- 1Yellow River Institute of Hydraulic Research, YRCC, Zhengzhou, China
- 2Henan Engineering Research Center of Hydropower Engineering Abrasion Test and Protection, Zhengzhou, China
- 3Guangdong ATV Academy for Performing Arts, Dongguan, China
- 4Nanchang Institute of Technology, Nanchang, China
- 5School of Computer Science and Technology, Huaibei Normal University, Huaibei, China
- 6School of Economics and Management, Nantong University, Nantong, China
- 7Department of Mathematics, Quaid-i-Azam University, Islamabad, Pakistan
- 8Department of Mathematic, College of Science, Taif University, Taif, Saudi Arabia
In this work, a CMFS method based on the analogy equation method, the radial basis function and the method of fundamental solutions for linear and nonlinear convection-diffusion equations in anisotropic materials is presented. The analog equation method is utilized to transform the linear and nonlinear convection-diffusion equation into an equivalent one. The expressions of the homogeneous solution and particular solution are derived by utilizing the radial basis function approximation and the method of fundamental solutions, respectively. By enforcing the desired solution to satisfy the original convection-diffusion equation with boundary conditions at boundary and internal collocation points yield a nonlinear system of equations, which can be solved by using the Newton-Raphson iteration or the Picard method of iteration. The error convergence curves of the proposed meshless method have been investigated by using different globally supported radial basis functions. Numerical experiments show that the proposed CMFS method is promising for anisotropic convection-diffusion problems with accurate and stable results.
1 Introduction
Partial differential equations (PDEs) are generally utilized in understanding and modeling of a considerable lot of realism matters show up in applied science and material science. The PDE models are utilized in numerous fields, for example, plasma physics, hydrodynamics, finance, biology and nonlinear optic [1–3]. It is pointed that it is hard to tackle nonlinear problems most of the cases, especially analytically. Numerous strategies have been developed by the researchers for the numerical solution of complex problems (see [4–6] and the references therein). Among these techniques, one of the most attractive group of techniques is radial basis function (RBF) based techniques.
The RBF techniques are attractive in numerical simulation thanks to their simple, flexible, and truly meshfree features. These techniques have been successfully applied to diverse problems in a simple-to-implement fashion. The popular RBF-based numerical methods include the Kansa’s method [7, 8], the method of fundamental solution (MFS) [9–12], the boundary knot method [13–15], the modified method of fundamental solutions [16–18] which have been well-developed and applied to a variety of boundary value problems.
In previous literatures, the polynomial RBFs, thin plate spline, Gaussians, and Multiquadrics are often used [19–21]. It is noted that the traditional RBF-based schemes are indirect and global in the sense that the expansion coefficients are used as the basic variables in the numerical solution procedure, while the global RBF interpolation leads to the full matrix. Roughly speaking, the RBF-based approaches can be classified as two types. The first category uses RBFs to approximate the particular solution of a partial differential equation (PDE) of interest, and the homogeneous part is obtained by means of numerical methods, like the boundary element method, the MFS, or the boundary knot method. The second category is the domain-type collocation methods. According to this approach, the RBF expansion is utilized directly for the unknown solution, and the collocation satisfies the governing equation and boundary conditions. The Kansa’s method is a typical domain-type RBF approach. In this paper, we will develop a RBF-based technique of the first type to investigate anisotropic materials.
Anisotropic materials, characterized by varied material properties along different directions, are ubiquitous in nature and difficult to be analyzed. If non-linear property is included, the problems become even more complicated. Previously, Shin and Elman [22] studied the effect of various element discretization strategies and iteration algorithms for nonlinear convection-diffusion problems with variable velocity in isotropic materials. Torsten [23] used the anisotropic streamline-diffusion finite element method to analyze homogeneous convection-diffusion problems with dominant convection. Onyejekwe [24] applied Green element method to 2D transient convection-diffusion problems with linear reaction and variable velocity. The lattice Boltzmann method is proposed for general nonlinear anisotropic convection-diffusion equations [25,26]. The anisotropic nonlinear convection-diffusion equations are also investigated by the finite volume method [27], the finite element method [28], the finite difference method [29], the virtual element method [30]. Shang et al. [31] proposed a discrete unified gas kinetic scheme for a general nonlinear convection-diffusion equation. Cao and Zhang studied a nonlinear diffusion-convection-reaction equation with a variable coefficient which has applications in many fields [32].
Based on the above-mentioned investigations, we aim to apply the MFS, in combination with the RBF and the analog equation method (AEM) [33], to analyze anisotropic nonlinear convection-diffusion problems. First, the AEM is utilized to transform the PDE into an equivalent one. Then, the expressions of the homogeneous and particular solutions are derived by utilizing RBF approximation and the MFS, respectively. Finally, enforcing the desired solution to satisfy the original PDE with boundary conditions at boundary and internal collocation points yield a nonlinear system of equations, which can be solved by using the Newton-Raphson iteration or the Picard method of iteration. Here, we will focus on the construction of Picard method of iteration, which should be carefully constructed to reach convergence.
The structure of this paper is arranged as follows. In Section 2, we give the depiction of nonlinear convection-diffusion problems in anisotropic media. Followed in Section 3, the detailed processes are derived to construct the proposed CMFS. Numerical investigation and results analysis are carried out in Section 4. Section 5 concludes this paper and provides some comments on the CMFS.
2 Nonlinear Convection-Diffusion Problems in Anisotropic Materials
Consider an open-bounded domain
subjected to Dirichlet boundary condition
and Neumann boundary condition related boundary flux
where
The boundary flux is defined as
It is observed that the smaller the determinant of
3 The CMFS Meshless Method
For the previous nonlinear problems, the proposed CMFS method is based on the combination of the AEM, globally supported RBF approximation and the MFS. Detailed processes are given below.
3.1 The Analog Equation Method
The AEM, which was improved by Burlon et al [34], was first proposed by Katsikadelis for the solution of nonlinear problems. Using the analog equation method, Eq. 1 can be converted into a Poisson type equation. Suppose
If the source distribution
Using to the principle of superposition, the solution of linear PDE Eq. 3 can be written in the form of the sum of the particular solution
Accordingly,
and
respectively. Furthermore, we must note that the particular solution
3.2 Radial Basis Function Approximation to the Particular Solution
This step is to derive the particular solution by RBF approximation. There are two schemes to fulfill this procedure. The standard approach to obtain the particular solutions is to integrate an operator by means of selected RBF. This scheme is just suitable to some simple operators and RBFs which is mathematically reliable. Another approach is a reverse differential process, which has no restriction on certain operators and RBFs, but the selected RBFs must be continuously differentiable with high orders. Here, the introduction of AEM replaces the original complicated operator with a simpler Laplacian operator, so it is feasible to evaluate the particular solution using the integrating process. To this end, the fictitious term introduced in Eq. 3 can be approximated by
where
Similarly, it is reasonable to express the particular solution
if the following relationship
holds, where
The accuracy and efficacy of the interpolation depend on the choice of the radial basis function
3.3 The Method of Fundamental Solutions for the Homogeneous Solution
Before introducing the MFS [36, 37], it is necessary to give the definition of the fundamental solutions. The fundamental solution
in an infinite domain, where
The fundamental idea of the MFS is to place a virtual boundary outside the domain interested. Here, to obtain a weak solution of Laplace Eq. 6, collocation points
which exactly satisfies Eq. 6.
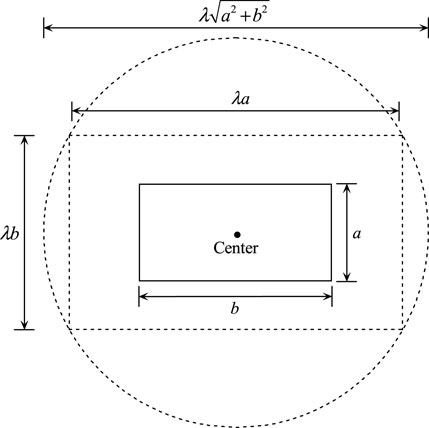
The proper usage of the MFS must concern three problems. The first case is the number of collocation points distributed on the physical boundary. However, too many collocation points may aggravate the ill-conditioned matrix. The virtual boundary shape is another important aspect. Theoretically, the virtual boundary shape can be arbitrarily chosen in the calculation. In practical computation, the virtual boundary shape is usually selected as a circle or similar shape to the actual boundary to keep algorithm versatile [38]. For example, for the rectangular domain, the rectangular or circular virtual boundaries can be used (see Figure 1).
The location of the fictitious source points is also an interesting issue. It has been investigated in several literatures [39–41]. In this paper, we consider a new way to find out the proper location of the virtual boundary, a ratio parameter
For example, in Figure 1, if the length and height of the rectangle domain are
3.4 The Construction of Solving Equations
According to the above process, the solution
which is also the solution of Eq. 1. Differentiating Eq. 14 yields
where
There are two different approaches to determine the unknowns
(1) Assume an initial guess
(2) During an iteration
(a) Linearization of Eq. 1:
(b) Using the AEM-RBF-MFS to produce the following linear solving equations
(c) The unknown coefficients
(d) Evaluating field values at
(e) Convergence criteria: if
(3) Once the iteration converges, Eq. 14 is used to evaluate quantities at arbitrary point in the domain and on the physical boundary.
4 Numerical Experiments
In this section, the convergence and accuracy of the CMFS are numerically examined by solving anisotropic nonlinear convection-diffusion problems. Since the Kansa’s method is a traditional RBF-based approach, comparisons are made between the CMFS and the Kansa’s method. To measure the accuracy of the approximation, the relative error
where
In order to investigate the condition number and convergence of the proposed CMFS, the linear anisotropic convection problem is tested in the first case, and then, nonlinear Burger’s equation and nonlinear anisotropic convection-diffusion equation are subsequently examined.
4.1 2D Linear Anisotropic Convection-Diffusion Problems
We first consider the linear anisotropic convection-diffusion equation in a square domain
where
The analytical solution shown is given as
for this case, which is also used to derive the Dirichlet boundary condition.
For the selection of interpolating points, different opinions always exist. Figure 2 shows the average relative error of polynomial
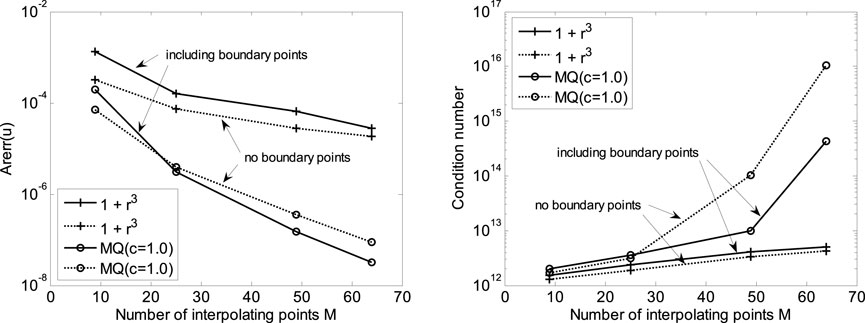
FIGURE 2. Effect of different interpolating schemes with boundary interpolating points and without boundary interpolating points.
For definite internal points number
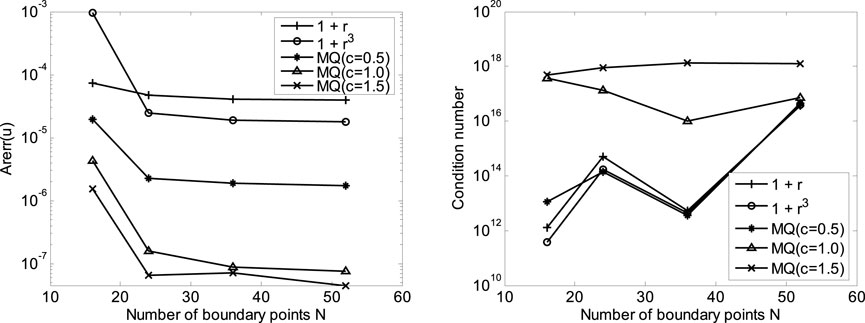
FIGURE 3. Convergence curves of average relative error and condition number with M = 64 by using different interpolating RBFs.
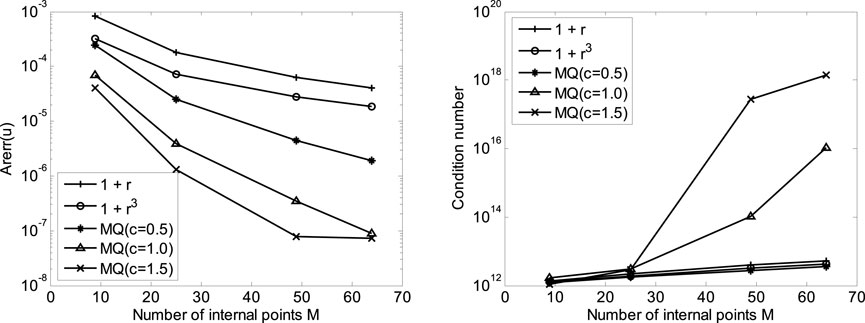
FIGURE 4. Convergence curves of average relative error and condition number with N = 36 by using different interpolating RBFs.
4.2 Nonlinear Inviscid Burger’s Equation
In this case, the nonlinear form for steady-state situation is considered
where the variable
Figure 6 shows the convergence curves of the CMFS using the Picard method of iteration with different RBFs. All convergence curves can be found with the increase of internal collocation points
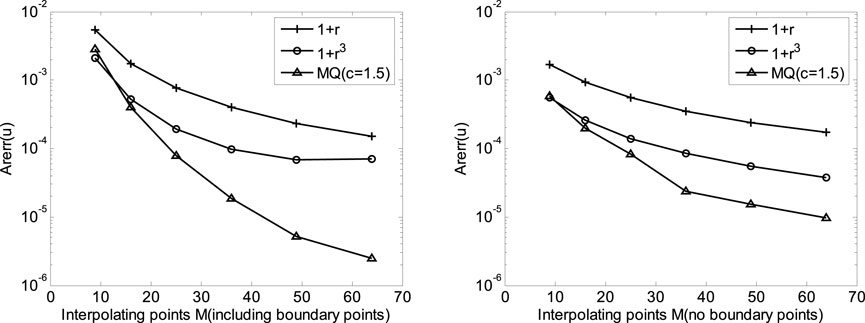
FIGURE 6. Convergence curves of average relative error for nonlinear Burger’s problems with N = 24 by using different interpolation schemes.
4.3 Nonlinear Anisotropic Convection-Diffusion Problem
Consider a 2D anisotropic convection-diffusion problem depicted by
with
Here, the similar Picard iteration scheme is employed and the initial guess of
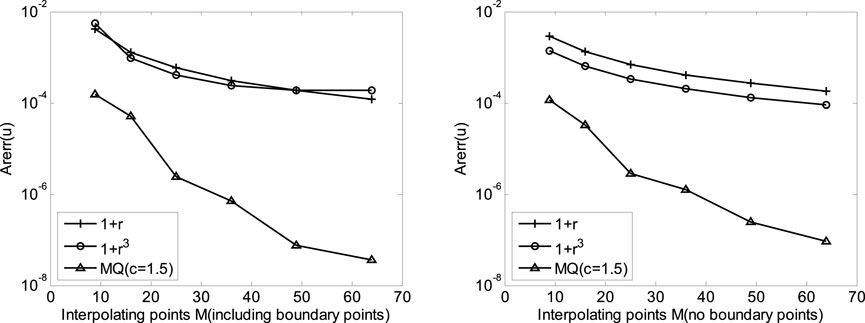
FIGURE 7. Convergence curves of average relative error for anisotropic nonlinear convection-diffusion problems with N = 24 by using different interpolation schemes.
5 Conclusion
In this paper, the CMFS, which is composed by the analog equation method, radial basis function approximation, and the method of fundamental solutions, is applied to the nonlinear anisotropic convection-diffusion problems. Numerical results reveal the efficiency and stability of the CMFS for the tested three cases. In a word, the proposed CMFS has the following features:
1) For linear cases, the approach is just one-step simple scheme. Meanwhile, no inverse of a matrix is involved.
2) The simple fundamental solution of Laplacian operator is employed, rather than one of the original PDE.
3) There are simple process and theoretical basis, so it is easy to program.
4) The related Picard iteration process is developed for nonlinear cases in isotropic and anisotropic media, respectively.
5) The proposed method is a truly meshfree method and no integrals are needed.
6) It can be easily extended to solve anisotropic un-homogeneous problems with variable parameter or the other problems [45].
Data Availability Statement
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.
Author Contributions
LZ supported found of the manuscript; FW developed the conceptualization, and wrote the manuscript; JZ worked on the mathematical development, performed the numerical analysis; SN and TN analyzed the data, and wrote the manuscript. All authors have read and agree to the published version of the manuscript.
Funding
This work is partially supported by the National Natural Science Foundation of China (Project No.U1965110) and the Natural Science Foundation of Anhui Provincial (Project No. 2008085MA11).
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
1. Wang F, Khan MN, Ahmad I, Ahmad H, Abu-Zinadah H, Chu Y-M. Numerical Solution of Traveling Waves in Chemical Kinetics: Time-Fractional Fishers Equations. Fractals (2022) 30(2):2240051. doi:10.1142/S0218348X22400515
2. Nadeem S, Fuzhang W, Alharbi FM, Sajid F, Abbas N, El-Shafay AS, et al. Numerical Computations for Buongiorno Nano Fluid Model on the Boundary Layer Flow of Viscoelastic Fluid towards a Nonlinear Stretching Sheet. Alexandria Eng J (2022) 61(2):1769–78. doi:10.1016/j.aej.2021.11.013
3. Zhang J, Anjal HA, Msmali A, Wang F, Nofal TA, Selim MM. Heat Transfer of Nanomaterial with Involve of MHD through an Enclosure. Case Stud Therm Eng (2022) 30:101747. doi:10.1016/j.csite.2021.101747
4. Wang F, Idrees M, Sohail A. "AI-MCMC" for the Parametric Analysis of the Hormonal Therapy of Cancer. Chaos, Solitons & Fractals (2022) 154:111618. doi:10.1016/j.chaos.2021.111618
5. Wang F, Azim Q-U -A, Sohail A, Nutini A, Arif R, R.S. Tavares JM. Computational Model to Explore the Endocrine Response to Trastuzumab Action in HER-2/neu Positive Breast Cancer. Saudi J Biol Sci (2022) 29(1):123–31. doi:10.1016/j.sjbs.2021.08.061
6. Zhang J, Wang F, Nadeem S, Sun M. Simulation of Linear and Nonlinear Advection-Diffusion Problems by the Direct Radial Basis Function Collocation Method. Int Commun Heat Mass Transfer (2022) 130:105775. doi:10.1016/j.icheatmasstransfer.2021.105775
7. Kansa EJ. Multiquadrics-A Scattered Data Approximation Scheme with Applications to Computational Fluid-Dynamics-I Surface Approximations and Partial Derivative Estimates. Comput Math Appl (1990) 19:127–45. doi:10.1016/0898-1221(90)90270-T
8. Zheng H, Yao GM, Kuo LH, Li XX. On the Selection of a Good Shape Parameter of the Localized Method of Approximated Particular Solutions. Aamm (2018) 10:896–911. doi:10.4208/aamm.OA-2017-0167
9. Rek Z, Šarler B. The Method of Fundamental Solutions for the Stokes Flow with the Subdomain Technique. Eng Anal Boundary Elem (2021) 128:80–9. doi:10.1016/j.enganabound.2021.03.020
10. Hematiyan MR, Mohammadi M, Tsai C-C. The Method of Fundamental Solutions for Anisotropic Thermoelastic Problems. Appl Math Model (2021) 95:200–18. doi:10.1016/j.apm.2021.02.001
11. Borachok I, Chapko R, Johansson BT. A Method of Fundamental Solutions for Heat and Wave Propagation from Lateral Cauchy Data. Numer Algor (2022) 89:431–49. doi:10.1007/s11075-021-01120-x
12. Gu Y, Fan C-M, Qu W, Wang F, Zhang C. Localized Method of Fundamental Solutions for Three-Dimensional Inhomogeneous Elliptic Problems: Theory and MATLAB Code. Comput Mech (2019) 64:1567–88. doi:10.1007/s00466-019-01735-x
13. Xiong J, Wen J, Liu Y-C. Localized Boundary Knot Method for Solving Two-Dimensional Laplace and Bi-harmonic Equations. Mathematics (2020) 8:1218. doi:10.3390/math8081218
14. Zhang L-P, Li Z-C, Huang H-T, Chen Z. Super-exponential Growth Rates of Condition Number in the Boundary Knot Method for the Helmholtz Equation. Appl Math Lett (2020) 105:106333. doi:10.1016/j.aml.2020.106333
15. Yue X, Wang F, Zhang C, Zhang H. Localized Boundary Knot Method for 3D Inhomogeneous Acoustic Problems with Complicated Geometry. Appl Math Model (2021) 92:410–21. doi:10.1016/j.apm.2020.11.022
16. Šarler B. Solution of Potential Flow Problems by the Modified Method of Fundamental Solutions: Formulations with the Single Layer and the Double Layer Fundamental Solutions. Eng Anal Boundary Elem (2009) 33:1374–82. doi:10.1016/j.enganabound.2009.06.008
17. Grabski JK. Numerical Solution of Non-newtonian Fluid Flow and Heat Transfer Problems in Ducts with Sharp Corners by the Modified Method of Fundamental Solutions and Radial Basis Function Collocation. Eng Anal Boundary Elem (2019) 109:143–52. doi:10.1016/j.enganabound.2019.09.019
18. Zhang L-P, Li Z-C, Huang H-T, Wei Y. The Modified Method of Fundamental Solutions for Exterior Problems of the Helmholtz Equation; Spurious Eigenvalues and Their Removals. Appl Numer Math (2019) 145:236–60. doi:10.1016/j.apnum.2018.09.00810.1016/j.apnum.2019.06.008
19. Wang F, Zheng K, Ahmad I, Ahmad H. Gaussian Radial Basis Functions Method for Linear and Nonlinear Convection-Diffusion Models in Physical Phenomena. Open Phys (2021) 19(1):69–76. doi:10.1515/phys-2021-0011
20. Schaback R. Limit Problems for Interpolation by Analytic Radial Basis Functions. J Comput Appl Math (2008) 212:127–49. doi:10.1016/j.cam.2006.11.023
21. Kazem S, Hatam A. Scattered Data Interpolation: Strictly Positive Definite Radial Basis/cardinal Functions. J Comput Appl Math (2021) 394:113580. doi:10.1016/j.cam.2021.113580
22. Shih Y, Elman HC. Iterative Methods for Stabilized Discrete Convection-Diffusion Problems. IMA J Numer Anal (2000) 20:333–58. doi:10.1093/imanum/20.3.333
23. Linß T. Anisotropic Meshes and Streamline-Diffusion Stabilization for Convection-Diffusion Problems. Commun Numer Meth Engng (2005) 21:515–25. doi:10.1002/cnm.764
24. Onyejekwe OO. Green Element Method for 2D Helmholtz and Convection Diffusion Problems with Variable Velocity Coefficients. Numer Methods Partial Differential Eq (2005) 21:229–41. doi:10.1002/num.20034
25. Zhao Y, Wu Y, Chai Z, Shi B. A Block Triple-Relaxation-Time Lattice Boltzmann Model for Nonlinear Anisotropic Convection-Diffusion Equations. Comput Math Appl (2020) 79:2550–73. doi:10.1016/j.camwa.2019.11.018
26. Chai Z, Shi B. Multiple-relaxation-time Lattice Boltzmann Method for the Navier-Stokes and Nonlinear Convection-Diffusion Equations: Modeling, Analysis, and Elements. Phys Rev E (2020) 102:023306. doi:10.1103/PhysRevE.102.023306
27. Cancès C, Chainais-Hillairet C, Herda M, Krell S. Large Time Behavior of Nonlinear Finite Volume Schemes for Convection-Diffusion Equations. SIAM J Numer Anal (2020) 58:2544–71. doi:10.1137/19M1299311
28. Zhelnin MS, Kostina AA, Plekhov OA. Variational Multiscale Finite-Element Methods for a Nonlinear Convection-Diffusion-Reaction Equation. J Appl Mech Tech Phy (2020) 61:1128–39. doi:10.1134/S0021894420070226
29. Jha N, Singh B. Fourth‐order Compact Scheme Based on Quasi‐variable Mesh for Three‐dimensional Mildly Nonlinear Stationary Convection-Diffusion Equations. Numer Methods Partial Differential Eq (2020). doi:10.1002/num.22702
30. Arrutselvi M, Natarajan E. Virtual Element Method for Nonlinear Convection-Diffusion-Reaction Equation on Polygonal Meshes. Int J Comput Math (2021) 98:1–25. doi:10.1080/00207160.2020.1849637
31. Shang J, Chai Z, Wang H, Shi B. Discrete Unified Gas Kinetic Scheme for Nonlinear Convection-Diffusion Equations. Phys Rev E (2020) 101:023306. doi:10.1103/PhysRevE.101.023306
32. Cao Z, Zhang LJ, Zhang L. Symmetries and Conservation Laws of a Time Dependent Nonlinear Reaction-Convection-Diffusion Equation. Discrete Cont Dyn-S (2020) 13:2703–17. doi:10.3934/dcdss.2020218
33. Katsikadelis JT. The Analog Equation Method: A Boundary-Only Integral Equation Method for Nonlinear Static and Dynamic Problems in General Bodies. Theor Appl Mech (Belgr) (2002) 27:13–38. doi:10.2298/TAM0227013K
34. Burlon A, Failla G, Arena F. An Improved Analog Equation Method for Non-linear Dynamic Analysis of Time-Fractional Beams with Discontinuities. Meccanica (2020) 55:649–68. doi:10.1007/s11012-020-01130-4
35. Magoulès F, Diago LA, Hagiwara I. Efficient Preconditioning for Image Reconstruction with Radial Basis Functions. Adv Eng Softw (2007) 38:320–7. doi:10.1016/j.advengsoft.2006.08.012
36. Fairweather G, Karageorghis A. The Method of Fundamental Solutions for Elliptic Boundary Value Problems. Adv Comput Math (1998) 9:69–95. doi:10.1023/A:1018981221740
37. Liu C-S. The Method of Fundamental Solutions for Solving the Backward Heat Conduction Problem with Conditioning by a New Post-conditioner. Numer Heat Transfer, B: Fundamentals (2011) 60:57–72. doi:10.1080/10407790.2011.588134
38. Gorzelańczyk P, Kołodziej JA. Some Remarks Concerning the Shape of the Source Contour with Application of the Method of Fundamental Solutions to Elastic Torsion of Prismatic Rods. Eng Anal Boundary Elem (2008) 32:64–75. doi:10.1016/j.enganabound.2007.05.004
39. Fasshauer GE, Zhang JG. On Choosing “Optimal” Shape Parameters for RBF Approximation. Numer Algor (2007) 45:345–68. doi:10.1007/s11075-007-9072-8
40. Schaback R. Adaptive Numerical Solution of MFS Systems. In: CS Chen, A Karageorghis, and YS Smyrlis, editors. The Method of Fundamental Solutions-A Meshless Method. Atlanta: Dynamic Publishers (2008). p. 1–27.
41. Reddy GMM, Nanda P, Vynnycky M, Cuminato JA. An Adaptive Boundary Algorithm for the Reconstruction of Boundary and Initial Data Using the Method of Fundamental Solutions for the Inverse Cauchy-Stefan Problem. Comp Appl Math (2021) 40:99. doi:10.1007/s40314-021-01454-1
42. Bavestrello H, Avery P, Farhat C. Incorporation of Linear Multipoint Constraints in Domain-Decomposition-Based Iterative Solvers - Part II: Blending FETI-DP and Mortar Methods and Assembling Floating Substructures. Comput Methods Appl Mech Eng (2007) 196:1347–68. doi:10.1016/j.cma.2006.03.024
43. Liu C-S, Chang C-W. A Simple Algorithm for Solving Cauchy Problem of Nonlinear Heat Equation without Initial Value. Int J Heat Mass Transfer (2015) 80:562–9. doi:10.1016/j.ijheatmasstransfer.2014.09.053
44. Wang F, Hou E, Ahmad I, Ahmad H, Gu Y. An Efficient Meshless Method for Hyperbolic Telegraph Equations in (1 + 1) Dimensions. Cmes-comput Model Eng (2021) 128(2):687–98. doi:10.32604/cmes.2021.014739
Keywords: radial basis function, meshless method, convection-diffusion problems, nonlinear partial difference equation, boundary value problem
Citation: Zhang L, Wang F, Zhang J, Wang Y, Nadeem S and Nofal T (2022) Novel Numerical Method Based on the Analog Equation Method for a Class of Anisotropic Convection-Diffusion Problems. Front. Phys. 10:807445. doi: 10.3389/fphy.2022.807445
Received: 02 November 2021; Accepted: 03 March 2022;
Published: 04 April 2022.
Edited by:
Horacio Sergio Wio, Institute of Interdisciplinary Physics and Complex Systems (CSIC), SpainReviewed by:
Yang Liu, Inner Mongolia University, ChinaChoonkil Park, Hanyang University, South Korea
Hussein A. Z. AL-bonsrulah, Iran University of Science and Technology, Iran
Copyright © 2022 Zhang, Wang, Zhang, Wang, Nadeem and Nofal. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: J Zhang, emo4MDExMDZAMTYzLmNvbQ==
 L Zhang
L Zhang FZ Wang
FZ Wang J Zhang
J Zhang YY Wang6
YY Wang6 S Nadeem
S Nadeem