Disentangling the Effects of Restriction and Exchange With Diffusion Exchange Spectroscopy

1 Introduction

Multidimensional NMR and MRI techniques [1] are a powerful means of studying heterogeneous samples [2]. Such methods can reveal correlations between distinct relaxation or diffusion components or pools within a heterogeneous sample [3]. A prominent multidimensional NMR methodology is diffusion exchange spectroscopy (DEXSY) [4], which looks at diffusion-diffusion correlations along the same gradient encoding direction. DEXSY can reveal the exchange dynamics between different diffusive microenvironments [5] and can interrogate steady-state water exchange without the use of exogenous contrast agents. DEXSY is thus a valuable tool for the noninvasive study of porous materials such as biological tissue. DEXSY and DEXSY-based methods are ideally suited for studying transmembrane water transport in cells and tissues [6–21].

In DEXSY, two unidirectional diffusion encodings with diffusion weightings b₁ and b₂ are separated by a mixing time, t_m [4, 22]. Signal is acquired at the second echo. The normalized echo intensity, I/I₀, is typically fit by assuming Gaussian diffusion [4, 5, 15, 16, 23, 24] such that the spin echo signal decays exponentially with the degree of each diffusion weighting, characterized by the b-value. In this framework, the DEXSY signal may be expressed as

$\frac{I}{I_0}={\int }_0^{\infty }{\int }_0^{\infty }P\left(D_1,D_2,t_m\right)\exp \left(-b_1{D}_1-b_2{D}_2\right)d{D}_{1}d{D}_2,(1)$

where P(D₁, D₂, t_m) is the joint probability density function (PDF) of diffusivities over both encoding periods for some t_m. The P(D₁, D₂) for a fixed t_m can thus be measured by acquiring I/I₀ at sufficiently many (b₁, b₂) pairs and then performing a numerical 2-D inverse Laplace transform (ILT) in the (b₁, b₂) domain [25]. Off-diagonal peaks in P(D₁, D₂) (i.e., lying off the 45° line) are interpreted as signatures of exchange between compartments [5]. These peaks may be integrated to quantify the extent of exchange during t_m. Repeating the process and varying t_m provides information about the exchange dynamics, which are typically modelled using first-order rate equations [26].

Although Eq. 1 is the most common way to interpret DEXSY data, diffusion is not necessarily Gaussian within heterogeneous samples [27]. According to conventional models of the spin echo attenuation due to diffusion, non-Gaussian signal behavior due to restrictions appears in many experimental cases [28–33]. Grebenkov [34] points out that at high diffusion weighting, the non-Gaussian signal behavior can manifest itself approximately as an exponential attenuation decaying with b^1/3 rather than b. In the presence of such behavior, P(D₁, D₂) must be interpreted with caution. To avoid potential misinterpretation, the data can instead be studied in the (b₁, b₂) acquisition domain—without transforming them—as we have proposed in prior studies that detail rapid variations of DEXSY [15, 19, 35]. More specifically, based on a method proposed by Song et al. [36] for the robust identification of exchange from T₂ − −T₂ (a.k.a. relaxation exchange spectroscopy, REXSY) time-domain features, we proposed to acquire DEXSY signal along a diagonal of constant total diffusion weighting, b₁ + b₂ [35]. Applying this similarity transformation to the (b₁, b₂) domain effectively separates or disentangles the effects of exchange and non-Gaussian signal behavior due to restrictions from the attenuation due to Gaussian diffusion [19, 35].

To complement our prior work, we argue here that 1) based on conventional signal models, the presence of non-Gaussian signal behavior is expected within biological specimen, 2) non-Gaussian signal behavior can lead to illusory features in the ILT-derived P(D₁, D₂), and 3) features in the (b₁, b₂) domain at various t_m—including, critically, t_m near 0—can be used as an alternative way to study exchange and to characterize the non-Gaussian signal behavior due to restrictions within a sample. We develop a combined acquisition scheme to independently characterize these effects in a time-efficient manner. We then present corroborating experimental findings on ex vivo neonatal mouse spinal cord utilizing a low-field permanent magnet NMR device known as the mobile universal surface explorer (NMR-MOUSE) with a strong static gradient. The neonatal mouse spinal cord contains mostly gray matter and very little myelin [37, 38]. Diffusion microstructural models for gray matter have become an important and challenging area of research [39–41] and our results facilitate future studies on this topic.

2 Theory

2.1 Models of the Spin Echo Signal Attenuation due to Diffusion

According to Hurlimann̈ et al. [32] and others [31, 42, 43], the spin echo decay due to diffusion can be separated, roughly speaking, into three regimes. For simplicity, a spin echo formed under a constant (or static) magnetic field gradient g with echo time 2τ is considered. The three regimes are associated with three length scales: 1) the diffusion length, ${\ell }_d=\sqrt{D_0\tau }$, where D₀ is the free diffusion coefficient; 2) the gradient dephasing length, ${\ell }_g={(D_0/\gamma g)}^{1/3}$, where γ is the gyromagnetic ratio; and 3) the structural length, ℓ_s, which is the length scale over which spins are restricted along the gradient direction. The diffusion length ℓ_d is the mean distance travelled by spins over the duration of each gradient application, τ. The gradient dephasing length ℓ_g can be qualitatively considered as the distance that spins must travel to significantly de-correlate their phases given they shared the same initial position [32, 44]. The structural length, ℓ_s, is the length scale that characterizes the extent of the restricted pore in the direction of the static gradient vector.

The smallest of the three length scales determines the diffusion regime (see Figure 1A) [32]. The simplest case is when ℓ_d is smallest; diffusion is effectively free and the well-known result [45] for the normalized spin echo decay under a constant gradient holds:

$\begin{array}{c}I/I_0=\exp \left(-b{D}_0\right),\\ b=\frac{2}{3}{\gamma }^2{g}^2{\tau }^3.\end{array}(2)$

Eq. 2 corresponds to a Gaussian distribution of net spin displacements during the measurement. If spins are confined by barriers, however, then the distribution of displacements will deviate from a Gaussian, resulting in non-Gaussian signal behavior.

FIGURE 1

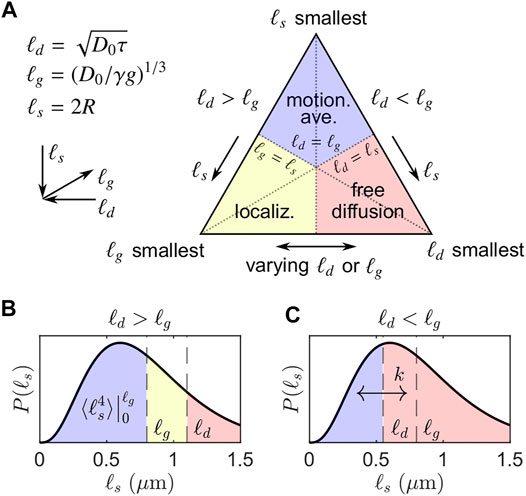
FIGURE 1. Simplified visualization of signal regimes adapted from Moutal and Grebenkov [44]. (A) The three asymptotic regimes of signal behavior determined by the smallest of the three length scales: ℓ_d, ℓ_g, ℓ_s. (B) Regimes when ℓ_d > ℓ_g and ℓ_g = 0.8 μm, corresponding to the left side of the triangle in (A). A representative distribution of ℓ_s with PDF P(ℓ_s) is shown. For ℓ_s > ℓ_d, diffusion remains approximately free. Note that the signal decay of the motionally averaged signal fraction is not dependent on ℓ_d and exhibits ensemble-averaged behavior over ℓ_s = [0, ℓ_g], leading to persistent signal even for large ℓ_d. (C) Regimes when ℓ_d < ℓ_g and ℓ_g = 0.8 μm, corresponding to the right side of the triangle in (A). We conjecture that exchange with some first-order exchange rate k may occur between restricted and free microenvironments encoded by non-Gaussian and Gaussian signal attenuation. The DEXSY experiment with ℓ_d ≳ ℓ_g takes advantage of the persistence of the non-Gaussian signal I/I₀ ∝ exp(−b^1/3) relative to the rapid attenuation of Gaussian signal I/I₀ ∝ exp(−b) to maximize sensitivity to exchange between restricted and free microenvironments.

Outside of the “free diffusion” regime, significantly slower echo dephasing—i.e., a slower increase in the phase variance of the spin ensemble—is observed due to confining barriers. When ℓ_g is smallest, signal from spins localized near barriers (within a distance of ℓ_g) dephases much more slowly than signal from spins that are farther from barriers. This localized signal dominates, producing the so-called “localization” regime [31, 46]. In the long τ limit (i.e., large ℓ_d), signal at a distance greater than ℓ_g from barriers has completely dephased and the decay of the persistent localized signal, assuming no exchange across barriers, is, to a first-order approximation [31],

$\frac{I}{I_0}\simeq \frac{a_0}{{\ell }_s}{\left(\frac{D_0}{\gamma g}\right)}^{1/3}\exp \left(-a_1{D}_0^{1/3}{\gamma }^{2/3}{g}^{2/3}\tau \right)\propto \exp \left(-b^{1/3}\right),{\ell }_d\gg {\ell }_g(3)$

where a₀ is a geometry-dependent prefactor (e.g., a₀ = 5.8841 for parallel plates [32]) and a₁ = 1.0188 is a universal prefactor. The signal behavior in the localization regime is complicated, however, and higher order terms may be significant [31, 47].

When ℓ_s is smallest, spins can diffuse across the restricted volume without significant dephasing. Put another way, spins in this regime are confined within a space that is much smaller than a turn of the phase winding helix imposed by a diffusion-weighting gradient. Spins thus experience a limited range of frequencies, resulting in the “motional averaging” or narrowing regime [30, 48]. For a spherical geometry of radius R (such that ℓ_s = R), again in the long τ or large ℓ_d limit, the signal decay in the motional averaging regime is well-approximated by [30].

$\begin{array}{cc}\hfill \frac{I}{I_0}& \simeq \exp \left(-\frac{8}{175}\frac{{\gamma }^2{g}^2{R}^4}{D_0}\left[2\tau -\frac{581}{840}\frac{R^2}{D_0}\right]\right),{\ell }_d\gg R\hfill \\ \hfill & \approx \exp \left(-b^{1/3}\left[\frac{16}{175}\frac{{\gamma }^{4/3}{g}^{4/3}{R}^4}{{\left(2/3\right)}^{1/3}{D}_0}\right]\right)=\exp \left(-b^{1/3}c\right),\hfill \end{array}(4)$

where the final approximation drops the small (R²/D₀) term. For compactness, we pull out a constant for the exponential scaling of the motionally averaged signal decay with b^1/3 (base units of m^2/3s^−1/3),

$c=\frac{16}{175}\frac{{\gamma }^{4/3}{g}^{4/3}{R}^4}{{\left(2/3\right)}^{1/3}{D}_0}.(5)$

The slower signal decay in both the localization and motional averaging regimes is characterized by a limiting exponential scaling of I/I₀ with τ (∝ b^1/3), as compared to τ³ (∝ b) for the free Gaussian diffusion regime. This difference in scaling distinguishes the Gaussian and non-Gaussian signal regimes. Generally, lengthening τ to increase b has a much smaller effect on I/I₀ in these non-Gaussian signal regimes. Note that our distinction of Gaussian vs. non-Gaussian signal behavior refers to any deviation from free diffusion and exponential signal decay with b; this differs from the usual definition of a Gaussian phase distribution approximation [30, 32, 42] in which the signal decays exponentially with g². Under that definition, the motionally averaged signal behavior remains Gaussian. To avoid confusion, we hereafter refer to water decaying in the motionally averaged and localized regimes as “restricted” since this water feels the effects of surfaces during diffusion encoding. Non-Gaussian signal behavior, as defined here, encompasses the effects of restriction.

2.2 Signal Behavior in Heterogeneous Samples

In heterogeneous samples such as biological tissue, with potentially hierarchically organized compartments, there may exist many water pools or volumes with distributed effective ℓ_s values. Individual sub-ensembles of water spins may reside in the regimes described above. For static gradient systems, ℓ_g is fixed such that only two cases arise, depending on the relationship between ℓ_d and ℓ_g. If ℓ_d < ℓ_g, then there are freely diffusing and motionally averaged sub-ensembles, presuming that some ℓ_s values extend below ℓ_g (motivated below). If ℓ_d > ℓ_g, then there are motionally averaged, localized, and free sub-ensembles. These two cases are visualized in Figure 1, where exemplar ℓ_d and ℓ_g values are overlaid on a representative PDF of distributed ℓ_s values, P(ℓ_s). As seen in Figures 1B,C, if any portion of P(ℓ_s) extends below ℓ_g, then some degree of restricted signal will be present in diffusion NMR experiments, regardless of ℓ_d. For the first case, ℓ_d < ℓ_g, little overall signal attenuation is expected and thus the free and motionally averaged sub-ensembles are not well separated. For the second case, ℓ_d > ℓ_g, free sub-ensembles attenuate much more rapidly with ℓ_d and the remaining signal becomes insignificant relative to the motionally averaged and localized sub-ensembles. While it is challenging to model the diffusion signal attenuation arising from a heterogeneous system containing all of these sub-ensembles, it is straightforward to utilize the characteristics of the attenuation to filter out free water sub-ensembles; by choosing ℓ_d ≳ ℓ_g, the remaining signal resides largely in the localized and motionally averaged sub-ensembles. Presuming extracellular water to be predominantly free and motionally averaged water to be predominantly intracellular, choosing ℓ_d ≳ ℓ_g provides a simple means to measure transmembrane water exchange with high SNR and a small number of data points via DEXSY, motivating the signal model discussed in the following section.

A similar picture applies for pulsed gradient experiments, in which ℓ_d is generally fixed and ℓ_g is varied. Note that ℓ_g is equivalently defined in the limit that the gradient pulse duration is equal to the diffusion encoding time: δ = Δ—i.e., when the pulsed gradients resemble the uninterrupted application of a static gradient—as opposed to the commonly used narrow gradient pulse approximation: δ ≪Δ (see Refs. [44, 49] for comparisons between these limits).

How do these cases apply to practical NMR experiments on biological tissue? That is, what is the range of salient ℓ_s values in tissue (i.e., cells) and what is the range of attainable experimental ℓ_g values? Electron microscopy (EM) imaging reveals a range of membrane-bound structures: cells, organelles, and even vesicles, which suggests that the range of salient ℓ_s values within tissue spans several orders of magnitude, from tens to thousands of nanometers. In comparison, an approximate lower bound for ℓ_g is provided by high static gradients, such as produced by stray fields [50] or some permanent magnets used in low-field NMR [51], which can attain, e.g., ℓ_g = 0.8 μm for g = 15.3 T/m and D₀ = 2.15 μm²/ms [15] (see also Refs. [52–54]). Thus, at least some ℓ_s values will invariably be smaller than ℓ_g ∼ 1 μm, so the presence of restricted signal within biological tissue is expected, given that the residence time within such restrictions is longer than the diffusion encoding time. In practice, this may manifest itself as a persistent signal component that exhibits little to no decay due to diffusion, especially at smaller gradient amplitudes.

Others [55, 56] have likewise pointed out that Gaussian diffusion is almost always violated to some degree in the study of biological tissue using diffusion NMR due to restrictions, but exchange from restricted compartments should also be important. Biological membranes control permeability to water and other substances through lipid membrane composition and through expression of membrane transport proteins. To water, membranes both reflect and hence restrict on some timescale but allow passage through and are permeable on some longer timescales. It may be feasible, therefore, to ignore restriction or exchange by probing the appropriate timescales.

Due to the potentially distributed nature of ℓ_s, however, both restriction and exchange may be relevant over a large range of probe-able timescales. Measurement of time-dependent diffusion in yeast samples over extremely short sub-millisecond timescales shows a deviation from the linear surface-to-volume ratio (S/V) scaling expected for the short-time limit [57], consistent with the effect of membrane permeability [58]. Static gradient spin echo diffusion attenuation in the spinal cord model utilized below shows the non-Gaussian signature of b^1/3 signal scaling even at extremely high diffusion weighting out to b = 3,000 ms/μm² with corresponding diffusion time τ = 6.6 ms [15]. Explorations of the “dot” compartment in gray matter appear to reveal a persistent, non-exchanging water pool at b = 15 ms/μm² and diffusion times up to 35.5 ms [59]. Taken together, these and other results over a large range of timescales and gradient strengths (see Refs. [55, 60, 61]) suggest that, in general, exchange cannot be completely ignored at short timescales, nor does exchange fully average out the effects of membranes at longer timescales. Therefore, restriction and exchange must both be accounted for to better understand what the diffusion NMR signal can reveal about the underlying tissue microstructure. Fortunately, unlike with single pulsed-field gradient or single diffusion encoding, with double diffusion encoding incorporating a mixing time, specifically with DEXSY, we can naturally separate the encoding of diffusion from the encoding of exchange. We now utilize the models for spin echo signal attenuation due to diffusion to develop a simplified DEXSY signal model for heterogeneous samples such as biological tissue.

2.3 A Minimal Diffusion Exchange Spectroscopy Signal Model for ℓ_d ≳ ℓ_g

This picture of distributed ℓ_s values hews close to the notion of a crowded cellular milieu, but does not lend itself to interpreting experimental data. Thus, we propose a simplified DEXSY signal model when ℓ_d ≳ ℓ_g using the picture provided in Figure 1B (cf. Moutal et al. [62]). We assume that relatively little signal exhibits localization behavior when ℓ_d is not much larger than ℓ_g such that the signal may be approximated as arising from two equilibrium signal fractions, f_m and f_e, corresponding to a motionally averaged (ℓ_s ≲ ℓ_g) and a free or extracellular sub-ensemble (ℓ_s > ℓ_g), respectively. More specifically, we assume that the signal behavior for ℓ_g < ℓ_s < ℓ_d resembles that of free diffusion because dephasing can occur within the extent of ℓ_s and the signal that is localized near boundaries does not yet dominate as it would in the limit of large ℓ_d. The gradient dephasing length ℓ_g demarcates the approximate boundary between the sub-ensembles. For the motionally averaged signal fraction f_m, we assume that ℓ_d ≫ ℓ_s for most ℓ_s < ℓ_g such that the signal behavior may be approximated by Eq. 4 whilst dropping the (R²/D₀) term. Again, we pull out a constant for the scaling with b^1/3, here ensemble-averaged over ℓ_s = [0, ℓ_g],

$⟨c⟩=\frac{16}{175}\frac{{\gamma }^{4/3}{g}^{4/3}⟨R^4⟩}{{\left(2/3\right)}^{1/3}{D}_0},⟨R^4⟩\approx {\int }_0^{{\ell }_g}P\left({\ell }_s\right){\ell }_s^{4}d{\ell }_s,(6)$

where P(ℓ_s) is the PDF of ℓ_s (e.g., Figures 1B,C). Because we are principally concerned with experiments performed under a static gradient, we treat g as a constant and leave the g^4/3 term in ⟨c⟩. Note that for pulsed gradients with varying g, a different representation would be necessary.

Assuming no exchange during diffusion encoding periods, no surface relaxation effects, and ignoring relaxation processes for the time being (i.e., spin-lattice relaxation T₁ during t_m and spin-spin relaxation T₂ during the encodings), I/I₀ for a DEXSY experiment may be written as arising from four signal fractions:

$\begin{array}{cc}\hfill \frac{I}{I_0}=& f_{m,m}\exp \left(-\left[b_1^{1/3}+b_2^{1/3}\right]⟨c⟩\right)+f_{m,e}\exp \left(-b_1^{1/3}⟨c⟩-b_2{D}_0\right)\hfill \\ \hfill & +f_{e,m}\exp \left(-b_1{D}_0-b_2^{1/3}⟨c⟩\right)+f_{e,e}\exp \left(-\left[b_1+b_2\right]D_0\right),\hfill \end{array}(7)$

where f_m = f_m,e + f_m,m, f_m,e and f_e,m are signal fractions that exchange between the two sub-ensembles or compartments during t_m, and f_m,m and f_e,e are signal fractions that do not, exhibiting the same signal behavior during both encodings. For static gradient experiments, b₁ and b₂ are varied by changing τ, i.e., $b_1=(2/3){\gamma }^2{g}^2{\tau }_1^3$ and $b_2=(2/3){\gamma }^2{g}^2{\tau }_2^3$. If exchange between f_m and f_e is assumed to be driven by passive diffusion, then the exchange will obey first-order rate kinetics with rate constant k:

$k=3\kappa /\langle R\rangle ,\langle R\rangle \approx {\int }_0^{{\ell }_g}P\left({\ell }_s\right){\ell }_{s}d{\ell }_s,(8)$

where κ is the barrier permeability (base units of m/s) and ⟨R⟩ is an ensemble-averaged, effective spherical radius for the motionally averaged sub-ensemble. The radius ⟨R⟩ may also be written as ⟨R⟩ = 3V/S, such that k = κ (S/V), where S/V is the surface-to-volume ratio of all restrictions for which ℓ_s ≲ ℓ_g. Finally, assuming detailed mass balance (i.e., no net flux): f_m,e = f_e,m, the total exchanging fraction may be written as [19].

$f_{exch}\left(t_m\right)=f_{m,e}+f_{e,m}=2f_e{f}_m\left[1-\exp \left(-t_{m}k\right)\right],(9)$

where the factor 2f_ef_m = 2f_m(1 − f_m) is a steady-state exchange fraction corresponding to complete mass turnover as t_m ≫ 1/k. Altogether, Eqs. 7, 9 provide a three-parameter model (f_m, ⟨c⟩, k) for the DEXSY signal as a function of (b₁, b₂, t_m).

While such a signal model is parsimonious and makes several assumptions—particularly in ignoring transitional signal behavior when ℓ_g < ℓ_s < ℓ_d and in assuming a single effective exchange rate between f_e and f_m—it may suffice as a coarse-grained description of the signal behavior in heterogeneous tissue suitable for obtaining apparent parameters. This model is amenable to both static gradient DEXSY (in which ℓ_g is constant) and pulsed gradient DEXSY in the limit that δ = Δ (in which ℓ_g is varied and ℓ_d is constant). Broadly speaking, this ℓ_d ≳ ℓ_g signal model is a two-compartment model with a first-order exchange rate that, unlike the standard Kärger model for diffusion exchange [63], incorporates restriction, represented here by a motionally averaged signal fraction f_m with some effective exponential decay rate ⟨c⟩ proportional to b^1/3g^4/3. This model is used throughout to simulate data and to fit experimental data.

3 Results

3.1 Simulated Data and Diffusion-Diffusion Spectra

To simulate data using Eq. 7, we set f_m = f_e = 0.5 and choose $⟨c⟩=1.2{(\mu {\mathrm{m}}^2/\mathrm{m}\mathrm{s})}^{1/3}$ such that complete signal attenuation and therefore stable ILTs can be achieved within reasonable b-values. Note that in reality, ⟨c⟩ may be much smaller, e.g., in the range of $⟨c⟩\sim 0.01-0.1{(\mu {\mathrm{m}}^2/\mathrm{m}\mathrm{s})}^{1/3}$ as reported in Williamson and Ravin et al. [15] for fixed neonatal mouse spinal cord. Nonetheless, the simulations here are demonstrative, and the observed behavior in the ILTs should translate to any signal model that consists of a freely diffusing signal fraction f_e exchanging with some restricted signal fraction exhibiting exponential decay with b^1/3.

Simulated signals at different t_m in relation to k $(t_m=\left[\mathrm{0,1}/(2k),1/k\right])$ are plotted vs. (b₁, b₂) in Figure 2, along with the ILT-derived P(D₁, D₂) and marginal P(D₁) distributions. Gaussian noise with a signal-to-noise ratio (SNR) of 100 was added prior to the inversion of simulated data. An example with t_m = 0 and no noise is also presented for comparison. The ILTs were performed using non-negative least squares (NLS) with L₂ regularization [64, 65]. The regularization parameter was chosen to produce a residual sum of squares (RSS) $\approx 1/$SNR for the t_m = 0 case and held constant for the t_m = 1/(2k) and 1/k cases, representative of moderate regularization. The simulated signal shows the expected transition from Gaussian to non-Gaussian signal behavior with increasing b-values (Figures 2A,B) and resembles previously reported data [15]. Both restriction and exchange result in curvature in the iso-signal contours, shown in Figure 2A. The cases with exchange show faster initial decay due to exchange from f_m to f_e, which is clearly visible in Figure 2B.

FIGURE 2

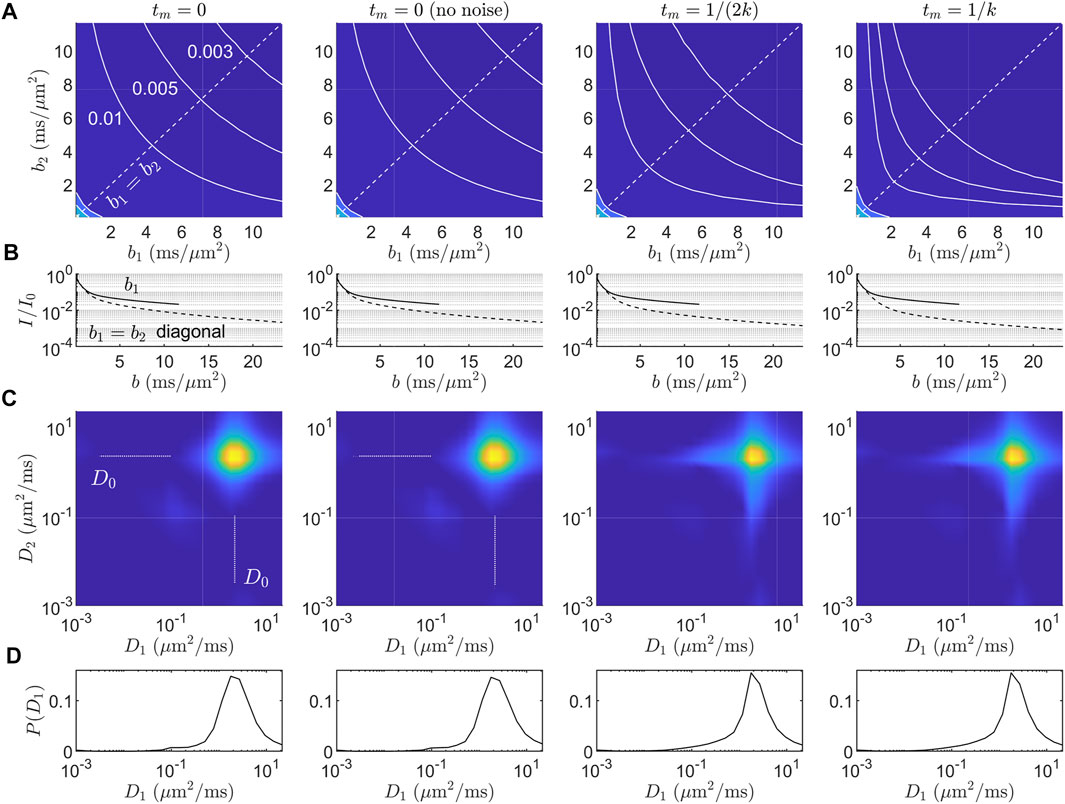
FIGURE 2. Simulated data and diffusion-diffusion spectra for the ℓ_d ≳ ℓ_g signal model in Eq. 7. (A) Simulated DEXSY signal in the (b₁, b₂) acquisition domain for four cases: t_m = 0, t_m = 0 without noise, t_m = 1/(2k), and t_m = 1/k. Gaussian noise with SNR = 100 was added unless otherwise specified. Iso-signal contours at I/I₀ = (0.01, 0.005, 0.003) are shown. (B) 1-D signal behavior from (A) along b₂ = 0 (solid line) and the b₁ = b₂ diagonal, i.e., b_d = 0 (dashed line). Increased exchange results in faster decay along the b_d = 0 diagonal. (C) ILT-derived diffusion-diffusion spectra P(D₁, D₂). The range of diffusivities given for the inversion was (D₁, D₂) ∈ (1 × 10^–3, 22.5) μm²/ms. The L₂ regularization parameter was chosen to produce an RSS $\approx 1/$SNR for the t_m = 0 case and held constant for the other cases. Broadening of the (D₀, D₀) component into a star-like shape is observed, even in the absence of noise. In exchanging cases, distributed exchanging components along D₀ are visible. (D) Marginal P(D₁) distribution from (C). Note the long tail of distributed, small diffusivities.

The inverted P(D₁, D₂) spectra (Figures 2C,D) contain illusory features. Namely, the presence of restricted signal results in 1) broadening of the (D₀, D₀) component into a star-like shape in both the on- and off-diagonal directions, even in the absence of noise and exchange (t_m = 0), and 2) with exchange, the off-diagonal components are distributed and are not consistent with the “ground-truth” two-compartment model, Eq. 7, used to simulate the data. The marginal P(D₁) distributions (Figure 2D) have a distributed tail of small diffusivities. With less regularization, the tail splits into multiple peaks (data not shown), an effect known as “pearling” [2]. This long tail of diffusivities is also seen in previous experimental P(D) distributions in which motionally averaged signal behavior was observed (see Refs. [66–68] as well as Figures 2C, 3A in Williamson and Ravin et al. [15]). Thus, while ILTs may be able to detect the exchange process in general via an increase in the off-diagonal components in P(D₁, D₂), the location and shape of these components cannot be meaningfully interpreted in the presence of non-Gaussian signal behavior due to restrictions. Furthermore, spurious off-diagonal components may be detected even in the absence of exchange, due primarily to the star-like broadening of the (D₀, D₀) component.

3.2 Diffusion Exchange Spectroscopy Acquisition Scheme and Signal Model Motivated by Features in the Acquisition Domain

As shown in Figure 2A, the curvature of the iso-signal contours in the (b₁, b₂) domain is sensitive to exchange, which provides a means to vastly reduce the number of samples needed to measure exchange at a given t_m. Rather than fully or partially sampling the (b₁, b₂) domain, one can instead obtain a finite difference approximation to the curvature along a contour or curve of constant total diffusion weighting, b₁ + b₂, at different t_m in order to estimate k, thereby obviating the ILT altogether and avoiding its potential confounds entirely.

Previously, we presented a rapid, five-point method to measure an apparent exchange rate (AXR) while removing the effects of the diffusion-weighted T₁ on the signal [19]. Here, we perform the same signal re-parameterization, but in the context of the minimal ℓ_d ≳ ℓ_g signal model, Eq. 7. We find that f_m and ⟨c⟩ can be related to the curvature depth at t_m = 0, providing a unique method of characterizing the non-Gaussian signal behavior due to restrictions from a series of DEXSY experiments with short t_m or from double spin echo experiments, akin to DEXSY with zero t_m. Further, we present a combined acquisition scheme which uses multiple t_m to determine all relevant restriction and exchange parameters: f_m, ⟨c⟩, and k or the AXR.

3.2.1 Signal Re-Parameterization

To look at the curvature of the signal attenuation in the (b₁, b₂) domain, we re-parameterize the sum, b_s, and difference, b_d, of the b-values.

$\begin{array}{c}{b}_s=b_1+b_2,b_d=b_1-b_2,\\ b_1=\frac{b_d-b_s}{2},b_2=\frac{b_s+b_d}{2},\end{array}(10)$

Substituting Eq. 10, Eq. 7 can be rewritten as

$\begin{array}{cc}\hfill \frac{I}{I_0}=& f_{m,m}\exp \left(-{\left[\frac{b_s+b_d}{2}\right]}^{1/3}\langle c\rangle -{\left[\frac{b_s-b_d}{2}\right]}^{1/3}\langle c\rangle \right)\hfill \\ \hfill & +f_{m,e}\exp \left(-{\left[\frac{b_s+b_d}{2}\right]}^{1/3}\langle c\rangle -\left[\frac{b_s-b_d}{2}\right]D_0\right)\hfill \\ \hfill & +f_{e,m}\exp \left(-{\left[\frac{b_s-b_d}{2}\right]}^{1/3}\langle c\rangle -\left[\frac{b_s+b_d}{2}\right]D_0\right)\hfill \\ \hfill & +f_{e,e}\exp \left(-b_s{D}_0\right)\hfill \end{array}(11)$

Calculating the second partial derivative of I/I₀ with respect to b_d evaluated about b_d = 0 (i.e., the central curvature of the signal along a slice of constant b_s), and rearranging,

$\begin{array}{cc}\hfill {\left.\left(\frac{{\partial }^2}{\partial b_d^2}\frac{I}{I_0}\right)\right|}_{b_d=0}=& \left(f_m-\frac{f_{exch}}{2}\right)\frac{⟨c⟩}{9}{\left(\frac{2}{b_s}\right)}^{5/3}\exp \left(-2{\left[\frac{b_s}{2}\right]}^{1/3}⟨c⟩\right)\hfill \\ \hfill & +a_0{f}_{exch}\exp \left(-{\left[\frac{b_s}{2}\right]}^{1/3}⟨c⟩-\frac{b_s}{2}{D}_0\right),\hfill \end{array}(12)$

where f_m,m = f_m − f_exch/2 has been substituted by mass balance, and a₀ is a factor given by

$a_0={\left(\frac{\langle c\rangle }{3\left[2^{1/3}{b}_s^{2/3}\right]}-\frac{D_0}{2}\right)}^2+\frac{2^{2/3}\langle c\rangle }{9b_s^{5/3}}.(13)$

Note that the contribution due to f_e,e disappears from Eq. 12. Computing the curvature thus separates the effects of restriction and exchange—both of which introduce curvature—from the effects of non-exchanging signal fractions that exhibit mono-exponential decay with b—which do not.

Rewriting Eq. 12 in terms of f_exch,

$f_{exch}=\frac{2\left(\mathrm{\Delta }I-f_m{a}_1{b}_s^2\right)}{b_s^2\left[a_0\exp \left(-2^{-1/3}{b}_s^{1/3}⟨c⟩-2^{-1}{b}_s{D}_0\right)-a_1\right]},(14)$

where now the curvature has been replaced with a three-point finite difference approximation assuming symmetry across the b_d = 0 axis (i.e., assuming that I/I₀ is the same at b_d = ±b_s),

${\left.\left(\frac{{\partial }^2}{\partial b_d^2}\frac{I}{I_0}\right)\right|}_{b_d=0}=\frac{2\mathrm{\Delta }I}{b_s^2},(15)$

where ΔI is the difference between the I/I₀ endpoint(s) and midpoint along b_d,

$\mathrm{\Delta }I={\left.\left(I/I_0\right)\right|}_{b_d=\pm b_s}-{\left.\left(I/I_0\right)\right|}_{b_d=0}(16)$

and for compactness we let

$a_1=\frac{\langle c\rangle }{18}{\left(\frac{2}{b_s}\right)}^{5/3}\exp \left(-2{\left[\frac{b_s}{2}\right]}^{1/3}\langle c\rangle \right).(17)$

The exchanging fraction f_exch can in principle be obtained from a single ΔI measurement with a priori knowledge of f_m and ⟨c⟩. However, if these quantities are not known, additional experiments are able to determine the apparent values of f_m and ⟨c⟩. Note that by using ΔI as the measured value (i.e., a difference in signal), the effect of T₁ during t_m is removed, as shown in Ref. [19].

3.2.2 Determining the Motionally Averaged Signal Fraction and Decay Constant

Going one step further, f_m and ⟨c⟩ can be isolated by measuring ΔI at t_m = 0. With t_m = 0, the exchanging fractions are approximately 0 such that f_m = f_m,m and f_e = f_e,e. From Eq. 11, it can be seen that taking ΔI removes the f_e contribution, yielding a simple expression for ΔI as a function of b_s,

$\mathrm{\Delta }I\left(b_s,t_m=0\right)=f_m\left[\exp \left(-b_s^{1/3}\langle c\rangle \right)-\exp \left(-2^{2/3}{b}_s^{1/3}\langle c\rangle \right)\right].(18)$

The apparent f_m is proportional to ΔI at t_m = 0 and can be determined at a single b_s if ⟨c⟩ is known (and vice versa). If either parameter is unknown, then ΔI at t_m = 0 can be measured at two or more b_s values and a two-parameter fit to Eq. 18 can be performed, yielding f_m and ⟨c⟩ simultaneously. In such a fit, ⟨c⟩ is a shape parameter and f_m is a scale parameter, which supports robust NLS fitting. It is important to note that the range of appropriate b_s values for the fit is not arbitrary, and is tightly constrained by the assumption that ℓ_d ≳ ℓ_g. The rationale behind selecting b_s values is discussed in more detail in Section 3.3.2.

To gain further insight into how fitted f_m and ⟨c⟩ values might reflect the underlying P(ℓ_s), forward simulations of the signal difference ΔI(b_s) in impermeable spheres with gamma distributed radii were performed using analytical expressions [30]. Eq. 18 was fit to simulated data and results are presented in the Supplementary Material. We find that the two-parameter model, Eq. 18, can adequately describe ΔI(b_s) in a truncated b_s range (see Section 3.3.2) and that fitted f_m and ⟨c⟩ values trend correctly with changes in the simulated P(ℓ_s) or P(R). We emphasize, however, that these are apparent parameters.

3.2.3 Accounting for Confounds at Small Mixing Time

In previous work [15] to quantify the AXR or k from the t_m dependence of DEXSY experiments, Eq. 9 required some modification to account for curvature (ΔI) observed at short t_m. An intercept term f₀ was introduced,

$f_{exch}\left(t_m\right)=\left(2f_m\left[1-f_m\right]-f_0\right)\left[1-\exp \left(-t_{m}k\right)\right]+f_0.(19)$

The ΔI due to f_m,m partially explains the need for an f₀ parameter. Other effects may also contribute to f₀: 1) exchange during the encoding periods, 2) exchange between compartments with different T₂ during the measurement, and 3) the change in ℓ_d between diffusion encoding periods when τ₁ ≠ τ₂, which is unavoidable for experimental setups with a static field gradient. The last effect 3), particularly, can result in large apparent exchange when no time-dependent exchange has occurred. Looking at Figures 1B,C, shifting ℓ_d left or right between encodings may produce f_m,e or f_e,m signal fractions, respectively. The same effect 3) can occur with pulsed gradients, in which ℓ_g is varied while ℓ_d stays constant. All of these confounding effects are lumped into f₀.

Another ad hoc approach to the correction for these effects is to remove the ΔI observed at t_m = 0 when calculating f_exch. Modifying Eq. 14 and explicitly including the t_m dependence,

$f_{exch}\left(t_m\right)=\frac{2\left[\mathrm{\Delta }I\left(t_m\right)-\mathrm{\Delta }I\left(t_m=0\right)-f_m{a}_1{b}_s^2\right]}{b_s^2\left[a_0\exp \left(-2^{-1/3}{b}_s^{1/3}⟨c⟩-2^{-1}{b}_s{D}_0\right)-a_1\right]}.(20)$

By performing the correction at this stage—prior to fitting for k—an intercept term is no longer necessary and Eq. 9 may be used as is to determine k from measurements of f_exch at one or more t_m.

3.2.4 Combined Acquisition Scheme

With Eqs 6–20 in mind, a combined acquisition scheme is designed to determine apparent values of ⟨c⟩, f_m, and k without prior knowledge of P(ℓ_s). As described in Section 3.2.2, ΔI measured at two or more b_s values at t_m = 0 can be fit to Eq. 18, yielding f_m and ⟨c⟩. With f_m and ⟨c⟩ known, a₀ and a₁ can be calculated from Eqs. 13, 17, respectively, after which Eq. 20 can be used to calculate f_exch from DEXSY experiments with various t_m > 0, using the previous measurement(s) for the ΔI(t_m = 0) correction term. Finally, calculated f_exch(t_m) values can be fit to Eq. 9, yielding k. Note that the steady-state exchange fraction 2f_m(1 − f_m) is presumed to be known such that Eq. 9 is truly a single parameter model. Furthermore, two points along b₁ or b₂ = 0 may be used to obtain the diffusion-weighted T₁ in order to interpolate the marginal b₁ or b₂ = 0 points for further data reduction, if desired [19]. In total, I₀ and three values of ΔI (two at t_m = 0 and one at t_m > 0) are sufficient to determine all parameters, although more data are likely required for practical fitting purposes. Throughout all measurements, the source of contrast ΔI lies in the difference between double diffusion encodings with equal diffusion weighting (b₁ = b₂, b_d = 0) and single diffusion encodings with the same total diffusion-weighting (b_s = b₁ + b₂). We thus term the method: Restriction and Exchange from Equally-weighted Double and Single Diffusion Encodings, abbreviated REEDS-DE. REEDS-DE is, in essence, a sub-sampling of conventional DEXSY data. This combined acquisition scheme is visualized in Figure 3.

FIGURE 3

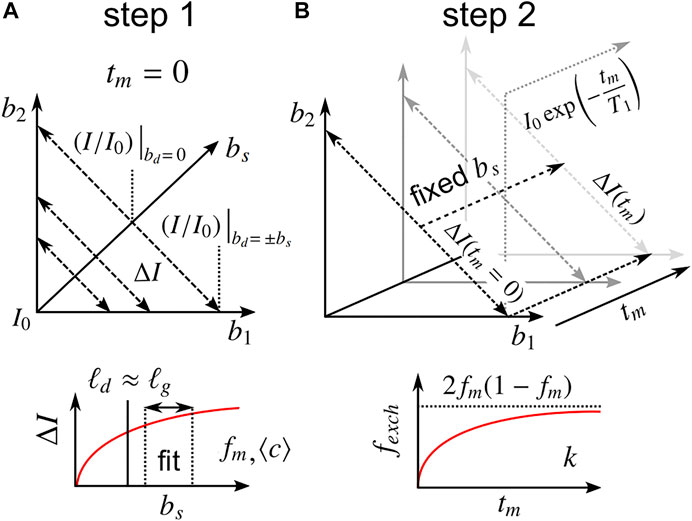
FIGURE 3. Description of the proposed REEDS-DE NMR acquisition scheme. Parameters are obtained in two steps. (A) In the first step, ΔI values measured at two or more b_s near t_m = 0 are fit to Eq. 18, yielding f_m and ⟨c⟩. The b_s values should be chosen to satisfy ℓ_d ≳ ℓ_g. (B) In the second step, ΔI values measured at one or more t_m > 0 at a fixed b_s are used to calculate f_exch(t_m) from Eq. 20, utilizing the first step for the correction term, ΔI(t_m = 0) (see Section 3.2.3). Finally, the t_m dependence of f_exch is fit to Eq. 9, yielding k. The steady-state f_exch at long t_m should agree with 2f_m(1 − f_m). Marginal points along b₁ or b₂ = 0 may be used to measure the diffusion-weighted T₁.

3.3 Experimental Validation of the REEDS-DE Combined Acquisition Scheme

3.3.1 Materials and Methods

The curvature along slices of constant b_s and at t_m near zero was assessed using two different double diffusion encoding pulse sequences implemented on a PM-10 NMR-MOUSE single-sided magnet at ω₀ = 13.79 MHz, B₀ = 0.3239 T, with a large g = 15.3 T/m static gradient (SG). One method is to simply shorten t_m in the SG-DEXSY pulse sequence. Exchange will be negligible when t_m ≪ 1/k. In this study, t_m = 0.2 ms was chosen, which is much shorter than the reported 1/k ≈ 10 ms for fixed ex vivo neonatal mouse spinal cord [15]. Further details of this sequence are presented in Ref. [15]. Alternatively, the storage interval can be removed completely by using an SG-double spin echo (SG-SE-SE) sequence. This sequence combines the phase cycles of the classic double spin echo [69] with the standard NMR-MOUSE SG spin echo diffusion sequence [70]. For both sequences, the signal is acquired in a CPMG loop and summed to maximize SNR [71]. Both sequences are shown in Figure 4. The pulse sequences and phase cycles can be found in the Data Availability statement.

FIGURE 4

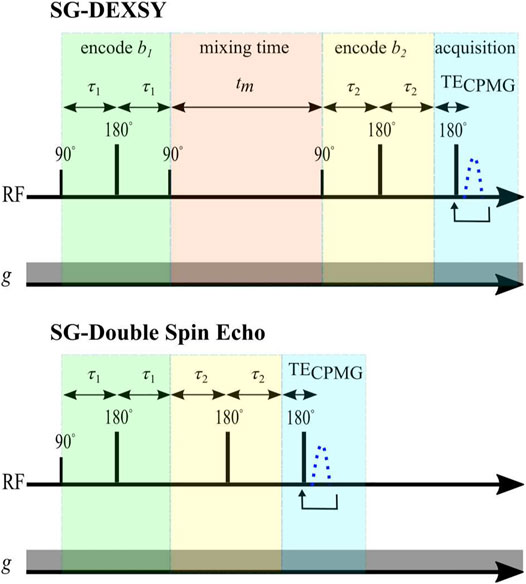
FIGURE 4. Pulse sequences. Static gradient DEXSY and static gradient double spin echo pulse sequences implemented on a low-field single-sided NMR system.

Sample preparation and test chamber details can be found in the Materials and Methods of Ref. [15]. Briefly, spinal cords were removed from Swiss Webster wild type mice (Taconic Biosciences, Rensselaer, NY) between postnatal day 1 and 4, under approved animal protocols (National Institute of Neurological Disorders and Stroke Animal Care and Use Committee (ACUC), Animal Protocol Number 1267–18 and National Institute of Child Health and Human Development ACUC Animal Protocol Number 21-025). Experiments were performed on either freshly dissected, viable spinal cords or on fixed spinal cords. Fixed spinal cords were fixed overnight in 4% paraformaldehyde and washed three times with artificial cerebrospinal fluid (aCSF) to remove residual paraformaldehyde. Spinal cords were placed within a 13 × 2 mm solenoid radiofrequency (RF) coil, built in-house. During experiments, spinal cords were bathed in aCSF with a surrounding gas environment of 95% O₂/5% CO₂. Temperature was monitored $(\approx 25\pm 1°\mathrm{C})$.

The SG-DEXSY and SG-SE-SE experiments were performed using the same experimental parameters. Curvature along b_d was assessed at b_s = (0.3, 1, 6) ms/μm². 6, 20, 21 points were spaced linearly in b_d across each b_s slice, respectively. With static gradients, b = 0 cannot be obtained and the minimum used here was b = 0.089 ms/μm². That is, the normalization point I₀ corresponds to b = 0.089 ms/μm². Accordingly, the b_d range along the slices of b_s was b_d = (−b_s + 0.089, b_s − 0.089) ms/μm². Points exactly at b_d = 0 were avoided due to the potential refocussing of unwanted coherence transfer pathways when τ₁ = τ₂. Other experimental parameters include: 90°/180° RF pulse lengths = 2/2 μs, pulse powers = −22/−16 dB, 2 s repetition time, 2000 or 8,000 echo CPMG train with 25 μs echo time, 8 points per echo, and 0.5 μs dwell time. With regards to relaxation processes, the effect of T₁ is normalized by using a difference in signals ΔI, as previously mentioned, and T₂ is assumed to negligibly affect the signal because the utilized τ values (≲ 1 ms) are small compared to the measured T₂ = 163 ms of the sample [15].

3.3.2 REEDS-DE Results

The curvature shape and depth (i.e., ΔI) from SG-DEXSY experiments with t_m = 0.2 ms and SG-SE-SE experiments performed on a freshly dissected, viable ex vivo neonatal mouse spinal cord are presented in Figure 5. At small b_s, no curvature is observed. As b_s increases, ΔI increases, as predicted by Eq. 18. It is worth noting that the SG-SE-SE experiment has anti-parallel gradient encodings whereas the SG-DEXSY experiment resembles an SE-SE experiment but the 90° RF storage pulses select coherence from both parallel and anti-parallel gradient encodings [72]. The SG-DEXSY experiment displays less attenuation than the SG-SE-SE experiment, likely corresponding to signal refocussing in the SG-DEXSY experiment due to reflections off of barriers that occurs on the timescale of the encoding, τ = τ₁ ≈ τ₂ [73, 74]. While substantive, this effect does not appear to affect ΔI such that, for our purposes, SG-SE-SE and SG-DEXSY experiments with t_m = 0.2 ms are functionally identical.

FIGURE 5

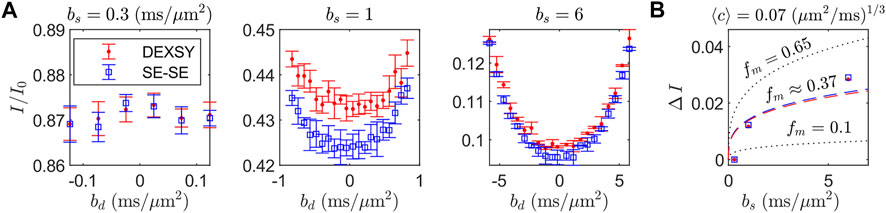
FIGURE 5. Exemplar curvature shape and depth ΔI for t_m at or near 0 measured at various b_s on a freshly dissected, viable ex vivo neonatal mouse spinal cord. (A) Normalized signal I/I₀ for the SG-DEXSY with t_m = 0.2 ms and SG-double spin echo (SE-SE) sequences, where I₀ was acquired at b = 0.089 ms/μm². I/I₀ is plotted as a function of b_d for three b_s = (0.3, 1, 6) ms/μm². ΔI increases with b_s, as predicted. Error bars = ±1 SD from three technical replicates. (B) ΔI vs. b_s from (A), where ΔI was measured as the difference between the average of the endpoints and the minimum I/I₀ point. Exemplar curves (dotted lines) are shown for f_m = (0.1, 0.65) and $⟨c⟩=0.07{(\mu {\mathrm{m}}^2/\mathrm{m}\mathrm{s})}^{1/3}$. NLS fits using this fixed ⟨c⟩ (dashed lines) yield f_m ≈ 0.37 (RSS = 1.3 × 10^–4). An initial guess of f_m = 0.2 was provided.

We assess the full REEDS-DE acquisition scheme (Figure 3) by retroactively analyzing the data presented in Appendix 7, Figure 2 of Ref. [15], which was acquired using the same SG-DEXSY protocol but on a different, fixed spinal cord. We choose to analyze a certain range of b_s values based on validity constraints of the ℓ_d ≳ ℓ_g signal model, Eq. 7. For this setup, g = 15.3 T/m and D₀ = 2.15 μm²/ms such that the point at which ℓ_d = ℓ_g = 0.8 μm occurs at τ = 0.3 ms and b = 0.3 ms/μm². As ℓ_d greatly exceeds this value, a significant portion of the remaining signal may exhibit localization behavior, invalidating the signal model (see Figure 1B). Furthermore, a longer τ results in more exchange during encodings such that the assumption of f_m,e = f_e,m = 0 at small t_m used to arrive at Eq. 18 may no longer be valid. A somewhat arbitrary heuristic is to keep ℓ_d ≲ 1.6 ℓ_g. Here, ℓ_d = 1.6 ℓ_g corresponds to τ = 0.76 ms and b = 5 ms/μm². Another constraint on validity comes from Eqs. 4, 6, in which we dropped the (R²/D₀) term on the basis of 2τ ≫ (581/840) (R²/D₀). This approximation is valid when ℓ_s ≪ ℓ_d. Thus, ℓ_d should be kept somewhat larger than ℓ_g such that ℓ_s ≪ ℓ_d for most ℓ_s < ℓ_g. These are competing validity constraints. As such, a narrow range of b_s should be used to measure ΔI. Here, we chose values in the range b_s = (2, 5) ms/μm²—or, equivalently, 1.23 ℓ_g ≤ ℓ_d ≤ 1.6 ℓ_g, where ℓ_d = 1.23 ℓ_g corresponds to b₁ = b₂ = 1 ms/μm². Results are summarized in Figure 6.

FIGURE 6

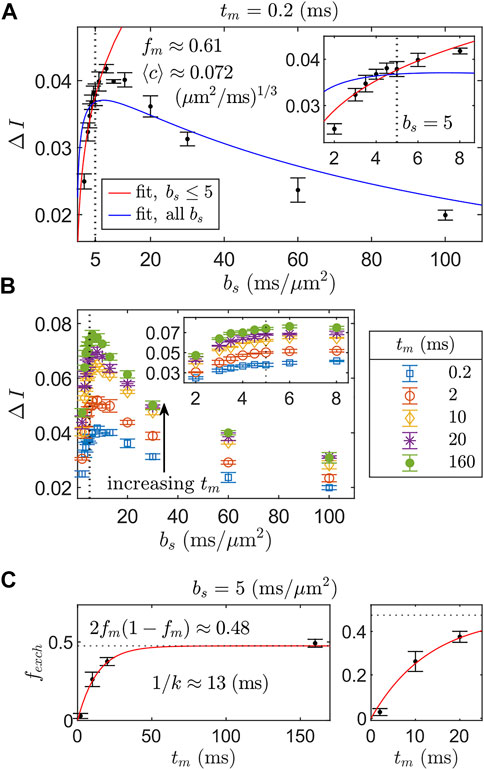
FIGURE 6. REEDS-DE acquisition and fitting scheme using SG-DEXSY data acquired on a fixed spinal cord. (A) ΔI vs. b_s curves for step 1 of REEDS-DE (Figure 3A). ΔI was measured at b_s = (2, 3, 3.5, 4, 4.5, 5, 6, 8, 10, 13, 20, 30, 60, 100) ms/μm² with t_m = 0.2 ms. Error bars = ± 1 SD from three technical replicates. Two fits to Eq. 18 are compared: one (red line) using the first six b_s values up to b_s = 5 ms/μm² (dotted line), whilst 1.23 ℓ_g ≤ ℓ_d ≤ 1.6 ℓ_g, and the other (blue line) using all b_s values. The truncated fit evaluated over the truncated region has RSS = 1.3 × 10^–4 vs. 5.8 × 10^–4 for the full fit and yields f_m ≈ 0.61, $⟨c⟩=0.072{(\mu {\mathrm{m}}^2/\mathrm{m}\mathrm{s})}^{1/3}$. The data are best fit near ℓ_d ≳ ℓ_g. An initial guess of f_m = 0.2 and $⟨c⟩=1\times 10^{-4}{(\mu {\mathrm{m}}^2/\mathrm{m}\mathrm{s})}^{1/3}$ was provided. Inset shows zoomed plot. (B) ΔI vs. b_s curves acquired at t_m = [0.2, 2, 10, 20, 160] ms for step 2 of REEDS-DE (Figure 3B). Error bars = ± 1 SD from three technical replicates. Inset shows zoomed plot. (C) f_exch calculated from points in (B) at a fixed b_s = 5 ms/μm² using Eq. 20. The t_m = 0.2 ms point was used for the correction term, ΔI(t_m = 0). Values were fit to Eq. 9, yielding k = 75 s⁻¹ and 1/k ≈ 13 ms (RSS = 0.013). An initial guess of k = 70 s⁻¹ was provided. The measured steady-state exchange fraction, f_exch(t_m = 160 ms) = 0.49 ± 0.03, agrees with 2f_m(1 − f_m) ≈ 0.48. Zoomed plot shown to the right.

For the first step of the REEDS-DE acquisition scheme (Figure 3A), ΔI was measured at six points b_s = (2, 3, 3.5, 4, 4.5, 5) ms/μm² using the SG-DEXSY sequence with t_m = 0.2 ms and data was fit to Eq. 18, yielding f_m ≈ 0.61 and $⟨c⟩\approx 0.072{(\mu {\mathrm{m}}^2/\mathrm{m}\mathrm{s})}^{1/3}$, shown in Figure 6A. This ⟨c⟩ value corresponds to ⟨R⁴⟩ ≈ 2.3 × 10^–2 μm⁴. Data was truncated from a full data set with b_s up to 100 ms/μm². Using all ΔI measured at up to b_s = 100 ms/μm² results in a poorer fit, perhaps due to increased exchange during encodings and the transition from freely diffusing to localized signal behavior in sub-ensembles for which ℓ_g < ℓ_s < ℓ_d. This behavior is expected, and supports that a narrow range of b_s corresponding to ℓ_d ≳ ℓ_g is where the signal model in Eq. 18 is most valid.

For the second step of REEDS-DE (Figure 3B), ΔI was measured using the SG-DEXSY sequence over the same range of b_s values with t_m = (0.2, 2, 10, 20, 160) ms, shown in Figure 6B. Then, b_s was fixed at 5 ms/μm² to calculate f_exch(t_m) from Eq. 20, shown in Figure 6C. Finally, f_exch(t_m) values were fit to Eq. 9, yielding k ≈ 75 s⁻¹ or 1/k ≈ 13 ms. This measured k agrees with previous results using a similar method (see “Method 2” in Ref. [15]). The observed steady-state exchange fraction (i.e., at the longest t_m = 160 ms ≫ 1/k) agrees with the predicted steady-state fraction of 2f_m(1 − f_m) ≈ 0.48, providing further evidence that the truncated fit in Figure 6A accurately characterizes the non-Gaussian signal behavior of the sample. All data was analyzed in MATLAB R2021b and fit using the lsqnonlin function. Overall, we demonstrate the feasibility of the REEDS-DE acquisition scheme and obtain good fits to the presented signal models.

Note that the truncated fit systematically overestimates ΔI at smaller and larger b_s (see Figure 6A inset). The direction of deviation is expected. At smaller b_s, ΔI may be overestimated due to the dropped (R²/D₀) term in Eq. 4, which, when included, results in a smaller effective ⟨c⟩ (i.e., a slower rise in ΔI vs. b_s). At larger b_s (and ℓ_d), ΔI may be overestimated as the localized signal behavior in the f_e signal fraction becomes significant, decreasing the difference in the signal decay of the f_m and f_e signal fractions. More explicitly, the f_e signal fraction no longer resembles the free diffusion regime as ℓ_d ≫ ℓ_g and a more complex relationship than Eq. 18 is needed to describe how the appearance of localized signal affects ΔI vs. b_s. Despite this shortcoming, the data support that the maximal ΔI is observed before localized signal behavior becomes prohibitively significant, at around b_s = 8 ms/μm². Thus, for the purposes of measuring apparent restriction and exchange parameters with maximal SNR efficiency, it may be acceptable and even preferable to truncate the b_s range and thereby avoid the localization regime. In a more thorough analysis, a variety of truncation points spanning b_s = (3, 100) ms/μm² were utilized. Results are presented in the Supplementary Material. We find that fit parameters converge on expected values as the truncation region decreases—i.e., 2f_m(1 − f_m) converges on the observed steady-state exchange fraction of 0.48, and ⟨c⟩ values stabilize—supporting our use of a limited range of b_s.

4 Discussion

4.1 Adapting REEDS-DE to High Field Scanners

Adapting REEDS-DE to pre-clinical or clinical scanners may prove challenging from a practical and modelling standpoint. On conventional MRI scanners, g may be orders of magnitude smaller (≲ 350 mT/m) than what is available on some low-field, single-sided NMR systems, resulting in a larger ℓ_g. Typically, ℓ_g ≳ 3 μm on pre-clinical and clinical scanners, as compared to ℓ_g = 0.8 μm here. Due to this larger ℓ_g, entirely different exchange processes may be measured because the effective boundary between the restricted and freely diffusing sub-ensembles has moved. This may result in a smaller observed k because the motionally averaged sub-ensemble spans ${\ell }_s=\left[0,{\ell }_g\right]$; a larger ℓ_g may decrease the apparent, ensemble-averaged S/V (see Eq. 8). Different gradient strengths may significantly influence the apparent exchange rate. Indeed, exchange rates found in the literature for neural tissue vary greatly [75, 76], possibly due to this ℓ_g dependence. The ℓ_d ≳ ℓ_g condition of REEDS-DE also necessitates longer diffusion times, which decreases the available signal due to T₂ and may make exchange during encodings more substantial. Exchange during encodings may be difficult to model out of Eq. 18 in the first step of REEDS-DE without further assumptions.

Another challenge for combining REEDS-DE with imaging is the presence of a non-zero-mean noise floor. With the NMR-MOUSE, summing up the real component of the complex signal preserves zero-mean Gaussian noise [15]. With imaging, the signal magnitude is typically used, leading to non-zero-mean Rician noise [77]. The persistent signal from motionally averaged water may be difficult to accurately model and separate from the noise floor, which may affect estimates of f_m and ⟨c⟩.

While the methods discussed here are potentially amenable to experiments in which gradient strength and direction is varied, some alterations to the modelling are needed. In particular, the motionally averaged signal decays exponentially with b^1/3g^4/3. The g^4/3 term, which is considered as a constant in Eqs. 4, 6 to pull out ⟨c⟩, will need to be accounted for when g is varied. The described method also ignores the transitional signal behavior when all three length scales ℓ_d, ℓ_g, ℓ_s are similar, although such behavior may be significant in both the intracellular and extracellular space [34]. Alternatively, more general diffusion MR signal models may be used to interpret REEDS-DE measurements, as opposed to the exchanging, two-compartment model presented here. To model signal resulting from simple restricted geometries probed by arbitrary gradient waveforms, the multiple correlation function framework can be utilized [27, 78]. Another way to model the signal is using time-dependent frameworks [79–81] that—similar to the ℓ_d ≳ ℓ_g signal model, Eq. 7—are valid when there are only free and motionally averaged signal fractions (i.e., when the Gaussian phase distribution approximation [42] holds in all sub-ensembles). Probing multiple gradient directions provides the opportunity for combinations with a diffusion tensor imaging framework [82], but the exchange rate is expected to vary with direction in anisotropic tissue regions [9]. We emphasize that REEDS-DE and the fitting approach described here is merely one way to interpret data from double diffusion encodings and that the above discussion concerning conventional MR scanners is speculative.

4.2 Comparison to Other Diffusion Exchange Spectroscopy-Based Methods

This work contributes to the existing body of literature attempting to accelerate DEXSY and obtain exchange parameters without the intensive data requirements of a conventional numerical ILT. Some approaches aim to accelerate the ILT itself [83, 84], e.g., by constraining the inversion using the marginal P(D) distributions [24, 85]. Approaches which rely on an ILT, however, remain limited by the confounds discussed in Section 3.1 and are thus unable, at present, to disentangle the effects of restriction and exchange. One potential direction would be to develop a simultaneous Gaussian and non-Gaussian inversion, similar to a simultaneous Gaussian and exponential inversion developed for relaxation data [86].

Other approaches are more similar to the one presented here and remain in the acquisition domain. Notably, filter exchange spectroscopy (FEXSY) uses a large, fixed b₁ to attenuate the free water population (i.e., f_e) and views the decay at various b₂ as being exchange-limited [6, 17, 18]. Visually, FEXSY slices the (b₁, b₂) domain horizontally, rather than diagonally, potentially conflating the effects of restriction and exchange. Simulated data and experimental observations, however, show that slicing diagonally along constant b₁ + b₂ = b_s maximally isolates the effects of (and provides the greatest sensitivity to) non-Gaussian signal behavior due to restrictions and exchange—see the DEXSY signal contours in Figure 2A. Thus, REEDS-DE and other approaches based on estimating the diagonal curvature or ΔI offer improved isolation from Gaussian diffusion and potentially improved SNR compared to FEXSY.

4.3 Relation of Our Findings to Those of Others

REEDS-DE can be viewed as a diffusion microstructural model of signals acquired with double diffusion encodings. The model incorporates a restricted intracellular compartment and exchange between intra- and extracellular compartments, consistent with classic microstructural imaging studies, e.g., Stanisz et al. (1997) [87]. From an extensive in vivo study of diffusion in human corticospinal tract, Nilsson et al. (2009) concluded that exchange must be included in two compartment models in which one compartment is restricted [60]. However, many microstructural models have focused on restriction and ignored exchange. For example, exchange is ignored in the Combined Hindered and Restricted Model of Diffusion (CHARMED) [88]. More generally, the field has posited a CHARMED-like “standard model” of brain microstructure consisting of 1) water confined in myelinated axons and neurites, modelled as impermeable sticks or cylinders, and 2) extra-cellular water presumed to undergo hindered, Gaussian diffusion [55, 89]. Extensions of this “standard model,” e.g., soma and neurite density imaging (SANDI) similarly ignore exchange [39]. While such models have been effective for understanding white matter, they have failed to translate to gray matter [55, 61, 90]. This is perhaps due to the higher expected membrane permeabilities of gray matter components including of soma, unmyelinated axons, dendrites and glia/glial processes such as astrocytes which highly express aquaporin water channels [91]. A growing body of literature suggests that exchange rates in gray matter are faster than have been previously assumed, with mean residence times on the order of 1/k ∼ 10 ms [15, 41, 90, 92], as reported here.

On the other hand, studies of exchange using diffusion NMR typically exclude the effects of restriction—following the seminal Kärger model [63]—and instead model the intracellular or restricted component(s) as having a small intrinsic diffusivity but otherwise Gaussian diffusion [41, 62, 93, 94]. This assumption may lead to the vast underestimation of exchange rates, as the slower exponential scaling of the signal decay in the high b-value regime is attributed not to non-Gaussian signal behavior, but to a slower exchange rate, when the former effect may be significant. Consider that 1-D diffusion MR data along b can be adequately fit using Kärger models or restriction models—both are capable of explaining the transition to slower exponential decay observed at high b-values [40, 41] (e.g., Figure 2B). The effects are ambiguated. If exchange is ignored, restriction length scales may be overestimated; if restriction is ignored, exchange rates may be underestimated. Ironically, slow exchange rates measured while ignoring restriction are sometimes used, perhaps erroneously, to justify the exclusion of exchange in signal models of tissue that do include the effects of restriction, such as CHARMED [88] and SANDI [39]. Overall, we should be cautious not to make modeling assumptions using findings from different, incompatible signal models.

Here, we provide a constructive method to merge the disparate signal models for restriction and exchange in tissue while retaining sensitivity to both effects in isolation. Unlike conventional diffusion MR experiments, multidimensional methods such as REEDS-DE and its attendant DEXSY experiments can efficiently disentangle these effects. Indeed, restriction and exchange parameters are fit separately using the REEDS-DE acquisition scheme. Furthermore, the relatively small number of parameters—arising from the presented argument that any underlying P(ℓ_s) is adequately described by a two-compartment model when ℓ_d ≳ ℓ_g—minimizes SNR requirements and supports robust NLS fitting. The theory and double diffusion encoding methods presented in this paper can be considered a step towards incorporating exchange into microstructural signal models, for which there is a vast body of prior literature. REEDS-DE and similar approaches may help to answer longstanding questions within the field, namely the relevance of exchange in gray matter.

5 Conclusion

Non-Gaussian signal behavior confounds the interpretation of 1- and 2-D diffusion coefficient distributions obtained using numerical ILTs of diffusion NMR and DEXSY data. On the other hand, non-Gaussian signal behavior is a signature of restriction and enhances sensitivity to transmembrane water exchange in tissue. A method to characterize the non-Gaussian signal behavior due to restrictions in itself and in tandem with exchange represents a valuable contribution. To that end, we have developed a diffusion NMR acquisition scheme that independently characterizes both restriction and exchange: Restriction and Exchange from Equally-weighted Double and Single Diffusion Encodings (REEDS-DE). Although the method has not yet been validated for general use (i.e., using conventional scanners), we present experimental NMR data collected on ex vivo neonatal spinal cord using a strong, static gradient system which support the validity of REEDS-DE and its accompanying signal model in the regime of ℓ_d ≳ ℓ_g.

REEDS-DE leverages multidimensional NMR data along the b₁, b₂, and t_m dimensions of DEXSY experiments. The method uses a simple two-point difference metric ΔI along an axis of constant total diffusion weighting b_s = b₁ + b₂ to remove the effects of Gaussian diffusion (and T₁ relaxation). This difference is then acquired at various t_m including t_m near 0 with experimental parameters that satisfy ℓ_d ≳ ℓ_g—i.e., $\sqrt{D_0\tau }\gtrsim {(D_0/\gamma g)}^{1/3}$ — in order to further disentangle the effects of restriction and exchange. The method yields three apparent parameters that characterize restrictions with an effective spherical radius R smaller than or similar to ℓ_g: f_m, ⟨c⟩, and k, corresponding to the volume fraction, ensemble-averaged decay rate with b^1/3g^4/3, and first-order exchange rate, respectively. The method provides a novel means of rapidly and comprehensively characterizing time-varying diffusion behavior in biological tissue without the potential pitfalls of numerical ILTs, and may prove useful in the study of tissue that has been historically difficult to characterize, such as gray matter.

Data Availability Statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Ethics Statement

The animal study was reviewed and approved by the National Institute of Neurological Disorders and Stroke Animal Care and Use Committee, Animal Protocol Number 1267–18.

Author Contributions

TC developed the theory and performed simulations. TC and NW analyzed the data. TC, NW, and RR designed experiments. NW and RR performed experiments and collected data. TC and NW drafted the manuscript and wrote the Supplementary Material. PB supervised the project. All authors edited the manuscript. All authors have read and approved the contents of the manuscript.

Funding

TC, RR, and PB were all supported by the IRP of the NICHD, NIH. TC is a graduate student in the NIH-Oxford Cambridge Scholars program. NW was funded by the NIGMS PRAT Fellowship Award # FI2GM133445-01.

Conflict of Interest

RR was self-employed by Celoptics, Inc.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

We thank Dr. Alexandru Avram and Dr. Michal Komlosh for helpful discussions about double diffusion encoding, Dr. Denis Grebenkov for discussions about the implications of non-Gaussian signal attenuation in ILT spectra, and Dr. Petrik Galvosas for the 2-D ILT code.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2022.805793/full#supplementary-material

References

1. Jeener J, Meier BH, Bachmann P, Ernst RR. Investigation of Exchange Processes by Two‐dimensional NMR Spectroscopy. J Chem Phys (1979) 71:4546–53. doi:10.1063/1.438208

CrossRef Full Text | Google Scholar

2. Callaghan P. Translational Dynamics and Magnetic Resonance Principles of Pulsed Gradient Spin Echo NMR. Oxford, UK: Oxford University Press (2011).

Google Scholar

3. Bernin D, Topgaard D. Nmr Diffusion and Relaxation Correlation Methods: New Insights in Heterogeneous Materials. Curr Opin Colloid Interf Sci (2013) 18:166–72. doi:10.1016/j.cocis.2013.03.007

CrossRef Full Text | Google Scholar

4. Callaghan PT, Furó I. Diffusion-diffusion Correlation and Exchange as a Signature for Local Order and Dynamics. J Chem Phys (2004) 120:4032–8. doi:10.1063/1.1642604

CrossRef Full Text | Google Scholar

5. Qiao Y, Galvosas P, Adalsteinsson T, Schönhoff M, Callaghan PT. Diffusion Exchange Nmr Spectroscopic Study of Dextran Exchange through Polyelectrolyte Multilayer Capsules. J Chem Phys (2005) 122:214912. doi:10.1063/1.1924707

CrossRef Full Text | Google Scholar

6. Åslund I, Nowacka A, Nilsson M, Topgaard D. Filter-exchange PGSE NMR Determination of Cell Membrane Permeability. J Magn Reson (2009) 200:291–5. doi:10.1016/j.jmr.2009.07.015

CrossRef Full Text | Google Scholar

7. Lasič S, Nilsson M, Lätt J, Ståhlberg F, Topgaard D. Apparent Exchange Rate Mapping with Diffusion Mri. Magn Reson Med (2011) 66:356–65. doi:10.1002/mrm.22782

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Nilsson M, Lätt J, van Westen D, Brockstedt S, Lasič S, Ståhlberg F, et al. Noninvasive Mapping of Water Diffusional Exchange in the Human Brain Using Filter-Exchange Imaging. Magn Reson Med (2013) 69:1572–80. doi:10.1002/mrm.24395

CrossRef Full Text | Google Scholar

9. Sønderby CK, Lundell HM, Søgaard LV, Dyrby TB. Apparent Exchange Rate Imaging in Anisotropic Systems. Magn Reson Med (2014) 72:756–62.

PubMed Abstract | Google Scholar

10. Lasič S, Oredsson S, Partridge SC, Saal LH, Topgaard D, Nilsson M, et al. Apparent Exchange Rate for Breast Cancer Characterization. NMR Biomed (2016) 29:631–9. doi:10.1002/nbm.3504

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Lampinen B, Szczepankiewicz F, van Westen D, Englund E, C Sundgren P, Lätt J, et al. Optimal Experimental Design for Filter Exchange Imaging: Apparent Exchange Rate Measurements in the Healthy Brain and in Intracranial Tumors. Magn Reson Med (2017) 77:1104–14. doi:10.1002/mrm.26195

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Tian X, Li H, Jiang X, Xie J, Gore JC, Xu J. Evaluation and Comparison of Diffusion Mr Methods for Measuring Apparent Transcytolemmal Water Exchange Rate Constant. J Magn Reson (2017) 275:29–37. doi:10.1016/j.jmr.2016.11.018

CrossRef Full Text | Google Scholar

13. Eriksson S, Elbing K, Söderman O, Lindkvist-Petersson K, Topgaard D, Lasič S. NMR Quantification of Diffusional Exchange in Cell Suspensions with Relaxation Rate Differences between Intra and Extracellular Compartments. PLoS One (2017) 12:e0177273. doi:10.1371/journal.pone.0177273

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Schilling F, Ros S, Hu D-E, D'Santos P, McGuire S, Mair R, et al. Mri Measurements of Reporter-Mediated Increases in Transmembrane Water Exchange Enable Detection of a Gene Reporter. Nat Biotechnol (2017) 35:75–80. doi:10.1038/nbt.3714

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Williamson NH, Ravin R, Benjamini D, Merkle H, Falgairolle M, O'Donovan MJ, et al. Magnetic Resonance Measurements of Cellular and Sub-cellular Membrane Structures in Live and Fixed Neural Tissue. eLife (2019) 8:e51101. doi:10.7554/eLife.51101

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Breen-Norris JO, Siow B, Walsh C, Hipwell B, Hill I, Roberts T, et al. Measuring Diffusion Exchange across the Cell Membrane with Dexsy (Diffusion Exchange Spectroscopy). Magn Reson Med (2020) 84:1543–51. doi:10.1002/mrm.28207

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Scher Y, Reuveni S, Cohen Y. Constant Gradient Fexsy: A Time-Efficient Method for Measuring Exchange. J Magn Reson (2020) 311:106667. doi:10.1016/j.jmr.2019.106667

CrossRef Full Text | Google Scholar

18. Bai R, Li Z, Sun C, Hsu Y-C, Liang H, Basser P. Feasibility of Filter-Exchange Imaging (Fexi) in Measuring Different Exchange Processes in Human Brain. NeuroImage (2020) 219:117039. doi:10.1016/j.neuroimage.2020.117039

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Williamson NH, Ravin R, Cai TX, Benjamini D, Falgairolle M, O’Donovan MJ, et al. Real-time Measurement of Diffusion Exchange Rate in Biological Tissue. J Magn Reson (2020) 317:106782. doi:10.1016/j.jmr.2020.106782

CrossRef Full Text | Google Scholar

20. Schillmaier M, Kaika A, Schilling F. Chapter 6. Disentangling Intercompartment Exchange from Restricted Diffusion. Adv Diffusion Encoding Methods MRI (2020) 24:154–85. doi:10.1039/9781788019910-00154

CrossRef Full Text | Google Scholar

21. Ludwig D, Laun FB, Ladd ME, Bachert P, Kuder TA. Apparent Exchange Rate Imaging: On its Applicability and the Connection to the Real Exchange Rate. Magn Reson Med (2021) 86:677–92. doi:10.1002/mrm.28714

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Callaghan PT, Manz B. Velocity Exchange Spectroscopy. J Magn Reson Ser A (1994) 106:260–5. doi:10.1006/jmra.1994.1036

CrossRef Full Text | Google Scholar

23. Neudert O, Stapf S, Mattea C. Diffusion Exchange NMR Spectroscopy in Inhomogeneous Magnetic fields. J Magn Reson (2011) 208:256–61. doi:10.1016/j.jmr.2010.11.014

CrossRef Full Text | Google Scholar

24. Benjamini D, Komlosh ME, Basser PJ. Imaging Local Diffusive Dynamics Using Diffusion Exchange Spectroscopy MRI. Phys Rev Lett (2017) 118:158003. doi:10.1103/physrevlett.118.158003

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Lee JH, Labadie C, Springer CS, Harbison GS. Two-dimensional Inverse Laplace Transform Nmr: Altered Relaxation Times Allow Detection of Exchange Correlation. J Am Chem Soc (1993) 115:7761–4. doi:10.1021/ja00070a022

CrossRef Full Text | Google Scholar

26. Washburn KE, Callaghan PT. Tracking Pore to Pore Exchange Using Relaxation Exchange Spectroscopy. Phys Rev Lett (2006) 97:175502. doi:10.1103/physrevlett.97.175502

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Grebenkov DS. NMR Survey of Reflected Brownian Motion. Rev Mod Phys (2007) 79:1077–137. doi:10.1103/revmodphys.79.1077

CrossRef Full Text | Google Scholar

28. Wayne RC, Cotts RM. Nuclear-magnetic-resonance Study of Self-Diffusion in a Bounded Medium. Phys Rev (1966) 151:264–72. doi:10.1103/physrev.151.264

CrossRef Full Text | Google Scholar

29. Robertson B. Spin-echo Decay of Spins Diffusing in a Bounded Region. Phys Rev (1966) 151:273–7. doi:10.1103/physrev.151.273

CrossRef Full Text | Google Scholar

30. Neuman CH. Spin echo of Spins Diffusing in a Bounded Medium. J Chem Phys (1974) 60:4508–11. doi:10.1063/1.1680931

CrossRef Full Text | Google Scholar

31. de Swiet TM, Sen PN. Decay of Nuclear Magnetization by Bounded Diffusion in a Constant Field Gradient. J Chem Phys (1994) 100:5597–604. doi:10.1063/1.467127

CrossRef Full Text | Google Scholar

32. Hürlimann MD, Helmer KG, Deswiet TM, Sen PN. Spin Echoes in a Constant Gradient and in the Presence of Simple Restriction. J Magn Reson Ser A (1995) 113:260–4. doi:10.1006/jmra.1995.1091

CrossRef Full Text | Google Scholar

33. Moutal N, Demberg K, Grebenkov DS, Kuder TA. Localization Regime in Diffusion Nmr: Theory and Experiments. J Magn Reson (2019) 305:162–74. doi:10.1016/j.jmr.2019.06.016

CrossRef Full Text | Google Scholar

34. Grebenkov DS. Diffusion Mri/nmr at High Gradients: Challenges and Perspectives. Microporous Mesoporous Mater (2018) 269:79–82. doi:10.1016/j.micromeso.2017.02.002

CrossRef Full Text | Google Scholar

35. Cai TX, Benjamini D, Komlosh ME, Basser PJ, Williamson NH. Rapid Detection of the Presence of Diffusion Exchange. J Magn Reson (2018) 297:17–22. doi:10.1016/j.jmr.2018.10.004

CrossRef Full Text | Google Scholar

36. Song R, Song Y-Q, Vembusubramanian M, Paulsen JL. The Robust Identification of Exchange from T2-T2 Time-Domain Features. J Magn Reson (2016) 265:164–71. doi:10.1016/j.jmr.2016.02.001

CrossRef Full Text | Google Scholar

37. Henry AM, Hohmann JG. High-resolution Gene Expression Atlases for Adult and Developing Mouse Brain and Spinal Cord. Mamm Genome (2012) 23:539–49. doi:10.1007/s00335-012-9406-2

PubMed Abstract | CrossRef Full Text | Google Scholar

38. Sengul G, Puchalski RB, Watson C. Cytoarchitecture of the Spinal Cord of the Postnatal (P4) Mouse. Anat Rec (2012) 295:837–45. doi:10.1002/ar.22450

PubMed Abstract | CrossRef Full Text | Google Scholar

39. Palombo M, Ianus A, Guerreri M, Nunes D, Alexander DC, Shemesh N, et al. Sandi: A Compartment-Based Model for Non-invasive Apparent Soma and Neurite Imaging by Diffusion Mri. NeuroImage (2020) 215:116835. doi:10.1016/j.neuroimage.2020.116835

PubMed Abstract | CrossRef Full Text | Google Scholar

40. Lee H-H, Papaioannou A, Novikov DS, Fieremans E. In Vivo observation and Biophysical Interpretation of Time-dependent Diffusion in Human Cortical gray Matter. NeuroImage (2020) 222:117054. doi:10.1016/j.neuroimage.2020.117054

PubMed Abstract | CrossRef Full Text | Google Scholar

41. Jelescu IO, de Skowronski A, Palombo M, Novikov DS. Neurite Exchange Imaging (Nexi): A Minimal Model of Diffusion in gray Matter with Inter-compartment Water Exchange. arXiv:2108.06121 (2021).

Google Scholar

42. Axelrod S, Sen PN. Nuclear Magnetic Resonance Spin Echoes for Restricted Diffusion in an Inhomogeneous Field: Methods and Asymptotic Regimes. J Chem Phys (2001) 114:6878–95. doi:10.1063/1.1356010

CrossRef Full Text | Google Scholar

43. Sukstanskii AL, Yablonskiy DA. Gaussian Approximation in the Theory of Mr Signal Formation in the Presence of Structure-specific Magnetic Field Inhomogeneities. J Magn Reson (2003) 163:236–47. doi:10.1016/s1090-7807(03)00131-9

CrossRef Full Text | Google Scholar

44. Moutal N, Grebenkov DS. The Localization Regime in a Nutshell. J Magn Reson (2020) 320:106836. doi:10.1016/j.jmr.2020.106836

CrossRef Full Text | Google Scholar

45. Torrey HC. Bloch Equations with Diffusion Terms. Phys Rev (1956) 104:563–5. doi:10.1103/physrev.104.563

CrossRef Full Text | Google Scholar

46. Stoller SD, Happer W, Dyson FJ. Transverse Spin Relaxation in Inhomogeneous Magnetic fields. Phys Rev A (1991) 44:7459–77. doi:10.1103/physreva.44.7459

PubMed Abstract | CrossRef Full Text | Google Scholar

47. Grebenkov DS, Helffer B. On Spectral Properties of the Bloch--Torrey Operator in Two Dimensions. SIAM J Math Anal (2018) 50:622–76. doi:10.1137/16m1088387

CrossRef Full Text | Google Scholar

48. Mitra PP, Halperin BI. Effects of Finite Gradient-Pulse Widths in Pulsed-Field-Gradient Diffusion Measurements. J Magn Reson Ser A (1995) 113:94–101. doi:10.1006/jmra.1995.1060

CrossRef Full Text | Google Scholar

49. Kiselev VG. Microstructure with Diffusion Mri: what Scale We Are Sensitive to? J Neurosci Methods (2021) 347:108910. doi:10.1016/j.jneumeth.2020.108910

CrossRef Full Text | Google Scholar

50. Kimmich R, Unrath W, Schnur G, Rommel E. Nmr Measurement of Small Self-Diffusion Coefficients in the Fringe Field of Superconducting Magnets. J Magn Reson (1969) (1991) 91:136–40. doi:10.1016/0022-2364(91)90416-q

CrossRef Full Text | Google Scholar

51. Blümich B, Blümler P, Eidmann G, Guthausen A, Haken R, Schmitz U, et al. The Nmr-Mouse: Construction, Excitation, and Applications. Magn Reson Imaging (1998) 16:479–84. doi:10.1016/s0730-725x(98)00069-1

PubMed Abstract | CrossRef Full Text | Google Scholar

52. Köpf M, Corinth C, Haferkamp O, Nonnenmacher TF. Anomalous Diffusion of Water in Biological Tissues. Biophysical J (1996) 70:2950–8. doi:10.1016/s0006-3495(96)79865-x

CrossRef Full Text | Google Scholar

53. Carlton KJ, Halse MR, Strange JH. Diffusion-weighted Imaging of Bacteria Colonies in the Strafi Plane. J Magn Reson (2000) 143:24–9. doi:10.1006/jmre.1999.1959

CrossRef Full Text | Google Scholar

54. Mazur W, Krzyżak AT. Attempts at the Characterization of In-Cell Biophysical Processes Non-invasively-quantitative NMR Diffusometry of a Model Cellular System. Cells (2020) 9:2124. doi:10.3390/cells9092124

PubMed Abstract | CrossRef Full Text | Google Scholar

55. Novikov DS, Fieremans E, Jespersen SN, Kiselev VG. Quantifying Brain Microstructure with Diffusion Mri: Theory and Parameter Estimation. NMR Biomed (2019) 32:e3998. doi:10.1002/nbm.3998

PubMed Abstract | CrossRef Full Text | Google Scholar

56. Jensen JH, Helpern JA. Mri Quantification of Non-gaussian Water Diffusion by Kurtosis Analysis. NMR Biomed (2010) 23:698–710. doi:10.1002/nbm.1518

PubMed Abstract | CrossRef Full Text | Google Scholar

57. Mitra PP, Sen PN, Schwartz LM. Short-time Behavior of the Diffusion Coefficient as a Geometrical Probe of Porous media. Phys Rev B (1993) 47:8565–74. doi:10.1103/physrevb.47.8565

CrossRef Full Text | Google Scholar

58. Cai TX, Williamson NH, Witherspoon VJ, Ravin R, Basser PJ. A Single-Shot Measurement of Time-dependent Diffusion over Sub-millisecond Timescales Using Static Field Gradient Nmr. J Chem Phys (2021) 154:111105. doi:10.1063/5.0041354

CrossRef Full Text | Google Scholar

59. Tax CMW, Szczepankiewicz F, Nilsson M, Jones DK. The Dot-Compartment Revealed? Diffusion Mri with Ultra-strong Gradients and Spherical Tensor Encoding in the Living Human Brain. NeuroImage (2020) 210:116534. doi:10.1016/j.neuroimage.2020.116534

PubMed Abstract | CrossRef Full Text | Google Scholar

60. Nilsson M, Lätt J, Nordh E, Wirestam R, Ståhlberg F, Brockstedt S. On the Effects of a Varied Diffusion Time In Vivo: Is the Diffusion in white Matter Restricted? Magn Reson Imaging (2009) 27:176–87. doi:10.1016/j.mri.2008.06.003

PubMed Abstract | CrossRef Full Text | Google Scholar

61. Novikov DS, Jensen JH, Helpern JA, Fieremans E. Revealing Mesoscopic Structural Universality with Diffusion. Proc Natl Acad Sci U.S.A (2014) 111:5088–93. doi:10.1073/pnas.1316944111

PubMed Abstract | CrossRef Full Text | Google Scholar

62. Moutal N, Nilsson M, Topgaard D, Grebenkov D. The Kärger vs Bi-exponential Model: Theoretical Insights and Experimental Validations. J Magn Reson (2018) 296:72–8. doi:10.1016/j.jmr.2018.08.015

PubMed Abstract | CrossRef Full Text | Google Scholar

63. Kärger J. Nmr Self-Diffusion Studies in Heterogeneous Systems. Adv Colloid Interf Sci (1985) 23:129–48. doi:10.1016/0001-8686(85)80018-x

CrossRef Full Text | Google Scholar

64. Venkataramanan L, Yi-Qiao Song YQ, Hürlimann MD. Solving Fredholm Integrals of the First Kind with Tensor Product Structure in 2 and 2.5 Dimensions. IEEE Trans Signal Process (2002) 50:1017–26. doi:10.1109/78.995059

CrossRef Full Text | Google Scholar

65. Godefroy S, Callaghan PT. 2d Relaxation/diffusion Correlations in Porous media. Magn Reson Imaging (2003) 21:381–3. doi:10.1016/s0730-725x(03)00144-9

PubMed Abstract | CrossRef Full Text | Google Scholar

66. Pfeuffer J, Provencher SW, Gruetter R. Water Diffusion in Rat Brain In Vivo as Detected at Very Largeb Values Is Multicompartmental. Magma (1999) 8:98–108. doi:10.1007/bf02590526

PubMed Abstract | CrossRef Full Text | Google Scholar

67. Ronen I, Moeller S, Ugurbil K, Kim D-S. Analysis of the Distribution of Diffusion Coefficients in Cat Brain at 9.4 T Using the Inverse Laplace Transformation. Magn Reson Imaging (2006) 24:61–8. doi:10.1016/j.mri.2005.10.023

PubMed Abstract | CrossRef Full Text | Google Scholar

68. Benjamini D, Basser PJ. Water Mobility Spectral Imaging of the Spinal Cord: Parametrization of Model-free Laplace Mri. Magn Reson Imaging (2019) 56:187–93. doi:10.1016/j.mri.2018.12.001

PubMed Abstract | CrossRef Full Text | Google Scholar

69. Fabich HT, Nandi P, Thomann H, Conradi MS. Diffusion Measurements Using the Second echo. Concepts Magn Reson A (2018) 47A:e21462. doi:10.1002/cmr.a.21462

CrossRef Full Text | Google Scholar

70. Rata DG, Casanova F, Perlo J, Demco DE, Blümich B. Self-diffusion Measurements by a mobile Single-Sided Nmr Sensor with Improved Magnetic Field Gradient. J Magn Reson (2006) 180:229–35. doi:10.1016/j.jmr.2006.02.015

CrossRef Full Text | Google Scholar

71. Casanova F, Perlo J, Blümich B. Single-Sided NMR. Berlin, Heidelberg: Springer (2011). p. 1–10. doi:10.1007/978-3-642-16307-4_1

CrossRef Full Text | Google Scholar

72. Khrapitchev AA, Callaghan PT. Double Pgse Nmr with Stimulated Echoes: Phase Cycles for the Selection of Desired Encoding. J Magn Reson (2001) 152:259–68. doi:10.1006/jmre.2001.2402

CrossRef Full Text | Google Scholar

73. Komlosh ME, Horkay F, Freidlin RZ, Nevo U, Assaf Y, Basser PJ. Detection of Microscopic Anisotropy in gray Matter and in a Novel Tissue Phantom Using Double Pulsed Gradient Spin echo Mr. J Magn Reson (2007) 189:38–45. doi:10.1016/j.jmr.2007.07.003

PubMed Abstract | CrossRef Full Text | Google Scholar

74. Avram AV, Özarslan E, Sarlls JE, Basser PJ. In Vivo detection of Microscopic Anisotropy Using Quadruple Pulsed-Field Gradient (Qpfg) Diffusion Mri on a Clinical Scanner. NeuroImage (2013) 64:229–39. doi:10.1016/j.neuroimage.2012.08.048

PubMed Abstract | CrossRef Full Text | Google Scholar

75. Nilsson M, van Westen D, Ståhlberg F, Sundgren PC, Lätt J. The Role of Tissue Microstructure and Water Exchange in Biophysical Modelling of Diffusion in white Matter. Magn Reson Mater Phy (2013) 26:345–70. doi:10.1007/s10334-013-0371-x

CrossRef Full Text | Google Scholar

76. Yang DM, Huettner JE, Bretthorst GL, Neil JJ, Garbow JR, Ackerman JJH. Intracellular Water Preexchange Lifetime in Neurons and Astrocytes. Magn Reson Med (2018) 79:1616–27. doi:10.1002/mrm.26781

PubMed Abstract | CrossRef Full Text | Google Scholar

77. Sijbers J, Den Dekker AJ. Maximum Likelihood Estimation of Signal Amplitude and Noise Variance from Mr Data. Magn Reson Med (2004) 51:586–94. doi:10.1002/mrm.10728

PubMed Abstract | CrossRef Full Text | Google Scholar

78. Özarslan E, Shemesh N, Basser PJ. A General Framework to Quantify the Effect of Restricted Diffusion on the Nmr Signal with Applications to Double Pulsed Field Gradient Nmr Experiments. J Chem Phys (2009) 130:104702. doi:10.1063/1.3082078

CrossRef Full Text | Google Scholar

79. Stepišnik J. Analysis of Nmr Self-Diffusion Measurements by a Density Matrix Calculation. Physica B+C (1981) 104:350–64.

Google Scholar

80. Stepišnik J. Time-dependent Self-Diffusion by Nmr Spin-echo. Physica B Condensed Matter (1993) 183:343–50.

Google Scholar

81. Ning L, Setsompop K, Westin C-F, Rathi Y. New Insights about Time-Varying Diffusivity and its Estimation from Diffusion Mri. Magn Reson Med (2017) 78:763–74. doi:10.1002/mrm.26403

PubMed Abstract | CrossRef Full Text | Google Scholar

82. Basser PJ, Mattiello J, LeBihan D. Mr Diffusion Tensor Spectroscopy and Imaging. Biophysical J (1994) 66:259–67. doi:10.1016/s0006-3495(94)80775-1

CrossRef Full Text | Google Scholar

83. Bai R, Cloninger A, Czaja W, Basser PJ. Efficient 2d Mri Relaxometry Using Compressed Sensing. J Magn Reson (2015) 255:88–99. doi:10.1016/j.jmr.2015.04.002

CrossRef Full Text | Google Scholar

84. Bai R, Benjamini D, Cheng J, Basser PJ. Fast, Accurate 2d-Mr Relaxation Exchange Spectroscopy (Rexsy): Beyond Compressed Sensing. J Chem Phys (2016) 145:154202. doi:10.1063/1.4964144

CrossRef Full Text | Google Scholar

85. Benjamini D, Basser PJ. Use of Marginal Distributions Constrained Optimization (MADCO) for Accelerated 2D MRI Relaxometry and Diffusometry. J Magn Reson (2016) 271:40–5. doi:10.1016/j.jmr.2016.08.004

PubMed Abstract | CrossRef Full Text | Google Scholar

86. Washburn KE, Anderssen E, Vogt SJ, Seymour JD, Birdwell JE, Kirkland CM, et al. Simultaneous Gaussian and Exponential Inversion for Improved Analysis of Shales by Nmr Relaxometry. J Magn Reson (2015) 250:7–16. doi:10.1016/j.jmr.2014.10.015

CrossRef Full Text | Google Scholar

87. Stanisz GJ, Wright GA, Henkelman RM, Szafer A. An Analytical Model of Restricted Diffusion in Bovine Optic Nerve. Magn Reson Med (1997) 37:103–11. doi:10.1002/mrm.1910370115

PubMed Abstract | CrossRef Full Text | Google Scholar

88. Assaf Y, Basser PJ. Composite Hindered and Restricted Model of Diffusion (Charmed) Mr Imaging of the Human Brain. NeuroImage (2005) 27:48–58. doi:10.1016/j.neuroimage.2005.03.042

PubMed Abstract | CrossRef Full Text | Google Scholar

89. Veraart J, Fieremans E, Novikov DS. On the Scaling Behavior of Water Diffusion in Human Brain white Matter. NeuroImage (2019) 185:379–87. doi:10.1016/j.neuroimage.2018.09.075

PubMed Abstract | CrossRef Full Text | Google Scholar

90. Jelescu IO, Palombo M, Bagnato F, Schilling KG. Challenges for Biophysical Modeling of Microstructure. J Neurosci Methods (2020) 344:108861. doi:10.1016/j.jneumeth.2020.108861

CrossRef Full Text | Google Scholar

91. Papadopoulos MC, Verkman AS. Aquaporin Water Channels in the Nervous System. Nat Rev Neurosci (2013) 14:265–77. doi:10.1038/nrn3468

PubMed Abstract | CrossRef Full Text | Google Scholar

92. Veraart J, Fieremans E, Rudrapatna U, Jones D, Novikov DS. Biophysical Modeling of the gray Matter: Does the “Stick” Model Hold. In: Proceedings of the 27th Annual Meeting of ISMRM; 16-21 June. 2018; Paris, France (2018).

Google Scholar

93. Fieremans E, Novikov DS, Jensen JH, Helpern JA. Monte Carlo Study of a Two-Compartment Exchange Model of Diffusion. NMR Biomed (2010) 23:711–24. doi:10.1002/nbm.1577

PubMed Abstract | CrossRef Full Text | Google Scholar

94. Nilsson M, Alerstam E, Wirestam R, Sta˚hlberg F, Brockstedt S, Lätt J, et al. Evaluating the Accuracy and Precision of a Two-Compartment Kärger Model Using Monte Carlo Simulations. J Magn Reson (2010) 206:59–67. doi:10.1016/j.jmr.2010.06.002

PubMed Abstract | CrossRef Full Text | Google Scholar