- 1Department of Physics, Ramakrishna Mission Vivekananda Educational and Research Institute, Howrah, India
- 2Quantitative Life Sciences Section, ICTP-Abdus Salam International Centre for Theoretical Physics, Trieste, Italy
- 3Bhaurao Kakatkar College, Jyoti Compound Camp, Club Road Belgaum, India
Stochastic processes offer a fundamentally different paradigm of dynamics than deterministic processes that one is most familiar with, the most prominent example of the latter being Newton’s laws of motion. Here, we discuss in a pedagogical manner a simple and illustrative example of stochastic processes in the form of a particle undergoing standard Brownian diffusion, with the additional feature of the particle resetting repeatedly and at random times to its initial condition. Over the years, many different variants of this simple setting have been studied, including extensions to many-body interacting systems, all of which serve as illustrations of peculiar non-trivial and interesting static and dynamic features that characterize stochastic dynamics at long times. We will provide in this work a brief overview of this active and rapidly evolving field by considering the arguably simplest example of Brownian diffusion in one dimension. Along the way, we will learn about some of the general techniques that a physicist employs to study stochastic processes. Relevant to the special issue, we will discuss in detail how introducing resetting in an otherwise diffusive dynamics provides an explicit optimization of the time to locate a misplaced target through a special choice of the resetting protocol. We also discuss thermodynamics of resetting, and provide a bird’s eye view of some of the recent work in the field of resetting.
Introduction: Brownian Motion
Brownian diffusion models random motion of a mesoscopic particle that is immersed in a fluid and is being constantly buffeted by the fluid molecules. Starting from this simple context, the paradigm of Brownian diffusion has been successfully employed to discuss a wide range of dynamical scenarios in physics, astronomy, chemistry, biology and mathematics, and even in finance and computer science. Consider a Brownian particle undergoing diffusion in free space in one dimension. Its dynamics is conveniently described by the so-called overdamped Langevin equation for the displacement of its center of mass, and is given by [1]:
where η(t) is a Gaussian, white noise with the properties
Here, angular brackets denote average over noise realizations. The parameter D > 0, called the diffusion coefficient, sets the strength of the noise.
The dynamics (1) is an example of a Markov process, namely, a process that evolves in continuous time and for which if one wants to know at any instant of time the future state of the process, it suffices to know the state of the process at that instant, and one does not need to know the entire history of the process until that instant. Indeed, it is evident from Eq. 1 that to know at any instant of time t the future state x(t + Δt); Δt > 0, one requires to know just x(t) and not the entire history from the initial state x(t = 0) to x(t). Note that the state space spanned by values of x is continuous.
For a given initial condition x(t = 0) = x0, Eq. 1 may be integrated to obtain
which implies that for a given initial condition, the position of the particle at time t may have many different values depending on the trajectory of the noise η between times 0 and t. Eq. 1 is an example of what are known as stochastic processes, in which one may have many different final outcomes for the same initial condition. This latter fact may be contrasted with what happens under deterministic processes, the most prominent example of which would perhaps be the Newton’s laws of motion, which have the property of yielding a unique final outcome for a given initial condition. Eq. 1 is more specifically known as a stochastic differential equation: a differential equation in which one or more terms is a stochastic process, and whose solution is consequently also a stochastic process.
The average position of the particle at time t, averaged over the different noise trajectories, is obtained from Eq. 3 on using Eq. 2 as ⟨x(t)⟩ = x0, while the variance, measured with respect to the initial location of the particle, reads
Position Probability Distribution
Now, it is instructive to ask: given that the position of the particle at time t has many different values, what is the full distribution of the position at time t? In other words, what is the form of P(x, t), defined such that P(x, t)dx is the probability to find the particle between positions x and x + dx at time t, given that the particle started from position x0 at time t = 0: P(x, 0) = δ(x − x0). The probability density is of course normalized as ∫dx P(x, t) = 1 ∀ t. The question just posed may be answered by writing down and solving the so-called Fokker-Planck equation for the time evolution of P(x, t). The equation reads
and needs to be solved subject to the initial condition P(x, 0) = δ(x − x0).
The Fokker-Planck equation may be derived by noting down the ways in which the probability density P(x, t) changes in a small time 0 < Δt ≪ 1, and finally taking the limit Δt → 0. One has
where ϕΔt(Δx) is the probability density for x to change by an amount Δx in time Δt, and is taken to be independent of x. The probability density satisfies the normalization ∫d(Δx) ϕΔt(Δx) = 1. Note that Eq. 1 implies that this jump probability is independent of the value of x from which the jump is taking place. In Eq. 6, the second term on the right hand side (rhs) denotes gain in probability due to a change taking place from x − Δx to x, while the third term on the rhs denotes loss in probability due to a change taking place from x. Next, noting that the dynamics (1) implies that for small Δt, the change Δx that x undergoes is also small, and assuming that P(x, t) is a slowly varying function of x, we may Taylor expand the left hand side (lhs) of Eq. 6 in powers of Δt and the second term on the right hand side in powers of Δx. Executing such an expansion, and noting that Eq. 1 implies that ⟨Δx⟩≡∫d(Δx) Δx ϕΔt(Δx) = 0 and ⟨(Δx)2⟩≡∫d(Δx) (Δx)2 ϕΔt(Δx) = 2DΔt, one obtains Eq. 5.
The solution to Eq. 5 is readily obtained by expressing P(x, t) in terms of its Fourier component
which is a Gaussian distribution centred at x0. Eq. 7 implies that the probability of finding the particle at a given distance from its initial location grows with time. Consequently, as time goes by, one has an increased probability of finding the particle far off from its initial location, although at any given time, the most probable location of the particle is at its initial location. These features are evident from the plot of P(x, t) at different times depicted in Figure 1.
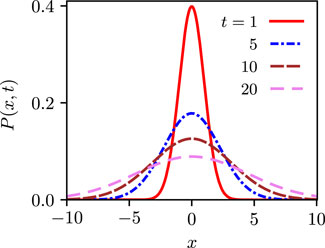
FIGURE 1. The distribution (7) at different times, showing the broadening of the distribution with time. Here, we have taken x0 = 0.0, D = 0.5.
The mean-squared displacement (MSD) of the particle about its initial location is obtained straightforwardly from Eq. 7 as
matching with the result (4), and which implies that the MSD grows forever as a function of time. Such a behavior in which the MSD grows linearly in time is referred to as normal diffusive behavior.
The aspect of the probability of finding the particle far off from x0 increasing with time may be traced back to the fact that since the particle is diffusing in free space, it is no wonder that at longer times, it would have spread to a larger region of the available space than at shorter times. Let us then ask this question: Is there a way to stop this spread? Well, one possible way could be to have the particle diffuse not in free space but in a bounded domain of finite extent, say, between points x = − L and x = + L on the x-axis. In this case, the probability of finding the particle at a given location would keep increasing with time, until it can increase no further, that is, until the system attains a stationary state. In this state, attained in the limit t → ∞, it may be argued that this probability would be the same at all locations inside the bounded domain. In other words, the particle would be equally likely to be found anywhere within the region x ∈ [ − L, L].
Brownian Motion in Presence of Resetting
In the above backdrop, one may ask: Is there a way to induce a stationary state in the system by not tweaking the boundary conditions but by modifying the dynamics in a way that it continues to take place in the free space and yet has a stationary state? Of course, one way could be to subject the motion of the particle to take place in a bounded potential. In this respect, tweaking the boundary condition so that the particle diffuses not in free space but in a bounded domain of finite extent is tantamount to a potential that is zero everywhere except at the boundaries where one has an infinitely-high potential barrier. As an interesting alternative to using a potential, it turns out that there is a rather simple and instructive way to achieve the goal of inducing a stationary state, through the introduction of stochastic resetting in the dynamics [2]. To this end, let us modify the dynamics of free diffusion by stipulating that the particle in addition to evolving according to the rule (1) has also the option of resetting its position to its initial value. More specifically, at time t, the particle has in the ensuing infinitesimal time interval dt the following options for updating its location x(t): with probability rdt, it resets its position to initial value x0, while with the complementary probability 1 − rdt, it evolves according to Eq. 1. Thus, we have [2]:
Here, r ≥ 0 is a dynamical parameter, whose value when set to zero reduces the modified dynamics to that of free diffusion. In practical terms, a typical trajectory of the particle would involve free diffusion interspersed with events of reset to x0, as shown in Figure 2. It is evident from Eq. 9 that introducing resetting into the dynamics (1) retains the Markov nature of the dynamics.
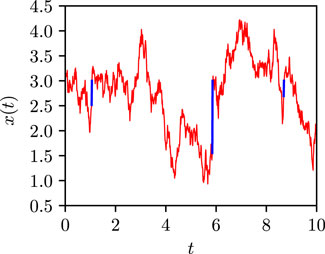
FIGURE 2. The plot shows a typical trajectory of a particle starting at location x0 = 3.0 and performing free diffusion in one dimension, with stochastic resets to x0 at random times. The parameter values are D = 0.5, and r = 0.25. The jumps in x values corresponding to resets are marked in blue.
Position Probability Distribution
Suppose we ask: what is the probability for the next reset to happen after a certain time t, in the interval [t, t + dt]? Let us discretize time in equal steps of length 0 < Δt ≪ 1; we will eventually consider the limit Δt → 0. The number of such steps during time duration t is obviously given by
Note that as mentioned earlier, the dynamics (1) represents infinitesimal change in x in infinitesimal time interval dt, while incorporating resetting into the dynamics has in the resulting dynamics reset events leading to any amount of change in x in infinitesimal interval dt. Indeed, the reset destination is always the same, namely, x0, irrespective of the location the particle resets from, so that the particle may execute a very long jump during a reset event.
It should be apparent from the aforementioned dynamical rules that introducing resetting into the dynamics would not let the particle go at any time, long or short, very far from the initial location. Is it actually the case? To answer this, we need to study just as in the case of free diffusion discussed above the time evolution of the probability density Pr(x, t) in presence of resetting, which may be derived by writing down the ways in which Pr(x, t) changes in a small time 0 < Δt ≪ 1 and then taking the limit Δt → 0. One has
Here, the second and the third term arise from diffusion, while the fourth and the fifth term are owing to resetting events. While the former two terms are as in the free diffusion case, Eq. 6, the latter two terms may be understood as follows. For r ≠ 0, there is a loss in probability at all locations other than x0 due to resetting events, which is represented by the fourth term on the rhs of Eq. 10, while the corresponding gain in probability at x = x0, given by rΔtδ(x − x0)∫dx Pr(x, t) = rΔtδ(x − x0), yields the last term on the rhs. Here we have used the normalization condition ∫dx Pr(x, t) = 1 ∀ t. Implementing appropriate Taylor expansions on both sides of Eq. 10, then taking the limit Δt → 0, the probability Pr(x, t) may be shown to be satisfying the Fokker-Planck equation [2]
The initial condition is Pr(x, 0) = δ(x − x0). Eq. 11 may be solved for Pr(x, t); here, we report only the solution, referring the reader to Ref. [3] for details of obtaining it:
where
Eq. 12 implies that in the limit t → ∞, one has a stationary-state form [2]:
Correspondingly, the MSD relaxes at long times to the stationary-state value
Figure 3 shows the probability distribution Pr(x, t) in presence of resetting and at four different times, as given by Eq. 12, showing in particular convergence in time to the stationary state (14).
The stationary-state distribution is an exponential centred at the resetting location; since the particle keeps resetting to x0 in time, it is no wonder that the most likely position of the particle is x0. More importantly, an exponential profile implies that there is a characteristic length scale within which the particle is to be found with significant probability and beyond which one has an exponentially-small probability of finding the particle. In conclusion, we have been able to achieve our goal: by modifying not the boundary conditions but rather the dynamics of free diffusion, one induces a stationary state in the system. While we have discussed in the foregoing the case of resetting at exponentially-distributed random times, the case of resetting at power-law-distributed random times has also been considered in the literature, see Ref. [4]. We remark in passing that resetting creates a source of probability at x0 and a sink at all other locations x ≠ x0, so that the condition of detailed balance, which characterizes an equilibrium stationary state [5], is manifestly violated in the stationary state induced by resetting. Consequently, the stationary state (14) is a generic nonequilibrium stationary state [2].
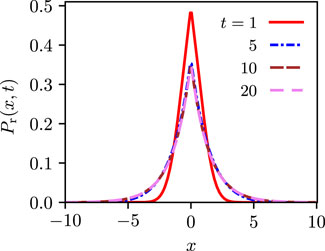
FIGURE 3. Probability distribution Pr(x,t) in presence of resetting and at four different times, as given by Eq. 12, showing convergence in time to a stationary state in which the distribution no longer changes with time. The latter is given by Eq. 14. The parameter values are x0 = 0.0, D = 0.5, and r = 0.25.
First-Passage Time Distribution
Now that we have seen a stationary state emerging in presence of stochastic resetting, one may wonder if besides this issue of theoretical relevance there is any practical utility of the process of stochastic resetting. Here, we will discuss one very interesting application of stochastic resetting, namely, in the context of search processes.
The Case of Brownian Motion
In order to discuss the concept and utility of first-passage times, let us come back to free diffusion. Referring to Figure 4, suppose we ask: when does a trajectory of free diffusion starting at x0 > 0 at time t = 0 cross the origin for the first time? Clearly the time tf that it happens, aptly termed the first-passage time (FPT), is a random variable that varies from trajectory to trajectory, and one may ask: what is the form of its distribution
where the angular brackets denote averaging with respect to the distribution
In order to proceed, we now derive a differential equation for
where the average denoted by the angular brackets is to be performed over all realizations of Δx. Now, Δτ being small implies that so is Δx, so that the quantity
Here, the prime denotes derivative with respect to x0. Now, Eq. 1 gives Δx = η(0)Δτ, so that averaging with respect to Δx is equivalent to averaging with respect to different realizations of η(0). Using ⟨η(0)⟩ = 0 and ⟨η2(0)⟩ = 2D/Δτ (see Appendix) so that ⟨Δx⟩Δx = 0 and
The above equation, referred to as the backward Fokker-Planck equation, is to be solved subject to two boundary conditions: 1)
On performing inverse Laplace transformation, one readily gets [6].
(For x0 < 0, the corresponding FPT distribution is obtained from the above equation with the replacement x0 → |x0|.) We thus find that the FPT distribution has a tail

FIGURE 4. Two sample trajectories x(t) corresponding to free diffusion (1) with initial condition x(0) = x0 = 3.0, and with D = 0.5. Here, the quantity tf is the first-passage time for the red trajectory.
The Case of Brownian Motion in Presence of Resetting
In order to proceed, define
Indeed, trajectories that did not have any reset during the time interval [0, t] (the probability of which, according to our earlier discussions, is exp( − rt)) give rise to the second term on the rhs of the second equality above. On the other hand, trajectories that at time t have had last reset in the interval [t − τ − dτ, t − τ] (the probability of which is exp( − rτ) rdτ), with τ ∈ [0, t], and have not hit the origin before that give rise to the first term on the rhs of the second equality.
Using Eq. 21 in Eq. 22, taking Laplace transform of both sides, and using Sr(x0, t = 0) = 1, we finally get
where the quantity A is defined as
Here, we have used
We see from Eq. 25 that for fixed x0 and D, the MFPT in presence of resetting is finite for finite r, so that resetting has a drastic consequence on rendering the MFPT of free diffusion finite. Moreover,
which has a unique non-zero solution z⋆ = 1.593 62 …. It then follows that there is an optimal resetting rate r⋆, such that the MFPT in presence of resetting attains its minimum as a function of r. The variation of
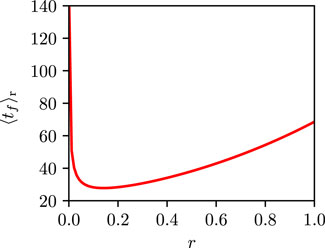
FIGURE 5. The mean first-passage time in presence of resetting given by Eq. (25) is shown as a function of r for x0 = 3.0 and D = 0.5. One may observe the existence of a distinct minimum.
Relevance of Resetting in Search Processes
What has then a minimum MFPT got to do with search processes? Imagine having misplaced one of your favourite or essential belongings. It could be your car key or your mobile phone. After getting into your office, you usually keep the key on your office table. Having misplaced it, a typical tendency to locate it is to begin searching in random directions for the key (well, you do not know beforehand which particular direction to search for, so random directions would be the best bet!) while starting from your office. Having searched unsuccessfully for sometime, you realize that perhaps you did not search well enough in the region around the table (after all, you usually keep the key on the table itself), so you return to the table, and re-initiate your search. You keep repeating the process until you locate the key, and of course the first time you locate it, you stop searching any further. Figure 6 models this search strategy in one dimension: the brown filled circle denotes your misplaced belonging, while searching in random directions for random times followed by re-initiation of the search process from your starting position may be modelled as free diffusion interspersed in time with stochastic resets to the initial location (the two space-time trajectories in the plot), namely, what has been our model of study in this work. Had there been no resets, that is, if you had continued searching in random directions without ever coming back to your initial location, we would arrive at the following conclusion based on our analysis of free diffusion pursued above. If you had repeated the process over and over again, then, in some realizations of the process, you would have located the brown circle in a finite time, while there would be happily a large number of other realizations in which you fail to locate it in finite time, so that the MFPT through the brown circle would diverge ! On the other hand, introducing stochastic resetting into the dynamics would make the MFPT finite, as our theoretical analysis of diffusion with stochastic resetting has revealed. Not just that, there exists an optimal value for the rate r at which stochastic resets are executed such that the corresponding MFPT attains its minimum value. Thus, stochastic resetting offers a very efficient way to locate your misplaced belonging. Of course, for resetting to be efficient, the quantity x0, the initial location of the searcher to which it repeatedly resets, has to be small enough. In other words, the location x0 has to be close enough to the target for resetting to do a good job. Indeed, as is evident from Eq. 25, if x0 is large, the MFPT would be very large, and then resetting would not help to locate the target in a finite time.
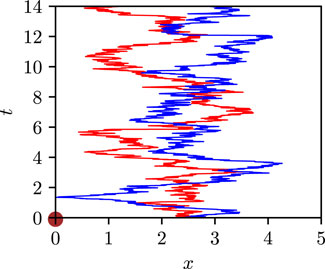
FIGURE 6. The plot shows a stationary target (misplaced belonging) denoted by the brown filled circle and located at the origin, and two space-time trajectories of a particle starting from x0 = 2.5 and executing stochastic resets to x0 at random times. The parameter values are D = 0.5 and r = 0.25. From the figure, we see that one of the trajectories has been able to detect the target, while the other one is yet to locate it.
Stochastic Thermodynamics of Resetting
In this section, we review briefly thermodynamics of systems subject to stochastic resetting, following Refs. [7, 8], and using basic principles extending thermodynamic laws to nonequilibrium systems laid down and reviewed in Ref. [9]. Consider first a Markov process in which the state space instead of being continuous, as in Eq. 1, is discrete. Let us denote the latter by non-zero integers i. The set of all possible states spans the state space of the system. Let N be the total number of states accessible to the system. The dynamics of the system is dictated by a set of transition rates Wi→j ≥ 0 giving the probability per unit time for the system to make a transition from state i to state j. We consider these transition rates to be time-independent. Define pi(t) to be the probability for the system to be in state i at time t, with the normalization
where the first term (respectively, the second term) on the right hand side summarizes all possible ways in which pi(t) increases (respectively, decreases) in an infinitesimal time interval [t, t + dt] due to transitions from all states j to the state i in question (respectively, due to transitions from state i to states j). Note that the Master Eq. 27 conserves in time the normalization of the probability pi(t). Let us note that the Brownian motion (1) may be considered as the continuous-space limit of a discrete-space continuous-time random walker moving with equal probability between the nearest-neighbour sites of a one-dimensional lattice [5]; in the latter case, the state space is constituted by the site indices, and we have Wi→j = Wj→i.
Now, for a given pair of states i and j, consider the following situation [8]: 1) Both the forward and backward transitions are allowed (denote the corresponding transition rates by Wi→j ≡ wi→j > 0 and Wj→i ≡ wj→i > 0). 2) Either the forward or the backward transition is allowed but not both (i.e., either we have Wi→j ≡ yi→j > 0 and Wj→i ≡ yj→i = 0, or, Wj→i ≡ yj→i > 0 and Wi→j ≡ yi→j = 0). The former dynamics is known as the bidirectional process, while the latter is referred to as the unidirectional process [8]. The reason we want to focus on this specific situation is that it models the resetting dynamics considered in this work. Indeed, a given state x(t) can in an infinitesimal time interval [t, t + dt] evolve to any other x value allowed by the dynamics (1), just as any other x value can evolve to the given value x(t) in an infinitesimal time interval [t, t + dt] provided of course the dynamics (1) allows that. On the contrary, the resetting dynamics is such that in an infinitesimal time interval [t, t + dt], any x value can evolve to the value x0, but the reverse move from x0 to any other x value via the resetting dynamics is not allowed (it is allowed only via the Brownian motion dynamics (1)). The Master Eq. 27 then reads [8].
where the summation in the second term on the right hand side is considered restricted to those pair of states for which the reverse transitions are not allowed (i.e., either we have yi→j > 0 and yj→i = 0, or, yj→i > 0 and yi→j = 0).
The (Shannon) entropy of the system at time t is given by (we work in units in which the Boltzmann constant is set to unity):
where pi(t) is to be obtained by solving the Master Eq. 28 subject to a given initial condition
where the dot denotes derivative with respect to time.
Let us for the moment disregard any resetting-like transitions in the system. Eq. 30 then reads
In the above, we have defined
That
In presence of resetting, Eq. 30 then leads to
where we have defined
Here,
In a stationary state, all the quantities
In an equilibrium stationary state, which is obtained in the absence of resetting (see the paragraphs following Eq. 15), one has the condition of detailed balance, wj→i pj = wi→j pi for all pairs of states i and j with time-independent pi’s. Consequently, one has
which is interpreted as the second law of thermodynamics in presence of resetting [7]. Considering the particular example of a discrete-space continuous-time random walker, for which one has wi→j = wj→i, we have
Eq. 36 when generalized to a Markov process with continuous state space reads [7].
For the case r(x) = r, a space-independent resetting rate, the situation we have considered in this work (see Eq. 9), we get
In the nonequilibrium stationary state (14), we get
We thus see explicitly that we have
In closing this section, we indicate how resetting may play a role in optimizing the efficiency of stochastic heat engines. We first describe briefly the principle of working of a stochastic heat engine constituted by a Brownian particle of mass m, which is placed in a fluid medium in equilibrium at a given temperature, thereby modelling a heat bath or a thermal reservoir [13]. For simplicity, let us consider the motion of the particle in one dimension x. The particle is subject to trapping due to an attractive force derived from a time-dependent potential U(x(t); t) and is also acted upon by a time-dependent non-conservative force F(x(t); t). The position x(t) and the velocity v(t) = dx(t)/dt of the particle evolve in time following the underdamped Langevin dynamics:
where γ is the friction coefficient accounting for the friction that the particle experiences while moving in the surrounding medium, while ξ(t) models the random force that the surrounding fluid molecules impart on the particle. One models ξ(t) as a Gaussian, white noise with zero mean and correlations in time given by ⟨ξ(t)ξ(t′)⟩ = 2γTδ(t − t′), where T is the temperature of the fluid medium in units of the Boltzmann constant. Note that in the absence of the potential U(x(t); t) and the non-conservative force F(x(t); t), when one considers the limit of large damping (the limit γ/m → ∞ at a fixed and finite m), the dynamics (44) takes the form of the overdamped Langevin dynamics (1). The dynamics (44) is what is known to physicists as the Brownian motion, while mathematicians prefer to refer to the overdamped dynamics (1) as the Brownian motion.
In using system (44) as a heat engine, one allows the temperature of the surrounding fluid medium to switch between a higher temperature Th and a lower temperature Tc, thus mimicking the hot and the cold thermal reservoir of an engine, respectively. A prominent example of an engine is the well-studied Carnot engine. Specifically, in our setup, considering U to be a harmonic potential, one varies the stiffness of this potential in time from times 0 to t1 to implement the isothermal expansion at temperature Th and from times t1 to t1 + t3 to implement the isothermal compression at temperature Tc of a Carnot cycle, while the adiabatic expansion and compression stages of the latter may be implemented by performing an instantaneous change in the stiffness at time instants t1 and t1 + t3, with concomitant jump in temperature from Th to Tc and from Tc to Th, respectively. Heat transfer takes place between the bath and the particle during the isothermal stages and not during the adiabatic stages. The aforementioned scenario defines a stochastic Carnot heat engine at the micro scale, with reasons of stochasticity being enhanced thermal fluctuations prevalent in the dynamics at such scales [14].
The heat transfer between the heat bath and the particle in time t and computed along the trajectory of the particle from x(0) to x(t) is given by
where ° implies that the integral on the right hand side is to be evaluated in the Stratonovich sense [15]. Similarly, the work done on the particle in time t equals
Note that both the heat and the work are stochastic functions of time that fluctuate between trajectories of the particle. Next, one invokes stochastic definition of efficiency as given by the ratio of the stochastic work extracted in a cycle to the stochastic heat transferred Qh(t) from the hot bath to the particle in a cycle, as
where t denotes the total duration of the cycle. On considering the ratio of average quantities, the corresponding efficiency
Resetting of Scaled and Fractional Brownian Motion
Scaled Brownian Motion
Until now, we have considered standard Brownian motion (1) in discussing the effects of stochastic resetting. We now discuss briefly the corresponding effects on the so-called scaled Brownian motion (SBM) [16, 17], which in appropriate limits reduces to the standard Brownian motion. SBM is used in such contexts as fluorescence recovery following photobleaching [18], anomalous diffusion in biophysics [19, 20], granular gas of viscoelastic particles [21], etc. In contrast to the standard Brownian motion (1) that involves a time-independent diffusion coefficient, the SBM involves a diffusion coefficient that is time dependent and in fact which scales as a power-law in time. Thus, the corresponding dynamics is given by [16].
with η(t) a Gaussian, white noise with properties
here, we have
with Kα a constant. Note that setting α = 1 and K1 = D reduces the SBM to the standard BM (1). In the case of the SBM, the position probability distribution may be shown to have the form [16].
which as expected reduces for α = 1 to the result (7). The MSD for the SBM reads [16].
The behavior of the MSD as a function of time depends explicitly on the value of α. Obviously, α = 1, the case of the standard BM, results in diffusive behavior. For 0 < α < 1, one has a subdiffusive behavior, while the behavior is superdiffusive for α > 1. For α = 2, one has ballistic growth of the MSD in time, and α > 2 results in superballistic behavior. In the limit α → 0, one has logarithmic time dependence of the MSD.
In discussing resetting of the SBM, two separate situations were considered: one in which only the position of the particle resets to its initial value (referred to as nonrenewal resetting [16]), and other in which both the position and the diffusion coefficient reset to their respective initial values (referred to as renewal resetting [17]). Let us discuss the effects of resetting in the two cases. In the case of nonrenewal resetting at exponentially-distributed random times (the set-up of Eq. 9), it was shown that in the long-time limit (more precisely, for times t satisfying
The above equation implies a probability distribution that is non-Gaussian and also time-dependent (unless α = 1), with a cusp at the location of resetting x = x0; For α = 1, the result yields the stationary-state (14) for the standard BM. The MSD in presence of resetting is given in the limit of long times by [16].
We thus see that with respect to the result for the SBM in absence of resetting, Eq. 52, the MSD in presence of resetting has a time dependence characterized by an exponent that is smaller by unity. For α = 1, Eq. 54 yields the stationary-state result (15) for the standard BM. For α = 2, when the SBM in absence of resetting shows ballistic motion, the MSD in presence of resetting exhibits normal diffusive behavior. Superdiffusive SBM corresponding to α in the range 1 < α < 2 exhibits a subdiffusive behavior in presence of resetting. For 0 < α < 1, when the SBM in absence of resetting shows a subdiffusive behavior, Eq. 54 shows that the MSD in presence of resetting decays to zero as a power law, implying thereby that the particle at long times remains in the close vicinity of the resetting location. We thus see that in the case of nonrenewal resetting of the SBM at exponentially-distributed random times, one ends up with a rather rich variety of behavior of the position probability distribution and the MSD depending on the value of α. In the foregoing, we discussed the case of resetting at exponentially-distributed times; for discussion on the effects of resetting at power-law-distributed times, the reader is referred to Ref. [16].
We now turn to the case of renewal resetting of the SBM. In this case, if there is a resetting at time instant tr, the particle resets its position to x0, and also the diffusion constant at a later time t > tr becomes
Not surprisingly, for α = 1, the above equation reproduces correctly the result (14) for the standard BM. Corresponding to the stationary state (55), the MSD attains the value [17].
where Γ(x) is the Gamma function. Again, for α = 1, one gets back the result (15) for the standard BM. On the basis of the above discussions we thus see a drastic difference between the cases of nonrenewal and renewal resetting. While in the former, resetting fails to induce a stationary position distribution, see Eq. 53, it does suffice to induce a stationary distribution in the renewal case, see Eq. 55. Of course, for α = 1, when the diffusion coefficient has no dependence on time, there is no difference between the two cases of resetting, and one has a stationary state. In Ref. [17], the MFPT has been investigated for the case of renewal resetting. Considering a stationary target located at the origin and an SBM starting at x0 > 0 and resetting to x0 at exponentially-distributed random times, the MFPT through the target is given by [17].
For α = 1, one recovers the result (25) for the standard BM. As a function of r, the above MFPT is minimized at r = r⋆ satisfying [17].
The above equation for α = 1 reduces correctly to the result (26) for the standard BM.
Fractional Brownian Motion
We now discuss the case of fractional Brownian motion (FBM), another variant of the standard BM (1). In this case, the dynamics is given by [22, 23].
with ηH(t) a Gaussian noise with zero mean, which unlike the standard BM and the SBM is correlated in time:
where H ∈ (0, 1) is the so-called Hurst exponent. The concept of FBM is invoked in discussions of subdiffusive dynamics [24], in investigating individual trajectories of fluorescently-labelled telomeres in the nucleus of living human cells [25], in discussing passive, thermally driven motion of micron-sized tracers in hydrogels of mucins, the main polymeric component of mucus [26], etc.
In absence of resetting, the MSD of the FBM behaves as
implying thereby normal diffusion for H = 1/2, subdiffusion for 0 < H < 1/2 and superdiffusion for 1/2 < H < 1. Resetting of FBM has been considered under the so-called fully-renewal scheme [27], whereby the memory of noise correlations given in Eq. 60 is completely erased at each resetting, and this is the case we consider here. In presence of exponential resetting, the MSD has the above behavior only for short times, while for times of order (1/r)[Γ(2H + 1)]1/(2H) shows saturation to a plateau (pl) value given by
Comparing the above result with the one for renewal resetting of the SBM at exponentially-distributed times, Eq. 56, we find that the value is the same as that in the SBM case with α = 2H. In the same manner, the FBM with exponential resetting has a stationary state characterized by a time-independent position probability distribution, which at intermediate-to-large displacements is given by the result (55) for the renewal resetting of the SBM, with the substitution α = 2H.
While the definition (61) for the MSD involves averaging at a given time instant t over ensemble of statistically-independent values of x(t), it is interesting to ask for the behavior of the MSD when computed along a single trajectory of x(t) as a function of time t, and enquire about ensemble-averaged versus time-averaged mean-squared displacements whose non-equivalence implies breaking of ergodicity of the underlying dynamics. The single-trajectory-based averaging along the time series of particle position x(t) defines the time-averaged-MSD (TAMSD) as
where Δ is the lag time and T is the length of the time series. On averaging over N statistically-independent TAMSD realizations, the mean TAMSD is obtained as
where the angular brackets denote averaging over noise realizations. Reference [27] performed a detailed study of the behavior of the TAMSD versus MSD to conclude that for short times, one has the MSD and the TAMSD behaving respectively as t2H and Δ2H for 0 < H < 1/2 and as t2H and Δ1 for 1/2 < H < 1, so that time averaging and ensemble averaging do not coincide for 1/2 < H < 1, while they do coincide for 0 < H < 1/2. For long times, however, the two averages coincide for all values of H and have the behavior as in Eq. 62. While the two averages coincide for the FBM in the absence of resetting, the foregoing suggests that the resetting dynamics of originally ergodic FBM for superdiffusive H > 1/2 exhibits weak ergodicity breaking at short times. For a more detailed survey of the topic, the reader is referred to Ref. [27].
Stochastic Resetting: A Bird’s Eye View of Recent Work and Applications
In this section, we provide a flavor of recent work on the theme of stochastic resetting through a random selection of a few articles. For a more exhaustive list, the reader is referred to the review [28]. We will also discuss some applications of the concept of resetting to physical systems.
Reference [29] addressed resetting of a diffusing particle for a space-dependent resetting rate, and resetting to a random position drawn from a resetting distribution, Ref. [30] studied effects of partial absorption on first-passage time problems in the case of diffusion with stochastic resetting, Ref. [31] considered in the setting of first-passage time problems for a diffusive particle with stochastic resetting the issue of optimal search time when compared against that of an effective equilibrium Langevin process with the same stationary distribution, Ref. [32] studied diffusion in arbitrary spatial dimension in presence of a resetting process. Reference [33] studied search process in one dimension by considering an immobile target and a searcher that undergoes a discrete-time jump process with successive jumps drawn independently from an arbitrary jump distribution. In Ref. [34], a simple random walk in one dimension was studied, wherein at each time step the walker resets to the maximum of the already visited positions, Ref. [35] considered a continuous-space and continuous-time diffusion process under resetting to a position chosen from the dynamical trajectory in the past according to a memory kernel, Ref. [36] studied stochastic resetting in the context of the fractional Brownian motion. Quantum dynamics in presence of stochastic reset was addressed in Ref. [37], stochastic resetting in the case of a particle undergoing run and tumble dynamics in one dimension, whereby its velocity reverses stochastically, was studied in Ref. [38], the issue of a stochastic process undergoing resetting in a manner that following each resetting, there a random refractory period during which the process is quiescent and remains at the resetting position was studied in Ref. [39]. Reference [40] considered several lattice random walk models with stochastic resetting to previously visited sites that are shown to exhibit a phase transition between an anomalous diffusive regime and a localization regime in which diffusion is suppressed; The transition is a result of a single impurity site at which the resetting rate is lower than on other sites, and around which the walker spontaneously localizes. Close to criticality, the localization length is shown to diverge with a critical exponent that falls in the same class as the self-consistent theory of Anderson localization of waves in random media. The distribution of additive functions of Brownian motion subject to stochastic resets was investigated in Ref. [41], while the well-known Ising model with stochastic resetting was addressed in Ref. [42]. Reference [43] is an experimental exploration of the optimal mean time for a free diffusing Brownian particle to reach a target in presence of resetting, while Ref. [44] analysed the non-equilibrium steady states and first-passage properties attained with a Brownian particle in an external confining potential that is switched on and off stochastically, and Ref. [45] computed the mean perimeter and the mean area of the convex hull of a two-dimensional isotropic Brownian motion in the presence of resetting.
Reference [46] studied the stationary state attained with a Brownian particle diffusing in an arbitrary potential and subject to stochastic resetting, Ref. [47] considered a Brownian particle diffusing in presence of time-dependent stochastic resetting, whereby the rate of resetting is a function of the time elapsed since the last reset event, Ref. [48] is devoted to developing a general approach to treat theoretically first passage under stochastic resetting, while its extension to also include branching was considered in Ref. [49]. Reference [50] investigated the dynamics of a Brownian particle diffusing in a one-dimensional interval with absorbing end points, Ref. [51] studied local time for a Brownian particle in presence of stochastic resetting: Given a Brownian trajectory, the local time is the time the trajectory spends in a vicinity of its initial position. A Landau-like theory to study phase transitions in resetting systems was developed in Ref. [52], while stochastic resetting in the context of the many-particle system of symmetric exclusion process was studied in Ref. [53]. Reference [54] considered diffusion with stochastic resetting in which the diffusing particle resets to the resetting location with a finite speed. Reference [55] took into account the fact that getting from place to place takes time, with places further away taking more time to be reached, in extending the theory of stochastic resetting to account for this inherent spatio-temporal coupling, while Ref. [56] reported on experimental realization of colloidal particle undergoing diffusion and resetting via holographic optical tweezers, Ref. [57] proposed a method of resetting in the context of a Brownian particle, whereby non-instantaneous returns are facilitated by an external confining trap potential centered at the resetting location. Reference [58] studied stochastic resetting in the context of the time that it takes to reach a stable equilibrium point in the basin of attraction of a dynamical system. Reference [59] studied an overdamped Brownian particle subject to stochastic resetting in one dimension in which the particle undergoes a finite-time resetting process facilitated by an external linear potential, while Ref. [60] investigated first-passage properties in the context of one-dimensional confined lattice random walks.
Reference [61] studied the case of stochastic search process in one, two, and three dimensions in which N diffusing searchers that all start at the same location search, with each searcher also resetting to its starting point, Refs. [62, 63] considered first-passage resetting, whereby the resetting of a random walk to a fixed position gets triggered by the first-passage event of the walk itself. Reference [64] studied the dynamics of predator-prey systems, whereby preys are confined to a region of space and predators move randomly according to a power-law dispersal kernel, and additionally, there is stochastic resetting of the predators to the prey patch, while the dynamics of random walks on arbitrary networks with stochastic resetting to the initial position was analysed in Ref. [65], and the case of resetting to multiple nodes was considered in Ref. [66]. Reference [67] investigated the effects of resetting on the reaction time between a Brownian particle and a stochastically-gated target. Reference [68] studied stochastic multiplicative process with reset events, Ref. [69] analyses large deviations of a ratio observable in discrete-time reset processes. where the ratio has the form of a current divided by the number of reset steps, Ref. [70] studied diffusive motion in presence of stochastic resetting of a test particle in a two-dimensional comb structure consisting of a main backbone channel with continuously-distributed side branches, Ref. [71] considered the Brownian motion with stochastic resetting of a particle in a bounded circular two-dimensional domain while searching for a stationary target on the boundary of the domain, Ref. [72] studied resetting in the context of the Sisyphus random walk, an infinite Markov chain whose dynamics is such that at every clock tick, the process can move rightward (or upward) one step or return to the initial state. A unified renewal approach to the problem of random search for several targets under resetting was developed in Ref. [73], while Ref. [74] considered a generalization of the basic set-up of stochastic resetting to the origin by a diffusing particle, whereby the diffusing particle may be only partially reset towards the trajectory origin or even overshoot the origin in a resetting step. Reference [75] studied stochastic resetting in the framework of the monotonic continuous-time random walks with a constant drift. In Ref. [76], for stochastic resetting of a random-walk process, a general perspective through derivation and analysis of mesoscopic (continuous-time random walk) equations for both jump and velocity models with stochastic resetting was offered. Reference [77] explored within the context of resetting the possibility of observing an interesting dynamics, including phase transitions for the minimization of the MFPT, for random walks with exponentially-distributed flights of constant speed, Ref. [78] studied the effects of a stochastic resetting within the ambit of the exactly solvable one-dimensional coagulation-diffusion process, Ref. [79] studied the effects of resetting on random processes that follow the so-called telegrapher’s equation. Reference [80] explored first-passage properties resulting from an interplay of stochastic resetting with trapping due to an external potential, in the framework of a diffusing particle in a one-dimensional trapping potential, while Ref. [81] studied how active transport processes in living cells can be modelled by using the framework of a directed search process with stochastic resetting and delays.
The concept of stochastic resetting has been invoked over the years in many different fields, from biology and ecology to computer science and psychology, to name a few. Resetting finds applications in discussing search algorithms in computer science, e.g., in discussing return to shallow points in a search tree by backtracking methods [82], and in addressing randomized search algorithms for hard combinatorial problems [83]; in the field of psychology, e.g., to discuss pattern learning and recognition [84], and to optimize visual search [85]; in the field of quantitative finance, e.g., in discussing reset options whereby the strike price of the option is reset periodically over the option’s lifetime, to bring out-of-the-money options back to being at the money [86], and in deriving a valuation equation for a European-style bear market warrant with a single reset date [87]; in biology, e.g., in considerations of a stochastic biophysical model for the motion of RNA polymerases during transcriptional pauses [88], and in the context of protein searching and recognition of targets on DNA [89]; in ecology, e.g., in addressing relocation of animals to already visited places [90], and in movement ecology [91].
Summary and Conclusion
Diffusion with stochastic resetting has been extensively studied in recent times, and Ref. [2] is considered a landmark contribution in recent times in the arena of nonequilibrium statistical physics, which has really ushered in a new beginning in studies of stochastic processes. While ours is a very brief review, with the contributions of one of the authors of the current article being Refs. [4, 92–95], we refer the reader to the recent exhaustive review [28] to get a broader view of this exciting topic of research. We hope that the current contribution will serve as an invitation to young minds to delve into the fascinating and exciting world of stochastic processes in general and stochastic resetting in particular.
Author Contributions
All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.
Funding
SG acknowledges support from the Science and Engineering Research Board (SERB), Government of India under SERB-TARE Scheme Grant No. TAR/2018/000023, SERB-MATRICS Scheme Grant No. MTR/2019/000560, and SERB-CRG Scheme Grant No. CRG/2020/000596.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Acknowledgments
SG thanks M. Chase, A. Gambassi, L. Giuggioli, S. N. Majumdar, A. Nagar, É. Roldán, G. Schehr, and G. Tucci for fruitful collaborations and insightful discussions on the topic of stochastic resetting. SG thanks Debraj Das, Sayan Roy and Mrinal Sarkar for comments on the manuscript and for help with figures. SG also thanks ICTP-Abdus Salam International Centre for Theoretical Physics, Trieste, Italy, for support under its Regular Associateship scheme.
References
2. Evans MR, Majumdar SN. Diffusion with Stochastic Resetting. Phys Rev Lett (2011) 106:160601–11606014. doi:10.1103/PhysRevLett.106.160601
3. Giuggioli L, Gupta S, Chase M. Comparison of Two Models of Tethered Motion. J Phys A: Math Theor (2019) 52:075001–-23. doi:10.1088/1751-8121/aaf8cc
4. Nagar A, Gupta S. Diffusion with Stochastic Resetting at Power-Law Times. Phys Rev E (2016) 93:060102-1–060102-5. doi:10.1103/PhysRevE.93.060102
5. Bertin E. Statistical Physics of Complex Systems: A Concise Introduction. Berlin: Springer (2016).
6. Majumdar SN. Universal First-Passage Properties of Discrete-Time Random Walks and Lévy Flights on a Line: Statistics of the Global Maximum and Records. Physica A: Stat Mech its Appl (2010) 389:4299–316. doi:10.1016/j.physa.2010.01.021
7. Fuchs J, Goldt S, Seifert U. Stochastic Thermodynamics of Resetting. EPL (2016) 113:60009–1600096. doi:10.1209/0295-5075/113/60009
8. Busiello DM, Gupta D, Maritan A. Entropy Production in Systems with Unidirectional Transitions. Phys Rev Res (2020) 2:023011–102301115. doi:10.1103/PhysRevResearch.2.023011
9. Seifert U. Stochastic Thermodynamics, Fluctuation Theorems and Molecular Machines. Rep Prog Phys (2012) 75:126001–112600158. doi:10.1088/0034-4885/75/12/126001
10. Pal A, Rahav S. Integral Fluctuation Theorems for Stochastic Resetting Systems. Phys Rev E (2017) 96:062135–106213511. doi:10.1103/PhysRevE.96.062135
11. Gupta D, Plata CA, Pal A. Work Fluctuations and Jarzynski equality in Stochastic Resetting. Phys Rev Lett (2020) 124:110608–11106087. doi:10.1103/PhysRevLett.124.110608
12. Pal A, Reuveni S, Rahav S. Thermodynamic Uncertainty Relation for Systems with Unidirectional Transitions. Phys Rev Res (2021) 3:013273-1–013273-15. doi:10.1103/PhysRevResearch.3.013273
13. Martínez IA, Roldán É, Dinis L, Rica RA. Colloidal Heat Engines: A Review. Soft Matter (2017) 13:22–36. doi:10.1039/C6SM00923A
14. Schmiedl T, Seifert U. Efficiency at Maximum Power: An Analytically Solvable Model for Stochastic Heat Engines. Europhys Lett (2007) 81:20003–-6. doi:10.1209/0295-5075/81/20003
16. Bodrova AS, Chechkin AV, Sokolov IM. Nonrenewal Resetting of Scaled Brownian Motion. Phys Rev E (2019) 100:012119-1–012119-0. doi:10.1103/PhysRevE.100.012119
17. Bodrova AS, Chechkin AV, Sokolov IM. Scaled Brownian Motion with Renewal Resetting. Phys Rev E (2019) 100:012120-1–012119-3. doi:10.1103/PhysRevE.100.012120
18. Saxton MJ. Anomalous Subdiffusion in Fluorescence Photobleaching Recovery: A Monte Carlo Study. Biophysical J (2001) 81:2226–40. doi:10.1016/S0006-3495(01)75870-5
19. Novikov DS, Fieremans E, Jensen JH, Helpern JA. Random Walks with Barriers. Nat Phys (2011) 7:508–14. doi:10.1038/nphys1936
20. Novikov DS, Jensen JH, Helpern JA, Fieremans E. Revealing Mesoscopic Structural Universality with Diffusion. Proc Natl Acad Sci (2014) 111:5088–93. doi:10.1073/pnas.1316944111
21. Bodrova A, Chechkin AV, Cherstvy AG, Metzler R. Quantifying Non-ergodic Dynamics of Force-free Granular Gases. Phys Chem Chem Phys (2015) 17:21791–8. doi:10.1039/C5CP02824H
22. Mandelbrot B. Une classe processus stochastiques homothétiques à soi; application à la loi climatologique. H E Hurst C R Acad Sci Paris (1965) 260:3274–7.
23. Jeon J-H, Metzler R. Fractional Brownian Motion and Motion Governed by the Fractional Langevin Equation in Confined Geometries. Phys Rev E (2010) 81:021103-1–021103-11. doi:10.1103/PhysRevE.81.021103
24. Magdziarz M, Weron A, Burnecki K, Klafter J. Fractional Brownian Motion versus the Continuous-Time Random Walk: A Simple Test for Subdiffusive Dynamics. Phys Rev Lett (2009) 103:180602–-4. doi:10.1103/PhysRevLett.92.17810110.1103/PhysRevLett.103.180602
25. Burnecki K, Kepten E, Janczura J, Bronshtein I, Garini Y, Weron A. Universal Algorithm for Identification of Fractional Brownian Motion. A Case of Telomere Subdiffusion. Biophysical J (2012) 103:1839–47. doi:10.1016/j.bpj.2012.09.040
26. Cherstvy AG, Thapa S, Wagner CE, Metzler R. Non-Gaussian, Non-ergodic, and Non-fickian Diffusion of Tracers in Mucin Hydrogels. Soft Matter (2019) 15:2526–51. doi:10.1039/C8SM02096E
27. Wang W, Cherstvy AG, Kantz H, Metzler R, Sokolov IM. Time Averaging and Emerging Nonergodicity upon Resetting of Fractional Brownian Motion and Heterogeneous Diffusion Processes. Phys Rev E (2021) 104:024105-1–024105-27. doi:10.1103/PhysRevE.104.024105
28. Evans MR, Majumdar SN, Schehr G. Stochastic Resetting and Applications. J Phys A: Math Theor (2020) 53:193001–-67. doi:10.1088/1751-8121/ab7cfe
29. Evans MR, Majumdar SN. Diffusion with Optimal Resetting. J Phys A: Math Theor (2011) 44:435001–-15. doi:10.1088/1751-8113/44/43/435001
30. Whitehouse J, Evans MR, Majumdar SN. Effect of Partial Absorption on Diffusion with Resetting. Phys Rev E (2013) 87:022118-1–022118-7. doi:10.1103/PhysRevE.87.022118
31. Evans MR, Majumdar SN, Mallick K. Optimal Diffusive Search: Nonequilibrium Resetting versus Equilibrium Dynamics. J Phys A: Math Theor (2013) 46:185001–118500113. doi:10.1088/1751-8113/46/18/185001
32. Evans MR, Majumdar SN. Diffusion with Resetting in Arbitrary Spatial Dimension. J Phys A: Math Theor (2014) 47:285001–-19. doi:10.1088/1751-8113/47/28/285001
33. Kusmierz L, Majumdar SN, Sabhapandit S, Schehr G. First Order Transition for the Optimal Search Time of Lévy Flights with Resetting. Phys Rev Lett (2014) 113:220602-1–220602-5. doi:10.1103/PhysRevLett.113.220602
34. Majumdar SN, Sabhapandit S, Schehr G. Random Walk with Random Resetting to the Maximum Position. Phys Rev E (2015) 92:052126-1–052126-13. doi:10.1103/PhysRevE.92.052126
35. Boyer D, Evans MR, Majumdar SN. Long Time Scaling Behaviour for Diffusion with Resetting and Memory. J Stat Mech (2017) 2017:023208–18. doi:10.1088/1742-5468/aa58b6
36. Majumdar SN, Oshanin G. Spectral Content of Fractional Brownian Motion with Stochastic Reset. J Phys A: Math Theor (2018) 51:435001–-11. doi:10.1088/1751-8121/aadef0
37. Mukherjee B, Sengupta K, Majumdar SN. Quantum Dynamics with Stochastic Reset. Phys Rev B (2018) 98:104309-1–104309-14. doi:10.1103/PhysRevB.98.104309
38. Evans MR, Majumdar SN. Run and Tumble Particle under Resetting: a Renewal Approach. J Phys A: Math Theor (2018) 51:475003–-18. doi:10.1088/1751-8121/aae74e
39. Evans MR, Majumdar SN. Effects of Refractory Period on Stochastic Resetting. J Phys A: Math Theor (2019) 52:01LT01–01LT01-15. doi:10.1088/1751-8121/aaf080
40. Boyer D, Falcón-Cortés A, Giuggioli L, Majumdar SN. Anderson-like Localization Transition of Random Walks with Resetting. J Stat Mech (2019) 2019:053204–27. doi:10.1088/1742-5468/ab16c2
41. den Hollander F, Majumdar SN, Meylahn JM, Touchette H. Properties of Additive Functionals of Brownian Motion with Resetting. J Phys A: Math Theor (2019) 52:175001–-23. doi:10.1088/1751-8121/ab0efd
42. Magoni M, Majumdar SN, Schehr G. Ising Model with Stochastic Resetting. Phys Rev Res (2020) 2:033182-1–033182-9. doi:10.1103/PhysRevResearch.2.033182
43. Besga B, Bovon A, Petrosyan A, Majumdar SN, Ciliberto S. Optimal Mean First-Passage Time for a Brownian Searcher Subjected to Resetting: Experimental and Theoretical Results. Phys Rev Res (2020) 2–032029-1032029-5. doi:10.1103/PhysRevResearch.2.032029
44. Mercado-Vásquez G, Boyer D, Majumdar SN, Schehr G. Intermittent Resetting Potentials. J Stat Mech (2020) 2020:113203–27. doi:10.1088/1742-5468/abc1d9
45. Majumdar SN, Mori F, Schawe H, Schehr G. Mean Perimeter and Area of the Convex hull of a Planar Brownian Motion in the Presence of Resetting. Phys Rev E (2021) 103:022135-1–022135-11. doi:10.1103/PhysRevE.103.022135
46. Pal A. Diffusion in a Potential Landscape with Stochastic Resetting. Phys Rev E (2015) 91:012113-1–012113-7. doi:10.1103/PhysRevE.91.012113
47. Pal A, Kundu A, Evans MR. Diffusion under Time-dependent Resetting. J Phys A: Math Theor (2016) 49:225001–122500119. doi:10.1088/1751-8113/49/22/225001
48. Pal A, Reuveni S. First Passage under Restart. Phys Rev Lett (2017) 118:030603-1–030603-6. doi:10.1103/PhysRevLett.118.030603
49. Pal A, Eliazar I, Reuveni S. First Passage under Restart with Branching. Phys Rev Lett (2019) 122:020602-1–020602-7. doi:10.1103/PhysRevLett.122.020602
50. Pal A, Prasad VV. First Passage under Stochastic Resetting in an Interval. Phys Rev E (2019) 99:032123-1–032123-11. doi:10.1103/PhysRevE.99.032123
51. Pal A, Chatterjee R, Reuveni S, Kundu A. Local Time of Diffusion with Stochastic Resetting. J Phys A: Math Theor (2019) 52:264002–-31. doi:10.1088/1751-8121/ab2069
52. Pal A, Prasad VV. Landau-like Expansion for Phase Transitions in Stochastic Resetting. Phys Rev Res (2019) 1:032001-1–032001-6. doi:10.1103/PhysRevResearch.1.032001
53. Basu U, Kundu A, Pal A. Symmetric Exclusion Process under Stochastic Resetting. Phys Rev E (2019) 100:032136-6-14–0321. doi:10.1103/PhysRevE.100.032136
54. Pal A, Kuśmierz Ł, Reuveni S. Time-dependent Density of Diffusion with Stochastic Resetting Is Invariant to Return Speed. Phys Rev E (2019) 100:040101-1101-6–040. doi:10.1103/PhysRevE.100.040101
55. Pal A, Kuśmierz Ł, Reuveni S. Invariants of Motion with Stochastic Resetting and Space-Time Coupled Returns. New J Phys (2019) 21:113024–-12. doi:10.1088/1367-2630/ab5201
56. Tal-Friedman O, Pal A, Sekhon A, Reuveni S, Roichman Y. Experimental Realization of Diffusion with Stochastic Resetting. J Phys Chem Lett (2020) 11:7350–5. doi:10.1021/acs.jpclett.0c02122
57. Gupta D, Plata CA, Kundu A, Pal A. Stochastic Resetting with Stochastic Returns Using External Trap. J Phys A: Math Theor (2020) 54:025003–-22. doi:10.1088/1751-8121/abcf0b
58. Ray A, Pal A, Ghosh D, Dana SK, Hens C. Mitigating Long Transient Time in Deterministic Systems by Resetting. Chaos (2021) 31:011103–-7. doi:10.1063/5.0038374
59. Gupta D, Pal A, Kundu A. Resetting with Stochastic Return through Linear Confining Potential. J Stat Mech (2021) 2021:043202–33. doi:10.1088/1742-5468/abefdf
60. Bonomo OL, Pal A. First Passage under Restart for Discrete Space and Time: Application to One-Dimensional Confined Lattice Random Walks. Phys Rev E (2021) 103:052129-1–052129-14. doi:10.1103/PhysRevE.103.052129
61. Bhat U, De Bacco C, Redner S. Stochastic Search with Poisson and Deterministic Resetting. J Stat Mech (2016) 2016:083401–25. doi:10.1088/1742-5468/2016/08/083401
62. De Bruyne B, Randon-Furling J, Redner S. Optimization in First-Passage Resetting. Phys Rev Lett (2020) 125:050602-1–050602-5. doi:10.1103/PhysRevLett.125.050602
63. De Bruyne B, Randon-Furling J, Redner S. Optimization and Growth in First-Passage Resetting. J Stat Mech (2021) 2021:013203–33. doi:10.1088/1742-5468/abcd33
64. Mercado-Vásquez G, Boyer D. Lotka-Volterra Systems with Stochastic Resetting. J Phys A: Math Theor (2018) 51:405601–-17. doi:10.1088/1751-8121/aadbc0
65. Riascos AP, Boyer D, Herringer P, Mateos JL. Random Walks on Networks with Stochastic Resetting. Phys Rev E (2020) 101:062147-1–062147-12. doi:10.1103/PhysRevE.101.062147
66. Riascos AP, Boyer D, Herringer P, Mateos JL. Random Walks on Networks with Stochastic Resetting. Phys Rev E (2020) 101:062126-1–062126-16. doi:10.1103/PhysRevE.101.062147
67. Mercado-Vásquez G, Boyer D. Search of Stochastically Gated Targets with Diffusive Particles under Resetting. J Phys A: Math Theor (2021) 54:444002–-17. doi:10.1088/1751-8121/ac27e5
68. Manrubia SC, Zanette DH. Stochastic Multiplicative Processes with Reset Events. Phys Rev E (1999) 59:4945–8. doi:10.1103/PhysRevE.59.4945
69. Coghi F, Harris RJ. A Large Deviation Perspective on Ratio Observables in Reset Processes: Robustness of Rate Functions. J Stat Phys (2020) 179:131–54. doi:10.1007/s10955-020-02513-3
70. Singh RK, Sandev T, Iomin A, Metzler R. Backbone Diffusion and First-Passage Dynamics in a Comb Structure with Confining Branches under Stochastic Resetting. J Phys A: Math Theor (2021) 54:404006–-21. doi:10.1088/1751-8121/ac20ed
71. Chatterjee A, Christou C, Schadschneider A. Diffusion with Resetting inside a circle. Phys Rev E (2018) 97:062106-1–062106-10. doi:10.1103/PhysRevE.97.062106
72. Montero M, Villarroel J. Directed Random Walk with Random Restarts: The Sisyphus Random Walk. Phys Rev E (2016) 94:032132-1–032132-10. doi:10.1103/PhysRevE.94.032132
73. Chechkin A, Sokolov IM. Random Search with Resetting: A Unified Renewal Approach. Phys Rev Lett (2018) 121:050601-1–050601-5. doi:10.1103/PhysRevLett.121.050601
74. Dahlenburg M, Chechkin AV, Schumer R, Metzler R. Stochastic Resetting by a Random Amplitude. Phys Rev E (2021) 103:052123-1–052123-2. doi:10.1103/PhysRevE.103.052123
75. Montero M, Villarroel J. Monotonic Continuous-Time Random Walks with Drift and Stochastic Reset Events. Phys Rev E (2013) 87:012116-1–012116-4. doi:10.1103/PhysRevE.87.012116
76. Méndez V, Campos D. Characterization of Stationary States in Random Walks with Stochastic Resetting. Phys Rev E (2016) 93:022106-1–022106-7. doi:10.1103/PhysRevE.93.022106
77. Campos D, Méndez V. Phase Transitions in Optimal Search Times: How Random Walkers Should Combine Resetting and Flight Scales. Phys Rev E (2015) 92:062115-1–062115-8. doi:10.1103/PhysRevE.92.062115
78. Durang X, Henkel M, Park H. The Statistical Mechanics of the Coagulation-Diffusion Process with a Stochastic Reset. J Phys A: Math Theor (2014) 47:045002–-17. doi:10.1088/1751-8113/47/4/045002
79. Masoliver J. Telegraphic Processes with Stochastic Resetting. Phys Rev E (2019) 99:012121-1–012121-12. doi:10.1103/PhysRevE.99.012121
80. Ahmad S, Nayak I, Bansal A, Nandi A, Das D. First Passage of a Particle in a Potential under Stochastic Resetting: A Vanishing Transition of Optimal Resetting Rate. Phys Rev E (2019) 99:022130-1–022130-8. doi:10.1103/PhysRevE.99.022130
81. Bressloff PC. Modeling Active Cellular Transport as a Directed Search Process with Stochastic Resetting and Delays. J Phys A: Math Theor (2020) 53:355001–-27. doi:10.1088/1751-8121/ab9fb7
83. Montanari A, Zecchina R. Optimizing Searches via Rare Events. Phys Rev Lett (2002) 88:178701-1–178701-4. doi:10.1103/PhysRevLett.88.178701
84. Noton D, Stark L. Scanpaths in Saccadic Eye Movements while Viewing and Recognizing Patterns. Vis Res (1971) 11:929–IN8. doi:10.1016/0042-6989(71)90213-6
86. Cheng W-Y, Zhang S. The Analytics of Reset Options. Jod (2000) 8:59–71. doi:10.3905/jod.2000.319114
87. Gray SF, Whaley RE. Valuing S&P 500 Bear Market Warrants with a Periodic Reset. Jod (1997) 5:99–106. doi:10.3905/jod.1997.407987
88. Roldán É, Lisica A, Sánchez-Taltavull D, Grill SW. Stochastic Resetting in Backtrack Recovery by RNA Polymerases. Phys Rev E (2016) 93:062411-1–062411-0. doi:10.1103/PhysRevE.93.062411
89. Cherstvy AG, Kolomeisky AB, Kornyshev AA. Protein−DNA Interactions: Reaching and Recognizing the Targets. J Phys Chem B (2008) 112:4741–50. doi:10.1021/jp076432e
90. Boyer D, Solis-Salas C. Random Walks with Preferential Relocations to Places Visited in the Past and Their Application to Biology. Phys Rev Lett (2014) 112:240601-1–240601-5. doi:10.1103/PhysRevLett.112.240601
91. Kenkre VM, Giuggioli L. Theory of the Spread of Epidemics and Movement Ecology of Animals. Cambridge: Cambridge University Press (2021).
92. Gupta S, Majumdar SN, Schehr G. Fluctuating Interfaces Subject to Stochastic Resetting. Phys Rev Lett (2014) 112:220601-1–220601-5. doi:10.1103/PhysRevLett.112.220601
93. Gupta S, Nagar A. Resetting of Fluctuating Interfaces at Power-Law Times. J Phys A: Math Theor (2016) 49:445001–-13. doi:10.1088/1751-8113/49/44/445001
94. Roldán É, Gupta S. Path-integral Formalism for Stochastic Resetting: Exactly Solved Examples and Shortcuts to Confinement. Phys Rev E (2017) 96:022130-1–022130-13. doi:10.1103/PhysRevE.96.022130
95. Tucci G, Gambassi A, Gupta S, Roldán É. Controlling Particle Currents with Evaporation and Resetting from an Interval. Phys Rev Res (2020) 2:043138-1–043138-24. doi:10.1103/PhysRevResearch.2.043138
Appendix: Discretization of Gaussian, White Noise
Here, we discuss discrete-time representation of the noise η(t) appearing in Eq. 1. To this end, we discretize time in small steps of length 0 < Δt ≪ 1, so that the ith time step is ti = iΔt, with
Then, in the limit Δt → 0, identifying
From the definition of the Dirac delta function, one has
On the basis of the above, we may write using Eq. 2 the following properties for the noise in discrete times:
with the understanding that the discrete-time representation of η(t) is ηi ≡ η(ti). In particular, we have ⟨η(0)⟩ = 0 and ⟨η2(0)⟩ = 2D/Δt, the properties we use in the main text preceding Eq. 19.
Keywords: stochastic processes, stochastic resetting, fokker-planck equation, stationary state, first-passage time
Citation: Gupta S and Jayannavar AM (2022) Stochastic Resetting: A (Very) Brief Review. Front. Phys. 10:789097. doi: 10.3389/fphy.2022.789097
Received: 04 October 2021; Accepted: 07 February 2022;
Published: 14 April 2022.
Edited by:
Reinaldo García García, Universidad de Navarra, SpainReviewed by:
Andrey Cherstvy, University of Potsdam, GermanyRainer Klages, Queen Mary University of London, United Kingdom
Copyright © 2022 Gupta and Jayannavar. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Shamik Gupta, c2hhbWlrZzFAZ21haWwuY29t
†Deceased
 Shamik Gupta
Shamik Gupta Arun M. Jayannavar3†
Arun M. Jayannavar3†