Analysis on Spatial Variability of SRM Based on Real-Time CT and the DIC Method Under Uniaxial Loading

Soil and rock mixture (SRM) consists of high-strength rock blocks and small-grained soils, which depend seriously on the rock size and the heterogeneity of structure. Because of inhomogeneous cementation between rock blocks, complex granulometric composition, and random distribution of rock blocks, these SRMs usually cause problems. Investigation of the localized deformation is critical for successful engineering designs, engineering safety assessment. In this work, uniaxial compression testing on the SRM with a rock block percentage of 40% (mass ratio) is performed under real-time computed tomography (CT) combined with digital image correlation (DIC) technology. Based on radial strain fields and shear fields, heterogeneity of strain fields and rock block motion is analyzed quantitatively by semi-variance. The results show that rock block is the main factor controlling the shear band geometry distribution. A localization strain band usually occurs along the soil and rock interfaces. From the experimental results by the DIC method, the damage factor is presented to describe the damage evolution of the SRM under uniaxial compression. The method proposed in this study can be used to quantitatively analyze the deformation characteristics of the SRM sample.

Introduction

Soil and rock mixture (SRM) is an extremely heterogeneous geomaterial, consisting of high-strength rock blocks and small-grained soils [1, 2]. Due to a wide distribution in the nature, the SRM is one of the most commonly encountered geomaterials in tunneling, slope engineering, and dam. However, because of inhomogeneity and discontinuity between rock blocks, complex granulometric composition, and random distribution of rock blocks, these SRMs usually cause problems [3, 4]. Therefore, how to define deformation and failure of the SRM is an important requirement for successful engineering designs, engineering safety assessment, and design of related engineering projects [2].

Many researchers have studied the mechanical properties and failure mechanism of the SRM from different points of view by using experimental and numerical methods, including meso-structural characteristics (block size, position, content, shape etc.) [3, 5–7], strength parameters [8–11], and shear strength [9, 12, 13]. Despite the fact that these research efforts used to obtain the macro-mechanical responses of the SRM, it is difficult to thoroughly reveal the meso-scale mechanical properties of the SRM. For example, the characteristics of the rock block size, shape, breakage, and morphology give rise to mesoscopic heterogeneity, but these factors are hard to separate. Mesoscopic evaluation is important for understanding many factors, significantly influencing the apparent strength of the SRM. In recent years, attempts have been made to study the inhomogeneous geomaterial by computed tomography (CT) [1, 14–17]. The 3D pattern of the sample was obtained in real-time by CT. 3D reconstruction techniques can intuitively show the spatial failure process of samples. The rock texture and internal structure and the fracture progressive process of the soil–rock mixture can be traced and analyzed nondestructively by multiple scans during testing. A serious of studies have employed CT to study the failure mechanism, such as the fracturing behavior (including area, volume, and fractal) [14, 15, 18], strength behavior [16, 19–21], and pore structure [1, 10, 18, 22]. Zhao et.al proposed a local threshold segmentation algorithm to describe the crack characteristics into five stages [23]. Zhou et.al separated the crack and pore structures to study the crack characteristics and the failure process based on CT slices [18]. It was found that cracks usually first appear on certain parts of the soil and rock block interfaces where the shear stress is prone to accumulate. CT slices, CT values, porosity, or the fracture mechanism is used to reveal the multi-scale deformation of samples. However, the method of CT is not commonly used in the SRM. Therefore, the mechanism on how to analyze and predict the mechanical behavior is critical for SRM samples.

Digital image correlation (DIC) technology is one of full-field non-contact digital image-based deformation measurement techniques, which could accurately measure the two-dimensional (2D) or three-dimensional (3D) displacements. This technology has been applied to the strain measurement of composites [24–26]. Fracture mechanisms, including displacement discontinuities, shear band characteristics and crack interfaces, are also analyzed by the DIC technology [27–30]. Zhou et al. studied crack types, real-time cracking behaviors, and mechanical properties by X-ray CT and DIC techniques in which five cracking stages were divided [31]. Bésuelle et al. used high resolution, fast X-ray micro tomography (synchrotron radiation) to evaluate the onset and evolution of strain localization in Callovo-Oxfordian argillite under deviatoric loading and focused on the ductile behavior at higher confining stress [32]. Tang et al. analyzed the progressive failure process of rocks under different confining pressures by the DIC method [33]. Based on the difference in the strain inside and outside the strain localization zone, they believed that as the confining pressure increases, the start-up phase of rock strain localization is delayed. It can be found that using the DIC method relatively large strains developed in the rock can be captured successfully, and spatial and temporal failure evolution can be detected and mapped.

As discussed previously, many researchers have explored the macro-mechanical responses of the SRM by physical tests. However, due to the effects of rock block sizes, rock block shape, cementation, and structural features, the deformation of the SRM is difficult revealed from the mesoscopic level. Based on the X-Ray technique, the structure and fracture distribution of samples can be reconstructed from the transverse CT slices. Unfortunately, real-time scanning under loading is not among the most common experiments at the laboratory scale. In our experiment, a real-time scanning system was conducted for the SRM with a rock block percentage of 40%. By image binarization, the size and distribution of the rock block was built. A series of displacement fields and strain fields can be directly obtained by the DIC technology. The strain localization distribution and progress of SRM under loading was first obtained in laboratory experimentation at the laboratory scale. In addition, semi-variance is adopted to qualitatively and quantitatively assess strain characteristics and rock motion under different stress strengths. The method proposed in this study is a new and effective approach for studying the deformation of the SRM.

Experiment and Methodology

Real-Time CT Under Uniaxial Loading Experiment

In this study, SRM specimens (cylindrical shape) with 40% rock block content were prepared. The diameter of the rock block is less than 6 mm and randomly distributed in the sample. The water content of the SRM is 9%. The size of the SRM sample was 50 mm in diameter and 100 mm in height. A 450 KV real-time CT in Institute Geology and Geophysics, Chinese Academy of Science is used in this study (as shown in Figure 1A). The loading device can rotate with the rotary table while scanning, which can avoid the disturbance, namely, the loading system and CT imaging system are working synchronously (real-time CT).

FIGURE 1

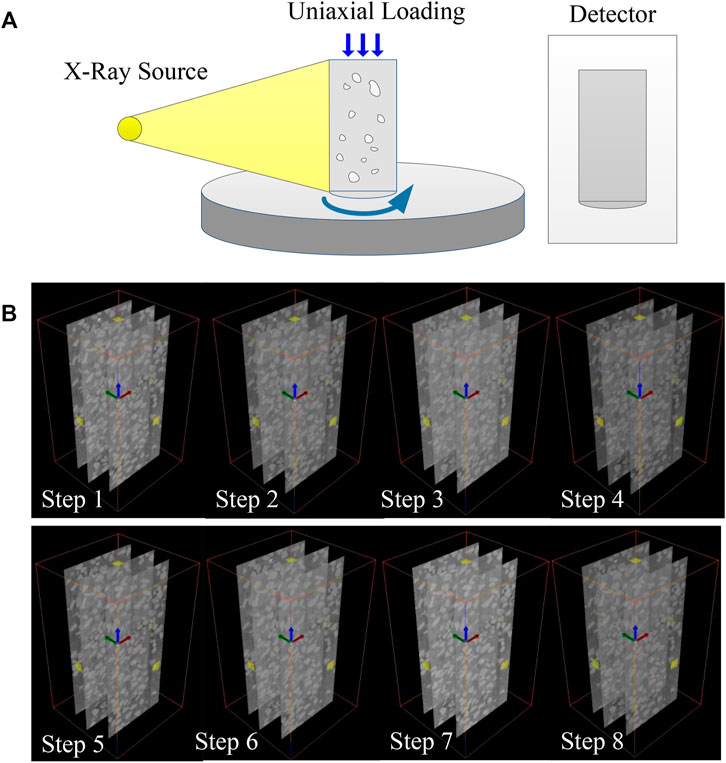
FIGURE 1. (A) Schematic diagram of the experimental setup. (B) 3D CT data of the SRM under different stress strengths.

The scanning step was 0.4°. A total of 900 projection data can be obtained, and 700 CT slices can be reconstructed for every CT scan. The CT slice is a bitmap with a size of 2048 × 2048 pixels. A pixel approximately represents 0.129 mm in size (as shown in Figure 1B).

Segmentation of Rock Blocks

The essence of CT imaging is attenuation coefficient imaging, which is bound up with the density of the sample. The density of the soil and rock, which composes the SRM, is quite different. Then, the components of the SRM have different distributions in the grayscale image, as shown in Figure 2, which is a selected vertical slice of the 3D sample images. The images obtained from 450 KV-CT were processed using the DIC technology. In this study, multi-threshold segmentation is used to determine the threshold for rocks, soil, and background, which involves a sequence of processes. In the first step, the grayscale image volume is “binarized” so that the SRM could be separated from the background. Binarization resulted in images in which voxels within the SRM have values of 1 and those without the SRM space have values of “nan” (“nan” means nothing). This is achieved by setting a global threshold value for the grayscale tomography images, in which voxels having values greater than this threshold would be recognized as the “SRM”. The next step is to separate the soil in the binary result into individual parts, which is referred to as “segmentation”. However, this method cannot obtain a satisfactory result due to the connected rocks. This is because voxels, which contains both rocks and soil, would be blurred (the partial-volume effect) and identified as rocks. Thus, for such areas, the threshold value is determined by trial and error so that reasonable binary images were obtained. The majority of rocks preserve the morphological features of original rocks reasonably well. Figure 2C shows the segmented rocks and soils within the sample in step 2, which are used for the following analysis.

FIGURE 2

FIGURE 2. Images of separating the rock block and soil from the vertical slices in the SRM. (A) SRM vertical CT slice. (B) Gray distribution. (C) Segmentation images of the rock (left) and soil (right), respectively.

Digital Image Correlation

The principle of DIC is based on the comparison of a reference image with a current image at subsequent deformed steps (shown in Figure 3). Reference images are the vertical CT slices in step 1. The current images are the vertical CT slices at each subsequent deformed step (refers to CT slices collected at scanning points 2–7). The displacement fields and strain fields can be obtained by searching the maximum value of image correlation in a sequence of CT slices captured at different loading levels. For example, there are two vertical CT slices in the same position of the sample. Based on the correlation searching, the point P is corresponding to a unique point P₁ (see Figure 3). With the loading consisting, the subsequent slices are regarded as the deformed images. Then, the displacement increment of these slices can be determined. The displacement and strain fields were obtained by comparing the initial state with the deformed states in DIC software [34].

FIGURE 3

FIGURE 3. Schematic diagram of the principle of the DIC method.

Real-time CT uniaxial compression was conducted on the SRM sample, and the axial strain was measured by using an extensometer during loading. The loading conditions at each step for the specimen are shown in Figure 4A. Eight stages of slices of samples are recorded by CT. The DIC method combined with X-ray tomography has been used in this study to obtain the series of strain fields in different stress strengths. After loading, CT slices are used to calculate the displacements and strains by the DIC technology. Then, six displacements were obtained by the comparison of a reference slice (step 1) and the subsequence slices (step 2 to step 7). Gradients of displacement at some local region were obviously larger than other areas; such behavior can be better demonstrated by strain fields. The strains can be obtained by equal (1), (2), and (3) at different stress levels

${\epsilon }_{xx}\left(k\right)=\frac{1}{2}\left(2\frac{\partial u_k}{\partial x}+{\left(\frac{\partial u_k}{\partial x}\right)}^2+{\left(\frac{\partial v_k}{\partial x}\right)}^2\right),(1)$

${\epsilon }_{yy}\left(k\right)=\frac{1}{2}\left(2\frac{\partial v_k}{\partial y}+{\left(\frac{\partial u_k}{\partial y}\right)}^2+{\left(\frac{\partial v_k}{\partial y}\right)}^2\right),(2)$

${\epsilon }_{xy}\left(k\right)=\frac{1}{2}\left(\frac{\partial u_k}{\partial y}+\frac{\partial v_k}{\partial x}+\frac{\partial u_k}{\partial y}\frac{\partial u_k}{\partial x}+\frac{\partial v_k}{\partial x}\frac{\partial v_k}{\partial y}\right),(3)$

where u and v indicate the displacement field along the x axis and y axis, respectively. The subscript “k” represents different scanning points: k = 2,3,4,5,6, 7. Then, the displacements were converted to three strain fields (normal strain field ɛ_xx, ɛ_yy along the x axis and y axis, respectively, and shear strain field ɛ_xy). The radial strain field in different scanning steps is shown in Figure 4B. Deformation evolution involving localization changes in the SRM is indirectly probed by the fracture progressive process from those CT images. Owing to the interaction between the rock blocks and the soil matrix, shear and tensile damage co-exist during deformation. It is difficult to observe such changes by the gray value method.

FIGURE 4

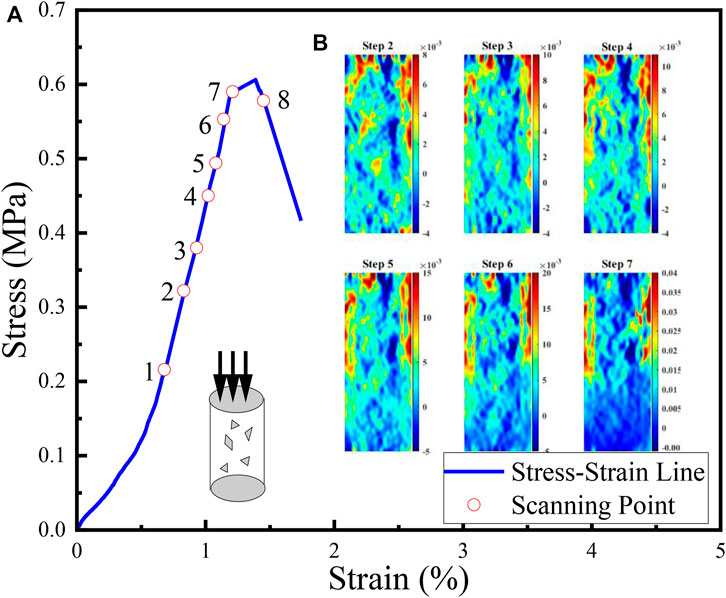
FIGURE 4. (A) Stress–strain curves for the SRM; (B) Radial deformation of the SRM under seven stress strengths (steps 2–7, respectively).

Semi-variance

Semi-variance is used to measure the spatial variation of the regionalized variable from a determined distance (h), which depends on the distance between the points. The plot of the semi-variances enables estimation of the variance for combinations of different pairs of points (shown in Figure 5). Sill (C₀+C), range (A), and nugget effect (C₀) are three main features in the semi-variance. Sill (C₀+C) is the ordinate value that the semi-variance levels off. The most important parameter is range (A), which is the abscissa value at which the semi-variance reaches the sill. A larger range represents a larger variability. The semi-variance at h = 0 is called the nugget variance, that is, the intercept. A nonzero nugget means variability at scales smaller than the smallest between the point distances. The structural ratio C/(C₀+C) is used to reflect the heterogeneity of the SRM under loading. A ratio of <25% indicated strong spatial dependence, between 25 and 75% indicated moderate spatial dependence, and >75% indicated weak spatial dependence [35]. Spatial variability of strain fields under different stress strengths was characterized from semi-variance modeling. Generally speaking, the larger the structural ratio is, the lower is the heterogeneity of the SRM . The semi-variance function is as follows:

$\gamma \left(h_i\right)=\frac{1}{2n\left(h_i\right)}{\displaystyle \sum _{i=1}^{n\left(h_i\right)}{\left(X\left(z_i\right)-X\left(z_i+h_i\right)\right)}^2},(4)$

where the experimental semi-variance at distance h, n(h) is the number of sampling pairs at distance h. X(z_i) and X(z_i+h_i) are the values regionalized variable at the location of z_i and z_i+h_i.

FIGURE 5

FIGURE 5. Schematic curve of semi-variance.

Result

Fitted Semi-variance Models of Strain Fields

Spatial variability of strains is an important behavior in the localization process of the SRM sample. During loading, rock block rotation, meso-structural adjustment, and strain localization occur simultaneously. With loading increase, strain bands continue to propagate in the soil matrix by passing the rock blocks, and multiple tortuous strain bands appear throughout the specimen eventually. To quantify localization behavior in the SRM, spatial variability of strain fields is investigated using semi-variances (including Range (a) and the ratio of the nugget to total semi-variance C/(C₀ + C)), expressed as a percentage, and is used to analyze progressive deformation (shown in Table 1). The strain fields in this section are fitted by the spherical model (shown in the Eq. 5).

$\gamma \left(h\right)=\{\begin{array}{l}0h=0\\ C_0+C\left[\frac{3}{2}\frac{h}{a}-\frac{1}{2}{\left(\frac{h}{a}\right)}^3\right]0<h\le a\\ C_0+Ch>a\end{array}(5)$

where a is the range, C₀ is the nugget effect, and C₀+C is the sill. The result is shown in Table 1. In Table 1, the parameters R₂ and RSS are used to measure the quality of the fitting results. The larger the R₂, the smaller the RSS is and the better the model fits. The resultant γ(h) of the strain fields in Table 1 shows which is approximated by the spherical model. From step 2 to step 4, the value of C/(C₀ + C) is larger than 0.75. Radial strain bands in these times expand discretely, and deformation has weak spatial dependence. The deformation of the SRM is the soil matrix deformation and disorderly rotation of rock blocks. In step 5, C/(C₀ + C) is decreased to less than 0.75. The radial strain bands gather to form some concentrated bands. As shown in Figure 2B, in the radial strain field, two parallel strain bands are formed on both sides of the sample. The localized bands propagated and coalesced in the soil matrix, and then, the main deformation plane formed. In step 7, the range increases dramatically, and C/(C₀ + C) is still less than 0.75, which means that a large number of macro cracks are generated. Due to the fact that the cracks’ width is less than the CT detection accuracy, these cracks are not detected in CT slices. The result can be shown that semi-variance can effectively and quantitatively describe the deformation process of the SRM sample.

TABLE 1

TABLE 1. Spatial variability of strain fields under different stress strengths.

Heterogeneity of Rock Block Motion

The development of the shear path in the SRM sample under different stress strengths is shown in Figure 6 (Black line). The shear bands expand along the interfacial transition zone between the rock and soil matrix, which indicates that the rock blocks are important for formation of the localization strain band. At last, as illustrated in Figure 6F, the shear paths gather to form some concentrated shear bands. The macro-mechanical responses of the SRM depend on the interaction of rock blocks in the mesoscopic level, and rotation is exactly one of the important influences on their interaction. Figure 6 shows the evolution of rock block rotation in the loading process for the SRM. Colors are used to show rotation in the direction of each rock block, and a different color shows the rotation value in the clockwise direction. As can be seen from Figure 6A, the motion of the rock block first occurred disorderly. With the increase of stress strength, the motion directions of rock blocks rotate gradually along the direction of shear bands. It can be seen that the movement of rock blocks becomes severe with the increase of axial deformation. In particular, at the top of the sample, rotation of rock blocks is much more serious than at other parts of the sample. In the shear band, the rock blocks show large rotation in their directions compared with other particles. Because of the effect of the rock blocks, stronger force chains might have formed between those blocks, which may have strongly controlled the distribution of the internal contact force. In step 7, the motion of rock blocks is more dramatically compared with previous steps. In order to quantify the rotation of the rock in the spatial structure, this section uses a semi-heterogeneous function to quantify the rotation of the rock block. The spherical model is also used to fit the rotation of the rock block. The result is shown in Table 2. From step 2 to step 6, the value of C/(C₀ + C) is less than 0.75, which indicates that the rotation of rock blocks has moderate spatial dependence. Soil deformation and localization shear bands lead to the rock block rotation. The value of range (a) decreases dramatically, which means the rock block contact as a cluster and macro-cracks is generated. At this moment, stress strength is near the peak strength, and a main shear band is formed. The result implies that the rock block is the main factor controlling the strain band geometry distribution and the associated deformation of the SRM.

FIGURE 6

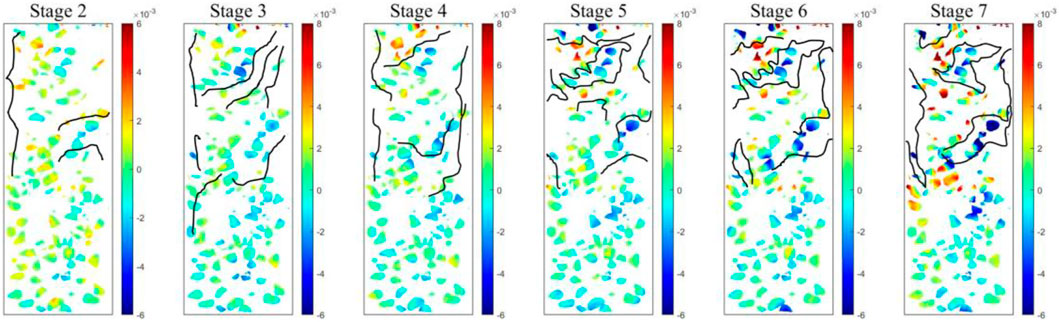
FIGURE 6. Shear strain in rock block under different stress strengths; shear bands are represented by black lines. (A) is the Stage 2, and (B–F) are the Stage 3–7, respectively.

TABLE 2

TABLE 2. Spatial variability of rock block rotation under different stress strengths.

Equal-Strain Fields

In previous studies, DIC has been used to evaluate the deformation and damage evolution processes in rocks [36–39]. However, these research studies are concentrated on external damage evolution. The objective of this method is to classify the onset and evolution of internal damage in the SRM. The cracks in the experiment can be classified as two types: original cracks (closing without loading) and new cracks (unclosing without loading). At a peak ratio of 53.67% (step 2), the strain band has appeared and approximately uniform distribution, with no obvious strain concentration zone, and original cracks are distributed in the sample. At a peak ratio of 75% (step 4), the dilatation behavior becomes severe. It means that the Poisson effect of the sample is obvious. The original cracks tend to connect, new cracks occur, and the SRM shows instability. At a peak ratio of 98.33% (step 7), two local strain concentration zones are clearly observed in the normal strain along the radial axis, which indicates the damage increased drastically.

Due to the appearance of crack and damage, the definitions of a strain [Equal (1), (2) and (3)] are no longer held true. Herein, the strain would be understood as the equivalent one, which has been used to investigate the evolution of damage [40]. The equivalent strain notion is as follows:

${\epsilon }_{eq}=\sqrt{{\displaystyle \sum _{i=1}^2{\epsilon }_i^2}},(6)$

where ɛ₁ and ɛ₂ denote the maximum principal strain and minimum principal strain, respectively.

The spatiotemporal internal damage evolution is quantitatively characterized based on the equivalent strain ɛ_eq (shown in Figure 7A–G). The magnitude of the equivalent strain is indicated by the color range. It can be found that the magnitude of ɛ_eq in the damage area is larger than other areas. The equivalent strain zone appears in the upper part of the specimen at the early step. With load increasing, it can be noted that the equivalent strain concentration zones gradually change to the upper left part and the upper right part of the SRM. The strain bands at the damage zone are along the axial direction. The concentration of the equivalent strains indicates the nucleation of macro-cracks. The strain zone distribution is almost the same as the macro-crack distribution (Figure 7G). The internal damage evolution can reflect the macroscopic failure pattern of the SRM.

FIGURE 7

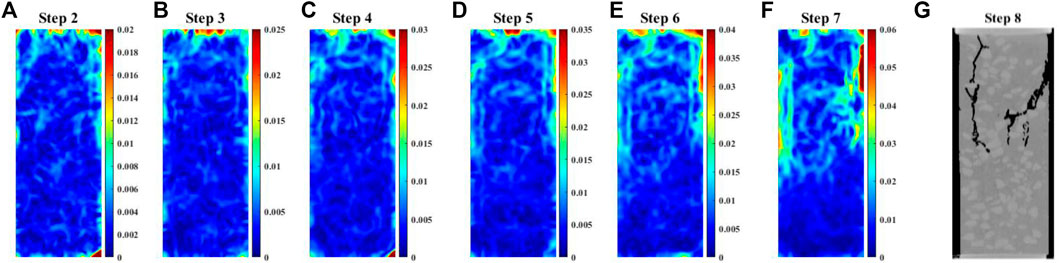
FIGURE 7. Equivalent strain filed. (A–F) Equivalent strain filed of the SRM under different stress levels. (G) Macro-crack distribution in the CT vertical slice.

The magnitude of ɛ_eq at damage regions or crack surfaces is significantly larger than that at the other regions; we will try to characterize the damage level in the sample in terms of ɛ_eq. Hao et al. [41] and Song et al. [37] analyzed the evolution of a non-uniform strain field based on fluctuation of strains. Here, we consider the damage evolution in this experiment is relevant to the equivalent strain, and the damage factor D is defined to describe the damage evolution.

$STD\_eq\left(k\right)=\sqrt{\frac{{\displaystyle \sum _{i=1,j=1}^N{\left({\epsilon }_{\text{eq}}\left(k\right)-\overline{{\epsilon }_{eq}}\right)}^2}}{N-1}},k=\mathrm{3,4,5,6,7,8}(7)$

$D\left(k\right)=STD\_eq\left(k\right)/\max \left\{STD\_eq\left(k\right)\right\},(8)$

where $\overline{{\epsilon }_{eq}}$ is the mean value of ${\epsilon }_{\text{eq}}$, k represents different steps, and max is the maximum value of the STD_eq(k) [42]. Then, the damage factor according to Eq. 7 can be calculated (Figure 8).

FIGURE 8

FIGURE 8. Volume strain curve and damage factor.

Based on the result of the stress–strain curve of the SRM and the aforementioned strain evolution characteristics, damage evolution can be divided into the initiation step, accumulation step, and acceleration step. The volume damage factor is increasing dramatically at the axial strain of 0.93% (step 3), which is the volume-expansion point. The Poisson effect under uniaxial compression is obvious in this experiment. Before this step, the few damages of the SRM first occur at the top section. The meso-physical mechanism of the volume expansion of the SRM means multiple new cracks are generated quickly. It means that the damage is accumulated at this time. The curve of the damage factor D accelerates apparently at the axial strain of 1.14% (step 6), which represents that plastic deformation happens. The strain localization becomes discontinuous due to the rock distribution. Due to the size and shape of rock blocks, the strain is propagated more tortuous and discontinuous. As Figure 7 shows, two macroscopic strain concentration bands are clearly observed in the left-up part and the right-up part of the specimen, respectively. Furthermore, the specimen shows both shear and tension failure modes, which results in the formation of macro-cracks. Then, the main failure plane formed along the strain localization bands. From these results, it was determined that tension failure causes damage, and shear failure causes failure in the SRM.

Conclusion

The objective of this work was to observe and quantify the onset and evolution of internal deformation processes in the SRM sample under uniaxial compression. The main element of the proposed approach is combining the state-of-the-art in situ X-ray tomography imaging with the DIC method. This makes it possible to assess the evolving strain field characteristic throughout loading. While X-ray imaging has been in the past applied to study the SRM deformation, the combination of these two methods to study the deformation evolution and shear formation is the first novel aspect of this work. Moreover, a deformation factor has been developed that shows the characteristic of the SRM. The following conclusions are acquired:

1. A proper method combined the digital image correlation, and in situ loading is an effective method to quantitatively study the strain characteristics of the SRM sample. During sample loading, strain bands and rock blocks are indirectly visible from strain fields. The localized strain band usually starts to appear at the soil and rock interfaces.

2. The semi-variance model analysis of the strain fields well characterizes the rock block motion. A number of indexes [range A, nugget C/(C₀ + C)] is allowed quantitatively to identify some essential properties of the strain propagation and rock motion. It is found that the rock block is the main factor controlling the strain band geometry distribution and the associated deformation of the SRM. Semi-variance can be used to quantitatively analyze the heterogeneity of the SRM.

3. From the experimental results by the DIC method, the damage factor is presented to describe the damage evolution of the SRM under uniaxial compression. The analyzing stress–strain curve can be divided into the stable damage evolution step, the damage accumulation step, and the damage acceleration step.

Data Availability Statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author Contributions

YW, LZ, and XL conceived and designed the experiments. YW and TM performed the experiments. YW and ML developed the dynamical model. YW, TM, and JZ collected and analyzed the data. YW and JZ analyzed the data. YW, LZ, and ML wrote the manuscript. All authors contributed to the manuscript and approved the submitted version.

Funding

This work was supported by the National Natural Science Foundation of China (Grants Nos. 42002279, 42090023, 41972287, and 11801398).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Li C-S, Zhang D, Du S-S, Shi B. Computed Tomography Based Numerical Simulation for Triaxial Test of Soil-Rock Mixture. Comput Geotechnics (2016) 73:179–88. doi:10.1016/j.compgeo.2015.12.005

CrossRef Full Text | Google Scholar

2. Jin L, Zeng Y, Xia L, Ye Y. Experimental and Numerical Investigation of Mechanical Behaviors of Cemented Soil-Rock Mixture. Geotech Geol Eng (2016) 35(1):337–54. doi:10.1007/s10706-016-0109-4

CrossRef Full Text | Google Scholar

3. Xu W-J, Wang S, Zhang H-Y, Zhang Z-L. Discrete Element Modelling of a Soil-Rock Mixture Used in an Embankment Dam. Int J Rock Mech Mining Sci (2016) 86:141–56. doi:10.1016/j.ijrmms.2016.04.004

CrossRef Full Text | Google Scholar

4. Wang S, Ji T, Xue Q, Shen Z, Zhang Q. Deformation and Failure Characteristics of Soil-Rock Mixture Considering Material Composition and Random Structure. Adv Mater Sci Eng (2019) 2019:1–13. doi:10.1155/2019/3165096

CrossRef Full Text | Google Scholar

5. Xu W, Hu R, Tan R, Zeng R, Yu H, et al. Study on Field Test of Rock-Soil Aggregate on Right Banl of Longpan in Tiger-Leaping Gorge Area. Chin J Rock Mech Eng (2006) 25(6).

Google Scholar

6. Li X, Liao QL, He JM. In-situ Tests and a Stochastic Structural Model of Rock and Soil Aggregate in the Three Gorges Reservoir Area, china. Int J Rock Mech Min (2004) 41. doi:10.1016/j.ijrmms.2003.12.030

CrossRef Full Text | Google Scholar

7. Afifipour M, Moarefvand P. Mechanical Behavior of Bimrocks Having High Rock Block Proportion. Int J Rock Mech Mining Sci (2014) 65:40–8. doi:10.1016/j.ijrmms.2013.11.008

CrossRef Full Text | Google Scholar

8. Avşar E. Contribution of Fractal Dimension Theory into the Uniaxial Compressive Strength Prediction of a Volcanic Welded Bimrock. B Eng Geol Environ (2020) 79(7):3605–19.

Google Scholar

9. Coli N, Berry P, Boldini D. In Situ non-conventional Shear Tests for the Mechanical Characterisation of a Bimrock. Int J Rock Mech Mining Sci (2011) 48(1):95–102. doi:10.1016/j.ijrmms.2010.09.012

CrossRef Full Text | Google Scholar

10. Krakowska P, Puskarczyk E, Jędrychowski M, Habrat M, Madejski P, Dohnalik M. Innovative Characterization of Tight Sandstones from Paleozoic Basins in Poland Using X-ray Computed Tomography Supported by Nuclear Magnetic Resonance and Mercury Porosimetry. J Pet Sci Eng (2018) 166:389–405. doi:10.1016/j.petrol.2018.03.052

CrossRef Full Text | Google Scholar

11. Zhang P, Li Q. Evaluation of Rock Size on the Mechanical Behavior and Deformation Performance of Soil-Rock Mixture: a Meso-Scale Numerical and Theoretical Study. Arab J Geosci (2021) 14(15). doi:10.1007/s12517-021-07854-1

CrossRef Full Text | Google Scholar

12. Verma R, Sharma PK, Pandey V. Study of Shear Strength Behaviour of Soil- Rock Mixture. Int J Eng Sci (2016) 5(8).

Google Scholar

13. Vallejo LE, Mawby R. Porosity Influence on the Shear Strength of Granular Material-clay Mixtures. Eng Geology (2000) 58(2):125–36. doi:10.1016/s0013-7952(00)00051-x

CrossRef Full Text | Google Scholar

14. Sun XK, Li X, Zheng B. Study on the Progressive Fracturing in Soil and Rock Mixture under Uniaxial Compression Conditions by CT Scanning. Eng Geol (2020) 279. doi:10.1016/j.enggeo.2020.105884

CrossRef Full Text | Google Scholar

15. Wang Y, Li CH, Hu YZ. 3D Image Visualization of Meso-Structural Changes in a Bimsoil under Uniaxial Compression Using X-ray Computed Tomography (CT). Eng Geology (2019) 248:61–9. doi:10.1016/j.enggeo.2018.11.004

CrossRef Full Text | Google Scholar

16. Meng HJ, Wang Y, Ren JY. In Situ X-Ray Computed Tomography (CT) Investigation on Localized Deformation and Crack Damage Evolution in a Bimrock by Tracking Rock Blocks. Adv Civil Eng (2020) 2020:1–14. doi:10.1155/2020/8851817

CrossRef Full Text | Google Scholar

17. Cnudde V, Masschaele B, Dierick M, Vlassenbroeck J, Hoorebeke LV, Jacobs P. Recent Progress in X-ray CT as a Geosciences Tool. Appl Geochem (2006) 21(5):826–32. doi:10.1016/j.apgeochem.2006.02.010

CrossRef Full Text | Google Scholar

18. Zhou X-P, Zhao Z, Li Z. Cracking Behaviors and Hydraulic Properties Evaluation Based on Fractural Microstructure Models in Geomaterials. Int J Rock Mech Mining Sci (2020) 130. doi:10.1016/j.ijrmms.2020.104304

CrossRef Full Text | Google Scholar

19. Duan Y, Li X, Zheng B, He J, Hao J. Cracking Evolution and Failure Characteristics of Longmaxi Shale under Uniaxial Compression Using Real-Time Computed Tomography Scanning. Rock Mech Rock Eng (2019) 52:3003–15. doi:10.1007/s00603-019-01765-0

CrossRef Full Text | Google Scholar

20. Yang S-Q, Yin P-F, Huang Y-H, Cheng J-L. Strength, Deformability and X-ray Micro-CT Observations of Transversely Isotropic Composite Rock under Different Confining Pressures. Eng Fracture Mech (2019) 214:1–20. doi:10.1016/j.engfracmech.2019.04.030

CrossRef Full Text | Google Scholar

21. Zhao Z, Zhou XP. Rapid Uniaxial Compressive Strength Assessment by Microstructural Properties Using X-ray CT Imaging and Virtual Experiments (2021).

Google Scholar

22. Munawar MJ, Lin C, Cnudde V. Petrographic Characterization to Build an Accurate Rock Model Using micro-CT: Case Study on Low-Permeable to Tight Turbidite sandstone from Eocene Shahejie Formation (2018). p. S0968432817304778.

Google Scholar

23. Zhao Z, Zhou X-P. Establishment of Numerical Cracking Constitutive Models Using 3D Reconstruction and X-ray CT Images of Geomaterials. Int J Mech Sci (2020) 183. doi:10.1016/j.ijmecsci.2020.105814

CrossRef Full Text | Google Scholar

24. Arai Y, Sakata S. Microscopic Full Field Strain Measurement of Unidirectionally Fiber Reinforced Plastics with the Kriging-Digital Image Correlation and Region Splitting Method. Compos Struct (2021) 260. doi:10.1016/j.compstruct.2020.113513

CrossRef Full Text | Google Scholar

25. Canal LP, González C, Molina-Aldareguía JM, Segurado J, LLorca J. Application of Digital Image Correlation at the Microscale in Fiber-Reinforced Composites. Composites A: Appl Sci Manufacturing (2012) 43(10):1630–8. doi:10.1016/j.compositesa.2011.07.014

CrossRef Full Text | Google Scholar

26. Mehdikhani M, Aravand M, Sabuncuoglu B, Callens MG, Lomov SV, Gorbatikh L. Full-field Strain Measurements at the Micro-scale in Fiber-Reinforced Composites Using Digital Image Correlation. Compos Structures (2016) 140(apr):192–201. doi:10.1016/j.compstruct.2015.12.020

CrossRef Full Text | Google Scholar

27. Dong W, Wu Z, Zhou X, Wang N, Kastiukas G. An Experimental Study on Crack Propagation at Rock-concrete Interface Using Digital Image Correlation Technique. Eng Fracture Mech (2017) 171:50–63. doi:10.1016/j.engfracmech.2016.12.003

CrossRef Full Text | Google Scholar

28. Munoz H, Taheri A, Chanda E. Pre-Peak and Post-Peak Rock Strain Characteristics during Uniaxial Compression by 3D Digital Image Correlation. Rock Mech Rock Eng (2016) 49(7). doi:10.1007/s00603-016-0935-y

CrossRef Full Text | Google Scholar

29. Nguyen TL, Hall SA, Vacher P. Fracture Mechanisms in Soft Rock: Identification and Quantification of Evolving Displacement Discontinuities by Extended Digital Image Correlation. Tectonophysics (2011) 503(1-2):117–28. doi:10.1016/j.tecto.2010.09.024

CrossRef Full Text | Google Scholar

30. Lenoir N, Bornert M, Desrues J, Bésuelle P, Viggiani G. Volumetric Digital Image Correlation Applied to X-ray Microtomography Images from Triaxial Compression Tests on Argillaceous Rock. Strain (2007) 43(3):193–205. doi:10.1111/j.1475-1305.2007.00348.x

CrossRef Full Text | Google Scholar

31. Zhou XP, Zhao Z, Liu Y. Digital Spatial Cracking Behaviors of fine‐grained sandstone with Precracks under Uniaxial Compression. Int J Numer Anal Methods Geomech (2020) 44(13):1770–87. doi:10.1002/nag.3088

CrossRef Full Text | Google Scholar

32. Bésuelle P, Viggiani G, Lenoir N. X-ray Micro CT for Studying Strain Localization in Clay Rocks under Triaxial Compression (2006).

Google Scholar

33. Tang Y, Okubo S, Xu J, Peng S. Progressive Failure Behaviors and Crack Evolution of Rocks under Triaxial Compression by 3D Digital Image Correlation. Eng Geology (2019) 249:172–85. doi:10.1016/j.enggeo.2018.12.026

CrossRef Full Text | Google Scholar

34. Blaber J, Adair B, Antoniou A. Ncorr: Open-Source 2D Digital Image Correlation Matlab Software. Exp Mech (2015) 55(6):1105–22. doi:10.1007/s11340-015-0009-1

CrossRef Full Text | Google Scholar

35. Usowicz B, Lipiec J. Spatial Variability of Saturated Hydraulic Conductivity and its Links with Other Soil Properties at the Regional Scale. Sci Rep (2021) 11(1):8293. doi:10.1038/s41598-021-86862-3

PubMed Abstract | CrossRef Full Text | Google Scholar

36. Li S, Chen X, Guo S. Evaluation of Fracture Process Zone in the Flexural Response of Different Concrete Materials Using DIC Method. Ksce J Civ Eng (2020) 24(8):2435–48. doi:10.1007/s12205-020-0255-3

CrossRef Full Text | Google Scholar

37. Song H, Zhang H, Fu D, Kang Y, Huang G, Qu C, et al. Experimental Study on Damage Evolution of Rock under Uniform and Concentrated Loading Conditions Using Digital Image Correlation. Fatigue Fract Engng Mater Struct (2013) 36(8):760–8. doi:10.1111/ffe.12043

CrossRef Full Text | Google Scholar

38. Munoz H, Taheri A, Chanda EK. Pre-Peak and Post-Peak Rock Strain Characteristics during Uniaxial Compression by 3D Digital Image Correlation. Rock Mech Rock Eng (2016) 49(7):2541–54. doi:10.1007/s00603-016-0935-y

CrossRef Full Text | Google Scholar

39. Kramarov V, Parrikar PN, Mokhtari M. Evaluation of Fracture Toughness of Sandstone and Shale Using Digital Image Correlation. Rock Mech Rock Eng (2020) 53(9):4231–50. doi:10.1007/s00603-020-02171-7

CrossRef Full Text | Google Scholar

40. Marars J. A Description of Micro and Macroscale Damage of concrete Structures. Eng Fract Mech (1986) 25(5-6):729–37.

Google Scholar

41. Hao SW, Wang HY, Xia MF, Ke FJ, Bai YL. Relationship between Strain Localization and Catastrophic Rupture. Theor Appl Fracture Mech (2007) 48(1):41–9. doi:10.1016/j.tafmec.2007.04.006

CrossRef Full Text | Google Scholar

42. Wu Y, Tahmasebi P, Lin C, Zahid MA, Dong C, Golab AN, et al. A Comprehensive Study on Geometric, Topological and Fractal Characterizations of Pore Systems in Low-Permeability Reservoirs Based on SEM, MICP, NMR, and X-ray CT Experiments. Mar Pet Geology (2019) 103:12–28. doi:10.1016/j.marpetgeo.2019.02.003

CrossRef Full Text | Google Scholar