- School of Physics and Optoelectronics, South China University of Technology, Guangzhou, China
Many experimental observations have shown remarkably large or even giant spectral splitting in strongly-coupled micro/nanocavity-atom systems. Popularly, such a spectral splitting has been attributed to the Rabi splitting, a pure quantum mechanical effect. However, there are disputes regarding whether the spectral splitting caused by multiple emitters, such as excitons in J-aggregate of molecules, is a pure quantum effect or also contributed by classical optical effect. In this work, we address this difficult problem by building a model physical system of a practical Fabry-Perot high-Q optical microcavity involving Lorentz-dispersion atoms. Very interestingly, by performing evaluation and estimate upon several strongly-coupled cavity-atom systems, we have found that the classical optical splitting and quantum Rabi splitting can be in the same order of magnitude. Our studies clearly indicate that the phenomenon of “giant Rabi splitting” that has been extensively observed in many experiments can also be caused by classic optical effects in addition to quantum mechanical effect. In some cases, the contribution by classic optical effects may be comparable to or even exceeding the contribution from quantum effects. We expect that this work can constructing the true and complete physics picture underlying strong light-matter interaction in a micro/nanocavity system.
Introduction
Strong coupling of quantum emitter with cavity is important for a wide range of application and studies, such as quantum cryptography [17], quantum information processing [25], nano-optical circuits [29], single-photon switch [31], and single-atom laser [19]. Rabi oscillation, a natural phenomenon where the energy travels back and forth between single photon and a two-level quantum emitter, happens frequently in the realm of strong coupling [9], which induces Rabi splitting in the spectra of quantum emitter in high quality factor (high-Q) cavity [33]. The concepts (energy level, single photon) and treatment (dress state) involved in Rabi oscillation and Rabi splitting in cavity quantum electrodynamics stem from quantum mechanics, so Rabi splitting is a spectral splitting produced by quantum effects. Although the classical and the quantum treatments are identical results in some phenomena, there is not classical treatments in other phenomena such as Rabi splitting. For example, different dissipation has different predominant splitting types Sometimes the classical spectral splitting (absorption, transmission, reflectivity) is dominant, sometimes the quantum splitting (photoluminescence, Rabi splitting) is dominant. We should not believe that any type of the splitting has more physical importance that the others. They refer to different experiments [26]. It is more convincing to observe Rabi splitting with a single atom due to quantum effect [1, 11, 30]. However, it is difficult to fix such a tiny atom in the cavity. Even if human can trap single atom by an artful “relatively stationary” scheme, the coupling coefficient
Strong coupling between light and quantum emitter requires to satisfy the condition
A large number of scholars are committed to realizing strong coupling in high performance cavity to observe Rabi splitting. In 1992, the first realization of Rabi splitting on semiconductor was reported based on quantum wells as the emitters [36]. Nonetheless, there is controversy over whether or not it truly steps into the strong coupling regime [10, 11]. On the other hand, quantum dots, possessing discrete sates, becomes an excellent quantum emitter for realization of strong coupling [8], because their dipole moment
To increase the coupling coefficient
Although previous studies have demonstrated an extinct spectral splitting in the strong coupling regime with ingenious technology, most of them refer to the spectral splitting induced by multiple molecules as vacuum Rabi splitting, which implies that the effect of collective molecules interacting with photons is attributed to pure quantum mechanics. However, splitting resonance state splittings are not by themselves necessary signatures of anything truly quantum, for instance, two coupled classical oscillators also demonstrate strong coupling and a single resonance state is split into two resonance states [28]. Moreover, it was shown in 1990s that classical effects could produce spectral splitting [26, 40]. Limited by the experimental conditions at that time, there was no experiment of putting the J aggregates into the plasmon cavity to observe the “giant Rabi splitting”. The experiment used a single emitter such as atom and quantum well, so there is no doubt that the splitting could be a Rabi splitting. Nowadays, the J aggregates contain multiple emitters, but people barely make a scrutiny into the cause of the spectral splitting in their experiment and roughly conclude that the splitting is all quantum Rabi splitting. On the other hand, recently a purely classical model was presented in Ref. [37], where quantum versus optical interaction contribution to giant spectral splitting in a strongly coupled nanogap plasmon–molecules system was discussed in details. This theoretical work has modeled surface plasmon resonances and molecules as two kinds of Lorentzian oscillators in mutual strong optical interaction. It turns out that the splitting in spectrum is also proportional to
Nonetheless, the theoretical work discussed in Ref. [37] has used an approximation to model the nanogap (a nanocavity) plasmon background as a purely classical oscillator and the nanocavity plasmon-molecule interaction as an oscillator-oscillator interaction. It is thus highly desirable to use a more accurate model, optimally and preferably an analytical model, to describe the plasmon-molecule interaction and elucidate the underlying complete physics picture without big approximation. Yet, frankly speaking, this is never an easy task due to the complexity in both the optical and quantum aspects. In this work, we will attack this difficult issue by considering an ensemble of atoms (or other emitters, such as quantum wells, quantum dots, molecule and J aggregates) immersed within a Fabry-Perot high-Q optical microcavity, as a critical step towards fully modeling the practical plasmonic nanocavity used in most experiments. The optical response of an atom will be treated quantum mechanically that yields naturally a Lorentz spectrum lineshape characterized by the resonance frequency (or wavelength) and linewidth. The transmission spectrum of an incident light as probe signal can then be analyzed and it will deflect the spectral response of this microcavity-atoms coupled system, from which the influence of the classical optical interaction upon the atomic spectrum can be revealed and the underlying physical mechanism can be clarified. This system can well model and describe a practical cavity-molecule strong interaction. We will show that when the violent optical resonance of the Fabry-Perot microcavity matches the atomic resonance, the originally single-peak transmission spectrum lineshape will be greatly modified and shaped into a two-split peak spectrum lineshape. Besides, the splitting magnitude can be controlled by both the geometric and physical parameters of the microcavity-atoms coupled system. The establishment of this analytical model will propel people to take into account the abundant physical principles and mechanisms behind the practical experimental phenomenon in the strong coupling regime known as the giant spectral splitting. Furthermore, the building of an analytic model will help very much to elucidate the specific subtle contribution of each physical principle and mechanism to experimentally observed phenomena and settle down a solid understanding to the underlying physics. Through such an analytical theory, one can better appreciate the great role of classical optical interaction in creating the well-observed giant spectral splitting that seemingly has a pure quantum mechanical origin.
Model and Theory
A practical optical microcavity model that is adopted in this work is illustrated in Figure 1A. The microcavity is a one-dimensional (1D) Fabry-Perot cavity made from two symmetric high-reflection mirrors with a sandwiched dielectric medium thin film (such as vacuum or silica glass), and the atoms are dispersed within the dielectric medium. The whole microcavity system is placed in the air background where the incident, reflected and transmitted light transport. The refractive index of the sandwiched medium in the cavity is
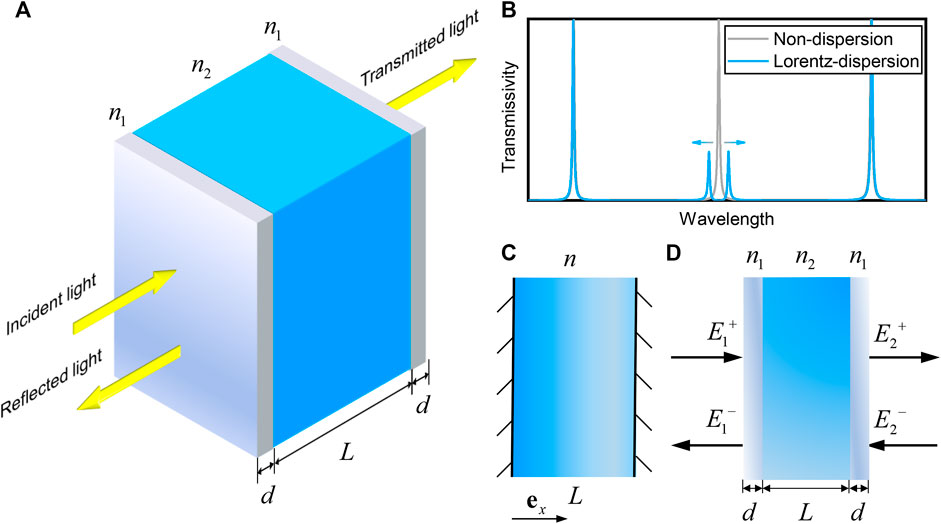
FIGURE 1. Schematic diagram for a Fabry-Perot optical microcavity used to probe cavity-atom interactions. (A) Schematic diagram for a practical Fabry-Perot optical microcavity system involving a dielectric medium embedded with atoms sandwiched between two high-reflection and loss-free mirrors. A classical splitting in spectrum can be observed in this model. (B) Diagram for transmission spectrum of optical microcavity exhibiting the splitting for Lorentz-dispersion cavity medium. (C) Schematic diagram for an ideal Fabry-Perot optical microcavity system to analyze theoretically the cause of classical spectral splitting observed in the practical optical microcavity system. (D) Schematic diagram for solution to the transmission/reflection spectrum in the Fabry-Perot optical microcavity system using a transfer-matrix method.
Note that we are studying the interaction between photon and a bulk of homogenous emitters which are embedded in the entire resonant cavity. Here, there are two points worth noting. Firstly, in addition to atoms, the emitters considered in our manuscript could include quantum dots and others. Atoms are just an example we choose to illustrate the problem clearly. Our model can be applicable to any quantum dot or molecule excitons, if their permittivity is known. Secondly, we have looked upon a large number of emitters as a continuous media, so the permittivity of the emitters is the same as the resonance permittivity for the continuous media in cavity.
An incident probe signal light is propagating from the left side to the right side, penetrating through the left mirror, inducing multiple reflection within the sandwiched cavity medium, and finally penetrating through the right mirror. Interaction of the incident light (wavelength
It is well known that for a classical Fabry-Perot cavity, the spectrum of transmitted light is an array of separate peak for a non-dispersion cavity medium, such as pure silica glass in the visible band, as shown in Figure 1B (gray line), and these discrete transmission peaks match exactly with the standing wave condition to form discrete cavity modes within the Fabry-Perot cavity. In contrast, we find that the spectrum of transmitted light will split into two peaks for a Lorentz-dispersion cavity medium (e.g., made from Lorentz-dispersion atoms embedded in non-dispersion background medium) (blue line) when the atomic resonant frequency is eminently close to the cavity mode resonance frequency. In the following sections, we will study systematically such a spectral splitting phenomenon that is caused entirely by classic electromagnetic/optical interaction effects. Firstly, we will calculate the transmission spectrum of the practical optical microcavity based on the well-established transfer-matrix method. And then, we will closely examine the effect of the cavity length, plasma frequency, atomic dissipation, and cavity wall dissipation to the spectral splitting. Finally, we theoretically explain the mechanism of the above four factors on the spectral splitting by analyzing the ideal Fabry-Perot cavity model (with perfect-reflection mirrors and dissipation-free cavity medium) [3, 7] as shown in Figure 1C.
The transfer-matrix method is widely used in the calculation of light transport in multi-layer medium models. It is efficient and convenient to analyze the transmission spectrum when the considered system consists of many layers of slab. Our Fabry-Perot microcavity model can be regarded as a three-layer medium (left metal mirror, sandwiched atoms-involved cavity layer, right metal mirror) placed in the air, as shown in Figure 1D. The transport of light can be described by the following transfer matrix formula
Assuming that the elements of the transfer matrices can be written as
then the expression of the matrix elements is
and
With the above formula, we can readily calculate the total transfer matrix
Then, the transmittance of energy flow at normal incidence (hereinafter referred to as transmittance) is
where “det” denotes determinant and the vertical lines denote complex modulus. Based on Eq. 3, we can calculate the transmission spectrum
Yet, as is well known, every medium in nature has the characteristics of absorption and dispersion, because atoms comprising the medium have different response behaviors to photons of different frequencies. This feature can be explained by the Schrödinger equation governing the quantum nature of atoms and electrons, and finally the Lorentz lineshape that describes the dispersion behavior of the medium can be obtained. Here we briefly recall this process and present it to the readers so that they can better understand how to bridge the microscopic quantum response, in particular the atomic dipole moment of an individual atom and the macroscopic optical properties, in particular the permittivity and refractive index of the atomic layer in our model. This will set the basis for understanding the optical response, in particular the transmission spectrum of the whole atoms-embedded Fabry-Perot microcavity. It also allows one to construct the physical picture about the classical optical interaction between the atoms and microcavity in the strong modulation and fundamental modification of the transmission spectrum lineshape.
It is well known that the evolution of any quantum state of atom
where the Hamiltonian
and the initial condition is
Here, bold letter indicates operators and upper arrows indicate vectors.
The Schrödinger equation with given initial conditions is solved in two pivotal steps:
First, according to the principle of state superposition, any state
where
Second, the equation with initial condition can be solved by a perturbation method. Expand the state
where the transition frequency
The average value of the electric dipole moment of an atom in any state can also be expanded into a perturbation series, where the first two orders are
Substitute Eqs 9, 10 into the above formula to get
Because the electric polarization intensity
Besides, because of the relationship between the linear susceptibility of medium
For simplicity we have assumed the case of a
Finally, let
then combining Eq. 14 with the above equation, omitting
Eq. 16 is thought of as Lorentz lineshape. Here we consider a practical case where there is a transition frequency
Table 1 presents various geometric and physical parameters of the practical optical microcavity model as shown in Figure 1A adopted in this work, and thus determines its physical properties. In all our calculations and discussions, the geometric and physical parameters are pre-designated explicitly in this table, unless additional instructions are made specially in the context. When considering the influence of the dispersive medium on the transmission spectrum, the dispersion is determined by Eq. 17. Note that the center frequency
Results of Spectral Splitting
Figure 2A shows the transmission spectrum nearby the first resonance peak of microcavity under the model parameters of Table 1 as calculated by the transfer-matrix method. The dispersion of the cavity medium leads to an apparent split spectrum, which changes from one peak (569.34 nm) when there is no dispersion (without the atoms and with only
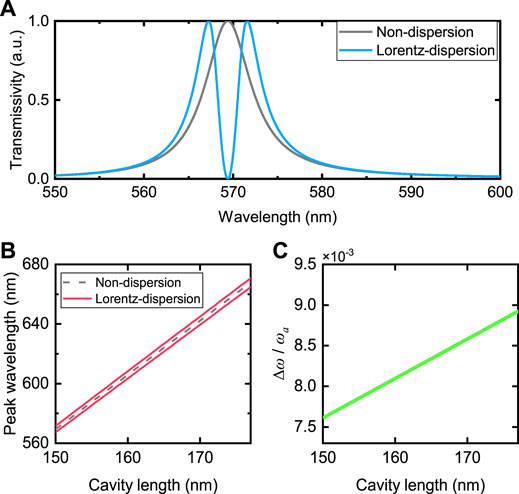
FIGURE 2. (A) Transmission spectrum nearby the first order resonance. When the medium is non-dispersive dielectric, there is one peak at 569.34 nm (2.1777 eV). When the medium is Lorentz-dispersive dielectric, there are two peaks at 567.20 nm (2.1859 eV) and 571.56 nm (2.1692 eV), respectively. That is, a spectral splitting has been created with an interval of 16.7 meV. (B) Position of transmission peaks versus the cavity length. As the cavity length increases, all peaks red shift and the splitting is so tightly close to the center wavelength that it is hard to distinguish the three lines. (C) The relative splitting degree
Figure 2B shows that the two split transmission peaks when there is dispersion are always on both sides of the single peak when there is no dispersion in all scale of variation of cavity length. In order to further study the influence of cavity length on splitting, we use the relative splitting degree
Many previous experimental works reported that a suitable adjustment of resonant micro/nanocavity parameters can improve the quantum interacting effect to obtain a “giant Rabi splitting”, which is in fact reflected from practical experimental observation of giant spectral splitting. But we find that the classic dispersion effect of cavity medium can also induce a tunable spectral splitting whose magnitude can be large. The parameters of cavity length, plasma frequency, atom dissipation and cavity wall dissipation all will affect the spectral splitting. In the remainder of this section, we will investigate systematically how these important factors influence the spectral splitting: the plasma frequency, atom dissipation and cavity wall dissipation.
The most effective approach to increase the spectral splitting is to increase the plasma frequency
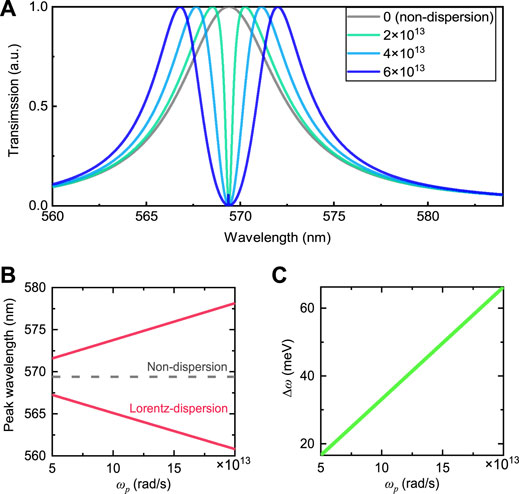
FIGURE 3. Transmission spectral splitting in various magnitudes of atom plasma frequency
The atom dissipation
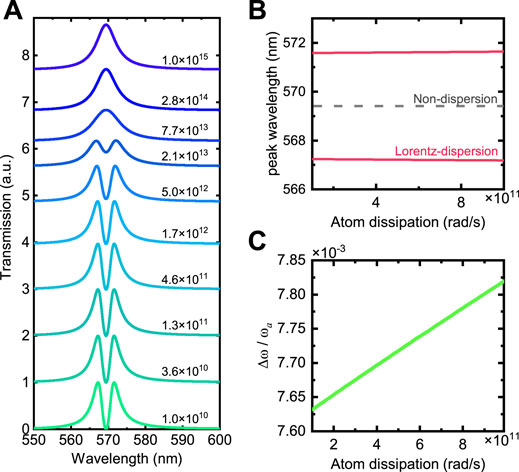
FIGURE 4. The change of transmission peaks under the change of atom dissipation. (A) Transmission spectrum in Lorentz-dispersion changed by atom dissipation
The practical optical microcavity as depicted in Figure 1A looks different from an ideal Fabry-Perot cavity. But we can approach the ideal cavity by increasing the reflectivity of the mirror film, or decreasing its transmittance equivalently. The calculation result of the transmission spectrum is shown in Figure 5A with gray line, where the cavity medium is non-dispersive dielectric. It can be seen that the spectrum is a single-peak profile. The transmission peak red shifts to 600 nm, a value anticipated by the Fabry-Perot cavity theory and the line width narrows, as the transmittance of mirror wall decreases. When the transmittance is approaching zero, the spectral line will become so narrow that it is somehow hard to calculate by computer. In fact, the ideal cavity model is a special case of practical optical microcavity, which provides a theoretical basis for analyzing various features as mentioned above, and this will be done soon. The spectral splitting varying along with the transmittance of mirror wall is also depicted in Figure 5A with blue line, where the cavity medium is Lorentz-dispersive. It can be seen that the spectrum is a double-peak profile, which changes in a trend similar to the single-peak profile.
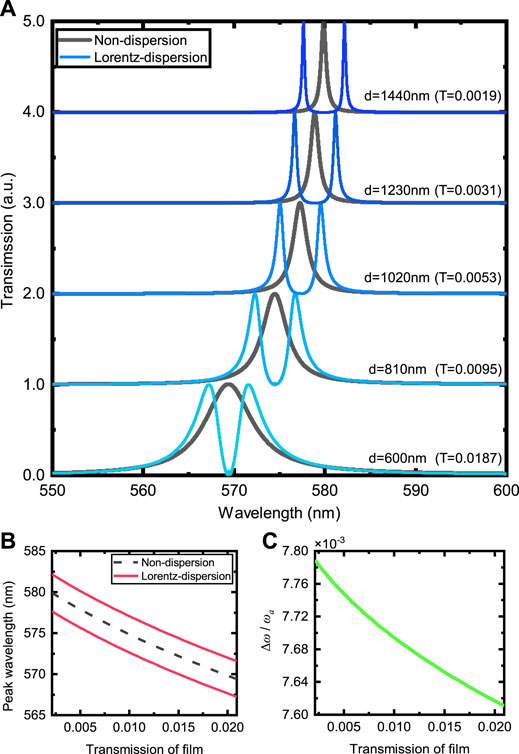
FIGURE 5. The change of transmission peaks along with the transmission of the cavity mirror film by changing the thickness of the mirror wall. (A) Transmission spectrum in the non-dispersion situation. The peak red shifts and narrows as the thickness of the wall increases (the transmission of mirror wall decreases). The notes on the curve indicate the wall thickness in unit of nm, together with the wall transmittance in the basket. (B) The transmission peaks position. Two peaks in Lorentz-dispersion (red solid line) surround the single peak in non-dispersion (gray dotted line). (C) The relative splitting degree
Furthermore, we study the influence of the reflectivity of the mirror wall on the case when the medium in the cavity is Lorentz-dispersive dielectric. Figure 5B shows the splitting close to the center wavelength in various transmittance of the mirror film, and all peaks red shift as the transmittance of the mirror film decreases, consistent with the analysis above. Figure 5C shows that the relative splitting degree
Application to Nanocavity-Atom Coupling System
As an example of applying the theory developed in this article, we consider the 1s → 2p atomic transition in hydrogen with 137 nm transition wavelength
Perhaps the example of hydrogen atoms is slightly beyond ordinary practice. The hydrogen atom has almost no effect on the resonance permittivity in the cavity because of their low density and low electric dipole moment. Actually, no one has used hydrogen atoms as objects to study Rabi splitting in a nanophotonic system. We use the example of hydrogen atoms for three considerations. First, the data on hydrogen atoms is readily available, which can be easily adopted to calculate for answering our question. Second, the hydrogen atoms are the simplest atoms. Placing them into our model as an example can epitomize the simplicity of our model, and it is our aim to get a theoretically analytical model. Third, our model is general and does not depend on the kinds of emitter. So, we can make certain reasonable prediction on a bulk of hydrogen atoms, even if the experiment still cannot be performed and implemented.
Let’s go back to the calculation and analysis of our model on hydrogen atoms. This cavity-atoms coupled system could induce two kinds of spectral splitting. One of them is the widely concerned Rabi splitting whose gap can be calculated from the above data. The electric field strength per photon
Notice that the best way to understand deeply the physics of a strong-coupling atom/molecule-micro/nanocavity system is to develop an analytical theory with good prediction power for everything upon the system. As generally the nanocavity in practice has a complicated 3D geometry, rigorous analytical theory is not possible, and some approximation must be adopted. In our work, we have taken the model of 1D microcavity interacting with not a single atom/molecule, but with a series of atom/molecule comprising a homogeneous dilute gas medium of atom/molecule. We have made an approximate assumption that if there is an emitter in the hot spot of 3D naoncavity, the basic physics, in particular, the spectral lineshape produced by this system is similar to that produced by multiple emitters at the same density embedded within the 1D microcavity. In fact, some researchers have used such model and method to explain their experiment and achieved a satisfactory result, where alone dye molecule is regarded as a continuous dispersive media with a thickness of 1 nm [4]. However, they did not discuss the essential physical picture underlying this method and merely got a numerical solution by FDTD simulations. Our current studies now would provide such a picture analytically. Incidentally, the similar idea is also used in the design of nanophotonic systems [21].
Another thing that is worth mentioning is that in our current model of 1D microcavity interacting with atom gas, the density of atom is dilute. Then practically each photon only interacts with atom once, and multiple interactions causing the atom to be excited and re-illuminate can be neglected. In this case the atom gas cannot change the cavity permittivity and transmittivity considerably, except at resonance. For a practical 3D nanocavity containing single molecule or only few molecules, the size of molecule is generally far smaller than the hot spot size, so that this system can still be modeled as a dilute atom system, and our current model can be well generalized to handle this strongly-coupled nanocavity-molecule system.
Based on the above approximation, we can consider the other instance raised from a plasmon-molecules system. In this system, methylene blue molecules, a kind of J aggregate, serve as the quantum emitters embedded in the nanogap of a promising nanoparticle-on-mirror (NPoM) geometry [33]. The NPoM geometry forms a localized surface plasmon as a nanocavity. Whereupon, the system with methylene blue molecules and NPoM nanocavity geometry can be referred to as an achievement of interaction between matter and light where the fascinating quantum Rabi splitting emerges in the strong coupling regime [4]. Incidentally, a classical spectral splitting also appears. One can repeat the above method to calculate the gap for both spectral splitting, just pay attention to substitute the effective electric field for stand wave
Ideal Optical Microcavity Mode Analysis and Empirical Formula
As shown in Figure 5A, an ideal Fabry-Perot optical microcavity is an ideal model of practical optical microcavity. It is a good opportunity to use the Fabry-Perot cavity model to reveal the true physical mechanism underlying the abundant phenomena that have been disclosed about the spectrum evolution and splitting against various geometric and physical parameters. Besides, this ideal model can help to construct a complete physics picture on how to engineer the spectral splitting. More importantly, we can derive a famous empirical formula in quantum experiment in pure classical way, which would provide another proof to ascertain that classical optical splitting is akin to the quantum Rabi splitting and that the large or even giant spectral splitting from multiple emitters may largely originate from classical optical interaction.
The Fabry-Perot cavity is composed of a dielectric medium sandwiched between two perfectly reflecting planar mirror wall as diagrammed in Figure 1C. The refractive index of the cavity medium
and the relative permittivity
Substituting the wave vector
Let
where
Combining Eqs. 24, 19, 28, we get
Further consider a non-detuning condition, then the center frequency of the atomic Lorentz lineshape should be equal to the resonance frequency of the cavity without dispersion, that is
Substituting Eq. 21 into the above equation, we get
Using the above equation, we can eliminate
Eq. 25 is a linear quadratic equation about
If using the graphical method to solve the problem, we can draw the function on the left side of Eq. 25 as
Then the point of intersection of the two functions is the solution of Eq. 25, and the calculation results are shown in Figure 6A. The two splitting peaks of Eq. 25 using the parameter in Table 1 (as mentioned above, take
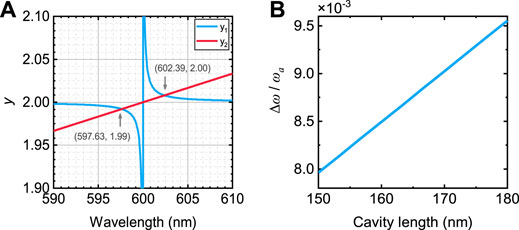
FIGURE 6. Process and result of graphical method or formula for roots to solve Eq. 25. (A) Graph of the two functions in Eq. 26 for graphical method. The abscissa of two points of intersection correspond to the two splitting peaks in the transmission spectrum for cavity medium with Lorentz-dispersion. (B) Theoretical analysis results of the influence of cavity length on the relative splitting degree
On the other hand, if using the analytical formula for solution of roots, we square and transpose Eq. 25 on both sides to get
The quadratic equation discriminant is
Thus, there are two real roots as
Because
we have
Thus, there are two positive real roots. Therefore, there must exist two positive real solutions of Eq. 25, which correspond to the two transmission peaks and read
Using the parameter in Table 1, we get the two solutions as 597.6 and 602.4 nm, respectively, which are identical with the solution of drawing method.
We can use this method to analyze the variation of the splitting with the length of cavity. In terms of the two transmission peaks for frequency determined by Eq. 29, we get the splitting interval
which is a classical spectral splitting, and will be used to compare the result of the quantum Rabi splitting obtained by Hamiltonian approach.
Using Eq. 21, 30, we can plot the trend of the relative splitting degree
Integrating this analytical theory developed in this section into an estimate on the atom dens1ity
Now one sees that we can derive the empirical formula through purely classical optical method, and thus there is strong reason to believe that the classical optical effect exists in the spectral splitting phenomenon of multiple emitters, which is contrary to the view that the spectral splitting all comes from quantum effects (Rabi splitting).
Based on our analytical model, we give two arguments to emphasize the non-negligible role of classical optical effects in the phenomenon of spectral splitting, which is different from the popular point of views upon “giant Rabi splitting.” On the one hand, we quantitatively estimate that in a practical micro/nanocavity, the quantum Rabi splitting is of the same order of magnitude as the classical optical splitting. On the other hand, we get the empirical formula of quantum experiment by classical method. All of these clearly indicate that one should pay more attention to the classical optical splitting in quantum experiment upon a cluster of emitters.
Conclusion
In summary, we have built up a model physical system to attack the difficult problem of classical optical interaction versus quantum interaction contribution to the experimentally observed giant spectral splitting in a strongly coupled system of atom and micro/nanocavity. The model system is a practical Fabry-Perot high-Q optical microcavity involving Lorentz-dispersion atoms, and it allows us to analytically study cavity-atom interaction and related spectral splitting phenomenon. In this model, the microscopic optical response of an individual atom upon an illuminating light is represented by its electric dipole moment, whose magnitude is solved quantum mechanically using the semi-classical theory. The macroscopic optical response of the cavity dielectric medium involving an ensemble of atoms dispersed within a background medium is described by the electric permittivity, dielectric constant, and refractive index. The spectral response, namely the optical response against light at different frequencies, of the individual atoms and the overall cavity medium is then described by a Lorentz dispersion lineshape. With these analytical formulae for all the relevant microscopic and macroscopic physical quantities of the atoms and cavity medium at hand, the macroscopic optical spectrum, namely, the reflection, transmission, and absorption spectrum, can all be solved readily in the framework of classical electromagnetics, electrodynamics, and optics. The characteristics of macroscopic spectrum can in turn be used to reflect and probe the microscopic physical properties of atoms against light. In this regard, this model system has involved features of microscopic atoms, mesoscopic microcavity, and macroscopic optical spectrum, and their contributions and roles to a specific physics entity can be qualitatively and quantitatively calculated, analyzed, traced, and induced in high accuracy and precision. Therefore, this model system is very suitable to serve as a wonderful high-pass bridge connecting these three fundamental categories of physics world.
In particular, we have theoretically studied and analyzed the classic causes of spectral splitting in optical microcavity involving atoms, in an aim to clarify the true physical reasons, mechanisms and pictures underlying observations made in many previous experimental works, in particular observations of optical spectral modulation and resonant peak splitting. Nowadays, these phenomena are popularly and dominantly attributed to quantum strong-coupling induced Rabi splitting, a pure quantum mechanical effect of atomic energy splitting under the strong action of single photons. We have used the transfer-matrix method to calculate the transmission spectrum against the incident probe signal light under different geometric and physical parameters with analytical exactness and accuracy. We have found that the classic electromagnetic effect alone can produce tunable splitting phenomenon in the microcavity, where the originally single transmission peak for a non-dispersion medium microcavity becomes two symmetrically split transmission peaks when the Lorentz-dispersion atoms are immersed within this cavity medium.
We have further considered an ideal Fabry-Perot microcavity where all atom dissipation and cavity wall leakage are removed, and get the explicit analytical formula for the spectral splitting between the two resonance modes. The analytical results are in good agreement with the transmission spectrum calculations against a practical Fabry-Perot microcavity with the atom dissipation and cavity wall leakage loss being fully incorporated. Using this ideal Fabry-Perot cavity model, we can successfully explain the causes of the spectral splitting theoretically, which confirms again the pure classical optical interaction effect can serve as the major physical origin behind the theoretically observed giant spectral splitting.
Our calculations and model analyses have shown that the spectral splitting will occur when the medium in the cavity is a dispersion dielectric. In contrast, for a purely dielectric medium neglecting Lorentz dispersion, only single transmission peak exists corresponding to the resonance mode of the Fabry-Perot microcavity. Importantly, there are at least four geometric and physical factors that are able to tune such splitting: the cavity length, plasma frequency, atom dissipation, and cavity wall dissipation. Among them, the main factor affecting the appearance and morphology of the spectral splitting is the atom dissipation, while the main factor affecting the degree of the spectral splitting is the plasma frequency of atom system. In some specific situations this spectral splitting can reach a remarkably large value of ∼70 meV, comparable to the results reported by previous experimental observations. This indicates that it is possible to get a “giant splitting” by designing proper parameters of the micro/nanocavity, which reaches out to be comparable with the magnitude of the reported quantum Rabi splitting. Yet, the spectral splitting is induced by the modulation upon the effective medium dielectric permittivity and refractive index of cavity and the consequent modification and splitting upon the cavity resonance peak. This is of course a purely classical optical interaction effect, instead of the popularly assumed quantum Rabi splitting effect.
We have calculated the quantitative value of quantum Rabi splitting and classical optical splitting for several typical strongly-coupled cavity-atom systems, such as a plasmon cavity filled with J aggregates, and found that the two splitting can be in the same order of magnitude. This indicates that we have no reason to ignore the classical optical effect and only emphasize on the quantum effect. Moreover, our model and theory has given the same empirical rule of
The atom-embedded 1D Fabry-Perot microcavity offers an excellent platform to comprehensively investigate and understand the cavity-atom interaction in various aspects from both the classical optical level and quantum mechanical level. This model system is very simple in geometry, so it allows for easy analytical solution to many classical optical problems as to light transport, cavity resonance, spectrum profile and spectral splitting. The explicit analytical expression for these physical quantities enables one to get deep insight and complete picture about some seemingly complicated issues. This model has fully shown the great power of physical model and mathematical analysis in comparison with pure numerical simulation and experimental measurements against a practical physical system of high complexity.
The analytical model developed in this work can allow us to explore deeply various physical effects that might be involved with this well-observed spectral splitting in an optical micro/nanocavity involving cavity-atom interaction. The occurrence of many natural phenomena is often accompanied by complex mechanisms, especially for the practical cavity-atom interaction system involving all the three categories of physical world: the microscopic atoms, mesoscopic micro/nanocavity, and macroscopic light. Starting from a completely classic electromagnetic theory, the current work shows that spectral splitting can take place naturally in the resonant cavity under the simple classic optical dispersion of materials originated from microscopic atoms, and the magnitude of spectral splitting can become remarkably large. In some cases, the classic effects may be comparable to or even overwhelm the quantum effects. Although in the current work we only focus on the purely classical optical effects leading to the remarkable spectral splitting of microcavity-atoms interaction system, we believe this 1D Fabry-Perot microcavity involving atoms should allow for extension to take into account the quantum mechanical effects such as quantum Rabi splitting due to single photon in strong coupling with atomic energy levels. In the near future, we hope to use the current model system to study fruitful intracavitary physical phenomena of micro/nanocavity-atoms/molecules strong coupling system under the joint action of quantum and classical interaction in the framework of joint classical and quantum theories. We believe abundant new physics in a new Frontier of physics and science are waiting there for somebody to discover, analyze and appreciate.
Data Availability Statement
The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.
Author Contributions
Z-YL contributed to conception and design of the study. JZ organized the data, performed the special analysis, wrote the first draft of the manuscript. Z-YL wrote sections of the manuscript. All authors contributed to manuscript revision, read, and approved the submitted version.
Funding
The authors are grateful for the financial support from National Key R&D Program of China (2018YFA0306200), National Natural Science Foundation of China (11974119), Guangdong Innovative and Entrepreneurial Research Team Program.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
1. Agarwal GS. Vacuum-field Rabi Splittings in Microwave Absorption by Rydberg Atoms in a Cavity. Phys Rev Lett (1984) 53:1732–4. doi:10.1103/physrevlett.53.1732
2. Boca A, Miller R, Birnbaum KM, Boozer AD, Mckeever J, Kimble HJ. Observation of the Vacuum Rabi Spectrum for One Trapped Atom. Phys Rev Lett (2004) 93:233603. doi:10.1103/physrevlett.93.233603
3. Born M, Wolf E. The Fabry–Perot Interferometer. In: Principles of Optics: Electromagnetic Theory of Propagation, Interference and Diffraction of Light. 7th ed. United Kingdom: ECambridge University Press (1999). p. 366–80.
4. Chikkaraddy R, De Nijs B, Benz F, Barrow SJ, Scherman OA, Rosta E, et al. Single-molecule strong Coupling at Room Temperature in Plasmonic Nanocavities. Nature (2016) 535:127–30. doi:10.1038/nature17974
5. Ciracì C, Hill RT, Mock JJ, Urzhumov Y, Fernández-Domínguez AI, Maier SA, et al. Probing the Ultimate Limits of Plasmonic Enhancement. Science (2012) 337:1072–4. doi:10.1126/science.1224823
6. Hakala TK, Toppari JJ, Kuzyk A, Pettersson M, Tikkanen H, Kunttu H, et al. Vacuum Rabi Splitting and strong-coupling Dynamics for Surface-Plasmon Polaritons and Rhodamine 6G Molecules. Phys Rev Lett (2009) 103:053602. doi:10.1103/PhysRevLett.103.053602
7. Hecht E. The Fabry–Perot Interferometer. In: Optics. America: Pearson Education (2017). p. 429–33.
8. Hennessy K, Badolato A, Winger M, Gerace D, Atatüre M, Gulde S, et al. Quantum Nature of a Strongly Coupled Single Quantum Dot-Cavity System. Nature (2007) 445:896–9. doi:10.1038/nature05586
9. Jaynes ET, Cummings FW. Comparison of Quantum and Semiclassical Radiation Theories with Application to the Beam Maser. Proc IEEE (1963) 51:89–109. doi:10.1109/proc.1963.1664
10. Khitrova G, Gibbs HM, Jahnke F, Kira M, Koch SW. Nonlinear Optics of normal-mode-coupling Semiconductor Microcavities. Rev Mod Phys (1999) 71:1591–639. doi:10.1103/revmodphys.71.1591
11. Khitrova G, Gibbs HM, Kira M, Koch SW, Scherer A. Vacuum Rabi Splitting in Semiconductors. Nat Phys (2006) 2:81–90. doi:10.1038/nphys227
12. Kimble HJ. Strong Interactions of Single Atoms and Photons in Cavity QED. Physica Scripta (1998) T76:127. doi:10.1238/physica.topical.076a00127
13. Kleemann M-E, Chikkaraddy R, Alexeev EM, Kos D, Carnegie C, Deacon W, et al. Strong-coupling of WSe2 in Ultra-compact Plasmonic Nanocavities at Room Temperature. Nat Commun (2017) 8:1296. doi:10.1038/s41467-017-01398-3
14. Li J, Guo H, Li Z-Y. Microscopic and Macroscopic Manipulation of Gold Nanorod and its Hybrid Nanostructures [Invited]. Photon Res (2013) 1:28–41. doi:10.1364/prj.1.000028
15. Li ZY. Mesoscopic and Microscopic Strategies for Engineering Plasmon-Enhanced Raman Scattering. Adv Opt Mater (2018) 6:1701097. doi:10.1002/adom.201701097
16. Liu R, Zhou Z-K, Yu Y-C, Zhang T, Wang H, Liu G, et al. Strong Light-Matter Interactions in Single Open Plasmonic Nanocavities at the Quantum Optics Limit. Phys Rev Lett (2017) 118:237401. doi:10.1103/physrevlett.118.237401
17. Lo H-K, Chau HF. Unconditional Security of Quantum Key Distribution over Arbitrarily Long Distances. science (1999) 283:2050–6. doi:10.1126/science.283.5410.2050
18. Marzin J-Y, Gérard J-M, Izraël A, Barrier D, Bastard G. Photoluminescence of Single InAs Quantum Dots Obtained by Self-Organized Growth on GaAs. Phys Rev Lett (1994) 73:716–9. doi:10.1103/physrevlett.73.716
19. Mckeever J, Boca A, Boozer AD, Buck JR, Kimble HJ. Experimental Realization of a One-Atom Laser in the Regime of strong Coupling. Nature (2003) 425:268–71. doi:10.1038/nature01974
20. Meystre P, Sargent M. Field Quantization. In: Elements of Quantum Optics. 4th ed. New York: Springer Science and Business Media (2007). p. 299–325. doi:10.1007/978-3-540-74211-1_13
21. Panda SS, Hegde RS. A Learning Based Approach for Designing Extended Unit Cell Metagratings. Nanophotonics (2021) 11:345–358. doi:10.1515/nanoph-2021-0540
22. Peter E, Senellart P, Martrou D, Lemaître A, Hours J, Gérard JM, et al. Exciton-photon strong-coupling Regime for a Single Quantum Dot Embedded in a Microcavity. Phys Rev Lett (2005) 95:067401. doi:10.1103/PhysRevLett.95.067401
23. Prodan E, Radloff C, Halas NJ, Nordlander P. A Hybridization Model for the Plasmon Response of Complex Nanostructures. Science (2003) 302:419–22. doi:10.1126/science.1089171
24. Reithmaier JP, Sęk G, Löffler A, Hofmann C, Kuhn S, Reitzenstein S, et al. Strong Coupling in a Single Quantum Dot-Semiconductor Microcavity System. Nature (2004) 432:197–200. doi:10.1038/nature02969
25. Sato Y, Tanaka Y, Upham J, Takahashi Y, Asano T, Noda S. Strong Coupling between Distant Photonic Nanocavities and its Dynamic Control. Nat Photon (2012) 6:56–61. doi:10.1038/nphoton.2011.286
26. Savona V, Andreani LC, Schwendimann P, Quattropani A. Quantum Well Excitons in Semiconductor Microcavities: Unified Treatment of Weak and strong Coupling Regimes. Solid State Commun (1995) 93:733–9. doi:10.1016/0038-1098(94)00865-5
27. Scully MO, Zubairy MS. Quantization of the Free Electromagnetic Field. In: Quantum Optics. United Kingdom: Cambridge University Press (1999). p. 2–7.
28. Sun J, Li Y, Hu H, Chen W, Zheng D, Zhang S, et al. Strong Plasmon-Exciton Coupling in Transition Metal Dichalcogenides and Plasmonic Nanostructures. Nanoscale (2021) 13:4408–19. doi:10.1039/d0nr08592h
29. Thompson JD, Tiecke TG, De Leon NP, Feist J, Akimov AV, Gullans M, et al. Coupling a Single Trapped Atom to a Nanoscale Optical Cavity. Science (2013) 340:1202–5. doi:10.1126/science.1237125
30. Thompson RJ, Rempe G, Kimble HJ. Observation of normal-mode Splitting for an Atom in an Optical Cavity. Phys Rev Lett (1992) 68:1132–5. doi:10.1103/physrevlett.68.1132
31. Tiecke TG, Thompson JD, De Leon NP, Liu LR, Vuletić V, Lukin MD. Nanophotonic Quantum Phase Switch with a Single Atom. Nature (2014) 508:241–4. doi:10.1038/nature13188
32. Törmä P, Barnes WL. Strong Coupling between Surface Plasmon Polaritons and Emitters: a Review. Rep Prog Phys (2014) 78:013901. doi:10.1088/0034-4885/78/1/013901
34. Wang B, Zeng X-Z, Li Z-Y. Quantum versus Optical Interaction Contribution to Giant Spectral Splitting in a Strongly Coupled Plasmon-Molecules System. Photon Res (2020) 8:343–51. doi:10.1364/prj.375135
35. Wang H, Brandl DW, Le F, Nordlander P, Halas NJ. Nanorice: A Hybrid Plasmonic Nanostructure. Nano Lett (2006) 6:827–32. doi:10.1021/nl060209w
36. Weisbuch C, Nishioka M, Ishikawa A, Arakawa Y. Observation of the Coupled Exciton-Photon Mode Splitting in a Semiconductor Quantum Microcavity. Phys Rev Lett (1992) 69:3314–7. doi:10.1103/physrevlett.69.3314
37. Yoshie T, Scherer A, Hendrickson J, Khitrova G, Gibbs HM, Rupper G, et al. Vacuum Rabi Splitting with a Single Quantum Dot in a Photonic crystal Nanocavity. Nature (2004) 432:200–3. doi:10.1038/nature03119
38. Zengin G, Wersäll M, Nilsson S, Antosiewicz TJ, Käll M, Shegai T. Realizing Strong Light-Matter Interactions between Single-Nanoparticle Plasmons and Molecular Excitons at Ambient Conditions. Phys Rev Lett (2015) 114:157401. doi:10.1103/physrevlett.114.157401
39. Zhong XL, Li ZY. All-analytical Semiclassical Theory of Spaser Performance in a Plasmonic Nanocavity. Phys Rev B (2013) 88:085101. doi:10.1103/physrevb.88.085101
Keywords: light-emitter interactions, cavity, rabi splitting, strong coupling, analytical solution
Citation: Zeng J and Li Z-Y (2022) Analytical Model and Solution Illustrating Classical Optical Contribution to Giant Spectral Splitting in Strongly-Coupled Micro/nanocavity-atom System. Front. Phys. 10:734841. doi: 10.3389/fphy.2022.734841
Received: 01 July 2021; Accepted: 05 January 2022;
Published: 27 January 2022.
Edited by:
Umberto Lucia, Politecnico di Torino, ItalyReviewed by:
Shunping Zhang, Wuhan University, ChinaSergey Vyatchanin, Lomonosov Moscow State University, Russia
Copyright © 2022 Zeng and Li. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Zhi-Yuan Li, cGh6eWxpQHNjdXQuZWR1LmNu
 Jian Zeng
Jian Zeng Zhi-Yuan Li
Zhi-Yuan Li