Asymmetric localized states at a nonlinear interface of fractional systems with optical lattices

We investigate the existence and stability of localized gap states at a non-linear interface of non-linear fractional systems in a one-dimensional photonic lattice. By using the direct numerical simulations and linear stability analysis, we obtain the stability of the asymmetric localized gap states in the first and second finite gaps. Our theoretical results show that the power of the localized gap states decrease gradually as the increase of propagation constant and the non-linear landscape (non-linear coefficient ratio between the left and right interface), providing insights into soliton physics in non-linear periodic systems with fractional-order diffraction.

1 Introduction

Fractional order has been introduced in many branches of sciences in past decades, including the calculus theory [1], image processing [2], quantum mechanics [3–5], and system control [2], to name a few. In 2002, Laskin first proposed fractional Schrödinger equation (FSE) in quantum mechanics, describing the fractional quantum mechanics, with the Riemann integral over the Brownian trajectory being replaced by the Lévy flight trajectory; and by the way, the Riemann path on the brown trajectory is well described by the standard Schrödinger equation [3–5]. Subsequently, many phenomena in the systems with the fractional effect have been disclosed, such as fractional Hall effect [6], fractional quantum oscillation [7], etc. In 2015, Longhi proposed a spherical optical resonator that may realize the FSE in optics [8]. In recent years, the research based on the FSE became a subject of great interest.A myriad of numerical studies have been reported, including the propagation dynamics of various beams under fractional diffraction: zigzag and funnel-shaped propagation trajectory of chirped Gaussian beam [9], non-diffracting beam and conical diffraction of non-chirped Gaussian beam [10], abnormal interaction of Airy beam [11], self-focusing dynamics of Airy Gaussian vortex beam [12], and beam propagation management [13], etc. The stationary solutions of non-linear Schrödinger equation have always been an interesting field. Therefore, when the non-linear Schrodinger equation is expanded from the standard integer order to the fractional order, that is non-linear fractional Schrödinger equation(NLFSE), many intriguing localized states/modes were revealed, including spatial solitons supported by PT-symmetry, symmetric and antisymmetric solitons, fundamental solitons, multipole gap solitons, discrete vortex solitons, vortex solitons and gap solitons and so forth in Kerr nonlinearity [14–33].

On another hand, studies of solitons in periodic potentials have recently been extended to nonlinear scenarios, namely nonlinear lattices [34–40]. Besides, the emergent soliton phenomena in nonlinear media with inhomogeneous modulation of non-linearity have attracted a great interest of scientists from nonlinear community; various soliton structures were thus found, including localized states [41, 43–48], fundamental solitons [42], dissipative solitons [49, 50], vortex solitons [45, 46], truncated-Bloch-wave solitons [51], vortex soliton tori [46], and twisted vortex solitons rings [52].

Up to now, solitonic studies in the fractional nonlinear Schrodinger equation with periodic potentials are mainly focused on the homogeneous modulation of nonlinearity, while the solitons under the inhomogeneous modulation of nonlinearity have not been well studied. Relevant research reports in recent years also indicate that fractional diffraction has varying degree of influence on the properties of various solitons. Therefore, the physical system with fractional diffraction and inhomogeneous modulation of non-linearity may provide new insights into the formation and stability of localized states.

Herein we aim to investigate the shift degree and the corresponding power change of the localized states at a nonlinear interface of one-dimensional photonic lattices with inhomogeneous modulation of non-linearity and fractional diffraction. By using the linear stability analysis and direct perturbed propagation, we report numerical simulations for one-dimensional localized gap states, lying into the first finite gap and the second one of the associated linear Bloch spectrum, under value-changing Kerr nonlinear modulation, and obtain the corresponding stability properties and power dependency.

2 Model

The propagation of light in a one-dimensional photonic lattice with fractional diffraction can be described by the normalized NLFSE, which yields:

$i\frac{\partial \psi }{\partial z}=-\frac{1}{2}{\left(\frac{{\partial }^2}{\partial x^2}\right)}^{\alpha /2}\psi +V\left(x\right)\psi +h\left(x\right){\left|\psi \right|}^2\psi (1)$

Here, $\psi$ is the slowly varying amplitude of the optical beam, $z$ and $x$ being the normalized longitudinal antransverse coordinates; ${\left({\partial }^2/\partial x^2\right)}^{a/2}$ is the one-dimensional fractional Laplacian operator, with the value of Lévy index $\alpha$, which is set to the interval $1<\alpha \le 2$. When $\alpha =2$, Eq. 1 restores to the standard non-linear Schrödinger equation with second-order diffraction. $V\left(x\right)$ is the photonic lattice (linear periodic modulation of refractive index)

: $V\left(x\right)=V_0{\sin }^2\left(x\right)$, where $V_0$ being modulation depth of the lattice. We set $V_0=6$ throughout. The remaining $h\left(x\right)$ represents the value-changing (domain wall-like) Kerr non-linear coefficient along the transverse coordinate $x$, following:

$h\left(x\right)=\left\{\begin{array}{l}{\mathrm{g}}_1\left(x\right)\\ {\mathrm{g}}_2\left(x\right)\end{array}\right.=\left\{\begin{array}{l}1,x<0\\ 20,x\ge 0\end{array}\right.(2)$

here, we define the associated non-linear coefficient ratio as $m=\frac{{\mathrm{g}}_2\left(x\right)}{{\mathrm{g}}_1\left(x\right)}$ for discussion. Here, the constant coefficients ${\mathrm{g}}_1\left(x\right)$ and ${\mathrm{g}}_2\left(x\right)$ are at the same sign, and both are self-defocusing Kerr nonlinear, thus the change is only for nonlinear strength. In experiments, such non-linear landscape can be controlled by a technique called Feshbach resonance in the field of BEC, and may be realized by appropriate forms of optics or direct current electric field induction in optics context [34]. In the linear case (ignoring the last term), the Eq. 1 could produce the linear band structure for the photonic lattice, Figure 1 shows such case at the Lévy index value $\alpha =1.4$. It is seen that, in addition to a semi-infinite gap, there are several finite band gaps. In this paper, we mainly consider the localized states populated within the first finite gap and the second one, and both gaps are within propagation constant $\beta$: $-3.382\le \beta \le -1.373$ and $-4.804\le \beta \le -3.457$, respectively.

FIGURE 1

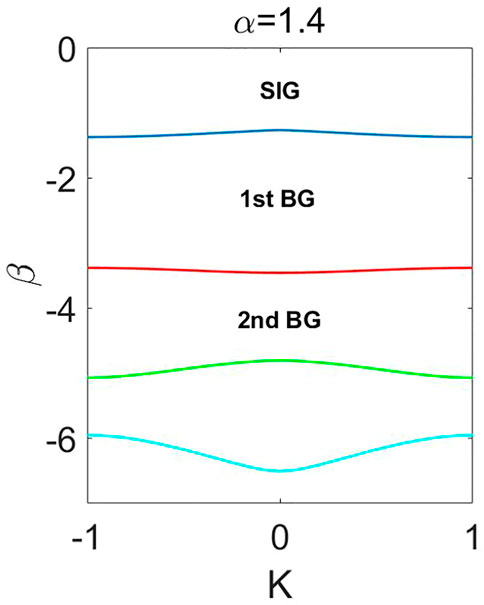
FIGURE 1. (Color online) Band-gap structure of linear spectrum $\beta \left(K\right)$ for optical lattice $V\left(x\right)=V_0{\sin }^2\left(x\right)$ at $V_0=6$ and Lévy index $\alpha =1.4$. Regions SIG, 1st BG and 2nd BG denote, respectively, the semi-infinite gap, the first and second band gaps.

Next, we take the stationary soliton solution as $\psi \left(x,z\right)=\varphi \left(x\right)\exp \left(-i\beta z\right)$ in Eq. 1, we then obtain:

$\beta \varphi =-\frac{1}{2}{\left(\frac{{\partial }^2}{\partial x^2}\right)}^{\alpha /2}\varphi +V_0{\sin }^2\left(x\right)\varphi +h\left(x\right){\varphi }^3(3)$

Here, $\varphi$ is the transverse profile of the light beam. Eq. 3 can be numerically solved by the modified square operator iterative method [48]. The total power P of the localized state yields $P={\int }_{-\infty }^{+\infty }{\left|\varphi \left(x\right)\right|}^{2}dx$.

The stability is a very important issue for localized states. To this end, it is necessary to perform linear stability analysis of them. We take the perturbation solution of Eq. 3 as:

$\psi =\left[\varphi +v\exp \left(\lambda z\right)+iw\exp \left(\lambda z\right)\right]\exp (-i\beta z)(4)$

Here, $v$ and $w$ are the real and imaginary parts of the perturbation eigenvalue function, satisfying $\left|v\right|\ll \left|\varphi \right|$, $\left|w\right|\ll \left|\varphi \right|$. $\lambda$ is the corresponding unstable growth rate. By substituting Eq. 4 into Eq. 1 and linearizing it, we can obtain the following eigenvalue problem:

$i\lambda v=-\frac{1}{2}{\left(\frac{{\partial }^2}{\partial x^2}\right)}^{\alpha /2}w+\left[\beta +V_0{\sin }^2\left(x\right)\right]w+h\left(x\right){\varphi }^{2}w(5)$

$i\lambda w=-\frac{1}{2}{\left(\frac{{\partial }^2}{\partial x^2}\right)}^{\alpha /2}v+\left[\beta +V_0{\sin }^2\left(x\right)\right]v+h\left(x\right){\varphi }^{2}v(6)$

Then, by using the Fourier collocation method [54], we can obtain the unstable growth rate, and judge the linear stability of the localized states according to the real part $\mathrm{R}\mathrm{e}\left(\lambda \right)$. The corresponding localized state is linearly unstable provided that $\mathrm{R}\mathrm{e}\left(\lambda \right)\ne 0$, and stable otherwise.

3 Numerical simulation and discussion

For discussion, the Lévy index is fixed at $\alpha =1.4$ throughout. We try to find the stability regions of stable and the unstable localized states in the form of gap solitons in the first and the second finite gaps. To study the profile changes of localized states under non-uniform nonlinear modulation, in addition to the case of nonlinear coefficient ratio $m=20$, we also cons-ider two cases of uniform non-linear modulation with non-linear coefficient ratio g=1 as reference, where the non-linear coefficients are $\gamma =1$ and $\gamma =20$ respectively. In fact, the localized states under uniform non-linearity may be called symmetric modes, while the cases for non-uniform nonlinear modulation being asymmetric modes [55]. As an example of stable transmission, we choose a situation in the middle of the first gap with propagation constant $\beta =-1.8$, whose profile is shown in Figure 2A. In comparison, the localized states under two uniform non-linearity conditions are shown in Figure 2B. We can find that compared with the localized states in uniform non-linearity, the localized state under non-uniform nonlinear modulation has a little position shift, and its intensity and profile of the localized state are in between, according to the Figures 2A, B. Subsequently, the perturbed evolution (propagation) of localized states in non-uniform nonlinear modulation is simulated numerically under the framework of Eq. 1, and is verified by the above-mentioned linear stability analysis. As shown in Figures 2C, D we can see that the localized state can stably transmit over 400 unit lengths, and there are no other real eigenvalues in its linear stability spectrum except for their imaginary counterparts, we thus can safely say that the localized state is stable under certain perturbations.Then we consider an unstable situation in the second band gap, the profile of such unstable localized state at $\beta =-3.5$ is shown in Figure 3A. As comparison, the profiles of the symmetrical counterparts under two constant non-linear strengths are shown in Figure 3B. Comparing both figures, we can see that the localized state under value-changing Kerr non-linear modulation shares the properties of stable one in Figure 2, such as takes a position shift toward its geometric center ($x=0$), and its profile (and thus the module and intensity) lies in between the two symmetric modes. For the unstable localized state in Figure 3A, we have also presented its transmission in Figure 3C and linear-stability eigenvalue in Figure 3D. It is observed from the former that the nonperiodic oscillation occurs in the process of transmission, demonstrating the unstable situation, which is confirmed by its instability eigenvalue spectrum with a pair of quadrupole eigenvalues for the latter. The dependence between the power of localized states and propagation constant is a well-known important property for soliton study. It is discussed fully here, as collected in Figure 4A for the particular case of nonlinear coefficient ratio g=20, where shows the selected propagation constant interval within the first and second finite gaps, $-4.5\le \beta \le -1.5$. We can find that as the propagation constant gradually reduces, i.e., from the first finite gap to the second gap, the power of these localized states presents a general trend of increase. We stress that the unstable localized states are only excited near the edges of the first and second band gaps. Moreover, we also discuss the effect of non-linear coefficient ratios on the power of asymmetric modes. At the fixed propagation constant $\beta =-4.0$, changing the non-linear coefficient ratios from 1 to 100, we obtain such relationship in Figure 4B, showing the decrease of the power of localized states with an increase of non-linear coefficient ratio, reaching a critical power around g=80, such critical power equates $\mathrm{P}=1.56$.

FIGURE 2

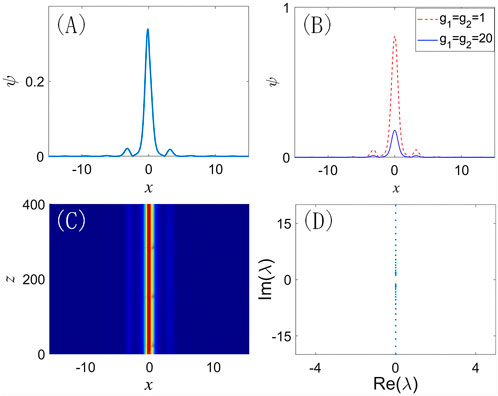
FIGURE 2. (Color online) First-gap localized modes under propagation constant $\beta =-1.8$. (A) Intensity profiles of stable localized mode in non-uniform nonlinearity. (B) Profiles of localized modes supported by one-dimensional photonic lattices and different constant nonlinear types (the red dotted line and blue dash line are uniform non-linearities with nonlinear coefficients of 1 and 20 respectively). (C) Evolution of the localized mode with the transmission distance of $z=400$. (D) Eigenvalue spectrum of linear stability analysis for the localized mode in (A).

FIGURE 3

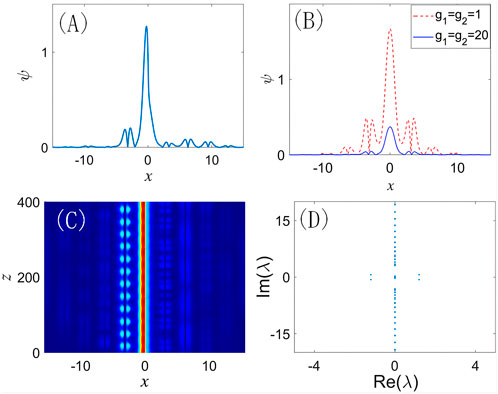
FIGURE 3. (Color online) Second-gap localized modes under propagation constant $\beta =-3.5$. (A) Intensity profiles of unstable localized mode in non-uniform nonlinearity. (B) Profiles of localized modes supported by one-dimensional photonic lattices and different constant nonlinear types (the red dotted line and blue dash line are uniform nonlinearities with nonlinear coefficients of 1 and 20 respectively). (C) Evolution of the localized mode with the transmission distance of $z=400$. (D) Eigenvalue spectrum of linear stability analysis for the localized mode in (A).

FIGURE 4

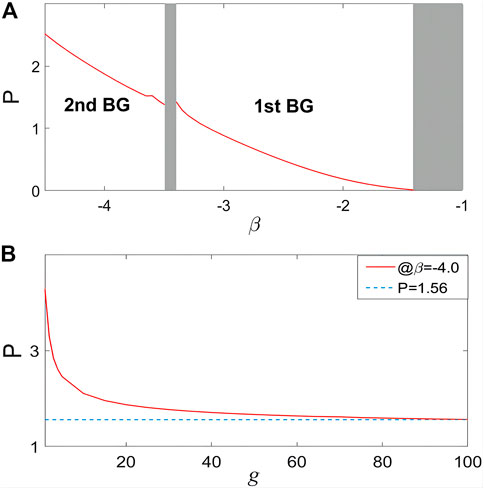
FIGURE 4. (Color online) Power of localized modes versus the associated propagation constant (A) and nonlinear coefficient ratio (B). (A) Nonlinear coefficient ratio $m=20$. (B) Propagation constant $\beta =-4.0$.

4 Conclusion

In the framework of the NLFSE, we studied numerically the dynamics of asymmetric modes in one-dimensional photonic lattices with the domain wall-like Kerr nonlinearity, in the first and second gaps of the underlying linear spectrum. We analyzed the properties of these localized states and studied their stability through direct numerical simulation and linear stability analysis. A significant feature is that the power of the asymmetric modes gradually decreases with increasing propagation constant and nonlinear coefficient ratio respectively. Our findings provide a controllable way to generate and manipulate localized states in physical systems with fractional diffraction and inhomogeneous non-linearity.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

SZ: Data Curation, Software, Visualization, Writing-Original Draft, Formal Analysis; JZ: Conceptualization, Methodology, Project Administration, Supervision, Validation, Visualization, Writing-Review and editing; YQ: Funding Acquisition, Project Administration.

Funding

This work was supported by the National Natural Science Foundation of China (NSFC) (61675184, 61275124 and 61405178).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Ortigueira MD, Tenreiro Machado JA. What is a fractional derivative? J Comput Phys (2015) 293:4–13. doi:10.1016/j.jcp.2014.07.019

CrossRef Full Text | Google Scholar

2. Piotr O. Discrete fractional calculus: Applications in control and image processing. Singapore: World Scientific (2015).

Google Scholar

3. Laskin N. Fractional quantum mechanics and Lévy path integrals. Phys Lett A (2000) 268:298–305. doi:10.1016/s0375-9601(00)00201-2

CrossRef Full Text | Google Scholar

4. Laskin N. Fractional quantum mechanics. Phys Rev E (2000) 62:3135–45. doi:10.1103/physreve.62.3135

CrossRef Full Text | Google Scholar

5. Laskin N. Fractional schrödinger equation. Phys Rev E (2000) 66:056108. doi:10.1103/physreve.66.056108

CrossRef Full Text | Google Scholar

6. Laughlin RB. Anomalous quantum Hall effect: An incompressible quantum fluid with fractionally charged excitations. Phys Rev Lett (1983) 50:1395–8. doi:10.1103/physrevlett.50.1395

CrossRef Full Text | Google Scholar

7. Olivar-Romero F, Rosas-Ortiz O. Fractorization of the quantum fractional oscillator. J Phys Condens Matter (2016) 698:012025. doi:10.1088/1742-6596/698/1/012025

CrossRef Full Text | Google Scholar

8. Longhi S. Fractional Schrödinger equation in optics. Opt Lett (2015) 40:1117–20. doi:10.1364/ol.40.001117

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Zhang Y, Liu X, Belić MR, Zhong W, Zhang Y, Xiao M. Propagation dynamics of a light beam in a fractional Schrödinger equation. Phys Rev Lett (2015) 115:180403. doi:10.1103/physrevlett.115.180403

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Zhang Y, Zhong H, Belić MR, Ahmed N, Zhang Y, Xiao M. Diffraction-free beams in fractional Schrödinger equation. Sci Rep (2016) 6:23645. doi:10.1038/srep23645

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Zhang L, Zhang X, Wu. H, Li C, Pierangeli D, Gao Y, et al. Anomalous interaction of Airy beams in the fractional nonlinear Schrödinger equation. Opt Express (2019) 27:27936. doi:10.1364/oe.27.027936

PubMed Abstract | CrossRef Full Text | Google Scholar

12. He S, Malomed BA, Mihalache D, Peng X, Deng D, Yu X, et al. Propagation dynamics of abruptly autofocusing circular Airy Gaussian vortex beams in the fractional Schrödinger equation. Chaos, Solitons and Fractals. (2021) 142:110470. doi:10.1016/j.chaos.2020.110470

CrossRef Full Text | Google Scholar

13. Huang C, Dong L. Beam propagation management in a fractional Schrödinger equation. Scientific Rep (2017) 7:5422. doi:10.1038/s41598-017-05926-5

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Wu Z, Cao S, Che W, Yang F, Zhu X, He Y. Solitons supported by parity-time-symmetric optical lattices with saturable nonlinearity in fra -ctional Schrödinger equation. Results Phys (2020) 19:103381. doi:10.1016/j.rinp.2020.103381

CrossRef Full Text | Google Scholar

15. Bo W, Liu W, Wang Y. Symmetric and antisymmetric solitons in the fractional nonlinear Schrödinger equation with saturable nonlinearity and PT-symmetric potential: Stability and dynamics. Optik (2022) 255:168697. doi:10.1016/j.ijleo.2022.168697

CrossRef Full Text | Google Scholar

16. Shi J, Zeng J. 1D solitons in saturable nonlinear media with space fractional derivatives. Annalen der Physik (2020) 532:1900385. doi:10.1002/andp.201900385

CrossRef Full Text | Google Scholar

17. Ren X, Deng F. Fundamental solitons in optical lattices with fractional-order diffraction. Opt Commun (2021) 495:127039. doi:10.1016/j.optcom.2021.127039

CrossRef Full Text | Google Scholar

18. Zhu X, Yang F, Cao S, Xie J, He Y. Multipole gap solitons in fractional Schrodinger equation with parity-time-symmetric optical lattices. Opt Express (2020) 28:1631–9. doi:10.1364/oe.382876

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Mejía-Cortés C, Molina MI. Fractional discrete vortex solitons. Opt Lett (2021) 46:2256–9. doi:10.1364/ol.421970

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Li P, Malomed BA, Mihalache D. Vortex solitons in fractional nonlinear Schrödinger equation with the cubic-quintic nonlinearity. Chaos, Solitons and Fractals (2020) 137:109783. doi:10.1016/j.chaos.2020.109783

CrossRef Full Text | Google Scholar

21. Zeng L, Zeng J. One-dimensional gap solitons in quintic and cubic-quintic fractional nonlinear Schrodinger equations with a periodically modulated linear potential. Nonlinear Dyn (2019) 98:985–95. doi:10.1007/s11071-019-05240-x

CrossRef Full Text | Google Scholar

22. Li P, Malomed BA, Mihalache D. Symmetry-breaking bifurcations and ghost states in the fractional nonlinear Schrödinger equation with a PT-symmetric potential. Opt Lett (2021) 46:3267. doi:10.1364/ol.428254

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Liu X, Malomed BA, Zeng J. Localized modes in nonlinear fractional systems with deep lattices. Adv Theor Simul. (2022) 5:2100482. doi:10.1002/adts.202100482

CrossRef Full Text | Google Scholar

24. Huang C, Dong L. Gap solitons in the nonlinear fractional Schrödinger equation with an optical lattice. Opt Lett (2016) 41:5636–9. doi:10.1364/ol.41.005636

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Dong L, Huang C. Double-hump solitons in fractional dimensions with a 𝒫𝒯–symmetric potential. Opt Express (2018) 26:10509–18. doi:10.1364/oe.26.010509

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Huang C, Dong L. Dissipative surface solitons in a nonlinear fractional Schrödinger equation. Opt Lett (2019) 44:5438–5441. doi:10.1364/ol.44.005438

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Xiao J, Tian Z, Huang C, Dong L. Surface gap solitons in a nonlinear fractional Schrödinger equation. Opt Express (2018) 26:2650–2658. doi:10.1364/oe.26.002650

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Su W, Deng H, Dong L, Huang Z, Huang C. Stabilization of fundamental solitons in the nonlinear fractional Schrödinger equation with PT-symmetric nonlinear lattices. Chaos, Solitons and Fractals (2020) 141:110427. doi:10.1016/j.chaos.2020.110427

CrossRef Full Text | Google Scholar

29. Huang C, Deng H, Dong L, Ye F. Fundamental solitons in the nonlinear fractional Schrödinger equation with a $\mathcal{PT}$ -symmetric potential. EPL (2018) 122:24002. doi:10.1209/0295-5075/122/24002

CrossRef Full Text | Google Scholar

30. Chen J, Zeng J. Spontaneous symmetry breaking in purely nonlinear fractional systems. Chaos (2020) 30:063131. doi:10.1063/5.0006050

PubMed Abstract | CrossRef Full Text | Google Scholar

31. Zeng L, Zeng J. Fractional quantum couplers. Chaos, Solitons and Fractals (2020) 140:110271. doi:10.1016/j.chaos.2020.110271

CrossRef Full Text | Google Scholar

32. Li L, Li H, Wen R, Leng F, Luo X. Gap solitons in parity-time-symmetric lattices with fractional-order diffraction. J Opt Soc Am B (2020) 37:488. doi:10.1364/josab.376975

CrossRef Full Text | Google Scholar

33. Zeng L, Zeng J. Preventing critical collapse of higher-order solitons by tailoring unconventional optical diffraction and nonlinearities. Comm Un Phys (2020) 3:26. doi:10.1038/s42005-020-0291-9

CrossRef Full Text | Google Scholar

34. Kartashov YV, Malomed BA, Torner L. Solitons in nonlinear lattices. Rev Mod Phys (2011) 83:247–305. doi:10.1103/revmodphys.83.247

CrossRef Full Text | Google Scholar

35. Kartashov YV, Vysloukh VA, Torner L. Soliton shape and mobility control in optical lattices. Prog Opt (2009) 52:63.

CrossRef Full Text | Google Scholar

36. Malomed BA. Soliton management in periodic systems. Heidelberg: Springer (2006).

Google Scholar

37. Guo D, Xiao J, Dong L, Jin H. One- and two-dimensional bright solitons in inhomogeneous defocusing nonlinearities with an antisymmetric periodic gain and loss. Physica.D. (2017) 343:1–6. doi:10.1016/j.physd.2016.11.005

CrossRef Full Text | Google Scholar

38. Zeng L, Zeng J. One-dimensional solitons in fractional Schrödinger equation with a spatially periodical modulated nonlinearity: Nonlinear lattice. Opt Lett (2019) 44:2661–2664. doi:10.1364/ol.44.002661

CrossRef Full Text | Google Scholar

39. Maimistov AI. Solitons in nonlinear optics. Quan Electron (2010) 40:756–81. doi:10.1070/qe2010v040n09abeh014396

CrossRef Full Text | Google Scholar

40. Dudley John M, Frédéric D, Miro E, Goëry G. Instabilities, breathers and rogue wave in optics. Nat.photon. (2014) 8:755.

CrossRef Full Text | Google Scholar

41. Liangwei D, Huang C, Qi W. Nonlocal solitons in fractional dimensions. Opt.Lett. (2019) 44:4917–4920. doi:10.1364/ol.44.004917

PubMed Abstract | CrossRef Full Text | Google Scholar

42. Borovkova OV, Kartashov YV, Torner L, Malomed BA. Bright solitons from defocusing nonlinearities. Phys.Rev E (2011) 84:035602. doi:10.1103/physreve.84.035602

PubMed Abstract | CrossRef Full Text | Google Scholar

43. Driben R, Kartashov YV, Malomed BA, Meier T, Torner L. Soliton gyroscopes in media with spatially growing repulsive nonlinearity. Phys Rev Lett (2014) 112:020404. doi:10.1103/physrevlett.112.020404

PubMed Abstract | CrossRef Full Text | Google Scholar

44. Huang C, Li C, Dong L. Gap solitons in fractional dimensions with a quasi-periodic lattice. Annalen Der Physik (2019) 531:1900056. doi:10.1002/andp.201900056

CrossRef Full Text | Google Scholar

45. Chen R, Dai C. Three-dimensional vector solitons and their stabilities in a Kerr medium with spatially inhomogeneous nonlinearity and transverse modulation. Nonlinear Dyn (2017) 88:2807–2816. doi:10.1007/s11071-017-3413-5

CrossRef Full Text | Google Scholar

46. Li L, Liu Y, Yu F. Some reverse space (RS) rational solutions for the nonlocal coupled nonlinear Schrödinger equations on the plane wave backgrounds. Appl Math Lett (2022) 129:107976. doi:10.1016/j.aml.2022.107976

CrossRef Full Text | Google Scholar

47. Li L, Yu F, Duan C. A generalized nonlocal Gross-Pitaevskii(NGP) equation with an arbitrary time-dependent linear potential. Appl Math Lett (2020) 110:106584. doi:10.1016/j.aml.2020.106584

CrossRef Full Text | Google Scholar

48. Yu FJ, Liu CP, Li L. Broken and unbroken solutions and dynamic behaviors for the mixed local-nonlocal Schrödinger equation. Appl Math Lett (2021) 117:107075. doi:10.1016/j.aml.2021.107075

CrossRef Full Text | Google Scholar

49. Huang C, Dong L, Zhang X. Asymmetric dissipative solitons in a waveguide lattice with non-uniform gain–loss distributions. Opt Lett (2020) 45:6699–6702. doi:10.1364/ol.409577

PubMed Abstract | CrossRef Full Text | Google Scholar

50. Wang R, Wang Y, Dai C. Dissipative solitons of the nonlinear fractional Schrödinger equation with PT-symmetric potential. Optik (2022) 254:168639. doi:10.1016/j.ijleo.2022.168639

CrossRef Full Text | Google Scholar

51. Dong L, Tian Z. Truncated-Bloch-wave solitons in nonlinear fractional periodic systems. Ann Phys (2019) 404:57–65. doi:10.1016/j.aop.2019.02.017

CrossRef Full Text | Google Scholar

52. Kartashov YV, Malomed BA, Shnir Y, Torner L. Twisted toroidal vortex solitons in inhomogeneous media with repulsive nonlinearity. Phys Rev Lett (2014) 113:264101. doi:10.1103/physrevlett.113.264101

PubMed Abstract | CrossRef Full Text | Google Scholar

53. Yang J, Lakoba TI. Universally-convergent squared-operator iteration methods for solitary waves in general nonlinear wave equations. Stud Appl.Math (2007) 118(2):153–197. doi:10.1111/j.1467-9590.2007.00371.x

CrossRef Full Text | Google Scholar

54. Yang J. Nonlinear waves in integrable and nonintegrable systems. Philadelphia: SIAM (2010).

Google Scholar

55. Shi J, Zeng J. Asymmetric localized states in periodic potentials with a domain wall-like Kerr nonlinearity. J Phys Commun (2019) 3:035003. doi:10.1088/2399-6528/ab07d1

CrossRef Full Text | Google Scholar