Lamb waves manipulation by piezoelectric metasurface with tunable diffraction orders

1 Introduction

The wave control method based on wavefront-manipulated metasurface has attracted much attention owing to its capability of accurately adjusting the wave phase. Metasurfaces have been developed for manipulating electromagnetic waves [1, 2], acoustic waves [3, 4], and elastic waves [5, 6]. Based on the generalized Snell’s law (GSL) [7], the phase-gradient metasurface is designed to adjust the relationship between the wave vectors of scattering and incident waves for achieving abnormal functions, such as wavefront shaping [3, 4, 8], cloaking [9], mode conversion [10–12], and splitting [13].

According to the classical GSL, the incident wave should be within a critical angle to obtain a non-zero refracted wave. However, recent studies indicate that high-order-mode diffraction may occur when the incident angle is greater than the critical angle, which provides a new approach for manipulating acoustic waves [14, 15] and elastic waves [16] for negative refraction or reflection with broad angles [17–19], asymmetric transmission [20–24], wave absorption [25], wave isolation [26], and wave guiding [27]. These phenomena and functions have broken the limitation of the GSL. Therefore, the mechanism of high-order-mode diffraction should be explored for manipulating wave propagation far beyond the GSL.

Compared with the acoustic wave, guided waves in structures with multiple modes and complex dispersive nature bring big challenges to control wave propagation, and their different desired functions are realized by different configurations of metasurfaces. Based on +1st-order and −1st-order diffraction, Li et al. [24] fabricated two kinds of zigzag metasurfaces with different supercells, realizing the symmetric transmission and asymmetric transmission, respectively. Based on 0th-order diffraction, Liu et al. [26] designed a circular meta-slab to isolate the flexural waves by total reflection, Cao et al. [23] used a dual-layer elastic gradient metasurface to achieve the asymmetric transmission of flexural waves, and Hu et al. [27] realized the ultrathin waveguides using a channel bounded by two metasurfaces. The functionality of these metasurfaces depends on their diffraction orders. However, the diffraction order is determined by the fixed geometric configuration of the metasurface, whose diffraction order switching is difficult to realize. Moreover, for the metasurface based on the structural configuration, broadband application is hard to be achieved because the wave phase of the metasurface is sensitive to wavelength. Accordingly, it is urgent to introduce a tunable metasurface into the manipulation of high-order-mode diffraction, especially realizing the adjustment of diffraction order by the same metasurface.

Multi-physics coupling effect has good performance in tunable modulation of elastic waves without structural reconfiguration. Therefore, electromechanical coupling effects are favored by their capabilities of circuitry integration and controllability, whether in passive designs [28, 29] or active designs [30–36]. According to the GSL, when the metasurface is composed of PZT (lead zirconate titanate) patches connected with shunting circuits and is attached to the host plate, the tunable manipulations of anti-symmetric mode Lamb wave [37], shear horizontal wave [38], and multi-mode guided waves [39] in the plate can be realized by adjusting the parameters of the circuits. However, within severe constraints of the GSL, many fantastic performances of the metasurface cannot be realized. In addition, without changing the physical configuration, how to use the shunting circuit to achieve the control of diffraction order is still a key problem.

In this study, for conquering the limitation of the GSL on high-order diffraction, a tunable piezoelectric metasurface is proposed for controlling the anti-symmetric mode Lamb wave propagation with tunable diffraction order. The remainder of the paper is organized as follows: Section 2 introduces the integer parity design in the high-order-mode diffraction, and a metasurface that can control the diffraction order is further designed and investigated. To show the tunable control of diffraction orders, +1st, −1st, and 0th orders of diffraction are investigated as examples in the paper, and the corresponding special functions are investigated and exhibited in Section 3 and Section 4. In Section 3, the high-order anomalous refractions including symmetric transmission and asymmetric transmission are realized based on +1st and −1st orders of diffraction. Then, in Section 4, the omnidirectional reflection and channelized waveguides are realized based on 0th-order diffraction. Finally, Section 5 summarizes the paper and provides conclusions.

2 Modulation of diffraction order

2.1 Integer parity design

The distribution of phase-shift gradient is an important factor in the study of high-order-mode diffraction. Here, the phase shift is described as the difference in wave phases between the incident wave and the transmitted wave changed by the metasurface. By designing a phase-gradient metasurface, which is equivalent to a periodic lattice, the diffraction mechanism [17, 22] in the metasurface can be described as

$\left(\sin {\theta }_{\text{tra}/\mathrm{r}\mathrm{e}\mathrm{f}}-\sin {\theta }_{\text{inc}}\right)k=\xi +n_{G}G,(1)$

where θ_inc is the angle of the incident wave, θ_tra/ref is the angle of the transmitted or reflected wave, k = 2π/λ is the wavenumber, λ is the wavelength (assuming that the incident area and transmitted area have the same medium), ξ is the phase gradient along the metasurface, n_G is an integer which represents the effect of periodicity, and G is the lattice constant of reciprocal lattice. In Eq. 1, the phase gradient ξ can be expressed as ξ = dϕ/dx₂, where ϕ is the phase shift and x₂ is the coordinate axis along the metasurface. ξ can be assumed as positive because the positive and negative phase gradients are physically equivalent.

To simplify the design of the metasurface, a supercell with length S in the metasurface is introduced by including m functional units as shown in Figure 1A to realize the distribution of the phase gradient over a complete 0 ∼ 2π range. Therefore, the phase shift of the jth functional unit in the supercell is set at ${\varphi }_j=2\pi j/m\left(j=1,2,\dots ,m\right)$. For the functional unit with a fixed width W, the width of the supercell is determined by including m function units, that is, S = mW. Thus, ξ can be written as the gradient of phase shifts in adjacent functional units, that is, ξ = Δϕ/W. In the supercell with m functional units, it can also be written as ξ = (mΔϕ)/(mW) = 2π/S. In addition, G can be written as G = 2π/p for a one-dimensional case, where p = S is the lattice constant of primitive lattice. So, G = 2π/S, and the values of ξ and G are naturally equal. For a single supercell, Eq. 1 is rewritten as

$\sin {\theta }_{\text{inc}}+n\frac{\lambda }{S}=\sin {\theta }_{\text{tra}/\mathrm{r}\mathrm{e}\mathrm{f}},(2)$

where n = n_G+1 is the diffraction order $\left(n=0,\pm 1,\pm 2,\dots \right)$. λ/S in Eq. 2 plays a role similar to the phase gradient, so it is not distinguished from the phase gradient in the following sections. The positive and negative angles are specified in Figure 1A, which is the same as traditional refraction and reflection theories.

FIGURE 1

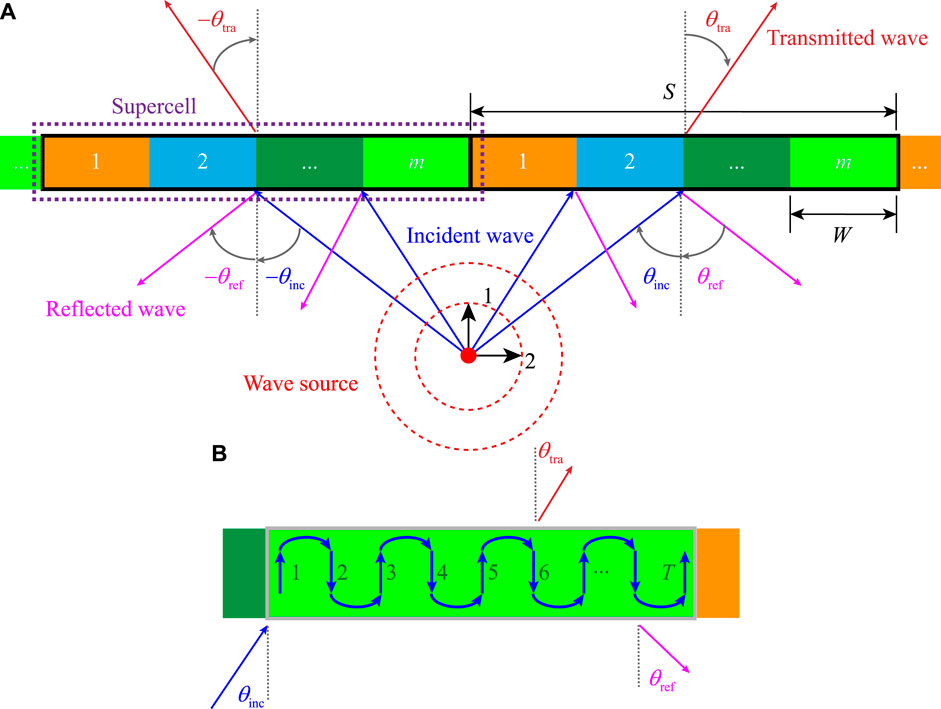
FIGURE 1. (A) Metasurface designed by supercells, and each supercell includes m functional units. (B) Wave propagation path in each functional unit.

For the case of n = 1, Eq. 2 can be reduced to the GSL. For the case of n ≠ 1, the wave diffraction can be described as the result of multiple reflections of the wave in the functional unit. Figure 1B illustrates the process of wave propagating in the functional unit for T times to reach its boundary. For example, if T = 1, it means that the incident wave passes through the functional unit directly as the transmitted wave. If T = 2, it means that the incident wave has one-time reflection in the functional unit and then leaves it at the incident side to be the reflected wave. Considering two adjacent functional units in the supercell, if both have (T−1) times inside reflections, the difference between their phase shifts becomes the cumulative phase of T-time wave propagation, that is, $\mathrm{\Delta }\varphi =T\left({\varphi }_{j+1}-{\varphi }_j\right)=2\pi T/m$. Thus, the +1st-order diffraction (GSL) can also be considered to have the shortest path with T = 1. For the case of n > 1, because λ/S is positive, the GSL will also be satisfied, if Eq. 2 is satisfied for the nth-order diffraction. However, the diffraction orders with n > 1 can be neglected, and the +1st order diffraction can replace them with the shortest path; this is because the wave diffraction prefers to follow the tendency for the shortest path of wave propagation [40]. Therefore, the actual range of n is reduced to n = +1, 0, − 1, − 2, ….

For the case of n ≤ 0, the difference between phase shifts of two adjacent functional units can also be written as Δϕ′ = 2πn/m according to Eq. 2, which is the nth-order diffraction wave. Furthermore, the relationship of phase shifts between two adjacent functional units can be established by using the plane wave expression method as e^iΔϕ = e^iΔϕ′, that is, $e^{i\left(2\pi T/m\right)}=e^{i\left(2\pi n/m\right)}$. For the diffraction order n ≤ 0, a positive integer Z is introduced to lead 2πT/m = 2πn/m + 2πZ, which is simplified to T = n + mZ. Because the wave propagates following the shortest path in the functional unit, the number Z is taken as 1, and then a relationship in a supercell with m functional units can be established as

$T=m+n.(3)$

If T is an odd number, the incident wave transmits through the supercell, and if T is an even number, the total reflection occurs. Consequently, by combining Eqs 2 and 3, the diffraction relation is summarized as

$\begin{array}{cc}\hfill \sin {\theta }_{\text{inc}}+n\frac{\lambda }{mW}& =\sin {\theta }_{\text{tra}},T=m+n\mathrm{i}\mathrm{s}\mathrm{o}\mathrm{d}\mathrm{d},\hfill \\ \hfill \sin {\theta }_{\text{inc}}+n\frac{\lambda }{mW}& =\sin {\theta }_{\text{ref}},T=m+n\mathrm{i}\mathrm{s}\mathrm{e}\mathrm{v}\mathrm{e}\mathrm{n}.\hfill \end{array}(4)$

Therefore, the relationship between transmission/reflection of the wave and diffraction order n of the supercell is established by the wave propagating path, which is related to the addition of m and n. It means that the performance of wave propagation can be altered by changing the number of functional units m in a supercell or the diffraction order n.

2.2 Tunable capability of the piezoelectric functional unit

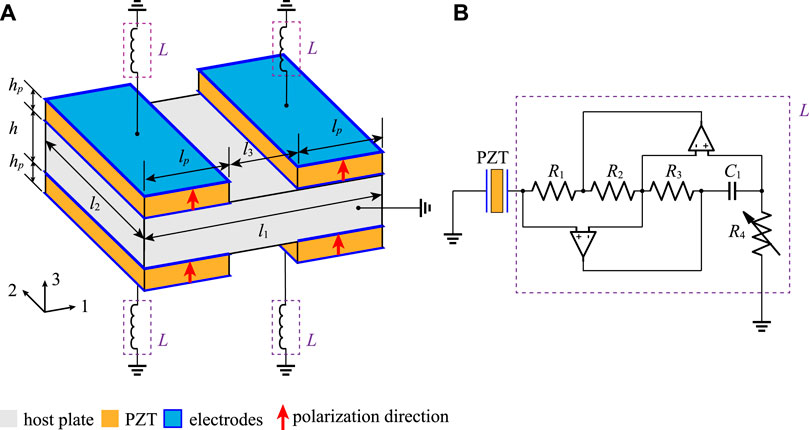
According to Eq. 4, the transmission or reflection of a wave can be controlled by the number of functional units m when the diffraction order n is determined. Actually, m and n are not independent in a strict sense. The applicable diffraction order of the existing metasurface is set by the distribution of the phase gradient in the supercell with fixed m. Recent studies [23–27] only used different structures of metasurfaces to realize different functional units m and then obtain the desired diffraction orders. In order to obtain a variable number m in the same metasurface, a basic functional unit based on the electromechanical coupling effect is designed by attaching PZT patches on both surfaces of the host plate as shown in Figure 2A. In the functional unit, four PZT patches (orange) with thin electrodes (blue) are symmetrically attached on both surfaces of the host plate (gray). To realize the manipulation of Lamb waves in the plate, each PZT patch is polarized along three directions [37], which are marked with red arrows in Figure 2A, and connected to an adjustable inductance L through the electrode on its surface. The effective capacitance of the PZT patch C_p and the shunting inductance L form a capacitance–inductance resonant system to alter the equivalent stiffness of the PZT patch [41, 42]. By adjusting the value of shunting inductance L, the equivalent stiffness of the PZT patch can be adjusted accordingly, and then the propagation of Lamb waves can be manipulated by the functional unit.

FIGURE 2

FIGURE 2. (A) Functional unit with shunting inductance L. (B) Equivalent inductance circuit.

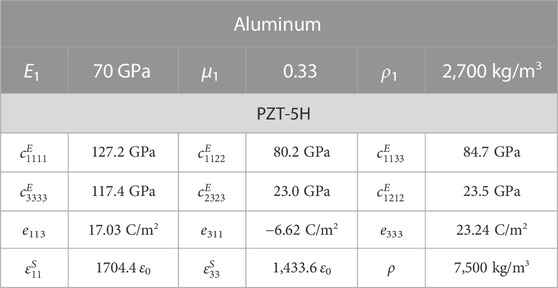
In fact, it is difficult to realize continuous adjustment of inductance using a real inductor. An adjustable synthetic inductor is achieved by using Antonio’s circuit [42] as shown in Figure 2B, which consists of two operational amplifiers, a capacitor (C₁), three resistors (R₁, R₂, and R₃), and an adjustable resistor (R₄). The equivalent inductance of the synthetic circuit is induced by L = R₁R₃R₄C₁/R₂, which is easily and continuously tuned by changing R₄. The host plate in the functional unit is designed as l₁ × l₂ = 12 mm × 8 mm with the height h = 2 mm. The size of the PZT patch is l_p × l₂ × h_p = 5 mm × 8 mm × 1 mm, and the gap between two PZT patches is l₃ = 2 mm. The material parameters of the host plate (aluminum) and PZT patch (PZT-5H) are listed in Table 1, where the crystal symmetry of PZT-5H is 4 mm.

TABLE 1

TABLE 1. Material parameters.

Without the loss of generality, the propagation of the anti-symmetric mode Lamb wave A₀ in the aluminum plate is studied. To quantitatively evaluate the capability of a functional unit for manipulating A₀-mode Lamb wave propagation, wave propagation in a host aluminum plate with one functional unit is considered, as shown in Figure 3A. To illustrate the propagation of the A₀-mode Lamb wave in the plate, the incident A₀-mode Lamb wave is excited at the left side of the functional unit, periodic boundary conditions are applied to both upper and lower sides of the host plate, and the perfectly matched layers (PMLs) are attached to both left and right sides of the host plate. The wave propagation process is calculated by the finite element method (FEM) via commercial software COMSOL Multiphysics. To obtain reliable calculation results, the functional unit is meshed by quadratic serendipity elements with a size smaller than one-tenth of the wavelength, and the mesh is appropriately encrypted near PZT patches. For the stable A₀-mode Lamb wave excited at a frequency of 14 kHz with the wavelength λ = 0.037 m, the transmission ratio, which is described as the ratio of amplitudes of out-of-plane displacements (|w|) for the transmitted signal to the incident signal, and the phase shifts are calculated as the shunting inductance L changing from 0.095 H to 0.140 H as shown in Figure 3B. The results show that the phase shifts of the functional unit cover a full 0 ∼ 2π range, and the transmission ratio is relatively high (above 0.8). Consequently, the functional unit can be an elementary unit of the supercell to achieve an arbitrary phase shift in a 0 ∼ 2π range by only adjusting the shunting inductance. For a metasurface fabricated by a series of proposed functional units, the number of functional units m in a supercell can be changed by appropriately selecting the phase shift of each functional unit, and the supercell makes the diffraction order to be changeable in the same metasurface.

FIGURE 3

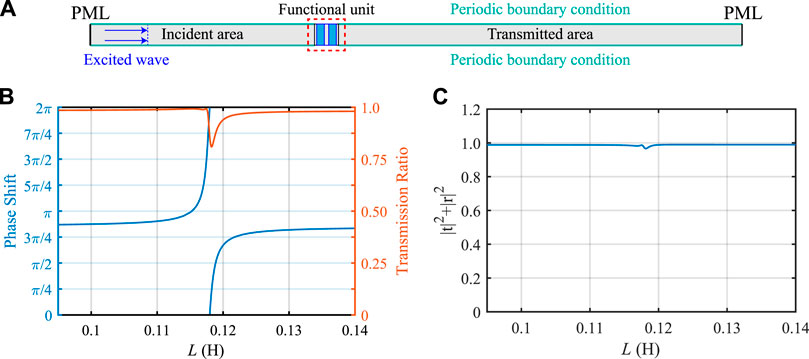
FIGURE 3. (A) Plate with one functional unit. (B) Phase shift and transmission ratio and (C) the sum of square of the transmission ratio and square of the reflection ratio of the A₀-mode Lamb wave at frequency 14 kHz with varying L.

In addition, Figure 3C illustrates the sum of the square of the transmission ratio |t|² and square of the reflection ratio (the ratio of |w| for the reflected signal to incident signal) |r|² to show the energy loss of the A₀-mode Lamb wave at frequency 14 kHz. The wave phase changes due to the local resonance of the PZT patch with a shunting circuit, which will inevitably consume energy. Therefore, the total energy is slightly less than 1, especially near the formant frequency. However, the sum is close to 1 with altering inductance L in general. It means that there is almost no strong energy loss and mode conversion of the wave by passing though the functional unit. Furthermore, the phase shifts, transmission ratios, and reflection ratios of the functional unit at an arbitrary frequency in the range from 10 to 30 kHz can also be calculated by FEM via commercial software COMSOL Multiphysics, and the effectivity of the functional unit to manipulate the A₀-mode Lamb wave by adjusting the shunting inductance L is verified.

3 High-order anomalous refraction

To avoid the effect of higher order diffraction, the relation between the wavelength λ and the length of the supercell S should be

$1<\lambda /S<2.(5)$

In addition, because the value of (sin θ_tra/ref − sin θ_inc) ranges from −2 to 2, according to Eq. 2, only three diffraction orders (n = +1, 0, − 1) exist for any incident angle. It is noteworthy that the 0th-order diffraction may occur, that is, θ_inc = θ_tra or θ_inc = θ_ref. Eq. 3 indicates that, for the case of n ≤ 0, the 0th-order diffraction is the longest path. Hence, if other order diffraction waves exist, the amplitude of the 0th order diffraction wave is very small.

3.1 Symmetric transmission

If two A₀-mode Lamb waves are incident with two opposite angles about the normal line of the metasurface, their transmitted angles are still opposite to each other, so they should satisfy the following condition:

$\begin{array}{cc}\hfill \sin \left(-{\theta }_{\text{inc}}\right)+n_1\frac{\lambda }{S}& =\sin {\theta }_{\text{tra}},\hfill \\ \hfill \sin \left(+{\theta }_{\text{inc}}\right)+n_2\frac{\lambda }{S}& =\sin \left(-{\theta }_{\text{tra}}\right),\hfill \end{array}(6)$

and n₁ = −n₂, for realizing the symmetric transmission. Obviously, the symmetric transmission cannot be achieved by the GSL. Considering Eq. 5, only diffraction of +1st, −1st, and 0th orders exists in the metasurface, so that the diffraction orders of symmetric transmission in Eq. 6 are n₁ = −n₂ = 1. The incident wave with the negative incident angle −θ_inc is noted as NI and with the positive incident angle +θ_inc is noted as PI. Eq. 6 indicates that for the angles of NI and PI with axial symmetry about the normal line of the metasurface, their transmitted waves manipulated by the metasurface can have the axial symmetry and travel at the same side of incident waves.

According to Eq. 4, T = m + n should be an odd number to guarantee that the wave will transmit through the metasurface. For the critical incident angle of the +1st-order diffraction (GSL) θ_c1 = arcsin(1 − λ/S), the incident angle of NI should satisfy −θ_inc < θ_c1, while the angle of PI should satisfy +θ_inc > θ_c1 with the existence condition of −1st-order diffraction, −1 < sin(+θ_inc) − λ/S < 1.

There are 64 functional units to be arranged as the tunable metasurface in an aluminum plate as shown in Figure 3A for manipulating the A₀-mode Lamb wave at frequency 14 kHz. An interval l₄ = 0.001 m is set between all adjacent functional units to ensure that the phase shift modulation of the wave by each functional unit is independent and free from interference. Therefore, the length of the supercell can be obtained as S = m(l₂+l₄). When the difference in phase shifts between two adjacent functional units is π/2, a supercell needs four functional units, m = 4, to form the distribution of phase shifts in the range of 0 ∼ 2π as shown in Figure 4A, so the metasurface totally includes 16 supercells. In Figure 4A, the orange rectangles represent the functional units. The length of the supercell with four functional units as shown in Figure 4A is S_m=4 = 0.036 m, and it satisfies the condition expressed in Eq. 5. The critical angle of +1st-order diffraction is θ_c1 = −1.59°, which means that most of the incident angles can realize the symmetric transmission. For the incident angles of 30° and 15°, the transmitted angles θ_tra can be calculated by Eq. 6, and the values are 31.86° (θ_inc = 30°) and 50.26° (θ_inc = 15°), respectively. FEM is conducted to verify the analytical result, and the numerical results of out-of-plane displacement fields about incident and transmitted waves with NI and PI of 30° are shown in Figures 4B1, B2, respectively, while Figures 4C1, C2 show the results with NI and PI of 15°, respectively. The white arrows in Figures 4B, C point out the designed propagation directions of incident and transmitted waves. Compared with the displacement fields of wave motion, the propagation of refraction waves is in good agreement with designs. The results shown in Figures 4B, C illustrate that two incident angles with the same value but contrary signs can manipulate the refraction waves by the metasurface to transmit waves at the same sides along the designed transmitted angles with axial symmetry about the normal line of the metasurface.

FIGURE 4

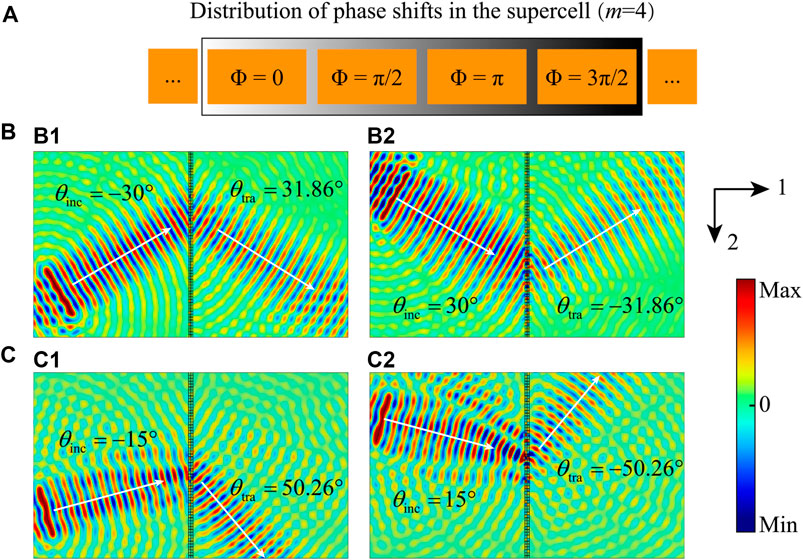
FIGURE 4. (A) Distribution of phase shifts along the supercell with m = 4. Out-of-plane displacement fields of (B) ± 30° and (C) ± 15° incident angles.

3.2 Asymmetric transmission

In general, for the angles of NI and PI with axial symmetry about the normal line of the metasurface, their transmitted waves manipulated by the metasurface can be without axial symmetry and propagate along arbitrary directions and are called as asymmetric transmission. Here, we consider one special case of generalized asymmetric transmission, which is that the angles of NI and PI have axial symmetry about the normal line of the metasurface; however, NI can pass through the metasurface, while PI is reflected by the metasurface. The corresponding condition for this case is

$\begin{array}{cc}\hfill \sin \left(-{\theta }_{\text{inc}}\right)+n_1\frac{\lambda }{S}& =\sin {\theta }_{\text{tra}},\hfill \\ \hfill \sin \left(+{\theta }_{\text{inc}}\right)+n_2\frac{\lambda }{S}& =\sin \left(-{\theta }_{\text{ref}}\right),\hfill \end{array}(7)$

where n₁ = 1 and n₂ = −1 are the diffraction orders of NI and PI, respectively. In Eq. 7, the angles of NI and PI still have axial symmetry, and even the angles of transmitted/reflected waves maintain numerical axial symmetry. NI transmits through the metasurface following the GSL, and according to Eq. 3, T = m + n₂ = m−1 should be an even number to make sure that the PI will be reflected by the metasurface. Figure 5A illustrates the distribution of phase shifts along the supercell with three functional units, m = 3. For manipulating the A₀-mode Lamb wave at frequency 14 kHz, according to Eq. 5, the ratio λ/S_m=3 = 1.370 makes sure that only −1st, +1st, and 0th orders of diffraction can exist in the metasurface. The critical angle of the +1st-order diffraction can be calculated as θ_c1 = −21.74°. Different from the symmetric transmission of NI and PI in the supercell with m = 4, the limitation to the incident angle should be considered to realize asymmetric transmission. If the incident angle is smaller than θ_c1 = −21.74°, according to Eq. 7, only n₁ = n₂ = 0 satisfies the diffraction equations and only reflected waves occur for both NI and PI.

FIGURE 5

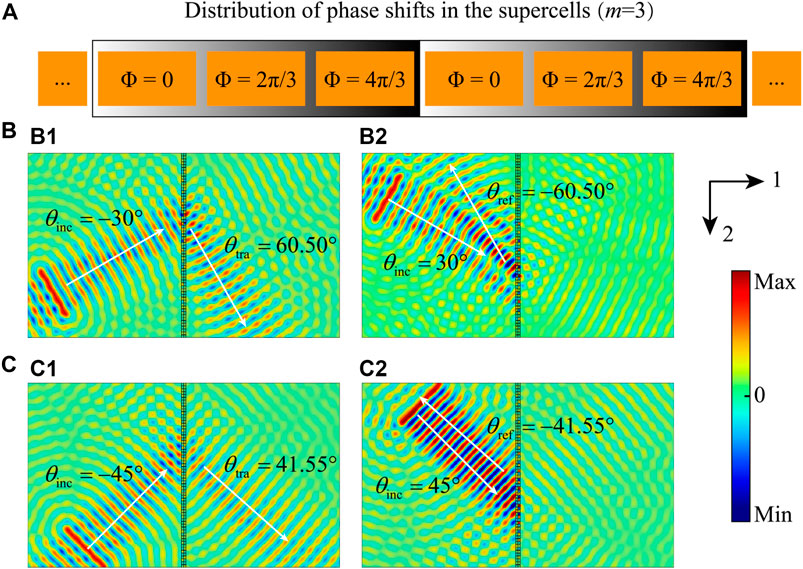
FIGURE 5. (A) Distribution of phase shifts along the supercell with m = 3. Out-of-plane displacement fields of (B) ± 30° and (C) ± 45° incident angles.

Figures 5B, C show the out-of-plane displacement fields of A₀-mode Lamb waves calculated by FEM for the cases with the NI and PI angles of 30° and 45°, respectively. The transmitted or reflected angles θ_tra/ref of both cases can be calculated according to Eq. 7 to be 60.50° (θ_inc = 30°) and 41.55° (θ_inc = 45°), respectively. The white arrows in Figures 5B, C illustrate the designed propagation directions of waves, and the results are in good agreement with the designed angles. In Figures 5B1, B2, the angles of NI and PI are axial symmetry with 30°, but for the NI in Figure 5B1, the wave transmits through the metasurface with the designed angle 60.50°, while for the PI in Figure 5B2, the wave reflects backward by the metasurface with the designed angle −60.50°. The same tendency can be observed by the NI and PI cases of axial symmetry with angle 45° in Figures 5C1, C2. In addition, there are very low fluctuations to be observed in Figures  4B, C, 5B, C. There are two reasons that cause the chaotic disturbance. One is because the phase gradient of the realistic metasurface is discrete, so a few waves directly pass through the metasurface. The other one is because the 0th-order diffraction still exists in the symmetric and asymmetric transmissions based on +1st- and −1st- orders of diffraction but with negligible low amplitudes.

It should be noted that the transmission of NI and reflection of PI in asymmetric transmission are determined for the positive phase gradient. Their functions can be exchanged when the sign of the phase gradient is inverted, which is also applied in symmetric transmission. The symmetric and asymmetric transmissions are realized by the same metasurface based on the tunability of diffraction orders. It also means that the function is tunable to meet different demands and conquer the main drawback of the existing metasurfaces.

4 Omnidirectional reflection and channelized waveguides

4.1 Omnidirectional reflection

In Section 3, the relation between wavelength and length of the supercell is restricted by Eq. 5 to avoid the generation of higher order diffraction in the metasurface. The 0th-order diffraction has the longest path among all the diffraction orders with n ≤ 0 in the same supercell according to Eq. 3. Thus, if the 0th-order diffraction is used for designing the metasurface with a higher amplitude, all the other order diffraction should be suppressed. Based on Eq. 2, the supercell should be designed to satisfy the condition of λ/S > 2 to make sure that no diffraction wave exists except n = 0. As an example, for the A₀-mode Lamb wave at frequency 14 kHz, the supercell with two functional units, m = 2, can satisfy the condition λ/S_m=2 = 2.06 > 2. Accordingly, when n = 0, T = m + n = 2 is an even number and Eq. 4 becomes sin θ_inc = sin θ_ref, which means that the wave only reflects directly along the same angle as the incident one no matter which angle the incident wave is. Therefore, the omnidirectional reflection wave is easily realized by the 0th-order diffraction.

For the supercell with two functional units, m = 2, the distribution of phase shifts is illustrated in Figure 6A. There are three cases of A₀-mode Lamb waves at frequency 14 kHz with the angles of NI as 0°, 30°, and 60°, respectively, to be calculated by FEM, and their out-of-plane displacement fields are shown in Figure 6B. The white arrows in Figure 6B mark the designed directions of incident waves and reflected waves. The results in Figure 6B are in good agreement with the designed arrows and show nearly total reflections in these cases.

FIGURE 6

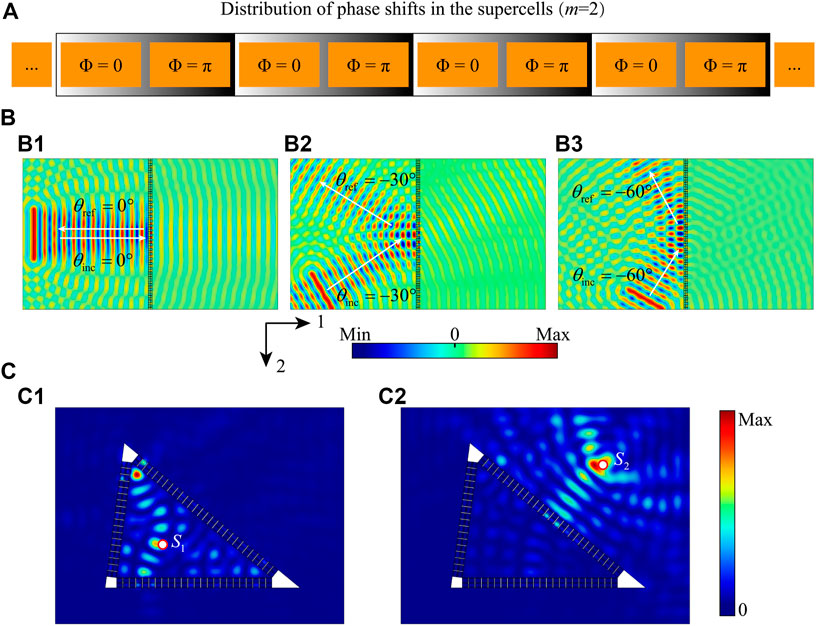
FIGURE 6. (A) Distribution of phase shifts along the supercell with m = 2. (B) Out-of-plane displacement fields of 0°, −30°, and −60° incident angles. (C) Energy field when a point source is placed inside and outside the triangle-shaped metasurface.

To further demonstrate that wave reflection is independent of the incident angle, a triangle-shaped metasurface is constructed by the supercell with m = 2. A point source (S₁) is placed in a random position inside the triangle-shaped metasurface, and the energy field (represented by |w|²) is shown in Figure 6C1. The result shows that the wave energy is enclosed in the triangle, and no wave is transmitted anywhere outside the triangle. When the point source (S₂) is moved outside the triangle-shaped metasurface, the wave energy can be isolated by the triangle as the energy field (|w|²) as shown in Figure 6C2. Therefore, the metasurface with the capability of omnidirectional reflection can make the wave energy to be concentrated inside the structure or isolated outside the structure, which exhibits exciting prospects for wave isolation.

4.2 Channelized waveguide

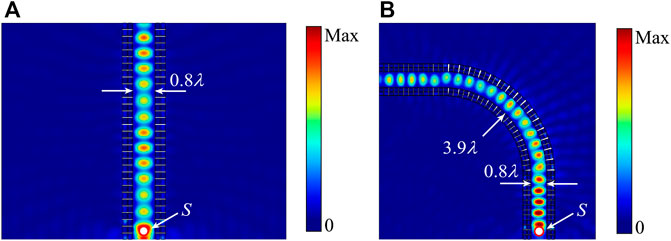
The supercell with m = 2 shows the strong ability to reflect the wave energy with an arbitrary incident angle. To deeply utilize the property, a channel is constructed by two metasurfaces as the route for wave propagation. When the wave propagates in the channel, it will be reflected by the metasurface boundary regardless of the incident angle. The channel can provide only one way for the wave to travel, despite its shape, that is, straight or curved. Figure 7 shows two examples of channelized waveguides for the A₀-mode Lamb wave at frequency 14 kHz: one is a straight line and the other is in “L” shape. Figure 7A shows the energy field of out-of-plane displacement (|w|²) in a straight channel formed by metasurfaces based on the supercell with m = 2. The white dot with a red circle marks the location of the wave source. The width of the channel is selected smaller than the wavelength as 0 .8λ to avoid the generation of wave interference [27]. The result shows that the wave is trapped in the channel and propagates straight forward. If the channel is turned to form an “L”-shaped channel by metasurfaces, the energy field shows that the wave travels through the channel with high amplitude as shown in Figure 7B. Therefore, for two metasurfaces with omnidirectional reflection using the 0th-order diffraction, different shapes of waveguides can be designed to realize wave propagation along any designed route in the plate.

FIGURE 7

FIGURE 7. Energy field of (A) a linear waveguide and (B) an “L”-shaped waveguide.

5 Conclusion

In this paper, a tunable piezoelectric metasurface is introduced to manipulate anomalous transmission and reflection of the anti-symmetric mode Lamb wave for achieving specific functions. The functional unit of the metasurface is symmetrically attached to piezoelectric patches with shunting inductance circuits on the host plate, and its phase shift can be arbitrarily tuned in the range of 0 ∼ 2π with wide frequency by adjusting the shunting inductance circuits. Without changing the physical configuration of the piezoelectric metasurface, the functional unit number of a supercell in the metasurface can be flexibly reprogrammed by properly adjusting the shunting inductance circuits for the desired phase shift distribution, and it can meet different requirements of manipulating wave propagation by the design and utilization of different orders of diffraction. Four kinds of exceptional functions are realized by tuning the diffraction orders in the metasurface. By utilizing the +1st-order and −1st-order diffraction, a couple of axis symmetric incident waves can achieve two functions: one is the symmetric transmission to obtain two transmitted waves with axis symmetry, and the other one is the asymmetric transmission to produce two separate transmitted and reflected waves with the same angle but contrary sign. By utilizing the 0th-order diffraction, the omnidirectional reflection can be achieved and arbitrary channelized waveguides can be designed. Similarly, other specific functions with higher order diffraction can also be realized by the same metasurface. Consequently, this proposed metasurface can promote the research beyond generalized Snell’s law by adjusting the shunting inductance circuits to achieve tunable high-order diffraction, and it has robustness, intelligence, and multifunctionality for manipulation of wave propagation. The metasurface has exhibited fair prospects of potential applications in wave motion control, wave isolation, and other fields.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material. Further inquiries can be directed to the corresponding author.

Author contributions

SS: conceptualization, methodology, software, validation, visualization, and writing—original draft. JC: validation and visualization. RX: software, validation, and writing—review and editing. ZL: conceptualization, funding acquisition, supervision, and writing—review and editing.

Funding

This work was supported by the National Natural Science Foundation of China under Grant Nos 11890681 and  12172008.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Aieta F, Genevet P, Yu N, Kats MA, Gaburro Z, Capasso F. Out-of-plane reflection and refraction of light by anisotropic optical antenna metasurfaces with phase discontinuities. Nano Lett (2012) 12:1702–6. doi:10.1021/nl300204s

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Yu N, Capasso F. Flat optics with designer metasurfaces. Nat Mater (2014) 13:139–50. doi:10.1038/nmat3839

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Li Y, Liang B, Gu ZM, Zou XY, Cheng JC. Reflected wavefront manipulation based on ultrathin planar acoustic metasurfaces. Scientific Rep (2013) 3:2546. doi:10.1038/srep02546

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Li Y, Jiang X, Liang B, Cheng JC, Zhang L. Metascreen-based acoustic passive phased array. Phys Rev Appl (2015) 4:024003. doi:10.1103/PhysRevApplied.4.024003

CrossRef Full Text | Google Scholar

5. Zhu H, Semperlotti F. Anomalous refraction of acoustic guided waves in solids with geometrically tapered metasurfaces. Phys Rev Lett (2016) 117:034302. doi:10.1103/PhysRevLett.117.034302

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Liu Y, Liang Z, Liu F, Diba O, Lamb A, Li J. Source illusion devices for flexural Lamb waves using elastic metasurfaces. Phys Rev Lett (2017) 119:034301. doi:10.1103/PhysRevLett.119.034301

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Yu N, Genevet P, Kats MA, Aieta F, Tetienne JP, Capasso F, et al. Light propagation with phase discontinuities: Generalized laws of reflection and refraction. Science (2011) 334:333–7. doi:10.1126/science.1210713

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Qiu H, Li F. Manipulation of shear horizontal guided wave with arbitrary wave fronts by using metasurfaces. J Phys D: Appl Phys (2020) 53:285301. doi:10.1088/1361-6463/ab850d

CrossRef Full Text | Google Scholar

9. Li H, Hou Z, Pei Y. The holographic algorithm and design for propagation of flexural Lamb waves and particles manipulation using elastic metasurfaces. Extreme Mech Lett (2022) 54:101765. doi:10.1016/j.eml.2022.101765

CrossRef Full Text | Google Scholar

10. Kim MS, Lee WR, Kim YY, Oh JH. Transmodal elastic metasurface for broad angle total mode conversion. Appl Phys Lett (2018) 112:241905. doi:10.1063/1.5032157

CrossRef Full Text | Google Scholar

11. Lee SW, Seung HM, Choi W, Kim M, Oh JH. Broad-angle refractive transmodal elastic metasurface. Appl Phys Lett (2020) 117:213502. doi:10.1063/5.0026928

CrossRef Full Text | Google Scholar

12. Li X, Chen Y, Zhang X, Huang G. Shaping elastic wave mode conversion with a piezoelectric-based programmable meta-boundary. Extreme Mech Lett (2020) 39:100837. doi:10.1016/j.eml.2020.100837

CrossRef Full Text | Google Scholar

13. Su X, Lu Z, Norris AN. Elastic metasurfaces for splitting SV- and P-waves in elastic solids. J Appl Phys (2018) 123:091701. doi:10.1063/1.5007731

CrossRef Full Text | Google Scholar

14. Assouar B, Liang B, Wu Y, Li Y, Cheng JC, Jing Y. Acoustic metasurfaces. Nat Rev Mater (2018) 3:460–72. doi:10.1038/s41578-018-0061-4

CrossRef Full Text | Google Scholar

15. Park JH, Ma PS, Lee HJ. Integrated acoustic multilayer metasurfaces for high degree of diffractive functionality. Int J Mech Sci (2022) 233:107653. doi:10.1016/j.ijmecsci.2022.107653

CrossRef Full Text | Google Scholar

16. Cao L, Yang Z, Xu Y. Steering elastic SH waves in an anomalous way by metasurface. J Sound Vib (2018) 418:1–14. doi:10.1016/j.jsv.2017.12.032

CrossRef Full Text | Google Scholar

17. Xie Y, Wang W, Chen H, Konneker A, Popa BI, Cummer SA. Wavefront modulation and subwavelength diffractive acoustics with an acoustic metasurface. Nat Commun (2014) 5:5553. doi:10.1038/ncomms6553

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Liu B, Zhao W, Jiang Y. Apparent negative reflection with the gradient acoustic metasurface by integrating supercell periodicity into the generalized law of reflection. Sci Rep (2016) 6:38314. doi:10.1038/srep38314

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Liu B, Zhao W, Jiang Y. Full-angle negative reflection realized by a gradient acoustic metasurface. AIP Adv (2016) 6:115110. doi:10.1063/1.4967430

CrossRef Full Text | Google Scholar

20. Shen C, Xie Y, Li J, Cummer SA, Jing Y. Asymmetric acoustic transmission through near-zero-index and gradient-index metasurfaces. Appl Phys Lett (2016) 108:223502. doi:10.1063/1.4953264

CrossRef Full Text | Google Scholar

21. Li Y, Shen C, Xie Y, Li J, Wang W, Cummer SA, et al. Tunable asymmetric transmission via lossy acoustic metasurfaces. Phys Rev Lett (2017) 119:035501. doi:10.1103/PhysRevLett.119.035501

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Fu Y, Shen C, Cao Y, Gao L, Chen H, Chan CT, et al. Reversal of transmission and reflection based on acoustic metagratings with integer parity design. Nat Commun (2019) 10:2326. doi:10.1038/s41467-019-10377-9

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Cao L, Xu Y, Assouar B, Yang Z. Asymmetric flexural wave transmission based on dual-layer elastic gradient metasurfaces. Appl Phys Lett (2018) 113:183506. doi:10.1063/1.5050671

CrossRef Full Text | Google Scholar

24. Li B, Hu Y, Chen J, Su G, Liu Y, Zhao M, et al. Efficient asymmetric transmission of elastic waves in thin plates with lossless metasurfaces. Phys Rev Appl (2020) 14:054029. doi:10.1103/PhysRevApplied.14.054029

CrossRef Full Text | Google Scholar

25. Cao L, Yang Z, Xu Y, Fan SW, Zhu Y, Chen Z, et al. Flexural wave absorption by lossy gradient elastic metasurface. J Mech Phys Sol (2020) 143:104052. doi:10.1016/j.jmps.2020.104052

CrossRef Full Text | Google Scholar

26. Liu F, Shi P, Xu Y, Cao L, Shen Y, Yang Z. Total reflection of flexural waves by circular meta-slab and its application in vibration isolation. Int J Mech Sci (2021) 212:106806. doi:10.1016/j.ijmecsci.2021.106806

CrossRef Full Text | Google Scholar

27. Hu Y, Zhang Y, Su G, Zhao M, Li B, Liu Y, et al. Realization of ultrathin waveguides by elastic metagratings. Commun Phys (2022) 5:62. doi:10.1038/s42005-022-00843-0

CrossRef Full Text | Google Scholar

28. Xia R, Zhu J, Yi J, Shao S, Li Z. Guided wave propagation in multilayered periodic piezoelectric plate with a mirror plane. Int J Mech Sci (2021) 204:106539. doi:10.1016/j.ijmecsci.2021.106539

CrossRef Full Text | Google Scholar

29. Xia R, Shao S, Yi J, Zheng K, Negahban M, Li Z. Tunable asymmetric transmission of Lamb waves in piezoelectric bimorph plates by electric boundary design. Compos Struct (2022) 300:116111. doi:10.1016/j.compstruct.2022.116111

CrossRef Full Text | Google Scholar

30. Li X, Chen Y, Hu G, Huang G. A self-adaptive metamaterial beam with digitally controlled resonators for subwavelength broadband flexural wave attenuation. Smart Mater Struct (2018) 27:045015. doi:10.1088/1361-665X/aab167

CrossRef Full Text | Google Scholar

31. Kumar S, Pueh Lee H. Recent advances in active acoustic metamaterials. Int J Appl Mech (2019) 11:1950081. doi:10.1142/S1758825119500819

CrossRef Full Text | Google Scholar

32. Li X, Chen Y, Zhu R, Huang G. An active meta-layer for optimal flexural wave absorption and cloaking. Mech Syst Signal Process (2021) 149:107324. doi:10.1016/j.ymssp.2020.107324

CrossRef Full Text | Google Scholar

33. Yi J, Ma Z, Xia R, Negahban M, Chen C, Li Z. Structural periodicity dependent scattering behavior in parity-time symmetric elastic metamaterials. Phys Rev B (2022) 106:014303. doi:10.1103/PhysRevB.106.014303

CrossRef Full Text | Google Scholar

34. Wu Q, Shivashankar P, Xu X, Chen Y, Huang G. “Multifunctional composites for autonomic, adaptive and self-sustaining systems”. Engineering nonreciprocal wave dispersion in a nonlocal micropolar metabeam. J Compos Mater (2022) 002199832211405. doi:10.1177/00219983221140562

CrossRef Full Text | Google Scholar

35. Wu Q, Zhang X, Shivashankar P, Chen Y, Huang G. Independent flexural wave frequency conversion by a linear active metalayer. Phys Rev Lett (2022) 128:244301. doi:10.1103/PhysRevLett.128.244301

PubMed Abstract | CrossRef Full Text | Google Scholar

36. Ma F, Wang C, Liu C, Wu JH. Structural designs, principles, and applications of thin-walled membrane and plate-type acoustic/elastic metamaterials. J Appl Phys (2021) 129:231103. doi:10.1063/5.0042132

CrossRef Full Text | Google Scholar

37. Li S, Xu J, Tang J. Tunable modulation of refracted lamb wave front facilitated by adaptive elastic metasurfaces. Appl Phys Lett (2018) 112:021903. doi:10.1063/1.5011675

CrossRef Full Text | Google Scholar

38. Xia R, Yi J, Chen Z, Li Z. In situ steering of shear horizontal waves in a plate by a tunable electromechanical resonant elastic metasurface. J Phys D: Appl Phys (2020) 53:095302. doi:10.1088/1361-6463/ab5cbc

CrossRef Full Text | Google Scholar

39. Shao S, Xia R, Li Z. Tunable piezoelectric metasurface for manipulating multi-mode guided waves in plate. Eng Struct (2022) 270:114917. doi:10.1016/j.engstruct.2022.114917

CrossRef Full Text | Google Scholar

40. Saleh BE, Teich MC. Fundamentals of photonics. Hoboken: John Wiley & Sons (2019).

Google Scholar

41. Hagood N, von Flotow A. Damping of structural vibrations with piezoelectric materials and passive electrical networks. J Sound Vib (1991) 146:243–68. doi:10.1016/0022-460X(91)90762-9

CrossRef Full Text | Google Scholar

42. Wang G, Chen S, Wen J. Low-frequency locally resonant band gaps induced by arrays of resonant shunts with Antoniou’s circuit: Experimental investigation on beams. Smart Mater Struct (2011) 20:015026. doi:10.1088/0964-1726/20/1/015026

CrossRef Full Text | Google Scholar