Abstract
In this paper proposes a sensitivity analysis method based on a Polynomial Chaos Expansion (PCE) surrogate model for flexoelectric materials. The non-uniform rational B-splines (NURBS) basis functions to discretize the fourth-order partial differential equation for flexoelectricity and obtains a deterministic solution (electric potential). The mathematical expressions of surrogate model for the flexoelectric materials are established by considering uncertain parameters such as independent Young’s modulus, concentrated load and flexoelectric constants. The sensitivity expression is found by derivation the mathematical expression for the surrogate model. Moreover the finite difference method (FDM) are conducted in numerical examples to demonstrate the validity and correctness of the proposed algorithm.
1 Introduction
Flexoelectricity is a new electromechanical energy conversion mechanism that can be an alternative to piezoelectricity [1]. The flexoelectricity is relatively weak in bulk crystalline materials, resulting in little attention. However, with the advancement of nanotechnology, huge strain gradients can be obtained at small-length scales, leading to a new understanding of the flexoelectricity as a size-dependent phenomenon [2]. As compared to piezoelectricity, flexoelectricity theoretically be present in all dielectrics, including those with centrosymmetric crystal structures, and is therefore a more versatile electromechanical coupling mechanism [3]. The traditional Lagrangian interpolation function of Finite Element Method (FEM) can only provide C0 continuity requirements. The C0 continuity of the FEM cannot satisfy the C1 continuity requirement of the fourth-order partial differential equation for flexoelectricity. This requires other numerical methods to achieve the C1 continuity requirement. Isogeometric analysis (IGA) is one of the most popular numerical methods. It satisfies the continuity of C1 by enhancing the order of NURBS basis function [4]. IGA initially developed to unify computer-aided design (CAD) and computer-aided engineering (CAE), but the remarkable characteristics of IGA basis functions such as NURBS has been applied to many applications including mechanics of fracture [5], electromagnetics [6], acoustics [7–10], and optimizations [11–14].
The input parameters of simulation models are often characterized by high uncertainty, and the model parameters are difficult and inaccurate to estimate [15]. This can largely lead us to make erroneous judgments about the issues of concern. The uncertainty quantification of input parameters is an efficient way to address uncertainty, and it examines the uncertainty in the model from the input parameters. Uncertainty analysis methods including Monte Carlo simulation (MCs) [16–18], the random spectral approach [19, 20] and the perturbation technique [21, 22] are frequently used to take into account the impact of uncertainty on the system response. However, with improving accuracy requirements, modeling of target simulation has become extremely complex, and its implementation is costly and time-consuming. The commonly used MCs approach is costly and challenging to implement for uncertainty quantification when many samples and model observations are required [23]. The surrogate modeling approach uses the relationship between inputs and outputs in a basic mathematical model to establish a new method for replacing complex analytical or computational models. The development of surrogate modeling techniques appropriate for solving practical engineering problems provides the required model observations and can reduce the computational cost of uncertainty quantification.
The Polynomial Chaos Expansion (PCE) becomes a prominent alternative modeling method in the field of uncertainty quantification (UQ) with low training cost when modeling extremely complex systems. The main implementation process of PCE is to use several polynomials to expand the response of random variables. The model response is expressed as a polynomial function of the input by determining the PCE coefficients of the polynomial components. These polynomial functions are orthogonal to the probability density functions of the input variables, which makes the calculation easier. The non-intrusive method does not require information about the control equations and is more suitable than the intrusive method for most problems when solving for the PCE coefficients. The non-intrusive methods include projection methods [24] and regression methods [25, 26] in which regression methods are more popular because of their efficiency in dealing with multivariate problems [27]. The sensitivity analysis (SA) quantitatively measures which the uncertainty of different input parameters contributes to the output uncertainty [28]. The sensitivity index is usually used to indicate the influence of each individual input parameter on the output [29]. Some complex problems in practical engineering do not have a definite input-output mathematical expression. It makes it difficult for engineers to perform sensitivity analysis on complex problems. The technique of surrogate modeling, such as PCE, can easily quantify the influence of the input parameters on the output by building mathematical expressions for the mechanical properties of complex problems depending on the inputs and outputs.
This paper lays out a procedure for solving the sensitivity problems of flexoelectric materials. This approach consists of two novel points:
1 The IGA-FEM and PCE are employed to establish a surrogate model for the flexoelectric materials.
2 The sensitivity expressions of the surrogate model are established by considering three kinds of different material parameters, respectively.
The remaining sections of the essay are structured as follows. The foundations of PCE in uncertainty quantification are presented in Section 2. Three introduces the principles of the isogeometric Finite Element Method for the statics of flexoelectric materials. Section 4 validates the IGA-FEM, PCE surrogate models and the sensitivity values of PCE surrogate models of the flexoelectric structure using numerical examples, followed by conclusions in Section 5.
2 Basic formula of polynomial chaos expansion
The basic idea of PCE is to replace the system model with an orthogonal polynomial defined by random variables, and then obtain a surrogate model expression by solving for the PCE coefficients. For the system model with n-dimensional independent random variables, the output function of the truncated PCE model with total expand order p can be expressed aswhere the total number N of polynomial terms of order p is computed by N = (n+p)!/(n!p!). θα are polynomial coefficients that are unknown. Ψα are multivariate orthogonal polynomials defined by the tensor product of univariate orthogonal polynomials aswhere is a univariate polynomial with respect to the random variable ri. The inner product of any two functions defined by Ψs(r) and Ψt(r), and the probability density function P(r) of r is:where is the expectation operator. δst is the Kronecker symbol, which is equal to one when s = t and otherwise zero.
In general, the probability density functions for different distributions correspond to different orthogonal polynomials, e.g., Legendre polynomials correspond to uniform distributions and Gaussian distributions correspond to Hermite polynomials. Table 1 lists the common univariate orthogonal polynomials and their corresponding probability distributions. There are various approaches to calculating the polynomial chaos expansion coefficient θα. The collocation method and the least-squares minimization problem are commonly employed to obtain the PCE coefficients. The orthogonal matrix and the PCE coefficient vector can be obtained according to Eq. 1 as [30].where Z is the number of random variables sample points. The PCE coefficient vector can be expressed aswhere . In this paper, an orthogonal polynomial with random variables satisfying a Gaussian distribution is used as an example. The recurrence relation for the Hermite orthogonal polynomials corresponding to the Gaussian distribution iswhere is an integer and less than or equal to r denotes the random variable. The three-term recurrence equation for the Hermite orthogonal polynomial is expressed as
TABLE 1
| Distribution type of random variable | Orthogonal polynomials | Interval |
|---|---|---|
| Gamma | Laguerre | |
| Weibull | ||
| Normal | Hermit | |
| Uniform | Legendre | [a, b] |
| Beta | Jacobi | [a, b] |
| Poisson | Charlier | {0, 1, 2, …, } |
| Negative binomial | Meixner-Chaos | {0, 1, 2, …, } |
| Binomial | Krawtchouk | {0, 1, 2, …, n} |
| Hypergeometric | Hahn-Chaos | {0, 1, 2, …, n} |
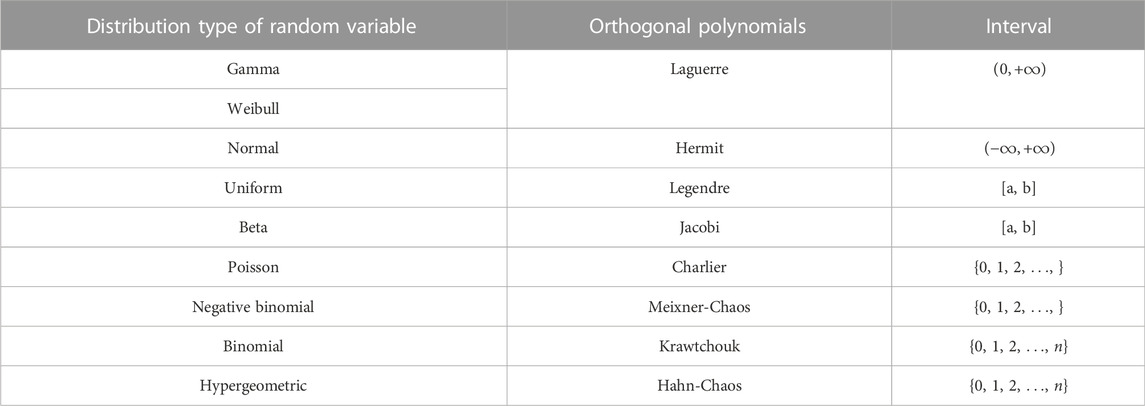
The probability distributions of different random variables and corresponding orthogonal polynomials [4].
The first six polynomials of Hα(r) are
3 IGA discretization of the control equations for flexoelectricity
In this section, we summarize the controlling equations for dielectric solids considering the flexoelectric effect. More information see [31–33] and references included therein. The weak form of the flexoelectric control equation iswhere ui denotes displacement; φ denotes the electric potential; Cijkl represents the fourth-order elasticity tensor; the mechanical strain is denoted by Sij, eijk is the third-order piezoelectric tensor, the electric field is defined as Ei = −φi; the fourth-order total flexoelectric tensor is denoted by μijkl; κij is dielectric tensor of second order; denotes the mechanical traction; ω is surface charge density. The physical domain is denoted by Ω, with boundaries Γt and ΓD corresponding to mechanical traction and electric displacements, respectively. In order to obtain the FEM form of the governing Eq. 9, the B-spline basis function Ni,p(ξ) obtained by recursively defining the Cox-de-Boor formula isand for p = 1, 2, 3,
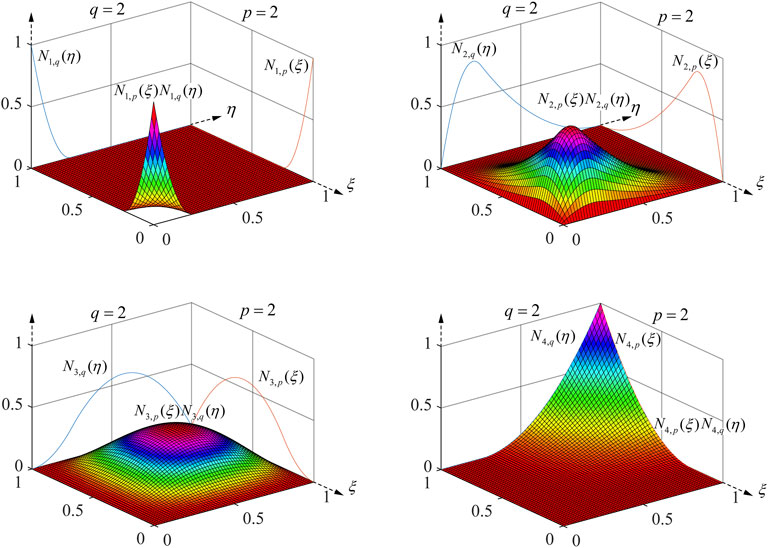
Figure 1 illustrates the results of visualizing the B-spline basis functions for both directional knot vectors with and . The Ni,p and Ni,q are 2nd order basis functions. The richness of B-spline basis function can be intuitively seen in Figure 1. The richness of the basis functions provides the groundwork for solving the fourth-order partial differential equation for flexoelectricity. Using Eqs. 10, 11 to discretize Eq. 9, the linear algebraic system of equations for the flexoelectricity control equation is obtained aswhere the matrix corresponding to the displacements isandwhere ν is Poisson’s ratio and Y is the Young’s modulus. The matrix of displacement and electric field coupling areThe electric field and Hessian matrices are
FIGURE 1
The specific B-spline basis functions.
The piezoelectric constants and flexoelectric constants matrices are
The matrix corresponding to the electric field iswhere the permittivity constant matrix is
The force and electrical load vectors areThe subscript e in Ωe, Γte and ΓDe represents the eth finite element in Eqs. 13, 16, 19, 21.
4 Numercial examples
In this section, we verify the accuracy of the IGA-FEM for solving the fourth-order partial differential equation using a benchmark example of a cantilever beam. After that, some random variable sample points are selected to obtain the output of IGA-FEM, which is used to build a polynomial chaos expansion surrogate model. Finally, the sensitivity results of the surrogate model for the mechanical properties of flexoelectric materials are verified by several numerical examples. For the cantilever beam model, we postulate that the model satisfies plane strain linear elastic isotropy.
4.1 Model verification
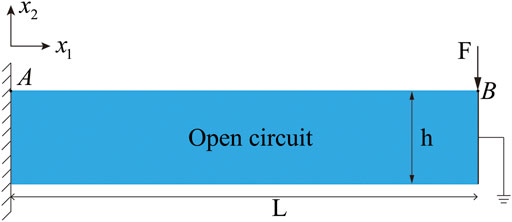
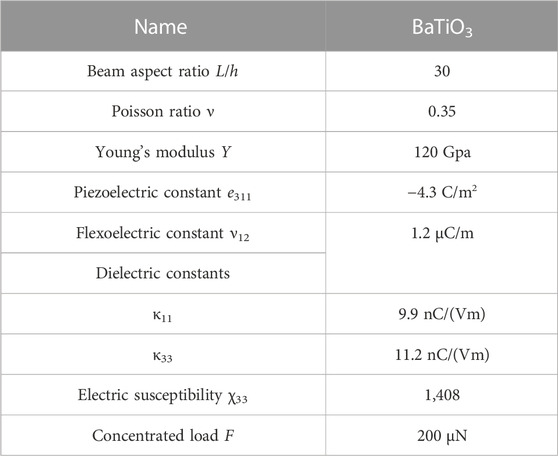
The cantilever beam model with open-circuit electrical boundary conditions and the top free edge subjected to a concentrated load of 200 μN is depicted in Figure 2. The most commonly used BaTiO3 material was selected for the cantilever beam model, as summarized in Table 2. The mesh and control point information is demonstrated in Figure 3. The boundary condition of the cantilever beam potential is specified on the right side as 0 V. The FEM uses the traditional Lagrangian basis function, which requires a lot of meshing to achieve higher accuracy, but the processing efficiency is lower. However, IGA-FEM uses NURBS basis functions to reduce the preprocessing time by enhancing the order, which improves the computational efficiency. This is the main motivation for using IGA-FEM in this work.
FIGURE 2
Cantilever beam model with open circuit electric boundary conditions.
TABLE 2
| Name | BaTiO3 |
|---|---|
| Beam aspect ratio L/h | 30 |
| Poisson ratio ν | 0.35 |
| Young’s modulus Y | 120 Gpa |
| Piezoelectric constant e311 | −4.3 C/m2 |
| Flexoelectric constant ν12 | 1.2 μC/m |
| Dielectric constants | |
| κ11 | 9.9 nC/(Vm) |
| κ33 | 11.2 nC/(Vm) |
| Electric susceptibility χ33 | 1,408 |
| Concentrated load F | 200 μN |
Material parameters for cantilever beam.
FIGURE 3
FEM discretization showing the control points as green dots.
The general definition of the electromechanical coupling coefficient isFor the one-dimensional cantilever beam problem, there are only stresses T11 and electric fields E2 [31]. The electromechanical coupling coefficient of the cantilever beam problem is [34].For comparison purposes, we introduce a normalized expression for the electromechanical coupling coefficient asand
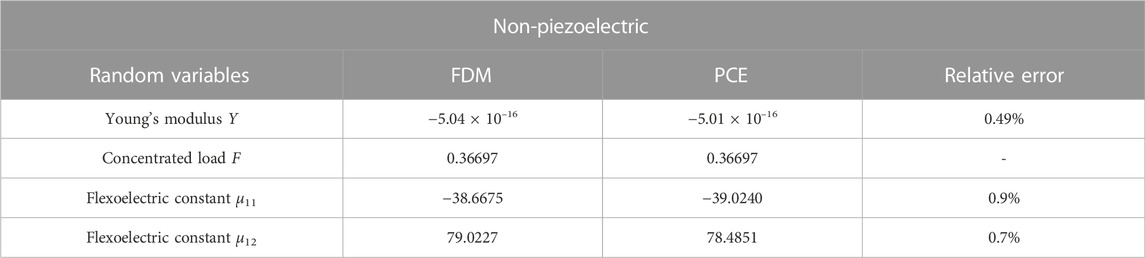
The one-dimensional model can be obtained by setting the Poisson’s ratio, the piezoelectric constant e333, flexoelectric constant μ11 in the two-dimensional model to zero. The non-piezoelectric material is obtained by setting e311 = 0. The normalized electromechanical coupling coefficients obtained by IGA-FEM and analytical solutions are presented in Tables 3, 4. From the Tables 3, 4, it can be seen that the normalized electromechanical coupling coefficients obtained by IGA-FEM are very close to the analytical solution, and the relative errors are within a small range. The increase in standardized thickness will decrease the mechanical properties (electric potential) of the flexoelectric material.
TABLE 3
| Non-piezoelectric materials | |||
|---|---|---|---|
| Normalized thickness h′ | IGA-FEM | Analytical solution | Relative error (%) |
| 1 | 3.4642 | 3.4641 | 0.003 |
| 2 | 1.7323 | 1.7321 | 0.012 |
| 3 | 1.1549 | 1.1547 | 0.017 |
| 4 | 0.8662 | 0.866 | 0.023 |
| 5 | 0.6929 | 0.6928 | 0.014 |
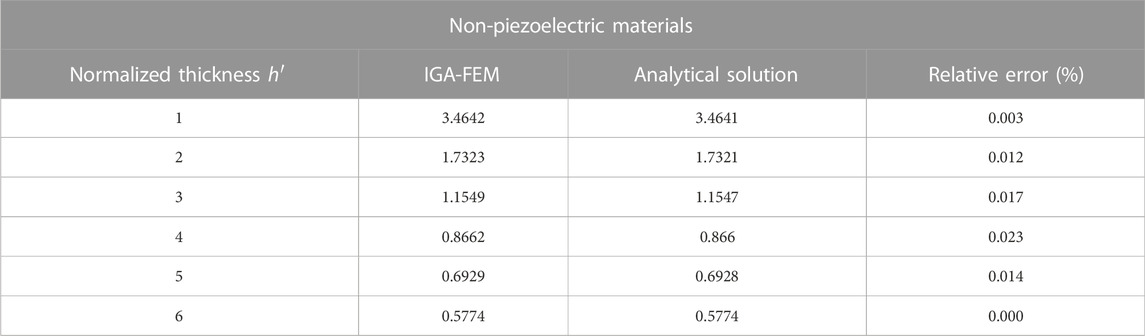
| 6 | 0.5774 | 0.5774 | 0.000 |
The normalized electromechanical coupling coefficient of non-piezoelectric materials with changing normalized thickness h′.
TABLE 4
| Piezoelectric materials | |||
|---|---|---|---|
| Normalized thickness h′ | IGA-FEM | Analytical solution | Relative error (%) |
| 1 | 3.5565 | 3.6056 | 1.36 |
| 2 | 1.9793 | 2.0000 | 1.04 |
| 3 | 1.5156 | 1.5275 | 0.78 |
| 4 | 1.3152 | 1.3229 | 0.58 |
| 5 | 1.2112 | 1.2166 | 0.44 |
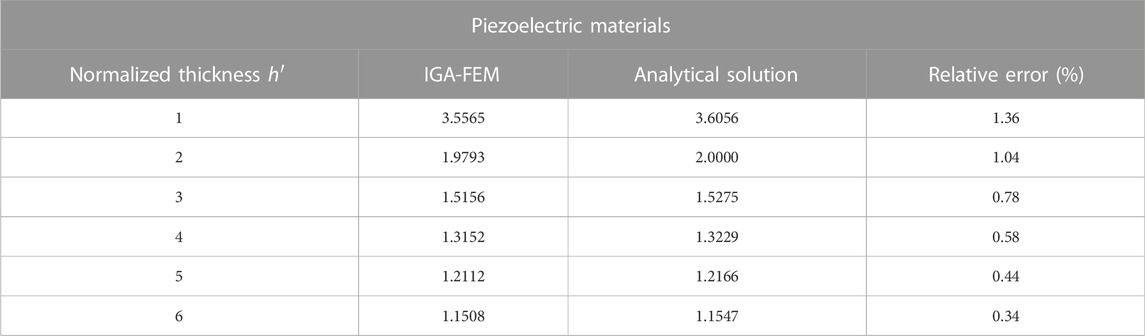
| 6 | 1.1508 | 1.1547 | 0.34 |
The normalized electromechanical coupling coefficient of piezoelectric materials with changing normalized thickness h′.
4.2 PCE surrogate model verification
In this section, the output of the IGA-FEM of the cantilever beam model is used to build the PCE surrogate model. The Young’s modulus, concentrated load and two flexoelectric constants as the random input variables are adopted, respectively. Table 5 lists the mean vlues, coefficients of variation, and ranges of sample points for the different random input variables. In this paper, we have used 500 sample points as input parameters for the random variables of the PCE. The Latin Hypercube Sampling (LHS) random number generation module in Matlab is utilized to obtain sample points of random variables. Owing to the potential distribution at the fixed edge is the most obvious, point A is selected as the reference point when establishing the surrogate model.
TABLE 5
| Variables | Mean values | Coefficient of variation γ | The limits of variables: [lower, upper] |
|---|---|---|---|
| Young’s modulus Y | 120 GPa | 0.1 | [84,156] |
| Concentrated load F | 200 μN | 0.12 | [128,272] |
| Flexoelectric constant μ11 / μ12 | 1.2 μC/m | 0.14 | [0.7,1.7] |
Definitions and the statistical characteristics of the random input variables.
Figure 4 presents the comparison results of PCE and IGA-FEM for piezoelectric and non-piezoelectric materials with Young’s modulus as random variable. As can be seen from Figure 4, the electric potential decreases as the Young’s modulus increases. The PCE calculation results are basically consistent with the IGA-FEM calculation results, which verifies the effectiveness of the algorithm.
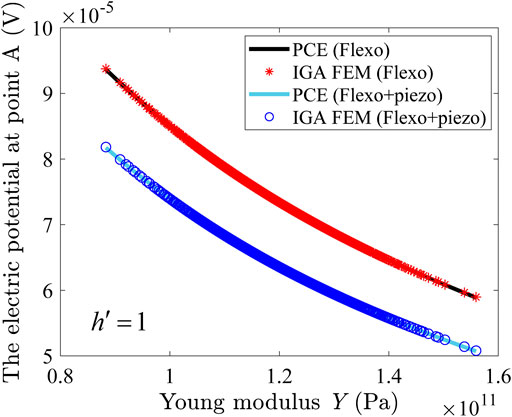
FIGURE 4
The electric potential at point A of cantilever beam where the Young’s modulus Y is a random variable.
Figure 5 depicts the electric potential obtained by PCE and IGA-FEM for piezoelectric and non-piezoelectric materials with concentrated load as random variables. As can be seen from Figure 5, the electric potential of point A increases with increasing concentrated load. The electric potential of a piezoelectric material subjected to the same concentrated force F is less than that of a non-piezoelectric material.
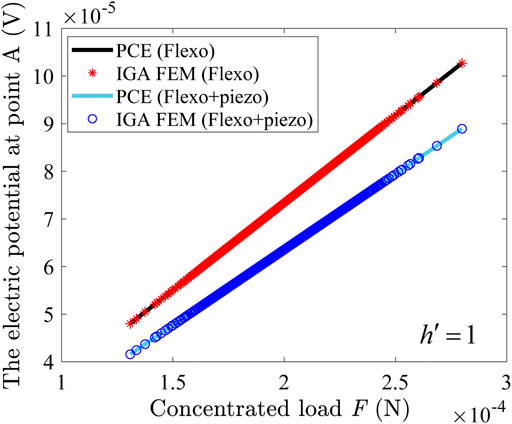
FIGURE 5
The electric potential at point A of cantilever beam where the concentrated load F is a random variable.
The results of PCE and IGA-FEM for piezoelectric and non-piezoelectric materials are shown in Figure 6, where the random variables are the flexoelectric constants μ11 and μ12. It can be seen from Figure 6 that the electric potential presents reverse changes as the two different flexoelectric constants are changed.
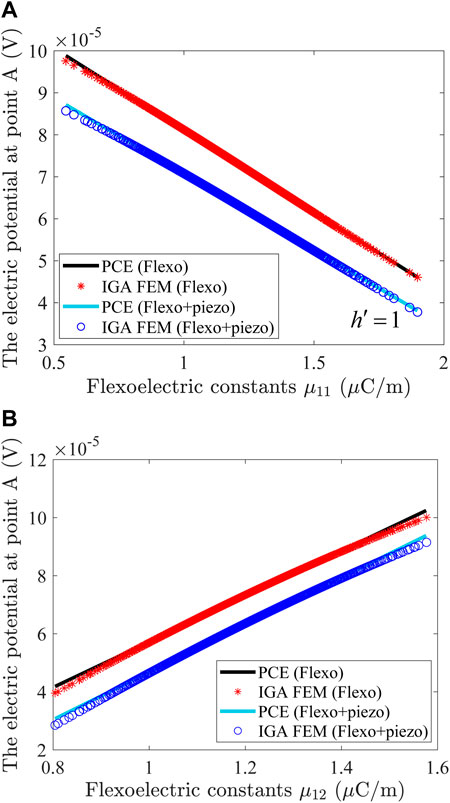
FIGURE 6
The electric potential at point A of the cantilever beam for different random variables. (A) The electric potential at point A of the cantilever beam when the random variable is μ11. (B) The electric potential at point A of the cantilever beam when the random variable is μ12.
4.3 Sensitivity analysis
In this section, we perform a sensitivity analysis of the surrogate model for the mechanical properties of flexoelectric materials obtained in Section 4.2. The sensitivity expression of the surrogate model for the mechanical properties of flexoelectric materials without considering piezoelectric effect are
The sensitivity expression of the surrogate model for the mechanical properties of flexoelectric materials considering piezoelectric effect are
The sensitivity values obtained from the PCE surrogate model are compared with the global finite difference method (FDM) defined by
To investigate the accuracy of DSM and FDM, one gives the relative error of DSM and FDM for different random variable r. The relative error of the sensitivity results obtained by FDM and PCE is
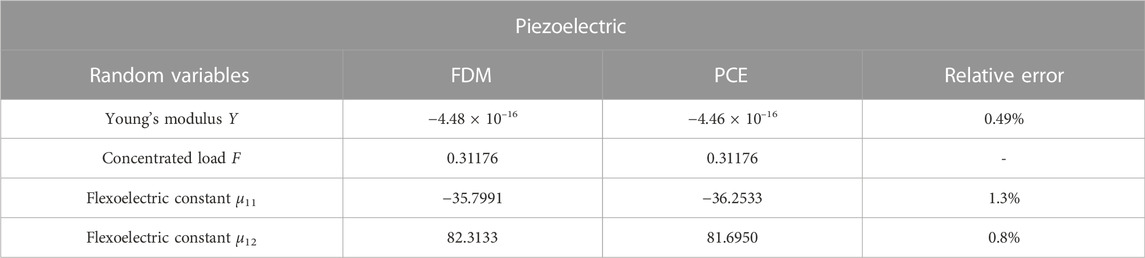
Owing to the first sensitivity expressions in Eqs. 27, 28 are a quadratic function of Young’s modulus. Therefore, we need to calculate the sensitivity value of the surrogate model through the mean value of Young’s modulus. The mean value of Young’s modulus is lists in Table 5. The rest of the sensitivity values are directly selected from the derivative results. Tables 6, 7 present a comparison of the sensitivity values of PCE and FDM for non-piezoelectric and piezoelectric materials. From Tables 6, 7, it can be seen that the sensitivity values obtained by PCE and FDM are basically the same, and the relative errors are very small. In terms of the value of sensitivity, the flexoelectric constant μ12 has a greater effect on the electric potential of the flexoelectric material and the material is more sensitive to the flexoelectric constant μ12.
TABLE 6
| Non-piezoelectric | |||
|---|---|---|---|
| Random variables | FDM | PCE | Relative error |
| Young’s modulus Y | −5.04 × 10–16 | −5.01 × 10–16 | 0.49% |
| Concentrated load F | 0.36697 | 0.36697 | - |
| Flexoelectric constant μ11 | −38.6675 | −39.0240 | 0.9% |
| Flexoelectric constant μ12 | 79.0227 | 78.4851 | 0.7% |
Comparison of PCE and FDM of sensitivity results for non-piezoelectric materials.
TABLE 7
| Piezoelectric | |||
|---|---|---|---|
| Random variables | FDM | PCE | Relative error |
| Young’s modulus Y | −4.48 × 10–16 | −4.46 × 10–16 | 0.49% |
| Concentrated load F | 0.31176 | 0.31176 | - |
| Flexoelectric constant μ11 | −35.7991 | −36.2533 | 1.3% |
| Flexoelectric constant μ12 | 82.3133 | 81.6950 | 0.8% |
Comparison of PCE and FDM of sensitivity results for non-piezoelectric materials.
5 Conclusion
In this paper, a sensitivity analysis method of surrogate model based on isogeometric stochastic Finite Element Method is proposed for flexoelectric materials. The NURBS basis functions with high-order continuity are used to discretize the fourth-order partial differential equation for flexoelectricity. The Polynomial Chaos Expansion (PCE) is utilized to develop a surrogate model for the mechanical properties of flexoelectric materials. The sensitivity values of the surrogate model are obtained by considering three kinds of different parameters, respectively. Numerical examples illustrate the flexoelectric material is more sensitive to the flexoelectric constant μ12. Additionally, the current technology will also be used to three-dimensional piezoelectric and flexoelectric problems.
Statements
Data availability statement
The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.
Author contributions
Conceptualization, HL; Data curation, HL; Formal analysis, YC and YX; Investigation, XG; Methodology, HL and JZ; Project administration, XY, Software, HL and JZ; Supervision, XY; Validation, YX; Visualization, YC; Writing—original draft, HL and XG. All authors have read and agreed to the published version of the manuscript.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
1.
HamdiaKMGhasemiHZhuangXAlajlanNRabczukT. Sensitivity and uncertainty analysis for flexoelectric nanostructures. Comput Methods Appl Mech Eng (2018) 337:95–109. 10.1016/j.cma.2018.03.016
2.
AhmadpoorFSharmaP. Flexoelectricity in two-dimensional crystalline and biological membranes. Nanoscale (2015) 7:16555–70. 10.1039/C5NR04722F
3.
YudinPVTagantsevAK. Fundamentals of flexoelectricity in solids. Nanotechnology (2013) 24:432001. 10.1088/0957-4484/24/43/432001
4.
HughesTJCottrellJABazilevsY. Isogeometric analysis: CAD, finite elements, NURBS, exact geometry and mesh refinement. Comput Methods Appl Mech Eng (2005) 194:4135–95. 10.1016/J.CMA.2004.10.008
5.
ChenLWangZPengXYangJWuPLianH. Modeling pressurized fracture propagation with the isogeometric BEM. Geomechanics Geophys Geo-Energy Geo-Resources (2021) 7:51. 10.1007/s40948-021-00248-3
6.
ChenLLianHXuYLiSLiuZAtroshchenkoEet alGeneralized isogeometric boundary element method for uncertainty analysis of time-harmonic wave propagation in infinite domains. Appl Math Model (2023) 114:360–78. 10.1016/j.apm.2022.09.030
7.
ChenLLuCLianHLiuZZhaoWLiSet alAcoustic topology optimization of sound absorbing materials directly from subdivision surfaces with isogeometric boundary element methods. Comput Methods Appl Mech Eng (2020) 362:112806. 10.1016/j.cma.2019.112806
8.
ChenLLianHLiuZGongYZhengC-JBordasS. Bi-material topology optimization for fully coupled structural-acoustic systems with isogeometric FEM-BEM. Eng Anal Boundary Elem (2022) 135:182–95. 10.1016/j.enganabound.2021.11.005
9.
ChenLMarburgSZhaoWLiuCChenH. Implementation of isogeometric fast multipole boundary element methods for 2d half-space acoustic scattering problems with absorbing boundary condition. J Theor Comput Acoust (2018) 27:1850024. 10.1142/S259172851850024X
10.
ChenLLuCZhaoWChenHZhengC-J. Subdivision surfaces—boundary element accelerated by fast multipole for the structural acoustic problem. J Theor Comput Acoust (2020) 28:2050011. 10.1142/S2591728520500115
11.
ChenLLiuCZhaoWLiuL. An isogeometric approach of two dimensional acoustic design sensitivity analysis and topology optimization analysis for absorbing material distribution. Comput Methods Appl Mech Eng (2018) 336:507–32. 10.1016/j.cma.2018.03.025
12.
ChenLLianHLiuZChenHAtroshchenkoEBordasS. Structural shape optimization of three dimensional acoustic problems with isogeometric boundary element methods. Comput Methods Appl Mech Eng (2019) 355:926–51. 10.1016/j.cma.2019.06.012
13.
ChenLZhangYLianHAtroshchenkoEDingCBordasSP. Seamless integration of computer-aided geometric modeling and acoustic simulation: Isogeometric boundary element methods based on catmull-clark subdivision surfaces. Adv Eng Softw (2020) 149:102879. 10.1016/j.advengsoft.2020.102879
14.
ChenLLianHNatarajanSZhaoWChenXBordasS. Multi-frequency acoustic topology optimization of sound-absorption materials with isogeometric boundary element methods accelerated by frequency-decoupling and model order reduction techniques. Comput Methods Appl Mech Eng (2022) 395:114997. 10.1016/j.cma.2022.114997
15.
ChengKLuZ. Adaptive sparse polynomial chaos expansions for global sensitivity analysis based on support vector regression. Comput Structures (2018) 194:86–96. 10.1016/j.compstruc.2017.09.002
16.
HurtadoJBarbatA. Monte Carlo techniques in computational stochastic mechanics. Arch Comput Methods Eng (1998) 5:3–29. 10.1007/BF02736747
17.
ChenLChengRLiSLianHZhengCBordasSP. A sample-efficient deep learning method for multivariate uncertainty qualification of acoustic–vibration interaction problems. Comput Methods Appl Mech Eng (2022) 393:114784. 10.1016/j.cma.2022.114784
18.
XuYLiHChenLZhaoJZhangX. Monte Carlo based isogeometric stochastic finite element method for uncertainty quantization in vibration analysis of piezoelectric materials. Mathematics (2022) 10:1840. 10.3390/math10111840
19.
HondaR. Stochastic BEM with spectral approach in elastostatic and elastodynamic problems with geometrical uncertainty. Eng Anal Boundary Elem (2005) 29:415–27. 10.1016/j.enganabound.2005.01.007
20.
LiuWKBelytschkoTManiA. Random field finite elements. Int J Numer Methods Eng (1986) 23:1831–45. 10.1002/nme.1620231004
21.
KamińskiM. Stochastic perturbation approach to engineering structure vibrations by the finite difference method. J Sound Vibration (2002) 251:651–70. 10.1006/jsvi.2001.3850
22.
KamińskiM. On generalized stochastic perturbation-based finite element method. Commun Numer Methods Eng (2006) 22:23–31. 10.1002/cnm.795
23.
ZhangB-YNiY-Q. A hybrid sequential sampling strategy for sparse polynomial chaos expansion based on compressive sampling and Bayesian experimental design. Comput Methods Appl Mech Eng (2021) 386:114130. 10.1016/j.cma.2021.114130
24.
Le MaîtreOKnioOM. Spectral methods for uncertainty quantification: With applications to computational fluid dynamics. Berlin, Germany: Springer Science & Business Media (2010).
25.
BlatmanGSudretB. Sparse polynomial chaos expansions and adaptive stochastic finite elements using a regression approach. Comptes Rendus Mécanique (2008) 336:518–23. 10.1016/j.crme.2008.02.013
26.
PalarPSTsuchiyaTParksGT. Multi-fidelity non-intrusive polynomial chaos based on regression. Comput Methods Appl Mech Eng (2016) 305:579–606. 10.1016/j.cma.2016.03.022
27.
ZhouYLuZChengKShiY. An expanded sparse Bayesian learning method for polynomial chaos expansion. Mech Syst Signal Process (2019) 128:153–71. 10.1016/j.ymssp.2019.03.032
28.
SaltelliARattoMAndresTCampolongoFCariboniJGatelliDet alGlobal sensitivity analysis: The primer. New York, NY, USA: John Wiley & Sons (2008).
29.
HamdiaKMSilaniMZhuangXHePRabczukT. Stochastic analysis of the fracture toughness of polymeric nanoparticle composites using polynomial chaos expansions. Int J Fracture (2017) 206:215–27. 10.1007/s10704-017-0210-6
30.
HauseuxPHaleJSBordasSP. Accelerating Monte Carlo estimation with derivatives of high-level finite element models. Comput Methods Appl Mech Eng (2017) 318:917–36. 10.1016/J.CMA.2017.01.041
31.
MajdoubMSSharmaPCaginT. Enhanced size-dependent piezoelectricity and elasticity in nanostructures due to the flexoelectric effect. Phys Rev B (2008) 77:125424. 10.1103/PhysRevB.77.125424
32.
GhasemiHParkHSRabczukT. A level-set based Iga formulation for topology optimization of flexoelectric materials. Comput Methods Appl Mech Eng (2017) 313:239–58. 10.1016/j.cma.2016.09.029
33.
GhasemiHParkHSAlajlanNRabczukT. A computational framework for design and optimization of flexoelectric materials. Int J Comput Methods (2020) 17:1850097. 10.1142/S0219876218500974
34.
AbdollahiAPecoCMillánDArroyoMAriasI. Computational evaluation of the flexoelectric effect in dielectric solids. J Appl Phys (2014) 116:093502. 10.1063/1.4893974
Summary
Keywords
isogeometric analysis, polynomial chaos expansion, surrogate model, uncertainty quantification, sensitivity analysis
Citation
Li H, Zhao J, Guo X, Cheng Y, Xu Y and Yuan X (2022) Sensitivity analysis of flexoelectric materials surrogate model based on the isogeometric finite element method. Front. Phys. 10:1111159. doi: 10.3389/fphy.2022.1111159
Received
29 November 2022
Accepted
12 December 2022
Published
22 December 2022
Volume
10 - 2022
Edited by
Pei Li, Xi’an Jiaotong University, China
Reviewed by
Yunfei Gao, Hohai University, China
Chuang Lu, University of Science and Technology of China, China
Updates
Copyright
© 2022 Li, Zhao, Guo, Cheng, Xu and Yuan.
This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Xiaohui Yuan, yxh@xynu.edu.cn
This article was submitted to Statistical and Computational Physics, a section of the journal Frontiers in Physics
Disclaimer
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.