Spatiotemporal shaping of high power laser pulses based on stimulated brillouin scattering

We proposed and numerically demonstrated the combination of temporal and spatial shaping of high power nanosecond laser pulses based on stimulated Brillouin scattering (SBS) in this paper. With the intensity-dependence characteristic of SBS, the higher intensity parts of the laser beam obtain higher reflectivity, and the incident non-uniform high power laser beam would be well smoothed. A parameter adjustable feedback control loop was used to tailor the output temporal profile by pre-compensating the temporal profile of the input pump. In our numerical simulation, a 3 ns super-Gaussian shaped single-frequency laser pulse with a 527 nm wavelength was used as the pump. And the heavy fluorocarbon FC-70 was chosen as the Brillouin medium. Simulation results show that the laser spatial modulation can be significantly pulled down when the energy efficiency is maintained above 90% in our beam smoothing system with suitable laser intensity. The flat-toped laser pulses both in temporal and spatial domain were demonstrated to be achievable simultaneously. The method proposed here paves a simple and effective way to optimizing the near field pattern and temporal shape of high power laser systems.

1 Introduction

High-power lasers have broad applications in various fields [1–4], especially in the research of inertial confinement fusion for clean energy exploring. Controlling the uniformity of laser spatial and temporal profile acts a significant role in mitigating laser-induced damage and laser transmission in high-power laser systems. The spatial non-uniformity in a laser beam is mainly comes from the uneven gain in the active laser medium and the diffraction modulation caused by the intensity and phase perturbation of laser components. Because the optics damage in high power laser systems is closely related to the local intensity, the over-high local intensity should be suppressed by spatial beam shaping.

In the past decades, laser system engineering has accumulated several techniques to avoid excessive spatial modulation by using liquid crystal spatial light modulators (SLMs) [5–7], random phase plates [8], far-field spatial filter [9], and so on. Randomized phase plates is randomly arranged by hundreds of small units with 0 or π phase delay, and the far-field smoothing is realized through the superposition of diffraction of each unit. It is insensitive to wave-front distortion, but it has some problems such as low diffraction efficiency and easy to be affected by incident wavelength. In general, SLM combined with spatial filtering can realize arbitrary spatial shaping in high-power laser systems. SLM is an active programmable beam shaping device, which can pre-compensate the non-uniformity of laser beam profile by adjusting the transmissivity of each pixel, with good results. However, the total transmissivity of SLM devices is relatively low [7], and the beam quality is improved at the cost of the output energy. In our previous research, we proposed a more effective method based on SBS to enhance laser near-field uniformity with high energy transmittance [10, 11]. SBS attracts extensive attention owing to its wide applications both in high quality laser generation [12–15], optical amplification [16, 17] and distributed optical fiber sensing [18]. In addition to the above applications, a special application called SBS optical limiting has attracted extensive attention [19–21]. When high power lasers with uneven beam profiles are injected into Brillouin medium and SBS is excited, the transmitted light energy and power will be limited to a certain level. A flat-topped profile in temporal or spatial domain can be obtained as a result of the non-linear properties of SBS [19]. This kind of optical limiting is easier to be realized in non-focusing scheme than multiphoton absorption and intensity dependent polarization rotators based optical limiting for its simpler structure and lower threshold [22, 23].

The SBS beam smoothing benefits from the higher reflectivity of higher intensity parts of laser beam, then a non-linear distortion occurs between profiles of output and input pulses. To obtain a flat-topped profile both in temporal and spatial domain, the input laser pulse shape should be pre-compensated strictly before introducing into the medium cell. In this paper, we demonstrate the temporal shaping of the output laser pulse from a Brillouin beam smoothing system by controlling the temporal profile of the pump laser with a feedback control loop. A top hat profile both in the temporal and spatial domain are obtained simultaneously in our numerical simulation with an energy efficiency of about 90%, which paves the way for the application of SBS in optical field shaping of high power laser systems.

2 Theory

The purpose of our work is to obtain top hat laser pulses both in temporal and spatial domain with SBS. The temporal pulse shape controlling and spatial beam smoothing process can be described by the following equations:

${\nabla }_{\mathit{T}}^{\mathbf{2}}{\mathit{A}}_{\mathit{P}}+\frac{\partial {\mathit{A}}_{\mathit{P}}}{\partial \mathit{z}}+\frac{\mathit{n}}{\mathit{c}}\frac{\partial {\mathit{A}}_{\mathit{P}}}{\partial \mathit{t}}=\mathit{i}\mathit{g}\mathit{\rho }{\mathit{A}}_{\mathit{S}}(1)$

${\nabla }_{\mathit{T}}^{\mathbf{2}}{\mathit{A}}_{\mathit{S}}+\frac{\partial {\mathit{A}}_{\mathit{S}}}{\partial \mathit{z}}-\frac{\mathit{n}}{\mathit{c}}\frac{\partial {\mathit{A}}_{\mathit{S}}}{\partial \mathit{t}}=-\mathit{i}\mathit{g}{\mathit{\rho }}^{*}{\mathit{A}}_{\mathit{P}}(2)$

$\frac{\partial \mathbf{\rho }}{\partial \mathit{t}}+\frac{\mathbf{1}}{\mathbf{2}}\mathit{\Gamma }\mathit{\rho }=\frac{\mathit{i}\mathit{\gamma }{\mathit{q}}^{\mathbf{2}}}{\mathbf{16}\mathit{\pi }{\mathit{\Omega }}_{\mathit{B}}}{\mathit{A}}_{\mathit{P}}{\mathit{A}}_{\mathit{S}}^{*}+\mathit{f}(3)$

where the amplitude of the pump and Stokes are represented as A_p and A_s, and ρ is the amplitude of acoustic wave; n is the refractive index of the medium, c is the speed of light, g is the Brillouin gain coefficient, γ is the electrostrictive constant, q is wave vector of the acoustic wave, Ω_B and Γ denote the acoustic frequency and Brillouin linewidth, f is the thermal noise which initiates the spontaneous Brillouin scattering and it can be described as a Gaussian random function in our model. The first terms of the two optical field equations illustrate the diffraction of the pump and Stokes light, which can be used to study 3D property of SBS.

By numerically solving the equations, the SBS process with a large aperture pump can be simulated. In our simulation, the split-step Fourier method is used by assuming that in propagating the optical field over an iteration step, the diffraction and non-linear effects can be treated independently. In general, diffraction and non-linear effects act together along the length of the medium cell, but the above assumption acts well when the iteration step size is small enough. Fast Fourier transformation method is utilized to deal with the laser diffraction, while an implicit finite differencing in time and a backward differencing scheme in space are used for the algorithm of non-linear effects calculation.

The main parameters of non-linear medium and laser source used in our simulation are set as follows: the wavelength of pump light is 0.527 μm, the pump pulse duration is 3 ns, the refraction index of the non-linear material is 1.303, the Brillouin gain coefficient is 0.2 cm/GW, the acoustic frequency is 2.14 GHz and the phonon time is 5 ps (parameters above are corresponds to heavy fluorocarbon liquid materials FC-70 [11]). The beam diameter used in our simulation is 40 mm. The length of the medium cell is 350 mm.

3 Numerical results and discussions

3.1 Beam smoothing effect by SBS

With the proposed numerical model, spatial beam smoothing effect of a large aperture high power laser was studied. When the mean intensity of the pump is set to 1.68 GW/cm², the calculated 3D intensity distribution of the input and output laser in the near field are shown in Figures 1A, B. It can be seen clearly from the pictures that after propagating through the medium and exciting SBS, hot spots have been cleaned up, and the near field pattern was smoothed obviously. The energy conversion efficiency of the beam shaping system is calculated to be above 95%. The spatial modulation caused by the high spatial frequency components (see Figure 1A) can easily be removed in the far-field by conventional spatial filtering of the high-order spatial frequencies. But the pinhole spatial filtering system needs a high vacuum environment to prevent air breakdown at the focal point from polluting the optical element and requires complicated design to avoid ghost damage. The simple structure and high energy efficiency are the main advantages of our beam smoothing method compared with the traditional scheme.

FIGURE 1

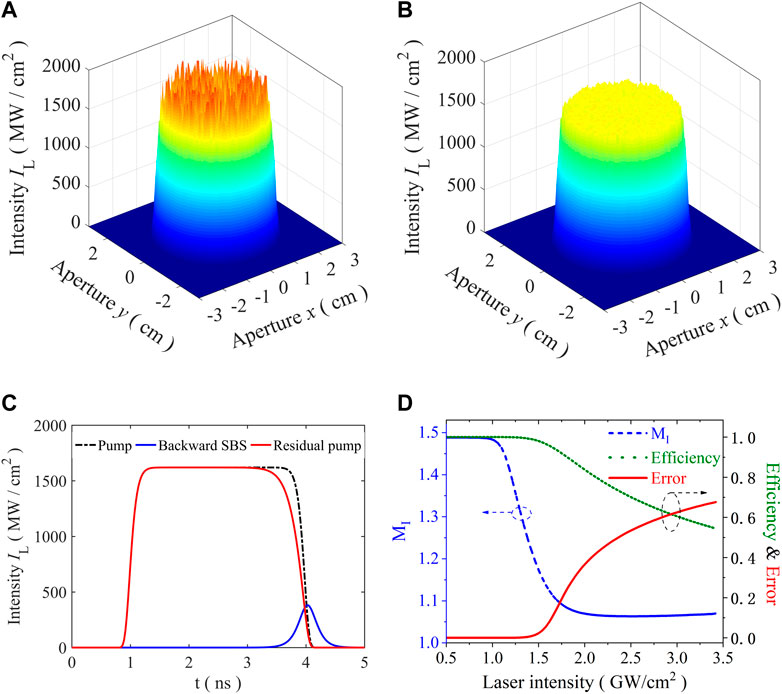
FIGURE 1. Numerical results of SBS beam smoothing. (A) Near field pattern of the pump (B) Near field pattern of the output light (C) Typical waveforms of the pump, Stokes and output pulse (residual pump) (D) Evolution of MI, η and PDR with the increasing of laser intensity.

The above simulation results verified that the near field of high power laser could be well cleaned up by SBS. However, when we focus on the time domain, the waveform of output pulse becomes distorted compared with the input laser pulse. Simulation results are shown in Figure 1C, the black dash line denotes the waveform of the pump pulse, the solid red line represents the temporal profile of the output laser pulse (the residual pump), and the solid blue line stands for that of the backward SBS. The parameters used here are the same as those above. It can be seen clearly from this figure that the transmitted laser is distorted noticeably in the trailing edge of the pump pulse. The main reason for this phenomenon is that part of the pump energy is taken off by the reflected Stokes light due to the non-linear development of SBS process. This distortion is harmful for applying the proposed beam smoothing scheme in high-power laser systems.

To quantitatively evaluate the SBS beam shaping effect, three parameters named the near field intensity modulation index (MI), energy efficiency (η) and pulse distortion ratio (PDR) were utilized. MI is defined as the ratio of the peak intensity to the average intensity in the flat top area of the laser field. Energy efficiency is related to the percentage of the output laser energy out of the total input laser energy. PDR denotes the distortion degree of the output pulses, and it is calculated with the following equation (24):

$\mathit{P}\mathit{D}\mathit{R}=\sqrt{\frac{\sum {\left(\mathit{T}\left(\mathit{t}\right)-\frac{\sum \mathit{T}\left(\mathit{t}\right)\mathit{R}\left(\mathit{t}\right)}{\sum {\mathit{R}}^{\mathbf{2}}\left(\mathit{t}\right)}\mathit{R}\left(\mathit{t}\right)\right)}^{\mathbf{2}}}{\sum {\mathit{T}}^{\mathbf{2}}\left(\mathit{t}\right)}}(4)$

where T(t) and R(t) represent the temporal profile of the input (target) and the output (result) pulse shape, respectively. The above three parameters were calculated with the changing of pump laser intensity, and the results are shown in Figure 1D. The calculated results indicate that the MI factor decreases sharply with the raise of the pump intensity. The MI factor can be mitigated largely from 1.49 to 1.08 with an energy efficiency of 89.7% when the pump intensity is 1.82 GW/cm². The calculated energy efficiency of our scheme is much higher than that of the widely used method with SLM. However, time-domain distortion of the output pulse increases rapidly with the laser intensity, and the PDR was calculated to 0.25 when the pump laser intensity is 1.82 GW/cm². Thus, it is necessary to take some steps to balance the MI reduction and the PDR increase.

3.2 Pre-compensation of the laser pulses

According to the above explanation, the output laser pulse distortion in the time domain occurs in the falling edge of the pulse because of the avalanche increase of the Stokes light by extracting pump energy. Thus, it is easily comes to mind that the output pulse profile distortion would be weakened if the rear pulse edge has much higher intensity. Then, we utilize the following feedback compensation algorithm for pump pre-compensation, which is based on the ratio between the targeted and the obtained waveform. The pre-compensated pump profile can be described as:

${\mathit{I}}_{\mathit{n}}\left(\mathit{t}\right)={\mathit{I}}_{\mathit{n}-\mathbf{1}}\left(\mathit{t}\right)\bullet \left[\mathit{P}\left(\mathit{S}-\mathbf{1}\right)+\mathbf{1}\right](5)$

Where $I_{n-1}\left(t\right)$ represents the pump profile of the previous iteration, $\mathrm{S}=\frac{T\left(t\right)}{R_{n-1}\left(t\right)}$ denotes the difference between the target waveform and the output laser pulse of the previous iteration, and P stands for the additional parameter which ranges from 0 to 1. The process of the waveform compensation with Equation 5 is shown in Figure 2. During each iteration, we calculate the parameter S with the aimed waveform and the measured waveform, firstly. Then the optimized pump profile of this iteration can be obtained after multiplying the previous pump waveform by the calculated parameter S. When the optimized pump is injected into the Brillouin cell, the output pulse will turn out to be much closer to the aimed profile. We repeat the above procedure until the output pulse is identical to the aimed pulse waveform.

FIGURE 2

FIGURE 2. The process of the waveform pre-compensation.

To study the proposed feedback algorithms under test, we numerically simulated the compensation process with different laser intensities. The laser peak intensity used here were 1.6 GW/cm², 1.7 GW/cm² and 1.82 GW/cm² with a 3 ns pulse duration, and the parameter P of Equation 5 was set to 0.9. The calculated results are shown in Figure 3. Figures 3A, B draw the optimized pump and the related output pulses of each iteration with 1.6 GW/cm² pump. It can be seen from these two pictures that, when the proposed pre-compensation method is used, the back of the pump pulse rises and the output pulse distortion disappears gradually with the increase of the iteration times. A perfect flat-top output pulse can be obtained within four iterations. Figures 3C, D show the calculated results with a laser intensity of 1.7 GW/cm², the same phenomenon appears and the optimized flat-top output pulse was realized when five iterations were carried out. When the laser intensity was set to 1.82 GW/cm², seven iterations in our algorithm were needed to compensate the output pulse distortion (see Figures 3E, F). The energy conversion efficiencies of the SBS system for the optimized pump waveform with the above three peak intensities are calculated to be 92.3%, 81.1% and 52.3%, respectively. Then, we can conclude from the above simulation results that the output pulse profile can be pre-compensated with our algorithms perfectly, and the iteration times increase with the rise of pump intensity. The main reason is that much higher SBS reflectivity and more serious output pulse distortion occur with higher pump intensity. Meanwhile, it should be taken into consideration that the optimum temporal profiling necessitates a pronounced trailing edge of the pump pulse, whose required intensity is nearly one order of magnitude higher than that of the flat-top range when the laser intensity is 1.82 GW/cm². It is a challenge to produce such a laser pulse in practice, although pulse stacking technique has been widely used in high power laser systems. And it may even threatens the safe operation of the laser system when the trailing peak is too high. In view of these reasons, our temporal-spatial beam smoothing system should be operated slightly above the SBS threshold according to Figure 1D. This condition can be achieved by choosing suitable medium with low gain coefficient for powerful laser operation.

FIGURE 3

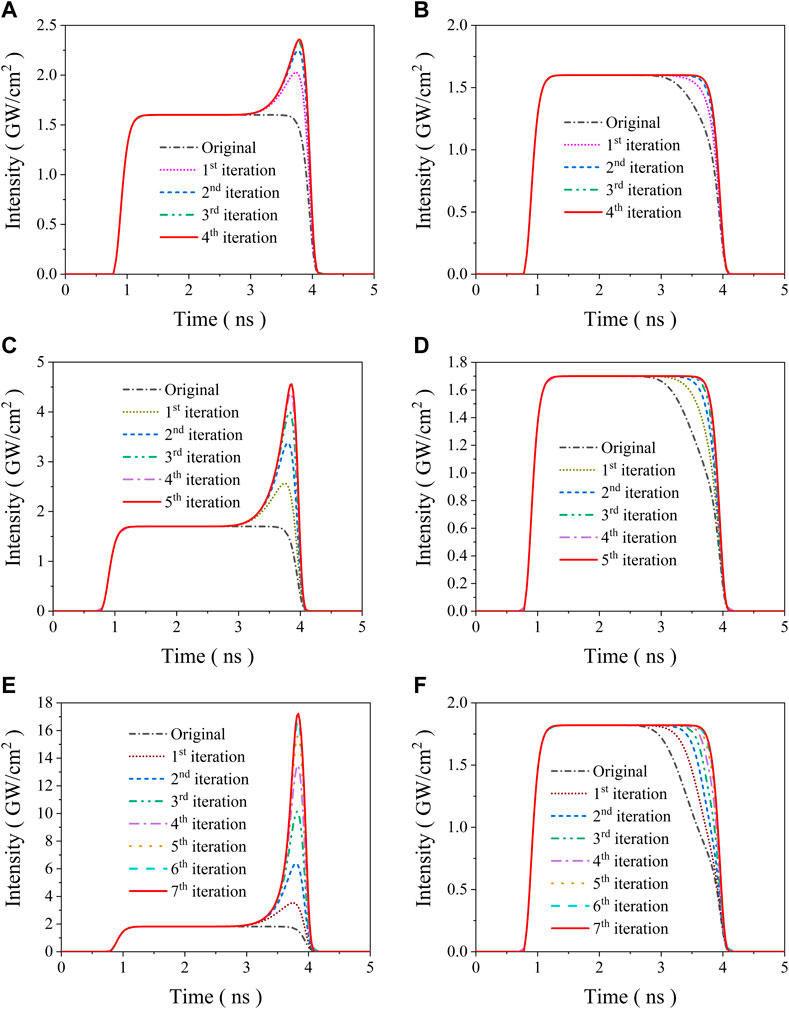
FIGURE 3. Simulation results of the pulse compensation with different pump intensities. (A,B) represent the pre-compensated pump waveforms and related output laser waveforms with the top-hat intensity of 1.6 GW/cm², (C,D) draw the correspond results with the top-hat intensity of 1.7 GW/cm², while (E,F) shows that of 1.82 GW/cm².

The proposed compensation algorithms shown in Equation 5 consist of an important parameter P, which controls the feedback depth of our method. Then, it is necessary to evaluate the influence of this parameter on output pulse pre-compensation. The above mentioned parameter PDR was calculated during each iteration with different P when the pump intensity was fixed as 1.82 GW/cm², the numerical results are shown in Figure 4. It can be seen clearly from this picture that the value of PDR drops sharply with the increase of iteration numbers, which indicates that the output pulse is compensated gradually with the proposed algorithms of this work. The compensate process develops more quickly with an increasing value of P. The output pulse can be optimized properly and the value of PDR remains nearly zero when the parameter P is below 0.9. But there exists an interesting phenomenon that the PDR index rebounds from bottom with the further increase of iteration number when the parameter P is set to 1, which indicates an instable compensation. From the above results we can draw a conclusion that the index P should be chosen slightly smaller than 1, and 0.9 is a proper value used in our calculation.

FIGURE 4

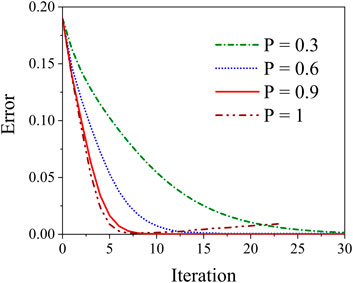
FIGURE 4. The relationship between output pulse distortion ratio and the calculation iteration with different parameter P.

4 Conclusion

In this paper, we have presented a method to correct the temporal pulse profile at the output of a Brillouin cell used for laser beam smoothing by changing the pump pulse utilizing a feedback loop. This method is applied simply using the knowledge of the input and of the output of the system. We numerically studied the dependence of the pulse compensation performance on the number of iterations and the proportionality factor P. In our numerical simulation, a 3 ns 20th order super-Gaussian shaped laser pulse with a 527 nm wavelength was used as the pump and FC-70 was chosen as the Brillouin medium. The calculated results indicate that the near field modulation index droops obviously with a proper laser intensity and the output pulse distortion decrease exponentially as a function of iterations. Our method minimizes the error between the output pulse profile and the target flat-top laser pulse, only about seven iterations are needed to complete the compensate process for 1.82 GW/cm² pump intensity (which is the proper laser intensity for beam smoothing in our simulation) with a parameter value of 0.9. This simple spatiotemporal shaping scheme has good application potential in the output optimization high power and energy nanosecond lasers.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

XZ: Conceptualization, Programming, Acquisition of data, Drafting the manuscript, Funding acquisition CL: Analysis of data, Data Curation QG: Investigation, Visualization HS: Writing–Review and Editing SS: Investigation, Validation.

Funding

This work was funded by the National Science Foundation of China (No: 11704083), the Key Program of Natural Science Foundation of Anhui Provincial Education Department (No: KJ2020A0347) and the Open Research Fund of Anhui Province Key Laboratory of Optoelectronic Materials Science and Technology (No: OMST201903).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Betti R, Zhou CD, Anderson KS, Perkins LJ, Theobald W, Solodov AA. Shock ignition of thermonuclear fuel with high areal density. Phys Rev Lett (2007) 98:155001. doi:10.1103/physrevlett.98.155001

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Ping Y, Amendt P, Baker K, Smalyuk VA, Chen H, Khan S, et al. Reaching 30% energy coupling efficiency for a high-density-carbon capsule in a gold rugby hohlraum on NIF. Nucl Fusion (2021) 61:086028. doi:10.1088/1741-4326/ac108d

CrossRef Full Text | Google Scholar

3. Rauscher P, Hauptmann J, Wetzig A, Beyer E. Domain refinement of grain oriented electrical steel with high power laser beam sources. Int J Mod Phys B (2014) 28:1442003. doi:10.1142/s021797921442003x

CrossRef Full Text | Google Scholar

4. Hambling D. Laser weapon shouts, then burns people. New Sci (2018) 240:14. doi:10.1016/s0262-4079(18)31924-9

CrossRef Full Text | Google Scholar

5. Ma H, Zhou P, Wang X, Ma Y, Xi F, Xu X, et al. Near-diffraction-limited annular flattop beam shaping with dual phase only liquid crystal spatial light modulators. Opt Express (2010) 18:8251–60. doi:10.1364/oe.18.008251

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Li JN, Tang Y, Kuang Z, Schille J, Loeschner U, Perrie W, et al. Multi imaging-based beam shaping for ultrafast laser-material processing using spatial light modulators. Opt Lasers Eng (2019) 112:59–67. doi:10.1016/j.optlaseng.2018.09.002

CrossRef Full Text | Google Scholar

7. Wu Y, Nie J, Shao L. Method to measure the phase modulation characteristics of a liquid crystal spatial light modulator. Appl Opt (2016) 55:8676–82. doi:10.1364/ao.55.008676

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Dixit SN, Thomas IM, Woods BW, Morgan AJ, Henesian MA, Wegner PJ, et al. Random phase plates for beam smoothing on the Nova laser. Appl Opt (1993) 33:2543–54. doi:10.1364/ao.32.002543

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Xiong H. Filtering differences and explanation of far-field spatial filters. J Russ Laser Res (2021) 42:181–9. doi:10.1007/s10946-021-09948-3

CrossRef Full Text | Google Scholar

10. Zhu X, Wu D, Wang G, Wang Z. High efficiency laser spatial beam smoothing based on stimulated Brillouin scattering. Laser Phys (2019) 29:065402. doi:10.1088/1555-6611/ab16e0

CrossRef Full Text | Google Scholar

11. Zhu X, Yang H, Wang G, Wu D, Qiu Y. Optimising of the material and laser parameters for high-power laser spatial beam smoothing based on stimulated Brillouin scattering. Laser Phys (2019) 29:075402. doi:10.1088/1555-6611/ab232a

CrossRef Full Text | Google Scholar

12. Wang H, Cha S, Kong HJ, Wang Y, Lu Z. Rotating off-centered lens in SBS phase conjugation mirror for high- repetition-rate operation. Opt Express (2019) 27:9895–905. doi:10.1364/oe.27.009895

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Wang Y, Zhu X, Lu Z, Zhang H. Generation of 360 ps laser pulse with 3 J energy by stimulated Brillouin scattering with a nonfocusing scheme. Opt Express (2015) 23:23318–28. doi:10.1364/oe.23.023318

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Yang F, Gyger F, Thevenaz L. Intense Brillouin amplification in gas using hollow-core waveguides. Nat Photon (2020) 14:700–8. doi:10.1038/s41566-020-0676-z

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Cui C, Wang Y, Lu Z, Yuan H, Wang Y, Chen Y, et al. Demonstration of 2.5 J, 10 Hz, nanosecond laser beam combination system based on non-collinear Brillouin amplification. Opt Express (2018) 26:32717–27. doi:10.1364/oe.26.032717

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Zhu ZH, Chen P, Li HW, Zhao B, Zhou ZY, Hu W, et al. Fragmentation of twisted light in photon-phonon nonlinear propagation. Appl Phys Lett (2018) 112:161103. doi:10.1063/1.5020082

CrossRef Full Text | Google Scholar

17. Zhu ZH, Gao W, Mu CY, Li HW. Reversible orbital angular momentum photon-phonon conversion. Optica (2016) 3(2):212–7. doi:10.1364/optica.3.000212

CrossRef Full Text | Google Scholar

18. Bashan G, London Y, Diamandi HH, Zadok A. Distributed cladding mode fiber-optic sensor. Optica (2020) 7:85–92. doi:10.1364/optica.377610

CrossRef Full Text | Google Scholar

19. Lu ZW, Hasi WLJ, Gong HP, Li Q, He WM. Generation of flat-top waveform by double optical limiting based on stimulated Brillouin scattering. Opt Express (2006) 14:5497–501. doi:10.1364/oe.14.005497

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Hasi WLJ, Lu ZW, Fu ML, Lu HH, Gong S, Lin DY, et al. Improved output energy characteristic of optical limiting based on double stimulated Brillouin scattering. Appl Phys B (2009) 95:711–4. doi:10.1007/s00340-009-3485-0

CrossRef Full Text | Google Scholar

21. Xu Y, Huang J, Wu Z, Lu Y. Non-linear optical limiting technology based on backward stimulated Brillouin scattering in grade-index optical fibres. Electron Lett (2021) 57:589–90. doi:10.1049/ell2.12204

CrossRef Full Text | Google Scholar

22. Gu B, Rui GH, Xue YX, He J, Cui YP. Large enhancement of optical limiting effects in anisotropic two-photon absorbers by radially polarized beams. J Opt Soc Am B (2016) 33:2512–7. doi:10.1364/josab.33.002512

CrossRef Full Text | Google Scholar

23. Lefort L, Barthelemy A. Intensity-dependent polarization rotation associated with type II phase-matched second-harmonic generation: Application to self-induced transparency. Opt Lett (1995) 20:1749–51. doi:10.1364/ol.20.001749

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Oliveira P, Addis S, Gay J, Ertel K, Galimberti M, Musgrave I. Control of temporal shape of nanosecond long lasers using feedback loops. Opt Express (2019) 27:6607–17. doi:10.1364/oe.27.006607

PubMed Abstract | CrossRef Full Text | Google Scholar