- 1Aviation and Automobile School, Chongqing Youth Vocational and Technical College, Chongqing, China
- 2College of Physics, Chongqing University, Chongqing, China
The topological phonon state is a new field that has sparked much interest. Weyl phonons in FeSi, for example, have been theoretically proposed and experimentally identified. In this work, via the first-principle calculation, we prove the ideal nodal net phonons exist in a realistic material Ag2O with
Introduction
Topological semimetals [1–10] with symmetry-protected bands crossing around the Fermi level have inspired enormous interest in condensed matter physics. As a typical family of topological semimetals, node-line semimetals [11–20] have high band degeneracy along a certain line in the Brillouin zone (BZ), and the resultant drumhead surface states at the boundary. Suppose more than one nodal line/ring appears in momentum space. In that case, these nodal lines/rings may form complex topological nodal structures in the three-dimensional (3D) Brillouin zone (BZ), such as nodal-chain [21–28], nodal-box [29], nodal-link [30–35], and nodal-net [36, 37] structures.
Topological state research has recently been extended to bosonic systems, such as photons in photonic crystals, phonon systems in 3D solids, and classical elastic waves in macroscopic artificial phononic crystals. In realistic materials, topological phonons [38–45] could play an essential role in thermal transports, electron-phonon coupling, and other phonon-related processes. Thus far, researchers have predicted some realistic materials [46–65] to host nodal net phonons. For example, using first-principles calculations, [66] discovered a nodal net state in the semiconductor copper chloride (CuCl). CuCl has a cubic crystal structure with the space group Pa3 (No. 205). In momentum space, the nodal net has a hexahedral shape and is made up of interconnected quadruple degenerate straight nodal lines. Moreover, with the help of first-principle calculations and symmetry analysis, [67] proposed the coexistence of the three-nodal surface and nodal net phonons in space groups with numbers 61 and 205. Some realistic materials, such as ZnSb with SG No. 61 and RuS2, P2Pt, and OsS2 with SG No. 205, hosting three-nodal surface and nodal net phonons have also been identified by [67].
In this paper, based on first-principles calculations, we contribute to one more realistic material with ideal nodal net phonons. Ag₂O is Cuprite structured and crystallizes in the cubic
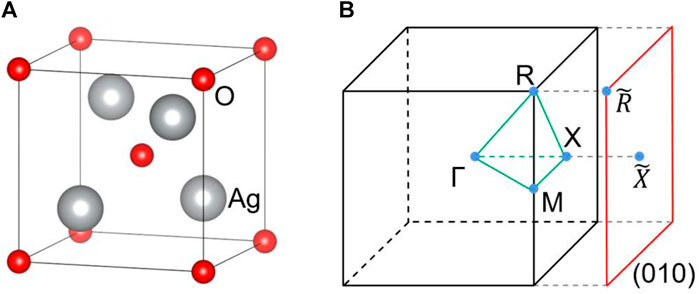
FIGURE 1. (A) The crystal structure of Ag2O, (B) 3D bulk Brillouin zone (BZ), and the two-dimensional (2D) surface BZ.
Methods
The calculations for the realistic material Ag2O were performed using the Vienna ab initio Simulation Package [69] and the framework of density functional theory. The calculation’s energy and force convergence criteria were set to 10−6 eV and −0.01 eV/A, respectively. The plane-wave expansion was truncated at 500 eV, and the entire BZ was sampled by a 7 × 7 × 7 Monkhorst-Pack grid. We used the PHONOPY code to generate the symmetry information and construct the constant force matrices for phonon spectra calculations. To calculate the phonon surface states, we used the WannierTools package [70] in conjunction with the iterative Green function method to construct the tight-binding model Hamiltonian.
Weyl nodal net phonons
Based on the determined lattice constants, the phonon dispersion for a 2 × 2 × 2 supercell of Ag2O is shown in Figure 2A. Note that the phonon-related properties in this work are calculated based on the density functional perturbation theory (DFPT). According to Figure 2A, there is no imaginary frequency in the phonon spectrum, indicating the dynamical stability of cubic Ag2O. Around the frequency of five THz, two phonon bands along X-R-Γ-M and Γ-X merged into one twofold degenerate phonon bands along the X-M path. We want to point out that a similar case can also be found around the frequency of 14 THz. Here, we only focus on the twofold degenerate phonon bands along the X-M path. The three-dimensional plot of the twofold degenerate phonon bands along the X-M is shown in Figure 2B, and one can see a cross-shaped nodal structure appears (see the dotted lines) in Figure 2B.
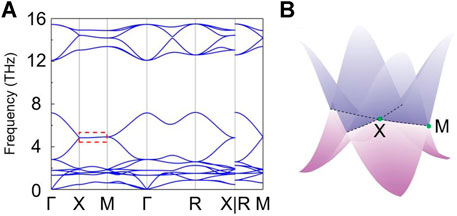
FIGURE 2. (A) Phonon dispersion of Ag2O along the Γ-X-M-Γ-R-X|R-M paths. (B) The 3D plot of the cross-shaped nodal structure.
To better view the cross-shaped nodal structure in the phonon dispersion of Ag2O, we plot the phonon band structure of the crossing branches in ky = π plane (See Figure 3A). The cross-shaped nodal structure in the ky = π plane is formed from crossing two straight Weyl nodal lines. We select some symmetry points along the X-M path and show the phonon dispersions for Ag2O along the a-b-a’, c-d-c’, e-f-e’, and g-h-g’ in Figure 3C. All the crossing points are doubly degenerate points with a linear phonon band dispersion (see Figure 3C). Note that the cross-shaped nodal structures can also exist in ky = -π, kx = ± π, kz = ± π plane. That is, these straight nodal lines are perpendicular to each other in different planes, forming a Weyl nodal net in the 3D BZ, as illustrated in Figure 3B.
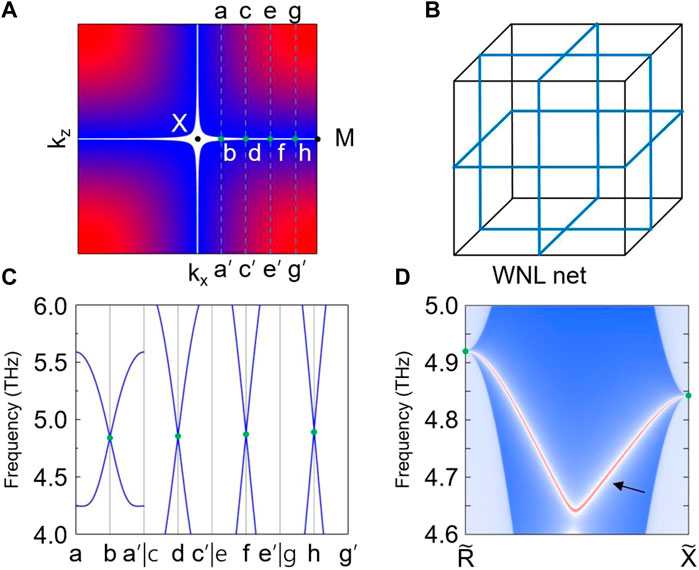
FIGURE 3. (A) A map of energy gaps between the two crossing branches around 5 THz in the ky = π plane. (B) A schematic diagram of Weyl nodal net in 3D BZ. (C) Phonon dispersions of Ag2O along the a-b-a’, c-d-c’, e-f-e’, and g-h-g’ paths. (D) Phononic drumhead-like surface states in (010) surface.
Phononic surface states
To examine the topological nature of the Weyl nodal net phonons in Ag2O, we calculate its Berry phase using the following formula:
Summary and remarks
We show that nodal net phonons exist in Ag2O using first-principles calculations. Straight lines constrained in the high-symmetry line X-M at the BZ boundary represent the nodal net. Because there is no spin in phononic systems, the nodal net phonons in Ag2O are resistant to time-reversal symmetry breaking. Before closing the paper, we would like to point out that our results can also guide the investigations of the Weyl nodal net in spinless electronic systems (such as topological semimetals without the consideration of spin-orbital coupling). We present a spinless lattice model to demonstrate the existence of Weyl nodal net states in spinless materials with SG 224. A unit cell with one site (0,0,0) was considered in this spinless lattice model, and s orbital was placed on this site. The four-band tight-binding (TB) Hamiltonian is shown as follows:
Data availability statement
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
Author contributions
Calculating, writing, and researching are done by YL.
Funding
This work is supported by the Science and Technology Research Program of Chongqing Municipal Education Commission (Grant No. KJZD-K202104101 and No. KJQN202204104) and the school-level Scientific Research Project of Chongqing Youth Vocational and Technical College (Grant No. CQY2021KYZ03).
Conflict of interest
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
The reviewer HZ declared a shared affiliation with the author(s) add initials here unless all authors are concerned to the handling editor at the time of review.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
2. Gao H, Venderbos JW, Kim Y, Rappe AM. Topological semimetals from first principles. Annu Rev Mater Res (2019) 49:153–83. doi:10.1146/annurev-matsci-070218-010049
3. Weng H, Dai X, Fang Z. Topological semimetals predicted from first-principles calculations. J Phys Condensed Matter (2016) 28(30):303rrrrrrrrrrr001. doi:10.1088/0953-8984/28/30/303001
4. Bernevig A, Weng H, Fang Z, Dai X. Recent progress in the study of topological semimetals. J Phys Soc Jpn (2018) 87(4):041001. doi:10.7566/jpsj.87.041001
5. Zhang X, Jin L, Dai X, Liu G. Topological type-II nodal line semimetal and Dirac semimetal state in stable kagome compound Mg3Bi2. J Phys Chem Lett (2017) 8(19):4814–9. doi:10.1021/acs.jpclett.7b02129
6. Tian L, Liu Y, Meng W, Zhang X, Dai X, Liu G. Spin–orbit coupling-determined topological phase: Topological insulator and quadratic Dirac semimetals. J Phys Chem Lett (2020) 11(24):10340–7. doi:10.1021/acs.jpclett.0c03103
7. Xu G, Wang W, Zhang X, Du Y, Liu E, Wang S, et al. Weak antilocalization effect and noncentrosymmetric superconductivity in a topologically nontrivial semimetal LuPdBi. Scientific Rep (2014) 4(1):5709–7. doi:10.1038/srep05709
8. Meng W, Zhang X, He T, Jin L, Dai X, Liu Y, et al. Ternary compound HfCuP: An excellent Weyl semimetal with the coexistence of type-I and type-II Weyl nodes. J Adv Res (2020) 24:523–8. doi:10.1016/j.jare.2020.05.026r
9. Chen DY, Wu Y, Jin L, Li Y, Wang X, Duan J, et al. Superconducting properties in a candidate topological nodal line semimetal SnTaS2 with a centrosymmetric crystal structure. Phys Rev B (2019) 100(6):064516. doi:10.1103/physrevb.100.064516
10. Wang X, Ding G, Cheng Z, Surucu G, Wang XL, Yang T. Rich topological nodal line bulk states together with drum-head-like surface states in NaAlGe with anti-PbFCl type structure. J Adv Res (2020) 23:95–100. doi:10.1016/j.jare.2020.01.017
11. Wang X, Ding G, Khandy SA, Cheng Z, Zhang G, Wang XL, et al. Unique topological nodal line states and associated exceptional thermoelectric power factor platform in Nb3GeTe6 monolayer and bulk. Nanoscale (2020) 12(32):16910–6. doi:10.1039/d0nr03704d
12. Wang X, Ding G, Cheng Z, Surucu G, Wang XL, Yang T. Novel topological nodal lines and exotic drum-head-like surface states in synthesized CsCl-type binary alloy TiOs. J Adv Res (2020) 22:137–44. doi:10.1016/j.jare.2019.12.001
13. Wang X, Cheng Z, Zhang G, Kuang M, Wang XL, Chen H. Strain tuning of closed topological nodal lines and opposite pockets in quasi-two-dimensional α-phase FeSi2. Phys Chem Chem Phys (2020) 22(24):13650–8. doi:10.1039/d0cp02334e
14. Zhou F, Liu Y, Kuang M, Wang P, Wang J, Yang T, et al. Time-reversal-breaking Weyl nodal lines in two-dimensional A3C2 (A= Ti, Zr, and Hf) intrinsically ferromagnetic materials with high Curie temperature. Nanoscale (2021) 13(17):8235–41. doi:10.1039/d1nr00139f
15. Zhou F, Cui C, Wang J, Kuang M, Yang T, Yu ZM, et al. Perovskite-type YRh3B with multiple types of nodal point and nodal line states. Phys Rev B (2021) 103(24):245126. doi:10.1103/physrevb.103.245126
16. Jin L, Zhang X, He T, Meng W, Dai X, Liu G. Topological nodal line state in superconducting NaAlSi compound. J Mater Chem C (2019) 7(34):10694–9. doi:10.1039/c9tc03464a
17. He T, Zhang X, Wang L, Liu Y, Dai X, Wang L, et al. Ideal fully spin-polarized type-II nodal line state in half-metals X2YZ4 (X= K, Cs, Rb, YCr, Cu, Z= Cl, F). Mater Today Phys (2021) 17:100360. doi:10.1016/j.mtphys.2021.100360
18. He T, Zhang X, Liu Y, Dai X, Wang L, Liu G. Potential antiferromagnetic Weyl nodal line state in LiTi2O4 material. Phys Rev B (2021) 104(4):045143. doi:10.1103/physrevb.104.045143
19. Yang Z, Hu J. Non-Hermitian Hopf-link exceptional line semimetals. Phys Rev B (2019) 99(8):081102. doi:10.1103/physrevb.99.081102
20. Li Y, Xia J. Cubic hafnium nitride: A novel topological semimetal hosting a 0-dimensional (0-D) nodal point and a 1-D topological nodal ring. Front Chem (2020) 8:727. doi:10.3389/fchem.2020.00727
21. Yu R, Wu Q, Fang Z, Weng H. From nodal chain semimetal to Weyl semimetal in HfC. Phys Rev Lett (2017) 119(3):036401. doi:10.1103/physrevlett.119.036401
22. Yan Q, Liu R, Yan Z, Liu B, Chen H, Wang Z, et al. Experimental discovery of nodal chains. Nat Phys (2018) 14(5):461–4. doi:10.1038/s41567-017-0041-4
23. Zhang X, Jin L, Dai X, Chen G, Liu G. Ideal inner nodal chain semimetals in Li2XY (X= Ca, Ba; Y= Si, Ge) materials. J Phys Chem Lett (2018) 9(18):5358–63. doi:10.1021/acs.jpclett.8b02204
24. Chang G, Xu SY, Zhou X, Huang SM, Singh B, Wang B, et al. Topological Hopf and chain link semimetal states and their application to Co2MnGa. Phys Rev Lett (2017) 119(15):156401. doi:10.1103/physrevlett.119.156401
25. Fu B, Fan X, Ma D, Liu CC, Yao Y. Hourglasslike nodal net semimetal in Ag2BiO3. Phys Rev B (2018) 98(7):075146. doi:10.1103/physrevb.98.075146
26. Chen C, Su Z, Zhang X, Chen Z, Sheng XL. From multiple nodal chain to Dirac/Weyl semimetal and topological insulator in ternary hexagonal materials. The J Phys Chem C (2017) 121(51):28587–93. doi:10.1021/acs.jpcc.7b11075
27. Bzdušek T, Wu Q, Rüegg A, Sigrist M, Soluyanov AA. Nodal-chain metals. Nature (2016) 538(7623):75–8. doi:10.1038/nature19099
28. Gao Y, Xie Y, Chen Y, Gu J, Chen Z. Spindle nodal chain in three-dimensional α′ boron. Phys Chem Chem Phys (2018) 20(36):23500–6. doi:10.1039/c8cp03874k
29. Sheng XL, Yu ZM, Yu R, Weng H, Yang SA. d orbital topological insulator and semimetal in the antifluorite Cu2S family: Contrasting spin Helicities, nodal box, and hybrid surface states. J Phys Chem Lett (2017) 8(15):3506–11. doi:10.1021/acs.jpclett.7b01390
30. Yan Z, Bi R, Shen H, Lu L, Zhang SC, Wang Z. Nodal-link semimetals. Phys Rev B (2017) 96(4):041103. doi:10.1103/physrevb.96.041103
31. Chang PY, Yee CH. Weyl-link semimetals. Phys Rev B (2017) 96(8):081114. doi:10.1103/physrevb.96.081114
32. Zhou Y, Xiong F, Wan X, An J. Hopf-link topological nodal-loop semimetals. Phys Rev B (2018) 97(15):155140. doi:10.1103/physrevb.97.155140
33. Liu Z, Lou R, Guo P, Wang Q, Sun S, Li C, et al. Experimental observation of Dirac nodal links in centrosymmetric semimetal TiB2. Phys Rev X (2018) 8(3):031044. doi:10.1103/physrevx.8.031044
34. Chen W, Lu HZ, Hou JM. Topological semimetals with a double-helix nodal link. Phys Rev B (2017) 96(4):041102. doi:10.1103/physrevb.96.041102
35. Tan X, Li M, Li D, Dai K, Yu H, Yu Y. Demonstration of Hopf-link semimetal bands with superconducting circuits. Appl Phys Lett (2018) 112(17):172601. doi:10.1063/1.5029439
36. Wang JT, Nie S, Weng H, Kawazoe Y, Chen C. Topological nodal-net semimetal in a graphene network structure. Phys Rev Lett (2018) 120(2):026402. doi:10.1103/physrevlett.120.026402
37. Feng X, Yue C, Song Z, Wu Q, Wen B. Topological Dirac nodal-net fermions in AlB2-type TiB2 and ZrB2. Phys Rev Mater (2018) 2(1):014202. doi:10.1103/physrevmaterials.2.014202
38. Wang X, Zhou F, Yang T, Kuang M, Yu ZM, Zhang G. Symmetry-enforced ideal lanternlike phonons in the ternary nitride Li6WN4. Phys Rev B (2021) 104(4):L041104. doi:10.1103/physrevb.104.l041104
39. Zhou F, Chen H, Yu ZM, Zhang Z, Wang X. Realistic cesium fluogermanate: An ideal platform to realize the topologically nodal-box and nodal-chain phonons. Phys Rev B (2021) 104(21):214310. doi:10.1103/physrevb.104.214310
40. Xie C, Liu Y, Zhang Z, Zhou F, Yang T, Kuang M, et al. Sixfold degenerate nodal-point phonons: Symmetry analysis and materials realization. Phys Rev B (2021) 104(4):045148. doi:10.1103/physrevb.104.045148
41. Wang X, Yang T, Cheng Z, Surucu G, Wang J, Zhou F, et al. Topological nodal line phonons: Recent advances in materials realization. Appl Phys Rev (2022) 9(4):041304. doi:10.1063/5.0095281
42. Ding G, Zhou F, Zhang Z, Yu ZM, Wang X. Charge-two Weyl phonons with type-III dispersion. Phys Rev B (2022) 105(13):134303. doi:10.1103/physrevb.105.134303
43. Liu Y, Chen X, Xu Y. Topological phononics: From fundamental models to real materials. Adv Funct Mater (2020) 30(8):1904784. doi:10.1002/adfm.201904784
44. Liu Y, Lian CS, Li Y, Xu Y, Duan W. Pseudospins and topological effects of phonons in a kekulé lattice. Phys Rev Lett (2017) 119(25):255901. doi:10.1103/physrevlett.119.255901
45. Liu Y, Zou N, Zhao S, Chen X, Xu Y, Duan W. Ubiquitous topological states of phonons in solids: Silicon as a model material. Nano Lett (2022) 22(5):2120–6. doi:10.1021/acs.nanolett.1c04299
46. Wang J, Yuan H, Kuang M, Yang T, Yu ZM, Zhang Z, et al. Coexistence of zero-one-and two-dimensional degeneracy in tetragonal SnO2 phonons. Phys Rev B (2021) 104(4):L041107. doi:10.1103/physrevb.104.l041107
47. Zhong M, Han Y, Wang J, Liu Y, Wang X, Zhang G. Material realization of double-Weyl phonons and phononic double-helicoid surface arcs with P213 space group. Phys Rev Mater (2022) 6(8):084201. doi:10.1103/physrevmaterials.6.084201
48. Xie C, Yuan H, Liu Y, Wang X, Zhang G. Three-nodal surface phonons in solid-state materials: Theory and material realization. Phys Rev B (2021) 104(13):134303. doi:10.1103/physrevb.104.134303
49. Feng Y, Xie C, Chen H, Liu Y, Wang X. Dirac point phonons at high-symmetry points: Towards materials realization. Phys Rev B (2022) 106(13):134307. doi:10.1103/physrevb.106.134307
50. Chen J, He J, Pan D, Wang X, Yang N, Zhu J, et al. Emerging theory and phenomena in thermal conduction: A selective review. Sci China Phys Mech Astron (2022) 65(11):117002–16. doi:10.1007/s11433-022-1952-3
51. Yang T, Xie C, Chen H, Wang X, Zhang G. Phononic nodal points with quadratic dispersion and multifold degeneracy in the cubic compound Ta3Sn. Phys Rev B (2022) 105(9):094310. doi:10.1103/physrevb.105.094310
52. Wang X, Zhou F, Zhang Z, Wu W, Yu ZM, Yang SA. Single pair of multi-Weyl points in nonmagnetic crystals. Phys Rev B (2022) 106(19):195129. doi:10.1103/physrevb.106.195129
53. Li J, Wang L, Liu J, Li R, Zhang Z, Chen XQ. Topological phonons in graphene. Phys Rev B (2020) 101(8):081403. doi:10.1103/physrevb.101.081403
54. Singh S, Wu Q, Yue C, Romero AH, Soluyanov AA. Topological phonons and thermoelectricity in triple-point metals. Phys Rev Mater (2018) 2(11):114204. doi:10.1103/physrevmaterials.2.114204
55. Süsstrunk R, Huber SD. Classification of topological phonons in linear mechanical metamaterials. Proc Natl Acad Sci (2016) 113(33):E4767–75. doi:10.1073/pnas.1605462113
56. Sreeparvathy PC, Mondal C, Barman CK, Alam A. Coexistence of multifold and multidimensional topological phonons in KMgBO3. Phys Rev B (2022) 106(8):085102. doi:10.1103/physrevb.106.085102
57. You JY, Sheng XL, Su G. Topological gimbal phonons in T-carbon. Phys Rev B (2021) 103(16):165143. doi:10.1103/physrevb.103.165143
58. Liu QB, Wang ZQ, Fu HH. Ideal topological nodal-surface phonons in RbTeAu-family materials. Phys Rev B (2021) 104(4):L041405. doi:10.1103/physrevb.104.l041405
59. Chen XQ, Liu J, Li J. Topological phononic materials: Computation and data. The Innovation (2021) 2(3):100134. doi:10.1016/j.xinn.2021.100134
60. Zhang T, Song Z, Alexandradinata A, Weng H, Fang C, Lu L, et al. Double-Weyl phonons in transition-metal monosilicides. Phys Rev Lett (2018) 120(1):016401. doi:10.1103/physrevlett.120.016401
61. Liu QB, Wang ZQ, Fu HH. Topological phonons in allotropes of carbon. Mater Today Phys (2022) 24:100694. doi:10.1016/j.mtphys.2022.100694
62. Jin YJ, Chen ZJ, Xia BW, Zhao YJ, Wang R, Xu H. Ideal intersecting nodal-ring phonons in bcc C8. Phys Rev B (2018) 98(22):220103. doi:10.1103/physrevb.98.220103
63. Miao H, Zhang TT, Wang L, Meyers D, Said AH, Wang YL, et al. Observation of double Weyl phonons in parity-breaking FeSi. Phys Rev Lett (2018) 121(3):035302. doi:10.1103/physrevlett.121.035302
64. Liu Y, Xu Y, Duan W, 2019. Research (2019). p. 1–8. doi:10.34133/2019/5173580Three-dimensional topological states of phonons with tunable pseudospin physicsResearch
65. Wang Z, Zhou W, Rudenko AN, Yuan S. Lattice dynamics and topological surface phonon states in cuprous oxide Cu2O. Phys Rev B (2021) 103(19):195137. doi:10.1103/physrevb.103.195137
66. Liu QB, Fu HH, Wu R. Topological phononic nodal hexahedron net and nodal links in the high-pressure phase of the semiconductor CuCl. Phys Rev B (2021) 104(4):045409. doi:10.1103/physrevb.104.045409
67. Wang J, Yuan H, Yu ZM, Zhang Z, Wang X. Coexistence of symmetry-enforced phononic Dirac nodal-line net and three-nodal surfaces phonons in solid-state materials: Theory and materials realization. Phys Rev Mater (2021) 5(12):124203. doi:10.1103/physrevmaterials.5.124203
68. Norby P, Dinnebier R, Fitch AN. Decomposition of silver carbonate; the crystal structure of two high-temperature modifications of Ag2CO3. Inorg Chem (2002) 41(14):3628–37. doi:10.1021/ic0111177
69. Sun G, Kürti J, Rajczy P, Kertesz M, Hafner J, Kresse G. Performance of the Vienna ab initio simulation package (VASP) in chemical applications. J Mol Struct THEOCHEM (2003) 624(1-3):37–45. doi:10.1016/s0166-1280(02)00733-9
Keywords: topological materials, DFT, DFPT calculation, Ag2O, phonon dispersion
Citation: Li Y (2023) Ideal nodal net phonons in
Received: 25 November 2022; Accepted: 15 December 2022;
Published: 04 January 2023.
Edited by:
Xiaoming Zhang, Hebei University of Technology, ChinaReviewed by:
Liying Wang, Tianjin University, ChinaHaopeng Zhang, Chongqing University of Posts and Telecommunications, China
Copyright © 2023 Li. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Yang Li, bGl5YW5nX3BoeXNpY3NAMTI2LmNvbQ==
 Yang Li
Yang Li