- 1Physical Research Laboratory, Ahmedabad, Gujarat, India
- 2Indian Institute of Technology Gandhinagar, Gandhinagar, Gujarat, India
- 3Department of Physics, Manipur University, Canchipur, Manipur, India
In this research, we study the bosonic fractional quantum Hall (FQH) states in a system of ultracold bosons in a two-dimensional optical lattice in the presence of a synthetic magnetic field, described by the bosonic Harper–Hofstadter Hamiltonian. We use the cluster Gutzwiller mean-field and exact diagonalization techniques in our work. We obtain incompressible states as ground states at various filling factors similar to those of the FQH states. We focus in particular on the ν = 1/2 FQH state, and it is characterized by the two-point correlation function and the many-body Chern number. We further investigate the effect of dipolar interaction on the ν = 1/2 FQH state. We find that the dipolar interaction stabilizes the FQH state against the competing superfluid state.
1 Introduction
Ultracold atoms in optical lattices are the subject of intense research as these systems are excellent proxies to study phenomena of quantum many-body physics. The strongly correlated regime is of particular interest as parameter domains were earlier inaccessible in condensed matter systems. For bosonic atoms, the physics of the system is described by the Bose–Hubbard model (BHM) [1, 2]. The interplay between the hopping strengths of the bosons onto neighboring lattice sites and the on-site repulsive interaction leads to the Mott insulator (MI) and superfluid (SF) phase in various parameter domains [3, 4]. Such systems allow unprecedented control over the system parameters for easy tunability in the experiments. Optical lattices are crystals of light and are generated by superimposing counter-propagating laser beams. The lattice parameters, like the depth of the potential wells, can be controlled by changing the intensity of the laser beams, and the lattice periodicity can be varied by choosing different wavelength lasers. Additionally, different lattice geometries like square, triangular, honeycomb, and kagome are synthesized for various choices of the angles between the lasers, and the lattice dimensionality can be increased by employing more sets of lasers in other orthogonal directions. Furthermore, these systems are clean and free of any defects. However, if needed, the defects can be introduced in a controlled manner, thus allowing a systematic study of the associated effects. This has allowed the study of various novel quantum phases and the experimental observation of quantum phase transitions with good control on the system parameters [5, 6]. They have been used extensively to study the quantum phases which have eluded experiments. Examples include the much-studied supersolid phase with dipolar bosons [7–9] and in various lattice geometries [10, 11]. The supersolid phase has been experimentally observed recently for the system of dipolar gases [12, 13] and with cavity-mediated interactions [14]. Other studies include the fermionic and bosonic mixtures and the physics of phase separation [15–17], collective excitations [18, 19], the effect of the synthetic magnetic field on the supersolid phase and the Bose glass phase in a disordered system [20, 21], Kibble–Zurek mechanism, and non-equilibrium dynamics [22–24].
Atoms being charged neutral, no Lorentz force is generated when an external magnetic field is applied. However, there is a host of phenomena in condensed matter physics associated with external magnetic fields. A prime example is the physics of quantum Hall states. This is now resolved with the recent experimental realization of synthetic gauge fields using lasers [25–27]. Thus, the system of neutral bosons in optical lattices is an ideal setup to study the physics of quantum Hall effect. This is due to the possibility of realizing high flux density per plaquette of the lattice, which is otherwise difficult in condensed matter systems [28]. This has opened the door to understand the strongly correlated physics of topological states like the integer quantum Hall and fractional quantum Hall states, proposals for their realization [29], and various theoretical studies on FQH states [30–33]. Recently, FQH states have been realized experimentally using ultracold atoms in optical lattices [34].
The integer quantum Hall effect (IQHE) is observed in electronic systems under the influence of strong magnetic fields at very low temperatures, where the resistivity of the system does not assume continuous values but is quantized in integer multiples of e2/h [35]. As a function of the magnetic field, the resistivity has plateaus corresponding to the integer values. Later, the discovery of the fractional quantum Hall effect (FQHE) in 1982 observed the resistivity quantized as the fractional multiple of e2/h [36]. It is understood to be arising from the electronic correlations, which play no role in the IQHE [37]. The FQH states are characterized by the fractional values of the filling factor ν, which quantifies the number of the flux quanta attached per electron. Earliest identified FQH states had ν = 1/3 and 2/3. Subsequently, several states were identified with ν = 1/5, 2/5, 3/7, 4/9, …, 4/3, 5/3, 7/5, 5/2, … [38]. The Jain sequence predicts FQH states for
In this work, we numerically study the FQH states exhibited by the ultracold bosons in a square optical lattice with a synthetic magnetic field described by the bosonic Harper–Hofstadter Hamiltonian. We use the cluster Gutzwiller mean-field (CGMF) and the exact diagonalization (ED) methods to probe the FQH states near the vacuum state. We have also studied the FQH states in the bosonic Harper–Hofstadter Hamiltonian extended by incorporating dipolar interactions. We focus, in particular, on the ν = 1/2 FQH state. This study adds to the previous literature on FQHE with dipolar interactions in the identification of the ground state among competing FQH and superfluid states obtained using the CGMF method. The superfluid state, obtained from the exact diagonalization method, has number density that is an integer multiple of the inverse of the system size and hence may not represent the ground state for the system in the thermodynamic limit. Thus, with ED, the metastability of the state is not determined. However, in order to identify the topological order of the state, we ultimately use exact diagonalization for a given number density. The FQH states are identified by studying their characteristic decaying trend of the two-point correlation function. These states are topological in nature and have fractional values of topological charge. The identification of the topological nature for these states is carried out by calculating the many-body Chern number (MBCN) [44].
2 Theory
Consider a system of bosonic atoms loaded in a 2D square optical lattice in the presence of a synthetic magnetic field. The system is described by the bosonic Harper–Hofstadter Hamiltonian, which is similar to the BHM except that the hopping term acquires a lattice-site-dependent Peierls phase. In the Landau gauge, the Hamiltonian is given by
where p (q) is the lattice site index along the x (y) directions,
The ground state is obtained by diagonalizing the Hamiltonian using the CGMF method with the appropriate cluster size. In the CGMF method, the lattice is tiled with clusters, and neighboring clusters are coupled through the mean field of the lattice sites at the boundary of clusters. Thus, the hopping term in the Hamiltonian in Eq. 1 is evaluated exactly for the intra-cluster hopping, while it is modified using mean-field prescription for the inter-cluster hopping [45]. In this approximation, the bosonic creation and annihilation operators of the inter-cluster hopping terms are written in terms of a mean-field plus a fluctuation. The bosonic operator corresponding to lattice sites surrounding the edges of a cluster is replaced by
where
where the first summation is restricted over lattice sites (p, q) such that their neighboring lattice sites (p+1, q) or (p, q+1) also lie within the cluster C. The last summation is over lattice sites (p, q) that lie at the boundary of the cluster C. Using the Gutzwiller ansatz, the ground state wavefunction of the system is defined as the tensor product of cluster wavefunctions expressed in terms of the coupled basis as follows:
where the cluster is chosen to be of dimension K × L. Then, for a M × N system, the number of clusters required to tile the system is M × N/(K × L). To obtain the ground state numerically, we start with an initial guess for the mean field ϕ, and the corresponding Hamiltonian matrix is calculated. The ground state wavefunction of each cluster is obtained by diagonalization of the cluster Hamiltonian. New values of ϕ are calculated for the lattice sites at the edge of the cluster, and these are used to update the cluster Hamiltonian as an improvement over the initial guess. This process is repeated for all the clusters and continued till self-consistency is achieved. For the present computations, we consider self-consistency is reached when the mean field converges upto an accuracy of
For specific values of the filling factor ν = ρ/α, where ρ is the number density, FQH states may be favored as the ground state. The quantum Hall states are identified by the plateaus in the plot of bosonic density ρ as a function of μ, which can also be referred to as the compressibility plot. Thus, the plateaus are the indicators of incompressible ground states and the signature of quantum Hall states. Among the states, those with the integer (fractional) value of ν can be the integer (fractional) quantum Hall states. The compressibility plot is obtained by the CGMF method with the appropriate cluster size. For the present work, we consider α = 1/4 and choose the Landau gauge. It should be mentioned that we choose experimentally achievable high values of α [26], as the lattice structure becomes more prominent at high flux strengths compared to the continuum limit at low values of α. For various choices of the flux strength α, FQHE has been studied extensively and has been reported in various works [31, 46–49]. For this choice of the magnetic field and the gauge employed, the magnetic unit cell consists of four lattice sites along the y direction. So the cluster size along the y direction should be in multiples of four lattice sites in order to respect the magnetic translational symmetry. To further verify that the plateaus represent quantum Hall states, we use the exact diagonalization method to compute properties of the quantum Hall states. In this method, all the terms of Hamiltonian are calculated exactly for a system with a fixed number of particles, that is, we work in the canonical ensemble. The quantum Hall states have a characteristic property related to the decaying behavior of the two-point correlation function defined by
This arises because the quantum Hall state is gapped in bulk but has a gapless edge at the boundary of the system.
To identify the topological order of the state, we calculate the MBCN using the method of [51]. On a torus geometry, the generalized boundary conditions are given by the single-particle translation along the lattice resulting in the original wavefunction but upto a phase or twist angles at the boundary. Depending on the direction along which the twist angle is applied, it could either represent magnetic flux along the axis of the torus or through the center of the torus. The ground state is a function of the twist angles, and the knowledge of the ground-state manifold across the grid of twist angles (θx, θy) is necessary to calculate MBCN. At the boundaries of the lattice, twist angles θx (θy) are applied in the hopping amplitude along x (y) directions, and then exact hopping is allowed at the boundary using periodic boundary conditions (pbc). The geometry of the system is thus that of a torus. With the implementation of the twist angles, the Hamiltonian is given by
where δxL is the Kronecker delta function. The ground-state manifold of the ν = 1/2 quantum Hall state is doubly degenerated on the torus geometry, so we calculate two states from the degenerated ground-state manifold Ψ0(θx, θy) and Ψ1(θx, θy) at various values of twist angles in the range [0,1] and calculate the ground-state manifold projector at (θx, θy):
To fix the gauge for the ground-state manifold, we choose two reference multiplets from the ground-state manifold at two different values of the twist angles
in either of the two complementary regions (identified by the regions where either ΛΦ or ΛΦ′ field is vanished). While counting the number of branch vortices, the vortices and anti-vortices should be summed with appropriate signs according to the vorticity [31, 48].
3 Results
3.1 FQH with Harper–Hofstadter Hamiltonian
In the phase diagram, considered in the μ/U−J/U plane, of the system defined by the Hamiltonian in Eq. 1, the quantum Hall states emerge as the incompressible states in the superfluid domain close to the Mott lobes. We scan for the FQH states outside the ρ = 0 vacuum state and obtain the compressibility plot (ρ vs. μ/U at fixed J/U) of the Hamiltonian given in Eq. 1. We employ the CGMF method with periodic boundary conditions (pbc) along x and y directions for a 12 × 12 lattice tiled with clusters of size 4 × 4 for α = 1/4. This choice of cluster size respects the magnetic translational symmetry. We allow the single-site occupancies to be at most unit filling, since at low values of J/U and near the ρ = 0 state, the probability of double occupancies at a site is negligible. For the ground state of the system, the average bosonic density ρ as a function of μ at fixed J/U = 0.01 is shown in Figure 1. We choose a small value of J to investigate the FQH states near the ρ = 0 vacuum state. At low density and near the ρ = 0 state, the probability of multiple occupancies per site is negligible, and hence the bosons can be treated as hard-core bosons. For such cases, if the strength J is tuned slightly, the compressibility plot is independent of J when plotted against μ/J. However, for large J = 0.1 U, hard-core boson treatment breaks down, and multiple occupancies per site should be allowed. We have carried out computations by considering the maximum single-site occupancy as 2 for densities close to ρ = 1/8, and note that the superfluid state is the ground state.
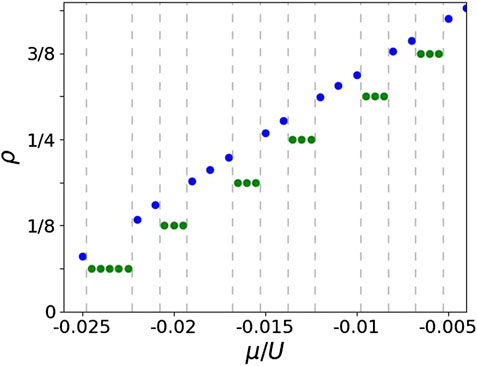
FIGURE 1. Compressibility plot: Ground state ρ as a function of μ/U at J = 0.01 U and α = 1/4. Green color dots represent the incompressible states, and the superfluid states are identified with blue color dots. The dashed gray line is a guide to the eye, separating the superfluid and incompressible state regimes. This plot is obtained using the CGMF method with the 4 × 4 cluster for a 12 × 12 lattice with pbc along both the directions.
In the figure, we see the compressible SF states (blue color) are associated with continuously varying number density against the chemical potential. However, in some regimes of μ/U, the density ρ does not change with the change in μ/U. These are incompressible states and form the plateaus (green color) in the compressibility plot. In these regimes, the incompressible states are the ground states, and the SF states are the competing metastable states. It is to be contrasted with the case of α = 1/3 and 1/5, where the SF state is the ground state and quantum Hall states are metastable [46, 49]. These incompressible states appear with ρ = 1/16, 1/8, 3/16, … corresponding to the filling factors ν = 1/4, 1/2, 3/4, …. These states residing on the plateaus in the compressibility plot can be quantum Hall states. The density and SF-order parameter distribution for the incompressible state at μ = −0.020U with ρ = 1/8 corresponding to ν = 1/2 with the 4 × 4 cluster for a 12 × 12 lattice is shown in Figure 2. In this figure, we see maximum bosonic density at the center of the 4 × 4 cluster, and it decreases with the radial distance from the center. It is to be noted that this incompressible ground state is nearly degenerate with the compressible SF state. This incompressible state has the energy per particle −0.00456 U, while the competing SF state is metastable with a higher number density and with the energy per particle −0.00446 U, and the gap between the two is 0.0001 U ∼ J/100. To investigate the finite size effects, we study the ρ = 1/8 plateau with system sizes as 8 × 8 and 16 × 16 for a range of μ values around this plateau. We note that this plateau is intact and robust against finite size effects.
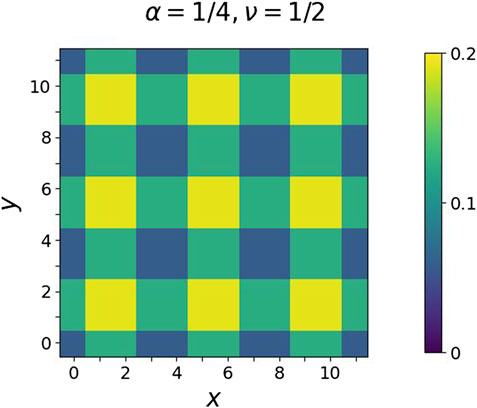
FIGURE 2. Density distribution for the ν = 1/2 incompressible state at μ/U = −0.02 obtained by CGMF with the 4 × 4 cluster for a 12 × 12 lattice with pbc.
To identify the incompressible states as FQH, we check the trend in the decay of the two-point correlation function for a larger system size using exact diagonalization. For a system of 4, 5, and 6 bosons on 8 × 4, 10 × 4, and 12 × 4 lattices, respectively, and with open boundary conditions, the plot of
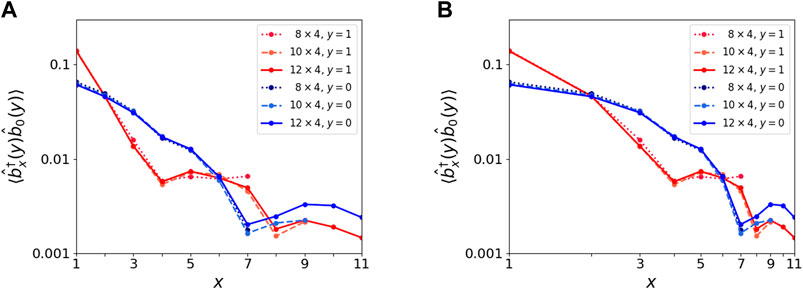
FIGURE 3. Two-point correlation function for the ρ = 1/8 state using open boundary conditions in the (A) log-linear scale and (B) log-log scale. Different shades of colors red and blue correspond to the row in the bulk (y = 1) and at the edge (y = 0). Dotted, dashed, and solid lines correspond to system sizes 8 × 4, 10 × 4, and 12 × 4, respectively.
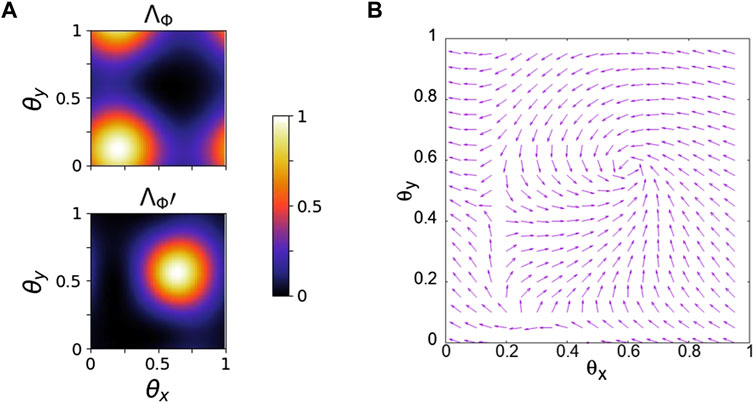
FIGURE 4. Plot of (A) reference gauge fields ΛΦ, ΛΦ′, and (B) argument field Ω as a function of the twist angles. In the region, where ΛΦ′ ≠ 0 and ΛΦ = 0, we see a vortex in the Ω field with a phase accumulation of 2π around it. Similarly, in the complementary region, we see an anti-vortex in the Ω field. Thus, there is only single-branch vortex in each region, which signifies that the many-body Chern number is equal to 1.
3.2 FQH with dipolar interactions
The quantum Hall states, as mentioned previously, are separated from excited states with an energy gap. The larger the gap, more robust the state is against perturbations. It is predicted that the dipolar interactions can increase the energy gap, and the results from exact diagonalization have shown that the energy gap increases with the dipolar interactions [31]. Here, using the CGMF method, we have shown that the incompressible states exist as the ground states with the addition of the dipolar interactions. Furthermore, we characterize the topological order to identify these incompressible states as the FQH states. To observe the effects of dipolar interactions on the occurrence of FQH states as the ground states, we incorporate the nearest-neighbor (NN) interactions with strength V, and the Hamiltonian of the system is given by the extended BHM. The interaction term in the Hamiltonian in Eq. 1 gets modified with the term corresponding to the nearest neighbor interactions and is given by
where (p′, q′) ∈ {p ± 1, q ± 1}.
Similar to the previous calculations, we obtain the compressibility plot by using the CGMF method with the 4 × 4 clusters. For the case of dipolar interaction of strength V = 2 J = 0.02 U, the compressibility plot is shown in Figure 5A. We observe the existence of incompressible states for densities ρ = 1/16, 1/8, and 3/16. The plateaus corresponding to the incompressible states now shift to higher μ/U than the case of V = 0. This is due to the influence of repulsive dipolar interactions. For a given value of μ, the system now energetically favors states with lower density to reduce the repulsive interaction energy. At μ/U = −0.015, the energy per particle for the incompressible state is −0.0084 U and −0.0079 U for the competing SF state with the energy gap 0.0005 U ∼ J/20. For larger V = 5 J = 0.05 U, the compressibility plot is shown in Figure 5B. We observe incompressible plateaus at ρ = 1/16 and 1/8. As expected, on increasing the strength of the dipolar interaction V, the plateaus corresponding to incompressible states shift to higher μ/U values. Itis also observed that the ρ = 1/8 incompressible state now exists in a larger parameter domain in the ground-state phase diagram. Near μ/U = −0.01, we find an incompressible state with ρ = 1/8 and the energy per particle is −0.0121 U, while the competing SF state has an energy per particle of −0.0111 U, and the energy gap is 0.001 U ∼ J/10. We find that the energy gap separating the incompressible state and the metastable state increases with the strength of dipolar interactions. Thus, the dipolar interactions stabilize the incompressible states. For the present work, the truncation of dipolar interactions to NN is sufficient as it qualitatively captures the effects of long-range interactions. For the case of dilute density considered here, we have examined the effect of the inclusion of the next-nearest neighbor interaction on the ρ = 1/8 plateau and observed that it is robust.
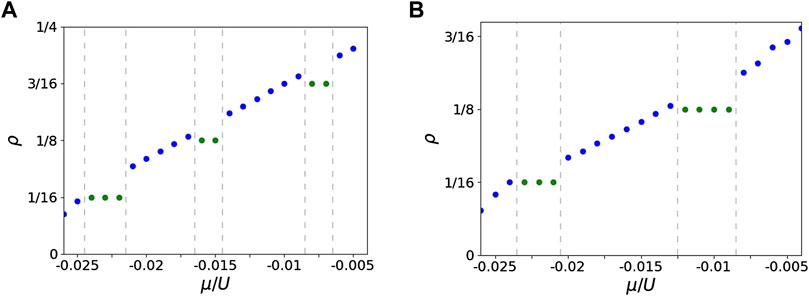
FIGURE 5. Compressibility plot: ρ as a function of μ/U for α = 1/4 with dipolar interaction strengths (A) V = 2J = 0.02 U and (B) V = 5J = 0.05 U. Green color dots represent the incompressible states, and the superfluid states are identified with blue color dots. The dashed gray line is a guide to the eye, separating the superfluid and incompressible state regimes. This plot is obtained using the CGMF method with the 4 × 4 cluster for a 12 × 12 lattice with pbc along both the directions.
To identify the ρ = 1/8 incompressible state as the ν = 1/2 FQH state, we check the behavior of the two-point correlation function
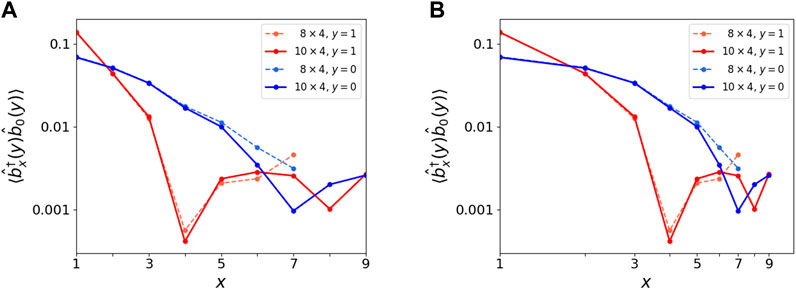
FIGURE 6. Two-point correlation function for the ρ = 1/8 state using open boundary conditions for V = 2 J = 0.02 U in the (A) log-linear scale and (B) log-log scale. Different shades of red and blue colors correspond to the row in the bulk (y = 1) and at the edge (y = 0). Dashed and solid lines correspond to system sizes 8 × 4 and 10 × 4, respectively.
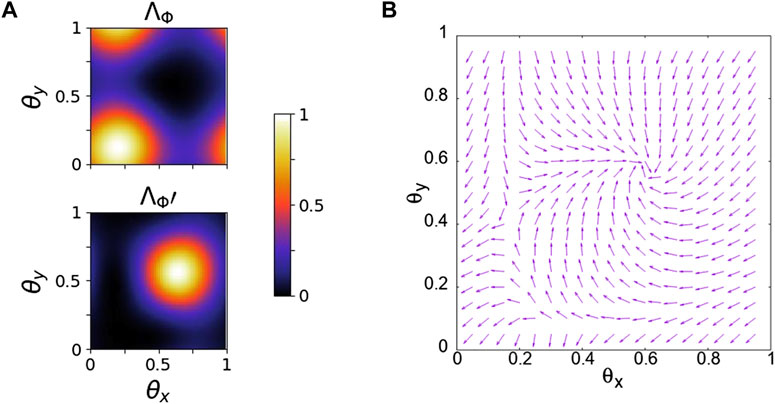
FIGURE 7. Plot of (A) reference gauge fields ΛΦ, ΛΦ′, and (B) argument field Ω as a function of the twist angles for the case of a dipolar interaction with strength V = 2 J = 0.02 U. In the region, where ΛΦ′ ≠ 0 and ΛΦ = 0, we see a vortex in the Ω field with a phase accumulation of 2π around it. Similarly, in the complementary region, we see an anti-vortex in the Ω field. Thus, there is only single-branch vortex in each region, which signifies that the many-body Chern number is equal to 1.
In this manuscript, we have confined our study to the case of closed systems. However, the effect of dissipation arising from the coupling with the environment on the robustness of topologically ordered phases becomes significant from an experimental perspective toward realizing these phases. Taking into account the two-body loss, studies, assuming the Markovian dynamics, find that the topological order of the phase survives; however, the state has a finite lifetime [53, 54]. The state preparation of FQH states with dissipative pumping of particles from higher to lower bands has been studied in [55]. The effect of non-Markovian environments has been studied for atom-cavity systems [56–59]. However, this effect needs to be explored for the topologically ordered phases.
4 Discussion
We have studied the FQH states of the bosonic Harper–Hofstadter Hamiltonian, which can be experimentally realized with ultracold atoms in optical lattices. We find FQH states as the ground state of the system for various parameter regimes. To calculate the ground state, we have used the CGMF method, which describes the quantum correlations well, and we find that incompressible states occur as the ground states for different regions in the parameter space. The filling factors of these states are similar to those of the FQH states. To verify that the states are indeed FQH states, we identify the topological order of the ν = 1/2 state by calculating the MBCN. With the introduction of dipolar interactions truncated to the nearest neighbor, we show that the extended Hamiltonian also supports the FQH states as the ground state. Thus, FQH states are robust against the dipolar interactions; in fact, we find that the dipolar interactions stabilize these states against the SF state. We have verified the robustness of the ν = 1/2 FQH state against the finite size effects and its stability against the tail of the dipolar interaction. This suggests the possibility of experimentally observing the ν = 1/2 FQH state with dipolar condensates in the optical lattice. Recent experimental realization of FQH states for ultracold gas of 87Rb atoms in the optical lattice [34] is a first step and can set a platform to further investigate the FQHE with dipolar condensates in the near future.
Data availability statement
The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.
Author contributions
DG, HS, and DA contributed to the initial conceptualization of the manuscript. DG performed the necessary numerical calculations. DG, HS, and DA analyzed and interpreted the results and contributed to the manuscript writing.
Acknowledgments
The results presented in the paper are based on the computations using Vikram-100, the 100 TFLOP HPC Cluster at the Physical Research Laboratory, Ahmedabad, India. We thank Rukmani Bai and Soumik Bandyopadhyay for their valuable insights and fruitful discussions.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
1. Hubbard J. Electron correlations in narrow energy bands. Proc R Soc. A (1963) 276:238. doi:10.1098/rspa.1963.0204
2. Fisher MPA, Weichman PB, Grinstein G, Fisher DS. Boson localization and the superfluid-insulator transition. Phys Rev B (1989) 40:546–70. doi:10.1103/PhysRevB.40.546
3. Jaksch D, Bruder C, Cirac JI, Gardiner CW, Zoller P. Cold bosonic atoms in optical lattices. Phys Rev Lett (1998) 81:3108–11. doi:10.1103/PhysRevLett.81.3108
4. Lewenstein M, Sanpera A, Ahufinger V, Damski B, Sen(De) A, Sen U. Ultracold atomic gases in optical lattices: Mimicking condensed matter physics and beyond. Adv Phys (2007) 56:243–379. doi:10.1080/00018730701223200
5. Greiner M, Mandel O, Esslinger T, Hänsch TW, Bloch I. Quantum phase transition from a superfluid to a Mott insulator in a gas of ultracold atoms. Nature (London) (2002) 415:39–44. doi:10.1038/415039a
6. Baier S, Mark MJ, Petter D, Aikawa K, Chomaz L, Cai Z, et al. Extended bose-hubbard models with ultracold magnetic atoms. Science (2016) 352:201–5. doi:10.1126/science.aac9812
7. Danshita I, Sá de Melo CAR. Stability of superfluid and supersolid phases of dipolar bosons in optical lattices. Phys Rev Lett (2009) 103:225301. doi:10.1103/PhysRevLett.103.225301
8. Bandyopadhyay S, Bai R, Pal S, Suthar K, Nath R, Angom D. Quantum phases of canted dipolar bosons in a two-dimensional square optical lattice. Phys Rev A (2019) 100:053623. doi:10.1103/PhysRevA.100.053623
9. Suthar K, Kraus R, Sable H, Angom D, Morigi G, Zakrzewski J. Staggered superfluid phases of dipolar bosons in two-dimensional square lattices. Phys Rev B (2020) 102:214503. doi:10.1103/PhysRevB.102.214503
10. Boninsegni M, Prokof’ev N. Supersolid phase of hard-core bosons on a triangular lattice. Phys Rev Lett (2005) 95:237204. doi:10.1103/PhysRevLett.95.237204
11. Bandyopadhyay S, Sable H, Gaur D, Bai R, Mukerjee S, Angom D. Quantum phases of dipolar bosons in a multilayer optical lattice. Phys Rev A (2022) 106:043301. doi:10.1103/PhysRevA.106.043301
12. Tanzi L, Lucioni E, Famà F, Catani J, Fioretti A, Gabbanini C, et al. Observation of a dipolar quantum gas with metastable supersolid properties. Phys Rev Lett (2019) 122:130405. doi:10.1103/PhysRevLett.122.130405
13. Norcia MA, Politi C, Poli E, Sohmen M, Mark MJ, Bisset RN, et al. Two-dimensional supersolidity in a dipolar quantum gas. Nature (2021) 596:357–61. doi:10.1038/s41586-021-03725-7
14. Landig R, Hruby L, Dogra N, Landini M, Mottl R, Donner T, et al. Quantum phases from competing short- and long-range interactions in an optical lattice. Nature (2016) 532:476–9. doi:10.1038/nature17409
15. Günter K, Stöferle T, Moritz H, Köhl M, Esslinger T. Bose-fermi mixtures in a three-dimensional optical lattice. Phys Rev Lett (2006) 96:180402. doi:10.1103/PhysRevLett.96.180402
16. Catani J, De Sarlo L, Barontini G, Minardi F, Inguscio M. Degenerate bose-bose mixture in a three-dimensional optical lattice. Phys Rev A (2008) 77:011603. doi:10.1103/PhysRevA.77.011603
17. Bai R, Gaur D, Sable H, Bandyopadhyay S, Suthar K, Angom D. Segregated quantum phases of dipolar bosonic mixtures in two-dimensional optical lattices. Phys Rev A (2020) 102:043309. doi:10.1103/PhysRevA.102.043309
18. Krutitsky KV, Navez P. Excitation dynamics in a lattice bose gas within the time-dependent gutzwiller mean-field approach. Phys Rev A (2011) 84:033602. doi:10.1103/PhysRevA.84.033602
19. Saito T, Danshita I, Ozaki T, Nikuni T. Detecting the superfluid critical momentum of bose gases in optical lattices through dipole oscillations. Phys Rev A (2012) 86:023623. doi:10.1103/PhysRevA.86.023623
20. Suthar K, Sable H, Bai R, Bandyopadhyay S, Pal S, Angom D. Supersolid phase of the extended bose-hubbard model with an artificial gauge field. Phys Rev A (2020) 102:013320. doi:10.1103/PhysRevA.102.013320
21. Pal S, Bai R, Bandyopadhyay S, Suthar K, Angom D. Enhancement of the bose glass phase in the presence of an artificial gauge field. Phys Rev A (2019) 99:053610. doi:10.1103/PhysRevA.99.053610
22. Shimizu K, Kuno Y, Hirano T, Ichinose I. Dynamics of a quantum phase transition in the bose-hubbard model: Kibble-zurek mechanism and beyond. Phys Rev A (2018) 97:033626. doi:10.1103/PhysRevA.97.033626
23. Zhou Y, Li Y, Nath R, Li W. Quench dynamics of rydberg-dressed bosons on two-dimensional square lattices. Phys Rev A (2020) 101:013427. doi:10.1103/PhysRevA.101.013427
24. Sable H, Gaur D, Bandyopadhyay S, Nath R, Angom D. Quantum quench dynamics of tilted dipolar bosons in 2d optical lattices (2021). arXiv:2106.01725v2.
25. Aidelsburger M, Atala M, Nascimbène S, Trotzky S, Chen Y-A, Bloch I. Experimental realization of strong effective magnetic fields in an optical lattice. Phys Rev Lett (2011) 107:255301. doi:10.1103/PhysRevLett.107.255301
26. Aidelsburger M, Atala M, Lohse M, Barreiro JT, Paredes B, Bloch I. Realization of the Hofstadter Hamiltonian with ultracold atoms in optical lattices. Phys Rev Lett (2013) 111:185301. doi:10.1103/PhysRevLett.111.185301
27. Jiménez-García K, LeBlanc LJ, Williams RA, Beeler MC, Perry AR, Spielman IB. Peierls substitution in an engineered lattice potential. Phys Rev Lett (2012) 108:225303. doi:10.1103/PhysRevLett.108.225303
28. Jaksch D, Zoller P. Creation of effective magnetic fields in optical lattices: The hofstadter butterfly for cold neutral atoms. New J Phys (2003) 5:56. doi:10.1088/1367-2630/5/1/356
29. Sørensen AS, Demler E, Lukin MD. Fractional quantum Hall states of atoms in optical lattices. Phys Rev Lett (2005) 94:086803. doi:10.1103/PhysRevLett.94.086803
30. Palmer RN, Jaksch D. High-field fractional quantum Hall effect in optical lattices. Phys Rev Lett (2006) 96:180407. doi:10.1103/PhysRevLett.96.180407
31. Hafezi M, Sørensen AS, Demler E, Lukin MD. Fractional quantum Hall effect in optical lattices. Phys Rev A (2007) 76:023613. doi:10.1103/PhysRevA.76.023613
32. Sterdyniak A, Cooper NR, Regnault N. Bosonic integer quantum hall effect in optical flux lattices. Phys Rev Lett (2015) 115:116802. doi:10.1103/PhysRevLett.115.116802
33. Kuno Y, Shimizu K, Ichinose I. Bosonic analogs of the fractional quantum Hall state in the vicinity of mott states. Phys Rev A (2017) 95:013607. doi:10.1103/PhysRevA.95.013607
34. Léonard J, Kim S, Kwan J, Segura P, Grudst F, Repellin C, et al. Realization of a fractional quantum hall state with ultracold atoms (2022). arXiv:2210.10919v2.
35. Klitzing Kv., Dorda G, Pepper M. New method for high-accuracy determination of the fine-structure constant based on quantized hall resistance. Phys Rev Lett (1980) 45:494–7. doi:10.1103/PhysRevLett.45.494
36. Tsui DC, Stormer HL, Gossard AC. Two-dimensional magnetotransport in the extreme quantum limit. Phys Rev Lett (1982) 48:1559–62. doi:10.1103/PhysRevLett.48.1559
37. Laughlin RB. Anomalous quantum Hall effect: An incompressible quantum fluid with fractionally charged excitations. Phys Rev Lett (1983) 50:1395–8. doi:10.1103/PhysRevLett.50.1395
38. Willett R, Eisenstein JP, Störmer HL, Tsui DC, Gossard AC, English JH. Observation of an even-denominator quantum number in the fractional quantum hall effect. Phys Rev Lett (1987) 59:1776–9. doi:10.1103/PhysRevLett.59.1776
39. Jain JK. Composite-fermion approach for the fractional quantum hall effect. Phys Rev Lett (1989) 63:199–202. doi:10.1103/PhysRevLett.63.199
40. Read N, Rezayi E. Beyond paired quantum hall states: Parafermions and incompressible states in the first excited landau level. Phys Rev B (1999) 59:8084–92. doi:10.1103/PhysRevB.59.8084
41. Rezayi EH, Read N. Non-abelian quantized hall states of electrons at filling factors 12/5 and 13/5 in the first excited landau level. Phys Rev B (2009) 79:075306. doi:10.1103/PhysRevB.79.075306
42. Harper PG. Single band motion of conduction electrons in a uniform magnetic field. Proc Phys Soc A (1955) 68:874–8. doi:10.1088/0370-1298/68/10/304
43. Hofstadter DR. Energy levels and wave functions of Bloch electrons in rational and irrational magnetic fields. Phys Rev B (1976) 14:2239–49. doi:10.1103/PhysRevB.14.2239
44. Niu Q, Thouless DJ, Wu Y-S. Quantized hall conductance as a topological invariant. Phys Rev B (1985) 31:3372–7. doi:10.1103/PhysRevB.31.3372
45. Lühmann D-S. Cluster Gutzwiller method for bosonic lattice systems. Phys Rev A (2013) 87:043619. doi:10.1103/PhysRevA.87.043619
46. Bai R, Bandyopadhyay S, Pal S, Suthar K, Angom D. Bosonic quantum hall states in single-layer two-dimensional optical lattices. Phys Rev A (2018) 98:023606. doi:10.1103/PhysRevA.98.023606
47. Bai R. Synthetic magnetic fields and multi-component BECs in optical lattices. Ph.D. thesis. Palaj, Gujarat: Indian Institute of Technology Gandhinagar (2018).
48. Gerster M, Rizzi M, Silvi P, Dalmonte M, Montangero S. Fractional quantum hall effect in the interacting hofstadter model via tensor networks. Phys Rev B (2017) 96:195123. doi:10.1103/PhysRevB.96.195123
49. Bai R, Bandyopadhyay S, Pal S, Suthar K, Angom D (2019). Quantum hall states for α = 1/3 in optical lattices. In Quantum collisions and confinement of atomic and molecular species, and photons (Singapore: Springer Singapore), 211–21. doi:10.1007/978-981-13-9969-5_20
50. He Y-C, Grusdt F, Kaufman A, Greiner M, Vishwanath A. Realizing and adiabatically preparing bosonic integer and fractional quantum hall states in optical lattices. Phys Rev B (2017) 96:201103. doi:10.1103/PhysRevB.96.201103
51. Hatsugai Y. Characterization of topological insulators: Chern numbers for ground state multiplet. J Phys Soc Jpn (2005) 74:1374–7. doi:10.1143/JPSJ.74.1374
52. Wen XG, Niu Q. Ground-state degeneracy of the fractional quantum hall states in the presence of a random potential and on high-genus riemann surfaces. Phys Rev B (1990) 41:9377–96. doi:10.1103/PhysRevB.41.9377
53. Yoshida T, Kudo K, Hatsugai Y. Non-hermitian fractional quantum hall states. Scientific Rep (2019) 9:16895. doi:10.1038/s41598-019-53253-8
54. Yoshida T, Kudo K, Katsura H, Hatsugai Y. Fate of fractional quantum hall states in open quantum systems: Characterization of correlated topological states for the full liouvillian. Phys Rev Res (2020) 2:033428. doi:10.1103/PhysRevResearch.2.033428
55. Liu Z, Bergholtz EJ, Budich JC. Dissipative preparation of fractional chern insulators. Phys Rev Res (2021) 3:043119. doi:10.1103/PhysRevResearch.3.043119
56. Shen HZ, Qin M, Yi XX. Single-photon storing in coupled non-markovian atom-cavity system. Phys Rev A (2013) 88:033835. doi:10.1103/PhysRevA.88.033835
57. Zhang R, Chen T, Wang X-B. Deterministic quantum controlled-phase gates based on non-markovian environments. New J Phys (2017) 19:123001. doi:10.1088/1367-2630/aa9510
58. Breuer H-P, Petruccione F. The theory of open quantum systems. Oxford, UK: Oxford University Press (2007). doi:10.1093/acprof:oso/9780199213900.001.0001
Keywords: FQHE (fractional quantum Hall effect), ultracold gases, optical lattices, Bose–Hubbard model, cluster Gutzwiller mean-field, exact diagonalization
Citation: Gaur D, Sable H and Angom D (2023) Fractional quantum Hall effect in optical lattices. Front. Phys. 10:1106491. doi: 10.3389/fphy.2022.1106491
Received: 23 November 2022; Accepted: 28 December 2022;
Published: 16 January 2023.
Edited by:
Ayan Khan, Bennett University, IndiaReviewed by:
Zhihao Lan, University College London, United KingdomH. Z. Shen, Northeast Normal University, China
Copyright © 2023 Gaur, Sable and Angom. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: D. Angom, ZGlsaXAuYW5nb21AbWFuaXB1cnVuaXYuYWMuaW4=
 Deepak Gaur
Deepak Gaur Hrushikesh Sable1,2
Hrushikesh Sable1,2