Photoelectron momentum distributions with twisted attosecond X waves carrying orbital angular momentum

We theoretically investigate the photoelectron momentum distributions of 1s and 2p_x,y states of hydrogen by twisted attosecond X waves carrying orbital angular momentum based on first-order perturbation theory. The photoionization spectra as a function of photoelectron energy and emission angle are analyzed respectively. The results indicate that there are interference fringes in the energy spectra and more nodes in the angular distributions. These angular nodes are attributed to both orbital structure and the temporal-spatial structure of X waves. We derive an equation that can quantitatively describe the angular nodes in the photoelectron angular distributions. Our results and analyses indicate that the angular distribution is an important observation for the investigation of the information of both orbitals and X waves.

1 Introduction

Advances of extreme ultraviolet (XUV) and soft x-ray pulses have opened up the intriguing opportunity of probing and control of electronic dynamics on the attosecond time scale (1 as = 10^–18 s) and Å spatial dimension (1 Å = 10^–10 m) [1–8]. The attosecond XUV and soft x-ray pulses can be accessible by high-order harmonic generation (HHG) [9–13] and free-electron lasers (FEL) [14, 15]. Based on the interaction of these shorter pulses with targets, a variety of applications, such as the ultrafast molecular orbital imaging [16–18], measurement of time delays in photoemission [19, 20], and detection of the charge migration in molecules, nanoparticles and materials [21–25], have been promised. In the majority of strong-field processes above, the adopted attosecond XUV and soft x-ray are general plane-wave pulses, which have been quite well understood.

Since the pioneering studies of Beth and Allen et al. [26, 27], one knows that, apart from the pulses with a plane-wave front, beams of light can possess a helical wavefront and carry orbital angular momentum (OAM) as well as their spin angular momentum (SAM). The polarization state of light is associated with its SAM, whereas the spatial distribution of the wave-front is related to the OAM of the light [27, 28]. Light with non-zero OAM is known as twisted or vortex light beams, such as the Bessel and Laguerre–Gaussian (LG) beams. Beyond the Bessel and LG pulses, another twisted beam, the X wave, formed by a superposition of Bessel beams, has also obtained much attention for its localization feature both in the spatial and temporal domain [29, 30]. These twisted light fields provide powerful capabilities for applications in the area of optical sensing and communication, quantum communication, optical tweezers and optical manipulation [31–36]. Until now, there are various ways to generate the twisted light pulses, such as spiral phase plates, axicons, computer-generated holograms and integrated ring resonators [37–41]. Although the OAM of light produced by these ways can be imprinted into waveforms over a large frequency range, it was not possible to generate the coherent light possessing OAM beyond the ultraviolet regime. So, the applications exploiting OAM interactions were limited to macroscopic systems using visible light. Fortunately, recent advances in HHG have broken this photonic limitation, producing the fully coherent attosecond XUV and soft X-ray pulses with designer OAM, which have opened up the possibility of monitoring and manipulating the OAM of light-matter interactions on the atomic scale [42–45].

Understanding photoionization in intense laser fields is of central importance in ultrafast optical sciences. In recent years, the twisted XUV pulses with OAM as a new powerful tool for probing ultrafast electron dynamics have gradually obtained much attention in theoretical and experimental studies on photoionization. For example, the twisted XUV Bessel and LG pulses have been used to theoretically study the above-threshold ionization and dichroism signals of targets [46, 47]. In an experiment [48], the attosecond vortex pulses have been applied to generate and manipulate, through photoionization, attosecond electron beams carrying OAM. Additionally, the energy spectrum of atoms irradiated by the twisted attosecond X wave has also been investigated [49, 50]. In contrast to plane-waves, a twisted X wave is a non-diffracting electromagnetic field in both space and time [30]. Most previous works, related to the attosecond X waves, mainly focused on the energy spectra [49, 50]. And the influence of the structure of orbitals on photoelectron angular distributions (PADs) have also been well studies. However, up to now, the PADs of different orbitals in the twisted attosecond X pulses have rarely been studied and the influence of the structure of X waves on the PADs have rarely been reported.

In this work, the PMDs of hydrogen atoms irradiated by twisted attosecond X waves are investigated based on first-order perturbation theory. Due to the temporal-spatial structure of X waves, interference fringes in the radial and more nodes in the angle direction of PMDs are observed. In order to interpret these phenomena in detail, we study the energy spectra and angular distributions by integrating the PMDs over emission angle and momentum, respectively. We derive a concise equation, which can quantitatively interpret the angular nodes in PADs. They are attributed to the spatial structures of orbitals and X waves. Our results and analyses indicate that the PADs can reveal the information about X waves and orbitals that cannot be revealed in energy spectra. Atomic units (m_e = q_e = ℏ = 1) are used throughout this work unless otherwise stated. The atomic units (a.u.) of time, distance, energy and momentum are τ₀ = 24.2 × 10^–18 s, a₀ = 0.053 × 10^–9 m, E₀ = 27.2 eV and v₀ = 2.18 × 10⁶ m/s.

2 Theoretical model

X waves are localized waves and formed by the superposition of Bessel beams ${\mathit{A}}_{m\mathrm{\Lambda }{\theta }_k}(\mathit{r},t)$, which are solutions of the wave equation:

$\left(\mathrm{\Delta }-{\alpha }^2\frac{{\partial }^2}{\partial t^2}\right){\mathit{A}}_{m\mathrm{\Lambda }{\theta }_k}\left(\mathit{r},t\right)=0,(1)$

in which m, Λ and θ_k are the projection of total angular momentum (PTAM), helicity and opening angle in momentum space. α is the electromagnetic fine structure constant. The cylindrical coordinates r = (r, ϕ_r, z) are applied. Distinguishing from plane-wave, ${\mathit{A}}_{m\mathrm{\Lambda }{\theta }_k}(\mathit{r},t)$ is also an eigenfunction of the PTAM,

${\widehat{J}}_z{\mathit{A}}_{m\mathrm{\Lambda }{\theta }_k}\left(\mathit{r},t\right)=m{\mathit{A}}_{m\mathrm{\Lambda }{\theta }_k}\left(\mathit{r},t\right),(2)$

where ${\widehat{J}}_z$ is the operator of PTAM. In general, the Bessel waves can be constructed with either linearly or circularly polarized plane-waves. Here, we just take the Bessel wave constructed with circularly polarized plane-waves with helicity Λ as an example to investigate the photoelectron momentum distributions of X waves [49],

${\mathit{A}}_{m\mathrm{\Lambda }{\theta }_k}\left(\mathit{r},t\right)=\int \frac{d^2{\mathit{k}}_{\perp }}{{\left(2\pi \right)}^2}{a}_{\kappa m}\left({\mathit{k}}_{\perp }\right)e^{i\left(\mathit{k}\cdot \mathit{r}-\omega t\right)}{\mathit{\epsilon }}_{\mathit{k}\mathrm{\Lambda }}(3)$

with the wave vector k = (k_⊥, k_z) = (κ, ϕ_k, k_z) and the Fourier coefficients

$a_{\kappa m}\left({\mathit{k}}_{\perp }\right)=\sqrt{\frac{2\pi }{\kappa }}{\left(-i\right)}^m{e}^{im{\varphi }_k}\delta \left(k_{\perp }-\kappa \right).(4)$

The opening angle is θ_k = arctan(κ/k_z). The polarization vector ɛ_kΛ describes a circularly polarized plane-wave with helicity Λ = ±1 and depends on the angles θ_k and ϕ_k in momentum space,

${\mathit{\epsilon }}_{\mathit{k}\mathrm{\Lambda }}=\frac{-\mathrm{\Lambda }}{\sqrt{2}}\left(\begin{array}{c}\hfill \cos {\theta }_k\cos {\varphi }_k-i\mathrm{\Lambda }\sin {\varphi }_k\hfill \\ \hfill \cos {\theta }_k\sin {\varphi }_k+i\mathrm{\Lambda }\cos {\varphi }_k\hfill \\ \hfill -\sin {\theta }_k\hfill \end{array}\right)(5)$

with the condition k ⋅ɛ_kΛ = 0. Note that, whether the Bessel pulses are constructed with linearly or circularly polarized pulses, the analyses and conclusions about the influence of X wave structures on PMDs is the same.Pulses applied in experiments of the light-target interactions possess a finite pulse duration T_X. Such pulses can be obtained by weighted non-monochromatic superposition of continuous Bessel beams [30]. The superposition with a fixed θ_k can construct X wave vector potential as

$\begin{array}{ll}\hfill {\mathit{A}}_X\left(\mathit{r},t\right)& ={\int }_0^{\infty }\frac{d\omega }{\sqrt{2\pi }\mathrm{\Delta }\omega }\exp \left[-\frac{1}{2}{\left(\frac{\omega -{\omega }_0}{\mathrm{\Delta }\omega }\right)}^2\right]\hfill \\ \hfill & \times {\mathit{A}}_{m\mathrm{\Lambda }{\theta }_k}\left(\mathit{r},t\right),\hfill \end{array}(6)$

where Δω = 1/T_X is the width of the Gaussian spectral distribution and the ω₀ is the central frequency.Eq. 3 is the most general form of the twisted states vector potential, which will be employed in the following discussions about the PMDs. For the sake of description of twisted X waves, we write the wave vector ${\mathit{A}}_{m\mathrm{\Lambda }{\theta }_k}(\mathit{r},t)$ in the Coulomb gauge on a spin basis

$\begin{array}{ll}\hfill {\mathit{A}}_{m\mathrm{\Lambda }{\theta }_k}\left(\mathit{r},t\right)& =e^{-i\left(\omega t-k_{z}z\right)}\sqrt{\frac{\kappa }{2\pi }}\sum _{m_s=0,\pm 1}{\mathit{\eta }}_{m_s}\hfill \\ \hfill & \times {\left(-i\right)}^{m_s}{c}_{m_s}{J}_{m-m_s}\left(\kappa r\right)e^{i\left(m-m_s\right){\varphi }_r},\hfill \end{array}(7)$

in which ${\mathit{\eta }}_{m_s}(m_s=0,\pm 1)$ are the eigenvectors of the spin projection operator ${\widehat{S}}_z$:

${\widehat{S}}_z{\mathit{\eta }}_{m_s}=m_s{\mathit{\eta }}_{m_s},{\mathit{\eta }}_0=\left(\begin{array}{c}\hfill 0\hfill \\ \hfill 0\hfill \\ \hfill 1\hfill \end{array}\right),{\mathit{\eta }}_{\pm 1}=\frac{\mp }{\sqrt{2}}\left(\begin{array}{c}\hfill 1\hfill \\ \hfill \pm i\hfill \\ \hfill 0\hfill \end{array}\right).(8)$

In Eq. 7, $J_{m-m_s}(\kappa r)$ are Bessel functions of the first kind. The coefficients are given by

$c_{\pm }=\frac{1}{2}\left(1\pm \mathrm{\Lambda }\cos {\theta }_k\right),c_0=\frac{\mathrm{\Lambda }}{\sqrt{2}}\sin {\theta }_k.(9)$

The set-up for the ionization of an atom by an X wave pulse is shown in Figure 1. The atom ionized is localized at position b = (b, ϕ_b = 0, b_z = 0). The XUV pulse propagates along the z-axis with helicity Λ = +1. We assume that the central frequency ω₀ = 3 a.u. is large enough and the intensity of the pulse is very weak. The single-photon ionization process can be induced. The pulse duration is T_X = 1.9 T_L0 with T_L0 = 110 a.u. = 2.7 fs. The photoelectron ionized from the atom is collected at the detector with the asymptotic momentum p = (p, ϕ_p, θ_p). We shall analyze the PMDs at the p_x-p_y plane for θ_p = π/2. Within first-order perturbation theory [49], the transition amplitude at impact parameter b reads as

${\mathcal{D}}_b\left(\mathit{p}\right)=-i{\int }_{-\infty }^{\infty }dt⟨{\mathrm{\Psi }}_f\left(t\right)|\widehat{\mathit{p}}\cdot {\mathit{A}}_X\left(\mathit{r},t\right)|{\mathrm{\Psi }}_i\left(t\right)⟩,(10)$

where Ψ_i and Ψ_f are the initial (bound) and final (continuum) wave functions. For hydrogen atoms, the wave functions can be analytically described. The continuum states are typically described by Volkov wave functions $|{\mathrm{\Psi }}_f(t)\rangle =|\mathit{q}(t)\rangle e^{-i{S}_V(t)}$, in which q(t) = p−A_X(r₀, t) is the kinetic momentum of the plane-wave electron at a specific position r₀. p is the conserved canonical momentum. The Volkov phase is given by $S_V(t)=\frac{1}{2}{\int }^{t}d{t}^{\prime }{[\mathit{p}+{\mathit{A}}_X(r_0,t^{\prime })]}^2$. For that ω₀ is large enough, A_X ≪ p, we can approximate q(t) ≈ p. The integration of Eq. 10 can be further simplified. Then, the photoionization probability can be obtained from Eq. 10 as

${\mathcal{P}}_b\left(\mathit{p}\right)=|{\mathcal{D}}_b\left(\mathit{p}\right){|}^2.(11)$

Substituting Eq. 6 into Eq. 10, we obtain the transition amplitude as a superposition of ${\mathcal{D}}_{\omega b}(\mathit{p})$

${\mathcal{D}}_b\left(\mathit{p}\right)={\int }_0^{\infty }\frac{d\omega }{\sqrt{2\pi }\mathrm{\Delta }\omega }\exp \left[-\frac{1}{2}{\left(\frac{\omega -{\omega }_0}{\mathrm{\Delta }\omega }\right)}^2\right]\times {\mathcal{D}}_{\omega b}\left(\mathit{p}\right),(12)$

where ${\mathcal{D}}_{\omega b}(\mathit{p})$ are the transition amplitudes of each ω Bessel beams. If r denotes the electronic coordinate with respect to the atomic nucleus, we have to replace r → r + b in the interactions of electron and photon. Based on Eq. 3, ${\mathcal{D}}_{\omega b}$ can be written as

${\mathcal{D}}_{\omega b}\left(\mathit{p}\right)=\int \frac{d^2{\mathit{k}}_{\perp }}{{\left(2\pi \right)}^2}{a}_{\kappa m}\left({\mathit{\kappa }}_{\perp }\right)e^{i\mathit{k}\cdot \mathit{b}}{\mathcal{D}}^{pl}\left(\mathit{p},\mathit{k}\right).(13)$

Here, ${\mathcal{D}}^{pl}(\mathit{p},\mathit{k})$ are the typical plane-wave transition amplitudes

$\begin{array}{ll}\hfill {\mathcal{D}}^{pl}\left(\mathit{p},\mathit{k}\right)& =-i{\int }_{-\infty }^{\infty }dt\mathit{q}\left(t\right)\cdot {\mathit{\epsilon }}_{\mathit{k}\mathrm{\Lambda }}\hfill \\ \hfill & \times ⟨\mathit{p}|e^{i\mathit{k}\cdot \mathit{r}}|{\mathrm{\Psi }}_i⟩e^{i\left(I_p-\omega \right)t+i{S}_V\left(t\right)},\hfill \end{array}(14)$

in which I_p is the ionization potential of Ψ_i.

FIGURE 1

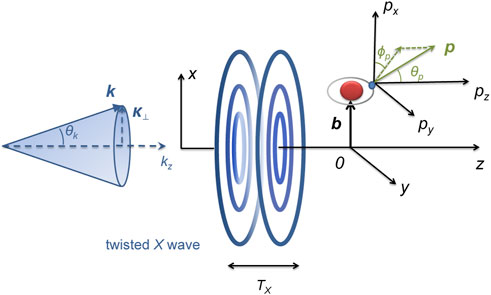
FIGURE 1. Ionization schematic of a hydrogen atom with twisted X wave with pulse duration T_X. Left panel: in momentum space, all wave vectors k contributing to Eq. 3 lie on a cone with opening angle θ_k = arctan(κ/k_z) with κ = |k_⊥|. k_z is parallel with z-axis. Right panel: the pulse propagates along z direction. An atom is localized at the impact parameter b=(b, ϕ_b = 0, z_b = 0) relative to the beam z-axis. Then, x-z plane is determined by the position of the target and the pulse propagation. The photoelectron is observed with asymptotic momentum p=(p, ϕ_p, θ_p) at the detector.

3 Results and discussions

We first calculate the PMDs of the hydrogen atom irradiated by the plane-wave pulses, which are the twisted X waves in the limit θ_k → 0 in Eq. 6. The results are presented in Figure 2. We display the modulus of the plane-wave pulse potential vector as a function of time t and distance r from the beam axis in Figure 2A. One can see that the vector potential is independent of r and exhibits a single maximum in time. For better visualization of the XUV pulse polarization and its temporal properties, we also plot the projection of the potential vector on A_X,x−A_X,y plane and the real part Re{A_X(r₀, t)} with r₀ = 11350 a.u. in Figures 2B,C. It is shown that the electric field is circularly polarized with helicity Λ = +1. In Figure 2C, only one XUV pulse is exhibited. The time-duration of the pulse is T_X. Then, we calculate the PMDs of 1s and 2p_x,y states of hydrogen atom placed at the impact parameter b = 11350 a.u. from the X wave beam axis. The results are shown in Figures 2D–F respectively. Note that, for a plane-wave pulse, the impact parameter b will not affect the results. In Figure 2D, the PAD of the 1s state is isotropic. For 2p_x,y states, the PADs present a distinct two-lobed structure in Figures 2E,F. The structures of PADs are attributed to the symmetry of the systems, which have been investigated in previous works [51, 52]. From Figures 2D–F, one can see that there are no interference structures and only one probability peak in the radial direction of PMDs. Besides, according to the energy conservation, the momentum corresponding to the maximum probability of PMDs satisfies

$|\mathit{p}|=\sqrt{2\left({\omega }_0-I_p\right)}.(15)$

So, for the 1s state with I_p = 1/2 a.u. and 2p_x,y states with I_p = 1/8 a.u., the momenta mentioned above are |p| = 2.2361 a.u. and |p| = 2.3979 a.u. respectively, which are very agree with the results in Figure 2D–F. Overall, Figure 2 illustrates that, in circular plane-wave pulses, the structures of PADs are only induced by orbitals. In this situation, the temporal-spatial structures of X waves play no role in PMDs at all.

FIGURE 2

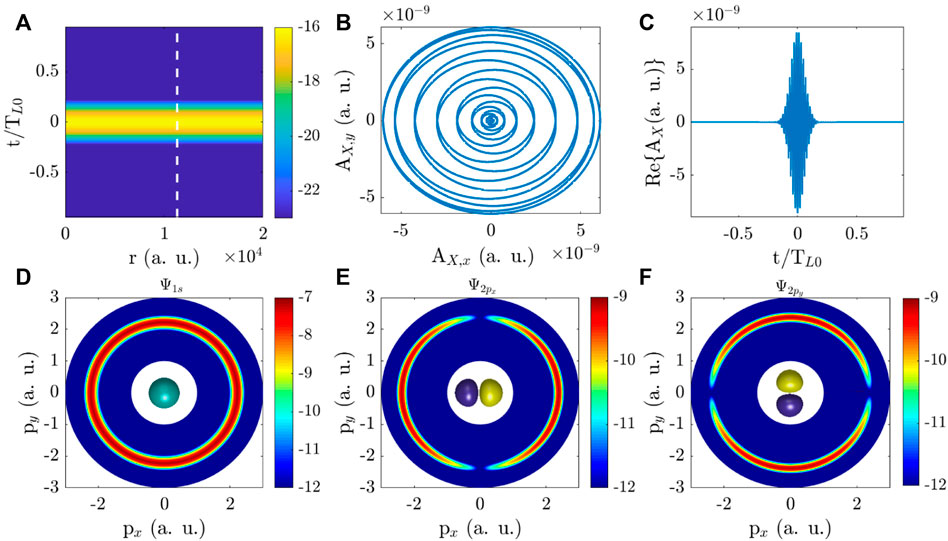
FIGURE 2. PMDs in plane-wave pulses. (A) Modulus of the pulse vector potential as a function of the distance r from the beam axis and time t on a logarithmic scale. r₀ = 11350 a.u. is labeled by the white dashed line. (B) The projection of the pulse vector potential on the A_X,x-A_X,y plane at position r₀. (C) Real part of the pulse vector potential Re{A_X(r₀, t)}. (D–F) PMDs of 1s, 2p_x and 2p_y states of a hydrogen atom at b = r₀. PMD of 1s state is isotropic and centered at zero momentum. For 2p states, there is a nodal plane in PMDs. The structures of PMDs in plane-wave pulses are contributed only by the orbital. The insets in (D–F) present the 1s, 2p_x and 2p_y orbitals of a hydrogen atom. The units of physical quantities in figures are atomic units (a.u).

Then, we study the PMDs in twisted X waves with larger θ_k. When the opening angle θ_k of the X pulses increases, the structure of X pulses changes, which will affect the PMDs. In Figures 3A,F, for θ_k = 5° and 60°, the moduli of X wave vector potential with m = 1 versus distance r and time t are plotted. By comparing with the vector potential in Figure 2A, one can see that the X wave vector potential splits into two pulses in the time domain. At a specific distance r₀, the time-delay τ between these two pulses is concerned with the opening angle θ_k of the X wave. For example, at r₀ = 11350 a.u., the time-delays are τ = 0.142 T_L0 for θ_k = 5° in Figure 3A and τ = 1.302 T_L0 for θ_k = 60° in Figure 3E. It is worth noting that, we are mainly concerned with the influence of θ_k and PTAM on PMDs through adjusting the time-delay rather than the spatial structure in the plane (r, ϕ). Additionally, under the conditions of the laser waves applied in our work, the maximum excursion distance of the electron is much smaller than the spatial size of the fields and the electron does not feel the spatial structure of the X waves. Thus, we can apply the local dipole approximation in the matrix element: ⟨p|e^ik⋅r|Ψ_i⟩ ≈ ⟨p|Ψ_i⟩ in Eq. 14. Then, the X wave pulse interacts with the hydrogen atom placed at the distance b = 11350 a.u. The PMDs of 1s and 2p_x,y states are presented in Figures 3B–D for θ_k = 5° and in Figures 3F–H for θ_k = 60°. From Figures 3B–D, one can see that, rather than a single probability peak of PMDs as shown in Figures 2D–F, two probability peaks appear in the radial direction of PMDs. In Figures 3F–H, there are more probability peaks in the radial direction of PMDs. For a clear visualization, momentum distributions outlined by white lines have been zoomed in. From the results in Figure 3, one can see that the opening angle θ_k of the twisted X pulses can affect the probability peaks of PMDs. These complex structures in the radial direction of PMDs are attributed to the interference of the ionization processes from the two split pulses, which will be discussed quantitatively below. In addition, the momentum corresponding to the maximum probability of PMDs still almost satisfies Eq. 15. In the angular direction, when θ_k increases, for 1s state, the isotropic PADs turn to a two-lobed distribution. For 2p_x,y states, some variations of the PAD also take place. A closer examination of PADs will be discussed in Figure 6.

FIGURE 3

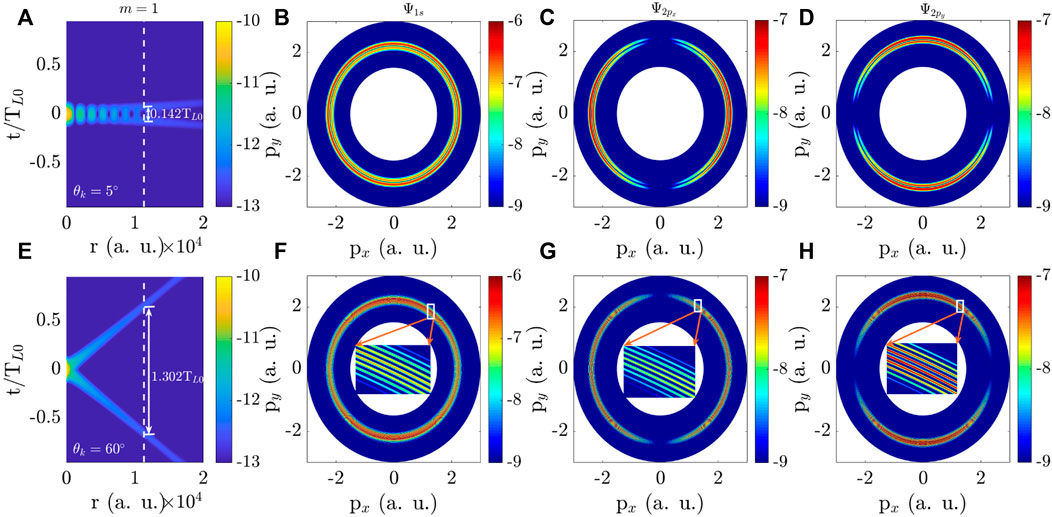
FIGURE 3. PMDs of an atom by the twisted X wave pulse at r = (r, ϕ_r = 0, z = 0). Moduli of the X wave vector potential as a function of the distance r to beam axis and time t for the PTAM m = 1 and two values of the opening angle (A) θ_k = 5° and (E) θ_k = 60° on a logarithmic scale. The time-delay τ between the two split pulses of the X wave at the position r₀ = 11350 a.u. labeled by the white dashed line is labeled by the solid line with double arrows. (B–D), (F–H) PMDs of 1 s, 2p_x and 2p_y states of a hydrogen atom at the impact parameter b = 11350 a.u. in the X waves for (A) and (E). The insets in (F–H) show the details of PMDs within the area outlined in white. The units of physical quantities in figures are a.u.

We have discussed the dependence of the PMDs on the opening angle θ_k in Figures 2,3. Next, we investigate the effect of PTAM m on PMDs. The moduli of X wave potential and the PMDs are displayed in Figure 4 for the same beam parameters as those in Figure 3, except for a different value of m = 20. As seen from Figures 4A,E, the structure of X waves changes compared with that in Figure 3. The first maximum of the X wave potential shifts away from the beam axis r = 0 to a larger distance in contrast to the wave with m = 1. Mathematically, this shift arises from the r dependence of the Bessel functions $J_{m-m_s}(\kappa r)$ in Eq. 7. In order to analyze the effects of PTAM m on PMDs, we place the hydrogen atom at the impact parameter b = 11350 a.u. in X fields with a different PTAM m = 20. The results are presented in Figures 4B–D for θ_k = 5° and in Figures 4F–H for θ_k = 60°. In the radial direction, it is found that, with m = 20, there is only one maximum probability peak of the PMDs for θ_k = 5°, which is different from that for m = 1 in Figures 3B–D. This one-peak structure can be explained by the comparison with the potential vector in Figure 4A: There is only one maximum value of the vector potential as a function of time t for θ_k = 5° and m = 20 at r₀ = 11350 a.u. No interference structure appears in PMDs. For a larger opening angle θ_k = 60°, there are also many interference fringes in PMDs, which are similar to the results in the case of m = 1. The mechanism of the interference fringes will be discussed in detail in Figure 5 below. In the angular direction, both the opening angle θ_k and PTAM of the X pulses have an influence on PADs, which will be discussed in detail in the following Figure 6.

FIGURE 4

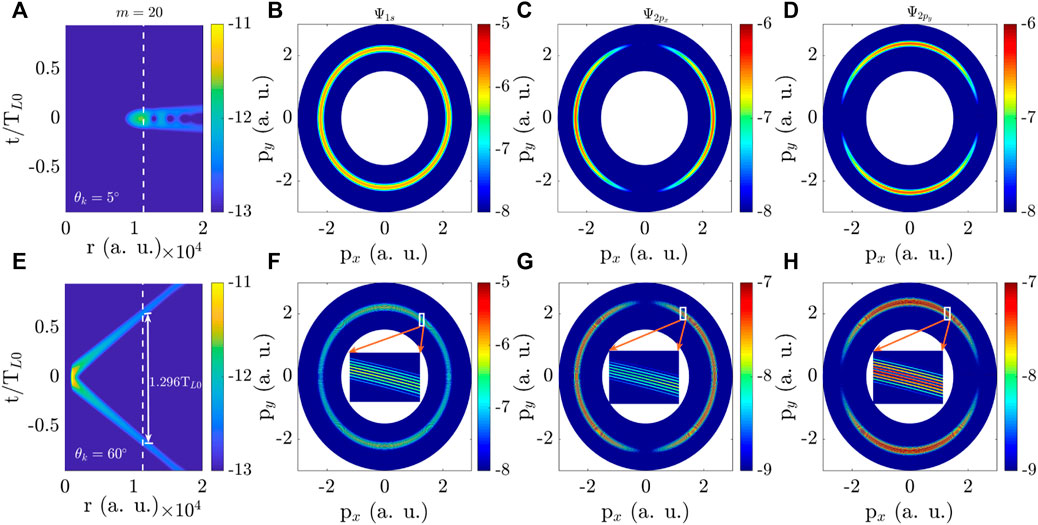
FIGURE 4. Same as Figure 3 but for a different PTAM m = 20 of the X wave. (A–D) θ_k = 5° and (E–H) θ_k = 60°.

FIGURE 5

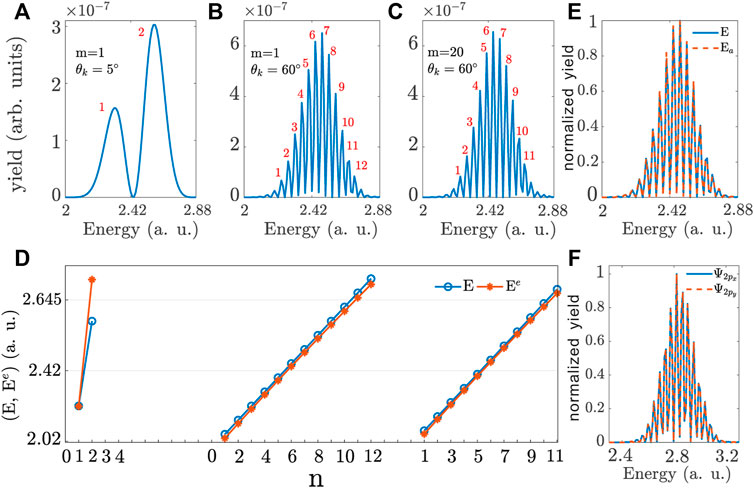
FIGURE 5. The energy spectra of 1s state of a hydrogen atom for ϕ_p = p_z = 0 with the PTAM and opening angle of the X wave (A) m = 1, θ_k = 5°, (B) m = 1, θ_k = 60° and (C) m = 20, θ_k = 60°. The red integers represent the peak numbers of the energy spectra. (D) Comparison of E (blue line) and E^e (red line) corresponding to the peak numbers in (A–C). E^e is the evaluated result according to Eq. 16 and E is the numerical result. The units of photoelectron yield are arbitrary units (arb. units) and the units of energy are a.u. (E) Comparison of the energy spectra of X wave (E labeled by the blue solid line) and double circular plane-wave pulses with the same time-delay τ as that in Figure 3E (E_a labeled by the red dashed line). (F) Comparison of the energy spectra of 2p_x,y orbitals corresponding to the PMDs in Figures 3G, H. The yield in (E) and (F) is normalized.

FIGURE 6

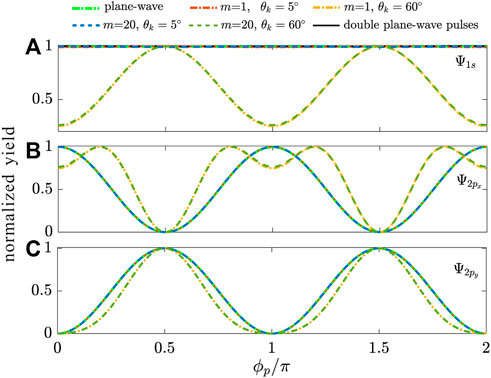
FIGURE 6. Photoelectron angular distributions by integration over the p of electrons emitted from (A) 1 s, (B) 2p_x and (C) 2p_y states of a hydrogen atom by plane-wave pulse and twisted X wave with m = 1, 20 and θ_k = 5°, 60°. The black solid line represents the PAD of double plane-wave pulses with the same time-delay τ as that in Figure 3E. The yield is normalized.

In order to interpret the interference fringes of PMDs in Figures 3,4, we propose a concise theoretical model. Here, we focus on the structure of energy spectra by integrating the PMDs over ϕ_p with θ_p = π/2. We define the transition amplitude of the photoelectron from one split pulse of the twisted X wave as ${\mathcal{D}}^e$. Considering the time-delay τ between the two split pulses, the transition amplitude from the other pulse is ${\mathcal{D}}^e\exp (-i{E}^e\tau )$, in which E^e is the evaluated photoelectron energy. Then, the yield of the energy spectrum in X wave pulses is evaluated by

$\begin{array}{ll}\hfill {\mathcal{P}}^e& ={\left|{\mathcal{D}}^e+{\mathcal{D}}^e\exp \left(-i{E}^e\tau \right)\right|}^2\hfill \\ \hfill & =2{\left|{\mathcal{D}}^e\right|}^2\left[1+\cos \left(E^e\tau \right)\right].\hfill \end{array}(16)$

From Eq. 16, one can determine the positions of the interference fringes based on E^e = 2nπ/τ (n is an integer). The numerical interference fringe of energy spectra can be obtained by integrating the PMDs over ϕ_p with θ_p = π/2. We take the case of 1s orbital as an example to verify that our theoretical model can precisely describe the interference fringes in the radial direction of PMDs. The energy spectra for Figures 3B,F,4F are plotted in Figures 5A–C. For ease of comparison with the evaluate results, the interference fringes are numbered. For the time-delay τ = 0.142T_L0, 1.302T_L0 and 1.296T_L0 presented in Figures 3B,F,4F respectively, the evaluate energy E^e can be calculated. Then, the comparison between the numerical (labeled by the blue hollow-circle lines) and evaluate (labeled by the red solid-circle lines) results is displayed in Figure 5D. From this figure, one can see that the evaluate results almost coincide with the numerical ones, which indicates that our theoretical model can reproduce the numerical results and quantitative interpret the mechanism of interference fringes. From Eq. 16, we know that the energy spectra are only dependent on the time-delay τ. They are independent of the spatial information of the orbital and X wave pulse. That is to say, the PTAM m and opening angle θ_k have an influence on the PAM through affecting the time-delay τ rather than the spatial structure of X waves. Besides, the information of orbital and X wave structures cannot be revealed only in these energy spectra. In order to demonstrate this point, we have calculated the photoelectron momentum distributions of 1s orbital in the double plane-wave pulses with the same time-delay τ as that in Figure 3E. The wavefront structure of these pulses is plane and different from the twisted wavefront of X waves. The comparison between the energy spectra of the two cases is presented in Figure 5E. One can see that the energy spectra are the same. Besides, we also compare the energy spectra of 2p_x,y orbitals for PMDs in Figures 3G, H. The results are plotted in Figure 5F. From this figure, one can see that the energy spectra are the same and orbital structures have no influence on them. Therefore, the discussions above demonstrate that, the interference fringes of PMDs are due to the two ionization events from the two split pulses, which can be interpreted by our theoretical model. Our model can also reproduce the interference fringe positions. Additionally, this model implies that the information of the X wave and orbital structures cannot be revealed in energy spectra.

At last, we discuss in detail the PADs, i.e., the photoionization yield versus azimuthal angle ϕ_p. We integrate the PMDs in Figures 2–4 over the momentum p: $W({\varphi }_p,{\theta }_p)={\int }_{p_1}^{p_2}{\mathcal{P}}_b(p,{\varphi }_p,{\theta }_p)dp$. The integration results with θ_p = π/2 and [p₁, p₂] = [2, 2.45] are presented in Figure 6. For a better comparison, W is normalized. The lime dot-dashed line represents the angular distribution W for plane-waves. The red and yellow dot-dashed lines represent W for θ_k = 5° and θ_k = 60° of X waves with m = 1. The blue and green dashed lines represent W for θ_k = 5° and θ_k = 60° of X waves with m = 20. More detailedly, for plane-wave and X wave with θ_k = 5°, W is almost isotropic for 1s orbital in Figure 6A and two-lobed for 2p_x,y orbitals in Figures 6B,C. These distribution structures are almost induced only by orbitals. For X wave with θ_k = 60°, more complex distribution structures are observed, such as an angular node for 1s orbital and the other angular node structure for 2p_x,y orbitals, which are attributed to the temporal-spatial structure of X waves. The results in Figure 6 also imply that the angular distributions can reflect the information of orbitals. For example, the photoelectron angular distributions for 2p_x,y orbitals are absolutely different. The above statements and phenomena in Figure 6 can be interpreted by the following equation. According to Eqs 13, 14, the photoionization probability satisfies

$\mathcal{P}\left(\mathit{p}\right)\propto \left[a_2+\left(a_1-a_2\right){\cos }^2{\varphi }_p\right]|{\mathrm{\Psi }}_i\left(\mathit{p}\right){|}^2,(17)$

in which Ψ_i(p) is the initial wave function in the momentum space. For 2p_x,y states, ${\mathrm{\Psi }}_{2p_x}\propto \cos ({\varphi }_p)$ and ${\mathrm{\Psi }}_{2p_y}\propto \sin ({\varphi }_p)$. For 1s states, the wave function is independent of ϕ_p. a₁ is |c₁J_m−1 + c₋₁J_m+1|² and a₂ is |c₋₁J_m+1−c₁J_m−1|². The terms a_1,2 are only related to the spatial structures of X waves. According to Eq. 17, one knows that, both the orbital and X wave have an influence on PADs. Moreover; Eq. 17 indicates that, the influence of orbitals and X waves can be analyzed individually. The first term on the right side is only determined by X waves and the second term by orbitals. For the case of plane-wave and X wave with θ_k = 5°, there is a₁ ≈ a₂ and a_1,2 are almost constants. Thus, according to Eq. 17, the first term related to X waves is a constant and independent of ϕ_p. Only the second term related to orbitals affects PADs. When θ_k increases to 60°, there is a₁ ≠ a₂. One can see from Eq. 17 that, besides the orbitals, X waves also affect PADs. The first term related to ϕ_p can contribute to other structures of PADs, such as a remarkable anisotropy for 1s orbital. Therefore, the equation we derived can clearly interpret the influence of both orbital and X wave on PADs. In order to further study the influence of the temporal-spatial structure of X waves on PADs, we also plot the result of double time-delayed plane-wave pulses in Figure 6A, which is labeled by the black solid line. The time-delay is the same as that in Figure 3E. The angular distribution of PMD in Figure 3E is labeled by the yellow dot-dashed line. By comparing the two results in Figure 6A, we find that the one for double plane-wave pulses is isotropic and the other one for the twisted X wave pulse is two-lobed. These two quite different PADs indicate that the structure of X waves plays a significant role in the PADs. Therefore, our results in Figure 6 illustrate that angular distribution is an important observation for the investigation of the information of both orbitals and X waves.

4 Conclusion

In conclusion, we investigated the PMDs of 1s and 2p_x,y states of hydrogen atoms irradiated by the twisted attosecond X waves carrying OAM using first-order perturbation theory. Different from the plane-wave, the X wave carrying orbital angular momentum can induce more complex structures in PMDs, such as the interference fringes in the radial direction and more nodes in the angle direction of PMDs. In order to interpret these structures in detail, we respectively analyzed the energy spectra and angular distributions. We found that the PADs can reveal the spatial information of orbitals and X waves. A concise equation is derived to quantitatively interpret the PADs. It describes the influence of orbitals and X waves on PADs individually. A comparison of the results in X waves and double time-delayed plane-wave pulses has been carried out to further demonstrate our point, i.e., PAD is an important observation encoding the structure information of X waves. X waves for their non-diffraction and OAM-carrying characteristics can be an ideal candidate in quantum communication and give the possibility to increase the amount of information that can be transferred in an undistorted way through the atmosphere. They can be also applied in other fields like acoustics, electromagnetism and even medicine. When X waves interact with complex molecules or solids, there may be more abundant strong-field phenomena, which are of great significance for stimulating new applications in various fields from quantum information to microscopy.

Data availability statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author contributions

XZ conceived the idea, conducted the simulations and wrote the manuscript. The data was analyzed by XZ and XM.

Funding

This work was supported by National Natural Science Foundation of China (NSFC) (Grants Nos. 11904269), the Natural Science Foundation of Hubei Province under Grant Nos. 2021CFB300, 2020CFB362, the Science Research Foundation of Wuhan Institute of Technology (Grant No. 21QD74).

Acknowledgments

We thank Feng Wang, Profs. Xiao-song Zhu and Qing Liao for the helpful discussion.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Paul PM, Toma ES, Breger P, Mullot G, Augé F, Balcou P, et al. Observation of a train of attosecond pulses from high harmonic generation. Science (2001) 292:1689–92. doi:10.1126/science.1059413

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Krausz F, Ivanov M. Attosecond physics. Rev Mod Phys (2009) 81:163–234. doi:10.1103/RevModPhys.81.163

CrossRef Full Text | Google Scholar

3. Mairesse Y, de Bohan A, Frasinski LJ, Merdji H, Dinu LC, Monchicourt P, et al. Attosecond synchronization of high-harmonic soft x-rays. Science (2003) 302:1540–3. doi:10.1126/science.1090277

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Kienberger R, Goulielmakis E, Uiberacker M, Baltuska A, Yakovlev V, Bammer F, et al. Atomic transient recorder. Nature (2004) 427:817–21. doi:10.1038/nature02277

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Allaria E, Appio R, Badano L, Barletta WA, Bassanese S, Biedron SG, et al. Highly coherent and stable pulses from the fermi seeded free-electron laser in the extreme ultraviolet. Nat Photon (2012) 6:699–704. doi:10.1038/nphoton.2012.233

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Smirnova O, Mairesse Y, Patchkovskii S, Dudovich N, Villeneuve D, Corkum P, et al. High harmonic interferometry of multi-electron dynamics in molecules. Nature (London) (2009) 460:972–7. doi:10.1038/nature08253

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Lan P, Ruhmann M, He L, Zhai C, Wang F, Zhu X, et al. Attosecond probing of nuclear dynamics with trajectory-resolved high-harmonic spectroscopy. Phys Rev Lett (2017) 119:033201. doi:10.1103/PhysRevLett.119.033201

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Shafir D, Soifer H, Bruner BD, Dagan M, Mairesse Y, Patchkovskii S, et al. Resolving the time when an electron exits a tunnelling barrier. Nature (London) (2012) 485:343–6. doi:10.1038/nature11025

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Sansone G, Benedetti E, Calegari F, Vozzi C, Avaldi L, Flammini R, et al. Isolated single-cycle attosecond pulses. Science (2006) 314:443–6. doi:10.1126/science.1132838

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Li J, Ren X, Yin Y, Zhao K, Chew A, Cheng Y, et al. 53-attosecond x-ray pulses reach the carbon k-edge. Nat Commun (2017) 8:186. doi:10.1038/s41467-017-00321-0

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Gaumnitz T, Jain A, Pertot Y, Huppert M, Jordan I, Ardana-Lamas F, et al. Streaking of 43-attosecond soft-x-ray pulses generated by a passively cep-stable mid-infrared driver. Opt Express (2017) 25:27506–27518. doi:10.1364/OE.25.027506

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Ferré A, Handschin C, Dumergue M, Burgy F, Comby A, Descamps D, et al. A table-top ultrashort light source in the extreme ultraviolet for circular dichroism experiments. Nat Photon (2015) 9:93–8. doi:10.1038/nphoton.2014.314

CrossRef Full Text | Google Scholar

13. Zhang X, Zhu X, Liu X, Wang F, Qin M, Liao Q, et al. Elliptical isolated attosecond-pulse generation from an atom in a linear laser field. Phys Rev A (2020) 102:033103. doi:10.1103/PhysRevA.102.033103

CrossRef Full Text | Google Scholar

14. Bostedt C, Boutet S, Fritz DM, Huang Z, Lee HJ, Lemke HT, et al. Linac coherent light source: The first five years. Rev Mod Phys (2016) 88:015007. doi:10.1103/RevModPhys.88.015007

CrossRef Full Text | Google Scholar

15. Huang S, Ding Y, Feng Y, Hemsing E, Huang Z, Krzywinski J, et al. Generating single-spike hard x-ray pulses with nonlinear bunch compression in free-electron lasers. Phys Rev Lett (2017) 119:154801. doi:10.1103/PhysRevLett.119.154801

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Villeneuve DM, Hockett P, Mjj V, Niikura H. Coherent imaging of an attosecond electron wave packet. Science (2017) 356:1150–3. doi:10.1126/science.aam8393

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Peng P, Marceau C, Villeneuve DM. Attosecond imaging of molecules using high harmonic spectroscopy. Phys Rev Lett (2019) 1:144–55. doi:10.1038/s42254-018-0015-1

CrossRef Full Text | Google Scholar

18. Bian XB, Bandrauk AD. Attosecond time-resolved imaging of molecular structure by photoelectron holography. Phys Rev Lett (2012) 108:263003. doi:10.1103/PhysRevLett.108.263003

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Schultze M, Fies M, Karpowicz N, Gagnon J, Korbman M, Hofstetter M, et al. Delay in photoemission. Science (2010) 328:1658–62. doi:10.1126/science.1189401

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Vos J, Cattaneo L, Patchkovskii S, Zimmermann T, Cirelli C, Lucchini M, et al. Orientation-dependent stereo wigner time delay and electron localization in a small molecule. Science (2018) 360:1326–30. doi:10.1126/science.aao4731

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Ranitovic P, Hogle CW, Rivière P, Palacios A, Tong XM, Toshima N, et al. Attosecond vacuum uv coherent control of molecular dynamics. Proc Natl Acad Sci USA (2014) 111:912–7. doi:10.1073/pnas.1321999111

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Liao Q, Cao W, Zhang Q, Liu K, Wang F, Lu P, et al. Distinction of electron dispersion in time-resolved photoemission spectroscopy. Phys Rev Lett (2020) 125:043201. doi:10.1103/PhysRevLett.125.043201

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Ellis JL, Hickstein DD, Xiong W, Dollar F, Palm BB, Keister KE, et al. Materials properties and solvated electron dynamics of isolated nanoparticles and nanodroplets probed with ultrafast extreme ultraviolet beams. J Phys Chem Lett (2016) 7:609–15. doi:10.1021/acs.jpclett.5b02772

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Ghimire S, DiChiara AD, Sistrunk E, Agostini P, DiMauro LF, Reis DA. Observation of high-order harmonic generation in a bulk crystal. Nat Phys (2011) 7:138–41. doi:10.1038/nphys1847

CrossRef Full Text | Google Scholar

25. Luu TT, Garg M, Kruchinin SY, Moulet A, Hassan MT, Goulielmakis E. Extreme ultraviolet high-harmonic spectroscopy of solids. Nature (London) (2015) 521:498–502. doi:10.1038/nature14456

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Beth RA. Mechanical detection and measurement of the angular momentum of light. Phys Rev 50 (1936) 115–25. doi:10.1103/PhysRev.50.115

CrossRef Full Text | Google Scholar

27. Allen L, Beijersbergen MW, Spreeuw RJC, Woerdman JP. Orbital angular momentum of light and the transformation of laguerre-Gaussian laser modes. Phys Rev A (1992) 45:8185–9. doi:10.1103/PhysRevA.45.8185

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Molina-Terriza G, Torres JP, Torner L. Twisted photons. Nat Phys (2007) 3:305–10. doi:10.1038/nphys607

CrossRef Full Text | Google Scholar

29. Saari P, Sonajalg H. Pulsed bessel beams. In: T Smith, editor. International workshop on laser Physics. Bristol, United Kingdom: IOP Publishing Ltd (1997). p. 32–9.

Google Scholar

30. Hernández-Figueroa HE. Localized waves. Hoboken: Wiley (2008).

Google Scholar

31. Willner AE, Huang H, Yan Y, Ren Y, Ahmed N, Xie G, et al. Optical communications using orbital angular momentum beams. Adv Opt Photon (2015) 7:66–106. doi:10.1364/AOP.7.000066

CrossRef Full Text | Google Scholar

32. Beaulieu S, Comby A, Descamps D, Fabre B, Garcia GA, Géneaux R, et al. Photoexcitation circular dichroism in chiral molecules. Nat Phys (2018) 14:484–9. doi:10.1038/s41567-017-0038-z

CrossRef Full Text | Google Scholar

33. Padgett M, Bowman R. Tweezers with a twist. Nat Photon (2011) 5:343–8. doi:10.1038/nphoton.2011.81

CrossRef Full Text | Google Scholar

34. Marrucci L, Manzo C, Paparo D. Optical spin-to-orbital angular momentum conversion in inhomogeneous anisotropic media. Phys Rev Lett (2006) 96:163905. doi:10.1103/PhysRevLett.96.163905

PubMed Abstract | CrossRef Full Text | Google Scholar

35. Forbes KA. Raman optical activity using twisted photons. Phys Rev Lett (2019) 122:103201. doi:10.1103/PhysRevLett.122.103201

PubMed Abstract | CrossRef Full Text | Google Scholar

36. Vicidomini G, Bianchini P, Diaspro A. Sted super-resolved microscopy. Nat Methods (2018) 15:173–82. doi:10.1038/nmeth.4593

PubMed Abstract | CrossRef Full Text | Google Scholar

37. Beijersbergen MW, Coerwinkel RPC, Kristensen M, Woerdman JP. Helical-wavefront laser beams produced with a spiral phaseplate. Opt Commun (1994) 112:321–7. doi:10.1016/0030-4018(94)90638-6

CrossRef Full Text | Google Scholar

38. Arlt J, Dholakia K. Generation of high-order bessel beams by use of an axicon. Opt Commun (2000) 177:297–301. doi:10.1016/S0030-4018(00)00572-1

CrossRef Full Text | Google Scholar

39. Heckenberg NR, McDuff R, Smith CP, White AG. Generation of optical phase singularities by computer-generated holograms. Opt Lett (1992) 17:221–3. doi:10.1364/OL.17.000221

PubMed Abstract | CrossRef Full Text | Google Scholar

40. Cai X, Wang J, Strain MJ, Johnson-Morris B, Zhu J, Sorel M, et al. Integrated compact optical vortex beam emitters. Science (2012) 338:363–6. doi:10.1126/science.1226528

PubMed Abstract | CrossRef Full Text | Google Scholar

41. Ninno GD, Wätzel J, Ribič PR, Allaria E, Coreno M, Danailov MB, et al. Photoelectric effect with a twist. Nat Photon (2020) 14:554–8. doi:10.1038/s41566-020-0669-y

CrossRef Full Text | Google Scholar

42. Dorney KM, Rego L, Brooks NJ, Román JS, Liao CT, Ellis JL, et al. Controlling the polarization and vortex charge of attosecond high-harmonic beams via simultaneous spin-orbit momentum conservation. Nat Photon (2019) 13:123–30. doi:10.1038/s41566-018-0304-3

CrossRef Full Text | Google Scholar

43. Rego L, Dorney KM, Brooks NJ, Nguyen QL, Liao CT, Román JS, et al. Generation of extreme-ultraviolet beams with time-varying orbital angular momentum. Science (2019) 364:9486. doi:10.1126/science.aaw9486

PubMed Abstract | CrossRef Full Text | Google Scholar

44. Kong F, Zhang C, Bouchard F, Li Z, Brown GG, Ko DH, et al. Controlling the orbital angular momentum of high harmonic vortices. Nat Commun (2017) 8:14970. doi:10.1038/ncomms14970

PubMed Abstract | CrossRef Full Text | Google Scholar

45. Gauthier D, Ribic̆ PR, Adhikary G, Camper A, Chappuis C, Cucini R, et al. Tunable orbital angular momentum in high-harmonic generation. Nat Commun (2017) 8:14971. doi:10.1038/ncomms14971

PubMed Abstract | CrossRef Full Text | Google Scholar

46. Boning B, Paufler W, Fritzsche S. Above-threshold ionization by few-cycle bessel pulses carrying orbital angular momentum. Phys Rev A (2018) 98:023407. doi:10.1103/PhysRevA.98.023407

CrossRef Full Text | Google Scholar

47. Baghdasaryan B, Boning B, Paufler W, Fritzsche S. Dichroism in two-color above-threshold ionization with twisted xuv beams and intense infrared laser fields. Phys Rev A (2019) 99:023403. doi:10.1103/PhysRevA.99.023403

CrossRef Full Text | Google Scholar

48. Geneaux R, Camper A, Auguste T, Gobert O, Caillat J, Taieb R, et al. Synthesis and characterization of attosecond light vortices in the extreme ultraviolet. Nat Commun (2016) 7:12583. doi:10.1038/ncomms12583

PubMed Abstract | CrossRef Full Text | Google Scholar

49. Muller RA, Seipt D, Beerwerth R, Ornigotti M, Szameit A, Fritzsche S, et al. Photoionization of neutral atoms by x waves carrying orbital angular momentum. Phys Rev A (2016) 94:041402. (R). doi:10.1103/PhysRevA.94.041402

CrossRef Full Text | Google Scholar

50. Boning B, Paufler W, Fritzsche S. Attosecond streaking with twisted x waves and intense infrared pulses. Phys Rev A (2017) 96:043423. doi:10.1103/PhysRevA.96.043423

CrossRef Full Text | Google Scholar

51. Faisal FHM. Multiple absorption of laser photons by atoms. J Phys B: Mol Opt Phys (1973) 6:L89–92. doi:10.1088/0022-3700/6/4/011

CrossRef Full Text | Google Scholar

52. Matula O, Hayrapetyan AG, Serbo VG, Surzhykov A, Fritzsche S. Atomic ionization of hydrogen-like ions by twisted photons: Angular distribution of emitted electrons. J Phys B: Mol Opt Phys (2013) 46:205002. doi:10.1088/0953-4075/46/20/205002

CrossRef Full Text | Google Scholar