Abstract
In the present study, the driven dynamics in a non-Hermitian Aubry–André (AA) model under the open boundary condition (OBC) are studied. For this model, non-Hermiticity is introduced by the non-reciprocal hopping, and this model undergoes a localization–skin effect phase transition depending on the strength of the quasi-periodic potential. Although the properties of non-Hermitian systems are very sensitive to the imposed boundary conditions, we find that the scaling behavior can also be described by the same set of the exponents under the periodic boundary condition (PBC). When the initial state is prepared deep in the localized phase and the potential strength is slowly driven through the critical point, we find that the driven dynamics of the localization length ξ and the inverse participation ratio (IPR) could be described by the Kibble–Zurek scaling (KZS). Then, we numerically verify these predictions for different initial states. Finally, the dynamical emergence of the skin effect state is found, and the dynamics can also be described by the Kibble−Zurek scaling with the same set of critical exponents.
1 Introduction
In recent years, the Anderson localization transition in quasi-periodic systems has attracted increasing interest [1–4]. The quasi-periodic system lacks a translational invariance but shows a long-range order, leading to some peculiar properties in comparison with the disordered system. For instance, the one-dimensional (1D) quasi-periodic system can show the Anderson localization transition [1]. A typical quasi-periodic example is the Aubry–André (AA) model, which undergoes a localization transition with the change of the potential strength [1, 4–7].
Many unusual characteristic features have been found in the AA model and generalized AA models [8–10], such as the self-similar energy spectra and non-trivial topological properties [1], the remarkable self-dual metal localization transition at a multifractal critical point [11], and many-body localization by including the interaction [6, 7, and 12–19]. Moreover, non-equilibrium dynamics in AA models have attracted increasing attention [20–25], and exotic properties, therein, have been discovered, e.g., the periodic driving can not only turn the localized eigenstates into extended eigenstates and vice versa [20 and 21] but also bring the system into the topological MBL phase [22]. For the driven dynamics in the AA model, it was shown that the driven dynamics from the initial state deep in the localized phase can be well described by the Kibble–Zurek scaling (KZS) [25].
On the other hand, the non-Hermitian systems have attracted enormous studies [26–40]. Due to the release of Hermiticity constraints, the non-Hermitian system exhibits rich phenomena without the Hermitian counterparts, e.g., the topological non-Hermitian skin effect under the open boundary condition (OBC), i.e., the wave functions in large systems under the OBC accumulate on the boundary [27–34], exceptional points [41–44], etc. The interplay of non-Hermiticity and the quasi-periodic system brings a new perspective for the localization phenomena [45–56]. Non-Hermiticity can affect the localization transition behavior, e.g., non-Hermiticity can destroy Anderson localization and lead to delocalization even in the 1D system, and it introduces a new scale and breaks down the one-parameter scaling, which is the central assumption of the conventional scaling theory of localization [57]. Furthermore, it has been demonstrated that non-Hermiticity can change the energy spectra of the disorder or the quasi-periodic system. A significant change of the energy spectra is the emergence of the imaginary parts, and the real-complex phase transition always appears accompanied by the localization transition [46, 48, 50, 53, and 58]. Very recently, the effect of the non-Hermiticity on the driven dynamics in a non-Hermitian AA model under the periodic boundary condition (PBC) has been studied [59]. It was found that the critical exponents for the non-Hermitian AA model under the PBC are different from those of the Hermitian AA model, and the driven dynamics of the localization–delocalization transition for different classes of initial states could be described by the KZS with the same set of critical exponents.
Although the driven dynamics of the non-Hermitian AA model under the PBC has been investigated, the driven dynamics of the non-Hermitian AA model under the OBC is still unknown. Since the skin effect, the non-Hermitian AA model undergoes a localization–skin effect transition under the OBC, which corresponds to a transition of the localization center of the wave functions from isolated sites to the boundary. Therefore, the behavior of the localization–skin effect transition under the OBC is different from that of the localization−delocalization transition under the PBC. Moreover, the energy spectrum under the OBC is different from that under the PBC [50]. Considering the effects of non-Hermiticity, it is interesting to investigate the driven dynamics of the non-Hermitian AA model under the OBC.
In the present paper, the static scaling behavior of the driven dynamics of the localization–skin effect transition in the non-Hermitian AA model under the OBC was studied. The non-Hermiticity of this model is induced by the non-reciprocal hopping [50]. Then, the static scaling behavior in the critical region of the localization–skin effect transition was studied, and the critical exponents were determined therein. Starting from the deep localized phase and slowly tuning the potential strength across the critical point, the driven dynamics in this model under the OBC were studied. It was shown that the driven dynamics of the localization–skin effect transition for the initial ground and excited states can be well described by the KZS with the same set of exponents. Finally, the dynamical emergence of the skin effect was observed, and the dynamics can be described by the KZS with the same set of exponents as well.
The rest of the paper is arranged as follows: the non-Hermitian AA model and phase diagram under the OBC are introduced in Section 2. The static scaling properties under the OBC are studied in Section 3, and the critical exponents are determined by the numerical study. Then, in Section 4, the driven dynamics are studied, and the KZS is numerically verified. A summary is given in Section 5.
2 The non-Hermitian AA model and phase diagram under the OBC
The Hamiltonian of the AA model is as follows [50]:in which is the creation (annihilation) operator of the hard-core boson, JL = Je−g and JR = Jeg are the asymmetry hopping amplitudes between the nearest neighboring (NN) sites, λ measures the amplitude of the quasi-periodic potential, is an irrational number, and ϕ ∈ [0, 1) is the phase of the potential. In the following calculation, the OBC is imposed.
In Figure 1A, the phase diagram of the non-Hermitian AA model for g > 0 is plotted. It is shown that the model is in the localized phase when λ > 2eg, while it is in the skin-effect phase when λ < 2eg. At λ = 2eg, the eigenstates of the system are all critical. Therefore, by varying λ through the critical point λc = 2eg, the system undergoes a localization–skin effect phase transition under the OBC.
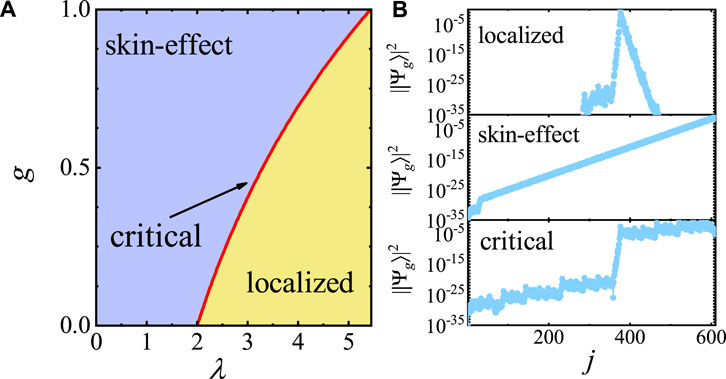
FIGURE 1
(A) Phase diagram of the non-Hermitian AA model under the OBC. (B) Typical spatial distributions of ‖Ψg⟩|2 in the skin effect phase, localized phase, and critical phase under the OBC. The lattice size is L = 610 and g = 0.5 in (B).
In different phases, the spatial distributions of the eigenstates show great different behaviors, which is an important characteristic feature in distinguishing these phases. Since the behavior of the spatial distributions of different eigenstates is similar to each other, the ground state is chosen as an example. As shown in Figure 1B, the spatial distribution of the ground states |Ψg⟩ in different phases is plotted. In the localized phase, one finds that the wave function is localized on some isolated sites. However, in the skin effect phase, the wave function is localized on the boundary due to the non-Hermitian skin effect. The wave function is localized near the right side, but different from the skin effect, where the wave function is not localized on the boundary. Therefore, the localization–skin effect transition corresponds to a transition of the localization center from some isolated sites to the boundary.
3 Static critical properties in the critical region of localization–skin effect transition
3.1 Static scaling forms in the critical region
In this section, the static properties in the critical region of the localization–skin effect transition are studied, and the critical exponents for the localization–skin effect transition are examined by studying the static behaviors of the energy gap between the first excited state and the ground state Δc, localization length ξ, and inverse participation ratio (IPR). We found that the critical exponents for the localization–delocalization transition under the PBC are still applicable in the localization–skin effect transition.
As in the usual quantum criticality, the energy gap between the first excited state and the ground state at the critical point is usually used to characterize the localization–skin effect transition. According to finite-size scaling, the energy gap Δc should scale as follows:
For the Hermitian AA model, z was determined as z = 2.37 [25], while z = 2 for the non-Hermitian AA model under the PBC [59].
The localization length ξ is defined as follows [25−59]:in which Pn is the probability of the wave function at site n, and nc ≡∑nPn is the localization center. Near a critical point, ξ scales with the distance to the critical point ɛ as follows:in which ɛ = λ–λc. Taken into account the finite-size scaling, the scaling form of ξ is given as follows:where f1 is the scaling function for the static ξ. For the Hermitian AA model and non-Hermitian AA model under the PBC, ν is determined as ν = 1 [25, 59, and 60].
The IPR is defined as follows [61 and 62]:where |Ψ(j)⟩ is the eigenvector. Under the OBC, the IPR shows a local minimum at the critical point, indicating the localization−skin effect transition [50]. Near the critical point, the IPR satisfies a scaling relation, shown as follows:
Taken into account the finite-size scaling, the scaling form of the IPR is given as follows:in which f2 is the scaling function for the static IPR. For the non-Hermitian AA model under the PBC, s is determined as s = 0.1196 [54 and 59].
3.2 Numerical results
By applying a finite-size scaling of Δc, the dynamical exponent z can be verified. The numerical results for Δc as a function of L are plotted in Figure 2. By a power-law fitting, one finds that Δc ∝ L−2.002 with the exponent very close to z = 2, confirming that z = 2 is also applicable under the OBC.
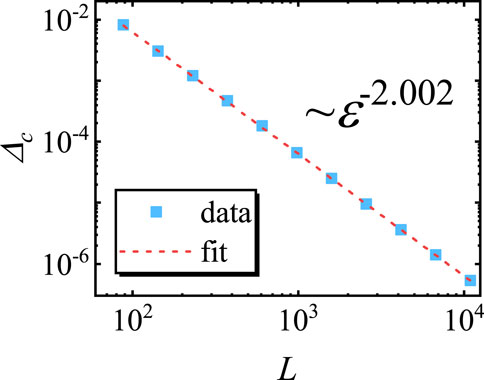
FIGURE 2
Energy gap between the ground and first excited states Δc as a function of the lattice size L. The power fit yields Δc ∝ɛ−2.002. Double-log scales are used. Here, g = 0.5, and the results are averaged for 100 choices of ϕ.
In the localized phase, the Eqs 5− 8 are tested, and the ground state is taken as an example. As shown in Figure 3 (A1), we calculate the curves of ξ versus ɛ for different lattice sizes. After rescaling ξ as ξL−1 and ɛ as ɛL1/ν with ν = 1, one finds that the rescaled curves match with each other very well, as plotted in Figure 3 (A2). In Figure 3 (B1), the curves of the IPR of the ground state versus ɛ for different lattice sizes are plotted. After rescaling the IPR as IPRLs/ν and ɛ as ɛL1/ν with ν = 1 and s = 0.1196, the rescaled curves collapse onto each other.
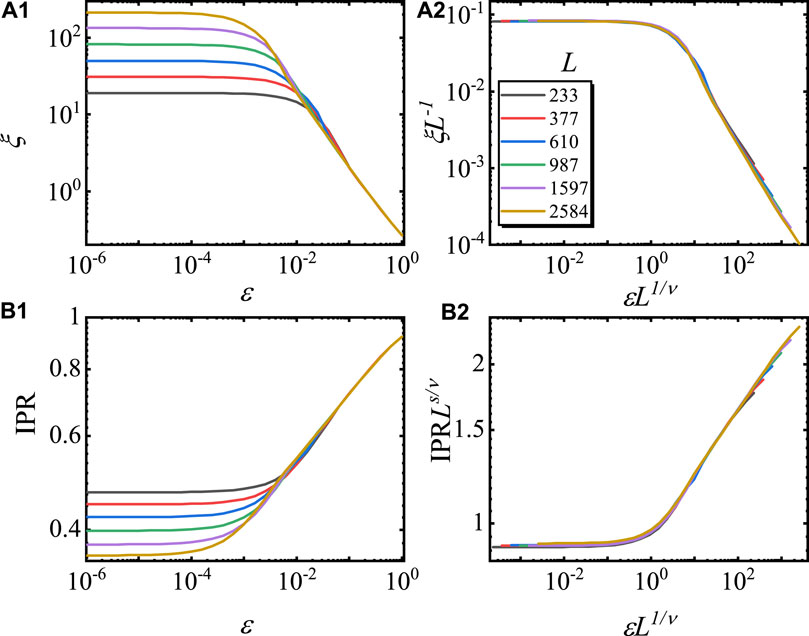
FIGURE 3
Finite scaling of ξ and IPR of the ground state in the localized phase. The curves of ξ versus ɛ before (A1) and after (A2) rescaling, according to Eq. 5 for different L values. The curves of the IPR versus ɛ before (B1) and after (B2) rescaling, according to Eq. 8 for different L values. Here, g = 0.5, ɛ > 0, and the model is in the localized phase region. Double-log scales are used, and the results are averaged for 100 choices of ϕ.
Different from the non-Hermitian AA model under the PBC, ξ and IPR are still well defined under the OBC when λ < 2eg. Therefore, the scaling functions of Eqs 5−8 are also verified in the skin effect phase. The numerical results are plotted in Figure 4. Figure 4 (A1) and (B1) show the ɛ dependence of ξ and IPR in the skin effect phase, respectively. After rescaling according to Eqs 5 and 8 with the same ν and s, we find that the rescaled curves collapse onto each other, as shown in Figure 4 (A2) and (B2).
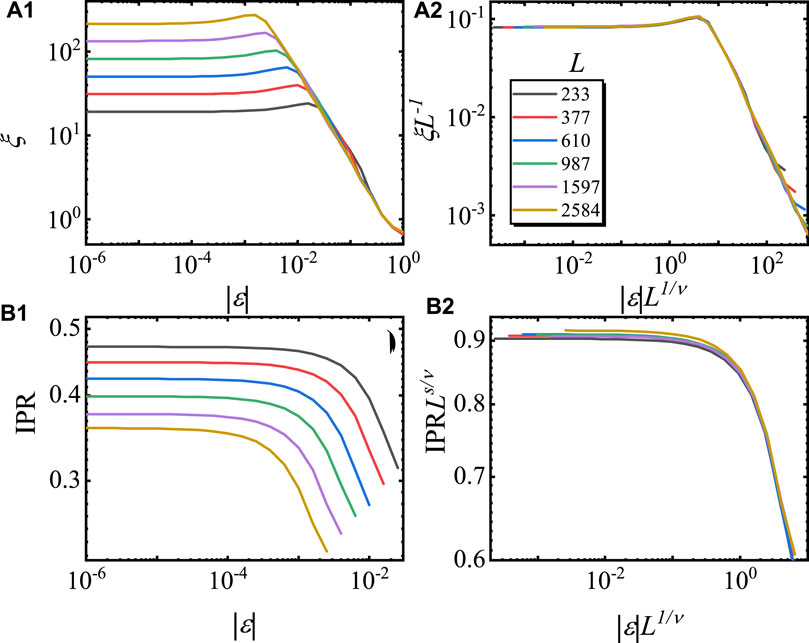
FIGURE 4
Finite scaling of ξ and IPR of the ground state in the skin effect phase. The curves of ξ versus |ɛ| before (A1) and after (A2) rescaling, according to Eq. 5 for different L values. The curves of the IPR versus |ɛ| before (B1) and after (B2) rescaling, according to Eq. 8 for different L values. Here, g = 0.5, ɛ < 0, and the model is in the skin effect phase region. Double-log scales are used, and the results are averaged for 100 choices of ϕ.
These results confirm that the same set critical exponent of the non-Hermitian AA model under the PBC is applicable for the localization–skin effect transition. These exponents, z, ν, and s, are usually enough to determine the critical behavior in the localization–skin effect critical region.
4 Kibble–Zurek scaling in the localization–skin effect transition
4.1 General theory of the KZS
Here, we slowly vary ɛ across the critical point from an initial state in the localized phase. ɛ varies as follows:where R is the varying rate. We choose the initial time as t0 = −ɛ0/R. According to the KZS, when |ɛ| > R1/νr with r = z+1/ν, the system can evolve adiabatically as the state has enough time to adjust to the change in the Hamiltonian. When |ɛ| < R1/νr, the system enters the impulse region and ceases to evolve as a result of the critical point slowing down.
Around the critical point, the driven dynamics of ξ satisfy the KZS, which is given as follows:where g1 is the scaling function for the driven dynamical ξ and r = z+1/ν. The driven dynamics of the IPR of the nth eigenstate around the critical point satisfy the following:where g2 is the scaling function for the driven dynamical IPR.
It should be noted that the scaling functions Eqs 10 and 11 are suitable to describe the driven dynamics of the localization–delocalization phase transition under the PBC since the exponents are the same under the PBC and OBC. The full scaling form for a quantity, e.g., Eqs 10 and 11 for ξ and IPR, has also been proposed from different perspectives in classical and quantum phase transitions [25, 63–69]. In the recent study, such scaling forms have been generalized to study the non-equilibrium dynamics in the non-Hermitian systems under the PBC [42, 59, and 70]. In this work, we perform this full scaling form in the dynamical localization–skin effect transition in the non-Hermitian AA model under the OBC.
4.2 Numerical results for the initial states deep in the localization phase
First, we verify the scaling function Eqs 10 and 11 with the initial state deep in the localized phase. We numerically solved the Schrodinger equation for the model (Eq. 1) under the OBC, and the finite difference method in the time direction is used. In the numerical calculation, the time interval is chosen as 10−3.
According to Eqs 10 and 11, at ɛ = 0, ξ and IPRn become the following:
In Figure 5, we take the ground state at ɛ0 = 1 as the initial state to test these predictions, where we plot the curves of ξR (ɛ = 0, R) and IPRn(ɛ = 0, R) as a function of R. The power-law fitting yields ξ(ɛ = 0, R) ∝ R−0.3367 and IPR(ɛ = 0, R) ∝ R0.0420, which are consistent with the predictions in Eqs 12 and 13.
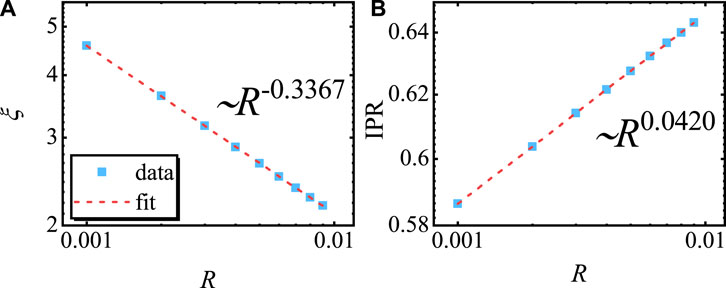
FIGURE 5
(A)ξ and (B) IPR at = 0 as a function of R. Here, we use g = 0.5 and L = 987. The results are averaged for 10 choices of ϕ.
In Figure 6 (A1), the curves of ξ versus ɛ with the initial ground state at ɛ = 1 for different R values are plotted. After rescaling ξ and ɛ with R, according to Eq. 10, the rescaled curves collapse onto each other very well, as plotted in Figure 6 (A2). It confirms the scaling law of Eq. 10. The numerical results of the IPR versus ɛ and rescaled curves according to Eq. 11 are plotted in Figure 6 (B1) and (B2). The collapse in Figure 6 (B2) confirms the scaling function Eq. 11.
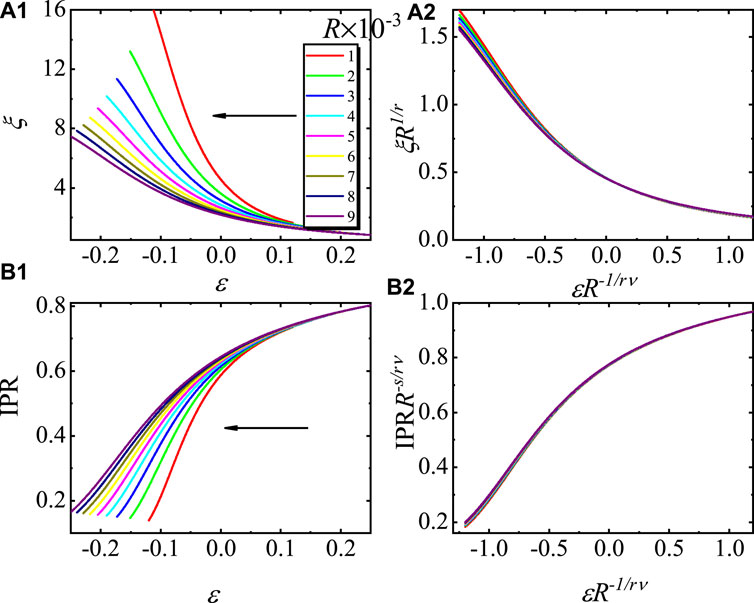
FIGURE 6
Driven dynamics with the initial ground state at ɛ = 1. (A1) Curves of ξ versus ɛ and (A2) the rescaled curves according to Eq. 10 for different R values. (B1) Curves of the IPRn versus ɛ and (B2) the rescaled curves according to Eq. 11 for different R values. Here, we use ɛ0 = 1, g = 0.5, and L = 987, and the results are averaged for 10 choices of ϕ. The arrows in (a1) and (b1) point to the direction of the changing ɛ.
In addition to the initial ground state, the scaling functions of Eqs 10 and 11 are also verified for the excited states. The 609th excited state at ɛ = 1 is selected as the initial state. Figure 7 (A1) and (B1) show the evolution of ξ and IPR, respectively, for the 609th excited state. After the rescaling according to Eqs 10 and 11 with the same set of the critical exponents, we find the rescaled curves collapse onto each other, as shown in Figure 7 (A2) and (B2). These results confirm that the rescaling functions of Eqs 10 and 11 are applicable for the excited eigenstates.
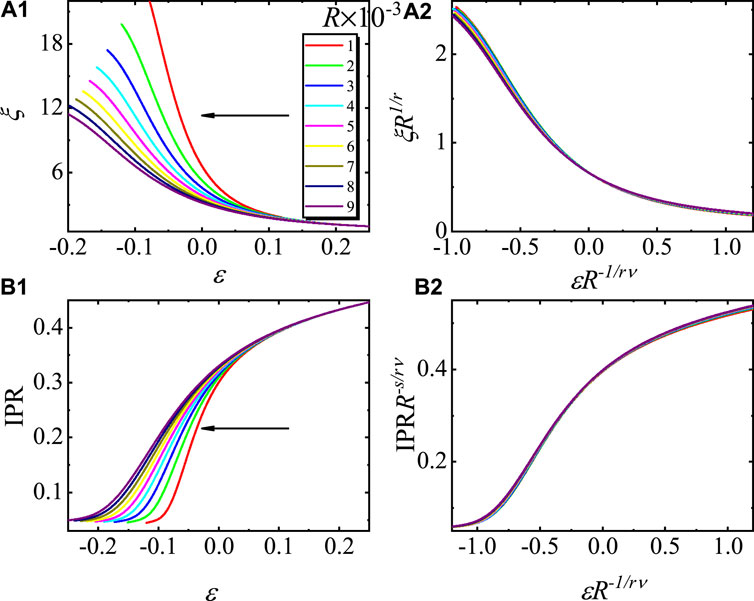
FIGURE 7
Driven dynamics with the initial 609th excited state at ɛ = 1. (A1) Curves of ξ versus ɛ, and (A2) the rescaled curves according to Eq. 10 for different R values. (B1) Curves of the IPRn versus ɛ and (B2) the rescaled curves according to Eq. 11 for different R values. Here, we use ɛ0 = 1, g = 0.5, and L = 987, and the results are averaged for 10 choices of ϕ. The arrows in (A1) and (B1) point to the direction of the changing ɛ.
4.3 Dynamical emergence of the skin effect
Since the critical exponents in the skin effect phase are identical to those in the localized phase, it is expected that the driven dynamics in the skin effect phase can also be described by the scaling functions of Eqs 10 and 11. To verify this prediction, we studied the driven dynamics with even smaller varying rates.
In Figure 8 (A1) and (B1), we calculate the curves of ξ and IPR versus ɛ for various R values. Here, we set the lattice size as L = 233; R values vary from 5 × 10−5 to 12 × 10−5, which is small enough to observe the behavior of the dynamical emergence of the skin effect. The ground state at ɛ = 1 is chosen as the initial state. By rescaling ξ and ɛ as ξR1/r and ɛR−1/rν, the rescaled curves collapse onto each other, as shown in Figure 8 (A2), confirming Eq. 10. As shown in Figure 8 (B1) and (B2), the curves of the IPR versus ɛ before and after rescaling according to Eq. 11 are plotted. We find that the rescaled curves, according to Eq. 11 with the same set of the critical exponents, collapse into a single curve. Furthermore, one finds that ξ shows a peak value and IPR shows a valley around ɛ = 0. Then, with the further decrease of ɛ, ξ decreases and IPR increases again. Such behaviors of ξ and IPR correspond to the dynamical emergence of the skin effect. These results confirm that Eqs 10 and 11 are still applicable in the dynamical emergence of the skin effect.
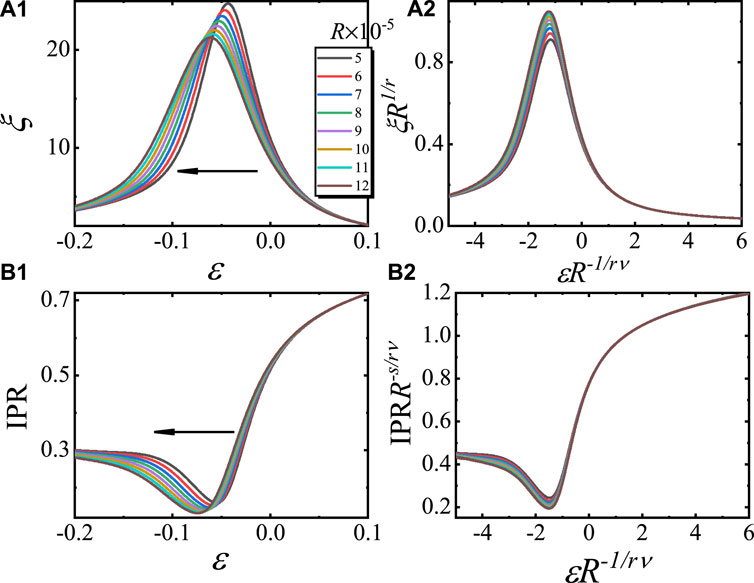
FIGURE 8
Dynamical emergence of the skin effect. (a1) Curves of ξ versus ɛ and (a2) the rescaled curves according to Eq. 10 for different R values. (b1) Curves of the IPRn versus ɛ and (b2) the rescaled curves according to Eq. 11 for different R values. Here, we use ɛ0 = 1, g = 0.5, and L = 233, and the results are averaged for 10 choices of ϕ. The arrows in (a1) and (b1) point to the direction of the changing ɛ.
5 Summary
In summary, we have studied the static scaling behavior and the driven dynamics of the localization–skin effect transition in a non-Hermitian AA model under the OBC. By investigating the static behavior of ξ, IPR, and Δc, respectively, it is shown that the same set of critical exponents of ν, s, and z under the PBC are also applicable under the OBC. The driven dynamics of the localization–skin effect transition for different initial states are studied, and we find that the driven dynamics in both the initial ground and excited states can be described by the KZS with the same set of critical exponents. Then, the dynamical emergence of the skin effect is observed with an even small varying rate R, and it is shown that the dynamical emergence of the skin effect can also be described by the same scaling functions with the same set of critical exponents. Our present work generalizes the KZS to the localization–skin effect transition in non-Hermitian systems under the OBC.
Statements
Data availability statement
The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.
Author contributions
All authors contributed to the writing of the manuscript and to the interpretation of the results. L-JZ was responsible for the numerical methods adopted in the manuscript and original draft preparation; H-YW was responsible for conceptualization and formal analysis; and L-LH and QG were responsible for the numerical calculation.
Funding
L-JZ was supported by the National Natural Science Foundation of China (Grant no. 11704161), the Zhongwu Youth Innovation Talent Support Plan of Jiangsu University of Technology, and the China Postdoctoral Science Foundation (Grant no. 2021M691535).
Acknowledgments
The authors would like to thank A. Sinha and S. Yin for their helpful discussions.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
1.
AubrySAndreG. Analyticity breaking and anderson localization in incommensurate lattices. Ann Isr Phys. Soc. (1980) 3:133.
2.
GoblotVŠtrkaljAPernetNLadoJLDorowCLemaîtreAet alEmergence of criticality through a cascade of delocalization transitions in quasiperiodic chains. Nat Phys (2020) 16:832–6. 10.1038/s41567-020-0908-7
3.
LüschenHPSchergSKohlertTSchreiberMBordiaPLiXet alSingle-particle mobility edge in a one-dimensional quasiperiodic optical lattice. Phys Rev Lett (2018) 120:160404. 10.1103/PhysRevLett.120.160404
4.
SkipetrovSESinhaA. Time-dependent reflection at the localization transition. Phys Rev B (2018) 97:104202. 10.1103/PhysRevB.97.104202
5.
GaneshanSSunKDas SarmaS. Topological zero-energy modes in gapless commensurate aubry-andré-harper models. Phys Rev Lett (2013) 110:180403. 10.1103/PhysRevLett.110.180403
6.
MastropietroV. Localization of interacting fermions in the aubry-andré model. Phys Rev Lett (2015) 115:180401. 10.1103/PhysRevLett.115.180401
7.
XuSLiXHsuYTSwingleBDas SarmaS. Butterfly effect in interacting aubry-andre model: Thermalization, slow scrambling, and many-body localization. Phys Rev Res (2019) 1:032039. 10.1103/PhysRevResearch.1.032039
8.
Das SarmaSHeSXieXC. Mobility edge in a model one-dimensional potential. Phys Rev Lett (1988) 61:2144–7. 10.1103/PhysRevLett.61.2144
9.
LiuFGhoshSChongYD. Localization and adiabatic pumping in a generalized aubry-andré-harper model. Phys Rev B (2015) 91:014108. 10.1103/PhysRevB.91.014108
10.
ThoulessDJ. Bandwidths for a quasiperiodic tight-binding model. Phys Rev B (1983) 28:4272–6. 10.1103/PhysRevB.28.4272
11.
AulbachCWobstAIngoldGLHänggiPVargaI. Phase-space visualization of a metal–insulator transition. New J Phys (2004) 6:70. 10.1088/1367-2630/6/1/070
12.
WangYChengCLiuXJYuD. Many-body critical phase: Extended and nonthermal. Phys Rev Lett (2021) 126:080602. 10.1103/PhysRevLett.126.080602
13.
ŠtrkaljADoggenEVHGornyiIVZilberbergO. Many-body localization in the interpolating aubry-andrè-fibonacci model. Phys Rev Res (2021) 3:033257. 10.1103/PhysRevResearch.3.033257
14.
ZhangSXYaoH. Universal properties of many-body localization transitions in quasiperiodic systems. Phys Rev Lett (2018) 121:206601. 10.1103/PhysRevLett.121.206601
15.
WangYZhangJHLiYWuJLiuWMeiFet alObservation of interaction-induced mobility edge in an atomic aubry-andré wire. Phys Rev Lett (2022) 129:103401. 10.1103/PhysRevLett.129.103401
16.
DaiCMZhangYYiXX. Dynamical localization in non-hermitian quasicrystals. Phys Rev A (Coll Park) (2022) 105:022215. 10.1103/PhysRevA.105.022215
17.
ZhouL. Floquet engineering of topological localization transitions and mobility edges in one-dimensional non-hermitian quasicrystals. Phys Rev Res (2021) 3:033184. 10.1103/PhysRevResearch.3.033184
18.
XuZHuangfuHZhangYChenS. Dynamical observation of mobility edges in one-dimensional incommensurate optical lattices. New J Phys (2020) 22:013036. 10.1088/1367-2630/ab64b2
19.
XuZChenS. Dynamical evolution in a one-dimensional incommensurate lattice with PT symmetry. Phys Rev A (Coll Park) (2021) 103:043325. 10.1103/PhysRevA.103.043325
20.
Morales-MolinaLDoernerEDanieliCFlachS. Resonant extended states in driven quasiperiodic lattices: Aubry-andrè localization by design. Phys Rev A (Coll Park) (2014) 90:043630. 10.1103/PhysRevA.90.043630
21.
BaireyERefaelGLindnerNH. Driving induced many-body localization. Phys Rev B (2017) 96:020201. 10.1103/PhysRevB.96.020201
22.
DeckerKSCKarraschCEisertJKennesDM. Floquet engineering topological many-body localized systems. Phys Rev Lett (2020) 124:190601. 10.1103/PhysRevLett.124.190601
23.
ModakRRakshitD. Many-body dynamical phase transition in a quasiperiodic potential. Phys Rev B (2021) 103:224310. 10.1103/PhysRevB.103.224310
24.
YangCWangYWangPGaoXChenS. Dynamical signature of localization-delocalization transition in a one-dimensional incommensurate lattice. Phys Rev B (2017) 95:184201. 10.1103/PhysRevB.95.184201
25.
SinhaARamsMMDziarmagaJ. Kibble-zurek mechanism with a single particle: Dynamics of the localization-delocalization transition in the aubry-andré model. Phys Rev B (2019) 99:094203. 10.1103/PhysRevB.99.094203
26.
AshidaYGongZUedaM. Non-hermitian physics. Adv Phys X (2021) 69:249–435. 10.1080/00018732.2021.1876991
27.
YaoSWangZ. Edge states and topological invariants of non-hermitian systems. Phys Rev Lett (2018) 121:086803. 10.1103/PhysRevLett.121.086803
28.
SongFYaoSWangZ. Non-hermitian skin effect and chiral damping in open quantum systems. Phys Rev Lett (2019) 123:170401. 10.1103/PhysRevLett.123.170401
29.
OkumaNKawabataKShiozakiKSatoM. Topological origin of non-hermitian skin effects. Phys Rev Lett (2020) 124:086801. 10.1103/PhysRevLett.124.086801
30.
KawabataKSatoMShiozakiK. Higher-order non-hermitian skin effect. Phys Rev B (2020) 102:205118. 10.1103/PhysRevB.102.205118
31.
BorgniaDSKruchkovAJSlagerRJ. Non-hermitian boundary modes and topology. Phys Rev Lett (2020) 124:056802. 10.1103/PhysRevLett.124.056802
32.
LonghiS. Unraveling the non-hermitian skin effect in dissipative systems. Phys Rev B (2020) 102:201103. 10.1103/PhysRevB.102.201103
33.
FuYHuJWanS. Non-hermitian second-order skin and topological modes. Phys Rev B (2021) 103:045420. 10.1103/PhysRevB.103.045420
34.
LiuJSHanYZLiuCS. A new way to construct topological invariants of non-hermitian systems with the non-hermitian skin effect. Chin Phys B (2020) 29:010302. 10.1088/1674-1056/ab5937
35.
XueWTHuYMSongFWangZ. Non-hermitian edge burst. Phys Rev Lett (2022) 128:120401. 10.1103/PhysRevLett.128.120401
36.
El-GanainyRMakrisKGKhajavikhanMMusslimaniZHRotterSChristodoulidesDN. Non-hermitian physics and pt symmetry. Nat Phys (2018) 14:11–9. 10.1038/nphys4323
37.
BenderCMBoettcherS. Real spectra in non-hermitian Hamiltonians having PT symmetry. Phys Rev Lett (1998) 80:5243–6. 10.1103/PhysRevLett.80.5243
38.
MostafazadehA. Pseudo-hermiticity versus pt symmetry: The necessary condition for the reality of the spectrum of a non-hermitian Hamiltonian. J Math Phys (2001) 43:205–14. 10.1063/1.1418246
39.
ZhangSJinLSongZ. Topology of a parity–time symmetric non-hermitian rhombic lattice. Chin Phys B (2022) 31:010312. 10.1088/1674-1056/ac364a
40.
ZhaiLJYinS. Out-of-time-ordered correlator in non-hermitian quantum systems. Phys Rev B (2020) 102:054303. 10.1103/PhysRevB.102.054303
41.
KawabataKBesshoTSatoM. Classification of exceptional points and non-hermitian topological semimetals. Phys Rev Lett (2019) 123:066405. 10.1103/PhysRevLett.123.066405
42.
YinSHuangGYLoCYChenP. Kibble-zurek scaling in the yang-lee edge singularity. Phys Rev Lett (2017) 118:065701. 10.1103/PhysRevLett.118.065701
43.
DoraBHeylMMoessnerR. The kibble-zurek mechanism at exceptional points. Nat Commun (2019) 10:2254. 10.1038/s41467-019-10048-9
44.
DingKMaGXiaoMZhangZQChanCT. Emergence, coalescence, and topological properties of multiple exceptional points and their experimental realization. Phys Rev X (2016) 6:021007. 10.1103/PhysRevX.6.021007
45.
HatanoNNelsonDR. Non-hermitian delocalization and eigenfunctions. Phys Rev B (1998) 58:8384–90. 10.1103/PhysRevB.58.8384
46.
LonghiS. Topological phase transition in non-hermitian quasicrystals. Phys Rev Lett (2019) 122:237601. 10.1103/PhysRevLett.122.237601
47.
LonghiS. Metal-insulator phase transition in a non-hermitian aubry-andré-harper model. Phys Rev B (2019) 100:125157. 10.1103/PhysRevB.100.125157
48.
LiuYWangYLiuXJZhouQChenS. Exact mobility edges, PT-symmetry breaking, and skin effect in one-dimensional non-Hermitian quasicrystals. Phys Rev B (2021) 103:014203. 10.1103/PhysRevB.103.014203
49.
CaiX. Localization and topological phase transitions in non-hermitian aubry-andré-harper models with p-wave pairing. Phys Rev B (2021) 103:214202. 10.1103/PhysRevB.103.214202
50.
JiangHLangLJYangCZhuSLChenS. Interplay of non-hermitian skin effects and anderson localization in nonreciprocal quasiperiodic lattices. Phys Rev B (2019) 100:054301. 10.1103/PhysRevB.100.054301
51.
JazaeriASatijaII. Localization transition in incommensurate non-hermitian systems. Phys Rev E (2001) 63:036222. 10.1103/PhysRevE.63.036222
52.
WangPJinLSongZ. Non-hermitian phase transition and eigenstate localization induced by asymmetric coupling. Phys Rev A (Coll Park) (2019) 99:062112. 10.1103/PhysRevA.99.062112
53.
ZhaiLJYinSHuangGY. Many-body localization in a non-hermitian quasiperiodic system. Phys Rev B (2020) 102:064206. 10.1103/PhysRevB.102.064206
54.
ZhaiLJHuangGYYinS. Cascade of the delocalization transition in a non-hermitian interpolating aubry-andré-fibonacci chain. Phys Rev B (2021) 104:014202. 10.1103/PhysRevB.104.014202
55.
TangLZZhangGQZhangLFZhangDW. Localization and topological transitions in non-hermitian quasiperiodic lattices. Phys Rev A (Coll Park) (2021) 103:033325. 10.1103/PhysRevA.103.033325
56.
CaiX. Localization and topological phase transitions in non-hermitian aubry-andré-harper models with p-wave pairing. Phys Rev B (2021) 103:214202. 10.1103/PhysRevB.103.214202
57.
KawabataKRyuS. Nonunitary scaling theory of non-hermitian localization. Phys Rev Lett (2021) 126:166801. 10.1103/PhysRevLett.126.166801
58.
HamazakiRKawabataKUedaM. Non-hermitian many-body localization. Phys Rev Lett (2019) 123:090603. 10.1103/PhysRevLett.123.090603
59.
ZhaiLJHuangGYYinS. Nonequilibrium dynamics of the localization-delocalization transition in the non-hermitian aubry-andré model. Phys Rev B (2022) 106:014204. 10.1103/PhysRevB.106.014204
60.
WeiBB. Fidelity susceptibility in one-dimensional disordered lattice models. Phys Rev A (Coll Park) (2019) 99:042117. 10.1103/PhysRevA.99.042117
61.
BauerJChangTMSkinnerJL. Correlation length and inverse-participation-ratio exponents and multifractal structure for anderson localization. Phys Rev B (1990) 42:8121–4. 10.1103/PhysRevB.42.8121
62.
FyodorovYVMirlinAD. Analytical derivation of the scaling law for the inverse participation ratio in quasi-one-dimensional disordered systems. Phys Rev Lett (1992) 69:1093–6. 10.1103/PhysRevLett.69.1093
63.
MonacoRMygindJRiversRJ. Zurek-kibble domain structures: The dynamics of spontaneous vortex formation in annular josephson tunnel junctions. Phys Rev Lett (2002) 89:080603. 10.1103/PhysRevLett.89.080603
64.
AnglinJRZurekWH. Vortices in the wake of rapid bose-einstein condensation. Phys Rev Lett (1999) 83:1707–10. 10.1103/PhysRevLett.83.1707
65.
AntunesNDGandraPRiversRJ. Is domain formation decided before or after the transition?Phys Rev D (2006) 73:125003. 10.1103/PhysRevD.73.125003
66.
DziarmagaJ. Dynamics of a quantum phase transition: Exact solution of the quantum ising model. Phys Rev Lett (2005) 95:245701. 10.1103/PhysRevLett.95.245701
67.
DamskiBZurekWH. Dynamics of a quantum phase transition in a ferromagnetic bose-einstein condensate. Phys Rev Lett (2007) 99:130402. 10.1103/PhysRevLett.99.130402
68.
ChandranAErezAGubserSSSondhiSL. Kibble-zurek problem: Universality and the scaling limit. Phys Rev B (2012) 86:064304. 10.1103/PhysRevB.86.064304
69.
TongXMengYMJiangXLeeCNetoGDDMGaoX. Dynamics of a quantum phase transition in the aubry-andré-harper model with p-wave superconductivity. Phys Rev B (2021) 103:104202. 10.1103/PhysRevB.103.104202
70.
ZhaiLJWangHYYinS. Hybridized kibble-zurek scaling in the driven critical dynamics across an overlapping critical region. Phys Rev B (2018) 97:134108. 10.1103/physrevb.97.134108
Summary
Keywords
non-Hermitian quasi-periodic system, Aubry–André model, localization–skin effect phase transition, driven dynamics, Kibble–Zurek scaling, Anderson localization
Citation
Zhai L-J, Hou L-L, Gao Q and Wang H-Y (2022) Kibble−Zurek scaling of the dynamical localization−skin effect phase transition in a non-Hermitian quasi-periodic system under the open boundary condition. Front. Phys. 10:1098551. doi: 10.3389/fphy.2022.1098551
Received
15 November 2022
Accepted
02 December 2022
Published
20 December 2022
Volume
10 - 2022
Edited by
Huan Yang, Shandong University, China
Reviewed by
Hai-Rui Wei, University of Science and Technology Beijing, China
Hongbin Yao, Xinjiang Institute of Engineering, China
Updates
Copyright
© 2022 Zhai, Hou, Gao and Wang.
This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Huai-Yu Wang, wanghuaiyu@mail.tsinghua.edu.cn
This article was submitted to Atomic and Molecular Physics, a section of the journal Frontiers in Physics
Disclaimer
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.