Image encryption scheme based on a controlled zigzag transform and bit-level encryption under the quantum walk

With the rapid development of science and technology and network technology, the study of information security has become a hot spot, and image encryption has potential value in this regard. In this paper, an image encryption scheme based on controlled zigzag transform and bit-level encryption under the quantum walk environment is proposed. First, the parameters of the alternating quantum walk are obtained using the SHA-256 method, and the probability matrix of the quantum distribution on the two-dimensional lattice is obtained by multiple walk measurements; second, the spatial dislocation and bit-level dislocation of the image are realized by performing controlled zigzag dislocation and three-dimensional tesseract-like rotational dislocation on the color image; finally, after preprocessing the probability matrix of the quantum distribution, the matrix is bitwise with the dislocated image to achieve the encryption protection of image information. The effectiveness of the encryption scheme is verified by simulation experiments, and the scheme has a significant encryption effect. Compared with other encryption schemes, this scheme has better key sensitivity and dislocation effect, which provides a new approach to the field of image quantum encryption.

1 Introduction

With the fast development and application of network technology, image information is more and more widely used in our daily life for different purposes such as medical images, scanned images, and remote sensing images Hossein Movafegh Ghadirli and Enayatifar [1]; Jianfeng Zhao et al. [2]; Sui and Gao [3]; Nanrun Zhou et al. [4]; Yuxin Shen et al. [5]; Xiaoyong Ji et al. [6]. To prevent image information from being attacked by hackers and other illegal elements during the network transmission process, which poses a threat to information security, researchers from various countries have studied various methods to hide and protect image information Gen Liu and Jiang [7]; Yuzhen Li et al. [8]; Xingyuan Wang and Cao [9]; Wang and Sun [10]; Vidhya and Brindha [11]. The current common image encryption methods are roughly divided into two parts: 1) the traditional scrambling algorithm is based on the spatial position of the image pixel value Gen Liu and Jiang [7]. It can transform the image information in the spatial position, which can achieve the visual encryption effect, but the whole image can be encrypted. The pixel values that are not processed are vulnerable to data analysis attacks and have poor security. 2) The image encryption algorithm is under the chaotic system Wang and Guan [12]; Li-Hua Gong et al. [13]; Wang and Liu [14]; Abitha and Bharathan [15]; AL-Hashemy and Mehdi [16]; Hegui Zhu et al. [17]; Gao [18]; Liu et al. [19]. Encryption technology based on the chaotic system was developed in the 1990s and has been continuously improved due to its sensitivity to initial conditions, ergodicity, and randomness, and it has become the most widely studied and used encryption algorithm. However, the chaotic sequence generated by the conventional chaotic algorithm generally has local linearity, and the correlation shows a certain periodicity, which affects the security of the image more or less.

In recent years, researchers are keen to combine traditional pixel-based spatial scrambling methods with chaotic systems and have proposed many “scrambling-diffusion” image encryption algorithms. Among them, the commonly used scrambling methods combined with chaotic systems are the following: Arnold transform Sui and Gao [3]; Nanrun Zhou et al. [4], zigzag transform Gen Liu and Jiang [7]; Yuzhen Li et al. [8]; Xingyuan Wang and Cao [9]; Wang and Guan [12], Knight Parade transform Xiaoyong Ji et al. [6], DNA encoding Wang and Liu [14]; Wang and Sun [10]; Li-Hua Gong et al. [13]; Yi-Nuo Wang et al. [20], Rubik’s cube transform Vidhya and Brindha [11]; Abitha and Bharathan [15]; AL-Hashemy and Mehdi [16]; Hegui Zhu et al. [17]; Jingbo Zhao et al. [21], and so on. In 2015, Yuzhen Li et al. took a combination of the zigzag scrambling transform and a 3-D logistic map chaotic structure into consideration and proposed an image encryption scheme, which increased the key space and improved the security of image information compared with the general chaotic encryption Yuzhen Li et al. [8]. In 2016, Abitha K.A combined the chaotic Baker with the Rubik’s cube principle to come up with a novel image encryption method, which increases the security of the cryptographic system Abitha and Bharathan [15]. In 2019, Xingyuan Wang put forward an image encryption method that takes the zigzag scrambling transform and LL compound chaotic system to improve the scrambling effect by improving the traditional zigzag scrambling transform Xingyuan Wang and Cao [9]; in the same year, Wang also proposed a combination of zigzag scrambling. The image encryption algorithm combining transformation and DNA-like encoding has higher security and sensitivity than the previous chaotic algorithm by improving zigzag scrambling transformation and DNA-like encoding Wang and Sun [10]. In 2021, Hegui Zhu came up with a bit-level image encryption algorithm based on the 3-D Rubik’s cube, which provided a new idea for the bit-level diffusion encryption of 2-D images Hegui Zhu et al. [17]. Although the chaotic algorithm generally has the characteristics of ergodicity and randomness, it can fully encrypt the image and can resist most attacks, but its periodic characteristics render the security of the image not well protected.

To cope with the periodic characteristics of chaotic systems, some researchers have introduced neural networks Zhang and bo Fang [22]; XingyuanWang and Li [23]. In 2015, Kun Zhang et al. proposed an image encryption algorithm based on a TD-ERCS system and wavelet neural network, using a wavelet neural network to study a TD-ERCS system to obtain an aperiodic-chaotic sequence Zhang and bo Fang [22]. In 2021, Xingyuan Wang et al. took the BP neural network into consideration , used it with PWLCM to produce a random and aperiodic key stream for image encryption, and finally obtained a good encryption scheme with good encryption effect and security XingyuanWang and Li [23]. Moreover, some researchers have found another new way of thinking to solve many problems that cannot be solved by classical computers against the background of the rapid development of quantum computing and quantum communication Elias Venegas-Andraca [24]; S. Marsh and Wang [25]; Fen Liu et al. [26]; Jing-Yi Dai and Zhou [27]; Ahmed et al. [28]; Alanezi et al. [29]; Ahmed et al. [30]; Nan-Run Zhou et al. [31]; Yulin Ma et al. [32]; Ahmed et al. [28]; Quan Lin et al. [33]. The quantum walk has been widely studied by researchers because of its non-periodicity in addition to the randomness of chaotic systems S. Marsh and Wang [25]. In 2020, Ahmed A. Abdel-Latif et al. proposed a quantum walk-based pseudo-random number generator, which has a good encryption effect in quantum image encryption Ahmed et al. [28]. In 2021, Bassem Abd-El-Atty et al designed a variety of new image encryption schemes using quantum walks A. Alanezi et al. [29]; Bassem Abd-El-Atty and El-Latif [34]; Ahmed et al. [30]. On the basis of various scholars, this paper uses the randomness and aperiodicity of quantum walks in two-dimensional space to propose an image encryption scheme combining zigzag and 3-D Rubik’s cube transformation under a two-dimensional quantum walk for the first time. The scheme not only uses the strong randomness of the quantum walk but also fully combines the zigzag scrambling transform and Rubik’s cube-like azimuth-level image encryption and achieves the expected image encryption effect. The organization of this paper is roughly arranged as follows: the introduction and arrangement of relevant knowledge are shown in Section 2, the third part is the experimental verification and analysis of the scheme; the experimental verification and analysis of the scheme are shown in Section 4; and finally, Section 5 shows a conclusion and provides the future of the scheme outlook for work and vision.

2 Preliminaries

2.1 Two-dimensional quantum walk

Quantum walk, which is known as quantum random walk, is the manifestation of particle random walk under quantum mechanics. Quantum walks can now be divided into two categories—continuous quantum walks and discrete quantum walks. This study uses discrete quantum walks. The Hilbert space H of the discrete quantum walk is mainly composed of the coin register space H_coin and the position state register space H_post tensors. The quantum walk process on the two-dimensional Hilbert space can be divided into two steps: the first is to determine the coin operator $\bar{C}$ used to represent the state of the coin and then the transfer operator $\bar{S}$ is used to determine the direction of one-step walking; this process can be dynamically expressed as a process in which a unitary operator $\bar{U}$ acts repeatedly in the superposition state.

$\bar{U}=\bar{S}\left(\bar{C}\otimes \bar{I}\right),(1)$

where $\bar{U}$ is a unitary operator, $\bar{S}$ is the transfer operator, $\bar{C}$ is the coin operator, and $\bar{I}$ is the identity gate which is shown as the identity matrix. The coin operator can usually be expressed as

$\bar{C}=\left(\begin{array}{cc}\hfill \cos \sigma \hfill & \hfill \sin \sigma \hfill \\ \hfill -\sin \sigma \hfill & \hfill \cos \sigma \hfill \end{array}\right),(2)$

where we choose the $\sigma =\frac{\pi }{4}$, and $\bar{C}$ is the Hadamard operator.

The transfer operator, also known as the offset operator, determines the offset of the superposition state. When the spin of the coin state is upward (that is, $\left|0⟩\right.$), the superposition state advances one unit in the positive direction; on the contrary, when the spin of the coin state is downward (that is, $\left|1⟩\right.$), the superposition state advances one unit in the opposite direction.

$\bar{S}=\left|1⟩⟨\left.1\right|\right.\otimes \sum \left|n-1⟩⟨\left.n\right|\right.+\left|0⟩⟨\left.0\right|\right.\otimes \sum \left|n+1⟩⟨\left.n\right|\right.(3)$

In a quantum walk on a two-dimensional lattice, H_post is determined by the positional state $\left\{\left|M,N⟩|M,N\in Z\right.\right\}$ tensor, so the unitary operator repeatedly acting on the superposition state can be expressed as

$\bar{U}={\bar{S}}_{Y,X}\left(\bar{H}\otimes \bar{I}\right),(4)$

${\bar{S}}_{Y,X}=\frac{1}{2}\left({\bar{S}}_X+{\left(-1\right)}^n{\bar{S}}_X\right)+\frac{1}{2}\left({\bar{S}}_Y+{\left(-1\right)}^{n+1}{\bar{S}}_Y\right),(5)$

${\bar{S}}_X=\left|1⟩⟨\left.1\right|\right.\otimes \sum _{M,N\in Z}\left|M-1,N⟩⟨\left.M,N\right|\right.+\left|0⟩⟨\left.0\right|\right.\otimes \sum _{M,N\in Z}\left|M+1,N⟩⟨\left.M,N\right|\right.(6)$

${\bar{S}}_Y=\left|1⟩⟨\left.1\right|\right.\otimes \sum _{M,N\in Z}\left|M,N-1⟩⟨\left.M,N\right|\right.+\left|0⟩⟨\left.0\right|\right.\otimes \sum _{M,N\in Z}\left|M,N+1⟩⟨\left.M,N\right|\right.(7)$

When the number of steps the particle walks is odd, ${\bar{S}}_Y$ acts on the superposition state; when the coin state is $\left|1⟩\right.$, the position state is one step forward in the negative direction of the Y-axis; and when the coin state is $\left|0⟩\right.$, the position state is one step forward in the positive direction of the Y-axis. On the contrary, when the number of steps taken by the particle is an even number, ${\bar{S}}_X$ acts on the superposition state; when the coin state is $\left|0⟩\right.$, the walker moves towards the positive X-axis. The direction is one step forward. When the coin state is $\left|1⟩\right.$, the position state is one step forward in the negative direction of the X -axis. Assuming that the initial state is φ_ini, the superposition state after the particle walks n steps is φ_n. Measuring the possibility of the superposition state of each point, we can get the probability matrix $P\left(Y,X,n\right)$.

$P\left(Y,X,n\right)=\sum _{\mathit{coin}}{\left|⟨y,x,coin|{\bar{U}}^n|{\phi }_{\mathit{inti}}⟩\right|}^2={\left|⟨y,x,0|{\bar{U}}^n|{\phi }_{\mathit{inti}}⟩\right|}^2+{\left|⟨y,x,1|{\bar{U}}^n|{\phi }_{\mathit{inti}}⟩\right|}^2.(8)$

2.2 Controlled zigzag transform

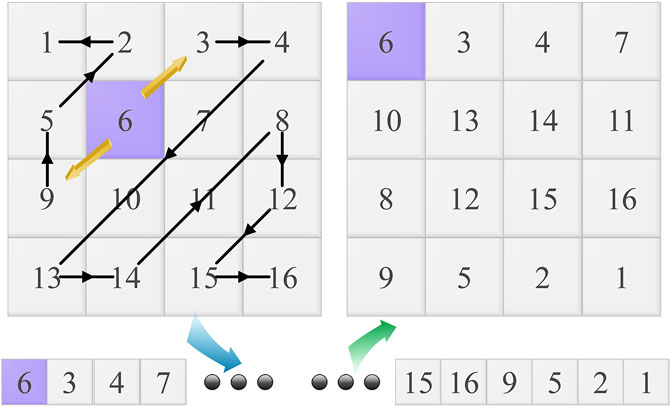
As a method of scanning and scrambled transformation, zigzag scrambling transformation means that the elements in the zigzag scrambling scanned image matrix are first saved in a one-dimensional array, and then they are rearranged into a two-dimensional matrix based on fixed rules. The order of the classic zigzag scrambling transform scan is zigzag from the upper left corner to the bottom right corner.

In order to make the scrambling effect better to overcome the periodicity of the traditional zigzag transformation, this paper proposes the zigzag transformation which is under the two-dimensional quantum walk (as shown in Figures 1, 2): the initial position of the zigzag transformation is determined by the quantum walk. The random sequence generated by the walk is determined, and the upper-right corner and upper-left corner of the pixel are zigzag scanning and stored in two sets of one-dimensional arrays in turn, and then the upper-right corner array is in front of the lower-left corner array and a new one-dimensional array is formed in the back, in a certain order.

FIGURE 1

FIGURE 1. Zigzag scrambling transform principle.

FIGURE 2

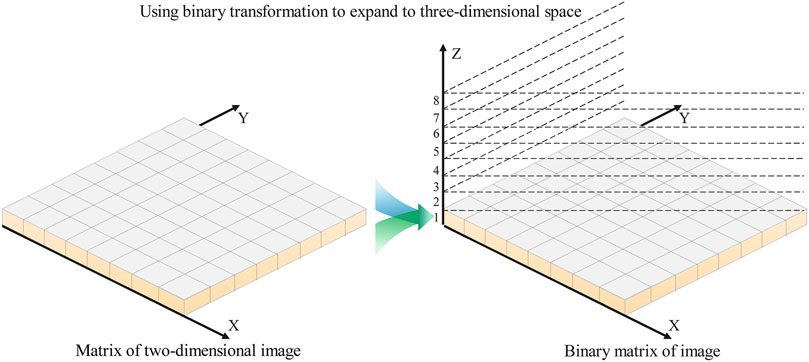
FIGURE 2. The bitwise expansion of a two-dimensional decimal matrix extended to a three-dimensional space to construct an eighth-order Rubik’s cube-like.

2.3 Rubik’s cube-like transform

The Rubik’s cube, also known as the magic cube, was first proposed by foreign scholar Erno Rubik and has been widely used in mechanical engineering; later, it entered everyone’s daily life as an educational toy for developing intelligence. Each layer of the Rubik’s cube can be rotated arbitrarily, and the more the betweenness, the more the rotation methods. By rotating the blocks of each layer, there will be a positional offset, and the Rubik’s cube can be restored by using the same reverse rotation. Based on this idea, we expand the image map like an eighth-order Rubik’s cube; the layers of the Rubik’s cube are selected through the random sequence obtained by the quantum walk, and the Rubik’s cube is rotated in a certain way to complete the pixel-value calculation. Also, the bit-level scrambling improves the security and confidentiality of image information.

$I_{0-255}={\left\{I_{8,}{I}_7,I_6{I}_5,I_4,I_3,I_2,I_1\right\}}_{\mathrm{0,1}},(9)$

$\left[\begin{array}{c}\hfill Y^{\prime }\hfill \\ \hfill X^{\prime }\hfill \end{array}\right]=ROTE\left(\theta \right)\left[\begin{array}{c}\hfill Y\hfill \\ \hfill X\hfill \end{array}\right],(10)$

$ROTE\left(\theta \right)=\left[\begin{array}{cc}\hfill \cos \theta \hfill & \hfill -\sin \theta \hfill \\ \hfill \sin \theta \hfill & \hfill \cos \theta \hfill \end{array}\right]=\cos \theta \left[\begin{array}{cc}\hfill 1\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 1\hfill \end{array}\right]+\sin \theta \left[\begin{array}{cc}\hfill 0\hfill & \hfill -1\hfill \\ \hfill 1\hfill & \hfill 0\hfill \end{array}\right]=\exp \left(\theta \left[\begin{array}{cc}\hfill 0\hfill & \hfill -1\hfill \\ \hfill 1\hfill & \hfill 0\hfill \end{array}\right]\right).(11)$

3 Methods

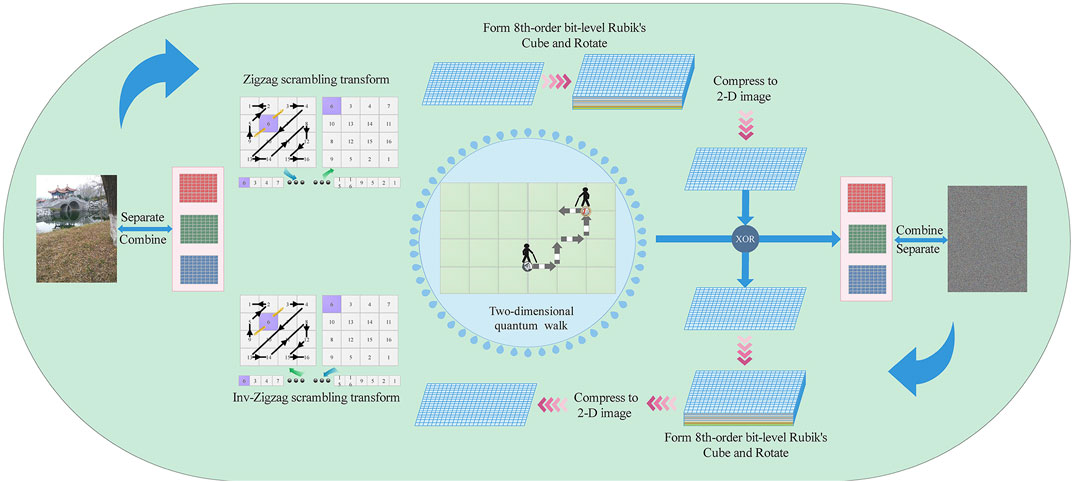
In this article, taking advantage of the chaotic and aperiodic characteristics of the quantum walk, a new image encryption scheme is proposed under the two-dimensional quantum walk, combining zigzag scrambling transformation with random position as the starting point and bit-level scrambling encryption of a 3-D Rubik’s cube rotation (the general content of the scheme is demonstrated in Figure 3).

FIGURE 3

FIGURE 3. Encryption algorithm under a 2-D quantum walk.

3.1 Image encryption

In this scheme, the color digital image is encrypted by combining the novel zigzag transform and 3-D Rubik’s cube under the two-dimensional quantum walk, as demonstrated in Figure 3. The specific steps of the encryption scheme are as follows.

Step 1: The color image I^color is separated to obtain three single-channel sub-images I^R, I^G, and I^B:

$I^{color}\stackrel{split}{\to }\left\{I^R,I^G,I^B\right\}.(12)$

Step 2: The information of the single-channel sub-image is analyzed, especially the size information of the image $I^R\left(M,N\right),I^G\left(M,N\right),I^B\left(M,N\right)$.

Step 3: Using the alternating random walk of parameters A and B obtained by calculating the hash value of the image on the two-dimensional grid, the probability matrix in the two-dimensional space is obtained (the size is the same as that of the processed single-channel sub-image matrix).

$P\left(Y,X,n\right)=\sum _{\mathit{coin}}{\left|⟨y,x,coin|{\bar{U}}^n|{\phi }_{\mathit{inti}}⟩\right|}^2={\left|⟨y,x,0|{\bar{U}}^n|{\phi }_{\mathit{inti}}⟩\right|}^2+{\left|⟨y,x,1|{\bar{U}}^n|{\phi }_{\mathit{inti}}⟩\right|}^2.(13)$

Step 4: The conversion probability matrix p is the control sequence Q1 and Q2 is to control the zigzag transformation (the sequence Q1 represents the initial row number position of the zigzag transformation, and the sequence Q2 represents the initial column number position of the zigzag transformation).

$Q1=fix\left(P\times {10}^{10}\right)modM(14)$

$Q2=fix\left(P\times {10}^{10}\right)modN.(15)$

Step 5: The initial position of the square matrix is determined according to the control sequence Q1 and Q2, and the iterative zigzag transformation is performed.

Step 6: Binary conversion is performed on the pixel matrix to obtain sub-bit-level images of each sub-image. The bit-level images of the image square matrix form an eighth-order Rubik’s cube-like F, and each binary bit represents a small cube.

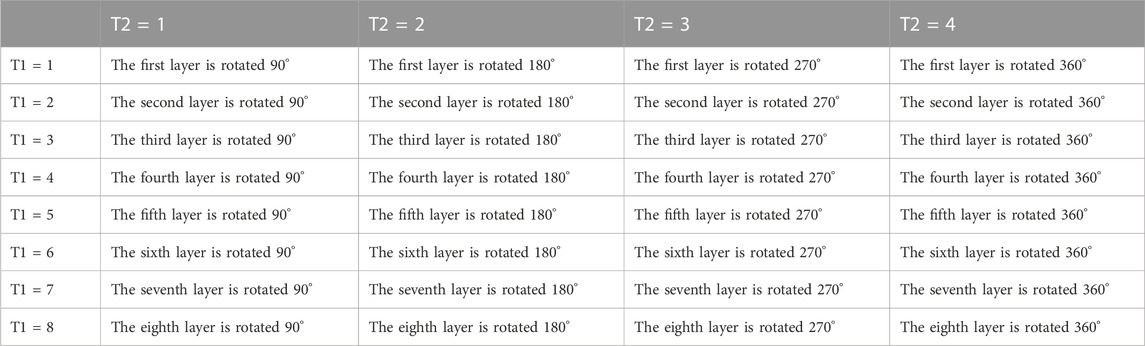
Step 7: The matrix p obtained by the quantum walk is converted into control sequences T1 and T2 to control the rotation of the Rubik’s cube-like. The way of the Rubik’s cube-like is shown in Table 1.

$T1=fix\left(P\times {10}^{12}\right)mod8+1,(16)$

$T2=fix\left(P\times {10}^{12}\right)mod4+1,(17)$

$F\prime \left(T1,T2\right)=SELETE\left[F,T1,ROTE\left(\frac{\pi }{2}\ast T2\right)\right].(18)$

Note: F′ = SELETE [F, ∂, ROTE(β)] means to select the Rubik’s cube’s ∂ layer and rotate β counterclockwise. F denotes the class tesseract composed of the original expansion, T1 denotes the sequence of selected tesseract layers, T2 is the parameter of rotation angle, and F′ denotes the result after rotation.

TABLE 1

TABLE 1. Eighth-order Rubik’s cube rotation mode.

Step 8: Each matrix is compressed into a two-dimensional image (convert the pixel value into decimal), and the bitwise circular principle of the Rubik’s cube is used to perform a circular shift L on the pixel value according to the control sequence T2 to obtain sub-images R, G, and B.

$L=3\ast T2.(19)$

Step 9: The probability matrix obtained by the quantum walk is converted into an encrypted matrix T3 and bitwise XOR processing on sub-images R, G, and B is performed to obtain encrypted sub-images R_EN, G_EN, and B_EN.

$T3=fix\left(P\times {10}^{12}\right)mod256,(20)$

$\left\{\begin{array}{c}\hfill R_{EN}=R\oplus T3\hfill \\ \hfill G_{EN}=G\oplus T3\hfill \\ \hfill B_{EN}=B\oplus T3\hfill \end{array}\right.(21)$

3.2 Decryption algorithm

This scheme belongs to a type of symmetric encryption. The decryption process is the inverse process of the encryption process. Here, we will not expand it in detail and provide a brief description of the steps:

Step 1: The encrypted image is separated into three channels, the quantum walk with the same parameters is used to generate a probability matrix, it is converted to obtain an encrypted matrix T3, and bitwise XOR is performed with each single-channel image.

$P\left(Y,X,n\right)={\left|⟨y,x,0|{\bar{U}}^n|{\phi }_{\mathit{inti}}⟩\right|}^2+{\left|⟨y,x,1|{\bar{U}}^n|{\phi }_{\mathit{inti}}⟩\right|}^2,(22)$

$T3=fix\left(P\times {10}^{12}\right)mod256,(23)$

$\left\{\begin{array}{c}\hfill \acute{R}=R_{EN}\oplus T3\hfill \\ \hfill \acute{G}=G_{EN}\oplus T3\hfill \\ \hfill \acute{B}=B_{EN}\oplus T3\hfill \end{array}\right.(24)$

Step 2: The probability matrix p obtained by the quantum walk is converted into control sequence T3, T3 is inverted to obtain sequence T4, and a reverse cyclic shift L′ is performed on the pixel value according to T5.

$T3=fix\left(P\times {10}^{12}\right)mod4+1,(25)$

$L^{\prime }=3\ast T4.(26)$

Step 3: The pixel values are converted into binary bits to form an eighth-order Rubik’s cubes-like $\breve{F}$.

Step 4: The probability matrix p obtained by the quantum walk is converted into control sequences T2 and T3, T2 and T3 are inverted to obtain sequences T5 and T6, and they are used to control the Rubik’s cube inversely.

$T2=fix\left(P\times {10}^{12}\right)mod8+1,(27)$

$T3=fix\left(P\times {10}^{12}\right)mod4+1,(28)$

$\breve{F^{\prime }}\left(T5,T6\right)=SELETE\left[\breve{F},T5,\breve{ROTE}\left(\frac{\pi }{2}\times T6\right)\right].(29)$

Note: $\breve{F^{\prime }}=SELETE[\breve{F},\partial ,\breve{ROTE}(\beta )]$ means to select the Rubik’s cube’s ∂ layer and rotate β counterclockwise.

Step 5: According to the conversion probability matrix p as the control sequence Q1 and Q2 performed the inverse zigzag transformation to obtain the sub-image.

$Q1=fix\left(P\times {10}^{10}\right)modM,(30)$

$Q2=fix\left(P\times {10}^{10}\right)modN.(31)$

Step 6: The three sub-images are combined to obtain a color image I_m.

4 Results and analysis

Aiming at the periodic characteristics of traditional color image chaotic encryption systems, this paper proposes an image encryption scheme combining a zigzag scrambling transform and 3-D Rubik’s cube under the quantum walk. To verify that this encryption scheme has a good encryption effect, experiments were carried out with color images of different sizes, and histogram analysis, information entropy analysis, correlation analysis, key security analysis, and anti-jamming analysis were carried out. The initial parameters used to perform a two-dimensional quantum walk are N = 600, T = 800, α, and β obtained from the hash value of the image.

4.1 Experiment results

To illustrate the encryption effect of the image, we encrypted and decrypted multiple images of different sizes, and the experimental results are shown in Figure 4. From this, we can see that the encrypted image has changed significantly, and no information can be obtained visually. The decrypted image restores the information elements it had before.

FIGURE 4

FIGURE 4. Experiment results: (A) is the encryption and decryption result of the bridge of size 1,440⋅1,080, (B,C) stand for the encryption and decryption result of the baboon of size 512⋅512, and the encryption and decryption result of the house whose size is 512⋅512.

4.2 Histogram distribution analysis

The histogram can visually represent the statistical information of the image, reflecting the distribution of each gray value in the image. A good image encryption algorithm should have a good histogram distribution. In this study, the histogram experiment is performed on the original image and the encrypted image, and the results are shown in Figure 5.

FIGURE 5

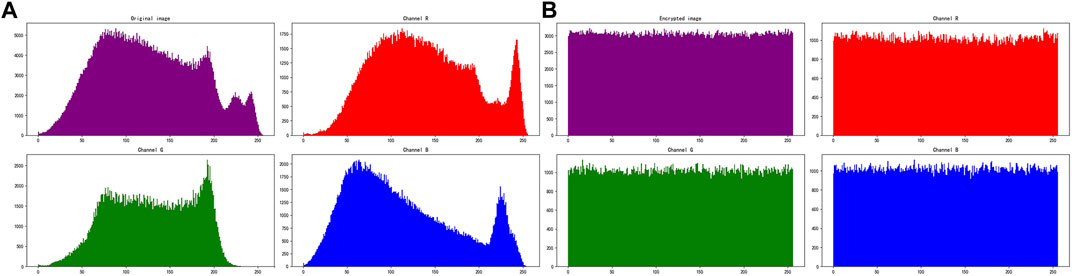
FIGURE 5. Histogram distribution of Baboon: (A) is original image’s histogram, and (B) is encrypted image’s histogram.

According to the experimental results, we found that the histogram distribution of the original image is uneven, while the histogram distribution of the encrypted image is uniform. It is difficult for an attacker to crack the transformation relationship between the plaintext image and the encrypted image through statistical analysis.

4.3 Information entropy analysis

Information entropy is mainly used to describe the complexity of objects and is often used in the field of images to measure the degree of the chaos of images. The degree of diffusion of pixels in each gray level of the image’s three channels is calculated to obtain the information entropy value of the different signal-color channels, the larger the value is, the more uniform the pixel distribution is, the stronger the randomness is, and the better the performance is against statistical attacks. The calculation method of information entropy can be expressed as

$H\left(p_i\right)=-\sum _{i=0}^{L}P\left(p_i\right){\log }_{2}P\left(p_i\right),(32)$

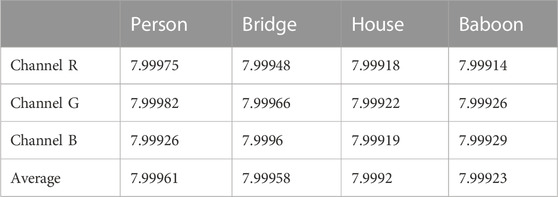
where L = 2⁸–1 = 255 indicates the possible grayscale values, p_i represents the pixel values, p (p_i) represents the possibility that the pixel value is p_i, and the H (p_i)’s ideal value is 8. Therefore, the closer the information entropy value is to eight, the more evenly distributed it is, and the better the encryption effect. We calculated the information entropy value of the encrypted image and compared it with other encryption algorithms. The experimental results are shown in Tables 2, 3. From Table 2, we can see that our information entropy reaches about 7.999, indicating that the image has a good distribution and the encryption scheme has a strong capability to resist statistical analysis.

TABLE 2

TABLE 2. Information entropy of three channels.

TABLE 3

TABLE 3. Information entropy of different encryption schemes.

4.4 Correlation analysis

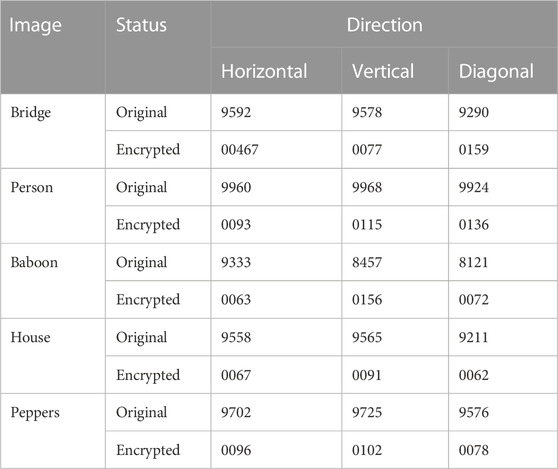
Correlation stands for the degree of intimacy of the relationship between two or more element variables. For color images, correlation represents the degree of closeness between adjacent pixels in each color channel; traditional color digital images have a strong correlation and are vulnerable to external analysis attacks, while the encrypted image is less relevant, and the lower the correlation is, the more outstanding the encryption effect of the image encryption scheme is. We randomly selected 3,000 pairs of adjacent pixels in color and encrypted images for horizontal, vertical, and diagonal experimental calculations, and the experimental results are shown in Tables 4, 5; Figure 6. Correlation is calculated as follows:

$D\left(p_x\right)=\frac{1}{N}\sum _{i=1}^N\left(p_{xi}-\frac{1}{N}\sum _{i=1}^N{p}_{xi}\right)2,(33)$

$ccov\left(p_x,p_y\right)=\frac{1}{N}\sum _{i=1}^N\left(p_{xi}-\frac{1}{N}\sum _{i=1}^N{p}_{xi}\right)\left(p_{yi}-\frac{1}{N}\sum _{i=1}^N{p}_{yi}\right),(34)$

$R_{XY}=\frac{ccov\left(p_x,p_y\right)}{\sqrt{D(p_x)}\sqrt{D(p_y)}}.(35)$

TABLE 4

TABLE 4. Image correlation.

TABLE 5

TABLE 5. Value of NPCR and UACI.

FIGURE 6

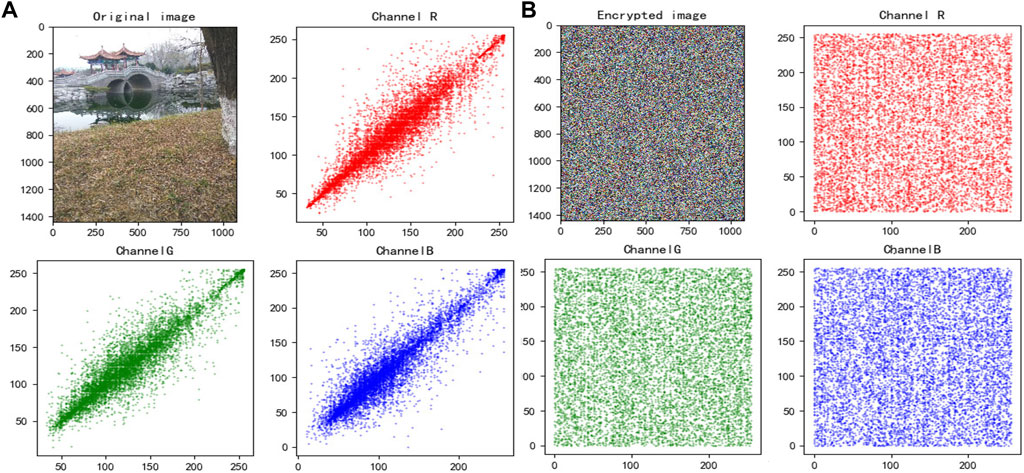
FIGURE 6. Bridge’s correction: (A) is original image’s correction, and (B) is encrypted image’s correction.

From the experimental test of correlation, we found that the pixel distribution of the color image before encryption is linearly correlated and the correlation coefficient is close to one, while the pixel distribution of the encrypted image is uniformly tiled and the correlation coefficient is close to zero. It shows that the color image has a strong correlation, and the adjacent pixels of the encrypted image is irrelevant and have an excellent capability to resist statistical analysis.

4.5 Key security analysis

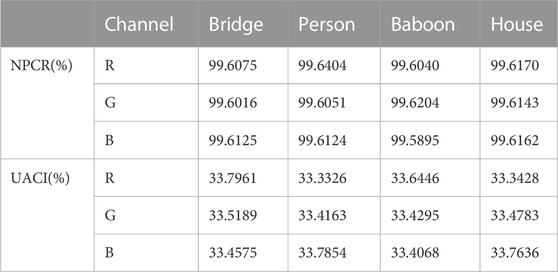
The security of the key is extremely essential in image encryption, which is reflected in the following two parts: one is a large enough key space, the bigger/broader the key space is, the stronger the key’s capacity of resistance to the brute force search is; the other is the key sensitivity: the more sensitive the key, the stronger the ability to be resistant to the brute force search attacks is. This study uses a two-dimensional alternating quantum walk with four parameters (N, T, α, and β) to obtain the key, where α and β are obtained from measuring the hash value of the image, so the encryption scheme has a large enough key space: 10¹⁶∗10¹⁶∗2^16∗8∗2^16∗8 = 10³²∗2²⁵⁶, which can resist various traditional brute force search attacks. To verify that the scheme has a sufficiently sensitive key, we measure the NPCR and UACI values between encrypted images before and after the key parameter change is calculated by changing a parameter (or bit) in the key. The calculation formulas of NPCR and UACI are as follows:

$T\left(i,j\right)=f\left(x\right)=\left\{\begin{array}{c}\hfill 0\begin{array}{cc}\hfill \hfill & \hfill ,C_{\mathit{KEY}}=C_{KE{Y}^{\prime }}\hfill \end{array}\hfill \\ \hfill 1\begin{array}{cc}\hfill \hfill & \hfill ,C_{\mathit{KEY}}\ne C_{KE{Y}^{\prime }}\hfill \end{array}\hfill \end{array}\right.,(36)$

$NPCR=\frac{{\sum }_{i,j}T\left(i,j\right)}{M\ast N}\ast 100,(37)$

$UACI=\frac{\sum \left(C_{\mathit{KEY}}\left(i,j\right)-C_{KE{Y}^{\prime }}\left(i,j\right)\right)}{M\ast N\ast 255}\ast 100,(38)$

where M means the length of the image, N represents the width of the image, C_KEY is the image encrypted with the initial key, and C_KEY’ is the image encrypted with the changed key. We obtained the experimental results as shown in Table 6. As we know, the closer the value of NPCR is to 99.6409%, the closer the value of UACI is to 33.4635%, indicating that the intensity of pixel change is greater, the key is more sensitive, and the encryption scheme is more secure.

TABLE 6

TABLE 6. Value of NPCR and UACI of different schemes.

4.6 Different attack analysis

In the process of information transmission, it will inevitably face interference from the outside world and even attacks. Therefore, an effective image encryption scheme can not only effectively protect the image information but also ensure that the information will not be lost when it is interfered with and attacked. This study conducts experimental tests on common interference and attacks. We not only simulate the encrypted image under different degrees of noise attack, and the experimental results are shown in Figure 7; we also simulate the situation when the encrypted image is subjected to different degrees of occlusion attack, and the experimental results are shown in Figure 8. It can be seen from the figure that we can recover a clearer image, indicating that our proposed scheme has the excellent ability to resist such common attacks.

FIGURE 7

FIGURE 7. Noise attack: (A) is the decryption result of adding 5% salt noise, (B) is the decryption result of adding 5% salt noise, (C) is the decryption result of adding 35% salt noise, and (D) is the decryption result of adding 1% gauss noise.

FIGURE 8

FIGURE 8. Occluded attack: (A) is the result of an experiment that occluded 16% of encrypted images, (B) is the result of an experiment that occluded 25% of encrypted images, (C) is the result of an experiment that occluded 36% of encrypted images, and (D) is the result of an experiment that occluded 49% of encrypted images.

4.7 Time and space complicity analysis

In the proposed image encryption scheme, Z scrambling transform and 3-D Rubik’s cube transform are combined. Assuming that the size of the image to be encrypted is M ⋅ N ⋅ 3, the time cost of a two-dimensional quantum random walk to generate a random sequence with image sensitivity is O (2 ⋅ M ⋅ N); the time complexity of the zigzag scrambling transform is O (T ⋅ M ⋅ N), where T is the sequence length of the selected random position; and the time complexity of a 3-D Rubik’s cube rotation and bitwise XOR processing of the image is O (2 ⋅ M ⋅ N). Therefore, the time complexity of the scheme is O ((4 + T) ⋅ M ⋅ N).

The space complexity of the proposed scheme is O (M ⋅ N). The space complexity of the random sequence key generated by two-dimensional quantum random walk is O (M ⋅ N), the space complexity of pixel space scrambling image obtained by zigzag scrambling transform is O (M ⋅ N), while the space complexity of diffusion encryption is O (M ⋅ N) + O (M ⋅ N) = O (M ⋅ N), and the space complexity of the encryption scheme is O (M ⋅ N) + O (M ⋅ N) + O (M ⋅ N) = O (M ⋅ N).

5 Summary and prospects

This paper proposed an image encryption scheme based on controlled zigzag transform and bit-level encryption under the quantum walk. To be specific, the work introduces the alternating quantum walk in quantum computing as the key generator of the penetration algorithm, improves the classical zigzag transform so that it is controlled by random sequences with non-periodicity, and constructs controlled three-dimensional tesseracts for rotational dislocation encryption in the pixel-value direction by expanding the dimension to achieve the “dislocation-diffusion” structure of the encryption algorithm. It increases the key space of traditional encryption algorithms, enhances key sensitivity, and improves the complexity of the encryption scheme and the ability to resist attacks. Through experimental tests, it is verified that the information entropy value of the encrypted image is about 7.999, the correlation coefficient is close to zero, the pixel distribution is uniform, and it has a good key security, which can effectively resist attacks such as statistical analysis, brute force search, and noise influence. The introduction of the quantum walk and control ideas in this scheme provides a new idea for image encryption. It is undeniable that this study needs to improve encryption efficiency. In the future, we will continue to combine quantum thinking and control thinking with traditional algorithms to design reliable encryption schemes.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

TZ designed the algorithm and verified it by experiment, and SW provided theoretical support.

Funding

This project was supported by the National Natural Science Foundation of China (no. 11975132), the Natural Science Foundation of Shandong Province (no. ZR2021MF049), and the National Natural Science Foundation of China—Shandong Joint Fund (no. ZR202108020011).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Hossein Movafegh Ghadirli AN, Enayatifar R. An overview of encryption algorithms in color images. Signal Process. (2019) 164:163–85. doi:10.1016/j.sigpro.2019.06.010

CrossRef Full Text | Google Scholar

2. Jianfeng Zhao YC, Wang S, Li X. A novel image encryption scheme based on an improper fractional-order chaotic system. Nonlinear Dyn (2015) 80:1721–9. doi:10.1007/s11071-015-1911-x

CrossRef Full Text | Google Scholar

3. Sui L, Gao B. Color image encryption based on gyrator transform and arnold transform. Opt Laser Tech (2013) 48:530–8. doi:10.1016/j.optlastec.2012.11.020

CrossRef Full Text | Google Scholar

4. Nanrun Zhou HLXT, Yan X, Li G, Tao X. Multi-image encryption scheme based on quantum 3d arnold transform and scaled zhongtang chaotic system. Quan Inf Process (2018) 17:338–538. doi:10.1007/s11128-018-2104-6

CrossRef Full Text | Google Scholar

5. Yuxin Shen MX, Tang C, Lei Z. Optical selective encryption based on the frfcm algorithm and face biometric for the medical image. Opt Laser Tech (2021) 138:106911. doi:10.1016/j.optlastec.2020.106911

CrossRef Full Text | Google Scholar

6. Xiaoyong Ji GZ, Sen B, Yan B, Bing Y. Image encryption and compression based on the generalized knight’s tour, discrete cosine transform and chaotic maps. Multimedia Tools Appl (2017) 76:12965–79. doi:10.1007/s11042-016-3684-8

CrossRef Full Text | Google Scholar

7. Gen Liu WJ, Jiang T-F. Color image scrambling based on zigzag transformation. Comput Eng Sci (2013).

Google Scholar

8. Yuzhen Li XJGZSGYTXZKZ, Li X, Wang Z, Zhao G, Ge S, Tian Y, et al. An image encryption algorithm based on zigzag transformation and 3-dimension chaotic logistic map. Appl Tech Inf Security (2015) 557:3–13. doi:10.1007/978-3-662-48683-2_1

CrossRef Full Text | Google Scholar

9. Xingyuan Wang JZ, Cao G, Guanghui C. An image encryption algorithm based on zigzag transform and ll compound chaotic system. Opt Laser Tech (2019) 119:105581. doi:10.1016/j.optlastec.2019.105581

CrossRef Full Text | Google Scholar

10. Wang X, Sun H. A chaotic image encryption algorithm based on zigzag-like transform and dna-like coding. Multimedia Tools Appl (2019) 78:34981–97. doi:10.1007/s11042-019-08085-z

CrossRef Full Text | Google Scholar

11. Vidhya R, Brindha M. A chaos based image encryption algorithm using rubik’s cube and prime factorization process (cierpf). J King Saud University-Computer Inf Sci (2022) 34:2000–16. doi:10.1016/j.jksuci.2019.12.014

CrossRef Full Text | Google Scholar

12. Wang X, Guan N. A novel chaotic image encryption algorithm based on extended zigzag confusion and rna operation. Opt Laser Tech (2020) 131:106366. doi:10.1016/j.optlastec.2020.106366

CrossRef Full Text | Google Scholar

13. Li-Hua Gong JW, Jin D, Zhou N-R. Image encryption scheme based on block scrambling, closed-loop diffusion, and dna molecular mutation. Security Commun Networks (2021) 2021:1–16. doi:10.1155/2021/6627005

CrossRef Full Text | Google Scholar

14. Wang X, Liu C. A novel and effective image encryption algorithm based on chaos and dna encoding. Multimedia Tools Appl (2017) 76:6229–45. doi:10.1007/s11042-016-3311-8

CrossRef Full Text | Google Scholar

15. Abitha KA, and , Bharathan K. Secure communication based on rubik’s cube algorithm and chaotic baker map. Multimedia Tools Appl (2016) 24:782–9. doi:10.1016/j.protcy.2016.05.089

CrossRef Full Text | Google Scholar

16. Al-Hashemy RH, Mehdi SA. A new algorithm based on magic square and a novel chaotic system for image encryption. J Intell Syst (2020) 29:1202–15. doi:10.1515/jisys-2018-0404

CrossRef Full Text | Google Scholar

17. Hegui Zhu YL, Dai L, Wu L. A three-dimensional bit-level image encryption algorithm with rubik’s cube method. Mathematics Comput Simulation (2021) 185:754–70. doi:10.1016/j.matcom.2021.02.009

CrossRef Full Text | Google Scholar

18. Gao X. Image encryption algorithm based on 2d hyperchaotic map. Opt Laser Tech (2021) 142:107252. doi:10.1016/j.optlastec.2021.107252

CrossRef Full Text | Google Scholar

19. Liu H, Kadir A, Xu C. Color image encryption with cipher feedback and coupling chaotic map. Int J Bifurcation Chaos (2020) 30:2050173. doi:10.1142/S0218127420501734

CrossRef Full Text | Google Scholar

20. Wang Y, Song Z, Ma Y, Hua N, Ma H Color image encryption algorithm based on dna code and alternating quantum random walk. Acta Physica Sinica (2021) 70:230302. doi:10.7498/aps.70.20211255

CrossRef Full Text | Google Scholar

21. Jingbo Zhao JJTF, Zhang T, Ma H, Fang T. Color image encryption scheme based on alternate quantum walk and controlled rubik’s cube. Scientific Rep (2022) 12:14253. doi:10.1038/s41598-022-18079-x

CrossRef Full Text | Google Scholar

22. Zhang K, bo Fang J. Color image encryption algorithm based on td-ercs system and wavelet neural network. Math Probl Eng (2015) 2015:1–10. doi:10.1155/2015/501054

CrossRef Full Text | Google Scholar

23. XingyuanWang SL, Li Y. Bit-level image encryption algorithm based on bp neural network and gray code. Multimedia Tools Appl (2021) 80:11655–70. doi:10.1007/s11042-020-10202-2

CrossRef Full Text | Google Scholar

24. Elias Venegas-Andraca S. Quantum walks: A comprehensive review. Quan Inf Process (2012) 11:1015–106. doi:10.1007/s11128-012-0432-5

CrossRef Full Text | Google Scholar

25. Marsh S, Wang JB. Deterministic spatial search using alternating quantum walks. Phys Rev A (2021) 104:022216. doi:10.1103/PhysRevA.104.022216

CrossRef Full Text | Google Scholar

26. Fen Liu P-AXZ-XH, Zhang X, Ma H-Y, He ZX. A quantum dialogue protocol in discrete-time quantum walk based on hyperentangled states. Int J Theor Phys (2020) 59:3491–507. doi:10.1007/s10773-020-04611-0

CrossRef Full Text | Google Scholar

27. Jing-Yi Dai YM, Zhou N-R. Quantum multi-image compression-encryption scheme based on quantum discrete cosine transform and 4d hyper-chaotic henon map. Quan Inf Process (2021) 20:246. doi:10.1007/s11128-021-03187-w

CrossRef Full Text | Google Scholar

28. Ahmed A, Abd El-Latif EM-N, BassemAbd-El-Atty and E.Venegas-Andraca S. Controlled alternate quantum walks based privacy preserving healthcare images in internet of things. Opt Laser Tech (2020) 124:105942. doi:10.1016/j.optlastec.2019.105942

CrossRef Full Text | Google Scholar

29. Alanezi A, Abd-El-Atty B, El-Latif AAA (2021). Quantum multi-image compression-encryption scheme based on quantum discrete cosine transform and 4d hyper-chaotic henon map, 176–81. doi:10.1109/CAIDA51941.2021.9425127

CrossRef Full Text | Google Scholar

30. AhmedAbd El-Latif AAMI, Abd-El-Atty B. An efficient visually meaningful quantum walks-based encryption scheme for secure data transmission on iot and smart applications. Mathematics (2021) 9:3131. doi:10.3390/math9233131

CrossRef Full Text | Google Scholar

31. Nan-Run Zhou X-WX, Zhang T-F, Wu J-Y. Hybrid quantum–classical generative adversarial networks for image generation via learning discrete distribution. Signal Processing: Image Commun (2022) 116891:116891. doi:10.1016/j.image.2022.116891

CrossRef Full Text | Google Scholar

32. Yulin Ma WZSW, Li N, Ma H-Y, Wang S. Image encryption scheme based on alternate quantum walks and discrete cosine transform. Opt Express (2021) 29:28338–51. doi:10.1364/OE.431945

PubMed Abstract | CrossRef Full Text | Google Scholar

33. Quan Lin K-KWLX, Qin H, Xue P, Xiao L. A two-dimensional quantum walk driven by a single two-side coin. Chin Phys B (2020) 29:110303. doi:10.1088/1674-1056/abaee8

CrossRef Full Text | Google Scholar

34. Bassem Abd-El-Atty AMI, El-Latif AAA, Abd El-Latif AA. A multi-image cryptosystem using quantum walks and Chebyshev map. Complexity (2021) 2021:1–16. doi:10.1155/2021/9424469

CrossRef Full Text | Google Scholar