- 1Beijing Academy of Quantum Information Sciences, Beijing, China
- 2Kavli Institute of Nanoscience, Delft University of Technology, Delft, Netherlands
We theoretically investigate the enhancement of the charging power in a Dicke quantum battery which consists of an array of N two-level systems (TLS)coupled to a single mode of cavity photons. In the limit of small N, we analytically solve the time evolution for the full charging process. The eigenvectors of the driving Hamiltonian are found to be pseudo-Hermite polynomials and the evolution is thus interpreted as harmonic oscillator like behaviour. Then we demonstrate the average charging power using a collective protocol is
1 Introduction
Batteries have become ubiquitous in modern technology, supplying power to devices as small as nano-robots and as large as automotive engines. However, the continuing miniaturization technology gradually pushes those traditional batteries into the atomic limit, i.e., the quantum world. This trend, rather than bringing us into an uncontrollable regime, offers the possibility of utilizing quantum properties for investigating and developing more efficient energy manipulations [1–5].
The topic of quantum batteries, started by Alicki and Fannes [6], is aimed at searching for adequate protocols based on quantum coherence and entanglement in order to achieve the efficient charging-discharging energy transfer. In general, a quantum battery is a system possessing discrete energy levels and interacting with external driving and consumption sources in a controllable fashion. The internal energy of a quantum battery is defined as tr [ρHB], with ρ the density matrix describing the state of the battery and HB the battery Hamiltonian (see Section 2). Charging (discharging) of a quantum battery means evolving into a higher (lower) energetic state ρ′ by cyclic operations. From the viewpoint that information is a form of energy, research on quantum batteries intrinsically involves using the notions and techniques of quantum information [7]. Questions like whether entanglement plays a role in speeding up the energy transfer and how does entropy (and related concepts) evolve in specific battery systems are under active research [8–16].
As an answer to these questions, Binder et al. suggested that energy can be deposited into an array of N working qubits with speedup in charging time T such that Tglobal = Tpar/N for the use of a globally entangling charging Hamiltonian compared to a parallel individual protocol [17]. In consequence, the average charging power defined by
Another practical setting for global charging is based on the Dicke model [19], which describes an array of two-level systems (TLS) enclosed in a photon cavity whose frequency is on resonance with the Zeeman splitting of those TLSs. A recent paper shows in the thermodynamic limit (i.e. the number of TLS N ≫ 1), quantum enhancement of charging power is proportional to
2 Model description
The model of a quantum battery, shown in Figure 1A, is an array of two level systems enclosed in a photon cavity. Since there is an equivalence between the ground/excited state of two level system to the spin down/up state of Zeeman splitting, we will refer to these TLSs as spins in the following. Without loss of generality, we set the spin down
where g* is the engineerable electron g-factor, μB is the Bohr magneton constant, and
where the frequency ωa can be tuned by changing the external magnetic field Bz. The initial energy for such a N-spin battery corresponds to be
In this paper, we focus on the time required to flip all spins down state
and the average charging power is
The cavity, as the charger, is set to stay in a single mode of the electromagnetic field. Its internal Hamiltonian reads Hc = ωca†a, with ωc the photon frequency and a†, a the creation and annihilation operators of cavity photons. We assume the cavity has high quality factor and the leakage of photons can be ignored. As the flipping duration is short enough, the relaxation and dephasing effect of TLS can also be safely neglected. Moreover, we assume that by tuning the external magnetic field Bz, the Zeeman splitting of the spins is on resonance with the cavity photons, i.e., ωc = ωa. Originating from magnetic dipole interactions, the coupling between the cavity photons and spins is modeled as the Dicke interaction Hint = g (a†+a) (S++S−), where
Here λ(t) is a time-dependent coupling signal set to be 1 during the charging period [0, τ] and 0 otherwise, as illustrated in Figure 1B. Before t = 0 there is no coupling between photons and spins, and the cavity is assumed to stay in a n-photon Fock state
At t = 0+ the coupling is turned on. Driven by the Dicke Hamiltonian (6) energy starts to be transferred from cavity photons to battery spins. The coupling is kept constant during this charging period t ∈ [0, τ] and shall be switched off at t = τ. The quantum state of the total system will then be static again with the battery spins expected to be fully flipped up. Similar process of start and pause of swapping has been achieved with high fidelity in recent experiment setup consists of superconducting quantum circuit within which multi qubits were inter-connected by the photon cavity [23].
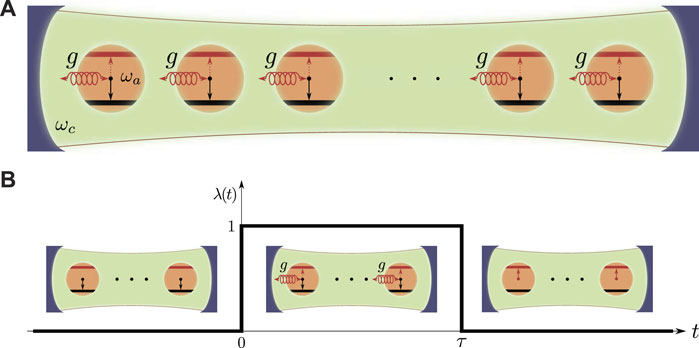
FIGURE 1. (A) Schematic representation of a Dicke quantum battery as an array of identical two level systems with energy splitting ℏωa. The ground state (black bar) and excited state (red bar) are equivalent to the states of spin down and up (see arrows). The batteries are charged inside a single cavity (green background) of photonic mode ωc and g is the coupling constant among TLSs and cavity photons. (B) Initially the coupling signal λ is set to be 0 and the batteries are prepared in the ground state. The coupling is switched on at time t =0+ and maintained as constant g for a period of τ. Then we turn off the coupling and the charging process therefore stops. Energy is transferred from cavity photons into the batteries whose final states are expected to be fully charged (all spins up).
In typical experiment settings, the coupling constant g is much smaller than cavity energy ωc so that the Dicke interaction can be simplified using the rotating wave approximation which results in the Tavis-Cumming Hamiltonian [24].
We point out four prominent properties of this charging protocol. I) When the photon frequency is on resonance with Zeeman energy, we have [H, a†a+Sz] = 0, i.e. the “excitation number” is conserved during the evolution. For example if we have 3 spins inside the cavity, the initial state can be denoted as
3 Collective charging of a Dicke quantum battery
We calculate the time of flipping the spins in Schrödinger picture by analytically solving the matrix representation of the charging Hamiltonian (8). Due to the conservation of excitation number, the quantum states of such charger-battery system flipping from
where each element
The charging Hamiltonian can be diagonalized as
Disregarding the common factor
with each of the column entries
The characteristic polynomials Pk(ξ) obey the recursion relation,
They are orthogonal to each other and alternating between even and odd parity. Actually, as the number of spins N approaches the thermodynamic limit, these polynomials converge into the Hermite polynomials. In particular, ξ = 0, 1, … , N so we have N−2ξ = N, N−1, … , − N. If we let N−2ξ = Nx, then the x goes from 1 to −1 in discrete steps and the recursion relation (13) reads
whose corresponding Rodrigues’ formula is
Eq. 14 is just the scaled version of the standard Hermite polynomials whose Rodrigues’ formula is
Equipped with the eigenvalues (10) and eigenvectors (11) of
can be rephrased into two algebraic equations with even and odd number of spins respectively. For odd numbers of spins N = 2m + 1, the algebraic formula corresponding to Eq. 16 is
One see that if
such that the left-hand side of Eq. 17 becomes
So in case N is odd, the flip duration
Similar to the odd-spin case, for
such that the left-hand side of Eq. 18 becomes
Thus in case N is even, the flip duration is also given by
Based on the above analysis, we now claim that if the time of flipping N spins equals
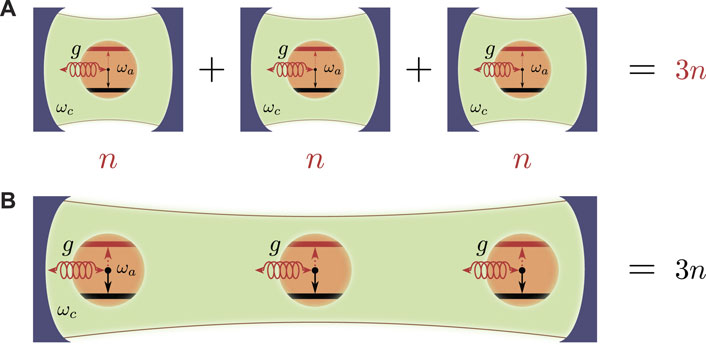
FIGURE 2. (A) Individually charging three spins in a parallel protocol. Each cavity is filled with n photons and in total 3n number of photons are used. (B) The three spins are collectively charged inside a single cavity. To make a fair comparison the same amount of photons should be provided as in the parallel protocol.
4 Quantum speedup originating from coherent cooperative interactions
In order to understand the origin of the speedup effect described in previous section, we first calculate the quantum speed limit (QSL) which forms the lower bound of the evolution duration that could possibly be achieved by corresponding Hamiltonian. For the parallel protocol, its energy variance reads
For collective charging, the energy variance for the same number of charging photons is
We see that due to the collective effect, the quantum speed limit has also been pushed down by a factor of
By taking partial trace of the density matrix of the collectively charged spins, we calculate and plot the development of entanglement during the evolution. As shown in Figure 3, no entanglement develops during the flipping process. Upon detailed numerical inspection, one finds all spins process exactly in step, i.e., follow the same evolution. This result differs from the conclusion of Ref. [20], which states that long-range entangling interactions among the spins will be formed due to the mediation of the common photon field inside the cavity. We have thus found an example where it is not the globally entangling operations that lead to the enhancement of charging. This raises the question for what is the source of quantum speedup in our model, if there is no entanglement involved.
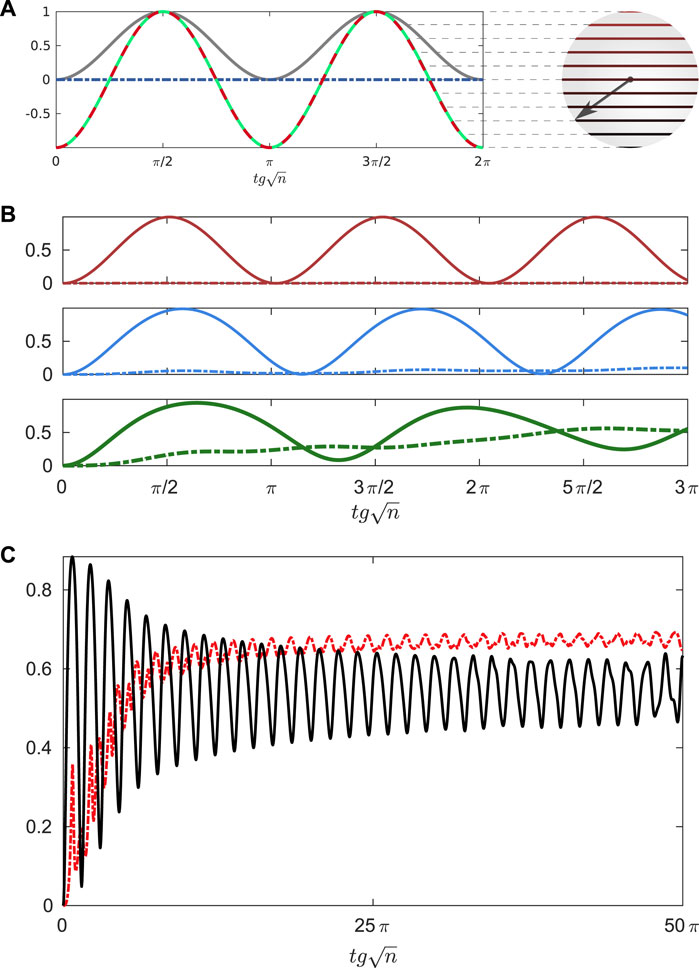
FIGURE 3. (A) The evolution of 10 spins under the 104 cavity driving photons with the charging Hamiltonian Eq. 8. The gray curve stands for the energy deposited into each battery
To answer this question we symbolically solve the von Neumann equation with Hamiltonian Eq. 8
Here j = 1, 2, … , N numbers the spins inside the cavity. Solving the dynamic equation for operator a(t) one finds
Substituting these expressions back into Eq. 21 we obtain the equation of motion for a single spin
Equation 23 shows that by integrating out the photon field, the effective force applied on an arbitrary spin j is proportional to
This final form explicitly shows the coupling strength of each spin has been increased by
As argued by Binder et al. quantum speedup originates from two different sources. One is the reduction of path length between initial and final state in projected Hilbert space
5 Conclusion and discussion
We have studied the energy transfer efficiency of an ideal Dicke quantum battery within the limit N/n ≪ 1. Under the constraint of full charging, we predicted a
Although the Dicke battery presented here only shows ‘half’ the amount of speedup (factor
Future work could focus on adding entangling interactions between the spins in order to further explore the remaining
Data availability statement
The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author.
Author contributions
This work is conducted by XZ under the supervisor MB.
Funding
This work was supported by China Postdoctoral Science Foundation, Grant No. 2022M710402.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
1. Crescente A, Carrega M, Sassetti M, Ferraro D. Charging and energy fluctuations of a driven quantum battery. New J Phys (2020) 22:063057. doi:10.1088/1367-2630/ab91fc
2. Caravelli F, Coulter-De Wit G, García-Pintos LP, Hamma A. Random quantum batteries. Phys Rev Res (2020) 2:023095. doi:10.1103/PhysRevResearch.2.023095
3. Barra F. Dissipative charging of a quantum battery. Phys Rev Lett (2019) 122:210601. doi:10.1103/PhysRevLett.122.210601
4. Liu J, Segal D, Hanna G. Loss-free excitonic quantum battery. The J Phys Chem C (2019) 123:18303–14. doi:10.1021/acs.jpcc.9b06373
5. Ghosh S, Chanda T, Sen(De) A. Enhancement in the performance of a quantum battery by ordered and disordered interactions. Phys Rev A (2020) 101:032115. doi:10.1103/PhysRevA.101.032115
6. Alicki R, Fannes M. Entanglement boost for extractable work from ensembles of quantum batteries. Phys Rev E (2013) 87:042123. doi:10.1103/PhysRevE.87.042123
7. Goold J, Huber M, Riera A, del Rio L, Skrzypczyk P. The role of quantum information in thermodynamics–a topical review. J Phys A: Math Theor (2016) 49:143001. doi:10.1088/1751-8113/49/14/143001
8. Giovannetti V, Lloyd S, Maccone L. The role of entanglement in dynamical evolution. Europhys Lett (2003) 62:615–21. doi:10.1209/epl/i2003-00418-8
9. Borras A, Zander C, Plastino AR, Casas M, Plastino A. Entanglement and the quantum brachistochrone problem. Europhys Lett (2008) 81:30007. doi:10.1209/0295-5075/81/30007
10. dos Santos EM, Duzzioni EI. Elucidating dicke superradiance by quantum uncertainty. Phys Rev A (2016) 94:023819. doi:10.1103/PhysRevA.94.023819
11. Henao I, Serra RM. Role of quantum coherence in the thermodynamics of energy transfer. Phys Rev E (2018) 97:062105. doi:10.1103/PhysRevE.97.062105
12. Andolina GM, Farina D, Mari A, Pellegrini V, Giovannetti V, Polini M. Charger-mediated energy transfer in exactly solvable models for quantum batteries. Phys Rev B (2018) 98:205423. doi:10.1103/PhysRevB.98.205423
13. Andolina GM, Keck M, Mari A, Campisi M, Giovannetti V, Polini M. Extractable work, the role of correlations, and asymptotic freedom in quantum batteries. Phys Rev Lett (2019) 122:047702. doi:10.1103/PhysRevLett.122.047702
14. Andolina GM, Keck M, Mari A, Giovannetti V, Polini M. Quantum versus classical many-body batteries. Phys Rev B (2019) 99:205437. doi:10.1103/PhysRevB.99.205437
15. Julià-Farré S, Salamon T, Riera A, Bera MN, Lewenstein M. Bounds on the capacity and power of quantum batteries. Phys Rev Res (2020) 2:023113. doi:10.1103/PhysRevResearch.2.023113
16. Zhang XM, Cui ZW, Wang X, Yung MH. Automatic spin-chain learning to explore the quantum speed limit. Phys Rev A (2018) 97:052333. doi:10.1103/PhysRevA.97.052333
17. Binder FC, Vinjanampathy S, Modi K, Goold J. Quantacell: Powerful charging of quantum batteries. New J Phys (2015) 17:075015. doi:10.1088/1367-2630/17/7/075015
18. Le TP, Levinsen J, Modi K, Parish MM, Pollock FA. Spin-chain model of a many-body quantum battery. Phys Rev A (2018) 97:022106. doi:10.1103/PhysRevA.97.022106
19. Dicke RH. Coherence in spontaneous radiation processes. Phys Rev (1954) 93:99–110. doi:10.1103/PhysRev.93.99
20. Ferraro D, Campisi M, Andolina GM, Pellegrini V, Polini M. High-power collective charging of a solid-state quantum battery. Phys Rev Lett (2018) 120:117702. doi:10.1103/PhysRevLett.120.117702
21. Emary C, Brandes T. Chaos and the quantum phase transition in the dicke model. Phys Rev E (2003) 67:066203. doi:10.1103/PhysRevE.67.066203
22. Wolfe E, Yelin SF. Certifying separability in symmetric mixed states of n qubits, and superradiance. Phys Rev Lett (2014) 112:140402. doi:10.1103/PhysRevLett.112.140402
23. Wang Z, Li H, Feng W, Song X, Song C, Liu W, et al. Controllable switching between superradiant and subradiant states in a 10-qubit superconducting circuit. Phys Rev Lett (2020) 124:013601. doi:10.1103/PhysRevLett.124.013601
24. Soykal OO, Flatté ME. Strong field interactions between a nanomagnet and a photonic cavity. Phys Rev Lett (2010) 104:077202. doi:10.1103/PhysRevLett.104.077202
25. Holstein T, Primakoff H. Field dependence of the intrinsic domain magnetization of a ferromagnet. Phys Rev (1940) 58:1098–113. doi:10.1103/PhysRev.58.1098
26. Kozierowski M, Mamedov AA, Chumakov SM. Spontaneous emission by a system of n two-level atoms in terms of the su(2)-group representations. Phys Rev A (1990) 42:1762–6. doi:10.1103/PhysRevA.42.1762
27. Chumakov SM, Klimov AB, Sanchez-Mondragon JJ. General properties of quantum optical systems in a strong-field limit. Phys Rev A (1994) 49:4972–8. doi:10.1103/PhysRevA.49.4972
28. Chiorescu I, Groll N, Bertaina S, Mori T, Myiashita S. Magnetic strong coupling in a spin-photon system and transition to classical regime. Phys Rev B (2010) 82:024413. doi:10.1103/PhysRevB.82.024413
29. Shankar R. Principles of quantum mechanics. New York: Springer US (1994). doi:10.1007/978-1-4757-0576-8
30. Kozierowski M, Chumakov SM, Światlowski J, Mamedov AA. Collective collapses and revivals in spontaneous emission of a partially inverted system of two-level atoms: Analytical solution. Phys Rev A (1992) 46:7220–7. doi:10.1103/PhysRevA.46.7220
31. Giovannetti V, Lloyd S, Maccone L. Quantum limits to dynamical evolution. Phys Rev A (2003) 67:052109. doi:10.1103/PhysRevA.67.052109
32. Binder FC, thesis PD. Work, heat, and power of quantum processes. Oxford: University of Oxford (2016). Section 3.6.
33. Soykal OO, Flatté ME. Size dependence of strong coupling between nanomagnets and photonic cavities. Phys Rev B (2010) 82:104413. doi:10.1103/PhysRevB.82.104413
34. Carlini A, Hosoya A, Koike T, Okudaira Y. Time-optimal quantum evolution. Phys Rev Lett (2006) 96:060503. doi:10.1103/PhysRevLett.96.060503
35. de Lange G, Wang ZH, Ristè D, Dobrovitski VV, Hanson R. Universal dynamical decoupling of a single solid-state spin from a spin bath. Science (2010) 330:60–3. doi:10.1126/science.1192739
36. Schröder T, Walsh M, Zheng J, Mouradian S, Li L, Malladi G, et al. Scalable fabrication of coupled nv center - photonic crystal cavity systems by self-aligned n ion implantation. Opt Mater Express (2017) 7:1514–24. doi:10.1364/OME.7.001514
37. Kubo Y, Ong FR, Bertet P, Vion D, Jacques V, Zheng D, et al. Strong coupling of a spin ensemble to a superconducting resonator. Phys Rev Lett (2010) 105:140502. doi:10.1103/PhysRevLett.105.140502
38. Bender CM, Brody DC, Jones HF. Complex extension of quantum mechanics. Phys Rev Lett (2002) 89:270401. doi:10.1103/PhysRevLett.89.270401
39. Liu YL, Wu R, Zhang J, Özdemir SK, Yang L, Nori F, et al. Controllable optical response by modifying the gain and loss of a mechanical resonator and cavity mode in an optomechanical system. Phys Rev A (2017) 95:013843. doi:10.1103/PhysRevA.95.013843
40. Bender CM, Boettcher S. Real spectra in non-hermitian Hamiltonians HavingPTSymmetry. Phys Rev Lett (1998) 80:5243–6. doi:10.1103/PhysRevLett.80.5243
41. Zhang D, Luo XQ, Wang YP, Li TF, You JQ. Observation of the exceptional point in cavity magnon-polaritons. Nat Commun (2017) 8:1368. doi:10.1038/s41467-017-01634-w
42. Bender CM, Brody DC, Jones HF, Meister BK. Faster than hermitian quantum mechanics. Phys Rev Lett (2007) 98:040403. doi:10.1103/PhysRevLett.98.040403
43. Kamin FH, Tabesh FT, Salimi S, Kheirandish F, Santos AC. Non-markovian effects on charging and self-discharging process of quantum batteries. New J Phys (2020) 22:083007. doi:10.1088/1367-2630/ab9ee2
Keywords: quantum battery, Tavis-Cumming Hamiltonian, Dicke model, pseudo-Hermite polynomials, quantum speedup
Citation: Zhang X and Blaauboer M (2023) Enhanced energy transfer in a Dicke quantum battery. Front. Phys. 10:1097564. doi: 10.3389/fphy.2022.1097564
Received: 14 November 2022; Accepted: 19 December 2022;
Published: 09 January 2023.
Edited by:
Jamal Berakdar, Martin Luther University of Halle-Wittenberg, GermanyReviewed by:
Levan Chotorlishvili, Rzeszów University of Technology, PolandH. Z. Shen, Northeast Normal University, China
Copyright © 2023 Zhang and Blaauboer. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Xiang Zhang, emhhbmd4aWFuZ0BiYXFpcy5hYy5jbg==
†These authors share first authorship
 Xiang Zhang
Xiang Zhang Miriam Blaauboer2
Miriam Blaauboer2