A perspective on complex networks in the stock market

Park, Jihun; Cho, Chang Hee; Lee, Jae Woo

doi:10.3389/fphy.2022.1097489

PERSPECTIVE article

Front. Phys., 23 December 2022

Sec. Social Physics

Volume 10 - 2022 | https://doi.org/10.3389/fphy.2022.1097489

This article is part of the Research Topic Taking Stock in Econophysics View all 5 articles

A perspective on complex networks in the stock market

Jihun Park

Chang Hee Cho

Jae Woo Lee*

Department of Physics, Inha University, Incheon, South Korea

A stock market is a complex system consisting of many interacting agents. We consider recent progress with complex networks constructed from cross-correlation of financial time series in the stock market. We review some methods and discuss the challenges in generating such complex networks that have a reasonable threshold.

1 Introduction

We consider complex networks in the stock market, which are generated by calculating cross-correlation coefficients of the logarithmic return between securities or stock indices. We connect two securities or indices with cross-correlation coefficients in descending order up to the number of links, $n = N - 1$ , without loops in a minimum spanning tree (MST) [1, 2]. In addition, we connect two securities up to $n = 3 (N - 2)$ without allowing crossings between links in a planar maximally filtered graph (PMFG), where $N$ is the total number of securities [3]. In a threshold network, we cut all links when the cross-correlation coefficients are less than the threshold value [4, 5]. The varying patterns of complex networks over time provide some important information on the stock market.

In this note, we discuss recent methods and applications of complex networks in the stock market and the pros and cons of threshold networks in the stock market.

2 Review

In a stock market, the indices or stock prices of individual companies become correlated with each other over time. The idea of complex networks applies to both stock markets and financial markets. We can construct a network based on world trade because the weights of the links are defined by trade flows, such as imports or exports among countries. In a stock market, one uses the cross-correlation coefficients of the stock indices or the prices of individual securities to generate a complex network. Consider a time series of a stock index on day $t$ , $P_{i} (t)$ , in the stock market. The logarithmic return is represented by $r_{i} (t) = [\log P_{i} (t) - \log P_{i} (t - 1)]$ . The cross-correlation function is

C_{i j} = \frac{< r_{i} (t) r_{j} (t) > - < r_{i} (t) > < r_{j} (t) >}{σ_{i} σ_{j}}, (1)

where $σ_{i}$ and $σ_{j}$ are the standard deviations of the logarithmic returns for two indices. We obtain an $N \times N$ correlation matrix $C$ . From this correlation matrix, we can generate complex networks in the stock market. Mantegna introduced a minimum spanning tree (MST) using metric distance.

d_{i j} = \sqrt{2 (1 - C_{i j})} . (2)

The MST is like a skeleton tree in the stock market, which is connected by tightly correlated indices or stock prices, with the number of links denoted as $n = N - 1$ [1]. Tumminello et al. introduced a planar maximally filtered graph (PMFG) with the number of links denoted as $n = 3 (N - 2)$ in the equity market, which is a topological generalization of the MST [2]. Onnela et al. reported networks of companies based on return correlations [6]. They added some links, allowing a loop structure from descending correlation coefficient ranks. Boginski et al. reported a market graph based on the correlation of stock prices [4]. Lee et al. introduced complex networks in a stock market by assigning a threshold value to normalized cross-correlation coefficients [5]. They reported a scale-free network from a restricted range of the threshold. Many stock markets have been studied using threshold methods for generating the stock network [7–17].

In the complex network of a stock market, the nodes are the stock indices or securities belonging to the stock market. When we consider cross-correlations among the indices of world markets, a node is a country’s stock index, such as the NYSE, the KOSPI, and the Nikkei. When we consider cross-correlation in intra-stock markets, nodes are securities such as Apple and Google in the U.S. stock market. We assign a link to the threshold networks when the cross-correlation coefficient between two companies is greater than a threshold value, such as

C_{i j} \geq θ . (3)

When one generates the threshold network, there is no concrete criterion for assigning threshold $θ$ . Many researchers heuristically choose a threshold value [4–16]. If the threshold value is close to 1, the threshold network is sparsely connected. In some cases, we can observe fragmented networks. When we decrease the threshold value, we obtain one giant connected network. In some ranges of a threshold value, threshold networks show a scale-free degree distribution. Intra-stock market time series of securities are highly correlated with each other; therefore, threshold networks have a high average degree and a high clustering coefficient.

Strongly connected links between two securities mean that they should behave synchronously. Therefore, when we build a portfolio, we can avoid choosing highly correlated or heavily connected securities from a threshold network. However, heuristic determination of the threshold value is an open issue in threshold networks. Nobi et al. chose a threshold value $θ = < C_{i j} > + n σ$ , where $n$ is a given value and $σ$ is the standard deviation [10, 11]. If $n = 0$ , the threshold is $θ = < C_{i j} >$ . If we choose the same value for $n$ , we can consistently compare threshold networks for different markets. In a stock index like the Korea Composite Stock Price Index (KOSPI), there are $N$ securities. When we calculate the cross-correlation, we choose a length for the time window $T$ in a time series. In general, we need criterion $T > N$ to avoid noise and obtain the statistical quality of the cross-correlation. We need an appropriate threshold value for the given set $(N, T)$ [10]. We considered the daily stock prices for 185 Korean securities listed on the KOSPI 200 for the period from 2 June 2006 to 30 June 2009. In this period, the 2008 global financial crisis occurred. We considered two time windows, such as before the crisis (2 June 2006–30 November 2007) and during the crisis (3 December 2007–30 June 2009). In Figure 1, we represent the threshold network with $θ = < C_{i j} > + 3 σ$ in the Korean stock market, where (a) illustrates before the 2008 global financial crisis $(< C_{i j} > = 0.23, σ = 0.098)$ and (b) illustrates during the global crisis $(< C_{i j} > = 0.35, σ = 0.11)$ . We observed a big change in threshold networks when the global financial crisis occurred. The number of nodes belonging to the largest cluster was 4.8% before the crisis and 20% during the crisis. Before the financial crisis, threshold networks with high cross-correlation were fragmented into many clusters. However, during the crisis, the threshold network formed a large network. The largest cluster of the threshold network during the crisis was 20% of the index. Before the crisis, the financial sector was separated into two clusters, and many sectors were observed in the threshold network. During the crisis, only two sectors (the financial sector and heavy industry and construction) belonged to the threshold network. The financial sector formed one large connected group, and the two sectors combined heavily with many links.

FIGURE 1

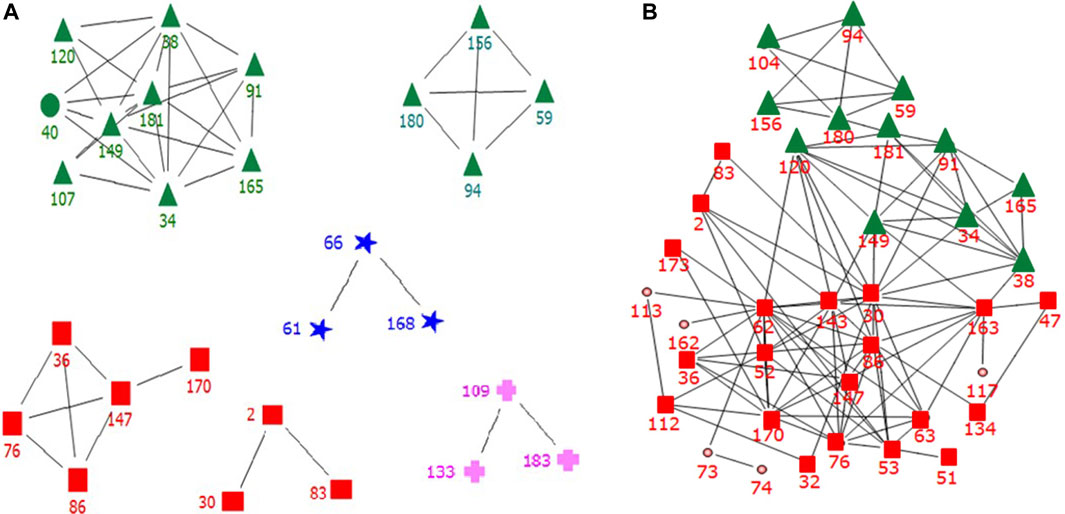
FIGURE 1. Threshold network with threshold $θ = < C_{i j} > + 3 σ$ in the Korean stock market: (A) before the 2008 global financial crisis $(< C_{i j} > = 0.23, σ = 0.098)$ and (B) during the global crisis $(< C_{i j} > = 0.35, σ = 0.11$ ). The labels indicate the companies, and the colors of the nodes indicate the sector of the stock market as follows: financial sector (green triangles), heavy industry and construction (red squares), iron and metal products (magenta plus), and non-metallic products (blue stars).

When we choose a threshold value, we can compare the distribution of the cross-correlation coefficients between the original time series and a shuffled time series. The shuffled time series destroys cross-correlation but maintains the distribution function of the returns. When we estimate the cross-correlation, a few high logarithmic returns heavily contribute to the value of the cross-correlation coefficients. This is an intrinsic problem in a time series if there are events with extreme values. In a threshold network, we obtain a unidirectional network. In the real world, the information flow between two securities is asymmetric and directional. Some researchers apply Granger causality, transfer entropy, causation entropy, and network entropy to generate a directional network in the stock market [18–22].

The strong points of a threshold network based on cross-correlation are that it is easy to construct the network and obtain intuitive relationships among the companies via the network. When we scan the changes in a threshold network over time, we can observe dynamic changes in the network, as shown in Figure 1. The properties of the threshold network help us understand the characteristics of the stock market. A weak point in the threshold network is that there is no concrete criterion for assigning the threshold. Therefore, if we change the threshold value, the connecting pattern changes heavily. When we obtain the threshold network, it does not give any causal relationships among companies because threshold networks are based on cross-correlation among time series.

The structural change of a complex network in the stock market can be applied to measure the impact of a crisis and the instability of the market [10, 15, 23–31]. A big shock on the market should change the structure of the stock network. The length of the minimum spanning tree experiences a drastic reduction when facing systemic risk [24]. The hierarchy of global trade networks increases during a period of recession [25]. Characteristics of complex networks, such as clustering coefficients, centrality, network size, and occupation ratio, are associated with systemic risk and instability in the stock market [23, 27].

In summary, we introduced a threshold method to generate a complex network via the cross-correlation of logarithmic returns in the stock market. We want to get some useful information from a complex network. We estimate properties like average degree, clustering coefficients, centrality, and community detection in the generated threshold networks. We need to relate these qualities to market stability, systemic risk in the market, investing strategies, etc. To accomplish these goals, we need to generate suitable complex networks for the stock market by using reasonable criteria.

3 Conclusion

We discussed methods of creating a threshold network using cross-correlation coefficients between securities or indices in stock markets. In the threshold method, we assigned a heuristic threshold value to generate the stock network. We need a more concrete criterion for choosing the threshold value for a threshold network. The dynamic changes of a threshold network in the stock market can be applied to understand the systemic risk and stability in the market.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.

Author contributions

JP, CC, and JL performed conception and design of the research, the acquisition and analysis of data, interpretation, writing, and revising.

Funding

This work was supported by Inha University Research Grant.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Mantegna R. Hierarchical structure in financial markets. Eur Phys J B (1999) 11:193–7. doi:10.1007/s100510050929