Commentary: Multidimensional discrete chaotic maps

A Commentary on
Commentary: Multidimensional discrete chaotic maps

by Bucolo M., Buscarino A., Fortuna L. and Gagliano S. (2022). Front. Phys. 10:862376. doi: 10.3389/fphy.2022.862376

1 Preliminaries

This commentary is addressed to multidimensional discrete chaotic maps discussed in [1]. The authors of the commented paper [1] note that the iterative logistic map of matrices is introduced in [2, 3]. Then, the authors of [1] introduce a multidimensional discrete chaotic map, define when this map is explosive, and prove two theorems describing the conditions when the map is not explosive, and when a chaotic behavior is observed for each scalar variable.

There are two issues commented in this commentary paper. The first one is related to the fact that multidimensional discrete chaotic maps have been already introduced in [4]. Secondly, both theorems describing the conditions when multidimensional discrete chaotic maps are not explosive, and when a chaotic behavior is observed for each scalar variable, do not hold true. Correct conditions when multidimensional discrete chaotic map is explosive are given in [2, 3] (for 2-dimensional discrete chaotic maps) and in [4] (for n-dimensional discrete chaotic maps). This commentary demonstrates that a multidimensional discrete chaotic map can be explosive even if the eigenvalues of the matrix of initial conditions are located in the convergence domain of the corresponding scalar discrete map. Necessary and sufficient conditions for a multidimensional discrete chaotic map to become explosive are discussed in [2, Theorem 3.2, p. 935], [3, Definition 3.3, p. 4433], [3, Comment 3, p. 4433], [3, Corollary 4, p. 4434], [4, Eq. 30, p. 7]. Moreover, a numerical example of a 2-dimensional discrete chaotic map is used to illustrate the fact that theorems 1 and 2 in [1] are incorrect.

2 2-dimensional discrete chaotic maps

Let us consider an iterative map

$x^{\left(k+1\right)}=f\left(x^{\left(k\right)}\right),k=\mathrm{0,1,2},\dots ,(1)$

where $x^{\left(k\right)}\in \mathbb{C}$ is a scalar variable and function f is an analytic function that can be expanded into the power series

$f\left(z\right)=\sum _{j=0}^{\infty }{c}_j\frac{z^j}{j!};c_j\in \mathbb{R}.(2)$

The scalar variable $x^{\left(k\right)}$ in Eq. 1 can be replaced by a square matrix ${\mathbf{X}}^{\left(k\right)}=\left[\begin{array}{cc}\hfill x_{11}^{\left(k\right)}\hfill & \hfill x_{12}^{\left(k\right)}\hfill \\ \hfill x_{21}^{\left(k\right)}\hfill & \hfill x_{22}^{\left(k\right)}\hfill \end{array}\right]$ of scalar variables $x_{11}^{\left(k\right)}$, $x_{12}^{\left(k\right)}$, $x_{21}^{\left(k\right)}$, $x_{22}^{\left(k\right)}$ [2, 3]. The 2-dimensional discrete map then reads:

${\mathbf{X}}^{\left(k+1\right)}=f\left({\mathbf{X}}^{\left(k\right)}\right),k=\mathrm{0,1,2},\dots .(3)$

It is shown in [2, 3] that the dynamics of the 2-dimensional discrete chaotic map depends not only on the fact that the eigenvalues of the matrix of initial conditions do (or do not) belong to the basin of attraction of the corresponding scalar map. A 2-dimensional discrete chaotic map can be explosive even if both eigenvalues of the matrix of initial conditions do belong to the basin of attraction of the corresponding scalar map.

Let us assume that the eigenvalues ${\lambda }_1^{\left(0\right)}$, ${\lambda }_2^{\left(0\right)}$ of the matrix of initial conditions ${\mathbf{X}}^{\left(0\right)}$ are different. Then ${\mathbf{X}}^{\left(0\right)}$ can be expressed in the form of an idempotent matrix:

${\mathbf{X}}^{\left(0\right)}={\lambda }_1^{\left(0\right)}{\mathbf{D}}_1+{\lambda }_2^{\left(0\right)}{\mathbf{D}}_2,(4)$

where D₁, D₂ are conjugate idempotents satisfying the following relations: det D₁ = det D₂ = 0, D₁ + D₂ = I, D₁⋅ D₁ = D₁, D₂ ⋅ D₂ = D₂, ${\mathbf{D}}_1\cdot {\mathbf{D}}_2={\mathbf{D}}_2\cdot {\mathbf{D}}_1=\left[\begin{array}{cc}\hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill \end{array}\right]$ (I denotes the identity matrix). In that case, the matrix preserves the form of an idempotent matrix with the same conjugate idempotents in every iteration [2, 3]:

${\mathbf{X}}^{\left(k+1\right)}={\lambda }_1^{\left(k+1\right)}{\mathbf{D}}_1+{\lambda }_2^{\left(k+1\right)}{\mathbf{D}}_2=f\left({\lambda }_1^{\left(k\right)}\right){\mathbf{D}}_1+f\left({\lambda }_2^{\left(k\right)}\right){\mathbf{D}}_2,k=\mathrm{0,1},\dots .(5)$

Therefore, such a 2-dimensional discrete map splits into two scalar maps of eigenvalues [2, 3]:

$\left\{\begin{array}{c}{\lambda }_1^{\left(k+1\right)}=f\left({\lambda }_1^{\left(k\right)}\right),\hfill \\ {\lambda }_2^{\left(k+1\right)}=f\left({\lambda }_2^{\left(k\right)}\right),\hfill \end{array}\right.k=\mathrm{0,1,2},\dots .(6)$

Then, the 2-dimensional discrete map is not explosive if and only if the eigenvalues ${\lambda }_1^{\left(0\right)}\ne {\lambda }_2^{\left(0\right)}$ do belong to the basin of attraction of the corresponding scalar map (Eq. 1).

Otherwise, if the matrix of initial conditions ${\mathbf{X}}^{\left(0\right)}$ has a single recurrent eigenvalue ${\lambda }_1^{\left(0\right)}={\lambda }_2^{\left(0\right)}={\lambda }_0^{\left(0\right)}$, then it can be expressed in the form of a nilpotent matrix:t

${\mathbf{X}}^{\left(0\right)}={\lambda }_0^{\left(0\right)}\mathbf{I}+\mathbf{N},(7)$

where N is a nilpotent satisfying the following relations: ${\mathbf{N}}^2=\left[\begin{array}{cc}\hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill \end{array}\right]$ and det N = 0. If the matrix of initial conditions ${\mathbf{X}}^{\left(0\right)}$ is a nilpotent matrix, then the matrices produced by the iterative map are also nilpotent matrices:

$\begin{array}{cc}\hfill {\mathbf{X}}^{\left(k+1\right)}& =f\left({\mathbf{X}}^{\left(k\right)}\right)=\sum _{j=0}^{\infty }\frac{c_j}{j!}{\left({\mathbf{X}}^{\left(k\right)}\right)}^j=\sum _{j=0}^{\infty }\frac{c_j}{j!}{\left({\lambda }_0^{\left(k\right)}\mathbf{I}+{\mu }_1^{\left(k\right)}\mathbf{N}\right)}^j\hfill \\ \hfill & =\sum _{j=0}^{\infty }\frac{c_j}{j!}\left(\left(\genfrac{}{}{0.0pt}{}{j}{0}\right){\left({\lambda }_0^{\left(k\right)}\right)}^j{\mathbf{I}}^j+\left(\genfrac{}{}{0.0pt}{}{j}{1}\right){\left({\lambda }_0^{\left(k\right)}\right)}^{j-1}{\mu }_1^{\left(k\right)}{\mathbf{I}}^{j-1}\mathbf{N}\right.\hfill \\ \hfill & \left.+\left(\genfrac{}{}{0.0pt}{}{j}{2}\right){\left({\lambda }_0^{\left(k\right)}\right)}^{j-2}{\left({\mu }_1^{\left(k\right)}\right)}^2{\mathbf{I}}^{j-2}{\mathbf{N}}^2+\cdots +\left(\genfrac{}{}{0.0pt}{}{j}{j}\right){\left({\mu }_1^{\left(k\right)}\right)}^j{\mathbf{N}}^j\right)\hfill \\ \hfill & =\sum _{j=0}^{\infty }\frac{c_j}{j!}\left({\left({\lambda }_0^{\left(k\right)}\right)}^j\mathbf{I}+j{\left({\lambda }_0^{\left(k\right)}\right)}^{j-1}{\mu }_1^{\left(k\right)}\mathbf{N}\right)\hfill \\ \hfill & =\left(\sum _{j=0}^{\infty }\frac{c_j}{j!}{\left({\lambda }_0^{\left(k\right)}\right)}^j\right)\mathbf{I}+\left(\sum _{j=0}^{\infty }\frac{c_j}{j!}j{\left({\lambda }_0^{\left(k\right)}\right)}^{j-1}\right){\mu }_1^{\left(k\right)}\mathbf{N}\hfill \\ \hfill & =f\left({\lambda }_0^{\left(k\right)}\right)\mathbf{I}+{\mu }_1^{\left(k\right)}{f}^{\prime }\left({\lambda }_0^{\left(k\right)}\right)\mathbf{N},\hfill \end{array}(8)$

where k = 0, 1, …, ${\mu }_1^{\left(0\right)}=1$; $f^{\prime }\left({\lambda }_0^{\left(k\right)}\right)$ denotes the derivative of f computed at ${\lambda }_0^{\left(k\right)}$ [2]. Therefore, the 2-dimensional discrete map splits into two intertwined scalar maps [2, 3]:

$\left\{\begin{array}{c}{\lambda }_0^{\left(k+1\right)}=f\left({\lambda }_0^{\left(k\right)}\right),\hfill \\ {\mu }_1^{\left(k+1\right)}={\mu }_1^{\left(k\right)}{f}^{\prime }\left({\lambda }_0^{\left(k\right)}\right),\hfill \end{array}\right.k=\mathrm{0,1,2},\dots ,{\mu }_1^{\left(0\right)}=1.(9)$

Then, the 2-dimensional discrete chaotic map can become explosive even if the recurrent eigenvalue does belong to the basin of attraction of Eq. 1. The discrete chaotic map becomes explosive if the Lyapunov exponent of the original scalar map is positive and the matrix of initial conditions is a nilpotent matrix [3].

The authors of [1] fail to observe the fact that a multidimensional discrete chaotic map can be explosive even if eigenvalues of the matrix of initial conditions do belong to the basin of attraction of the corresponding scalar map (Figure 1). For example, the 2-dimensional discrete logistic map ${\mathbf{X}}^{\left(k+1\right)}=3.6{\mathbf{X}}^{\left(k\right)}\left(\mathbf{I}-{\mathbf{X}}^{\left(k\right)}\right)$ can be explosive even when the eigenvalues of the matrix of initial conditions do belong to the basin of attraction of the corresponding scalar logistic map $x^{\left(k+1\right)}=3.6x^{\left(k\right)}\left(1-x^{\left(k\right)}\right)$. The matrix of initial conditions ${\mathbf{X}}^{\left(0\right)}=\left[\begin{array}{cc}\hfill 0.8\hfill & \hfill 0.4\hfill \\ \hfill -0.1\hfill & \hfill 0.3\hfill \end{array}\right]$ (${\lambda }_1^{\left(0\right)}=0.7$; ${\lambda }_2^{\left(0\right)}=0.4$) results into 4 stationary processes (Figure 1A). However, the 2-dimensional discrete logistic map becomes explosive (Figure 1B) at ${\mathbf{X}}^{\left(0\right)}=\left[\begin{array}{cc}\hfill -0.1\hfill & \hfill 0.4\hfill \\ \hfill -0.1\hfill & \hfill 0.3\hfill \end{array}\right]$ (${\lambda }_1^{\left(0\right)}={\lambda }_2^{\left(0\right)}={\lambda }_0^{\left(0\right)}=0.1$). The Lyapunov exponent of the corresponding scalar logistic map is L = 0.197 > 0. The evolution of $x_{11}^{\left(k\right)}$, $x_{12}^{\left(k\right)}$, $x_{21}^{\left(k\right)}$, and $x_{22}^{\left(k\right)}$ is depicted by the black, the green, the blue, and the red line respectively. In other words, Theorems 1 and 2 formulated in the commented paper [1] do not hold true.

FIGURE 1

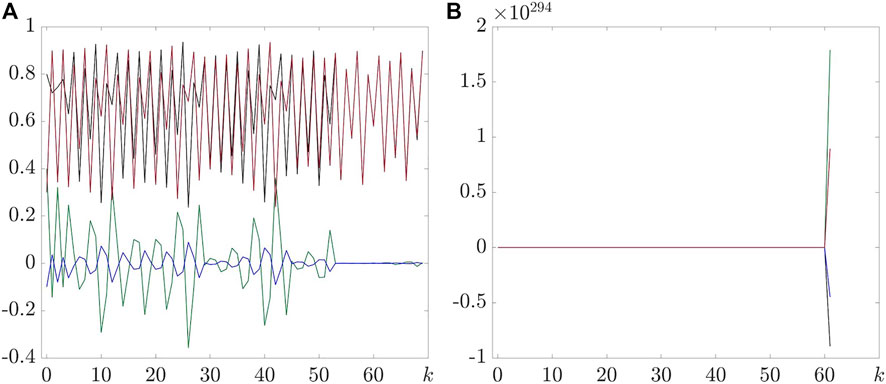
FIGURE 1. The 2-dimensional discrete logistic map can be explosive even when the eigenvalues of the matrix of initial conditions do belong to the basin of attraction of the corresponding scalar logistic map. The matrix of initial conditions ${\mathbf{X}}^{\left(0\right)}=\left[\begin{array}{cc}\hfill 0.8\hfill & \hfill 0.4\hfill \\ \hfill -0.1\hfill & \hfill 0.3\hfill \end{array}\right]$ (${\lambda }_1^{\left(0\right)}=0.7$; ${\lambda }_2^{\left(0\right)}=0.4$) results into 4 stationary processes [part (A)]. However, the map becomes explosive when ${\mathbf{X}}^{\left(0\right)}=\left[\begin{array}{cc}\hfill -0.1\hfill & \hfill 0.4\hfill \\ \hfill -0.1\hfill & \hfill 0.3\hfill \end{array}\right]$ (${\lambda }_1^{\left(0\right)}={\lambda }_2^{\left(0\right)}=0.1$) [part (B)]. The evolution of $x_{11}^{\left(k\right)}$, $x_{12}^{\left(k\right)}$, $x_{21}^{\left(k\right)}$, and $x_{22}^{\left(k\right)}$ is depicted by the black, the green, the blue, and the red line respectively.

3 N-dimensional discrete chaotic maps

It can be noted that a scalar variable in Eq. 1 can be also replaced by the nth order square matrix [4]. However, it appears that the dynamics of n-dimensional discrete chaotic maps becomes much more complicated compared to the dynamics of 2-dimensional discrete chaotic maps [4].

3.1 Packing and divergence codes

A multidimensional discrete chaotic map may become explosive if at least two eigenvalues of the matrix of initial conditions do coincide (even though all eigenvalues of the matrix are located in the convergence domain of the corresponding scalar discrete map). The multiplicity indexes of eigenvalues are directly related to the packing codes due to the classical bin packing problem [4]. Therefore, the study of packing codes becomes a topic of primary importance in the analysis of the divergence of multidimensional discrete chaotic maps [4]. Also, it is demonstrated in [4] that there exists a bijective correspondence between the packing and the divergence codes. On their turn, divergence codes define the rate of divergence of multidimensional discrete chaotic maps [4]. Let us illustrate the packing and the divergence codes for a 4-dimensional discrete chaotic map.

Packing and divergence codes at n = 4 are depicted in Table 10 [4, p. 9]. The set of packing codes does represent the classical bin packing problem since 4 × 1 = 1 × 2 + 2 × 1 = 2 × 2 = 1 × 3 + 1 × 1 = 1 × 4 = 4.

Firstly, let us consider the case when all four eigenvalues of the matrix of initial conditions are different $({\lambda }_1^{(0)}\ne {\lambda }_2^{(0)}\ne {\lambda }_3^{(0)}\ne {\lambda }_4^{(0)})$. The multiplicity index of all four eigenvalues is 1. Thus, the packing code reads: $\left[0004\right]$ (0 × 4 + 0 × 3 + 0 × 2 + 4 × 1) [4, Table 10, p. 9].

Analogous derivations to those performed for the 2-dimensional discrete chaotic maps yield four uncoupled scalar discrete maps of eigenvalues (Eq. 10). Note that multiplicity indexes of the iterated matrix variable do remain unchanged from the initial set of multiplicity indexes given by the matrix of initial conditions [4]. None of those four maps in Eq. 10 do comprise the auxiliary parameter μ. Therefore, the divergence code in Table 10 [4, p. 9] comprises four zeros [4].

$\left\{\begin{array}{c}{\lambda }_3^{\left(k+1\right)}=f\left({\lambda }_3^{\left(k\right)}\right);\hfill \\ {\lambda }_4^{\left(k+1\right)}=f\left({\lambda }_4^{\left(k\right)}\right);k=\mathrm{0,1,2},\dots \hfill \end{array}\right.(10)$

Secondly, let us investigate the scenario when only two eigenvalues do coincide but other two are different $({\lambda }_1^{(0)}={\lambda }_2^{(0)}={\lambda }_0^{(0)}\ne {\lambda }_3^{(0)}\ne {\lambda }_4^{(0)})$. The packing code now reads $\left[0012\right]$ (0 × 4 + 0 × 3 + 1 × 2 + 2 × 1 = 4). This packing code yields the divergence code $\left[0001\right]$ because Eq. 11 comprises a single map (the fourth scalar iterative map) with the auxiliary parameter ${\mu }_1^{(k)}$. Note that the value of ${\mu }_1^{(0)}$ is always equal to 1 in the first iteration [4].

$\left\{\begin{array}{c}{\lambda }_0^{\left(k+1\right)}=f\left({\lambda }_0^{\left(k\right)}\right);\hfill \\ {\lambda }_3^{\left(k+1\right)}=f\left({\lambda }_3^{\left(k\right)}\right);\hfill \\ {\lambda }_4^{\left(k+1\right)}=f\left({\lambda }_4^{\left(k\right)}\right);\hfill \\ {\mu }_1^{\left(k+1\right)}={\mu }_1^{\left(k\right)}{f}^{\prime }\left({\lambda }_0^{\left(k\right)}\right);k=\mathrm{0,1,2},\dots ;{\mu }_1^{\left(0\right)}=1.\hfill \end{array}\right.(11)$

Next, let us consider the packing code $\left[0020\right]$ (0 × 4 + 0 × 3 + 2 × 2 + 0 × 1 = 4) [4, Table 10, p. 9]. This situation corresponds to two pairs of identical eigenvalues $({\lambda }_1^{(0)}={\lambda }_2^{(0)};{\lambda }_3^{(0)}={\lambda }_4^{(0)})$. Eq. 12 contains two scalar iterative maps of parameters ${\mu }_1^{(k),1}$ and ${\mu }_1^{(k),3}$ interrelated with eigenvalues ${\lambda }_1^{(k)}$ and ${\lambda }_3^{(k)}$ respectively. Eq. 12 yields the divergence code $\left[0011\right]$ [4].

$\left\{\begin{array}{c}{\lambda }_1^{\left(k+1\right)}=f\left({\lambda }_1^{\left(k\right)}\right);\hfill \\ {\lambda }_3^{\left(k+1\right)}=f\left({\lambda }_3^{\left(k\right)}\right);\hfill \\ {\mu }_1^{\left(k+1\right),1}={\mu }_1^{\left(k\right),1}{f}^{\prime }\left({\lambda }_1^{\left(k\right)}\right);\hfill \\ {\mu }_1^{\left(k+1\right),3}={\mu }_1^{\left(k\right),3}{f}^{\prime }\left({\lambda }_3^{\left(k\right)}\right);k=\mathrm{0,1,2},\dots ;{\mu }_1^{\left(0\right),1}=1;{\mu }_1^{\left(0\right),3}=1.\hfill \end{array}\right.(12)$

Let us consider the fourth packing code in Table 10 [4, p. 9]. It describes the case when three eigenvalues do coincide but the fourth is different $({\lambda }_1^{(0)}={\lambda }_2^{(0)}={\lambda }_3^{(0)}={\lambda }_0^{(0)}\ne {\lambda }_4^{(0)})$. Eq. 13 comprises two scalar iterative maps, one iterative map with the auxiliary variable ${\mu }_1^{(k)}$, and one map with auxiliary variables ${\mu }_1^{(k)}$ and ${\mu }_2^{(k)}$ [4]. Thus, the packing code $\left[0101\right]$ (0 × 4 + 1 × 3 + 0 × 2 + 1 × 1 = 4) results into the divergence code $\left[0012\right]$ [4, Table 10, p. 9].

$\left\{\begin{array}{c}{\lambda }_0^{\left(k+1\right)}=f\left({\lambda }_0^{\left(k\right)}\right);\hfill \\ {\lambda }_4^{\left(k+1\right)}=f\left({\lambda }_4^{\left(k\right)}\right);\hfill \\ {\mu }_1^{\left(k+1\right)}={\mu }_1^{\left(k\right)}{f}^{\prime }\left({\lambda }_0^{\left(k\right)}\right);\hfill \\ {\mu }_2^{\left(k+1\right)}={\mu }_2^{\left(k\right)}{f}^{\prime }\left({\lambda }_0^{\left(k\right)}\right)+\frac{{\left({\mu }_1^{\left(k\right)}\right)}^2}{2!}{f}^{″}\left({\lambda }_0^{\left(k\right)}\right);\hfill \\ k=\mathrm{0,1,2},\dots ;{\mu }_1^{\left(0\right)}=1;{\mu }_2^{\left(0\right)}=1.\hfill \end{array}\right.(13)$

Finally, let us discuss the largest divergence code when all eigenvalues are equal $({\lambda }_1^{(0)}={\lambda }_2^{(0)}={\lambda }_3^{(0)}={\lambda }_4^{(0)}={\lambda }_0^{(0)})$. The packing code $\left[1000\right]$ (1 × 4 + 0 × 3 + 0 × 2 + 0 × 1 = 4) results into Eq. 14 which yields the divergence code $\left[0012\right]$ [4]:

$\left\{\begin{array}{c}{\lambda }_0^{\left(k+1\right)}=f\left({\lambda }_0^{\left(k\right)}\right);\hfill \\ {\mu }_1^{\left(k+1\right)}={\mu }_1^{\left(k\right)}{f}^{\prime }\left({\lambda }_0^{\left(k\right)}\right);\hfill \\ {\mu }_2^{\left(k+1\right)}={\mu }_2^{\left(k\right)}{f}^{\prime }\left({\lambda }_0^{\left(k\right)}\right)+\frac{{\left({\mu }_1^{\left(k\right)}\right)}^2}{2!}{f}^{″}\left({\lambda }_0^{\left(k\right)}\right);\hfill \\ {\mu }_3^{\left(k+1\right)}={\mu }_3^{\left(k\right)}{f}^{\prime }\left({\lambda }_0^{\left(k\right)}\right)+\frac{2{\mu }_1^{\left(k\right)}{\mu }_2^{\left(k\right)}}{2!}{f}^{″}\left({\lambda }_0^{\left(k\right)}\right)+\frac{{\left({\mu }_1^{\left(k\right)}\right)}^3}{3!}f‴\left({\lambda }_0^{\left(k\right)}\right);\hfill \end{array}\right.(14)$

where k = 0, 1, 2, …; ${\mu }_1^{(0)}={\mu }_2^{(0)}={\mu }_3^{(0)}=1$.

Packing and divergence codes for the n-dimensional discrete chaotic map are given in [4]. It is interesting to observe that the sequence of the packing codes does comprise the paradigmatic sequence A061196 from the OEIS (the Online Encyclopedia of Integer Sequences [5]), while the sequence of the divergence codes introduced in [4] does represent a new integer sequence.

3.2 The divergence of the 4-dimensional logistic map

The largest divergence code for the 4 × 4 matrix $\left[0123\right]$ yields iterative equations Eq. (30) [4, p. 7]. The multidimensional logistic map reduces those iterative equations because higher derivatives of the logistic mapping function do vanish:

$\left\{\begin{array}{c}{\lambda }_0^{\left(k+1\right)}=a{\lambda }_0^{\left(k\right)}\left(1-{\lambda }_0^{\left(k\right)}\right);\hfill \\ {\mu }_1^{\left(k+1\right)}=a{\mu }_1^{\left(k\right)}\left(1-2{\lambda }_0^{\left(k\right)}\right);\hfill \\ {\mu }_2^{\left(k+1\right)}=a{\mu }_2^{\left(k\right)}\left(1-2{\lambda }_0^{\left(k\right)}\right)-a{\left({\mu }_1^{\left(k\right)}\right)}^2;\hfill \\ {\mu }_3^{\left(k+1\right)}=a{\mu }_3^{\left(k\right)}\left(1-2{\lambda }_0^{\left(k\right)}\right)-2a{\mu }_1^{\left(k\right)}{\mu }_2^{\left(k\right)};\hfill \end{array}\right.(15)$

where ${\mu }_1^{(0)}={\mu }_2^{(0)}={\mu }_3^{(0)}=1$.

All four eigenvalues of ${\mathbf{X}}^{\left(0\right)}$ are set to 0.1 and fit into the convergence domain of the scalar logistic map. The positive Lyapunov coefficient (0.197 at a = 3.6) and the non-zero divergence code $\left[0123\right]$ yield the explosive divergence of the 4-dimensional logistic map [4, Figure 2, part (A), p. 15].

It is interesting to observe, that the divergence rate of the auxiliary parameters do depend not only on the Lyapunov coefficient, but also on their indexes. Detailed discussion of the rate of explosive divergence of multidimensional logistic maps is given in [4, p. 11].

4 Concluding remarks

This commentary paper demonstrates that a multidimensional discrete chaotic map can become explosive even if the eigenvalues of the matrix of initial conditions are located in the convergence domain of the corresponding scalar discrete map. The explosive divergence of the multidimensional discrete chaotic map does occur if the divergence code of the matrix of initial conditions is larger than zero (at least two eigenvalues of ${\mathbf{X}}^{\left(0\right)}$ do coincide), and the Lyapunov exponent of the corresponding scalar map is positive [4]. In other words, Theorems 1 and 2 given in the commented paper [1] are incorrect.

This fact has important implications for the study of discrete chaotic systems when the nodal complexity of the system is increased by expanding the dimension of the scalar variable [6–9]. Complex fractal patterns representing spatio-temporal divergence in the extended Kaneko model in [6], the development of a novel image hiding scheme in [7], spiral waves of divergence in [8], intermittent bursting in fractional logistic map in [9] are all based on divergence codes greater than zero. In other words, all these effects could not be observed if theorems 1 and 2 in [1] would hold true.

Author contributions

All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication. Both authors contributed equally to this work and have approved it for publication.

Funding

This research is funded by the European Social Fund under the No 09.3.3-LMT-K-712 “Development of Competences of Scientists, other Researchers and Students through Practical Research Activities” measure (Project No. 09.3.3-LMT-K-712-23-0235).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Bucolo M, Buscarino A, Fortuna L, Gagliano S. Multidimensional discrete chaotic maps. Front Phys (2022) 10:199. doi:10.3389/fphy.2022.862376

CrossRef Full Text | Google Scholar

2. Navickas Z, Smidtaite R, Vainoras A, Ragulskis M. The logistic map of matrices. Discrete & Continuous Dynamical Systems-B (2011) 16:927–44. doi:10.3934/dcdsb.2011.16.927

CrossRef Full Text | Google Scholar

3. Navickas Z, Ragulskis M, Vainoras A, Smidtaite R. The explosive divergence in iterative maps of matrices. Commun Nonlinear Sci Numer Simulation (2012) 17:4430–8. doi:10.1016/j.cnsns.2012.03.018

CrossRef Full Text | Google Scholar

4. Smidtaite R, Navickas Z, Ragulskis M. Clocking divergence of iterative maps of matrices. Commun Nonlinear Sci Numer Simulation (2021) 95:105589. doi:10.1016/j.cnsns.2020.105589

CrossRef Full Text | Google Scholar

5. Bottomley H. Entry A061196 in The On-Line Encyclopedia of Integer Sequences (2001). https://oeis.org/A061196

Google Scholar

6. Lu G, Smidtaite R, Navickas Z, Ragulskis M. The effect of explosive divergence in a coupled map lattice of matrices. Chaos, Solitons & Fractals (2018) 113:308–13. doi:10.1016/j.chaos.2018.06.016

CrossRef Full Text | Google Scholar

7. Lu G, Smidtaite R, Howard D, Ragulskis M. An image hiding scheme in a 2-dimensional coupled map lattice of matrices. Chaos, Solitons & Fractals (2019) 124:78–85. doi:10.1016/j.chaos.2019.04.038

CrossRef Full Text | Google Scholar

8. Smidtaite R, Ragulskis M. Spiral waves of divergence in the barkley model of nilpotent matrices. Chaos, Solitons & Fractals (2022) 159:112158. doi:10.1016/j.chaos.2022.112158

CrossRef Full Text | Google Scholar

9. Petkevičiūtė-Gerlach D, Šmidtaitė R, Ragulskis M. Intermittent bursting in the fractional difference logistic map of matrices. Int J Bifurcation Chaos (2022) 32:2230002. doi:10.1142/S0218127422300026

CrossRef Full Text | Google Scholar