- 1Center for Quantum Sciences and School of Physics, Northeast Normal University, Changchun, China
- 2School of Science, Shenyang University of Technology, Shenyang, China
It is known that the dynamics and geometric phase of a quantum system can be simulated by classical coupled oscillators using the quantum−classical mapping method without loss of physics. In this work, we show that this method can also be used to simulate the schemes of quantum shortcuts to adiabaticity, which can quickly achieve the adiabatic effect through a non-adiabatic process. By mapping quantum systems by classical oscillators, two schemes, Berry’s “transitionless quantum driving” and the Lewis−Riesenfeld invariant method, are simulated by a corresponding transitionless classical driving method, which keeps adiabatic phase trajectories and acquires Hannay’s angle and the classical Lewis−Riesenfeld invariant method by manipulating the configurations of classical coupled oscillators. The classical shortcuts to adiabaticity for the two coupled classical oscillators, which is the classical version of a spin-1/2 in a magnetic field, is employed to illustrate our results and compared with quantum shortcuts-to-adiabaticity methods.
1 Introduction
Adiabatic processes of quantum systems have become a significant ingredient in quantum information processing for various practical purposes in metrology, interferometry, quantum computing, and control of chemical interaction [1–4]. Achieving state preparation or transferring the population with high fidelity versus parameter fluctuations should take a long time [5–7]. However, there are many instances where we need to speed these operations up to prevent them from suffering decoherence, noise, or losses [8, 9]. Therefore, proposing a way to speed up the adiabatic approaches has drawn considerable attention [10–13]. So far, a variety of techniques to implement shortcuts to adiabaticity (STA) have been proposed [5, 8, 14–21]. Notably, there is a shortcut passage algorithm proposed by Berry called “transitionless quantum driving” (TQD) [10]. This method accelerates adiabatic evolution in a hurry by designing a time-dependent interaction followed by the system exactly [10]. Moreover, Chen et al. put forward another method to accelerate the adiabatic passage using the Lewis−Riesenfeld (LR) invariant to keep the eigenstates of a Hamiltonian from a specified initial to the final configuration in an arbitrary time [8].
Not only STA techniques are developed in quantum systems but there are also dissipationless classical drivings in classical systems [20, 22–26]. Moreover, it is already known that a quantum system in a Hilbert space possesses a mathematically canonical classical Hamiltonian structure in the phase space [27–41]. For example, the structures of their phase spaces are usually regarded as the same [42, 43]. Classical and quantum mechanics can also be embedded in a unified formulation as a quantum−classical hybrid system [44]. There is a way to devote elements of quantum mechanics to classical mechanics, in which we can simulate the microscopic quantum behavior by a transition of the average value from a quantum system Hamiltonian into a classical system consisting of oscillators without losing any physics [45–55]. Therefore, it is possible to map and generalize adiabatic processes and STA for quantum systems to classical systems by the quantum−classical mapping method. As a matter of fact, we are inspired to ask if we can simulate the STA in quantum systems by classical oscillators. Based on this mapping and simulation, can it give specific classical schemes for quantum schemes for the STA as the dissipationless classical driving did? What is the relation between the quantum and classical STA?
In this paper, we first introduce the quantum−classical mapping and the relation between the Berry phase for the original quantum system and Hannay’s angle for the mapped classical system in Section 2. In Section 3, we generalize and simulate the two kinds of STA methods, TQD and LR invariant-based methods, for quantum systems into the classical system through the quantum−classical mapping and construct a complete theoretical framework for both methods of achieving the STA in classical systems. On one hand, the TQD method which implements the STA by finding an additional Hamiltonian to drive the system can be simulated by adding an additional driving Hamiltonian to keep adiabatic phase trajectories and acquire Hannay’s angle [23, 24]. On the other hand, the LR invariant method which keeps energy eigenstates from a specified initial to the final configuration can also be simulated by manipulating the configurations of classical coupled oscillators [20, 22]. To illustrate these two classical methods, we study the quantum−classical mapping and the two STA methods for a spin-1/2 in a magnetic field, which corresponds to two coupled classical oscillators in Section 4. Finally, we give a conclusion in Section 5.
2 Adiabatic evolution in quantum−classical mapping
We consider an N-level quantum system governed by Hamiltonian
with the probability amplitudes ψn of the state |Ψ⟩ = ∑nψn(t)|ψn⟩ on the bare basis {|ψn⟩} and the mean value energy
with Unk = ⟨ψn|Ek(t)⟩. By the adiabatic theorem, the probability |φk(t)|2 remains unchanged in the adiabatic limit. The phase of the amplitudes φk accumulated via evolution includes a dynamic phase ∫Ek(t)dt and a Berry phase γk = ∫⟨Ek(t)|dtEk(t)⟩dt [56].
This quantum adiabatic evolution can be equivalently mapped into a classical one without losing any physics [45, 46, 52]. If we decompose ψn into real and imaginary parts
The Hamiltonian HC(ψ, ψ*, t) can be transformed into h(q, p, t), and the quantum dynamics in Eq. 1 can be represented by the classical evolution of the “position variable q(t)” and “momentum variable p(t)” in Eq. 3.
The adiabatic evolution of adiabatic states can also be mapped to a classical one. One can introduce a new pair of variables (θ, I) corresponding to the amplitudes on the adiabatic basis by
and the Hamiltonian changes into [52]
where Ek(t) corresponds to the eigenvalues of the Hamiltonian
between the position−momentum variable and action−angle variable, which corresponds to the quantum unitary transformation |Ek(t)⟩ = ∑nUnk(t)|ψn⟩ between the adiabatic basis and the bare basis. Under the adiabatic evolution, it has been proved that the two new variables θ(t) and I satisfy the same canonical equations as the angle−action variables in classical mechanics [46], given as follows:
Like the Berry phase, the adiabatic evolution will accumulate a dynamic angle ∫Ek(t)/ℏdt and an additional angle onto the angle variable called Hannay’s angle [57].
where
is the angle connection for Hannay’s angle [51]. The angular brackets ⟨⋯ ⟩θ denote the averaging over all angles θ (this averaging process is called the averaging principle, which can be treated as the classical adiabatic approximation), and ∂t is defined as
So far, a quantum adiabatic evolution and its Berry phase can be perfectly mapped to a classical one and its Hannay’s angle. Next, we will show that the two different methods for the quantum STA can also be mapped to classical systems. It will not only connect the current methods for the classical STA to the quantum ones but also shed more light on the classical methods.
3 Shortcut to adiabaticity: From a quantum to classical system
3.1 Transitionless classical driving
We first discuss the transitionless tracking algorithm. For the non-adiabatic quantum driving, the quantum evolution cannot be restricted to an eigenstate, whatever the initial state is. According to the STA proposed by Berry, for the Hamiltonian
of
To drive state Eq. 11, the first sum in Eq. 12 is exactly the original Hamiltonian
Similarly, for non-adiabatic classical driving, the evolution of the canonical coordinates q and p will also fail to keep the action variable I unchanged without the averaging principle, and their trajectories in the phase space will not follow adiabatic trajectories (see Figure 1B). Accordingly, the action variable I will be conserved in a classical evolution as long as the additional effects caused by the time-dependent canonical transformation are canceled. This means that if we want the Hamiltonian function driving the canonical variables as Eq. 7 without the average principle, the transitionless classical driving (TCD, no transition between action variables) Hamiltonian function can be written as follows [25]:
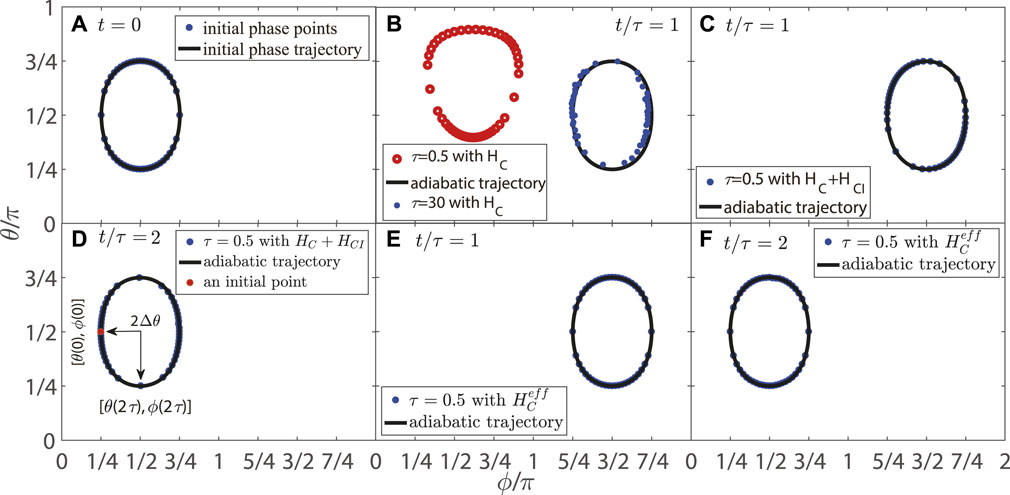
FIGURE 1. (A) Initial phase trajectory (solid line) and initial phase points (blue dots). (B) Final adiabatic trajectory (solid line) and final phase points driven by HC when t/τ = 1, τ = .5 (red dot blanks) and τ = 30 (blue dots). (C) Final adiabatic trajectory (solid line) and final phase points driven by HC + HCI, when t/τ = 1 and τ = .5 (blue dots). (D) Final adiabatic trajectory (solid line) and final phase points driven by HC + HCI, when t/τ = 2 and τ = .5 (blue dots). (E) Final adiabatic trajectory (solid line) and final phase points driven by
With the quantum−classical mapping method we introduced in the last section, we can derive a more explicit form of the TCD Hamiltonian
where ωn = En/ℏ and the angular brackets ⟨⋯ ⟩ denote the averaging over all angle variables
respectively. Like the TQD, the choice of eigenfrequencies ωn can be arbitrary and the geometric angles can be dropped for keeping the actions I conserved [10]. The simplest form of the Hamiltonian driving the canonical coordinates q and p with the conserved action I can be written as follows:
3.2 LR invariant-based scheme
A different approach to realize the quantum STA is based on the LR invariants [8, 58]. For the Hamiltonian
The eigenvalues λn of
via the dynamical evolution. By using the time-dependent unitary evolution operator
the Hamiltonian can be written as follows [8]:
where the second term can be used to drive the eigenstates |λn(t)⟩ of
For a classical system, we can also find similar classical time-dependent invariants that satisfy
By introducing a new pair of variables including the time-dependent invariants (ξ, J) (hereafter referred to as LR variables), we have the following canonical equations:
where G(ξ, t) = HC(ξ, J, t) + S(ξ, J, t) is the Hamiltonian after a classical transformation (q(t), p(t)) → (ξ(t), J) with the generating function S(q, I, t). Since Jk are invariants, the Hamiltonian G(ξ, t) does not contain the angle variables ξk. The changes of angles then can be rewritten as follows:
with
To determine the specific form of the classical LR invariant-based scheme, we define the probabilities amplitudes dk of |Ψ⟩ = ∑kdk|λk⟩ on the LR basis {|λk⟩} as
using the quantum−classical mapping method. The canonical transformation (q, p) → (ξ, J) between position−momentum variables and LR variables can correspond to the quantum unitary transformation |λk(t)⟩ = ∑nUnk(t)|ψn⟩ between the adiabatic basis and the bare basis given as follows:
Similar to the classical TQD scheme of the STA, the driving Hamiltonian should cancel the effect of the time-dependent transformation S and generate the angle Δξk. By Eqs 13–23, we have
with
According to the quantum−classical mapping, this classical Hamiltonian of LR invariants method is just the mean value of the quantum LR, given as follows:
Therefore, the form of LR variables can be determined by equating Hd and HC, and the boundary conditions are as follows:
On the contrary, we can design the classical Hamiltonian Hd from the evolution of LR variables to realize the classical LR invariant-based scheme.
4 Spin-1/2 in a magnetic field
To illustrate our results, we consider the adiabatic evolution and STA scheme for a simple two-level quantum system, i.e., a spin-half particle with the magnetic moment μ in an external magnetic field B = B(sin α cos β, sin α sin β, cos α). Its Hamiltonian reads
where
4.1 Transitionless classical driving
As we introduced in the previous section, if the two spin eigenstates |±⟩ are chosen as the basis, the Hamiltonian in Eq. 30 can be mapped to the classical Hamiltonian of a coupled oscillator, given as follows:
with |ψ⟩ = ψ1| − ⟩ + ψ2| + ⟩ and
It is interesting to note that by defining a vector S = (S1, S2, S3) with
the Hamiltonian function can be written as follows:
where the normalization condition of S is
We now move to calculate Hannay’s angle. Since the Hamiltonian in Eq. 30 has two eigenstates,
with eigenenergies −μB and μB, respectively. The canonical transformation (q, p) → (θ, I) and the mapped Hamiltonian function can be written as follows:
We can calculate the forms of variable I by the following:
with q = (q1, q2), p = (p1, p2), θ = (θ1, θ2), I = (I1, I2), and b = B/B.
Therefore, we obtain the angle one-form by Eq. 9, given as follows:
Hannay’s angles can, thus, be obtained by Eq. 10, given as follows:
which differ from the Berry phases in the original quantum Hamiltonian [58] only by a sign.
By Eq. 14, we have the following:
Therefore, we can get the TCD Hamiltonian function
which takes a similar form as the counter-adiabatic driving Hamiltonian for spin-1/2 system Eq. 30. This means that the TCD scheme can be treated like a classical version of the TQD scheme by representing coordinate−momentum variables by the classical “spin” defined by Eq. 33.
We illustrate the evolution of the states through their trajectories in the phase space. The evolution of the points on phase trajectories can be determined by the dynamic equation of classical “spin,” given as follows:
By defining θ = arccos S2 and ϕ = arctan S2/S1, the dynamics of the original Hamiltonian HC takes the following form:
The parameters of the magnetic field B are chosen as
and μB/ℏ = −1.
As shown in Figure 1B, the evolution of the canonical coordinates p and q will keep the action variable I almost unchanged, and their trajectories in the phase space will follow adiabatic trajectories when the frequency is slow.
For the TCD Hamiltonian HC + HCI, the effective magnetic field changes into the following:
The dynamics of the TCD Hamiltonian can, thus, be written as follows:
To drive the eigenstates using HC + HCI, the evolution of the canonical coordinates p and q will keep action variables I unchanged, and their trajectories in the phase space will follow adiabatic trajectories no matter how fast the frequency is (see Figures 1C, D). By tracing the same phase points of the initial phase trajectory (see Figure 1A) and the final adiabatic trajectory, we can find that there is an angle of shift after an adiabatic evolution. Also, the angle of shift after a whole period is double that after half a period.
Moreover, for the simplest Hamiltonian Eq. 41 [dropping the constant term and the term generating the Hannay’s angle Eq. 42], the dynamics of the simplest Hamiltonian
It is easy to find that the adiabatic trajectories will remain unchanged after any period (see Figures 1E, F).
4.2 Classical LR invariant
In the approach of the LR invariant, the eigenstates of the LR invariant parallel to the eigenstates in Eq. 36 can be constructed as follows [8]:
and the LR invariant can be expressed as follows:
In the classical expression of the adiabatic process, without loss of generality, the time-dependent classical invariants can be designed by classical spin Eq. 33 as follows:
where b′ = (sin η cos δ, sin η sin δ, cos η) is the scaling factor with the parameters (η, δ).
The canonical transformation between position−momentum variables (q, p) and LR variables (ξ, J) can be written as follows:
After this canonical transformation, the Hamiltonian h(q, p; B) becomes
We can calculate LR angles accumulated via the evolution process by Eq. 23, given as follows:
According to Eq. 26, the driving Hamiltonian of the LR invariant-based scheme becomes
where
The system invariant boundary conditions in Eq. 29 become
and the driving magnetic field in the Hamiltonian H can be chosen as
to realize the evolution from initial energy eigenstates |λn(0)⟩ to final energy eigenstates |λn(T)⟩.
By equating Hamiltonian Hd Eq. 56 and
In particular, there is still arbitrariness in the choice of parameters η and δ. To illustrate the adiabatic evolution driven by Eq. 56, we make the invariants of the initial and final moments satisfy the boundary conditions and Eq. 60. For example, to transfer the state from the first oscillator with canonical variables q1 and p1 to the second oscillator with canonical variables q2 and p2, we can set
To illustrate this result, we choose two different configurations of time-dependent parameters as shown in Figure 2. The first set of parameters
in Figure 2A which implements the adiabatic invariance of action variables can reproduce the evolution manipulated by the TQD Hamiltonian Eq. 43 as shown in Figure 2B. The action variables Ji exactly follow the adiabatic trajectories. The evolution of the phase trajectory is just like that in Figures 1A, E driven by
in Figure 2C can also realize the state transfer between the two oscillators with a nearly unchanged δ. Thus, the optional form of the parameters to implement the adiabatic invariance is not unique. These results can be perfectly related to the LR invariant method for the spin-1/2 system [59].
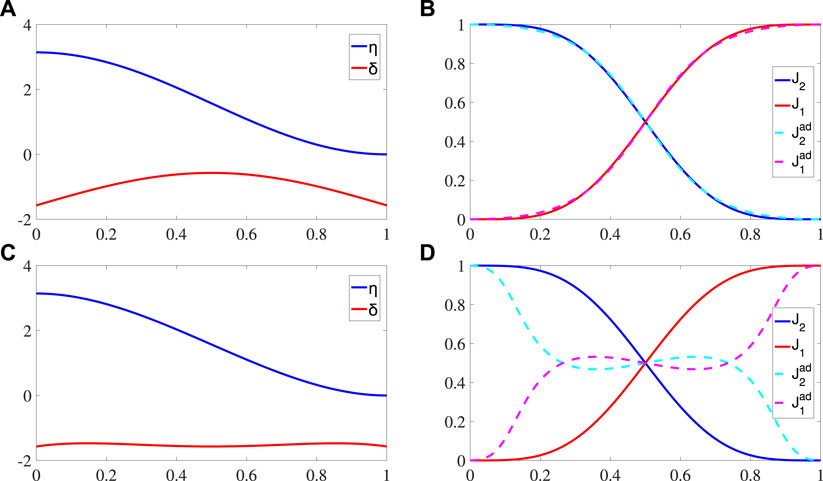
FIGURE 2. (A−C) Evolution of the parameters η (solid blue line) and δ (solid red line). (B−D) Time evolution of the action variables J1 (solid red line), J2 (solid blue line) driven by Hd, and adiabatic approximate invariants
5 Conclusion
To sum up, we use the quantum−classical mapping method to simulate the two schemes of the STA, i.e., the TQD and quantum LR invariant method, by the classical system consisting of coupled oscillators. On one hand, for the TQD, which implements the STA by finding an additional Hamiltonian to drive the system, we derived the explicit form of an additional driving Hamiltonian to keep the evolution of adiabatic phase trajectories and acquire the Hannay’s phase. This TCD method can perfectly simulate and match the TQD method. On the other hand, the Lewis−Riesenfeld invariant method, which keeps the energy eigenstates from a specified initial to the final configuration, can also be simulated by manipulating the configurations of classical coupled oscillators. Both of the approaches can accelerate the adiabatic process effectively under different circumstances and matches the quantum methods of the STA. These results prove that the protocol of the quantum−classical mapping can be used to generalize quantum schemes of the STA into the classical system. By this simulation, our theory could be expected to find applications of the STA for classical systems.
Data availability statement
The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding authors.
Author contributions
HL and HS initiated the idea. YL and HL wrote the main manuscript text. YL and YZ performed the calculations.
Funding
This work was supported by the National Natural Science Foundation of China (Contact Nos. 11875103 and 12147206).
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
1. Li YC, Chen X. Shortcut to adiabatic population transfer in quantum three-level systems: Effective two-level problems and feasible counterdiabatic driving. Phys Rev A (2016) 94:063411. doi:10.1103/PhysRevA.94.063411
2. Král P, Thanopulos I, Shapiro M. Colloquium: Coherently controlled adiabatic passage. Rev Mod Phys (2007) 79:53–77. doi:10.1103/RevModPhys.79.53
3. Saffman M, Walker TG, Mølmer K. Quantum information with rydberg atoms. Rev Mod Phys (2010) 82:2313–63. doi:10.1103/RevModPhys.82.2313
4. Vitanov NV, Rangelov AA, Shore BW, Bergmann K. Stimulated Raman adiabatic passage in physics, chemistry, and beyond. Rev Mod Phys (2017) 89:015006. doi:10.1103/RevModPhys.89.015006
5. Chen X, Ruschhaupt A, Schmidt S, del Campo A, Guéry-Odelin D, Muga JG. Fast optimal frictionless atom cooling in harmonic traps: Shortcut to adiabaticity. Phys Rev Lett (2010) 104:063002. doi:10.1103/PhysRevLett.104.063002
6. Longuet-Higgins HC, Öpik U, Pryce MHL, Sack RA. Studies of the jahn-teller effect. ii. the dynamical problem. Proc R Soc A: Math Phys Eng Sci (1958) 244 (1236):1–16. doi:10.1098/rspa.1958.0022
7. Pancharatnam S. Generalized theory of interference, and its applications. Proc Indian Acad Sci A (1956) 44:247–62. doi:10.1007/BF03046050
8. Chen X, Torrontegui E, Muga JG. Lewis-Riesenfeld invariants and transitionless quantum driving. Phys Rev A (2011) 83:062116. doi:10.1103/PhysRevA.83.062116
9. Rezek Y, Kosloff R. Irreversible performance of a quantum harmonic heat engine. New J Phys (2006) 8:83. doi:10.1088/1367-2630/8/5/083
10. Berry MV. Transitionless quantum driving. J Phys A: Math Theor (2009) 42:365303. doi:10.1088/1751-8113/42/36/365303
11. Ban Y, Chen X, Sherman EY, Muga JG. Fast and robust spin manipulation in a quantum dot by electric fields. Phys Rev Lett (2012) 109:206602. doi:10.1103/PhysRevLett.109.206602
12. Ban Y, Jiang LX, Li YC, Wang LJ, Chen X. Fast creation and transfer of coherence in triple quantum dots by using shortcuts to adiabaticity. Opt Express (2018) 26:31137–49. doi:10.1364/OE.26.031137
13. Chen X, Jiang RL, Li J, Ban Y, Sherman EY. Inverse engineering for fast transport and spin control of spin-orbit-coupled bose-einstein condensates in moving harmonic traps. Phys Rev A (2018) 97:013631. doi:10.1103/PhysRevA.97.013631
14. Zhang J, Shim JH, Niemeyer I, Taniguchi T, Teraji T, Abe H, et al. Experimental implementation of assisted quantum adiabatic passage in a single spin. Phys Rev Lett (2013) 110:240501. doi:10.1103/PhysRevLett.110.240501
15. del Campo A. Shortcuts to adiabaticity by counterdiabatic driving. Phys Rev Lett (2013) 111:100502. doi:10.1103/PhysRevLett.111.100502
16. del Campo A. Frictionless quantum quenches in ultracold gases: A quantum-dynamical microscope. Phys Rev A (2011) 84:031606. doi:10.1103/PhysRevA.84.031606
17. Chen YH, Shi ZC, Song J, Xia Y. Invariant-based inverse engineering for fluctuation transfer between membranes in an optomechanical cavity system. Phys Rev A (2018) 97:023841. doi:10.1103/PhysRevA.97.023841
18. Lu M, Xia Y, Shen LT, Song J, An NB. Shortcuts to adiabatic passage for population transfer and maximum entanglement creation between two atoms in a cavity. Phys Rev A (2014) 89:012326. doi:10.1103/PhysRevA.89.012326
19. Chen YH, Xia Y, Wu QC, Huang BH, Song J. Method for constructing shortcuts to adiabaticity by a substitute of counterdiabatic driving terms. Phys Rev A (2016) 93:052109. doi:10.1103/PhysRevA.93.052109
20. Deffner S, Jarzynski C, del Campo A. Classical and quantum shortcuts to adiabaticity for scale-invariant driving. Phys Rev X (2014) 4:021013. doi:10.1103/PhysRevX.4.021013
21. Chen X, Lizuain I, Ruschhaupt A, Guéry-Odelin D, Muga JG. Shortcut to adiabatic passage in two- and three-level atoms. Phys Rev Lett (2010) 105:123003. doi:10.1103/PhysRevLett.105.123003
22. Jarzynski C, Deffner S, Patra A, Subaşı Y. Fast forward to the classical adiabatic invariant. Phys Rev E (2017) 95:032122 (3). doi:10.1103/PhysRevE.95.032122
23. Okuyama M, Takahashi K. From classical nonlinear integrable systems to quantum shortcuts to adiabaticity. Phys Rev Lett (2016) 117:070401. doi:10.1103/PhysRevLett.117.070401
24. Jarzynski C. Generating shortcuts to adiabaticity in quantum and classical dynamics. Phys Rev A (2013) 88:040101. doi:10.1103/PhysRevA.88.040101
25. Deng J, Wang Q, Liu Z, Hänggi P, Gong J. Boosting work characteristics and overall heat-engine performance via shortcuts to adiabaticity: Quantum and classical systems. Phys Rev E (2013) 88:062122. doi:10.1103/PhysRevE.88.062122
26. Xiao G, Gong J. Suppression of work fluctuations by optimal control: An approach based on jarzynski’s equality. Phys Rev E (2014) 90:052132. doi:10.1103/PhysRevE.90.052132
27. Olavo L. Quantum mechanics as a classical theory; 2, relativistic theory. Tech. Rep. quant-ph/9503021 (1995).
28. Arnold VI. Mathematical methods of classical mechanics. In: Graduate texts in mathematics, Vol. 60. New York, NY: Springer-Verlag (1978). doi:10.1007/978-1-4757-1693-1
29. Peres A, Terno DR. Hybrid classical-quantum dynamics. Phys Rev A (2001) 63:022101. doi:10.1103/PhysRevA.63.022101
30. Elze HT. Linear dynamics of quantum-classical hybrids. Phys Rev A (2012) 85:052109. doi:10.1103/PhysRevA.85.052109
31. Gil V, Salcedo LL. Canonical bracket in quantum-classical hybrid systems. Phys Rev A (2017) 95:012137. doi:10.1103/PhysRevA.95.012137
32. Kantner M, Mittnenzweig M, Koprucki T. Hybrid quantum-classical modeling of quantum dot devices. Phys Rev B (2017) 96:205301. doi:10.1103/PhysRevB.96.205301
33. Briggs JS, Eisfeld A. Equivalence of quantum and classical coherence in electronic energy transfer. Phys Rev E (2011) 83:051911. doi:10.1103/PhysRevE.83.051911
34. Briggs JS, Eisfeld A. Coherent quantum states from classical oscillator amplitudes. Phys Rev A (2012) 85:052111. doi:10.1103/PhysRevA.85.052111
35. Briggs JS, Eisfeld A. Quantum dynamics simulation with classical oscillators. Phys Rev A (2013) 88:062104. doi:10.1103/PhysRevA.88.062104
36. Briggs JS. Equivalent emergence of time dependence in classical and quantum mechanics. Phys Rev A (2015) 91:052119. doi:10.1103/PhysRevA.91.052119
37. Radonjić M, Prvanović S, Burić N. System of classical nonlinear oscillators as a coarse-grained quantum system. Phys Rev A (2011) 84:022103. doi:10.1103/PhysRevA.84.022103
38. Radonjić M, Prvanović S, Burić N. Hybrid quantum-classical models as constrained quantum systems. Phys Rev A (2012) 85:064101. doi:10.1103/PhysRevA.85.064101
39. Radonjić M, Prvanović S, Burić N. Emergence of classical behavior from the quantum spin. Phys Rev A (2012) 85:022117. doi:10.1103/PhysRevA.85.022117
40. Burić N, Popović DB, Radonjić M, Prvanović S. Orbits of hybrid systems as qualitative indicators of quantum dynamics. Phys Lett A (2014) 378 (16):1081–1084. doi:10.1016/j.physleta.2014.02.037
41. Arsenović D, Burić N, Popović DB, Radonjić M, Prvanović S. Positive-operator-valued measures in the Hamiltonian formulation of quantum mechanics. Phys Rev A (2015) 91:062114. doi:10.1103/PhysRevA.91.062114
42. Polchinski J. Weinberg’s nonlinear quantum mechanics and the einstein-podolsky-rosen paradox. Phys Rev Lett (1991) 66:397–400. doi:10.1103/PhysRevLett.66.397
43. Chruściński D, Jamiołkowski A. Geometric phases in classical and quantum mechanics. In: Progress in mathematical physics, Vol. 36. Boston, MA: Springer Science and Business Media (2012). doi:10.1007/978-0-8176-8176-0
44. Zhang Q, Wu B. General approach to quantum-classical hybrid systems and geometric forces. Phys Rev Lett (2006) 97:190401. doi:10.1103/PhysRevLett.97.190401
45. Heslot A. Quantum mechanics as a classical theory. Phys Rev D (1985) 31:1341–8. doi:10.1103/PhysRevD.31.1341
46. Weinberg S. Testing quantum mechanics. Ann Phys (N Y) (1989) 194:336–86. doi:10.1016/0003-4916(89)90276-5
47. Weinberg S. Precision tests of quantum mechanics. Phys Rev Lett (1989) 62:485–8. doi:10.1103/PhysRevLett.62.485
48. Wu B, Liu J, Niu Q. Geometric phase for adiabatic evolutions of general quantum states. Phys Rev Lett (2005) 94:140402. doi:10.1103/PhysRevLett.94.140402
49. Zhang Q, Wu B. General approach to quantum-classical hybrid systems and geometric forces. Phys Rev Lett (2006) 97:190401. doi:10.1103/PhysRevLett.97.190401
50. Stone M. Born-oppenheimer approximation and the origin of wess-zumino terms: Some quantum-mechanical examples. Phys Rev D (1986) 33:1191–4. doi:10.1103/PhysRevD.33.1191
51. Gozzi E, Thacker WD. Classical adiabatic holonomy and its canonical structure. Phys Rev D (1987) 35:2398–406. doi:10.1103/physrevd.35.2398
52. Liu HD, Wu SL, Yi XX. Berry phase and hannay’s angle in a quantum-classical hybrid system. Phys Rev A (2011) 83:062101. doi:10.1103/PhysRevA.83.062101
53. Heslot A. Quantum mechanics as a classical theory. Phys Rev D (1985) 31:1341–8. doi:10.1103/PhysRevD.31.1341
54. Strocchi F. Complex coordinates and quantum mechanics. Rev Mod Phys (1966) 38:36–40. doi:10.1103/RevModPhys.38.36
55. Dirac PAM, Bohr NHD. The quantum theory of the emission and absorption of radiation. Proc R Soc Lond A (1927) 114:243–65. doi:10.1098/rspa.1927.0039
56. Berry MV. Quantal phase factors accompanying adiabatic changes. Proc R Soc Lond A (1984) 392 (1802):45–57. The Royal Society London. doi:10.1098/rspa.1927.0039
57. Berry MV. Classical adiabatic angles and quantal adiabatic phase. J Phys A: Math Gen (1985) 18:15–27. doi:10.1088/0305-4470/18/1/012
58. Lewis HR, Riesenfeld W. An exact quantum theory of the time-dependent harmonic oscillator and of a charged particle in a time-dependent electromagnetic field. J Math Phys (1969) 10:1458–73. doi:10.1063/1.1664991
Appendix: Derivation of the Schrödinger equation in the canonical form
The dynamical evolution of the N-level quantum system governed by the Hamiltonian
which can be expanded by the quantum state |Ψ⟩ = ∑ψn(t)|ψn⟩ as follows:
with the probability amplitudes ψn on the bare basis {|ψn⟩}. Since {|ψn⟩} is a time-independent bare basis, Eq. 64 becomes
Multiplying Eq. 65 by ⟨ψm|, we have the following:
with
which is just the same as Eq. 1.
Keywords: shortcut to adiabaticity, quantum−classical mapping, transitionless quantum driving, Lewis−Riesenfeld invariant, geometric phase
Citation: Liu Y, Zhang YN, Liu HD and Sun HY (2023) Simulation of quantum shortcuts to adiabaticity by classical oscillators. Front. Phys. 10:1090973. doi: 10.3389/fphy.2022.1090973
Received: 06 November 2022; Accepted: 28 December 2022;
Published: 13 January 2023.
Edited by:
Libin Fu, Graduate School of China Academy of Engineering Physics, ChinaReviewed by:
Arkajit Mandal, Columbia University, United StatesYue Ban, Basque Research and Technology Alliance (BRTA), Spain
Copyright © 2023 Liu, Zhang, Liu and Sun. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: H. D. Liu, bGl1aGQxMDBAbmVudS5lZHUuY24=; H. Y. Sun, c3VuaHk1MDdAbmVudS5lZHUuY24=
 Yang Liu
Yang Liu Y. N. Zhang1,2
Y. N. Zhang1,2 H. D. Liu
H. D. Liu