- 1China University of Petroleum East China, Qindao, China
- 2Institute of Computing Science and Technology, Guangzhou University, Guangzhou, China
- 3Department of Mathematics, University of Mazandaran, Babolsar, Iran
The cubic fuzzy graph structure, as a combination of cubic fuzzy graphs and fuzzy graph structures, shows better capabilities in solving complex problems, especially in cases where there are multiple relationships. The quality and method of determining the degree of vertices in this type of fuzzy graphs simultaneously supports fuzzy membership and interval-valued fuzzy membership, in addition to the multiplicity of relations, motivated us to conduct a study on the regularity of cubic fuzzy graph structures. In this context, the concepts of vertex regularity and total vertex regularity have been informed and some of its properties have been studied. In this regard, a comparative study between vertex regular and total vertex regular cubic fuzzy graph structure has been carried out and the necessary and sufficient conditions have been provided. These degrees can be easily compared in the form of a cubic number expressed. It has been found that the condition of the membership function is effective in the quality of degree calculation. In the end, an application of the degree of vertices in the cubic fuzzy graph structure is presented.
1 Introduction
Graphs have many applications in different fields such as computers, systems analysis, networks, transportation, operations research, and economics. Graphs are usually used to model relationships among objects. But there are many issues that are vague and uncertain as a result of the information loss, lack of evidence, incomplete statistical data, etc. In general, uncertainty exists in many real life problems and is an integral part of them. In a classical graph, for each vertex or edge, the probability of uncertainty existence or non-existence is assumed. Therefore, classical graphs cannot model uncertain problems. However, often real-life problems are uncertain, which makes it difficult to model using conventional methods. Zadeh [1] presented an extended version of sets, called fuzzy set (FS), where objects have different degrees of membership between zero and one. This concept quickly found wide applications in computer science, information science, system science, management science, theoretical mathematics and other fields of sciences. A decade after the introduction of FS, Zadeh [2] presented an interval-valued fuzzy set (IVFS) as a branch of FS in which an interval between 0 and 1 was used as the membership value instead of a fuzzy number. These two concepts gave rise to different types of graphs called fuzzy graphs, which were first introduced by Kaufman [3] in 1973. Later, fuzzy graph theory was developed as a generalization of graph theory by Rosenfeld [4] in 1975. He explained some concepts including tree, cut vertex, cycle, bridge, and end vertex in fuzzy graphs. The researchers studied different types of fuzzy graphs. Talebi [5] had a study on Kayley fuzzy graph. Borzooei et al. [6] had many studies on vague graphs. Atanassov [7] introduced the concept of intuitionistic fuzzy set (IFS) as a generalization of FS. Akram and Dudek [8] gave the idea of an interval-valued fuzzy graph (IVFG) in 2011. Talebi et al. [9, 10] introduced some new concepts of interval-valued intuitionistic fuzzy graph (IVIFG). Kosari et al. [11–13] studied new results in vague graph and vague graph structures. Some trend concepts in fuzzy graphs were explained by Pal et al. [14]. Samanta et al. [15, 16] reviewed some results from fuzzy k–competition graphs.
Graph structures were presented by Sampathkumar [17] in 2006 as a generalization of signed graphs and graphs with labeled or colored edges. Fuzzy graph structure (FGS) is more important than graph structure because uncertainty and ambiguity in many real-world phenomena often occur as two or more separate relationships. Dinesh [18] introduced the notion of an FGS and discussed some related properties. Ramakrishnan and Dinesh [19] generalized this concept in studies. Akram [20] presented new results on m-polar FGSs. Akram and Akmal [21–23] investigated the concepts of bipolar FGSs and intuitionistic FGSs. Akram et al. [24–28] defined new concepts of operations in FGSs. Kou et al. [29] studied vague graph structure. Continuing his studies in 2020, Denish [30] presented the concept of fuzzy incidence graph structure. Akram and Sitara [31] introduced decision-making with q-rung orthopair FGSs. Sitara and Zafar [32] studied the application of q-rung picture FGSs in airline services.
Fuzzy graphs were previously limited to one or more degrees of fuzzy membership or interval-valued fuzzy membership. Jun et al. [33] introduced the idea of a cubic fuzzy set (CFS) in the form of a combination of FS and IVFS, serving as a more general tool for modeling uncertainty and ambiguity. By applying this concept, various problems that arise from uncertainties can be solved and the best choice can be made using CFS in decision making. Jun et al. [34] combined the neutrosophic complex with CFS and proposed the idea of neutrosophic CFS. Jun et al., also, studied some CFS-based algebraic features including cubic IVIFSs [35], cubic structures [36], cubic sets in semigroups [37], cubic soft sets [38], and cubic intuitionistic structures [39]. Muhiuddin et al. [40] presented the stable CFSs idea. Kishore Kumar et al. [41] examined the regularity concept in CFG. Rashid et al. [42] introduced the concept of a CFG where they introduced many new types of graphs and their applications. A modified definition of a CFG is given by Muhiuddin et al [43] along with concepts such as the strong edge, path, path strength, bridge, and cut vertex. Rashmanlou et al [44] explained some of the concepts of the CFG.
The concept of node order and degree plays an important role in graph theory and its applications, including the analysis of social networks, road transmission networks, wireless networks, etc. Vertex degree is an accepted concept to represent the total number of relations of a vertex in a graph that can be used in graph analysis. Gani and Radha [45] offered the notation of the regular FG. Samanta and Pal [46] introduced the concept of the irregular bipolar fuzzy graphs. Borzooei et al. [47] investigated the Regularity of vague graphs. Gani and Lathi [48] defined the concept of irregularity, total irregularity, and total degree in an FG. Huang et al. [49] studied regular and irregular Neutrozophic graphs with real applications. Samanta et al. [50] investigated the completeness and regularity of generalized fuzzy graphs. These concepts have been gradually developed by researchers into different types of FGs.
Cubic fuzzy graph structure (CFGS), as a combination of FGS and CFG, has better flexibility in modeling and solving problems in ambiguous and uncertain fields. The study of regularity in the CFGS that supports multiple relationships is important and decisive in its own way. In fact, checking regularity is essential from the point of view that most of the issues around us are composed of several different relationships. The quality and method of determining the degree of the vertices in the cubic fuzzy graph structure, has fuzzy membership and interval-valued fuzzy membership at the same time besides the multiplicity of existing relations, made us carry out a study on the regularity of cubic fuzzy graph structures. In this paper, we introduce regularity in a CFGS. We were able to investigate the corresponding properties by defining the degree of a vertex and the total degree of a vertex. In the following, by introducing the order and size in the CFGS, some relevant results were studied. Finally, an application of the CFGS in the detection of bank criminals is presented.
2 Preliminaries
In this section, we have an overview of the basic concepts in fuzzy graphs in order to enter the main discussion.
A graph is a pair of G = (V, E), where V is a non-empty set of vertices and E is the set of edges of G. A graph structure (GS) of X = (V, E1, E2, …, Ek) consists of a set V with relations of E1, E2, …, Ek on V, all of which are mutually disjoint and each Ei is irreflexive and symmetric, for i = 1, 2, …, k. If (x, y) ∈ Ei for some i = 1, 2, …, k, then, it is called an Ei−edge and is simply written xy. A GS is complete whenever each Ei−edge appears at least once and between each pair of vertices of x, y ∈ V, xy ∈ Ei for some i = 1, 2, …, k. A path between two vertices of x and y consisting of only Ei−edges is named Ei−path. Reciprocally, Ei−cycle is a cycle consisting of only Ei−edges. A GS is a tree, if it is connected and contains no cycle. If the subgraph structure induced by Ei−edges is a tree, then, it is an Ei−tree. A GS is an Ei−forest, if the subgraph structure induced by Ei−edges is a forest [17].
A fuzzy graph (FG) on V is a pair of G = (τ, μ), where τ is a fuzzy subset (FS) of V and μ is a fuzzy relation on τ so that μ(x, y) ≤ τ(x) ∧ τ(y), ∀x, y ∈ V. The underlying crisp graph of G is the graph G* = (τ*, μ*), where τ* = {x ∈ ∣τ(x) > 0} and μ* = {xy ∈ V × V∣μ(xy) > 0}. An FG S = (λ, η) on V is a partial fuzzy subgraph of G if λ ≤ τ and η ≤ μ. A fuzzy subgraph S is a spanning fuzzy subgraph of G if τ = λ [14].
An interval-valued fuzzy set (IVFS) A on V is described by
where α and β are FSs of V so that α(x) ≤ β(x) for all x ∈ V. [14]
A cubic fuzzy set (CFS) [33]
where [α(z), β(z)] is named the interval-valued fuzzy membership degree and γ(z) is named the fuzzy membership degree of z, so that α, β, γ: V → [0, 1].
The CFS
Definition 2.1 [19]. Let Z = (V, E1, E2, …, Ek) be a GS. Then,
If ab ∈ supp(φi), then, ab is called a φi−edge of
Definition 2.2 [43]. A cubic fuzzy graph (CFG) on a non-empty set V is a pair of
Definition 2.3. Let V be a non-empty set and G* = (V, E1, E2, …, Ek) be a GS. Then,
If
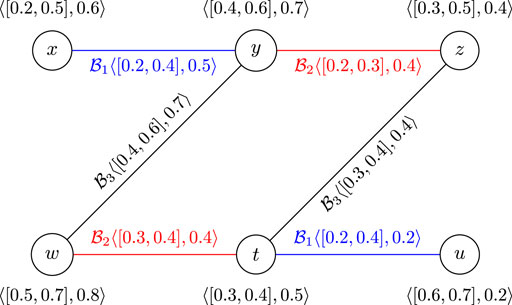
Example 2.4. Consider the GS G* = (V, E1, E2, E3) where V = {x, y, z, t, u, w}, E1 = {xy, tu}, E2 = {yz, tw}, and E3 = {wy, tz}. We define the CFSs
Then, the CFGS
Definition 2.5. A CFGS
If
Definition 2.6. A CFGS
Definition 2.7. A CFGS
Some abbreviations in the article are listed in Table 1.
3 Vertex regularity in cubic fuzzy graph structures
In this section, vertex regularity in cubic fuzzy graph structures is discussed and some of its properties are examined.
Definition 3.1. Let
Also,
The full-degree z is defined as
Definition 3.2. Let
Considering the membership degree of the vertex, we define the total degree of the vertex as follows:
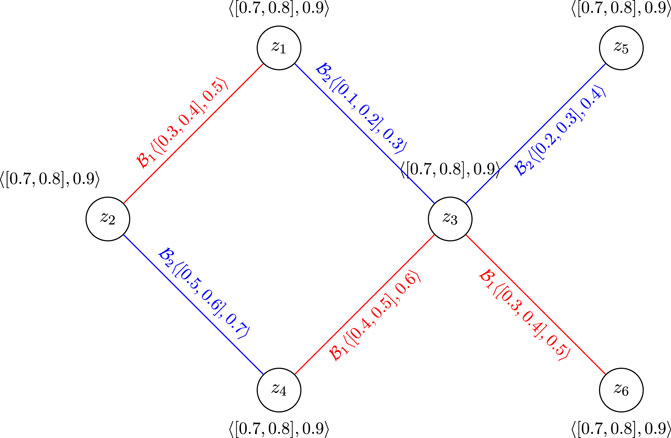
Example 3.3. Consider CFGS
The
Definition 3.4. Let
Also, total
where
The totally full-degree z is defined as
Definition 3.5. Let
The following definitions determine the maximum or minimum degree of a vertex in CFGS.
Definition 3.6. Let
Also, the minimum vertex
where
Definition 3.7. Let
Also, the maximum vertex
Definition 3.8. Let
Also, the minimum total vertex
where
Definition 3.9. Let
Also, the maximum total vertex
where
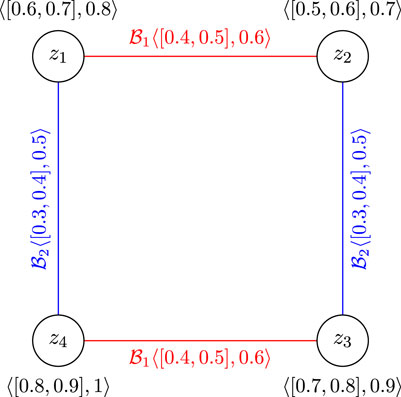
Example 3.10. Consider CFGS of
The total
Remark 3.11. A CFGS
and
Also,
and
Theorem 3.12. Let
Proof. Suppose
Thus, by definition
Therefore,
Hence,
The following example shows that the opposite of the above theorem is not necessarily true.
Example 3.13. Consider CFGS
Here,
Definition 3.14. Let
Remark 3.15. The
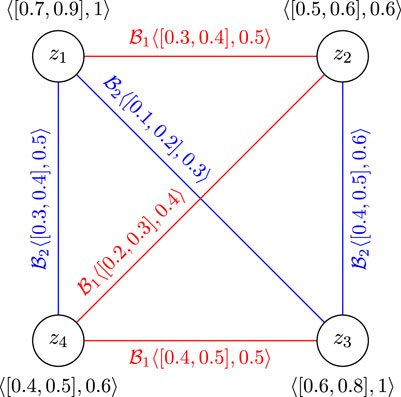
Example 3.16. Consider the CFGS
Theorem 3.17. Let
(1)
(2)
Proof. Suppose
(1) ⇒ (2) Let
On the other hand, we have
Therefore,
Therefore,
Thus,
Since
Corollary 3.18. Let
(1)
(2)
Proof. It is proved similar to the above theorem.
Corollary 3.19. Let
Definition 3.20. The order of a CFGS
The
The size of a CFGS
Theorem 3.21. Let
Proof. Suppose
On the other hand,
Therefore,
Hence,
Theorem 3.22. Let
Proof. Suppose
Therefore,
Correspondingly,
Example 3.23. Consider CFGS
Therefore,
Corollary 3.24. Let
Proof. The result is obtained from the above theorems.
4 Application
In today’s world, consumers demand instant access to services and money transfers, which provides opportunities for criminals. For example, payment service programs try to deliver money to users as quickly as possible while ensuring that money is not sent for illegal purposes. This requires real-time fraud detection.
Fraud detection is a process that identifies fraudsters and prevents their fraudulent activities. The implementation of this process is very important in banking, insurance, medicine and also government organizations.
Money laundering, cyber attacks, fake bank transactions and checks, identity theft and many other illegal activities are called fraudulent activities. As a result, organizations are implementing modern fraud detection and prevention technologies and risk management strategies to combat this growing fraudulent activity across multiple platforms.
These techniques employ adaptive and predictive analytics (machine learning) to detect fraud. This enables continuous monitoring of transactions and crimes in real-time condition and can also help decipher new and complex preventive measures through automation.
Graphs are the most widely used tools for visualization and analysis of complex communication data. This wide range of functions has made graphs one of the most useful tools in detecting financial corruption and fraud today. In large economic networks, in order to gain an intuition of the totality of relationships between entities and simultaneously access details, only a graph with the correct settings and readability can be useful. When looking at trades with graph technology, it is not just trades that can be modeled on graphs. Graphs are very flexible, denoting the fact that surrounding heterogeneous information can also be modeled. For example, customers’ IP addresses, ATM geographic locations, card numbers, and account IDs can all become nodes, and each type of connection can be an edge.
A CFGS can be used for fraud detection, especially in on line banking and ATM location analysis, because users can design fraud detection rules based on data sets. The following relationships are taken into account in the review of banking transactions of a bank’s customers:
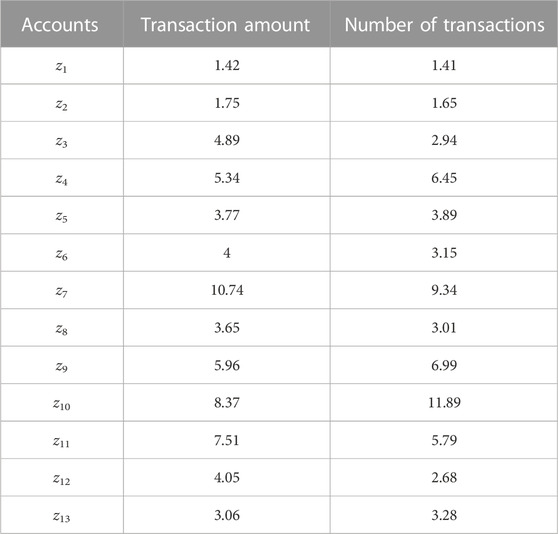
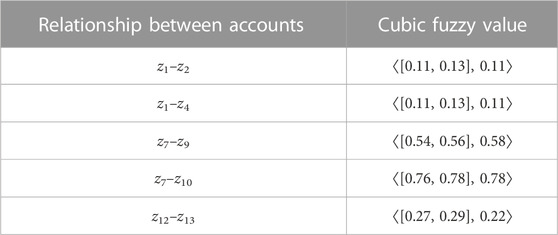
Today, by monitoring information and data, it is easy to obtain the statistics of banks and interbanks payments. One of these statistics is the number and amount of bank transactions in the payment network and the share of each account in these transactions. Table 2 shows some suspicious accounts found in the investigation of a bank, as well as the percentage share of each account in the total number and amount of related transactions.
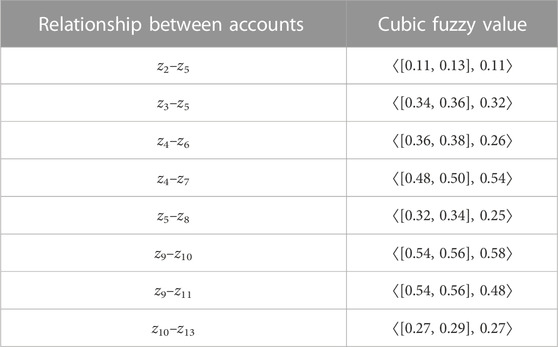
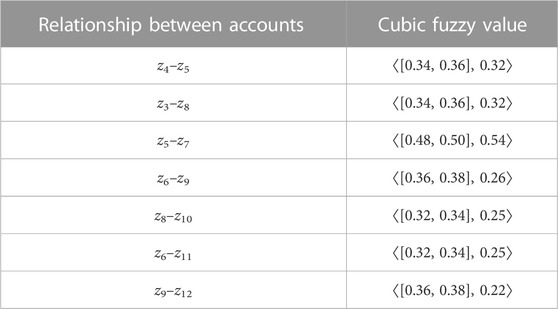
The cubic fuzzy values of each account are given in Table 3. To fuzzify the numbers, dividing each number by the maximum number is used. As in the connection between the accounts, the strongest connections were intended, therefore, all the edges are considered strong.The cubic fuzzy values related to each of the relations of
Considering accounts as vertices and relationships of
By examining the degrees of vertices, it is determined that:
The maximum
The maximum
The maximum
5 Conclusion
Cubic fuzzy graph structure (CFGS) as a combination of fuzzy graph structure and cubic fuzzy graph, has a better flexibility in modeling and solving problems in ambiguous and uncertain fields. In this article, we introduced vertex regularity in CFGS and examined their characteristics. Also, the total vertex regularity in CFGS is discussed and its results are studied. In this regard, a comparative study has been conducted between vertex regular and total vertex regular CFGSs and some necessary and sufficient conditions have been provided. These degrees are expressed as a cubic number so that they can be easily compared. It has been found that the membership function conditions in CFGS are effective in the degree calculation quality. The results show that some properties of vertex regular CFGSs are not true for the total vertex regular CFGSs. In our future work, we intend to express the properties of product operations on CFGSs.
Data availability statement
The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.
Author contributions
LL contributed to supervision, methodology, project administration, and formal analyzing. SK and SS contributed to investigation, resources, computations, and wrote the initial draft of the paper, which was investigated and approved by AT, who wrote the final draft. All authors have read and agreed to the submitted version of the manuscript.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
2. Zadeh LA. The concept of a linguistic variable and its application to approximate reasoning–I. Inf Sci (1975) 8(3):199–249. doi:10.1016/0020-0255(75)90036-5
3. Kauffman A Introduction a la Theorie des Sous-Emsembles Flous, 1. French: Masson: Issy-les-Moulineaux (1973).
4. Rosenfeld A Fuzzy Graphs, Fuzzy Sets and Their Applications. New York, NY, USA: Academic Press (1975). p. 77–95.
5. Talebi AA. Cayley fuzzy graphs on the fuzzy groups. Comp Appl Math (2018) 37(4):4611–32. doi:10.1007/s40314-018-0587-5
6. Borzooei RA, Rashmanlou H. New concepts of vague graphs. Int J Mach Learn Cybern (2016) 8(4):1081–92. doi:10.1007/s13042-015-0475-x
7. Atanassov K. Intuitionistic fuzzy sets. Fuzzy Sets Syst (1986) 20:87–96. doi:10.1016/s0165-0114(86)80034-3
8. Akram M, Dudek WA. Interval-valued fuzzy graphs. Comput Math Appl (2011) 61(2):289–99. doi:10.1016/j.camwa.2010.11.004
9. Talebi AA, Rashmanlou H, Sadati SH. New concepts on m-polar interval-valued intuitionistic fuzzy graph. TWMS J Appl Eng Math (2020) 10(3):808–16.
10. Talebi AA, Rashmanlou H, Sadati SH. Interval-valued intuitionistic fuzzy competition graph. J Multiple-Valued Logic Soft Comput (2020) 34:335–64.
11. Kosari S, Rao Y, Jiang H, Liu X, Wu P, Shao Z. Vague graph structure with application in medical diagnosis. Symmetry (2020) 12(10):1582–2. doi:10.3390/sym12101582
12. Rao Y, Kosari S, Shao Z. Certain properties of vague graphs with a novel application. Mathematics (2020) 8(10):1647. doi:10.3390/math8101647
13. Kou Z, Kosari S, Akhoundi M. A novel description on vague graph with application in transportation systems. J Math (2021) 2021:11. doi:10.1155/2021/4800499
15. Samanta S, Pal M. Fuzzy k-competition graphs and p-competition fuzzy graphs. Fuzzy Inf Eng (2013) 5(2):191–204.
16. Samanta S, Pal M, Pal A. Some more results on fuzzy k-competition graphs. Int J Adv Res Artif Intell (2006) 3(1):60–67.
18. Dinesh T. A study on graph structures, incidence algebras and their fuzzy analogues Ph.D. Thesis. Kannur, India: Kannur University (2011).
19. Dinesh T, Ramakrishnan T. On generalised fuzzy graph structures. Appl Math Sci (2011) 5(4):173–80.
20. Akram M, 371. Cham: Springer (2019). p. 209–33.m–polar fuzzy graph structuresM-polar Fuzzy Graphs Stud fuzziness soft Comput
21. Akram M, Akmal R. Application of bipolar fuzzy sets in graph structures. Applied Computational Intelligence and Soft Computing (2016).
22. Akram M, Akmal R. Intuitionistic fuzzy graph structures. Kragujevac J Math (2017) 41(2):219–37. doi:10.5937/kgjmath1702219a
23. Akram M, Akmal R. Operations on intuitionistic fuzzy graph structures. Fuzzy Inf Eng (2016) 8(4):389–410. doi:10.1016/j.fiae.2017.01.001
24. Akram M, Sitara M. Certain fuzzy graph structures. J Appl Math Comput (2019) 61(1):25–56. doi:10.1007/s12190-019-01237-2
25. Sitara M, Akram M, Yousaf Bhatti M. Fuzzy graph structures with application. Mathematics (2019) 7(1):63. doi:10.3390/math7010063
26. Akram M, Sitara M, Saeid AB. Residue product of fuzzy graph structures. J Multiple-Valued Logic Soft Comput (2020) 34(3-4):365–99.
27. Koam AN, Akram M, Liu P. Decision-making analysis based on fuzzy graph structures. Math Probl Eng (2020) 2020:1–30. doi:10.1155/2020/6846257
28. Akram M, Sitara M. Novel applications of single-valued neutrosophic graph structures in decision-making. J Appl Math Comput (2018) 56(1):501–32. doi:10.1007/s12190-017-1084-5
29. Kou Z, Akhoundi M, Chen X, Omidi S. A study on vague graph structures with an application. Adv Math Phys (2022) 2022:1–14. doi:10.1155/2022/3182116
31. Akram M, Sitara M. Decision-making with q-rung orthopair fuzzy graph structures. Granul Comput (2021) 7:505–26. doi:10.1007/s41066-021-00281-3
32. Sitara M, Zafar F. Selection of best inter-country airline service using q-rung picture fuzzy graph structures. Comp Appl Math (2022) 41(1):54–32. doi:10.1007/s40314-021-01714-0
34. Jun YB, Smarandache F, Kim CS. Neutrosophic cubic sets. New Math Nat Comput (2017) 13(01):41–54. doi:10.1142/s1793005717500041
35. Jun YB, Song SZ, Kim SJ. Cubic interval-valued intuitionistic fuzzy sets and their application in BCK/BCI-algebras. Axioms (2018) 7(1):7. doi:10.3390/axioms7010007
36. Jun YB, Lee KJ, Kang MS. Cubic structures applied to ideals of BCI-algebras. Comput Math Appl (2011) 62(9):3334–42. doi:10.1016/j.camwa.2011.08.042
37. Khan M, Jun YB, Gulistan M, Yaqoob N. The generalized version of Jun’s cubic sets in semigroups. J Intell Fuzzy Syst (2015) 28(2):947–60. doi:10.3233/ifs-141377
38. Ali A, Jun YB, Khan M, Shi FG, Anis S. Generalized cubic soft sets and their applications to algebraic structures. Ital J Pure Appl Math (2015) 35:393–414.
39. Senapati T, Jun YB, Muhiuddin G, Shum KP. Cubic intuitionistic structures applied to ideals of BCI-algebras. Analele Universitatii Ovidius Constanta - Seria Matematica (2019) 27(2):213–32. doi:10.2478/auom-2019-0028
41. Krishna KK, Rashmanlou H, Talebi AA, Mofidnakhaei F. Regularity of cubic graph with application. J Indonesian Math Soc (2019) 1–15. doi:10.22342/jims.25.1.607.1-15
42. Rashid S, Yaqoob N, Akram M, Gulistan M. Cubic graphs with application. Int J Anal Appl (2018) 16(5):733–50.
43. Muhiuddin G, Takallo MM, Jun YB, Borzooei RA. Cubic graphs and their application to a traffic flow problem. Int J Comput Intelligence Syst (2020) 13(1):1265–80. doi:10.2991/ijcis.d.200730.002
44. Rashmanlou H., Muhiuddin G., Amanathulla S. K., Mofidnakhaei F., Pal M. A study on cubic graphs with novel application. Journal of Intelligent & Fuzzy Systems (2021) 40(1):89–101. doi:10.3233/jifs-182929
47. Borzooei RA, Rashmanlou H, Samanta S, Pal M. Regularity of vague graphs. J Intell Fuzzy Syst (2016) 30(6):3681–9. doi:10.3233/ifs-162114
48. Nagoorgani A, Latha SR. Isomorphism on irregular fuzzy graphs. Int J Math Sci Eng Appl (2012) 6(3):193–208.
49. Huang L, Hu Y, Li Y, Kumar PK, Koley D, Dey A. A study of regular and irregular neutrosophic graphs with real life applications. Mathematics (2019) 7(6):551. doi:10.3390/math7060551
Keywords: cubic fuzzy graph structure, ℬi-degree, total ℬi-degree, ℬi-vertex regularity, total ℬi-vertex regularity, perfectly ℬi-vertex regular
Citation: Li L, Kosari S, Sadati SH and Talebi AA (2023) Concepts of vertex regularity in cubic fuzzy graph structures with an application. Front. Phys. 10:1087225. doi: 10.3389/fphy.2022.1087225
Received: 02 November 2022; Accepted: 05 December 2022;
Published: 20 April 2023.
Edited by:
Song Zheng, Zhejiang University of Finance and Economics, ChinaReviewed by:
Madhumangal Pal, Vidyasagar University, IndiaHossein Rashmanlou, Islamic Azad University Central Tehran Branch, Iran
Muhammad Akram, University of the Punjab, Pakistan
Copyright © 2023 Li, Kosari, Sadati and Talebi. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Saeed Kosari, c2FlZWRrb3NhcmkzOEB5YWhvby5jb20=
 Li Li1
Li Li1 Saeed Kosari
Saeed Kosari