- 1Department of Physics and Optoelectronic Engineering, Faculty of Science, Beijing University of Technology, Beijing, China
- 2School of Materials Science and Engineering, Hebei University of Technology, Tianjin, China
Topological semimetals have attracted wide attention due to their potential applications, such as electronic devices and electrocatalysis. Herein, based on the first-principles calculations and symmetry analysis, we first report that ternary compound pnnm-type LiRuO2 is a typical lantern-like nodal wall semimetal. Specifically, without considering spin-orbit coupling (SOC), one-dimensional (1D) two-fold degenerate bands on the ki = ±π (i = x, y) planes form the two-dimensional (2D) topological state (namely, nodal surface) under the constraint of multiple symmetry operations. In addition, the symmetry-enforced nodal network is formed on the kz = ±π planes. Finally, these nodal networks and nodal surfaces are coupled together to form lantern-like nodal walls. Remarkably, these topological states are protected by multiple symmetries, namely, nonsymmorphic two-fold screw-rotational symmetry [S2i (i = x, y)], time-reversal symmetry (T), inversion symmetry (I), glide plane symmetry (σz), and two-fold rotational symmetry (C2x/y). In addition, we further discuss the effect of spin-orbit coupling on the lantern-like nodal walls. We find that even if LiRuO2 contains S2z and T symmetries, these nodal surfaces and nodal networks are still broken. Then, due to the existence of I and T symmetries, Dirac nodal lines and Dirac points are formed in the low-energy region. Therefore, our work indicates that LiRuO2 is an excellent material platform for researching multiple topological states.
1 Introduction
Topological insulators (TIs) have attracted extensive attention in condensed matter physics due to the fact that they possess the Dirac cone feature on some specific surfaces [1–3]. Inspired by TIs, the researchers found that there exist multiple types of crossing points near the Fermi level in some electronic band structures with a metal feature. Under some symmetry operations, such as mirror plane symmetry, glide plane symmetry, and inversion/time-reversal symmetries, these crossing points generate topological states of different dimensions. It is well known that the high-dimensional fermions usually originate from topological states of a lower dimension. Among them, the most typical example is that the one-dimensional Weyl/Dirac nodal line [4–10] is actually formed by countless zero-dimensional Weyl/Dirac points [11–20]. In other words, a two-dimensional nodal surface [21–25] is made up of countless one-dimensional nodal lines. In this case, the classification of topological semimetals is greatly expanded. Thus, topological states with different dimensions exhibit a variety of interesting properties, such as opposite chirality [11–15], Fermi arc or drumhead-like surface states [4–10], and high surface density of states [26–29]. These properties make topological semimetals have important application prospects in electronic devices or electrocatalysis [e.g., hydrogen evolution reaction (HER) and N2 cleavage] [26–31].
It is well known that with the increase of dimensions, topological fermions usually require higher symmetry operations. So far, the topological fermion with the highest dimension has been theoretically proved to be a two-dimensional nodal surface. Wu et al. [21] and Yu et al. [32] analyzed that there exist only three possible for nodal surfaces, namely one (a), two (b), or three (c) nodal surfaces, as shown in Figures 1A–C. At present, in electronic systems, a large number of topological nodal surface semimetals have been reported [21–35], such as hexagonal compounds XTiO2 (X = Li, Na, and K Rb) [22], Ti3Al family [23], quasi-one-dimensional half-metals XYZ3 (X = Ca, Rb, Y = Cr, Cu, and Z = Cl, I) [24], electride Ba4Al5 [25], and Sr5X3 (X = As, Sb, and Bi) [33]. We can find that more nodal surface semimetals only exist in one nodal surface, while reported two and three nodal surfaces are mainly concentrated in phonon systems [36–38]. Interestingly, in these phonon systems, Wang et al. [38] found that P42/nmc-type Li6WN4 material possesses a novel topological phase, namely ideal lantern-like phonons. This lantern-like phonon is composed of two nodal surfaces and two symmetry-enforced nodal networks, as shown in Figure 1D. To the best of our knowledge, this novel topological phase may not have been reported in electronic systems. Therefore, it is urgent to find the real materials with this topological state in the electronic system.
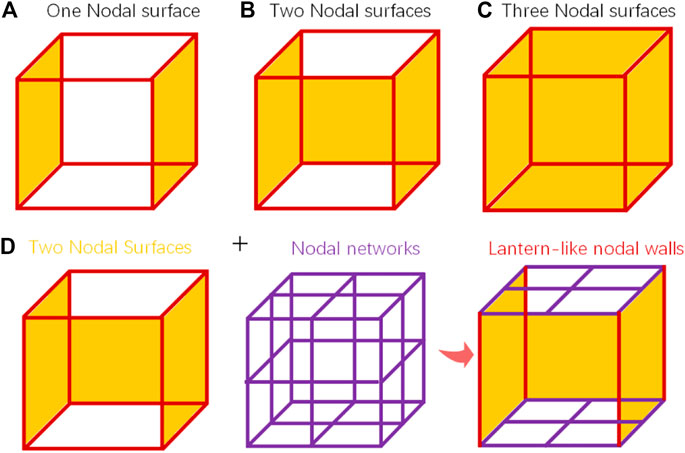
FIGURE 1. (A) Schematic diagrams of (A) one nodal surface, (B) two nodal surfaces, (C) three nodal surfaces, and (D) lantern-like nodal walls.
In this work, we first report that the synthesized ternary compound LiRuO2 possesses this novel type of topological state, namely lantern-like nodal wall. Specifically, in compound LiRuO2, there exist two-fold degenerate bands along k-paths X-S-R-U (kx = π) and Y-S-R-T (ky = π). Under the combined operation of S2x/y and T symmetries, these degenerate bands form two-dimensional nodal surfaces on kx = π and ky = π planes. In addition, a symmetry-enforced nodal network is formed on the kz = π surface due to the existence of a two-fold rotational symmetry (C2x/y) along the kx/y directions, glide plane (σz), inversion-reversal (I), and T symmetry. Finally, two nodal networks and two nodal surfaces form the lantern-like nodal wall. However, when spin-orbit coupling (SOC) is considered, the lantern-like nodal wall is broken and transformed into Dirac points (located at Z point) and Dirac nodal lines (on kz = 0 and ky = π planes) under IT symmetries.
2 Calculations and results
2.1 Crystal and electronic structures
Figures 2A,B show the crystal structure and the Brillouin zone (BZ) of LiRuO2. It possesses a typical orthorhombic structure and belongs to the space group Pnnm (No. 58). The primitive cell of LiRuO2 contains eight atoms [see 3) of Figure 2A], namely, two Li atoms at the 2c Wyckoff position (0,0, and 1/2), two Ru atoms at the 2a Wyckoff position (1/2, 1/2, and 1/2), and four O atoms at the 4 g Wyckoff position (0, 0.67, and 0.75). From the crystal structure, we can find that six O atoms form a tilted octahedron, and Ru atoms are contained in the body center, while Li atoms form a one-dimensional chain along the c-axis [see (I and 2) of Figure 2A]. In fact, LiRuO2 is the final configuration in which the abundant lithium ions are inserted into the anodic material RuO2. Specifically, researchers [39] have proved that RuO2 with a hexagonal structure is an excellent anode material. Then, RuO2 was ground into powder, mixed with Li in proportion, and placed in acetone and dibutyl phthalate to form the final lithium-ion battery LiRuO2 with an orthorhombic structure [see Figure 2C]. Interestingly, we find that LiRuO2 shows abundant degenerate bands near the Fermi level from its electronic band structure. As shown in Figure 2D, the k-paths Y-S-R-T-Y (kx = π), X-S-R-U-X (ky = π), and Z-U-R-T-Z (kz = π) are all two-fold degenerate bands, and these bands are mainly contributed by O atoms of octahedron and Ru atoms of body center, as shown in Figure 2E. Finally, these degenerate bands form a new type of lantern-like nodal wall under multiple symmetric operations.

FIGURE 2. Crystal structure (A) and Brillouin zone (B) of LiRuO2. Among them, the primitive cell (iii) of LiRuO2 is formed by countless O atoms with a tilted octahedron, Ru atoms with a body center, and Li atoms with a one-dimensional chain (ii). (C) Anode material RuO2 with a tetragonal structure forms the final LiRuO2 with an orthorhombic structure by inserting lithium ions. The electronic band structure without SOC (D) and the density of states (E) of LiRuO2, where the arrows point the two-fold degenerate bands of all k-paths.
2.2 Lantern-like nodal wall
Since the lantern-like nodal wall is composed of two nodal networks and two nodal surfaces, we will analyze the two topological states one by one from two aspects of symmetry operations and DFT calculations.
2.2.1 Analysis of symmetry
In space group (SG) 58, the symmetry operations contain: two-fold screw symmetries:
2.2.2 Nodal networks
By DFT calculation, we find that the calculated results in LiRuO2 compound are consistent with the symmetry analysis. Specifically, as shown in Figure 3A, we can find that these bands along k-paths Г-Y, Г-X, Г-Z are single band. Based on group theoretic analysis, the irreducible representations of these single bands are {R1, R2, R3, and R4}. Finally, these single bands form symmetry-enforced two-fold degenerate bands [namely open nodal line] along k-paths Y-S-R-T-Y (kx = π), X-S-R-U-X (ky = π), and Z-U-R-T-Z (kz = π) [See Figure 3B]. In addition, the irreducible representations of these nodal lines on kx = π, ky = π, and kz = π are {R2, R4}, {R6, R8}, and R5, respectively. Due to the existence of Mx/y/z symmetries, these nodal lines finally form the nodal network on different surfaces, as shown in Figure 3C. Remarkably, based on the symmetry analysis and the following DFT verification, the nodal network on the kx/y planes actually belongs to part of the two nodal surfaces. It is well known that a pair of Weyl points of opposite chirality are connected by a one-dimensional Fermi arc, as shown in 1) of Figure 3D. For LiRuO2 compound, these nodal lines on kz = π are composed of countless zero-dimensional Weyl points. Thus, the surface state of nodal line is connected by countless one-dimensional Fermi arcs, namely drumhead-like surface state, as shown in 2) of Figure 3D. In this case, compared with the Weyl semimetals, the surfaces of nodal line semimetals possess higher density of states (DOSs), as shown in 3) of Figure 3D. Based on some reports of topological catalysis [26–31], high surface DOS [namely (001) surface] may possess potential application prospects for the catalytic performance.
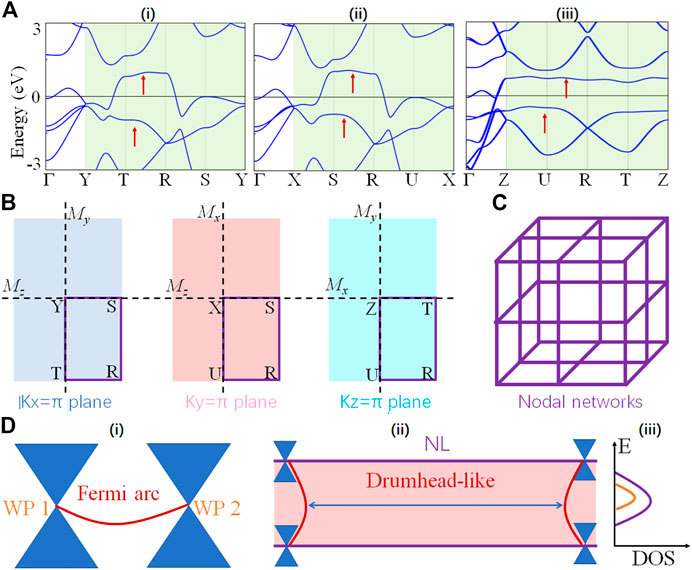
FIGURE 3. (A) Electronic band structures along k-paths (i) Y-S-R-T-Y (kx = π), (ii) X-S-R-U-X (ky = π), and (iii) Z-U-R-T-Z (kz = π) (B) Different surfaces of LiRuO2 in momentum space, where these purple lines represent the node lines. These nodal lines finally form the nodal networks on different surfaces (C). (D) Schematic diagram of the surface states for (i) Wey point (WP) and (ii) nodal line (NL).
2.2.3 Two nodal surfaces
By symmetry analysis, the nodal lines on the kx = π/ky = π planes should belong to a part of two nodal surfaces. In this section, we verify the existence of two nodal surfaces by DFT calculation. Figure 4A shows the electronic band structure along the highly symmetric paths on the kx = π/ky = π planes. Then, we denote the midpoints of the T-S (R-Y) and X-R (U-S) paths as B and D [See Figure 4B]. Obviously, we can clearly observe that the two linear single bands cross at B and D points, as shown in Figure 4C. In other words, the whole surfaces of kx = π/ky = π are double degenerate bands. Furthermore, the three-dimensional dispersion bands on kx = π and kx = 0.8π planes are calculated, as shown in Figure 4D. We find that when on the kx = π plane, the two single bands are combined to form a curved double degenerate surface. On the contrary, the bands on the kx = 0.8π plane evolves into four curved single bands due to the absence of S2x symmetry. Therefore, the aforementioned DFT calculations fully confirm that the kx = π/ky = π planes are the double degenerate surfaces, which agree well with the results of the symmetry analysis. In addition, the surface states of zero-dimensional nodal points and one-dimensional nodal lines are one-dimensional Fermi arcs and two-dimensional drumhead-like, respectively. In other words, the dimension of the surface state is one dimension higher than that of the topological fermion. Since the highest dimension of the projected surface in three-dimensional materials is a two-dimensional surface, there is no surface state for nodal surface.
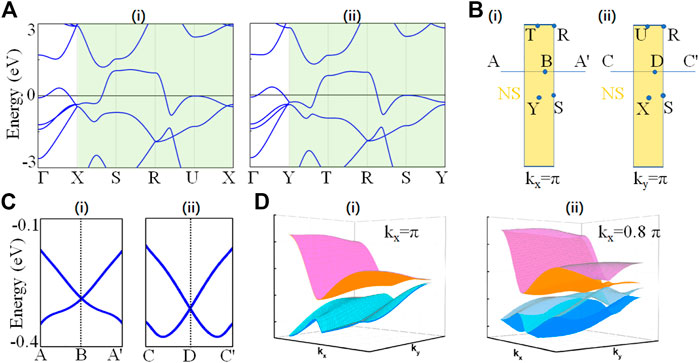
FIGURE 4. (A) Electronic band structures along k-paths (i) Y-S-R-T-Y (kx = π) and (ii) X-S-R-U-X (ky = π) (B) Some symmetry points of (i) kx = π/(ii) ky = π planes for LiRuO2 in momentum space. (C) Electronic band structure along k-paths (i) A-B-A′ and (ii) C-D-C’. (D) Three-dimensional dispersion bands on kx = π and kx = 0.8π planes.
3 Discussions and conclusion
Before concluding the discussion, we also discuss the effect of SOC on the lantern-like nodal wall. As reported by Wu et al. [21], all types of topological nodal surfaces may be destroyed after considering SOC but may be retained in containing the combined nonsymmorphic two-fold screw-rotational and T symmetries. For LiRuO2 compound, we find that even if this material contains S2z and T symmetries, the two nodal surfaces and two nodal networks are broken, as shown in Figure 5A. Due to the existence of IT symmetries, Dirac points and Dirac nodal lines are finally formed on the high symmetric point Z and the k-paths X-S-Y (kz = 0), S-R (ky = π), respectively [See Figures 5B,C]. It is worth noting that these Dirac points and Dirac nodal lines are composed of a pair of Weyl points with opposite chirality (C = ±1). In other words, the Chern number of these Dirac states are 0 (C = 0). That is, these Dirac states do not have topologically protected Fermi arc and drumhead surface states.
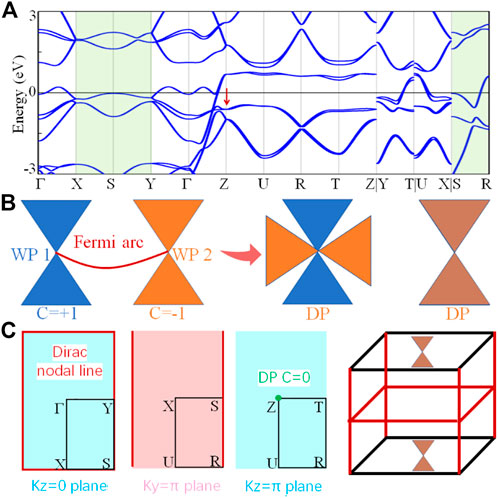
FIGURE 5. (A) Electronic band structures with SOC for LiRuO2 compound. (B) Schematic diagram of a pair of Weyl points with opposite chirality and Dirac point. Among them, the two Dirac points are formed by four single bands and two double degenerate bands. (C) Different surfaces of LiRuO2 in momentum space, where these red lines and green dot represent the node lines and Dirac point, respectively.
In conclusion, we find that two nodal surfaces exist on the kx = ±π and ky = ±π planes of LiRuO2. These nodal surfaces are protected by nonsymmorphic two-fold screw-rotational (S2x/S2y) and T symmetries and are classified to the second class (class-II) of nodal surfaces. In addition, the symmetry-enforced nodal network is formed on the kz = ±π surfaces due to the existence of a two-fold rotational symmetry (C2x/y), glide plane (σz), inversion-reversal (I), and T symmetries. Finally, the two nodal networks and two nodal surfaces form the lantern-like nodal wall.
4 Calculation methods
In this work, the first-principles calculations were performed in the framework of density functional theory (DFT) by using the Vienna ab initio simulation package (VASP) [40, 41]. For ionic potentials, the generalized gradient approximation (GGA) of the Perdew–Burke–Ernzerhof (PBE) method is used [42]. The cutoff energy was adopted as 550 eV, and the Brillouin zone was sampled with Γ-centered k-point mesh of 9 × 9×11 for both structural optimization and self-consistent calculations. The energy convergence criteria were chosen as 10−5 eV. In addition, the DFT + U method was used to calculate the band structures of compound LiRuO2 (URu = 3eV) [43]. We find that the change of the electronic band structure is weak at different U values, which is similar to some of the previous reports [13, 44].
Data availability statement
The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding authors.
Author contributions
HG and WM: manuscript writing, data computing, and data analysis LW: band analysis. JD: modifying the article.
Funding
This study was funded by the Beijing Nova Program (Beijing Municipal Science and Technology Commission, Grant No. Z211100002121079) and Post-graduate’s Innovation Fund Project of Hebei Province (Department of Education of Hebei Province, Grant No. CXZZBS2022036).
Acknowledgments
The authors acknowledge the computational support from the Texas Advanced Computing Center.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
1. Hasan MZ, Kane CL. Colloquium: Topological insulators. Rev Mod Phys (2010) 82:3045–67. doi:10.1103/revmodphys.82.3045
2. Qi X-L, Zhang S-C. Topological insulators and superconductors. Rev Mod Phys (2011) 83:1057–110. doi:10.1103/revmodphys.83.1057
3. Bansil A, Lin H, Das T. Colloquium: Topological band theory. Rev Mod Phys (2016) 88:021004. doi:10.1103/revmodphys.88.021004
4. Wang XT, Yang T, Cheng ZX, Surucu G, Wang J, Zhou F, et al. Topological nodal line phonons: Recent advances in materials realization. Appl Phys Rev (2022) 9:041304. doi:10.1063/5.0095281
5. Jin L, Zhang X, Liu Y, DaiShen XX, Wang L, Liu G, et al. Two-dimensional Weyl nodal-line semimetal in a d0 ferromagnetic K2N monolayer with a high Curie temperature. Phys Rev B (2020) 102:125118. doi:10.1103/physrevb.102.125118
6. Yang SA, Pan H, Zhang F. Dirac and Weyl superconductors in three dimensions. Phys Rev Lett (2014) 113:046401. doi:10.1103/physrevlett.113.046401
7. Yu R, Weng H, Fang Z, Dai X, Hu X. Topological node-line semimetal and Dirac semimetal state in antiperovskite Cu3PdN. Phys Rev Lett (2015) 115:036807. doi:10.1103/physrevlett.115.036807
8. Kim Y, Wieder BJ, Kane CL, Rappe AM. Dirac line nodes in inversion-symmetric crystals. Phys Rev Lett (2015) 115:036806. doi:10.1103/physrevlett.115.036806
9. He T, Zhang X, Wang L, Liu Y, Dai X, Wang L, et al. Ideal fully spin-polarized type-II nodal line state in half-metals X2YZ4 (X=K, Cs, Rb, Y=Cr, Cu, Z=Cl, F). Mater Today Phys (2021) 17:100360. doi:10.1016/j.mtphys.2021.100360
10. Li S, Yu ZM, Liu Y, Guan S, Wang SS, Zhang X, et al. Type-II nodal loops: Theory and material realization. Phys Rev B (2017) 96:081106. doi:10.1103/physrevb.96.081106
11. Armitage N, Mele E, Vishwanath A. Weyl and Dirac semimetals in three-dimensional solids. Rev Mod Phys (2018) 90:015001. doi:10.1103/revmodphys.90.015001
12. Wan X, Turner AM, Vishwanath A, Savrasov SY. Topological semimetal and Fermi-arc surface states in the electronic structure of pyrochlore iridates. Phys Rev B (2011) 83:205101. doi:10.1103/physrevb.83.205101
13. Meng WZ, Zhang XM, Liu Y, Dai XF, Liu GD. Lorentz-violating type-II Dirac fermions in full-Heusler compounds XMg2Ag (X = Pr, Nd, Sm). New J Phys (2020) 22:073061. doi:10.1088/1367-2630/ab9d55
14. Young SM, Zaheer S, Teo JCY, Kane CL, Mele EJ, Rappe AM. Dirac semimetal in three dimensions. Phys Rev Lett (2012) 108:140405. doi:10.1103/physrevlett.108.140405
15. Ding GQ, Zhou F, Zhang ZY, Yu ZM, Wang XT. Charge-two Weyl phonons with type-III dispersion. Phys Rev B (2022) 105:134303. doi:10.1103/physrevb.105.134303
16. Soluyanov AA, Gresch D, Wang ZJ, Wu QS, Troyer M, Dai X, et al. Type-II Weyl semimetals. Nature (2015) 527:495–8. doi:10.1038/nature15768
17. Liu ZK, Zhou B, Wang ZJ, Weng HM, Prabhakaran D, et al. Discovery of a three-dimensional topological Dirac semimetal, Na 3 Bi. Na3bi Sci (2014) 343:864–7. doi:10.1126/science.1245085
18. Gibson Q, Evtushinsky D, Zabolotnyy V, Buchner B, Cava RJ. Experimental realization of a three-dimensional Dirac semimetal. Phys Rev Lett (2014) 113:027603. doi:10.1103/physrevlett.113.027603
19. He TL, Zhang XM, Liu Y, Yu ZM, et al. Ferromagnetic hybrid nodal loop and switchable type-I and type-II Weyl fermions in two dimensions. Phys Rev B (2020) 102:075133. doi:10.1103/physrevb.102.075133
20. Young SM, Kane CL. Dirac semimetals in two dimensions. Phys Rev Lett (2015) 115:126803. doi:10.1103/physrevlett.115.126803
21. Wu WK, Liu Y, LiZhong SC, Yu ZM, Sheng XL et al Nodal surface semimetals: Theory and material realization. Phys Rev B (2018) 97:115125. doi:10.1103/physrevb.97.115125
22. Yang T, Jin L, Liu Y, Zhang XM, Wang XT. Spin-polarized type-II nodal loop and nodal surface states in hexagonal compounds XTiO2 (X= Li, Na, K, Rb). Phys Rev B (2021) 103:235140. doi:10.1103/physrevb.103.235140
23. Zhang XMYZM, Wu WK, Wang SS, Sheng XL, Sheng XL et al Nodal loop and nodal surface states in the Ti3Al family of materials. Phys Rev B (2018) 97:235150. doi:10.1103/physrevb.97.235150
24. He TL, Liu Y, Tian L, Zhang XM, Meng WZ, Dai XF, et al. Coexistence of fully spin-polarized Weyl nodal loop, nodal surface, and Dirac point in a family of quasi-one-dimensional half-metals. Phys Rev B (2021) 103:085135. doi:10.1103/physrevb.103.085135
25. Meng WZ, Zhang XM, Liu Y, Dai XF, Liu GD. Antiferromagnetism caused by excess electrons and multiple topological electronic states in the electride Ba4Al5·e-. Phys Rev B (2021) 104:195145. doi:10.1103/physrevb.104.195145
26. Wang LR, Zhang XM, Meng WZ, Liu Y, Dai XF, Liu GD. A topological quantum catalyst: The case of two-dimensional traversing nodal line states associated with high catalytic performance for the hydrogen evolution reaction. J Mater Chem A Mater (2021) 9:22453–61. doi:10.1039/d1ta06553j
27. Li G, Felser C. Heterogeneous catalysis at the surface of topological materials. Appl Phys Lett (2020) 116:070501. doi:10.1063/1.5143800
28. Li JX, Ma H, Xie Q, Feng SB, Ullah S, Li R et al Topological quantum catalyst: Dirac nodal line states and a potential electrocatalyst of hydrogen evolution in the TiSi family. Sci China Mater (2018) 61:23–9. doi:10.1007/s40843-017-9178-4
29. Rajamathi CR, Gupta U, Kumar N, Yang H, Sun Y, SuB V et al Weyl semimetals as hydrogen evolution catalysts. Adv Mater (2017) 29:1606202. doi:10.1002/adma.201606202
30. Yang Q, Li GW, Manna K, Fan FR, Felser C, Sun Y. Topological engineering of Pt-Group-Metal-Based chiral crystals toward high-efficiency hydrogen evolution catalysts. Adv Mater (2020) 32:1908518. doi:10.1002/adma.201908518
31. Liu W, Zhang XM, Meng WZ, Liu Y, Dai XF, Liu GD. Theoretical realization of hybrid Weyl state and associated high catalytic performance for hydrogen evolution in NiSi. iScience (2022) 25:103543. doi:10.1016/j.isci.2021.103543
32. Yu ZM, Zhang ZY, Liu GB, Wu WK, Li XP, Zhang RW, et al. Encyclopedia of emergent particles in three-dimensional crystals. Sci Bull (2022) 67:375–80. doi:10.1016/j.scib.2021.10.023
33. Khan MR, Bu K, Wang JT, Chen CF. Topological nodal surface semimetal states in Sr5X3 compounds (X=As, Sb, Bi). Phys Rev B (2022) 105:245152. doi:10.1103/physrevb.105.245152
34. Zhong CY, Chen YP, Xie Y, Yang SA, Cohen ML, Zhang SB. Towards three-dimensional Weyl-surface semimetals in graphene networks. Nanoscale (2016) 8:7232–9. doi:10.1039/c6nr00882h
35. Liang QF, Zhou J, Yu R, Wang Z, Weng HM. Node-surface and node-line fermions from nonsymmorphic lattice symmetries. Phys Rev B (2016) 93:085427. doi:10.1103/physrevb.93.085427
36. Xie CW, Yuan HK, Liu Y, Wang XT, Zhang G. Three-nodal surface phonons in solid-state materials: Theory and material realization. Phys Rev B (2021) 104:134303. doi:10.1103/physrevb.104.134303
37. Xie CW, Yuan HK, Liu Y, Wang XT. Two-nodal surface phonons in solid-state materials. Phys Rev B (2022) 105:054307. doi:10.1103/physrevb.105.054307
38. Wang XT, Zhou F, Yang T, Kuang MQ, Yu ZM, Zhang G, et al. Symmetry-enforced ideal lantern-like phonons in ternary nitride Li6WN4. Phys Rev B (2021) 104:L041104. doi:10.1103/physrevb.104.l041104
39. Hu YY, Liu ZG, Nam KW, Borkiewicz OJ, Cheng J, Hua X, et al. Origin of additional capacities in metal oxide lithium-ion battery electrodes. Nat Mater (2013) 12:1130–6. doi:10.1038/nmat3784
40. Kresse G, Joubert D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys Rev B (1999) 59:1758–75. doi:10.1103/physrevb.59.1758
41. Blochl PE. Projector augmented-wave method. Phys Rev B (1994) 50:17953–79. doi:10.1103/physrevb.50.17953
42. Perdew JP, Burke K, Ernzerhof M. Generalized gradient approximation made simple. Phys Rev Lett (1996) 77:3865–8. doi:10.1103/physrevlett.77.3865
43. Anisimov VI, Zaanen J, Andersen OK. Band theory and mott insulators: Hubbard U instead of stoner I. Phys Rev B (1991) 44:943–54. doi:10.1103/physrevb.44.943
Keywords: first-principles calculations, symmetry analysis, topological semimetals, lantern-like nodal walls, multiple-symmetry-protected
Citation: Gao H, Meng W, Wang L and Deng J (2022) Multiple-symmetry-protected lantern-like nodal walls in lithium-rich compound LiRuO2. Front. Phys. 10:1081708. doi: 10.3389/fphy.2022.1081708
Received: 27 October 2022; Accepted: 15 November 2022;
Published: 14 December 2022.
Edited by:
Yong Fang, Changshu Institute of Technology, ChinaReviewed by:
Xiaotian Wang, Southwest University, ChinaZhiming Yu, Beijing Institute of Technology, China
Copyright © 2022 Gao, Meng, Wang and Deng. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Hongli Gao, aGxnYW9AYmp1dC5lZHUuY24=; Weizhen Meng, bXd6MTk5NjA4MThAMTYzLmNvbQ==
 Hongli Gao
Hongli Gao Weizhen Meng
Weizhen Meng Lirong Wang2
Lirong Wang2