Features of the power-law fluid over cylinders in a channel via gap aspects: Galerkin finite element method (GFEM)-based study

The goal of this investigation is to carry out a comprehensive analysis of hydrodynamic forces, with particular attention being paid to the power-law fluid flow across cylinders and presence gap considerations. With the assistance of the Galerkin finite element method (GFEM), the discretization of the two-dimensional system of non-linear partial differential equations was successfully completed. The research is carried out with a significant variance of the flow behavior index $\left(n\right)$ from .3 to 1.7, gap aspects $\left(G_p\right)$ from 0 .0 to .3, and fixed Reynolds number $\left(Re\right)$ 20. To obtain an extremely accurate solution, first, a coarse hybrid computational mesh needs to be developed, and then, more refinement must take place. The selection of the best possible case can be determined by comparing flow patterns, coefficients of drag and lift, and cylinder gaps. The shear-thickening behavior of fluids has a substantially greater influence on the drag characteristics than either the Newtonian or the shear-thinning behavior of fluids do. In addition to this, the shear-thickening action causes the upstream obstacle’s drag coefficient to increase because the gap spacing becomes more widespread.

1 Introduction

Non-linear fluids past over cylinders are being studied by many researchers over the years. Engineering applications are designed and later modified based on the study of hydrodynamic forces and flow configurations. Product qualities are being improved by deep and modified investigations over the years. Flow patterns and their impact are also being investigated around more than one bluff body. It is also significant to note that the arrangement/placement of obstacles in the cross-flow also plays an important role and has a practical use. Extensive work conducted on the non-Newtonian fluid flow around a single cylinder has been summarized in the previous work [1–7]. This work is aimed to increase the stage of complicatedness concerning the nature of fluid and the number of obstacles to investigate the influence of hydrodynamic forces like drag and lift while changing the gap spacing around the circular cylinders in the power-law fluid. Lesser work is available in the literature on the incompressible power-law fluid flowing over cylinders of circular nature in tandem arrangement. Regarding the positioning of the two cylinders, many investigations into non-Newtonian fluids are available [8–12].

The flow around two side-by-side circular cylinders and tandem arrangements of circular cylinders simulated the results for different Reynolds numbers. Using several modeling methodologies based on a computational fluid dynamics solver, the authors suggest that the impacts of flow patterns such as the frequency of primary vortex shedding and the frequency of the secondary cylinder interaction may be seen for flow around two rows of staggered cylinders. The behavior of Reynolds numbers and gap spacing for the flow that occurs between side-by-side cylinders can be found using a numerical study [13–16]. These researchers investigated not only the effects of different gap spacings and Reynolds numbers but also the distinct flow patterns. [17] investigated the characteristics of flow behaviors and the action of fluid forces on two cylinders with a range of staggered configurations.

A lot of computational work has been conducted to investigate drag and lift forces on obstacles in the Newtonian flow field, but analyzing the influence of non-linear viscosity functions on drag and lift is still in its embryonic stage. Because of the examination of a wake, recycling zone length, and drag and lift features, the flow of incompressible flows over cylinders of varied cross-sectional areas makes for an attractive field of study. [18] investigated numerically the effects of the drag component on a heated circular cylinder for Reynolds number $\left(5\le \mathrm{R}\mathrm{e}\le 50\right)$.Determining solutions in the field of rheological fluid is a struggling mission for scientists because the study of flow behaviors around the obstacles with the influence of force parameters (drag and lift) has established the attention of scholars over an insufficient decade [19–21]. [22] analyzed numerically the influence of viscous fluid flows past confined cylinders using the LBM algorithm and also studied the effects of drag components of the cylinders. [23] offered an investigation of the laminar flow and heat transmission that was caused by a long circular cylinder that was either horizontal or vertical. The properties of MHD heat transport in a cavity were studied by [24, 25], who used the Galerkin finite element technique in their research. In addition, there is a general upward tendency in the average Nusselt number along the bottom wall of the tank and the right wall. There have been some interesting advancements in our understanding of the non-linear fluid flow recently, and they can be seen in [26–28].

The purpose of this investigation is to compute the fluid forces based on gap aspects that are exerted over an obstacle that is submerged in a power-law fluid flow. The CFD community has not previously conducted such an analysis of forces in this domain. In view of the numerous commercial uses of flow around dual cylinders, the scope of this work has been narrowed to include only some numerical results. The results of the circular cylinder are used as a point of comparison in this section. The following is the structure of this paper: the mathematical formulation is the topic of discussion in Section 2. In Sections 3 and 4, we will investigate the influence that the computing domain has and the effect that the grid points have. In Section 5, we talk about how the spacing ratio affects the aerodynamic forces, and in Section 6, we present our findings and draw some conclusions.

2 Mathematical formulation

The continuity and momentum equations for the incompressible shear rate model are given in their compact form and are written as follows [31]:

$\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}=0,(1)$

$u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial y}+\frac{\partial p}{\partial x}=\frac{1}{Re}\left(\frac{\partial {\tau }_{xx}}{\partial x}+\frac{\partial {\tau }_{xy}}{\partial y}\right),(2)$

$u\frac{\partial v}{\partial x}+v\frac{\partial v}{\partial y}+\frac{\partial p}{\partial y}=\frac{1}{Re}\left(\frac{\partial {\tau }_{yx}}{\partial x}+\frac{\partial {\tau }_{yy}}{\partial y}\right),(3)$

where

$\mathbf{\tau }=m{\left(\dot{\mathbf{\gamma }}\right)}^n,(4)$

where $m,n,\text{and}\dot{\gamma }$ are the fluid consistency parameter, power law index, and shear rate, respectively. For $n<1,$ the model obtained effects of the shear-thinning fluid, and for $n=1,$ the model decline to Newtonian fluid with constant viscosity. Also, $n>1$ represented the shear-thickening effects in the model.

The involved non-dimensionalized parameters are

$\mathrm{R}\mathrm{e}\equiv \frac{\rho U_{ref}{L}_{ref}}{{\mu }_p},(5)$

$C_D\equiv \frac{2F_d}{\rho U^{2}D},(6)$

$C_L\equiv \frac{2F_l}{\rho U^{2}D},(7)$

where $U_{ref}\text{and}{L}_{ref}$ are the velocity and length reference, and $C_D$ and $C_L$ are the drag and lift coefficient with drag and lift forces denoted by $F_d$ and $F_l,$ respectively.

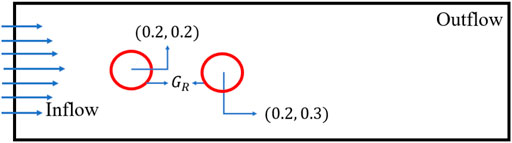
3 Problem description

Consider a channel of dimensions $\left(\mathrm{0,0}\right),\left(\mathrm{2.2,0}\right),\left(\mathrm{0,0.41}\right),\text{and}\left(2.2,0.41\right)$ are defined. The circular obstacle $C_1$ is located fixed at (.2, .2), and $C_2$ is placed with various gap spacings. Both the top and bottom walls of the channel are positioned so that u = v = 0. The inlet of the channel is subjected to an inflow parabolic profile with a maximum u velocity at .3, and a do-nothing boundary condition is selected for the outlet.

Let $D=0.1m$ be the diameter of the obstacles $C_1\text{and}{C}_2$, and also, $G_p$ is a confined space between the obstacles, as shown in Figure 1. This simulation was performed by using $H=4.1D,L_u=2D,L=4D,$ and $L_d=16D$ where $L_u\text{and}{L}_d$ are upstream and downstream distances from the centers of the obstacles to the inflow and outflow edge, respectively. To accurately reflect the hydrodynamic forces acting on the cylinder, additional components surrounding the obstruction are taken into consideration.

FIGURE 1

FIGURE 1. Schematic representation of the problem.

4 Numerical approach

At a constant Reynolds number Re = 20, it is well established that viscous fluid flows are laminar, two-dimensional, and characterized by symmetrical vortices and that these flows have a relatively constant shear rate. The numerical technique has been tested to identify the convergency, accuracy, and consistency of the outputs by evaluating the present study with the literature for viscous fluids. This was conducted in order to determine whether or not the results are convergent, accurate, and reliable.

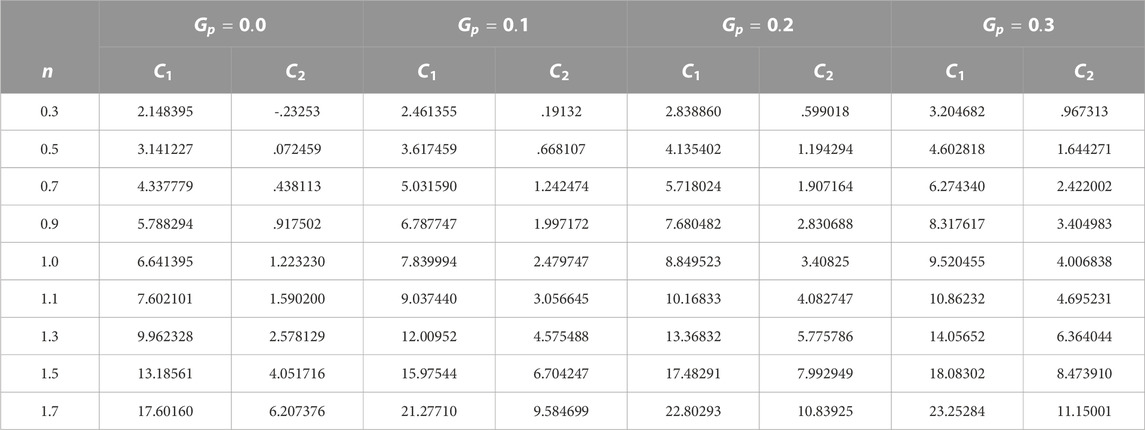
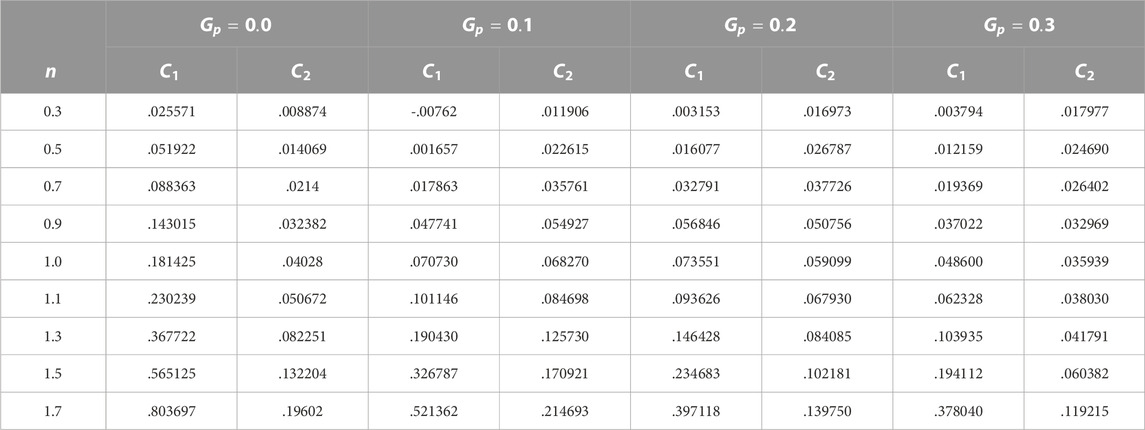
Table 1 shows the comparison between the past literature and current values for the Newtonian scenario, which is useful for code validation. The quantities of the drag coefficient for a single cylinder are maintained at a constant level of $C_D=5.5785$. Meshing is a crucial stage initial to set the boundary conditions for simulation because of the influence of convergence, accuracy, and outcome speed. It is fundamental to have a maximum number of cells. The term “meshing” refers to the process of discretizing a boundary with the intention that it enables the creation of well-shaped pieces. The size of the cell has an enormous impact on how accurately iterations are performed. Whenever the size of the cell is reduced, the accuracy rate increases, but this also considerably leads to the maximum amount of time spent computing. It only aids in the process of breaking down a physical domain into a small discrete volume in which sets of equations can be calculated.

TABLE 1

TABLE 1. Code validation test compared to Majeed et al. [30–36].

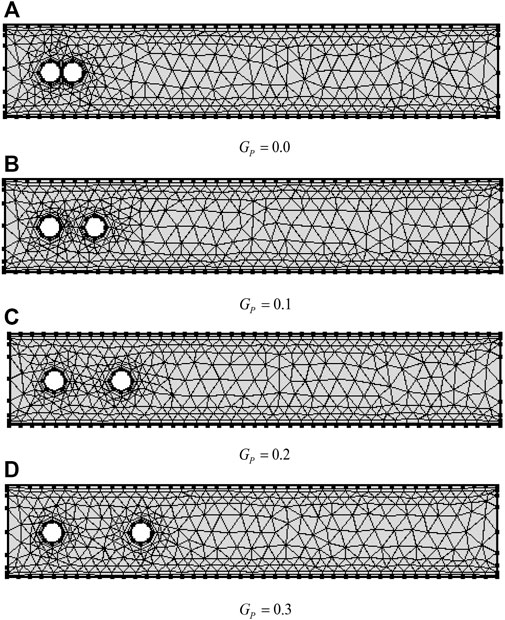
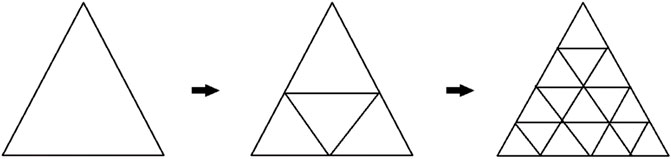
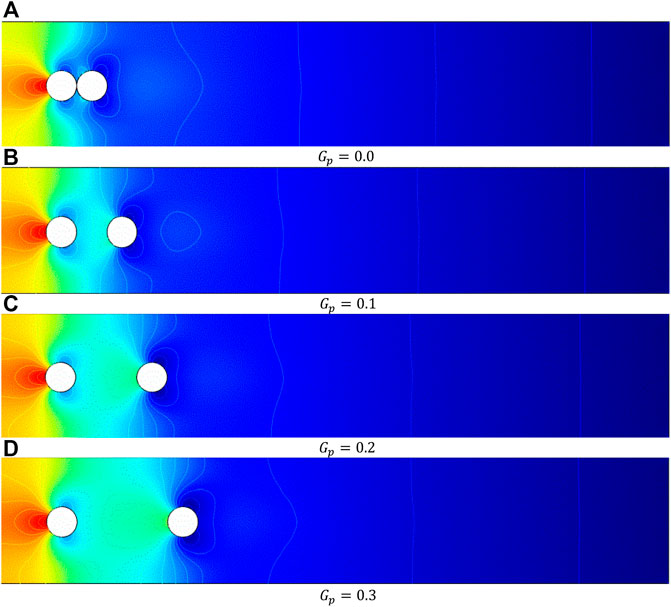
The computational coarse level grid for various gap spacings of obstacles is shown in Figure 2. For higher levels of optimization, convert one element into four narrow-size elements. The refinement mechanism is described in Figure 3.

FIGURE 2

FIGURE 2. Computational grid at the coarse level.

FIGURE 3

FIGURE 3. Sequence of grids on the space mesh level: 1, 2, and 3 (from left to right).

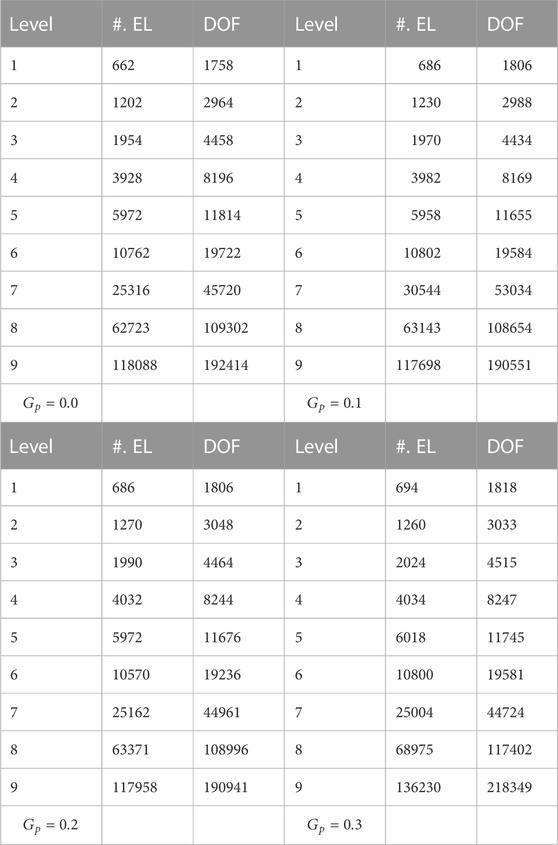
The number of elements and degrees of freedom at various stages of refinement are shown in Table 2, which was created under this method of refinement.

TABLE 2

TABLE 2. Data on meshes of varying refinement levels.

Table 2 contains several different depictions of the domain discretization of a channel that has a couple of cylinders arranged in a tandem configuration. These representations are facilitated at multiple levels of refinement. Based on the data that were examined on the degree of freedom at various $G_p=0.0,$ $G_p=0.1,$ $G_p=0.2,$ and $G_p=0.3$, it is concluded that for the high-refinement levels, the degree of freedom is 192414 at $G_p=0.0,$ whereas 190551 at $G_p=0.1,$ also 190941 at $G_p=0.2,$ and 218349 at $G_p=0.3$ with fixed $\mathrm{R}\mathrm{e}=20.$ According to Table 2, when the gap spacing is exceeded, not only does the number of domain elements but also the number of boundary elements grow from $G_p=0.1$ to $G_p=0.3$, which is a computed conclusion. The numerical scheme (FEM) for the numerous approximations of the Navier stokes equation with the hybrid grid was generated on a very high refinement level and also criteria of convergence for non-linear iteration, which is already described in [29–36]. Table 3 provides specifics on a number of different meshing levels that can occur in a flow pattern that includes a circular cylinder.

TABLE 3

TABLE 3. Grid convergence tests.

5 Results and discussions

(a) Impact on velocity and pressure:

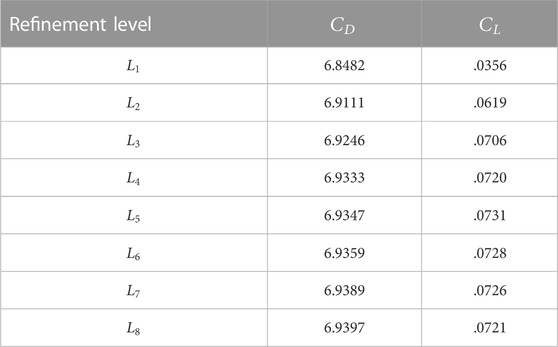
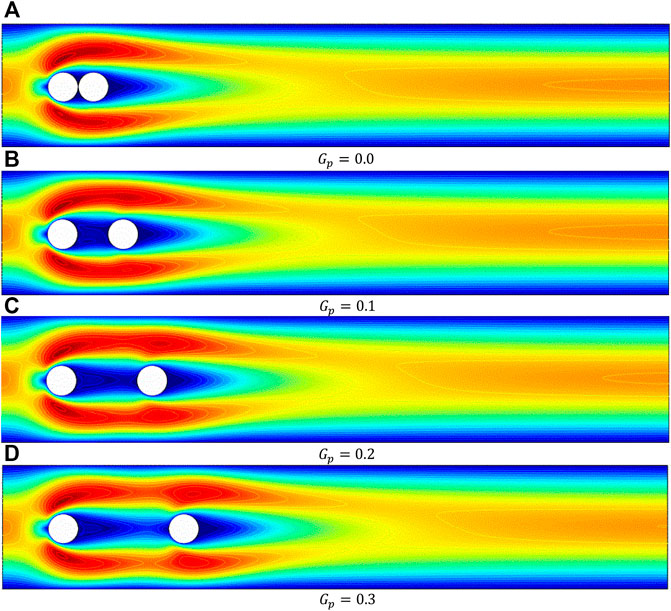
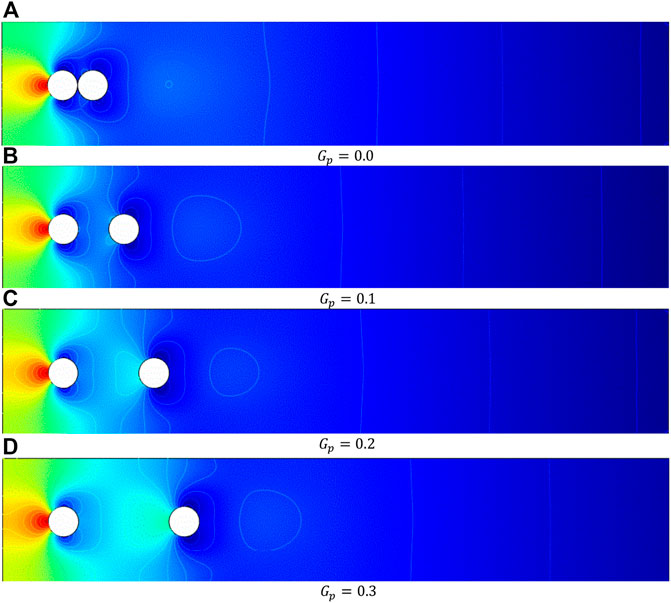
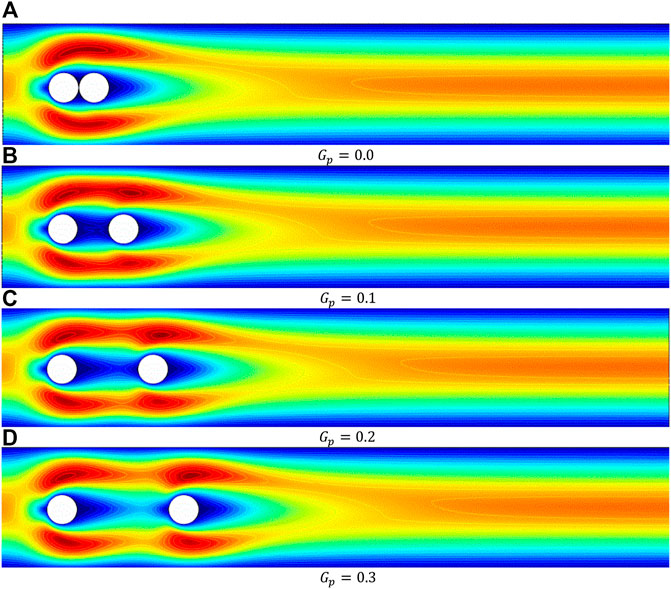
In the present work, the computations of incompressible flow have been carried out for the various quantities of the dimensionless parameters: the power law index, $n=\mathrm{0.5,1,1.5},$ thereby covering all the cases for $n<1,n=1$, and $n>1$ while several gaps with fixed Reynolds number $Re=20.$ Taking into account, the gap spacing ratio in the direction of the flow has an effect on the development of gap flow, which is the flow that happens between the two stationary cylinders in combination with a range of gap ratios. This flow can be affected by changing the gap ratios. Characteristics of the fluid flow can be determined inside the domain by conducting an analysis on the velocity profile, pressure field, force components, and the drag and lift coefficients. Figures 4, 5 reveal the impacts of velocity profile and pressure around the surface of confined tandem cylinders for the fluid value of Re and $n=0.5$ with the several ratios of gap spacing $\left(G_p\right),$ respectively. There is no pressure on the downstream cylinder at $G_p=0.0$, but pressure increases downstream due to increasing the gaps between the cylinders. Similarly, the flow pattern inside the cylinders increases for all cases of power law index due to variation of the spacing factor. Figures 6, 7 show the effects of $n=1$ fluid with different gap ratios on velocity and pressure field, while in all cases $n$, the pressure is steady at the downstream region, but continuously the steadiness decreases in the downstream region for increasing the gap ratios of the obstacles.

FIGURE 4

FIGURE 4. Influence on velocity for various gap spacings of a cylinder with $n=0.5$ and $\mathrm{R}\mathrm{e}=20.$

FIGURE 5

FIGURE 5. Influence on pressure for various gap spacings of cylinders with $n=0.5$ and $\mathrm{R}\mathrm{e}=20.$

FIGURE 6

FIGURE 6. Influence on velocity for various gap spacings of a cylinder with $n=1$ and $\mathrm{R}\mathrm{e}=20.$

FIGURE 7

FIGURE 7. Influence on pressure for various gap spacings of cylinders with $n=1$ and $\mathrm{R}\mathrm{e}=20.$

Figures 8, 9 reveal the impact of $n=1.5$ on flow patterns for various gap levels with fixed lower Reynolds numbers. Both the velocity field and the pressure field exhibit a considerable flow interaction between the two cylinders in shear-thinning and shear-thickening flow, according to a qualitative analysis of the data. In the case of extremely shear-thinning flow, flow separation did not take place, regardless of the gap spacing values that were used. In the shear-thickening instance, at the lower values of the gap ratios, the wake distraction hypothesis can be seen, as shown in Figures 3–9, when the wake of the upstream cylinder is being stifled as a result of the downstream barrier being so near to it.

(b) Line graph behavior:

FIGURE 8

FIGURE 8. Influence on velocity for various gap spacings of a cylinder with $n=1.5$ and $\mathrm{R}\mathrm{e}=20.$

FIGURE 9

FIGURE 9. Influence on pressure for various gap spacings of cylinders with $n=1.5$ and $\mathrm{R}\mathrm{e}=20.$

Figures 10A–E demonstrate the executed $u$-velocity at several power-law indexes. The maximum flow pattern is taken as $U_{\max }=0.3$, and in the present work also occurs as $U_{mean}=0.2.$ In detail, at $x=0.0$ the fluid is initially justified at the inlet of the channel is parabolic behavior. At the center of the cylinders $C_1$ and $C_2,$ it can be noticed that the velocity curves at $x=0.2$ and $x=0.6,$ the velocity profile gain large values due to the collision of the fluid with cylinders. For $x=0.4,$ the impact of cylinders on the fluid reduces. The velocity profile at $x=0.4$ is the minimum as the velocity at the center of the cylinders, while at the downstream region, at $x=2.2,$ the fluid seems low affected by the cylinders, and behavior almost goes to the initial velocity profile.

(c) Impact of drag and lift coefficients.

The influence of the gap ratio between the two tandem circular cylinders is at several Rein terms of force quantities, such as drag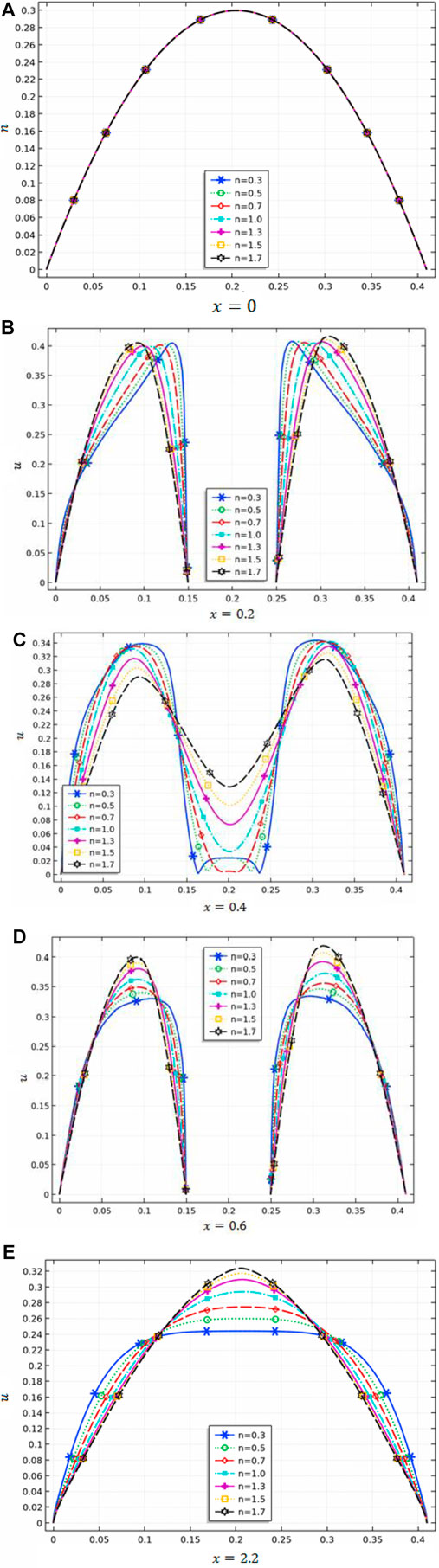 $\left(C_D\right)$ and lift $\left(C_L\right)$ coefficients. Tables 4, 5 reveal the numerous values of benchmark hydrodynamics quantities like drag and lift coefficients across the cylinders $C_1$ and $C_2.$ It is found that by increasing both gap ratios and the power-law parameter, both force coefficients upsurge. In the following statistical data, the drag coefficient upstream is greater than the downstream for the fixed Reynolds number $\left(\mathrm{R}\mathrm{e}=20\right),$ which is an interesting discussion. Table 4 reveals that the values of the parameter of the power law and gap ratio are increasing upstream, and the drag forces over both cylinders are also increasing. Similarly, in Table 5 analysis, the effects of the lift coefficient increase for the increasing power law index, while they decrease for maximum gap ratios at both upstream and downstream obstacles. The numerical values of the lift coefficient for a cylinder $C_1$ are greater than $C_2$ for the selected Reynolds number. The maximum value of drag and lift coefficient is 23.25284 and .378040 at upstream; also, for the downstream cylinder, values are 11.15001 and .119215, respectively, acquired at $\left(n,G_p\right)=\left(\mathrm{1.7,0.3}\right),$ where the flow is fully developed within the gap and the downstream region of the second cylinder.

FIGURE 10

FIGURE 10. Horizontal velocity along a vertical line at various places on the x-axis for different values of n.

TABLE 4

TABLE 4. Influence of the drag coefficient of both cylinders against $n$ with various gap spacing.

TABLE 5

TABLE 5. Influence of the lift coefficient of both cylinders against $n$ with various gap spacing.

6 Conclusion

We have used the GFEM to simulate how the power-law fluid flows around obstacles. It has been determined in great detail how much of an impact the flow behavior index and gap spacing have on the drag and lift coefficients of the cylinders. When calculating the drag and lift coefficients across cylinders, it has been discovered that the spacing performs a considerable role in the process. An increase in the gaps causes an increase in the amount of fluid flow that is directed toward the walls of the channel downstream of the obstacles. When there is more space between the cylinders, the pressure on the cylinder that is further downstream will be higher due to stagnation. When looking at any gap spacing, the correlation between the drag and lift coefficients is positive for the upstream cylinder, but when looking at the downstream cylinder, the correlation is negative. When it comes to tandem cylinders, the drag coefficient of both cylinders stays relatively the same even when the case involves shear-thinning.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding authors.

Author contributions

NF and YK was responsible for funding; NF, AHM, and HS computed the results; AM and YK wrote the original draft; NF and HS wrote the review draft; AHM performed modeling; YK contributed to conceptualization; YK, AM, and AHM performed validation.

Funding

This research work was funded by institutional fund projects under no. (IFP-A-2022-2-5-24).

Acknowledgments

Therefore, authors gratefully acknowledge technical and financial support from the ministry of education and University of Hafr Al Batin, Saudi Arabia.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Bearma PW, Wadcock AJ. The interaction between a pair of circular cylinders normal to a stream. J Fluid Mech (1973) 61:499–511. doi:10.1017/s0022112073000832

CrossRef Full Text | Google Scholar

2. Zdravkovich MM. REVIEW—review of flow interference between two circular cylinders in various arrangements. ASME J Fluids Eng (1977) 199:618–33. doi:10.1115/1.3448871

CrossRef Full Text | Google Scholar

3. Igarashi T. Characteristics of the flow around two circular cylinders arranged in tandem: 1st report. Bull Jpn Soc Mech Eng (1981) 24:323–31. doi:10.1299/jsme1958.24.323

CrossRef Full Text | Google Scholar

4. Stansby PK, Slaouti AA. A numerical study of vortex shedding from one and two circular cylinders. Aero Quart (1981) 99:48–71. doi:10.1017/s000192590000901x

CrossRef Full Text | Google Scholar

5. Igarashi T. Characteristics of the flow around two circular cylinders arranged in tandem: 2nd report, unique phenomenon at small spacing. Bull Jpn Soc Mech Eng (1984) 27:2380–7. doi:10.1299/jsme1958.27.2380

CrossRef Full Text | Google Scholar

6. Williamson CHK. Evolution of a single wake behind a pair of bluff bodies. J Fluid Mech (1985) 159:1–18. doi:10.1017/s002211208500307x

CrossRef Full Text | Google Scholar

7. Zdravkovich MM. The effects of interference between circular cylinders in cross flow. J Fluids Structures (1987) 1:239–61. doi:10.1016/s0889-9746(87)90355-0

CrossRef Full Text | Google Scholar

8. Ohya Y, Okajima A, Hayashi M. Wake interference and vortex shedding. Encycl. Fluid mech. Cheremisinoff. Houston: Gulf (1988).

Google Scholar

9. D'Alessio SJD, Pascal JP. Steady flow of a power-law fluid past a cylinder. Acta Mechanica (1996) 117(1-4):87–100. doi:10.1007/bf01181039

CrossRef Full Text | Google Scholar

10. Chhabra RP. Hydrodynamics of non-spherical particles in non-Newtonian fluids. In: NP Cheremisinoff, and PN Cheremisinoff, editors. Handbook of applied polymer processing Technology. New York: Marcel Dekker (1996). Chapter 1.

Google Scholar

11. Zadvkovich MM. Flow around circular cylinders, Vol. 1: Fundamentals. New York: Oxford University Press (1997).

Google Scholar

12. Chhabra RP. Heat and mass transfer in rheologically complex systems. In: D Siginer, D De Kee, and RP Chhabra, editors. Advances in the rheology and flow of non-Newtonian fluids. Amsterdan: Elsevier (1999).

CrossRef Full Text | Google Scholar

13. Sumner D, Price SJ, Paidoussis MP. Flow pattern identification for two staggered circular cylinders in cross-flow. J Fluid Mech (2000) 411:263–303. doi:10.1017/s0022112099008137

CrossRef Full Text | Google Scholar

14. Whitney MJ, Gregory JR. Force–velocity relationships for rigid bodies translating through unbounded shear-thinning power-law fluids. Int J non-linear Mech (2001) 36(6):947–53. doi:10.1016/s0020-7462(00)00059-7

CrossRef Full Text | Google Scholar

15. Zadvkovich MM. Flow around circular cylinders, Vol. 2. New York: FundamentalsOxford University Press (2003).

Google Scholar

16. Chhabra RP, Soares AA, Ferreira JM. Steady non–Newtonian flow past a circular cylinder: A numerical study. Acta Mechanica (2004) 172(1-2):1–16. doi:10.1007/s00707-004-0154-6

CrossRef Full Text | Google Scholar

17. Alam MM, Sakamoto H, Zhou Y. Determination of flow configurations and fluid forces acting on two staggered circular cylinders of equal diameter in cross-flow. J Fluids Structures (2005) 21:363–94. doi:10.1016/j.jfluidstructs.2005.07.009

CrossRef Full Text | Google Scholar

18. Soares AA, Ferreira JM, Chhabra RP. Flow and forced convection heat transfer in crossflow of non-Newtonian fluids over a circular cylinder. Ind Eng Chem Res (2005) 44(15):5815–27. doi:10.1021/ie0500669

CrossRef Full Text | Google Scholar

19. P Chhabra R. Bubbles, drops and particles in non-Newtonian fluids. 2nd ed. Boca Raton, FL: CRC Press (2006).

Google Scholar

20. Ding H, Shu C, Yeo KS, Xu D. Numerical simulation of flows around two circular cylinders by mesh-free-least-square-based finite difference methods. Int J Numer Methods Fluids (2007) 53:305–32. doi:10.1002/fld.1281

CrossRef Full Text | Google Scholar

21. Mossaz S, Jay P, Magnin A. Criteria for the appearance of recirculating and non-stationary regimes behind a cylinder in a viscoplastic fluid. J Non-Newtonian Fluid Mech (2010) 165(21-22):1525–35. doi:10.1016/j.jnnfm.2010.08.001

CrossRef Full Text | Google Scholar

22. Nejat A, Abdollahi V, Vahidkhah K. Lattice Boltzmann simulation of non-Newtonian flows past confined cylinders. J Non-Newtonian Fluid Mech (2011) 166(12-13):689–97. doi:10.1016/j.jnnfm.2011.03.006

CrossRef Full Text | Google Scholar

23. Turkyilmazoglu M. Exact solutions concerning momentum and thermal fields induced by a long circular cylinder. Eur Phys J Plus (2021) 136(5):483–10. doi:10.1140/epjp/s13360-021-01500-1

CrossRef Full Text | Google Scholar

24. Nazeer M, Ali N, Javed T, Nazir MW. Numerical analysis of the full MHD model with the Galerkin finite-element method. Eur Phys J Plus (2019) 134:204. doi:10.1140/epjp/i2019-12562-9

CrossRef Full Text | Google Scholar

25. Nazeer M, Ali N, Javed T, Razzaq M. Finite element simulations for energy transfer in a lid-driven porous square container filled with micropolar fluid: Impact of thermal boundary conditions and Peclet number. Int J Hydrogen Energ (2019) 44:7656–66. doi:10.1016/j.ijhydene.2019.01.236

CrossRef Full Text | Google Scholar

26. Raza R, Naz R, Abdelsalam SI. Microorganisms swimming through radiative Sutterby nanofluid over stretchable cylinder: Hydrodynamic effect. Num M Partial Dif Equs (2022) 39 (2), 975–994.

CrossRef Full Text | Google Scholar

27. Faizan M, Ali F, Loganathan K, Zaib A, Reddy CA, Abdelsalam SI. Entropy analysis of sutterby nanofluid flow over a riga sheet with gyrotactic microorganisms and cattaneo–christov double diffusion. Mathematics (2022) 10:3157. doi:10.3390/math10173157

CrossRef Full Text | Google Scholar

28. Abdelsalam SI, Zaher AZ. On behavioral response of ciliated cervical canal on the development of electroosmotic forces in spermatic fluid. Math Model Nat Phenom (2022) 17:27. doi:10.1051/mmnp/2022030

CrossRef Full Text | Google Scholar

29. Mahmood R, Bila S, Majeed AH, Khan I, Sherif EM. A comparative analysis of flow features of Newtonian and power law material: A new configuration. J Mater Res Technol (2020) 9:1978–87. doi:10.1016/j.jmrt.2019.12.030

CrossRef Full Text | Google Scholar

30. Mahmood R, Bilal S, Majeed AH, Khan I, Nisar KS. CFD analysis for characterization of non-linear power law material in a channel driven cavity with a square cylinder by measuring variation in drag and lift forces. J Mater Res Technol (2020) 9:3838–46. doi:10.1016/j.jmrt.2020.02.010

CrossRef Full Text | Google Scholar

31. Mahmood R, Bilal S, Majeed AH, Khan I, Nisar KS. Assessment of pseudo-plastic and dilatant materials flow in channel driven cavity: Application of metallurgical processes. J Mater Res Technol (2020) 9:3829–37. doi:10.1016/j.jmrt.2020.02.009

CrossRef Full Text | Google Scholar

32. Majeed AH, Mahmood R, Abbasi WS, Usman K. Numerical computation of MHD thermal flow of cross model over an elliptic cylinder: Reduction of forces via thickness ratio. Math Probl Eng (2021) 2021:1–13. doi:10.1155/2021/2550440

CrossRef Full Text | Google Scholar

33. Bilal S, Mahmood R, Majeed AH, Khan I, Nisar KS. Finite element method visualization about heat transfer analysis of Newtonian material in triangular cavity with square cylinder. J Mater Res Technol (2020) 9(3):4904–18. doi:10.1016/j.jmrt.2020.03.010

CrossRef Full Text | Google Scholar

34. Majeed AH, Jarad F, Mahmood R, Saddique I. Topological characteristics of obstacles and nonlinear rheological fluid flow in presence of insulated fins: A fluid force reduction study. Math Probl Eng (2021) 2021:2021–15. doi:10.1155/2021/9199512

CrossRef Full Text | Google Scholar

35. Ahmad H, Mahmood R, Hafeez MB, Hussain Majeed A, Askar S, Shahzad H. Thermal visualization of Ostwald-de Waele liquid in wavy trapezoidal cavity: Effect of undulation and amplitude. Case Stud Therm Eng (2022) 2021.

CrossRef Full Text | Google Scholar

36. Mehmood A, Mahmood R, Majeed AH, Awan FJ. Flow of the bingham-papanastasiou regularized material in a channel in the presence of obstacles: Correlation between hydrodynamic forces and spacing of obstacles. Model Simulation Eng (2021) 2021:1–14. doi:10.1155/2021/5583110

CrossRef Full Text | Google Scholar

Nomenclature

$u,v$ velocity component

$U_{in}$ inlet velocity

$U_{ref}$ reference velocity

$\dot{\gamma }$ shear rate

$p$ hydrodynamic pressure

$m$ viscosity index

n power-law index

$Re$ Reynolds number

D diameter of the obstacle

$L_{ref}$ reference length

#EL number of elements

# DOF number of degrees of freedom

$C_D$ drag coefficient

$C_L$ lift coefficient