An optically pumped atomic clock based on a continuous slow cesium beam

Herein, we report the scheme of an optically pumped atomic clock based on a cold cesium atomic beam source. We propose the laser system and physical mechanism of this atomic clock, wherein the atomic beam travels in an upper parabolic trajectory, thereby eliminating the light shift effect. In the experiments, when the length of the free evolution region was 167 mm, the line width of the Ramsey fringe was 37 Hz. When the expected signal-to-noise ratio of the Ramsey fringe that can be achieved is 36,000, the expected short-term frequency stability is about 3.6 × 10^–14/√τ, which is significantly higher than that of a conventional optically pumped cesium clock of similar volume.

1 Introduction

The current commercial atomic clocks are mainly microwave clocks, including hydrogen, cesium, and rubidium clocks. Owing to their excellent long-term stability and other properties, cesium beam atomic clocks are being used for time keeping [1]. Additionally, they are being widely used in many fields, such as precision measurement, positioning and navigation, and high-speed communication. However, most existing cesium beam atomic clocks utilize thermal atoms [2–5], and the thermal atoms move fast and the Ramsey fringe line width is difficult to decrease. Therefore, simultaneously meeting the requirements of small volume and high frequency stability is difficult [6]. Laser cooling and magneto-optical trap (MOT) technology [7, 8] reduce the atomic velocity and yields of fountain clocks, their frequency stability can reach the order of 10^–13/√τ [9–11]. However, they are too large and their frequency stability is limited by the Dick effect [12]. Therefore, although cold cesium atomic beam clocks have been studied by numerous researchers [13–15], only one is currently operational, which is very large and complicated [15].

Recently, we developed a compact cold cesium atomic beam source based on 2D⁺-MOT, as shown in Figure 1 [16], wherein the mechanical structure was simply connected to a conventional optically pumped cesium beam tube using a differential tube. The experimental results demonstrated that when the pushing light’s power was 180 μW and its frequency resonated with the 4 → 5' transition of the Cs D₂ line, the most probable longitudinal velocity of the outgoing cold atomic beam, width of velocity distribution, and atomic beam flux were 19.38 m/s, 8.1 m/s, and 1.7 × 10¹⁰ atoms/s, respectively. In the following experiments of the optically pumped atomic clock based on this cold cesium atomic beam source, when the length of the free evolution region was 167 mm, the line width of the Ramsey fringe was 37 Hz. Additionally, when the expected signal-to-noise ratio (SNR) of the Ramsey fringe that can be achieved in the experiment is 3,000, the expected short-term frequency stability is about 4 × 10^–13/√τ, which is considerably higher than that of a conventional optically pumped cesium clock with similar volume.

FIGURE 1

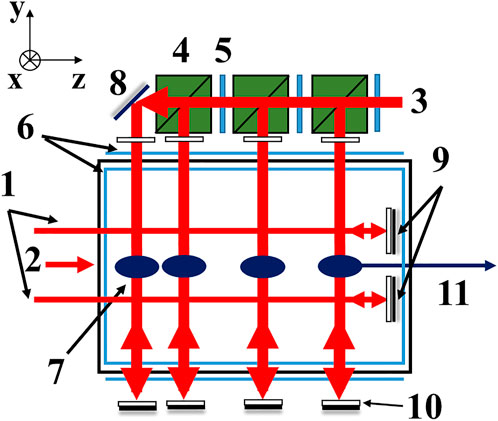
FIGURE 1. Schematic (yz plane) of the cold cesium atomic beam source [16]. 1: Hollow cooling light; 2: Pushing light; 3: Transverse cooling light; 4: Polarizing beam splitter prism; 5: λ/2 wave plate; 6: Magnetic field coil; 7: Cold atomic cloud; 8: Reflector; 9: λ/4 wave plate with center 1 mm hole and high reflective coating on the back; 10: λ/4 wave plate; 11: Cold cesium atomic beam.

2 Methods

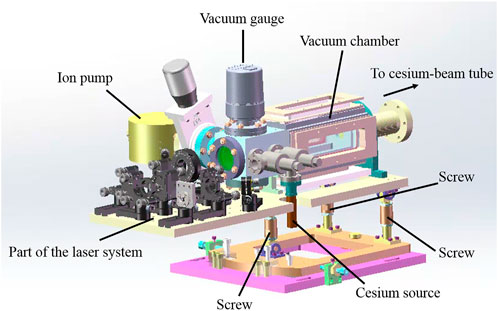
Figure 2 shows the overall design of the optically pumped cold cesium beam atomic clock. Its optical system is shown in Figure 3, which is an improvement on the optical system put forward by [16]. Additionally, multiple functions such as laser cooling, optical pumping, and optical detection of atoms can be realized, which improve the robustness of the system. After cesium atoms were emitted from the cold cesium beam source, they were mainly distributed in the ground state F = 4 energy level. When they traversed through the pumping region, they simultaneously interacted with the pumping lights one and 2. The frequency of pumping light one resonated with the 4 → 3' transition of Cs D₂ line, and the frequency of pumping light two resonated with the 3 → 3' transition. Pumping light two was π-polarized, and the polarization direction was the x direction, as shown in Figure 2, which was consistent with the direction of the applied magnetic field. The unpolarized pumping light one pumped cesium atoms to the F = 3 energy level, and pumping light two pumped cesium atoms to the |F = 3, m = 0> sub-levels. After many such transitions, most of the cesium atoms were pumped to the |F = 3, m = 0> sub-levels.

FIGURE 2

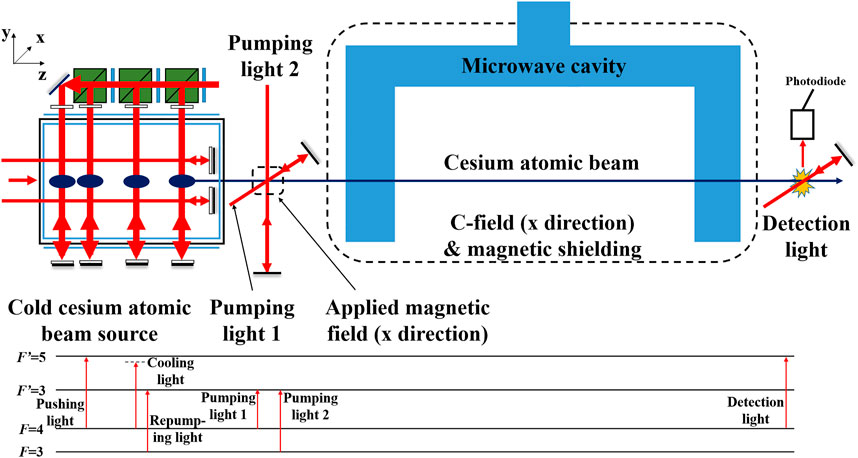
FIGURE 2. Schematic of the optically pumped cold cesium beam atomic clock. The upper part is the detailed structure of the atomic clock, and the lower part is a diagram of the transitions of Cs D₂ line used in each part of the atomic clock.

FIGURE 3

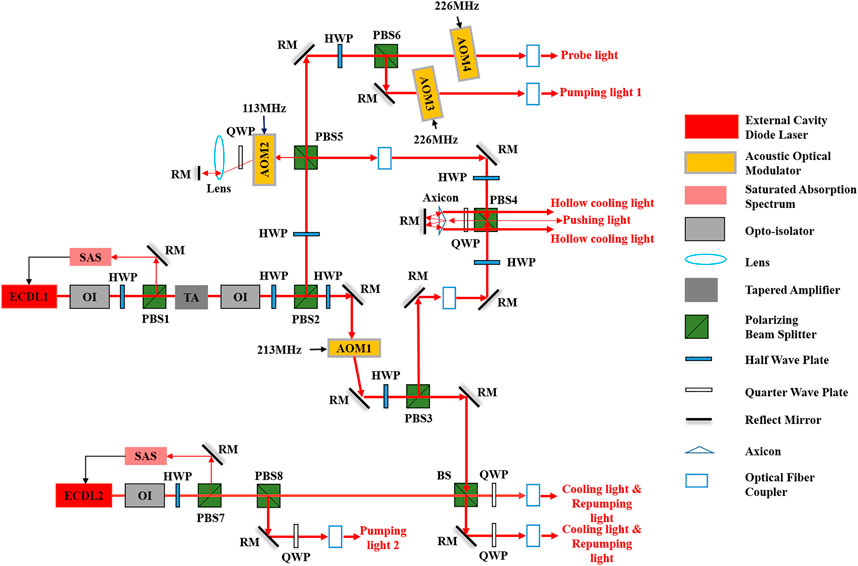
FIGURE 3. Schematic of the optical system of the optically pumped cold cesium beam atomic clock. Both ECDLs were frequency stabilized using a saturable absorption spectrum. All of the lasers were finally coupled into the fiber and output to the desired location. OI: optical isolator; HWP: λ/2 wave plate; PBS: polarizing beam splitter prism; RM: mirror; SAS: saturable absorption spectrum; TA: tapered amplifier; AOM: acousto-optic modulator; QWP: λ/4 wave lens: convex lens; BS: beam splitter prism.

The U-shaped microwave cavity can realize the Ramsey separated oscillating field. The microwave interacted with the cesium atomic beam when it passed through the microwave cavity. When the length of the region where the atom interacted with the microwave was fixed, the microwave power was adjusted according to the measured atom’s flight speed, so that the atoms experienced two π/2 pulses when passing through the microwave cavity twice. Similar to the existing optically pumped cesium beam atomic clocks, the C-field existed in the free evolution region and the two interaction regions. Moreover, the two ground-state hyperfine energy levels of the cesium atom were split into Zeeman sub-levels and the selected |F = 3, m = 0> → |F = 4, m = 0 > transition could be easily selected as the reference spectral lines of the clock frequency.

The microwave servo part utilized the local crystal oscillator to afford microwave frequencies near 9192631770 Hz through the frequency doubling synthesis chain and then feed it into the microwave cavity. Therefore, the microwave frequency proportionally changed with the local oscillator frequency. Consequently, it could be changed using a single-chip microcomputer scanning the local oscillator frequency.

After interacting with the microwave, some of the atoms in the F = 3 state were excited to the F = 4 state. The number of these cesium atoms could be determined from the fluorescence signal released due to the interaction between the detection laser and these atoms. The frequency of the detection laser resonated with the 4 → 5' cyclic transition line, and the probability of the cesium atoms excited to the F = 4 state was deduced from the magnitude of the detected fluorescence signal. A photodiode transformed the fluorescence signal into an electronic signal, which exhibited stripe-like fluctuations when the microwave frequency was scanned, i.e., the Ramsey fringe. The servo circuit processed the Ramsey fringe signal to obtain the clock frequency error signal to provide feedback for controlling the clock frequency.

3 Results

In the experiment, for easy operation, a large experimental bench was employed. The distance from the exit of the cold cesium atomic beam source to the detection area was about 650 mm, which was long, and thus, the flight trajectory was greatly affected by gravity. Consequently, a very slow atomic beam cannot be used. [16] showed that an atom’s flight speed was positively related to the pushing light power. When the pushing light power was high, the atomic beam flux was high when the light’s frequency resonated with the 4 → 5' transition line and it approached saturation with increasing power. Therefore, a pushing light of 120 μW with a resonant frequency was used to push out the cesium atomic beam. Then, by turning on the two pumping lights, feeding the microwave into the microwave cavity, turning on the detection light to detect the number of atoms excited by the microwave, and scanning the microwave frequency, the Ramsey fringe could be obtained (Figure 4).

FIGURE 4

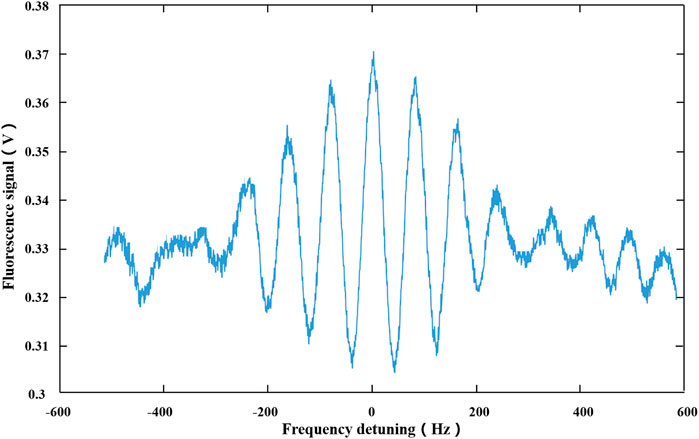
FIGURE 4. Ramsey fringe of a cold cesium atomic beam. The abscissa is the microwave frequency detuning, relative to the frequency of 3 → 4 transition of Cs D₂ line. The ordinate is the fluorescence signal amplitude detected by the photodiode.

Based on the measurements, the central line width of the Ramsey fringe was 37 Hz, and the SNR under the bandwidth of 1 Hz was about 300. Figure 4 shows that the Ramsey fringe has a certain amount of noise, and the two sides are not completely symmetrical. This may be because the aging of the tapered amplifier used in the experiment caused the laser power to become unstable, resulting in noise, and the σ transition caused by the incomplete parallelism between the C-field and the magnetic field of the microwave produced the Ramsey pulling effect, which caused the incomplete symmetry of the fringes.

4 Discussion

After cesium atoms were ejected from the cold cesium atomic beam source by the pushing light, the pushing light continued to move forward. If it was not separated from the cesium atoms in the microwave cavity, light shift would occur, which would affect the frequency stability of the atomic clock. Thus, to prevent light shift as much as possible, the cold cesium atomic beam source was fixed on a bracket with an adjustable angle (Figure 5).

FIGURE 5

FIGURE 5. Diagram of the physical part of the cold cesium atomic beam source.

The pitch angle and height of the cold cesium atomic beam source were adjusted by rotating the screws to adjust the atomic beam’s and the pushing light’s direction. The distance between the exit of the atomic beam and microwave cavity in the experimental platform was 430 mm, and the longitudinal velocity of the atomic beam was v_z = 17.5 m/s. Through adjustment, the pushing light and cesium atoms were both emitted at an angle of 0.3° to the horizontal plane. Since the cesium atomic beam was affected by gravity, the atoms traveled in a parabolic orbit, while the pushing light traveled in a straight line. Therefore, before reaching the first microwave cavity, the pushing light was separated from the cesium atomic beam by a distance that was simply estimated to be 430 × tan(0.3°) + g × (430/v_z)²/2 ≈ 5 mm. According to the light intensity distribution of the Gaussian beam,

$I=I_0\exp \left(-2r^2/w^2\right),(1)$

where I₀ is the light intensity on the optical axis, r is the distance from the optical axis, and w is the beam diameter that was equal to 1 mm. In the first microwave cavity, at the atomic beam’s position, the light intensity attenuated to 2 × 10^–22 of the light intensity of the optical axis. Thus, the influence of the light shift caused by the pushing light could be ignored. Simultaneously, a graphite tube was set between the two microwave cavities, which not only absorbed the divergent cesium atoms but also absorbed the pushing light. This tube was included to keep the pushing light away from the outer wall of the microwave cavity to prevent stray light. The trajectories of the pushing light and atomic beam in the cesium beam tube are shown in Figure 6.

FIGURE 6

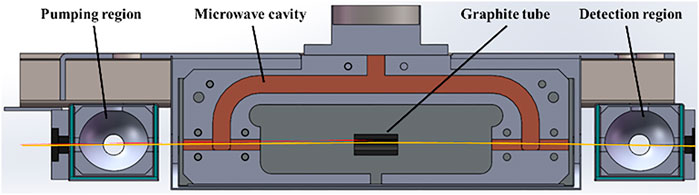
FIGURE 6. Schematic of the trajectories of the pushing light and atomic beam in the cesium beam tube. The red line denotes the laser beam, while the yellow line denotes the atomic beam.

When the short-term frequency stability expression of atomic clocks is applied to cold atomic clocks, it should be modified as [17].

${\sigma }_y\left(\tau \right)=\frac{1}{\pi }\frac{\Delta \nu }{{\nu }_{\mathrm{h}\mathrm{f}\mathrm{s}}}\frac{1}{SNR}\frac{1}{\sqrt{\tau /s}}.(2)$

According to the results of this study, when the Ramsey fringe line width is 37 Hz and the SNR is approximately 300, the short-term frequency stability of the proposed cold atomic clock is about 4 × 10^–12/√τ. Considerable scope still exists for improving the SNR of Ramsey fringes. The SNR limit is related to the number of available atoms [18]:

${\left(\frac{S}{N}\right)}_{\sqrt{\mathrm{H}\mathrm{z}}}=\frac{1}{2}\sqrt{\frac{\pi }{2}{I}_{\mathrm{a}}}.(3)$

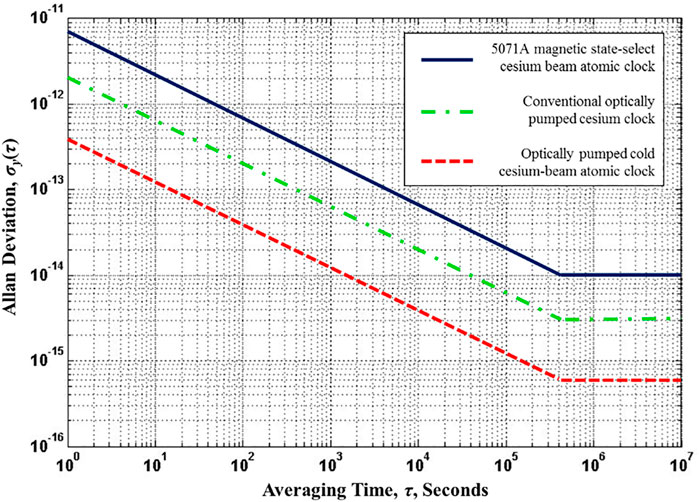
Here, I_a is the intensity of the atomic beam flux. According to [16], when the pushing light power is 120 μW, the measured atomic beam flux is 1.6 × 10¹⁰ atoms/s. Additionally, simulations have shown that the utilization rate of atoms after traversing through the microwave cavity is 20.6%. Thus, the number of atoms finally reaching the detection region is 3.3 × 10⁹ atoms/s. When the state preparation efficiency is 100%, according to Eq. 3, the theoretical maximum SNR is about 36 ,000 and the corresponding short-term frequency stability limit is 3.6 × 10^–14/√τ. In actual operation, this SNR limit is difficult to achieve. Considering the influence of factors such as state preparation efficiency, if the expected SNR in the experiment is 3,000, the expected short-term frequency stability is about 4 × 10^–13/√τ. Referring to the long-term frequency stability of existing cold atomic fountain clocks [15], the corresponding frequency stability curve is shown in Figure 7. The frequency stability of cold optically pumped cesium atomic clocks is considerably higher than that of the previous cesium beam clocks. The experimental measurements of the frequency stability have not been provided herein, as at the completion time of this paper, the reference hydrogen maser is still analyzing the frequency stability of a miniaturized optically pumped cesium beam atomic clock. Furthermore, we hope that better frequency stability can be obtained by improving the SNR of the Ramsey fringe and reducing the system noise. There are some possible methods. Firstly, the utilization efficiency of light power can be improved by improving the optical system, so that a stronger cold atomic beam can be obtained under the same cooling light power. Secondly, the cold atomic beam can be transversely cooled while being optically pumped, reducing the divergence angle of the atomic beam and improving the atomic utilization. Finally, optical elements should be fixed on a specially made ultra stable base to obtain a more stable atomic beam.

FIGURE 7

FIGURE 7. Comparison of the frequency stability of three atomic clocks.

5 Conclusion

This study introduced an optically pumped cold cesium beam atomic clock. Moreover, the scheme of the atomic clock was proposed and the experimental bench for the experiment was designed and assembled. A U-shaped microwave cavity can realize the separation of the oscillating field in the same phase while preventing the heating of the cold atoms by other excitation methods. Furthermore, this study performed the cold cesium atomic beam preparation, state preparation, microwave excitation, and state detection and subsequently obtained the Ramsey fringe. Compared with the thermal atoms, the cold atoms have lower flight speeds, and can obtain a longer free evolution time within the same free evolution length, thus greatly reducing the line width of the atomic resonance spectrum. The line width of the Ramsey fringe of this atomic clock was 37 Hz, which was 1/15 of the line width of the Ramsey fringe of 575 Hz [18] of a miniaturized optically pumped cesium beam atomic clock with the same free evolution region length of 167 mm. Finally, the system performance was analyzed, and a scheme of oblique upward emission of atomic beam for eliminating the light shift of the pushing light was proposed, which was more concise than the scheme proposed by [15] Additionally, the theoretical limit of the system frequency stability of 3.6 × 10^–14/√τ was obtained. When the expected SNR of the Ramsey fringe that can be achieved in the experiment is 3,000, the expected short-term frequency stability is about 4 × 10^–13/√τ. Of course, this is a laboratory result, further research will be carried out in the future to obtain frequency stability and make the scheme practical.

Data availability statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author contributions

WX designed the experimental setup, conducted the experiments, and wrote the paper. QW participated in the design of the experiment and provided guidance for the experiment. XH helped design the electrical part and participated in some of the experiments. ZY helped design the electrical part. SF designed the microwave source. NC provided ideas for the preparation of atomic states. ZX helped set up the experimental apparatus. JZ helped set up the vacuum system. XQ directed the experiment. SL participated in the revision of the paper. XC is the leader of the laboratory and provided overall guidance.

Acknowledgments

The authors would like to thank the Advanced Technology Institute of Peking University for their support of this research.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Wang Y, Wang Q, Fu J, Dong T. In: Y Li, editor. Principle of quantum frequency standards. Beijing: Science Press (1986). (in Chinese).

Google Scholar

2. Arditi M. A caesium beam atomic clock with laser optical pumping, as a potential frequency standard. Metrologia (1982) 18:59–66. doi:10.1088/0026-1394/18/2/003

CrossRef Full Text | Google Scholar

3. Makdissi A, Clercq E. Evaluation of the accuracy of the optically pumped caesium beam primary frequency standard of BNM-LPTF. Metrologia (2001) 38:409–25. doi:10.1088/0026-1394/38/5/6

CrossRef Full Text | Google Scholar

4. Hasegawa A, Fukuda K, Kajita M, Ito H, Kumagai M, Hosokawa M, et al. Accuracy evaluation of optically pumped primary frequency standard CRL-O1. Metrologia (2004) 41:257–63. doi:10.1088/0026-1394/41/4/006

CrossRef Full Text | Google Scholar

5. Schmeissner R, Favard P, Douahi A, Perez P, Mestre N, Baldy M, et al. Optically pumped Cs space clock development. In: 2017 Joint Conference of the European Frequency and Time Forum and IEEE International Frequency Control Symposium (EFTF/IFCS); 09-13 July 2017; Besancon, France (2017). doi:10.1109/fcs.2017.8088825

CrossRef Full Text | Google Scholar

6. Hermann V, Gazard M, Berthoud P, Lecomte S, Ruffieux R, Audoin C, et al. OSCC project: A space Cs beam optically pumped atomic clock for galileo. In: 2007 IEEE International Frequency Control Symposium Joint with the 21st European Frequency and Time Forum; 29 May 2007 - 01 June 2007; Geneva, Switzerland (2007). doi:10.1109/freq.2007.4319035

CrossRef Full Text | Google Scholar

7. Pritchard D, Raab E, Bagnato V, Wieman C, Watts R. Light traps using spontaneous forces. Phys Rev Lett (1986) 57:310–3. doi:10.1103/physrevlett.57.310

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Raab E, Prentiss M, Cable A, Chu S, Pritchard D. Trapping of neutral sodium atoms with radiation pressure. Phys Rev Lett (1988) 59:2631–4. doi:10.1103/physrevlett.59.2631

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Szymaniec K, Chalupczak W, Whibberley P, Lea S, Henderson D. Evaluation of the primary frequency standard NPL-CsF1. Metrologia (2005) 42:49–57. doi:10.1088/0026-1394/42/1/007

CrossRef Full Text | Google Scholar

10. Heavner T, Donley E, Levi F, Costanzo G, Parker T, Shirley J, et al. First accuracy evaluation of NIST-F2. Metrologia (2014) 51:174–82. doi:10.1088/0026-1394/51/3/174

CrossRef Full Text | Google Scholar

11. Fang F, Li M, Lin P, Chen W, Liu N, Lin Y, et al. NIM5 Cs fountain clock and its evaluation. Metrologia (2015) 52:454–68. doi:10.1088/0026-1394/52/4/454

CrossRef Full Text | Google Scholar

12. Santarelli G, Audoin C, Makdissi A, Laurent P, Dick GJ, Clairon A. Frequency stability degradation of an oscillator slaved to a periodically interrogated atomic resonator. IEEE Trans Ultrason Ferroelectr Freq Control (1998) 45:887–94. doi:10.1109/58.710548

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Wang H, Iyanu G. MOT-based continuous cold Cs-beam atomic clock. In: 2010 IEEE International Frequency Control Symposium; 01-04 June 2010; Newport Beach, CA, USA (2010). doi:10.1109/freq.2010.5556290

CrossRef Full Text | Google Scholar

14. Park S, Lee H, Shin E, Kwon T, Yang S, Cho H. Generation of a slow and continuous cesium atomic beam for an atomic clock. J Opt Soc Am B (2002) 19:2595. doi:10.1364/josab.19.002595

CrossRef Full Text | Google Scholar

15. Devenoges L, Stefanov A, Joyet A, Thomann P, Domenico G. Improvement of the frequency stability below the Dick limit with a continuous atomic fountain clock. IEEE Trans Ultrason Ferroelectr Freq Control (2012) 59:211–6. doi:10.1109/tuffc.2012.2181

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Xie W, Wang Q, He X, Fang S, Yuan Z, Qi X, et al. A cold cesium beam source based on a two-dimensional magneto-optical trap. AIP Adv (2022) 12:075124. doi:10.1063/5.0099415

CrossRef Full Text | Google Scholar

17. Riehle F. Frequency standards: Basics and applications 78. New Jersey, United States: John Wiley & Sons (2006).

Google Scholar

18. Xie W, Wang Q, He X, Chen N, Xiong Z, Fang S, et al. Frequency instability of a miniature optically pumped cesium-beam atomic frequency standard. Rev Sci Instrum (2020) 91:074705. doi:10.1063/5.0001749

PubMed Abstract | CrossRef Full Text | Google Scholar