- 1College of Physics and Information Engineering, Minnan Normal University, Zhangzhou, China
- 2Shandong Provincial Engineering and Technical Center of Light Manipulations & Shandong Provincial Key Laboratory of Optics and Photonic Devices, School of Physics and Electronics, Shandong Normal University, Jinan, China
- 3Department of Physics and Optical Science, University of North Carolina at Charlotte, Charlotte, NC, United States
- 4Department of Physics, University of Miami, Coral Gables, FL, United States
We investigate the behavior of the orbital angular momentum (OAM) flux density of partially coherent vortex (PCV) beams in atmospheric turbulence. It is shown that for PCV beams with different spatial coherence structures, the OAM flux density distribution exhibits rich variations along the propagation path. Our findings provide insight into the use of the OAM in free-space optical communications when turbulence effects are significant.
Introduction
During the past few decades, the study of vortex structures in optical fields, and more complicated wavefield singularities, has become a stand-alone area of investigation of modern optics, named singular optics [1–3]. Spatially coherent beams carrying optical vortices, called vortex beams, have attracted much interest due to their potential applications in many areas including coronagraph [4], coherence filtering [5], and free-space optical communication [6]. Since Allen et al. found that Laguerre–Gauss beams carry a well-defined OAM as a consequence of their vortex core [7], vortex beams have also found application in optical tweezing [8], optical spanning [9], design of light-driven machines [10], high-resolution microscopy [11], security holograms [12], quantum information transfer [13], and rotation measurements [14].
Partially coherent beams have been shown to benefit a number of applications, such as free-space optical communication [15], particle trapping [16], and atom cooling [17]. It is therefore of great interest to consider vortex structures in partially coherent beams. Unlike spatially coherent beams, however, partially coherent beams do not have a well-defined phase structure and their behavior can only be described using coherence functions. Some years ago, Schouten et al showed that these coherence functions can possess their own phase singularities (and optical vortices) that are closely related to their coherent counterparts [18], and since then, much attention has been given to these so-called coherence singularities or coherence vortices [19–23]. For partially coherent beams carrying vortex structures, which are called PCV beams, when the coherence decreases, coherence singularities are shown to be more robust than phase singularities [24].
Recently, it was found that the OAM of PCV beams exhibits a number of novel characteristics. For example, different types of PCV beams can have different distributions of the OAM flux density in their cross-sections. The OAM flux density can represent a Rankine vortex, a rigid body rotator, a fluid rotator, or even more rich varieties of OAM distributions; these results indicate that PCV beams can provide additional control over OAM than their coherence counterparts [25–28]. More recently, we found that one can manipulate the source coherence to change the OAM flux density of PCV beams on propagation in free space [29], and this effect joins correlation-induced spectral and polarization changes in a family of source coherence influenced propagation phenomena (for the summary see Ch. 4 of Ref. [30]).
However, despite the fact that free-space optical communication is one of the most significant applications of such beams, the propagation characteristics of the OAM flux density of PCV beams in atmospheric turbulence has yet to be studied. In this paper, we study the propagation of the OAM flux density of PCV beams in atmospheric turbulence. We derive analytic formulas showing how atmospheric turbulence affects the OAM flux density on propagation, and illustrate the changes with a number of model partially coherent beams with structured spatial coherence.
Theory
We consider a scalar, statistically stationary random source that is located in a plane perpendicular to the direction of propagation. The second-order statistical properties of the source can be characterized by the cross-spectral density (CSD) function [31],
where
To model a variety of partially coherent vortex beams, we consider isotropic Schell-model sources with a definite topological charge, of the form
with
representing the normalized Laguerre–Gauss mode of radial order 0 and azimuthal order l, and
where
The CSD function of the PCV beam after propagating in atmospheric turbulence can be calculated with the extended Collins integral [32].
where
where
Here,
If turbulence is governed by non-Kolmogorov statistics and the power spectrum
with
where
where
where
In the modeling of a partially coherent vortex beam, we begin with a planar, secondary Gaussian Schell-model vortex (GSMV) source, with a source spectral degree of coherence of the form
where
with
For a paraxial scalar PCV beam, the average OAM flux density can be shown to be related to the CSD function by the expression [25]
where
where
The total OAM
With the help of Eqs. 19, 21, we can calculate the distribution of normalized OAM flux density
To illustrate the possible effects of atmospheric turbulence on the distribution of the OAM flux density of PCV beams with different spatial coherence states, we will involve multi-Gaussian Schell-model vortex (MGSMV) source, for which the source spectral degree of coherence has the form
where
Here,
We will also consider a source that is the incoherent superposition of GSMV beams with equal and opposite topological charges but different coherence width
This source has a net zero OAM flux density but will exhibit OAM flux density changes on propagation due to the different correlation widths of the different OAM modes, even in free space [29].
With the help of Eqs. 16, 19, 21, the normalized OAM flux density
Results
To show the effect of atmospheric turbulence on the evolution of OAM of PCV beams on propagation, we calculate the normalized OAM flux density
Figure 1 shows the evolution of the normalized OAM flux density
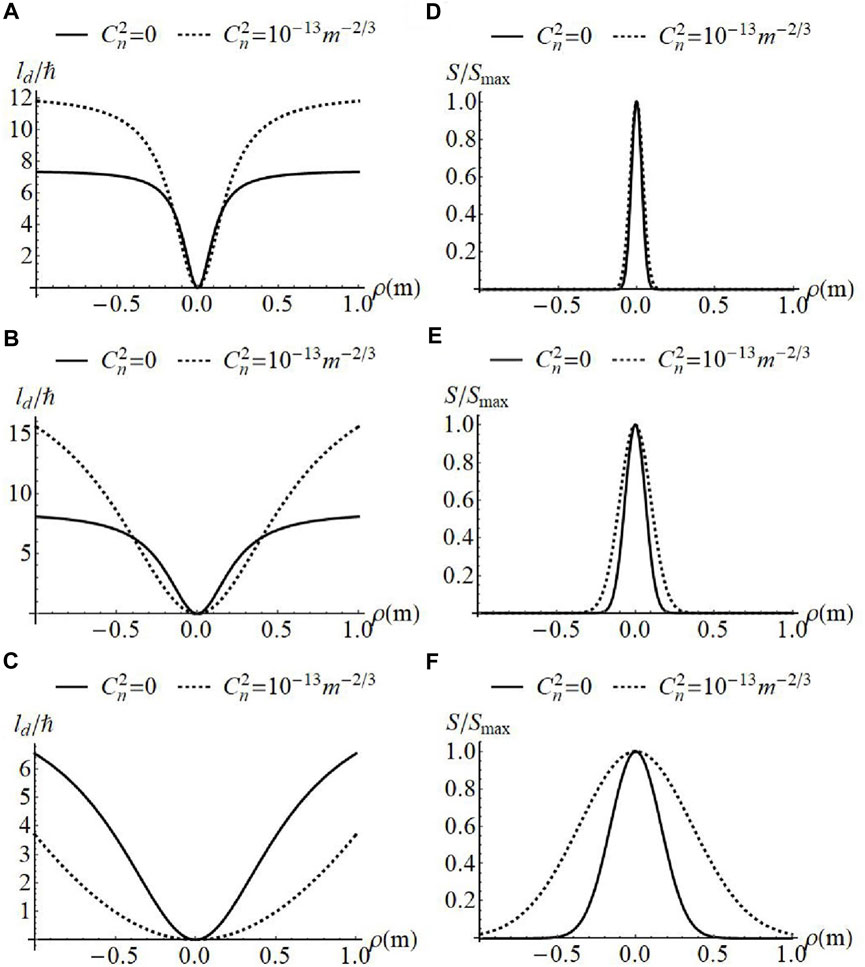
FIGURE 1. Normalized OAM flux density (A–C) and spectral density (D–F) of GSMV beams with w = 10 mm,
Figures 2, 3 show the evolution of OAM in atmospheric turbulence for
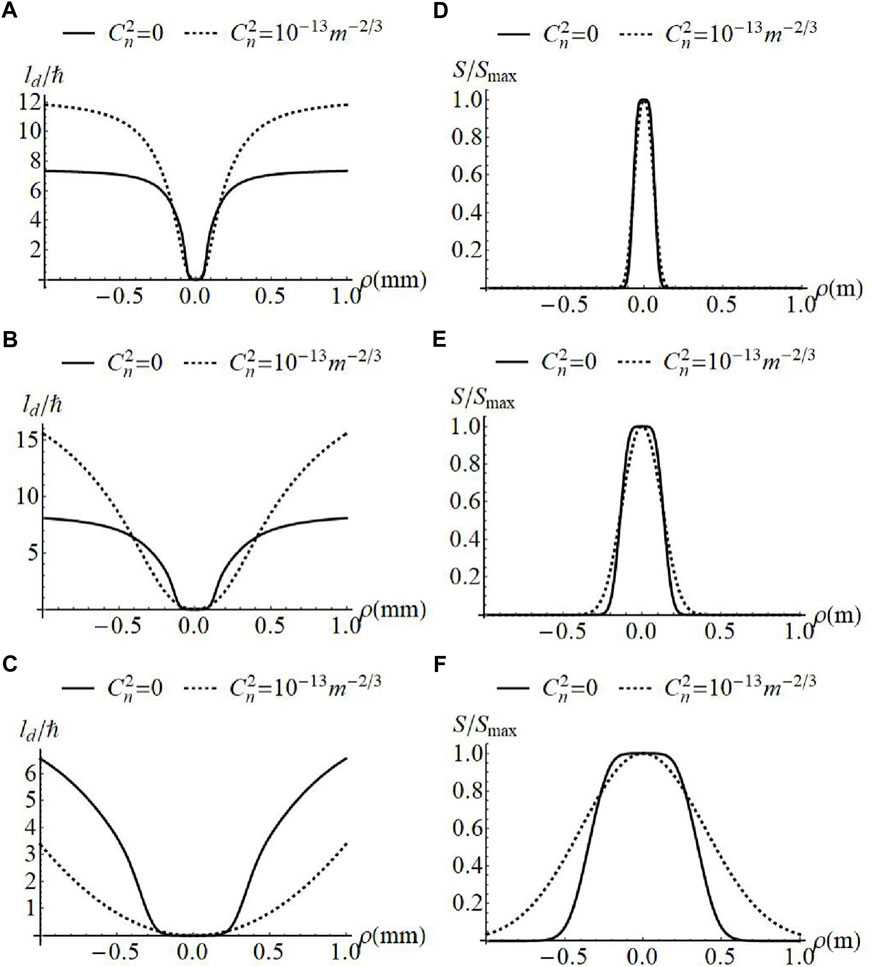
FIGURE 2. Normalized OAM flux density (A–C) and spectral density (D–F) of MGSMV beams with
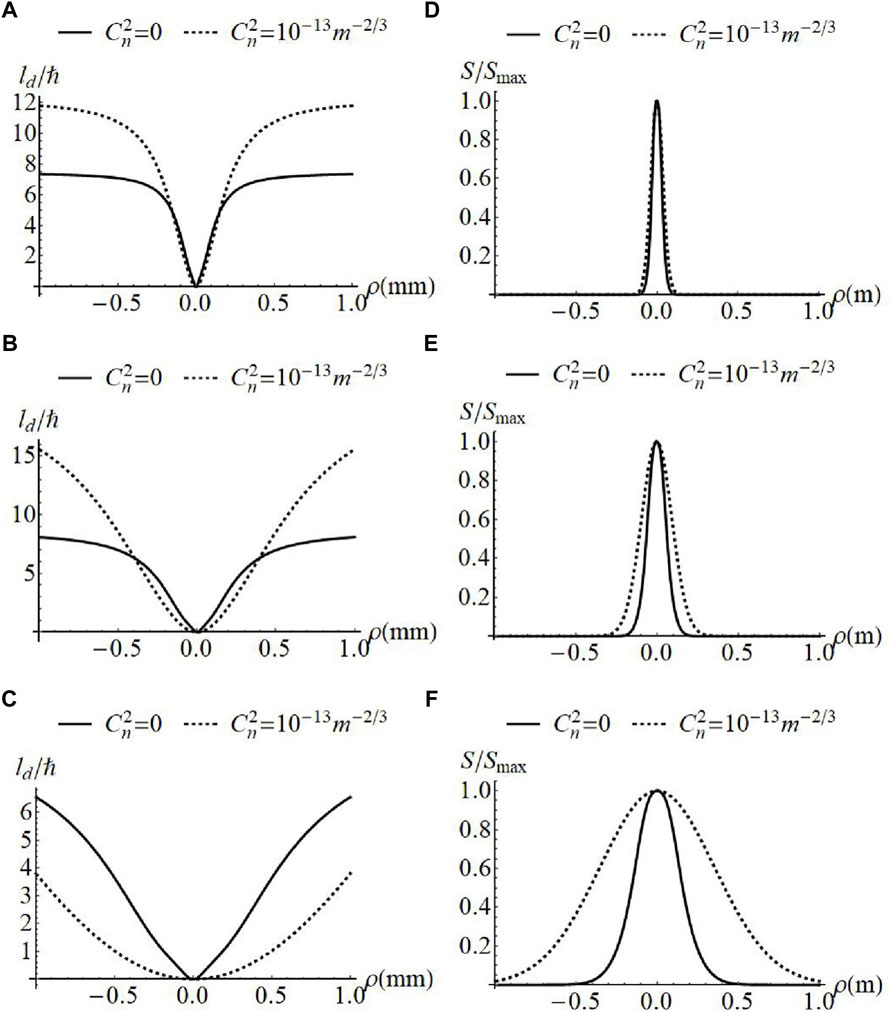
FIGURE 3. Normalized OAM flux density (A–C) and spectral density (D–F) of MGSMV beams with
Even more significant variations in the distribution of OAM can be made by the incoherent superposition of GSMV beams with equal and opposite topological charge. We label the positive contribution by the subscript “+” and the negative contribution by the subscript “-”. Figures 4, 5 give the evolution of OAM with the fixed correlation width of the positive vortex beam
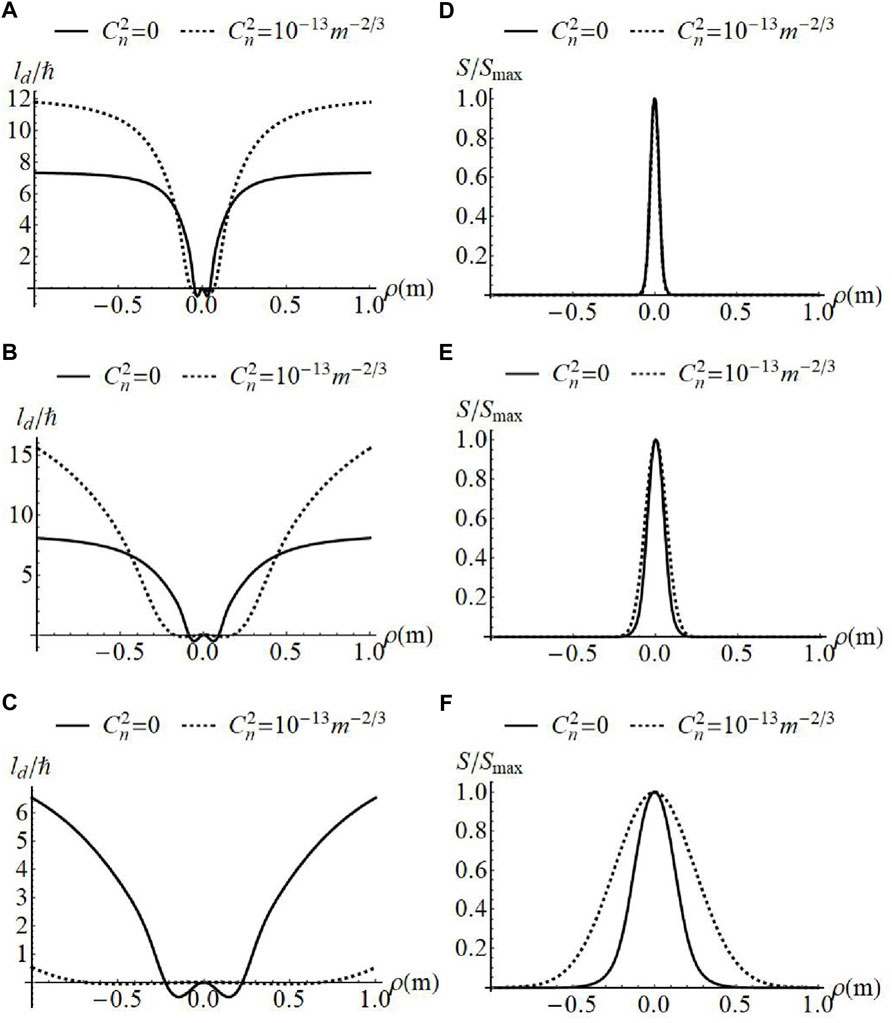
FIGURE 4. Normalized OAM flux density (A–C) and spectral density (D–F) of superposed GSMV beams with w = 10 mm,
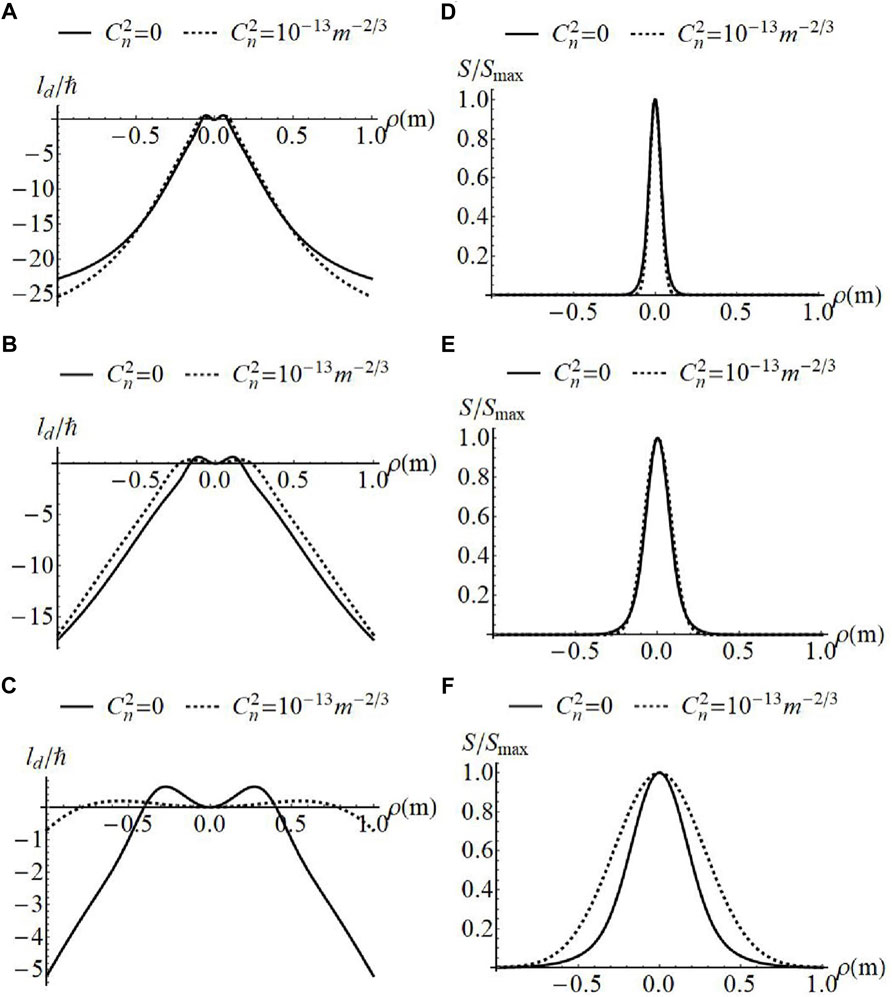
FIGURE 5. Normalized OAM flux density (A–C) and spectral density (D–F) of superposed GSMV beams with w = 10 mm,
It can be seen from the figures that this non-trivial counter-rotating structure can be maintained on propagation in atmospheric turbulence, even though the OAM
In comparing Figures 4, 5, it can be seen that the OAM distribution for
Discussion
In summary, we have studied the evolution of the OAM density flux in atmospheric turbulence for PCV beams with different coherence structures, i.e., GSMV beams, MGSMV beams, and the incoherent superposition of GSMV beams. The analytical expression of the average OAM flux density in atmospheric turbulence is derived, with which we illustrate the changes of OAM distribution on propagation. The results show that after propagating in atmospheric turbulence, the OAM distribution of PCV beams exhibits rich behavior. It is found that the OAM distribution in the outskirts is more affected by atmospheric turbulence than that near the core, which results in an interesting phenomenon that the OAM flux density is larger in atmospheric turbulence than that in free space for shorter propagation distances but becomes smaller at longer distances. Especially, for the MGSMV beams with
We have illustrated the possible OAM changes in air turbulence only for a very small portion of partially coherent beams; an entirely different behavior may be expected for non-Schell model beams, e.g., non-uniformly correlated, twisted beams or radially accelerating random beams. The calculation of the OAM flux is far from trivial even for general Schell-model beams, even in free space [39], and hence, better methods need to be developed for comprehensive analysis of the OAM flux density of beams with arbitrary coherence states, for propagation in both free space and turbulent media.
Data availability statement
The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.
Author contributions
All authors listed have made a substantial, direct, and intellectual contribution to the study and approved it for publication.
Funding
The authors thank the National Natural Science Foundation of China (12174173, 12004218), the Fujian Provincial Natural Science Foundation of China (2022J02047), and the Shandong Provincial Natural Science Foundation of China (ZR2020QA067). GG was supported by the Air Force Office of Scientific Research (FA9550-21-1-0171) and Office of Naval Research (MURI N00014-20-1-2558). OK was supported by the Cooper Fellowship of the University of Miami.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
1. Soskin MS, Vasnetsov MV. Singular optics. Prog Opt (2001) 42:219–76. doi:10.1016/s0079-6638(01)80018-4
2. Dennis MR, O’Holleran K, Padgett MJ. Singular optics: Optical vortices and polarization singularities. Prog Opt (2009) 53:293–363.
4. Lee JH, Foo G, Johnson EG, Swartzlander GA. Experimental verification of an optical vortex coronagraph. Phys Rev Lett (2006) 97:053901. doi:10.1103/physrevlett.97.053901
5. Palacios D, Rozas D, Swartzlander GA. Observed scattering into a dark optical vortex core. Phys Rev Lett (2002) 88:103902. doi:10.1103/physrevlett.88.103902
6. Gibson G, Courtial J, Padgett MJ, Vasnetsov M, Pas’ko V, Barnett SM, et al. Free-space information transfer using light beams carrying orbital angular momentum. Opt Express (2004) 12:5448–56. doi:10.1364/opex.12.005448
7. Allen L, Beijersbergen MW, Spreeuw RJC, Woerdman JP. Orbital angular momentum of light and the transformation of Laguerre-Gaussian laser modes. Phys Rev A (1992) 45:8185–9. doi:10.1103/physreva.45.8185
9. Simpson NB, Dholakia K, Allen L, Padgett MJ. Mechanical equivalence of spin and orbital angular momentum of light: An optical spanner. Opt Lett (1997) 22:52–4. doi:10.1364/ol.22.000052
10. Ladavac K, Grier DG. Microoptomechanical pumps assembled and driven by holographic optical vortex arrays. Opt Express (2004) 12:1144–9. doi:10.1364/opex.12.001144
11. Ritsch-Marte M. Orbital angular momentum light in microscopy. Phil Trans R Soc A (2017) 375:20150437. doi:10.1098/rsta.2015.0437
12. Ruffato G, Rossi R, Massari M, Mafakheri E, Capaldo P, Romanato F. Design, fabrication and characterization of Computer Generated Holograms for anti-counterfeiting applications using OAM beams as light decoders. Sci Rep (2017) 7:18011. doi:10.1038/s41598-017-18147-7
13. Erhard M, Fickler R, Krenn M, Zeilinger A. Twisted photons: New quantum perspectives in high dimensions. Light Sci Appl (2018) 7:17146. doi:10.1038/lsa.2017.146
14. Wang L, Ma J, Xiao M, Zhang Y. Application of optical orbital angular momentum to rotation measurements. Results Opt (2021) 5:100158. doi:10.1016/j.rio.2021.100158
15. Ricklin JC, Davidson FM. Atmospheric turbulence effects on a partially coherent Gaussian beam: Implications for free-space laser communication. J Opt Soc Am A (2002) 19:1794–802. doi:10.1364/josaa.19.001794
16. Zhao C, Cai Y, Lu X, Eyyuboğlu HT. Radiation force of coherent and partially coherent flat-topped beams on a Rayleigh particle. Opt Express (2009) 17:1753–65. doi:10.1364/oe.17.001753
17. Zhang J, Wang Z, Cheng B, Wang Q, Wu B, Shen X, et al. Atom cooling by partially spatially coherent lasers. Phys Rev A (2013) 88:023416. doi:10.1103/physreva.88.023416
18. Schouten HF, Gbur G, Visser TD, Wolf E. Phase singularities of the coherence functions in Young’s interference pattern. Opt Lett (2003) 28:968–70. doi:10.1364/ol.28.000968
19. Gbur G, Visser TD. Coherence vortices in partially coherent beams. Opt Commun (2003) 222:117–25. doi:10.1016/s0030-4018(03)01606-7
20. Gbur G, Visser TD, Wolf E. ‘hidden’ singularities in partially coherent wavefields. J Opt A: Pure Appl Opt (2004) 6:S239–42. doi:10.1088/1464-4258/6/5/017
21. Wang W, Takeda M. Coherence current, coherence vortex, and the conservation law of coherence. Phys Rev Lett (2006) 96:223904. doi:10.1103/physrevlett.96.223904
22. Raghunathan SB, Schouten HF, Visser TD. Correlation singularities in partially coherent electromagnetic beams. Opt Lett (2012) 37:4179–81. doi:10.1364/ol.37.004179
23. Stahl CSD, Gbur G. Complete representation of a correlation singularity in a partially coherent beam. Opt Lett (2014) 39:5985–8. doi:10.1364/ol.39.005985
24. Palacios DM, Maleev ID, Marathay AS, Swartzlander GA. Spatial correlation singularity of a vortex field. Phys Rev Lett (2004) 92:143905. doi:10.1103/physrevlett.92.143905
25. Kim SM, Gbur G. Angular momentum conservation in partially coherent wave fields. Phys Rev A (2012) 86:043814. doi:10.1103/physreva.86.043814
27. Stahl CSD, Gbur G. Partially coherent vortex beams of arbitrary order. J Opt Soc Am A (2017) 34:1793–9. doi:10.1364/josaa.34.001793
28. Zhang Y, Cai Y, Gbur G. Control of orbital angular momentum with partially coherent vortex beams. Opt Lett (2019) 44:3617–20. doi:10.1364/ol.44.003617
29. Zhang Y, Korotkova O, Cai Y, Gbur G. Correlation-induced orbital angular momentum changes. Phys Rev A (2020) 102:063513. doi:10.1103/physreva.102.063513
31. Wolf E. Introduction to the theory of coherence and polarization of light. New York: Cambridge University Press (2007). p. 222.
32. Andrews LC, Phillips RL. Laser beam propagation through random media. Bellingham, Washington: SPIE Press (1998). p. 775.
33. Shirai T, Dogariu A, Wolf E. Mode analysis of spreading of partially coherent beams propagating through atmospheric turbulence. J Opt Soc Am A (2003) 20:1094–102. doi:10.1364/josaa.20.001094
34. Shchepakina E, Korotkova O. Second-order statistics of stochastic electromagnetic beams propagating through non-Kolmogorov turbulence. Opt Express (2010) 18:10650–8. doi:10.1364/oe.18.010650
35. Korotkova O, Hyde I. Multi-Gaussian random variables for modeling optical phenomena. Opt Express (2021) 29:25771–99. doi:10.1364/oe.432227
36. Sahin S, Korotkova O. Light sources generating far fields with tunable flat profiles. Opt Lett (2012) 37:2970–2. doi:10.1364/ol.37.002970
37. Wang F, Korotkova O. Circularly symmetric cusped random beams in free space and atmospheric turbulence. Opt Express (2017) 25:5057. doi:10.1364/oe.25.005057
38. Korotkova O, Sahin S, Shchepakina E. Multi-Gaussian schell-model beams. J Opt Soc Am A (2012) 29:2159–64. doi:10.1364/josaa.29.002159
Keywords: atmospheric turbulence, propagation, partially coherent, orbital angular momentum, vortex
Citation: Zhang Y, Yu J, Gbur G and Korotkova O (2022) Evolution of the orbital angular momentum flux density of partially coherent vortex beams in atmospheric turbulence. Front. Phys. 10:1073662. doi: 10.3389/fphy.2022.1073662
Received: 18 October 2022; Accepted: 14 November 2022;
Published: 30 November 2022.
Edited by:
Carmelo Rosales-Guzmán, Centro de Investigaciones en Optica, MexicoCopyright © 2022 Zhang, Yu, Gbur and Korotkova. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Olga Korotkova, a29yb3Rrb3ZhQHBoeXNpY3MubWlhbWkuZWR1
 Yongtao Zhang
Yongtao Zhang Jiayi Yu2
Jiayi Yu2 Greg Gbur
Greg Gbur Olga Korotkova
Olga Korotkova