- Hubei Key Laboratory of Optical Information and Pattern Recognition, Wuhan Institute of Technology, Wuhan, China
Non-Hermitian skin effect (NHSE), where huge modes are accumulated at system boundaries, offers new possibility for steering the transport and localization of light by non-Hermiticity. Here, the direction-dependent NHSE is proposed in a photonic waveguide array via spatially complex modulation, where the skin modes tend to localize at different boundaries for opposite propagation directions. We utilize complex modulation to arouse anisotropic coupling between symmetric and anti-symmetric modes in multimode waveguides and further match the refractive index of adjacent waveguides. In this way, a non-Hermitian Su–Schrieffer–Heeger (SSH) lattice that supports NHSE is achieved. In particular, the anisotropic coupling is highly unidirectional. For forward direction, it allows mode conversion from antisymmetric modes to symmetric modes. However, the process is forbidden for backward direction. As a result, the skin modes tend to locate at lower boundary for forward propagation but the localization direction is reversed for backward injection. Our results provide a potential platform to investigate NHSE on photonic chips and may find applications in non-magnetic unidirectional devices.
Introduction
The ability to control the flow of light is of fundamental significance and desired for the next-generation of photonic integrated devices [1]. Inspired by band theory developed in solid state physics, its photonic analogies, such as photonic crystals [2], ring resonator arrays [3–5], and waveguide arrays [6–8], have sparked a wide range of applications by taking advantage of micro/nanofabrication technology. In particular, waves tunneling dynamics in coupled waveguides resembles that of electron hopping in crystals. Therefore, waveguide arrays are successfully utilized to simulate unique electron dynamics that may be difficult observed in electron crystal. Discrete diffraction [9], Bloch oscillation [10, 11], dynamic localization [12, 13], Anderson localization [14], and massless particle [15] were theoretically and experimentally demonstrated in different kinds of waveguides, which in turn provide new approaches to controlling light transport and localization. In addition, synthetical gauge fields can be generated by periodically bending waveguides [16], dynamical modulation of refractive index [17, 18], or using orbital coupling [6, 19], which give rise to Aharanov-Bohm caging [19], Fouquet topological insulator [20], high-order topological insulator, and semimetals [21, 22].
Recently, band theory in non-Hermitian photonic systems has also attracted a lot of attention with considering the influence of gain and loss. The early studies mainly focus on parity-time (PT) and anti-PT-symmetric systems where non-Hermiticity is introduced by on-site gain and loss [23, 24]. On the other hand, non-Hermiticity can also be produced by anisotropic coupling, which leads to intriguing non-Hermitian skin effect (NHSE) with a number of modes accumulated at system boundaries [25]. The discovery of NHSE deepens the previous understanding of bulk and topological edge modes in the sense that bulk modes can be localized but topological edge modes may become extended [26]. Therefore, the traditional bulk-boundary correspondence is broken down and non-Bloch band theory is subsequently developed to indicate the existence of topological modes. In addition, NHSE itself belongs to a topological phenomenon protected by spectral winding number, which develops a new way for manipulating light [27]. Abnormal phenomena were discovered with the aid of NHSE, such as light funneling [28], self-acceleration [29], self-healing [30], and anomalous single-mode lasing [31]. NHSE are reported in various platforms, such as quantum walks [32], cold atoms [33], electric circuits [34], acoustics [35], optical fibers [28], and photonic ring resonator arrays [4].
In this work, we present another platform by using modulated waveguide arrays to achieve NHSE. The waveguides undergo spatially refractive-index modulation and gain-loss modulation along light propagation direction at the same time, namely the complex modulation [36]. Such modulation yields one-way mode conversion in multimode waveguides, which was theoretically proposed in long-period grating and experimentally implemented in silicon waveguides [37–39]. Here, we utilize a set of modulated waveguides with each supporting two TE-polarized modes and further turn their refractive index to match the detuning of propagation constants of symmetric and anti-symmetric modes between adjacent waveguides. In this approach, we can create a non-Hermitian SSH photonic lattice that sustains NHSE with non-Hermitian anisotropic coupling induced by complex modulation. Since anisotropic coupling is unidirectional, NHSE inherits this direction-dependent behavior and tends to localize at different boundaries for different transport directions.
Theoretical model for anisotropic coupling
We start by investigating the anisotropic coupling aroused by complex modulation in a single photonic waveguide. Figure 1A shows the scheme of a waveguide where light propagates along z direction. The relative refractive indexes of cladding and core are denoted as n0 and ncore, respectively. For simplicity, we assume the cladding is air with n0 = 1. The waveguide holds two modes under TE polarization including symmetric and anti-symmetric modes, which propagation constants are denoted by kzs and kza. In Figure 1B, we plot the band structure of waveguides without modulation, namely, the propagation constant versus incident frequency. The insert illustrates the typical modal profiles of symmetric and anti-symmetric modes.
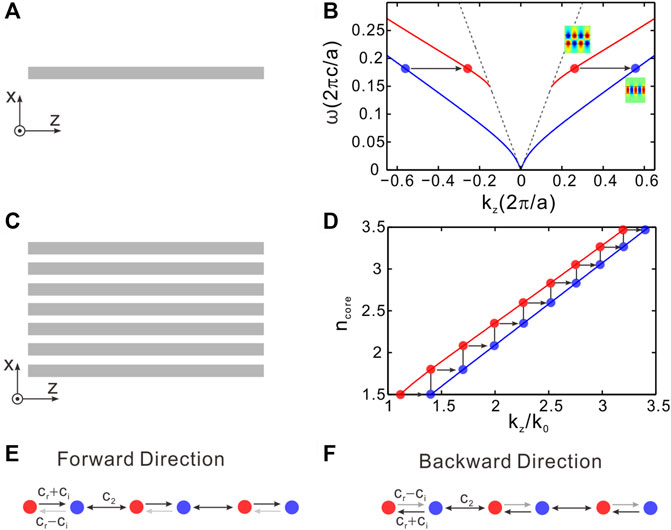
FIGURE 1. Schematic to construct non-Hermitian SSH lattice using complex modulation. (A) The diagram of a slab waveguide. (B) Band structures of the waveguide. The blue and red lines stand for symmetric and anti-symmetric modes. Their mode profiles (Ey) are shown in the insert. The two modes are coupled under spatial modulation. (C) The diagram of a waveguide array. (D) Propagation constants versus the refractive index of waveguide core. The width and incident wavelength are fixed at w = 1 μm and λ = 1.55 μm. (E) and (F) are the effective lattice for forward and backward directions, respectively. The intracell couplings are different for two lattices.
In general, the two modes are orthogonal to each other and thus the mode conversion is forbidden between them without modulation. To make them coupled, we add periodic modulation of complex permittivity along z direction. The modulation function reads as
where x0 denotes center location of the waveguide, Δεr and ΔεI are the amplitudes of the real and imaginary parts of the dielectric perturbation, Λ is the modulation period, and ϕ is the phase difference between real and imaginary modulation. The modulation profile is odd along x direction with respect to x0. When phase matching condition is satisfied with 2π/Λ = kzs—kza, the mode conversion is aroused between symmetric and antisymmetric modes. In the modulated region, the electric fields can be written as
where Es,a denote the modal profiles of symmetric and anti-symmetric mode, as and aa are their normalized amplitudes, respectively. When light is injected from the left side of the waveguide (forward direction), the real modulation is ahead of the imaginary modulation, and the phase difference is positive ϕ. By utilizing slowing varying approximation, one can derive the coupled mode equation in the modulated region for the forward propagation as follows
where the coupling coefficients are
The result indicates the complex modulation leads to complex coupling between symmetric and anti-symmetric modes. The phase difference ϕ between real and imaginary modulation acts as an effective gauge potential [40]. Its interaction with complex coupling finally leads to anisotropic coupling. It becomes more straightforward with considering a special case as ϕ = π/2, corresponding to PT-symmetric modulation [41]. In this case, the coupled mode equation reduces to
where the off-diagonal elements are different. When the real and imaginary modulations have the same strength with Δεr = Δεi, the two coupling coefficients are equal with cr = ci. In this case, it only allows mode transition from antisymmetric to symmetric modes while the inverse conversion is forbidden.
In contrast, for the backward propagation, the imaginary modulation is ahead of the real modulation. Then the effective gauge potential becomes negative with ϕ = −π/2. As a result, the coupled mode equation for the right-side injection reads as
with off-diagonal elements switched. As cr = ci, the mode conversion is reversed. The power can couple from symmetric to antisymmetric mode. However, no energy transfers from anti-symmetric mode to symmetric one. The one-way coupling behaviour is schematically indicated by the arrows in Figure 1B.
We further place an array of modulated multimode waveguides to realize a non-Hermitian SSH lattice, as shown in Figure 1C. Figure 1D plots the propagation constants of two modes as a function of the refractive index ncore with incident wavelength λ = 1.55 μm. The width of each waveguide is fixed at w = 1 μm. The blue and red lines stand for symmetric and antisymmetric modes, respectively. The two modes supported in a single waveguide are coupled by the complex modulation. We further adjust the refractive index of every waveguide such that the symmetric and anti-symmetric modes between adjacent waveguides have the same propagation constants and can be coupled. We first set the refractive index of the first waveguide to ncore = 1.5, then calculate the effective refractive index of the two modes in this waveguide, which are neff = 1.403 for symmetric mode and 1.116 for antisymmetric mode, respectively. In order to make the second waveguide couple with the previous waveguide, we should adjust the refractive index of second waveguide such that the antisymmetric mode of second waveguide is the same as that of the symmetric mode of the first waveguide. Then, the refractive index of the second waveguide is determined to be ncore = 2.084. Following this way, we can determine all refractive index of every waveguide. The refractive index from upper to lower waveguides is set to ncore = 1.50, 1.80, 2.08, 2.35, 2.598, 2.831, 3.053, 3.265, and 3.467. The materials for the parameters adopted can be SiO2 and Si. The refractive indexes of Si and SiO2 are 1.45 and 3.45, which cover the range of refractive index used above. Therefore, we could use the hybrid waveguide made by Si and SiO2 to design the proposed model. In this way, we could realize an effective coupled photonic lattice with non-Hermitian coupling, as indicated by the red and blue dots in Figure 1D. We have briefly shown the periodically modulation results in a coupled mode equation with complex coupling for mode conversion process. More intuitively, we indeed integrate on-site gain and loss into the waveguide. As the on-site dissipation is periodically varied, it can provide a wavevector to meet the mismatch between symmetric and antisymmetric modes. In this way, the two modes can be coupled and the effective coupling coefficients are imaginary. This complex coupling occurs in the momentum space between symmetric and anti-symmetric modes. We emphasis that the real-space coupling, that is, the couplings between neighboring waveguides, are still real-valued. To further consider the unidirectional coupling generated by complex modulation, the proposed SSH lattice is direction-dependent since it inherits the unidirectional behaviour. The effective lattices for forward and backward directions are shown in Figures 1E,F, respectively. The intracell couplings are inversed for opposite directions.
To further gain insights into the unidirectional coupling, we perform full wave simulation based on finite element method. As a comparison, we present the transport of light as only the real part of dielectric permittivity is modulated. The distributions of electric field (Ey) are shown in Figure 2A where light with wavelength λ = 1.55 μm is launched from the left side of waveguide, corresponding to forward propagation. Other parameters are set as w = 1 μm, ncore = 1.5, and n0 = 1. The propagation constants for symmetric and antisymmetric modes are figured out to be kzs = 5.69 μm−1 and kza = 4.52 μm−1, respectively. The modulation period is Λ = 2π/(kzs − kza) to match the detuning of two modes and the modulation amplitude is Δεr = 0.1. The insert plots the effective lattice in which the transition is bidirectional. The results show that the antisymmetric mode at the incidence evolves into symmetric mode and then transfers back to antisymmetric mode. The coupling is bidirectional and can be also reflected by plotting mode amplitudes, as indicated by the blue line for symmetric and red line for antisymmetric mode in Figure 2B. At propagation distance z = 25 μm, we see aa = 0 and as = 1, implying all light completely converts into symmetric modes. As propagation distance increases, aa increases and as decreases, indicating light transfers back to antisymmetric modes. The same behaviour applies in backward injection due to the reciprocity in momentum space [42]. Figure 2C shows the field distributions in forward propagation as the waveguide is under complex modulation. The real and imaginary modulation strength is equal as ΔεI = Δεr and the phase difference is ϕ = π/2. The coupling is completely unidirectional, as shown in the inset of Figure 2C. The injection of antisymmetric mode will stimulate symmetric mode. However, it will not transfer back. As a result, the symmetric mode is dominated at the output. We also plot the amplitudes of two modes as a function of propagation distance in Figure 2D. The amplitude of symmetric mode linearly increases (blue line) while the antisymmetric mode (red line) stays unchanged. For backward propagation, as shown in Figure 2E, the injected antisymmetric mode remains unchanged and cannot transfer to symmetric mode. This can be seen from mode amplitudes as well, as plotted in Figure 2F. The amplitude for antisymmetric mode (red line) keeps at unity for different z while it is vanished (blue line) for symmetric mode. Such one-way mode conversion clearly reflects the direction-dependent coupling due to complex modulation.
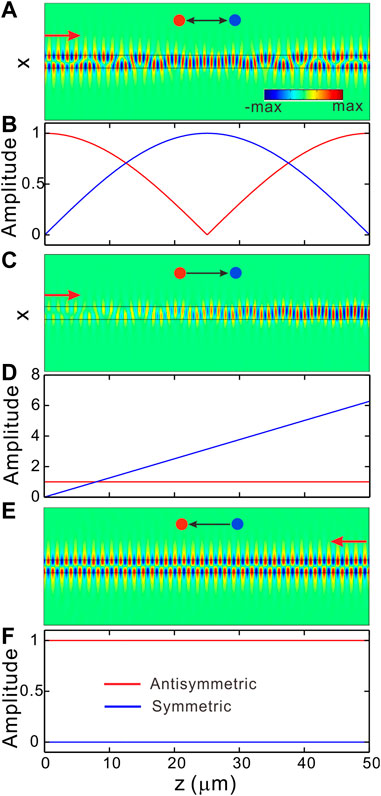
FIGURE 2. One-way mode conversion under complex modulation. (A) The simulated distribution of the electric field (Ey) under real modulation for the forward propagation. The red arrow indicates propagation direction. (B) The amplitudes of symmetric (blue line) and anti-symmetric (red line) modes along propagation distance z under real modulation. (C) and (E) are the distribution of the electric field under complex modulation for the forward and backward injections, respectively. (D) and (F) are amplitudes of two modes corresponding to C and E, respectively. The real and imaginary parts of permittivity perturbation are equal with Δεi = Δεr = 0.1. For complex modulation, the phase difference is fixed at ϕ = π/2.
We emphasis that we only use spatial modulation without time modulation. As a result, the proposed model does not break Lorentz reciprocity and cannot be used for optical isolators. We surely obtain asymmetric behavior in mode conversion. However, it is not necessary to break Lorentz reciprocity as our system still respects tij = tji with tij denoting transmission coefficients from j mode into i mode. By involving time modulation, Lorentz reciprocity can be broken and the transmission coefficients fulfill tij ≠ tji. In this case, it is possible to construct an isolator.
Non-Hermitian skin effect
As discussed above, a non-Hermitian version of SSH model can be realized by couple a set of modulated waveguides. We now analyse the eigenvalues and eigenvectors to clearly show the appearance of NHSE in the proposed systems. We consider the effective gauge potential is ϕ = π/2. Then the Bloch Hamiltonian for forward direction corresponding to Figure 1E is given as follows
with cr ± ci denoting intracell coupling, c2 signifying intercell coupling, and k representing Bloch momentum. Such a non-Hermitian model has been studied in various systems, exhibiting NHSE under OBC and non-Bloch bulk-boundary correspondence [26, 43, 44]. Here we focus on NHSE, which can be indicated by eigenvalue spectra. Figures 3A–C plot the eigenvalue spectra on the complex plane for three different anisotropic couplings with ci = 0, cr/2, and cr, respectively. Other parameters are fixed at cr = 1 and c2 = 0.5. The blue dots and red circles stand for PBC and OBC, respectively. As ci = 0, the intracell coupling is isotropic and the system is Hermitian. The spectra for OBC and PBC are real and almost identical to each other, as shown in Figure 3A. In this case, there is no NHSE under OBC. The corresponding distributions of eigenmodes are plotted in Figure 3D. The modes are extended throughout all sites. As ci = cr/2, the periodic spectrum forms closed loops in the complex plane. In contrast, the spectrum for OBC collapses into lines that resides within the loops for PBC. This is a typical feature of NHSE. According to bulk-boundary correspondence based on spectral winding, NHSE will take place under OBC if periodic spectra enclose any area. The spectral winding is given by
where Eb is any base point. The spectral winding number is to characterize the number of times of complex eigenvalues encircling Eb. The non-zero winding number indicates NHSE will appear in the system under OBC. If periodic spectra enclose any non-zero area, the base point can be chosen within the loop, which leads to W ≠ 0. In Figure 3E, we plot the distributions of eigenmodes, which are accumulated at the left boundary and exponentially decrease with distance away from the boundary. As we further increase the anisotropic degree with ci = cr, the enclosed area of periodic spectrum increases, as shown Figure 3C. NHSE effect becomes stronger in the sense that eigenmodes experience stronger localization at the left boundary, as shown in Figure 3F.
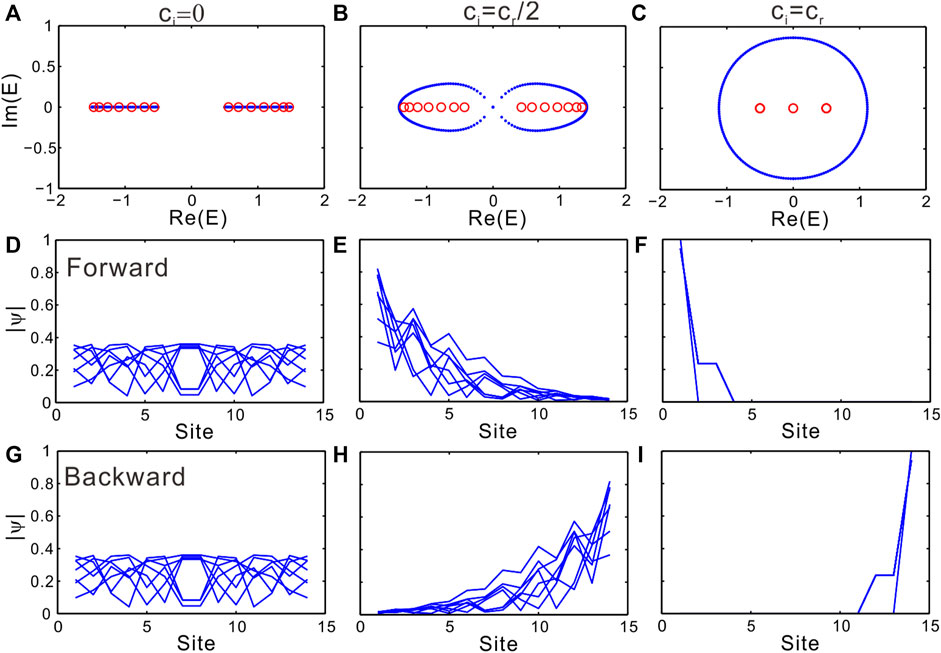
FIGURE 3. NHSE in modulated waveguide arrays. (A–C) Are the eigenvalue spectra for three different imaginary coupling strength with ci = 0, ci = cr/2, and ci = cr, respectively. The blue dots and red circles stand for periodic and open boundaries, respectively. (D–F) Are the distributions of eigenmodes under OBC for forward propagation. (G–I) Are eigenmode distributions for backward propagation.
For backward direction, the effective gauge field switches to negative value and the intracell coupling changes as well. The Bloch Hamiltonian corresponding to Figure 1F is given by
The spectra for backward direction are similar to that of forward propagation. However, the location of skin modes is reversed. Figures 3G–I plot the distributions of eigenmodes for backward direction for ci = 0, cr/2, and cr, respectively. As ci = 0, as shown in Figure 3G, there are no skin modes. The eigenmodes are distributed throughout all sites, just like forward case. In contrast, when ci = cr/2 and ci = cr, as shown in Figures 3G,H, one can observe NHSE and skin modes are exponentially accumulated at the right boundary.
The NHSE and the direction-dependent behavior can be directedly viewed from light propagation by full wave simulation. In Figure 4, we employ nine modulated waveguides to achieve a SSH lattice. Each waveguide underlies complex modulation with ϕ = π/2. The refractive index of each waveguide is the same as that in Figure 1D. To generate the same coupling strength between symmetric and antisymmetric modes in the same waveguide, the modulation amplitudes of different waveguides should be adjusted. From upper to lower, the modulation amplitudes of dielectric permittivity are Δεr = 0.12, 0.13, 0.15, 0.16, 0.18, 0.20.0.21, 0.23, and 0.24 with the modulation vectors 2π/Λ = 0.287k0, 0.303k0, 0.288k0, 0.270k0, 0.253k0, 0.238k0, 0.226k0, 0.215k0, and 0.204k0. As a result, the intracell couplings are identical, corresponding to cr = 0.0628 μm−1. On the other hand, the spatial spacing should be altered as well to make intercell couplings identical. The spacing from upper to bottom is d = 1.59 μm, 1.41 μm, 1.30 μm, 1.24 μm, 1.20 μm, 1.17 μm, 1.14 μm, and 1.12 μm, which leads to coupling coefficient c2 = 0.044 μm−1. In this way, a photonic SSH lattice is created. Then, we launch light from the second waveguide at the bottom with antisymmetric modes. Figures 4A–C show the light propagation for forward propagation as Δεi = 0, Δεr/2, and Δεr, respectively. As Δεi = 0, light spreads and more and more waveguides are excited during the propagation, displaying discrete diffraction [Figure 4A]. As Δεi = Δεr/2, light tends to localize at the lower boundary with the aid of NHSE [Figure 4B]. As we further increase imaginary modulation with Δεi = Δεr, the localization becomes stronger [Figure 4C]. These results indicate the skin modes tend to localize light at the bottom of waveguide array. We further inject light from the right side, corresponding to backward propagation, as shown in Figures 4D–F. As Δεi = 0 [Figure 1D], there is no NHSE and light spreads during the evolution, just the same as Figure 1A. In contrast, in the presence of NHSE, light tends to localize at the upper boundary for backward propagation [Figures 4E,F], significantly different from the forward direction. The results clearly show the direction-dependent behavior of NHSE using complex modulation. The wave propagation in Figure 4F is not very well confined into a single waveguide for the backward propagation. It may be caused by the following two reasons. Firstly, the input ports locate at the lower boundary, which is just near the location boundary for forward propagation but far from location boundary for backward injection. Secondly, the designed waveguide array is not perfectly equivalent to a tight-binding model and the coupling coefficients for the backward direction are not completely vanished. Anyway, the results can still reflect the unidirectional localization of NHSE.
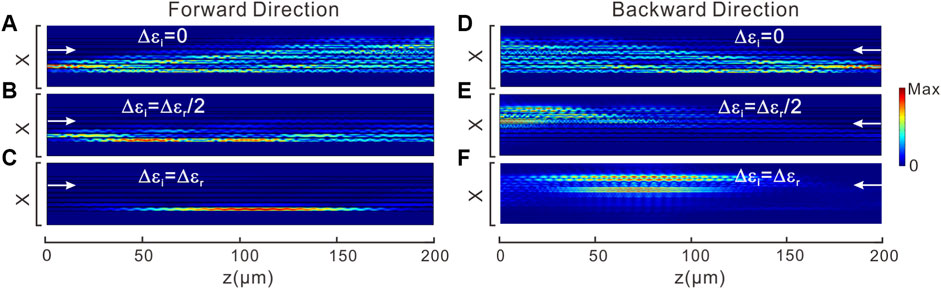
FIGURE 4. Wave dynamics for direction-dependent NHSE. (A–C) Are the distributions of electric fields (|E|) for forward direction with Δεi = 0, Δεr/2, and Δεr, respectively. (D–F) Are the field distributions for backward propagation. The arrow in the insert denotes the propagation direction.
Conclusion
In conclusion, we have proposed NHSE in waveguide arrays based on complex modulation. The complex modulation could arouse non-Hermitian coupling and effective gauge fields between symmetric and anti-symmetric modes, which interaction finally leads to anisotropic coupling. By coupling a set of waveguides and making the propagation constants of neighboring waveguides matched, we successfully create a photonic SSH lattice sustaining NHSE. Since the effective gauge fields switch its sign for opposite propagation directions, the anisotropic coupling changes its relative strength as well. Therefore, the localization direction of NHSE is direction-dependent in the sense that skin modes are accumulated to locate at the lower boundary for forward direction and upper boundary for backward direction. The proposed model may be experimentally implemented in dielectric waveguides. The modulation of real part of refractive index can periodically embed sinusoidal-shaped structure at the top of the silicon waveguide, while the imaginary part of modulation is realized by integrating periodically curved Ge or Cr layers [38]. In order to match the refractive index of adjacent waveguides, one can adjust the width and the height of Si. The difficulty may lie in how to fabricate a large-scale waveguide array together with each waveguide under complex modulation with different parameters. As NHSE is a topological phenomenon, the accuracy requirements of some parameters can be relaxed such as coupling coefficients, waveguide spacing, and the width of waveguides. We believe the proposed model can be realized soon. Here we only discussed skin modes but topological modes can also be explored in these systems to detect non-Bloch bulk-boundary correspondence and extended isolated modes [45]. Furthermore, the spatial modulation does not break optical reciprocity. The similar mechanism can be extended to dynamically modulated waveguides with involving temporal modulation. One could construct a special photon transition where transition can occur between two modes at different frequency for forward direction. However, for backward propagation, mode transition is forbidden due the wavevector mismatch, which may give rise to non-reciprocal transport of skin modes. Our results pave a way to chip-scale localization with the aid of NHSE and may find potential applications in non-magnetic unidirectional devices.
Data availability statement
The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding authors.
Author contributions
SK contributed to the conception and design of the study. YW and JZ performed the research and analyzed the data. YW and CJ wrote the first draft of the manuscript. XL and SK contributed to the revisions.
Funding
This research was funded by the National Natural Science Foundation of China (NSFC) (12204363), the 13th Graduate Education Innovation Fund of Wuhan Institute of Technology (CX2021380) and Innovation and Entrepreneurship Training Program Funded by Wuhan Institute of Technology (S202110490034).
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
1. Ozawa T, Price HM, Amo A, Goldman N, Hafezi M, Lu L, et al. Topological photonics. Rev Mod Phys (2019) 91:015006. doi:10.1103/RevModPhys.91.015006
2. Wang Z, Chong Y, Joannopoulos JD, Soljacic M. Observation of unidirectional backscattering-immune topological electromagnetic states. Nature (2009) 461:772–5. doi:10.1038/nature08293
3. Hafezi M, Mittal S, Fan J, Migdall A, Taylor JM. Imaging topological edge states in silicon photonics. Nat Photon (2013) 7:1001–5. doi:10.1038/nphoton.2013.274
4. Lin Z, Ding L, Ke S, Li X. Steering non-Hermitian skin modes by synthetic gauge fields in optical ring resonators. Opt Lett (2021) 46:3512–5. doi:10.1364/OL.431904
5. Jiang J, Ren J, Guo Z, Zhu W, Long Y, Jiang H, et al. Seeing topological winding number and band inversion in photonic dimer chain of split-ring resonators. Phys Rev B (2020) 101:165427. doi:10.1103/PhysRevB.101.165427
6. Jiang C, Wu Y, Qin M, Ke S. Topological bound modes with orbital angular momentum in optical waveguide arrays. J Lightwave Technol (2022) 2022 1–7. doi:10.1109/jlt.2022.3200139
7. Wu S, Song W, Gao S, Chen Y, Zhu S, Li T. Floquet π mode engineering in non-Hermitian waveguide lattices. Phys Rev Res (2021) 3:023211. doi:10.1103/PhysRevResearch.3.023211
8. Song W, Sun W, Chen C, Song Q, Xiao S, Zhu S, et al. Breakup and recovery of topological zero modes in finite non-hermitian optical lattices. Phys Rev Lett (2019) 123:165701. doi:10.1103/PhysRevLett.123.165701
9. Ke S, Liu Q, Zhao D, Liu W. Spectral discrete diffraction with non-Hermitian coupling. J OPT SOC AM B (2018) 35:2387. doi:10.1364/josab.35.002387
10. Peschel U, Pertsch T, Lederer F. Optical Bloch oscillations in waveguide arrays. Opt Lett (1998) 23:1701–3. doi:10.1364/OL.23.001701
11. Lenz G, Talanina I, De Sterke CM. Bloch oscillations in an array of curved optical waveguides. Phys Rev Lett (1999) 83:963–6. doi:10.1103/PhysRevLett.83.963
12. Longhi S, Marangoni M, Lobino M, Ramponi R, Laporta P, Cianci E, et al. Observation of dynamic localization in periodically curved waveguide arrays. Phys Rev Lett (2006) 96:243901. doi:10.1103/PhysRevLett.96.243901
13. Iyer R, Aitchison JS, Wan J, Dignam MM, De Sterke CM. Exact dynamic localization in curved AlGaAs optical waveguide arrays. Opt Express (2007) 15:3212–23. doi:10.1364/OE.15.003212
14. Segev M, Silberberg Y, Christodoulides DN. Anderson localization of light. Nat Photon (2013) 7:197–204. doi:10.1038/nphoton.2013.30
15. Xu B, Li T, Zhu S. Simulation of massless Dirac dynamics in plasmonic waveguide arrays. Opt Express (2018) 26:13416–24. doi:10.1364/OE.26.013416
16. Garanovich IL, Longhi S, Sukhorukov AA, Kivshar YS. Light propagation and localization in modulated photonic lattices and waveguides. Phys Rep (2012) 518:1–79. doi:10.1016/j.physrep.2012.03.005
17. Qin C, Wang B, Wong Z, Longhi S, Lu P. Discrete diffraction and Bloch oscillations in non-Hermitian frequency lattices induced by complex photonic gauge fields. Phys Rev B (2020) 101:064303. doi:10.1103/PhysRevB.101.064303
18. Jalas D, Petrov A, Eich M, Freude W, Fan S, Yu Z, et al. What is — And what is not — An optical isolator. Nat Photon (2013) 7:579–82. doi:10.1038/nphoton.2013.185
19. Jörg C, Queraltó G, Kremer M, Pelegrí G, Schulz J, Szameit A, et al. Artificial gauge field switching using orbital angular momentum modes in optical waveguides. Light Sci Appl (2020) 9:150–7. doi:10.1038/s41377-020-00385-6
20. Rechtsman MC, Zeuner JM, Plotnik Y, Lumer Y, Podolsky D, Dreisow F, et al. Photonic Floquet topological insulators. Nature (2013) 496:196–200. doi:10.1038/nature12066
21. Xie B, Liu H, Wang H, Cheng H, Tian J, Chen S. A review of topological semimetal phases in photonic artificial microstructures. Front Phys (2021) 9:621. doi:10.3389/fphy.2021.771481
22. Luo L, Wang HX, Lin ZK, Jiang B, Wu Y, Li F, et al. Observation of a phononic higher-order Weyl semimetal. Nat Mater (2021) 20:794–9. doi:10.1038/s41563-021-00985-6
23. Bender CM, Boettcher S. Real spectra in non-hermitian Hamiltonians HavingPTSymmetry. Phys Rev Lett (1998) 80:5243–6. doi:10.1103/PhysRevLett.80.5243
24. Ge L, Türeci HE. AntisymmetricPT-photonic structures with balanced positive- and negative-index materials. Phys Rev A (2013) 88:053810. doi:10.1103/PhysRevA.88.053810
25. Okuma N, Kawabata K, Shiozaki K, Sato M. Topological origin of non-Hermitian skin effects. Phys Rev Lett (2020) 124:086801. doi:10.1103/PhysRevLett.124.086801
26. Yao S, Wang Z. Edge states and topological invariants of non-hermitian systems. Phys Rev Lett (2018) 121:086803. doi:10.1103/PhysRevLett.121.086803
27. Zhang K, Yang Z, Fang C. Correspondence between winding numbers and skin modes in non-hermitian systems. Phys Rev Lett (2020) 125:126402. doi:10.1103/PhysRevLett.125.126402
28. Weidemann S, Kremer M, Helbig T, Hofmann T, Stegmaier A, Greiter M, et al. Topological funneling of light. Science (2020) 368:311–4. doi:10.1126/science.aaz8727
29. Longhi S. Non-Hermitian skin effect and self-acceleration. Phys Rev B (2022) 105:245143. doi:10.1103/PhysRevB.105.245143
30. Longhi S. Self-healing of non-hermitian topological skin modes. Phys Rev Lett (2022) 128:157601. doi:10.1103/PhysRevLett.128.157601
31. Zhu B, Wang Q, Leykam D, Xue H, Wang QJ, Chong YD. Anomalous single-mode lasing induced by nonlinearity and the non-hermitian skin effect. Phys Rev Lett (2022) 129:013903. doi:10.1103/PhysRevLett.129.013903
32. Xiao L, Deng T, Wang K, Zhu G, Wang Z, Yi W, et al. Non-Hermitian bulk–boundary correspondence in quantum dynamics. Nat Phys (2020) 16:761–6. doi:10.1038/s41567-020-0836-6
33. Li L, Lee CH, Gong J. Topological switch for non-hermitian skin effect in cold-atom systems with loss. Phys Rev Lett (2020) 124:250402. doi:10.1103/PhysRevLett.124.250402
34. Helbig T, Hofmann T, Imhof S, Abdelghany M, Kiessling T, Molenkamp LW, et al. Generalized bulk–boundary correspondence in non-Hermitian topolectrical circuits. Nat Phys (2020) 16:747–50. doi:10.1038/s41567-020-0922-9
35. Zhang L, Yang Y, Ge Y, Guan YJ, Chen Q, Yan Q, et al. Acoustic non-Hermitian skin effect from twisted winding topology. Nat Commun (2021) 12:6297. doi:10.1038/s41467-021-26619-8
36. Song AY, Shi Y, Lin Q, Fan S. Direction-dependent parity-time phase transition and nonreciprocal amplification with dynamic gain-loss modulation. Phys Rev A (2019) 99:013824. doi:10.1103/PhysRevA.99.013824
37. Greenberg M, Orenstein M. Unidirectional complex gratings assisted couplers. Opt Express (2004) 12:4013–8. doi:10.1364/opex.12.004013
38. Feng L, Ayache M, Huang J, Xu YL, Lu MH, Chen YF, et al. Nonreciprocal light propagation in a silicon photonic circuit. Science (2011) 333:729–33. doi:10.1126/science.1206038
39. Feng L, Xu YL, Fegadolli WS, Lu MH, Oliveira JE, Almeida VR, et al. Experimental demonstration of a unidirectional reflectionless parity-time metamaterial at optical frequencies. Nat Mater (2013) 12:108–13. doi:10.1038/nmat3495
40. Zheng L, Wang B, Qin C, Zhao L, Chen S, Liu W, et al. Chiral Zener tunneling in non-Hermitian frequency lattices. Opt Lett (2022) 47:4644–7. doi:10.1364/OL.470880
41. Fang K, Yu Z, Fan S. Photonic Aharonov-Bohm effect based on dynamic modulation. Phys Rev Lett (2012) 108:153901. doi:10.1103/PhysRevLett.108.153901
42. Wang W, Wang LQ, Xue RD, Chen HL, Guo RP, Liu Y, et al. Unidirectional excitation of radiative-loss-free surface plasmon polaritons in PT-symmetric systems. Phys Rev Lett (2017) 119:077401. doi:10.1103/PhysRevLett.119.077401
43. Yang Z, Zhang K, Fang C, Hu J. Non-hermitian bulk-boundary correspondence and auxiliary generalized brillouin zone theory. Phys Rev Lett (2020) 125:226402. doi:10.1103/PhysRevLett.125.226402
44. Jin L, Song Z. Bulk-boundary correspondence in a non-Hermitian system in one dimension with chiral inversion symmetry. Phys Rev B (2019) 99:081103. doi:10.1103/PhysRevB.99.081103
Keywords: non-Hermitian skin effect, waveguide array, modulation, anisotropic coupling, localization
Citation: Wu Y, Zou J, Jiang C, Li X and Ke S (2022) Direction-dependent non-Hermitian skin effect in modulated photonic waveguide arrays. Front. Phys. 10:1073295. doi: 10.3389/fphy.2022.1073295
Received: 18 October 2022; Accepted: 23 November 2022;
Published: 02 December 2022.
Edited by:
Haoran Xue, Nanyang Technological University, SingaporeReviewed by:
Yiqi Zhang, Xi’an Jiaotong University, ChinaJinhui Wu, Northeast Normal University, China
Copyright © 2022 Wu, Zou, Jiang, Li and Ke. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Xiaohong Li, eGlhb2hvbmdsaUB3aXQuZWR1LmNu; Shaolin Ke, a2VzaGFvbGluQHdpdC5lZHUuY24=
†These authors have contributed equally to this work
 Yanting Wu†
Yanting Wu† Shaolin Ke
Shaolin Ke