Influence of the focusing characteristics of near-infrared lasers on the maintenance of plasma luminescence

The interaction of 980-nm continuous laser radiation with the plasma of a continuous optical discharge in xenon lamps at a pressure of p = 12 atm has been studied. The threshold power and characteristics of the laser required to sustain the xenon plasma became our focus. According to the theory of Gaussian beam propagation, the laser parameters after collimation and focusing are obtained by combining ZEMAX simulation and the actual measurement. The influence of the beam waist ω₀, which determines the power density distribution at focus, and the Rayleigh range Z₀, which determines the energy concentration range, on the threshold maintenance power is expounded. The results show that there is a threshold power density for the generation of plasma, whose value is about 1,500–2,000 W/mm², and that the threshold maintenance power of the plasma shows an overall decreasing trend with decreasing ω₀. When ω₀ is reduced to a higher power density that can easily maintain the thermodynamic equilibrium process of the plasma, the mismatch between Z₀ and the plasma size caused by the decrease in Z₀ makes the threshold power tend to be stable and increasing.

1 Introduction

When high-power CW laser energy is radiated to the gas, the molecules or atoms in it will be ionized, forming a high-temperature and high-particle density plasma environment composed of electrons, ions, and neutral particles [1]. Under the conditions of Stark broadening, the electrons in the xenon lamp and mercury lamp with higher pressure undergo active free–free transition in the process of reverse bremsstrahlung radiation [2], producing highly bright and stable light with a stronger UV distribution [3, 4], which is widely used in many fields such as semiconductor measurement, material characterization, and hyperspectral imaging [5–7].

Since the photon energy is comparable to the excitation and ionization potentials of most gases, multiphoton absorption and cascade ionization are considered to be important mechanisms for plasma generation by laser–gas interactions [8], but even with xenon, which has the lowest thermal conductivity and ionization energy among all non-radioactive rare gases [9], the laser energy required to produce plasma is enormous. On the other hand, once the plasma is generated, the center of higher temperature and high-electron density is formed. At this time, the local thermodynamic equilibrium of the plasma [10] can be maintained by injecting lower energy to achieve long-term stable luminescence. The plasma in this state absorbs the energy of laser light through inverse bremsstrahlung [11, 12] to balance the energy loss generated by radiation and other processes, and this energy is far less than the breakdown threshold of gas.

In this work, a xenon lamp was selected as the object to generate plasma, and xenon in the lamp was pre-ionized by DC high-voltage ignition to form an initial plasma discharge channel, in which some atoms in the gas were transferred from the ground state to the excited state, obtaining more energy. Before pre-ionization, we focused the laser between the two electrodes of the lamp to maintain the continuous emission of the plasma generated by pre-ionization. Through preliminary maintenance experiments with the existing pressurized xenon lamps in the laboratory, a xenon lamp bulb with a charge pressure of 12 atm, which was the easiest to maintain, was selected. The threshold power of the laser required to maintain the plasma at this charging pressure was studied with the help of different lens combinations, and the regularity of the plasma maintenance process was analyzed in combination with the characteristics of the focused beam.

2 Research contents

In the literature [13], a spherical heat transfer model was developed for a focused laser beam, and the effect of plasma temperature on the laser power required for the equilibrium process was investigated from the perspective of laser absorption by the plasma. At a constant pressure P, the absorption coefficient ${\mu }_{\omega }\left(T_k\right)$ exists in a rising process due to the increase in plasma temperature T caused by laser injection; subsequently, the electron and ion density n decreases with the increase in temperature T and the absorption coefficient also decreases, as shown in Eqs 1, 2, where $\Theta \left(T_k\right)$ was the heat flux potential, which varied monotonically with temperature. Corresponding to the absorption of the laser by the plasma, there exists a threshold power $P_0$ enabling the plasma to enter a steady state, that is, a local thermodynamic equilibrium state, and when the plasma is unable to maintain this state, that is, the injected laser energy does not allow the plasma to reach the desired temperature, the ionization becomes so weak that the absorption of the laser can even be neglected.

$P_0\approx \frac{2\pi \Theta \left(T_k\right)}{{\mu }_{\omega }\left(T_k\right)},(1)$

$P\sim nT=constant.(2)$

2.1 Experimental setup

The laser-maintained plasma setup is shown in Figure 1. A semiconductor laser with a central output wavelength of 980 nm is selected as the laser source, and the output is fiber-coupled, with the pigtail being a multimode fiber of 106.5 μm core diameter produced by Everbright Photonics Co., Ltd.

FIGURE 1

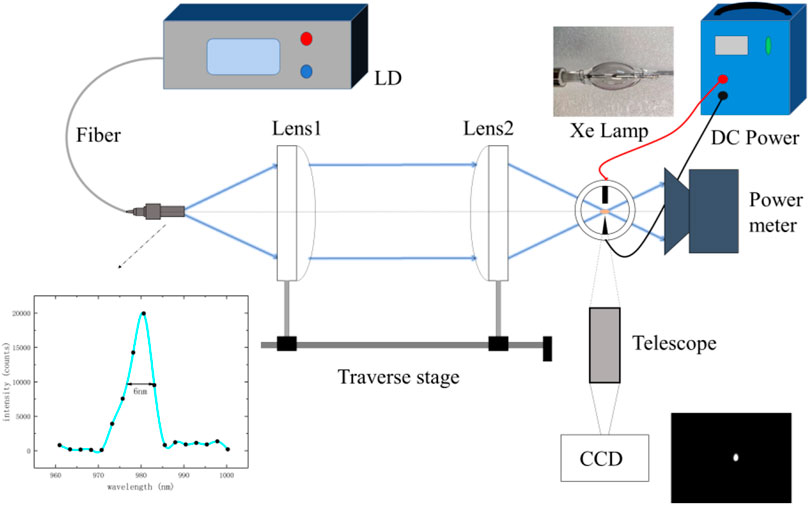
FIGURE 1. Experimental schematic diagram. The near-infrared semiconductor laser (illustrated as the spectrum of the central wavelength, FWHM is about 6 nm, and the laser can reach a maximum power of up to 70 W), after being collimated and focused by a position adjustable lens group, enters the middle of the electrode of the xenon lamp with a diameter of 18 mm and a pressure of 12 atm. The bulb is externally connected with a high-voltage arc excitation device to form the initial plasma (this voltage will be removed after laser injection) and uses a power meter (F150A-BB-26, Ophir) and a CCD camera (MV-CA016-10UM, Hikrobotics) to record the laser spot and plasma information.

Highly ionized plasma was formed by using a DC high voltage to break down the xenon gas between the electrodes, and then, continuous laser energy was focused on the location of the plasma to maintain its continuous and stable luminescence [14]. We measured the numerical aperture (NA) value of the outgoing laser using the knife-edge method [15], that is, 0.14, and it corresponded to the far-field divergence angle of the outgoing laser. In order to obtain a more concentrated laser distribution, the laser output from the fiber had gone through the collimation and focusing process of the lens group [16] before being focused between the two electrodes of the xenon lamp.

2.2 Experimental method

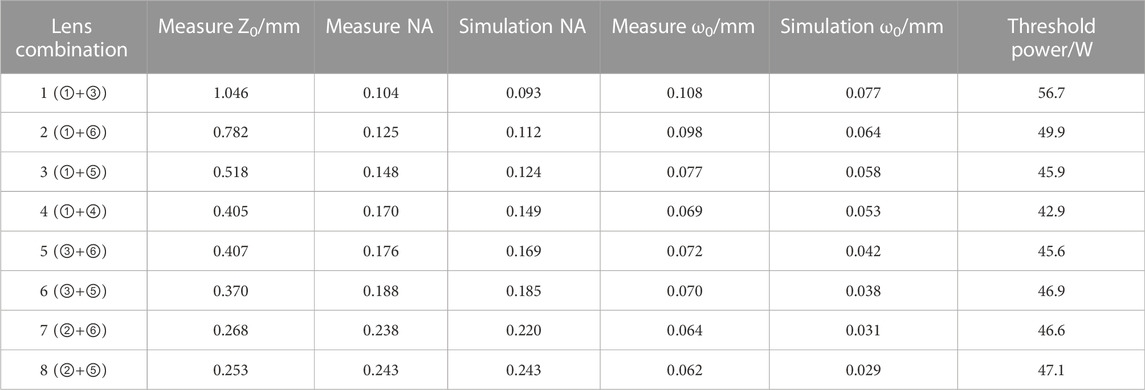
Lenses ①, ②, and ③ with numerical apertures of 0.79, 0.76, and 0.625 were selected as the collimating lenses, respectively, and lenses ④, ⑤, and ⑥ with focal lengths slightly greater than the bulb radius were selected as the focusing lenses, which were combined for the experimental study of the laser-maintained plasma. The aforementioned lenses were aspherical.

We selected the xenon lamp charging pressure of 12 atm, and the minimum laser power that can maintain the continuous and stable emission of plasma for more than 10 min was taken as the threshold power under this combination. The characteristic parameters of the focused beam under different combinations were obtained using ZEMAX simulation and actual measurements. The focused laser beam still propagates according to the characteristics of a Gaussian beam, and the radius of the beam waist, which affects the laser power density, and the Rayleigh length, which affects the degree of energy concentration, became the objects of our focus.

2.2.1 ZEMAX simulation

We took the lens combination ②+⑥ as an example and set the object height, wavelength, and object NA to 0.05 mm, 0.98 μm, and 0.14, respectively, in the lens data editor according to the parameters of the incident laser. We input the lens parameters into the lens data editor and set the corresponding initial distance, respectively, and then optimize the thickness of the distance between the exit surface of the optical fiber and the front surface of the collimating lens and the distance between the rear surface of the focusing lens and the image plane to obtain the best collimation and focusing effect. The optical path in the shadow mode is shown in Figure 2A.

FIGURE 2

FIGURE 2. Simulation result graph and actual measurement graph of the combination ②+⑥. (A) 3D layout of the beam in ZEMAX; (B) focal plane light map and diffuse spot images corresponding to object heights of 0 and ±0.05 mm; (C) schematic diagram of Gaussian beam propagation and its parametric relationships, is the waist radius, Z₀ is the Rayleigh length, θ is the far-field divergence angle, and λ is the wavelength; (D) spot radius at different positions and their hyperbolic fits (inset shows the spot images acquired by the CCD (VEN-161-61U3M-M05, China Daheng Group, Inc.) corresponding to each position).

Observing the distribution of the light beam on the image plane, the converged light beam obtained a good focusing effect. On the premise of ensuring that the aberration was as small as possible, the small spot output was realized and the spot size radius at the focal point was only 31 μm. This result was better reflected in the scattered spot distribution of the light beam, as shown in Figure 2B.

The simulation of the initial lens combination using ZEMAX was an aid for us to exclude the effect of optical path aberration and determine the radius of the focused beam to facilitate the selection of a lens set that met the plasma maintenance conditions.

2.2.2 Beam parameter measurement

According to the propagation characteristics of the Gaussian beam, as shown in Figure 2C, the focused beam can be fit well into the hyperbolic equation [17]. The CCD was used to record the spot image including the focus within a range of about 4 mm before and after the focus. A total of 11 photographs were collected, of which at least five points were within the Rayleigh length of the focused beam [18].

The attenuated laser was directly incident on the image surface of the CCD after focusing to obtain a clear spot image near the focal point. Again, using the combination ②+⑥ as an example, the spot image taken near the focal point is shown in Figure 2D.

Combined with the spot position, the focused laser transmission can be represented by fitting the hyperbolic equation:

${\omega \left(z\right)}^2=A{z}^2+Bz+C,(3)$

Where $\omega \left(z\right)$ corresponds to the radius of the spot at position $z$. $A$, $B$, and $C$ are the three coefficients obtained from the least squares fit; each parameter of the laser can be expressed by A, B, and C, respectively, as

$\left\{\begin{array}{c}{\omega }_0=\sqrt{C-B^2/4A}\\ \theta =\sqrt{A}\\ Z_0=\frac{\sqrt{AC-B^2/4}}{A}\end{array}\right.,(4)$

Where ${\omega }_0$, θ, and $Z_0$ denote the beam waist radius, beam divergence angle, and Rayleigh length at the focal plane, respectively. We took the combination ②+⑥ as an example, and its spot size and fitted data are shown in Figure 2D. The NA, beam waist radius, and Rayleigh length obtained according to Eq. 4 were 0.238, 63.903 μm, and 0.268 mm, respectively.

3 Result analysis

The aforementioned combination was simulated and compared with the focused beam characteristic parameters fitted after CCD measurement, and the results are shown in Table 1. It can be observed that the NA obtained by simulation and actual measurement data fitting was not much different, and the difference in the beam waist radius was also basically maintained at the same level. The difference was caused by the aberration of the optical path and the diffraction of the beam during the actual beam propagation [19]. With the increase in NA, the threshold power tended to decrease gradually. In order to analyze this reason, we first carried out simulation analysis on the selected combinations. The simulated data and the photographs recorded by the camera verified that some combinations showed obvious deviation from the simulation curve of ${\omega }_0$ in Figure 3A due to the existence of aberration. Other combinations met the characteristics of Gaussian beam propagation, that is, with the increase of NA, the beam waist radius gradually decreased. It was worth noting that in the actual beam transmission, the beam waist radius cannot be ideally reduced with the increase in NA; as obtained in the simulation, as shown in Figure 3A, after NA was greater than 0.15, the change slope of the measurement curve was smaller than that of the simulation curve, which will directly affect the threshold power density of the laser at the focal point.

TABLE 1

TABLE 1. Simulation and fitting parameters of the focused beam with different lens combinations.

FIGURE 3

FIGURE 3. (A) Plot of the beam waist radius versus NA under simulation and the actual measurement; (B) effect of on the threshold power and its density; (C) relationship between and Rayleigh length at the focal point; (D) schematic diagram of laser focusing and the formed plasma morphology under different NA values, with insets showing the plasma images collected under different NA values.

We studied the threshold power affected by the beam waist radius and Rayleigh length for eight combinations with small aberrations and no excessive energy loss (this energy loss is mainly reflected in the shading of the laser energy by the experimental device) and established its relationship with the threshold power, as shown in Figure 3B, with the beam waist radius as the independent variable. The threshold power density represents the average distribution of laser energy at the focal plane and was numerically equal to the ratio of the threshold power to the focal plane area, which showed an opposite trend to the threshold power with ${\omega }_0$, and this relationship can be better explained by the variation of the plasma luminescence size with the laser focusing NA in Figure 3D. If the NA was small, that is, ${\omega }_0$ and $Z_0$ is large, although the plasma size was larger at this time, but its longitudinal dimension was still less than the Rayleigh length of the focused laser, and the threshold power density at this time reflects the power conditions that should be met when the plasma was lit; as NA increases, $Z_0$ decreases to the same scale as the plasma length, the power density at the luminous edge still met the value required in the first case, and the power density at the focal plane was in a rising stage due to the decrease of ${\omega }_0$; this process continued until the Rayleigh length was smaller than the plasma length, that is, the case of large NA, and the power density beyond the Rayleigh length still met the threshold power density for maintaining the plasma under this condition, which also meant that the plasma needed more energy to maintain, and the maintenance power that should be continuously decreasing becomes stable and appears to increase. In addition, this trend was further increased by the fact that the decrease in ${\omega }_0$ tends to level off with increasing NA during the actual transmission. In summary, we believed that a certain threshold power density was necessary for the formation of a stable plasma; this value was in the approximate range of 1,500–2,000 W/mm², but the required laser power was also influenced by the Rayleigh range and the relative length of the plasma size when analyzed from the point of view of plasma maintenance. This was also better verified by combination 4 (circled in Figures 3B,C), that is, ①+④, which had a lower threshold power due to its larger Rayleigh length than the combination in the same ${\omega }_0$ conditions.

4 Discussion and conclusion

We adopted the method of combining simulation and experimental measurement to study the continuous and stable luminescence process of the laser-maintained xenon plasma at a fixed pressure. The following main conclusions were drawn for this process.

In the selection of optical path, the lens should be chosen from a lens group with small aberration and large energy transmission to obtain a focused beam, the poor focusing effect mainly occurred in the case of large NA, and ZEMAX in this process can play a preliminary screening role. In addition, the beam waist radius decreased with increasing NA, and the elevated power density was to some extent conducive to the reduction of the threshold power, but as the Rayleigh length also decreased along with it, the reduced energy concentration region reduced the plasma size, while the mismatch between the two sizes can make the plasma maintenance require higher power, and the threshold power no longer decreased or even appeared to increase slowly, and the two factors, ${\omega }_0$ and $Z_0$, each played a major role in maintaining the laser threshold of the plasma in different NA ranges.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.

Author contributions

YC conceived the project, LZ and XG conducted the experiment, LZ and YC wrote the manuscript, YS provided ZEMAX scheme guidance, TZ helped with the measurement, CZ and SJ provided theoretical guidance and supervised the project. And all authors contributed to discussions during its preparation.

Funding

This work was funded by the Fundamental Research Funds for the Provincial Universities of Zhejiang (No: 2021YW03).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2022.1072023/full#supplementary-material

References

1. Huddlestone RH, Leonard SL. Plasma diagnostic techniques. Massachusetts: Plasma Diagnostic Techniques (1965).

Google Scholar

2. Kozlov G, Kuznetsov V, Masyukov V. Radiative losses by argon plasma and the emissive model of a continuous optical discharge. Zh Eksp Teor Fiz (1974) 66:954–64.

Google Scholar

3. Silfvast W, Wood O. Comparison of radiation from laser-produced and dc-heated plasmas in xenon. Appl Phys Lett (1974) 25(5):274–7. doi:10.1063/1.1655470

CrossRef Full Text | Google Scholar

4. Biberman LM, Norman GÉ. Continuous spectra of atomic gases and plasma. Sov Phys Usp (1967) 10(1):52–90. doi:10.1070/pu1967v010n01abeh003199

CrossRef Full Text | Google Scholar

5. Taudt C, Baselt T, Nelsen B, Assmann H, Greiner A, Koch E, et al. Characterization of edge effects in precision low-coherence interferometry using broadband light sources. Opt Meas Syst Ind Inspection X (2017) 10329:748–53. doi:10.1117/12.2270318

CrossRef Full Text | Google Scholar

6. Ojaghi A, Fay ME, Lam WA, Robles FE. Ultraviolet hyperspectral interferometric microscopy. Sci Rep (2018) 8(1):9913–6. doi:10.1038/s41598-018-28208-0

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Taudt C, Baselt T, Nelsen B, Assmann H, Greiner A, Koch E, et al. Evaluation of the thermal stability of a low-coherence interferometer for precision surface profilometry. Photonic Instrumentation Eng IV (2017) 10110:302–8. doi:10.1117/12.2252375

CrossRef Full Text | Google Scholar

8. Bekefi G. Principles of laser plasmas. New York (1976).

Google Scholar

9. Wang Y. The reaseach based on the simulation of microwave plasma light source. University of Electronic Science and Technology of China (2015). (in chinese).

Google Scholar

10. Van Der Mullen J. On the atomic state distribution function in inductively coupled plasmas—II: The stage of local thermal equilibrium and its validity region. Spectrochimica Acta B: At Spectrosc (1990) 45(1-2):1–13. doi:10.1016/0584-8547(90)80078-W

CrossRef Full Text | Google Scholar

11. Seely JF, Harris EG. Heating of a plasma by multiphoton inverse bremsstrahlung. Phys Rev A (Coll Park) (1973) 7(3):1064–7. doi:10.1103/PhysRevA.7.1064

CrossRef Full Text | Google Scholar

12. Mora P. Theoretical model of absorption of laser light by a plasma. Phys Fluids (1982) 25(6):1051–6. doi:10.1063/1.863837

CrossRef Full Text | Google Scholar

13. Raĭzer YP. Optical discharges. Sov Phys Usp (1980) 23(11):789–806. doi:10.1070/pu1980v023n11abeh005064

CrossRef Full Text | Google Scholar

14. Zimakov V, Kuznetsov V, Solovyov N, Shemyakin A, Shilov A, Yakimov M, et al. Interaction of near-IR laser radiation with plasma of a continuous optical discharge. Plasma Phys Rep (2016) 42(1):68–73. doi:10.1134/s1063780x15110100

CrossRef Full Text | Google Scholar

15. Khosrofian JM, Garetz BA. Measurement of a Gaussian laser beam diameter through the direct inversion of knife-edge data. Appl Opt (1983) 22(21):3406–10. doi:10.1364/AO.22.003406

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Dickson LD. Characteristics of a propagating Gaussian beam. Appl Opt (1970) 9(8):1854–61. doi:10.1364/AO.9.001854

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Yan H. Evaluation of beam characteristics of high power semiconductor laser. Changchun University of Science and Technology (2019). (in chinese).

Google Scholar

18. Xiong X. The measuring system of laser beam parameter and quality. JiLin university (2007). (in chinese).

Google Scholar

19. Mouroulis P, Macdonald J, Macdonald J. Geometrical optics and optical design. New York: Oxford University Press (1997). p. 351p.

Google Scholar