Realisation of acoustic black holes using multi-material additive manufacturing

Acoustic black holes (ABHs) have been widely accepted as an effective passive vibration control technique, with multiple configurations investigated for different applications. However, traditional manufacturing techniques may limit the potential geometries and configurations of the ABH. For example, the required damping layer has to be applied to the surface of the ABH taper rather than being embedded throughout or within the taper. In addition, conventional subtractive manufacturing is particularly wasteful for the realisation of ABHs, which rely on the removal of material to create a tapering structure. Therefore, in this work, we investigate the use of multi-material additive manufacturing as a potential solution, which avoids waste material in the manufacturing process and is capable of realising complex geometries, such as enclosing one material inside another. An ABH taper in a beam termination application has been implemented using polymer multi-material inkjet printing. The additively manufactured ABH was modelled using finite element analysis, before being manufactured and experimentally tested to enable an investigation of the vibration attenuation capabilities of such an ABH realisation.

1 Introduction

Acoustic black holes (ABHs), as first proposed by Mironov [1], are used as a passive vibration control technique in beams and plates, as reviewed by Pelat et al. [2]. In beams, the ABH is implemented by gradually decreasing the thickness of the beam along its length, which results in a decreasing wavespeed along the taper. In the ideal theoretical case, the ABH tapers to zero thickness such that a wavespeed of zero is achieved. However, in practice, the ABH taper is terminated with a finite thickness, which means that, without the addition of damping material to the ABH taper, the wave is still reflected from the ABH termination despite the reduced wavespeed. Therefore, an additional layer of damping material is typically added to the ABH taper to dissipate the wave energy [3]. A practical ABH beam termination with an applied damping layer can be seen in Figure 1.

FIGURE 1

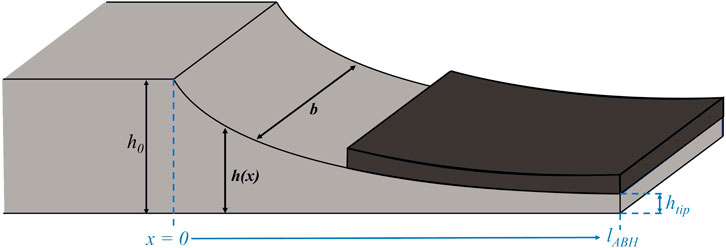
FIGURE 1. ABH beam termination with damping layer showing the beam thickness h₀, beam width b, ABH length l_ABH, ABH thickness profile h(x) and ABH tip height h_tip.

ABHs are well suited to applications in which the overall weight of a structure is particularly limited, since unlike most passive vibration control techniques where mass must be added, the ABH requires material to be removed from the beam, reducing its mass. Unfortunately, this means that production of ABH terminated beams produces significant waste material when realised using traditional subtractive manufacturing methods. Typically, a uniform beam will be milled or otherwise cut to achieve the characteristic ABH taper. This method also imposes a minimum tip height that can be achieved, since at small scales, manufacturing defects are more likely to damage the ABH during construction. In addition, the required damping layer must be added to the structure after machining the ABH taper and thus results in a multi-stage manufacturing process.

In addition to the conventional ABH design shown in Figure 1, a variety of more complex ABHs have also been proposed, as reviewed in [2]. Of particular interest to the work presented here, there have been a number of ABH configurations proposed that are challenging to produce with traditional manufacturing techniques. For example, the spiral ABH proposed by Park et al. [4] requires precise construction of a traditional ABH on a beam before applying damping to the surface and finally roll forming the ABH taper to reduce the footprint of the design. This is a time consuming and complex process, with each step introducing a new source of error between the ABH design and constructed ABH and this may benefit from additive manufacturing. Along similar lines, a modified ABH profile has recently been proposed to improve the fatigue life of the ABH. However, this modified design requires a relatively complex variation in the taper profile [5], which may also be more easily and sustainably manufactured using additive processes. Another alternative configuration is the functionally graded ABH, wherein the material properties are changed along the length of the beam as opposed to the geometry. Initial investigations into a multi-material ABH have taken place and have shown that such a design can provide a reduction in vibration without the introduction of thin structural sections [6]. The manufacture of such a system would be unfeasible in terms of time and complexity of construction using traditional manufacturing techniques and multi-material additive manufacturing provides a suitable manufacturing alternative.

The issues and challenges highlighted above regarding the manufacture of ABHs could potentially be avoided by using multi-material additive manufacturing (MMAM). Additive manufacturing (AM) has already been widely accepted in many industries for its ability to produce increasingly complex structures, whilst the layer-wise construction of products reduces waste production significantly compared to subtractive manufacturing methods [7–9]. In recent years, MMAM has allowed for simultaneous construction with multiple materials, allowing for one material to be enclosed or otherwise shielded by another in such a way that would not be possible to realise with traditional techniques [10].

Despite its advantages, MMAM is not without its limitations. For example, as with all AM techniques, discrepancies between the predicted properties based on the material used and the measured performance of the printed product do not perfectly align due to the inconsistencies in internal structures in AM parts [11]. Moreover, MMAM sometimes has issues with adhesion between dissimilar materials [12], causing material separation issues and damage to parts that cannot easily be repaired. There are also limitations on which materials can be used in one print, as materials with dissimilar printing requirements cannot be used together due to the risk of one material printing process leading to damage of another material [13] or introducing excessive complication to the build process.

The use of AM, and MMAM, in ABH design has been investigated by a number of researchers to-date. In [14], for example, the use of Fused Deposition Modelling (FDM) is investigated by realising three different ABH designs that maintain a constant thickness profile by increasing damping layer thickness as the ABH taper decreases in thickness. These designs would all be challenging to realise with subtractive manufacturing processes and would certainly require a multi-stage manufacturing process. MMAM has also been used in the realisation of ABHs with both decreasing thickness profile and graded material properties along the length of the taper [15]. This work used inkjet printing, where a photopolymer ink is deposited onto the build surface before being cured with UV light. Inkjet printing is capable of much finer build resolution in the final product compared to FDM [16]. Moreover, inkjet printing produces more consistent internal structures since each layer is cured simultaneously rather than material gradually cooling down throughout the print, as in FDM. However, inkjet printing is typically more expensive, since it requires more complex equipment and specialised materials. Nevertheless, [15] investigated the benefit of grading both the material and thickness profiles, as noted above, and compared the performance to a conventional ABH profile geometry without an added damping layer. This work demonstrated a significant advantage to using MMAM to realise ABHs, however, it did not explore the realisation of a conventional ABH thickness profile with an added damping layer. This specific design provides a clear benchmark in the field of ABHs and also poses potential challenges in MMAM due to the significant differences between the structural material and the damping material which may lead to adhesion issues between the materials. Therefore, the realisation of a conventional geometrical ABH with an added damping layer provides the main focus of the work presented in this paper.

In the first instance, Section 2 of this paper presents the methods associated with numerical modelling, manufacture and experimental testing of polymer ABH beams realised through MMAM. Section 3 presents the numerical and experimental results and analyses the performance of the ABH terminated beam. Section 4 discusses the suitability of this method for use in the design and manufacture of ABHs and the potential use cases for additively manufactured ABH beams.

2 Methods

2.1 ABH design

ABHs were originally theorised as a taper in a beam or plate with a tip height gradually reducing to zero [1]. Theoretically, this gradual decrease in profile height would induce a decrease in the wavespeed to zero at the ABH tip, with wavespeed, c, calculated as

$c={\left(\frac{Eh{\left(x\right)}^2}{12\rho }\right)}^{1/4}{\omega }^{1/2},(1)$

where E is the Young’s modulus of the material, h(x) is the height function of the ABH taper, ρ is the density of the material, and ω is the frequency of the propagating wave. In practice, it is not possible to reach zero thickness and, as such, this ideal ABH cannot be manufactured. Instead, the ABH is terminated with a truncated tip and a damping layer is added to the taper to dissipate the wave that propagates with a reduced speed [3]. Previous work by Ouisse et al. [17] has investigated the optimal damping layer configuration for a given ABH taper through a parametric study exploring the effect of the damping thickness and the relative area of the ABH taper that has the additional damping layer applied. This work demonstrated that the optimal configuration was dependent not only on the considered ABH geometry and construction, but also on the frequency range over which the performance was evaluated. Considering the operational frequency range of ABHs, it is well documented that the ABH effect occurs above a certain cut-on frequency. In the 1D ABH taper configuration considered here, the ABH cut-on frequency can be calculated as [2, 18].

$f_{\mathit{cut-on}}=\frac{h_0}{2\pi l_{\mathit{ABH}}^2}\sqrt{\frac{E\left(40-24\nu \right)}{12\rho \left(1-{\nu }^2\right)}}(2)$

where ν is the Poisson’s ratio of the material and l_ABH is the length of the ABH taper. As such, the minimum effective frequency of the ABH can easily be changed by varying the length of the taper, although this design parameter is often limited by the considered application in practice.

As well as considering the length of the ABH and the optimal application of the damping layer, a number of different ABH taper profiles have been investigated in the literature. A particularly thorough analytical comparison between various ABH profiles has been presented by Karlo et al. [19], where the power-law profile, an exponential profile, a power-cosine profile, a Gaussian profile and a compound power-law are compared. This study demonstrates that although the exponential profile shows the lowest general level of reflection from the ABH termination, it also exhibits higher levels of fluctuation over frequency. A compromise between these two characteristics can be achieved via the power-law profile, which tends to the exponential profile as the order of the power is increased, but can reach a performance compromise with a lower order power. This flexibility is one reason why the power-law profile is still the most commonly applied profile in the literature. In particular, it provides an effective compromise between impedance matching to the beam and wavespeed reduction within the taper. The power-law thickness profile can be described as [3].

$h\left(x\right)=ϵx^{\mu }+h_{\mathit{tip}},(3)$

where ϵ is a scaling factor, ϵ = h_beam−h_tip, μ is the exponent of the power law, and h_tip is the height of the truncated tip.

To evaluate the feasibility of realising a conventional ABH beam termination using MMAM, an ABH taper with a length of 7 cm, a tip height, h₀, of 0.5 mm and power law, μ, of four was selected. These design parameters were chosen to be consistent with ABH profiles described in the literature and realised using conventional manufacturing, for example [20]. These ABH profile parameters do not necessarily test the limits of what is possible with the MMAM approach, but they do provide a benchmark case to evaluate the realisability of a functional ABH using MMAM. The ABH termination was applied to a beam of length 18 cm, which with the added ABH termination of 7 cm corresponds to the maximum build dimension for the inkjet printer used in this study. The width of the beam was set to 4 cm and the beam thickness was 1 cm, both of which were chosen to minimise plate-type behaviour.

The MMAM has been carried out in this study using the Stratasys inkjet system and their range of digital materials. In particular, two materials from this range were used in the designs: VeroClear and Tango+. VeroClear is a rigid polymer, designed to simulate acrylic [21] and was used for the beam sections and ABH tapers of each design. Tango+ is a rubber-like polymer [22] that was used for the damping layer. VeroClear and Tango + have a nominal Young’s modulus of 2.3 GPa and 0.62 MPa and an isotropic loss factor of 0.06 and 1.05 respectively. Both materials have a density of 1160 kgm³. According to the geometry of the ABH and the material properties, it is relevant to note that, according to Eq. 2, the cut-on frequency for the ABH terminations is 954 Hz.

Three different beams configurations were investigated in this study: one constant thickness beam constructed from VeroClear with a length of 25 cm; one beam with an ABH termination as described above but no additional damping layer applied; and one beam with the same ABH termination, but an additional damping layer manufactured using the Tango + material. The designs were all printed using multi-material inkjet printing and could thus be constructed in one uninterrupted process. This set of three configurations has been chosen to provide insight into the effect of the geometrical ABH itself, and the influence of the damping layer. In order to design the damping layer, an investigation into the optimal damping layer configuration was performed similarly to that presented in [17] but for the ABH taper considered here. This study considered damping layer lengths between 1 and 7 cm and thicknesses between h_tip and 8 × h_tip with the objective of achieving the minimum average kinetic energy in the beam. The results of this study are not presented here for conciseness, however, they are consistent with the general conclusions in [17], and result in a 6 cm long and 4 mm thick damping treatment providing the best performance. The two ABH termination configurations considered here are presented in Figure 2.

FIGURE 2

FIGURE 2. Diagrams showing the two ABH configurations. (A) Geometric ABH with 0.5 mm tip height and no damping layer. (B) Geometric ABH with 0.5 mm tip height and additional damping layer.

2.2 Simulation methods

Each beam configuration described in Section 2.1 was modelled in COMSOL MultiPhysics using a 3D solid mechanics model in the frequency domain. A boundary load was applied to a small circular area, representing the mounting stud contact point used in the experiments and a 1 N load was applied acting to excite the beam flexurally. The remaining boundary conditions were defined to be free and a mesh convergence study was conducted at the upper frequency of interest. The final models for the uniform beam, undamped ABH and damped ABH configurations had 1578 elements, 1824 elements and 6507 elements respectively once fully converged. The elements were hexahedral in the uniform beam sections of each model and prismatic in the ABH tapers. To evaluate the performance of the three configurations, a uniform grid of 3 × 9 points covering the uniform beam section were used to extract the velocity response in the same direction as the force excitation, which was normal to the beam. The model was solved at frequencies between 20 Hz and 5 kHz, with a frequency resolution of 20 Hz. The extracted data was subsequently processed in MATLAB to estimate the kinetic energy in the beam section of each design based on the sum of the squared velocities measured at the 27 evaluation points. Although the kinetic energy could be directly extracted from the models, this process was adopted to be consistent with the experimental procedure described in the following section.

2.3 Experimental methods

The three beam configurations described in Section 2.1 have also been experimentally characterised. Each beam was suspended vertically on a wire to approximate the free boundary conditions assumed in the model. The beam was excited by a shaker driven by white noise up to 5 kHz and attached to the beam via a stinger and impedance head, which was used to measure the force of the excitation. The response of the beam was measured over a grid of 3 × 9 positions using three accelerometers attached across the width of the uniform beam section and nine repetitions with the accelerometers re-positioned at nine locations along the length of the beam. During each measurement, the acceleration and input force were measured when the beam was excited for 30 s.

The performance of the ABH termination was quantified by estimating the average kinetic energy of the uniform beam section per unit input force at each frequency. The energy was quantified relative to the magnitude of the input force to account for the resonance of the shaker as well as the differences between the excitation force applied in the finite element modelling compared to the experimental investigations.

3 Results

3.1 Multi-material printing

The three beam configurations described in Section 2.1 have been manufactured as described above and, upon visual inspection, there were no apparent issues with the printed ABH tapers in terms of build quality. Each taper was printed accurately with no voids or cavities in the beam, as would be desired in a solid inkjet print. The material boundaries between the taper and damping layer were clean and defined with no apparent blending between materials whilst still maintaining good adhesion between these materials. The printed beams with ABH tapers can be seen in Figure 3 (the constant thickness beam is omitted for conciseness).

FIGURE 3

FIGURE 3. Inkjet printed ABH beam configurations (A,C) 0.5 mm tip height ABH configuration with no damping layer (B,D) 0.5 mm tip height ABH configuration with additional damping layer.

3.2 Structural response analysis

The behaviour of the three beam configurations has been evaluated using both the simulated and experimental methods described in Section 2. Figure 4 shows the simulation 1) and measurement 2) results for the three beam configurations. Focusing firstly on the simulation results presented in Figure 4A, it can be seen that the uniform beam and the beam terminated by the undamped ABH show similar characteristics with clear resonance peaks. However, the location of these peaks varies between these two configurations, due to the combined effect of the differences in mass and stiffness of each configuration and the resonance behaviour of the ABH taper. The results corresponding to the damped ABH configuration clearly demonstrate its high performance capability, with the peaks above 1 kHz being heavily damped compared to the undamped ABH configuration. This can be attributed to the high isotropic loss factor of the Tango + damping layer effectively dissipating the energy in the ABH taper. It is interesting to note that although the ABH cut-on frequency is around 1 kHz, according to Eq. 2, the damped ABH termination still provides significant attenuation of the 360 Hz resonance, although this is unlikely to be due to the ABH effect directly.

FIGURE 4

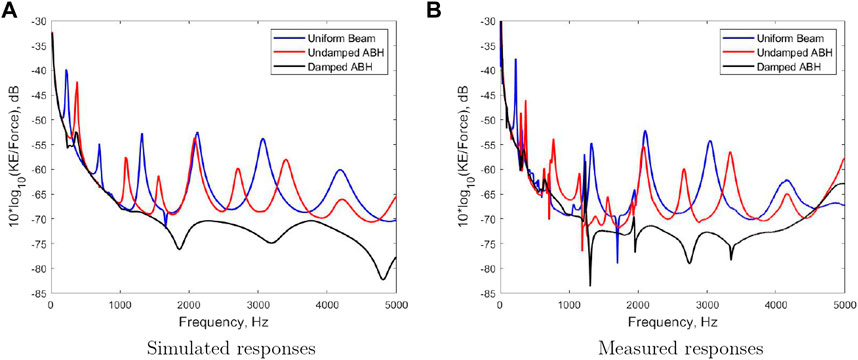
FIGURE 4. Kinetic energy normalised to the force input over frequency for the simulated (A) and measured (B) responses corresponding to the uniform beam (blue), undamped ABH (red) and damped ABH (black).

Figure 4B shows the corresponding set of results obtained from the experimental testing of the manufactured beams. From these results it can be seen that the characteristic behaviour is similar to that shown by the simulation results. The results for the uniform beam and the undamped ABH profiles, in particular, align closely with minimal difference between the location of the resonance peaks. The differences between simulation and measurement are more significant for the damped ABH profile. At freqencies above around 2 kHz, the experimental results show a similar level of vibration control to that demonstrated in simulation; below 2 kHz it can be seen that not all of the resonances are as strongly attenuated as predicted by the simulations, although a significant level of vibration control remains. There are a number of possible contributors to the differences between the characteristics of the results at lower frequencies. Firstly, there may be differences between the assumed and actual material properties, including the potential for frequency dependent properties in practice. There will also be differences between the boundary conditions and force excitation conditions that are not fully described by the COMSOL model. Nevertheless, the experimental results clearly demonstrate the need for the use of the additional damping layer, but also confirm the realisability of the ABH using MMAM.

4 Discussion

This work has demonstrated that it is possible to realise a geometric ABH termination on a beam using multi-material inkjet printing. It was possible to produce high quality printed prototypes with strong adhesion between the structural and damping materials.

The simulated and experimental responses of each beam configuration were consistent in their characteristics, demonstrating that the ABH with an applied damping layer provides an effective means of vibration control. There were some discrepancies between the measured and simulated results, particularly in the case of the damped ABH design, but these can be attributed to factors not fully captured by the numerical models used in the simulation study. Despite these differences, it has been shown in both simulation and experiment that a multi-material additively manufactured ABH with an additional damping layer provides an effective passive vibration control measure for the beam termination applications.

Future work may investigate the material properties of the printable materials in more detail, considering their potentially frequency dependent nature. This could then be used to update and improve the accuracy of the finite element modelling process to better predict the behaviour of the final printed beams and enable more reliable design optimisation processes to be carried out. Attempts to construct more complex ABH designs should now also be considered, such as the spiral ABH [4] and the fatigue optimised ABH [5] discussed in Section 1.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

BA produced the finite element models and completed the experiments undertaken in this work. JC aided in the design of the experiment and otherwise supervised the work undertaken in this paper. BA wrote the manuscript. JC edited the manuscript.

Funding

This work was supported by an EPSRC Prosperity Partnership (No. EP/S03661X/1).

Acknowledgments

The authors acknowledge the use of the IRIDIS High Performance Computing Facility and associated support services at the University of Southampton in the completion of this work. The authors acknowledge the contributions of Anil Bastola and the Centre for Additive Manufacturing at the University of Nottingham for the production of the test specimens.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Mironov MA. Propagation of a flexural wave in a plate whose thickness decreases smoothly to zero in a finite interval. Soviet Phys Acoustics-Ussr (1988) 34:318–9.

Google Scholar

2. Pelat A, Gautier F, Conlon SC, Semperlotti F. The acoustic black hole: A review of theory and applications. J Sound Vibration (2020) 476:115316. doi:10.1016/J.JSV.2020.115316

CrossRef Full Text | Google Scholar

3. Krylov VV, Tilman FJ. Acoustic ‘black holes’ for flexural waves as effective vibration dampers. J Sound Vibration (2004) 274:605–19. doi:10.1016/J.JSV.2003.05.010

CrossRef Full Text | Google Scholar

4. Park S, Kim M, Jeon W. Experimental validation of vibration damping using an Archimedean spiral acoustic black hole. J Sound Vibration (2019) 459:114838. doi:10.1016/j.jsv.2019.07.004

CrossRef Full Text | Google Scholar

5. Keys A. Modified acoustic black hole profile for improved fatigue performance. In: Proceedings of 2022 International Congress on Noise Control Engineering, INTER-NOISE2022 (2022).

Google Scholar

6. Austin B, Cheer J. Design of a multi-material acoustic black hole. In: Proceedings of 2022 International Congress on Noise Control Engineering, INTER-NOISE2022 (2022).

Google Scholar

7. Leal R, Barreiros FM, Alves L, Romeiro F, Vasco JC, Santos M, et al. Additive manufacturing tooling for the automotive industry. Int J Adv Manuf Technol (2017) 92:1671–6. doi:10.1007/s00170-017-0239-8

CrossRef Full Text | Google Scholar

8. Uriondo A, Esperon-Miguez M, Perinpanayagam S. The present and future of additive manufacturing in the aerospace sector: A review of important aspects. Proc Inst Mech Eng G: J Aerospace Eng (2015) 229:2132–47. doi:10.1177/0954410014568797

CrossRef Full Text | Google Scholar

9. Thompson A, McNally D, Maskery I, Leach RK. X-Ray computed tomography and additive manufacturing in medicine: A review. Int J Metrol Qual Eng (2017) 8:17. doi:10.1051/ijmqe/2017015

CrossRef Full Text | Google Scholar

10. Dalaq AS, Abueidda DW, Abu Al-Rub RK. Mechanical properties of 3D printed interpenetrating phase composites with novel architectured 3D solid-sheet reinforcements. Composites A: Appl Sci Manufacturing (2016) 84:266–80. doi:10.1016/j.compositesa.2016.02.009

CrossRef Full Text | Google Scholar

11. Tuan DN, Kashani A, Imbalzano G, Nguyen KT, Hui D. Additive manufacturing (3D printing): A review of materials, methods, applications and challenges. Composites B: Eng (2018) 143:172–96. doi:10.1016/j.compositesb.2018.02.012

CrossRef Full Text | Google Scholar

12. Vu IQ, Bass LB, Williams CB, Dillard DA. Characterizing the effect of print orientation on interface integrity of multi-material jetting additive manufacturing. Additive Manufacturing (2018) 22:447–61. doi:10.1016/j.addma.2018.05.036

CrossRef Full Text | Google Scholar

13. Riemenschneider J, Mitkus R, Vasista S. Integration of actuators by additive layer manufacturing. In: ASME 2017 Conference on Smart Materials, Adaptive Structures and Intelligent Systems (2017). doi:10.1115/SMASIS2017-3764

CrossRef Full Text | Google Scholar

14. Rothe S, Watschke H, Langer SC. Study on the producibility of additively manufactured acoustic black holes. In: 24th International Congress on Sound and Vibration, ICSV 2017 (2017).

Google Scholar

15. Huang W, Zhang H, Inman DJ, Qiu J, Cesnik CE, Ji H. Low reflection effect by 3D printed functionally graded acoustic black holes. J Sound Vibration (2019) 450:96–108. doi:10.1016/j.jsv.2019.02.043

CrossRef Full Text | Google Scholar

16. Han D, Lee H. Recent advances in multi-material additive manufacturing: Methods and applications. Curr Opin Chem Eng (2020) 28:158–66. doi:10.1016/j.coche.2020.03.004

CrossRef Full Text | Google Scholar

17. Ouisse M, Renault D, Butaud P, Sadoulet-Reboul E. Damping control for improvement of acoustic black hole effect. J Sound Vibration (2019) 454:63–72. doi:10.1016/j.jsv.2019.04.029

CrossRef Full Text | Google Scholar

18. Conlon SC, Feurtado PA. Progressive phase trends in plates with embedded acoustic black holes. The J Acoust Soc America (2018) 143:921–30. doi:10.1121/1.5024235

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Karlos A, Elliott SJ, Cheer J. Higher-order WKB analysis of reflection from tapered elastic wedges. J Sound Vibration (2019) 449:368–88. doi:10.1016/J.JSV.2019.02.041

CrossRef Full Text | Google Scholar

20. Hook K, Cheer J, Daley S. A parametric study of an acoustic black hole on a beam. J Acoust Soc America (2019) 145:3488–98. doi:10.1121/1.5111750

PubMed Abstract | CrossRef Full Text | Google Scholar

21.[Dataset] Stratasys. Vero clear: Rigid transparent 3D printing material (2020).

Google Scholar

22.[Dataset] Stratasys. Tango: A soft flexible 3D printing material — Stratasys (2021).

Google Scholar