- 1School of Mechanical Engineering, Hangzhou Dianzi University, Hangzhou, China
- 2School of Aerospace Engineering and Applied Mechanics, Tongji University, Shanghai, China
Acoustic metamaterials, artificial composite structures with exotic material properties used to control elastic waves, have become a new frontier in physics, materials science, engineering and chemistry. In this paper, the research progress and development prospect of acoustic metamaterials are reviewed. Related studies on passive acoustic metamaterials and active acoustic metamaterials are introduced and compared. Additionally, we discuss approaches to material structure design, including topology optimization approaches, as well as bio-inspired and fractal geometry-based approaches to structure design. Finally, we summarize and look forward to the prospects and directions of acoustic metamaterial research. With the development of additive manufacturing technology, the research potential of acoustic metamaterials is huge.
1 Introduction
Metamaterial is a material that obtains extraordinary physical properties that conventional materials do not possess by designing special artificial structures. Veselago, a Soviet physicist, demonstrated the feasibility of negative refractive index materials and named them in 1967 [1]. After that, the concept of electromagnetic metamaterials began to formally enter people’s sight. The researchs related to the application of electromagnetic metamaterials in various fields quickly attracted the interest of researchers [2, 3]. With the continuous deepening of research, it has been found that elastic waves will have elastic wave band gaps similar to the photonic band gaps of electromagnetic metamaterials when they propagate in periodic elastic composite media. As a result, the concept of acoustic metamaterials was proposed, and related researches continued [4–6]. Different crystal compositions and periodic structures lead to different band gap properties of elastic waves. This makes it adaptable to different situations and makes it applicable to various fields [7–10]. In particular, it provides a simple, low-cost, and easy-to-apply solution to engineering problems for the solution of vibration and noise [11–13].
One of the earliest and more popular acoustic metamaterials is phononic crystals, which is a new type of functional material formed by the periodic arrangement of elastic solids in another solid or fluid medium. The Bragg type of phononic crystals was proposed earlier and is relatively mature. But the lattice constant of Bragg diffraction-based phononic crystals is of the same order of magnitude as the band gap frequency. As a result, it cannot be used to control low frequency problems. Liu et al. [14] first proposed the concept of locally resonant phononic crystals (LRPCs). the band gap frequency of LRPCs with the same lattice size is much lower than the Bragg’s, which can be used to solve low-frequency problems. With the deepening of research, the potential of phononic crystals in various fields has gradually emerged, and related research has become more abundant [15–20]. Topology optimization is the most commonly used optimization design of phononic crystals. Among them, Ranjbar and Hosseinkhani [21–23] have made remarkable research achievements in this regard.
It is worth noting that metamaterials that combine mechanics and biology have emerged in recent years and have begun to attract the attention of researchers [24, 25], such as DNA-inspired chiral metamaterials [26], microtubules composed of Biological nanonetworks [27], layered cellular materials [28]. These biological systems-inspired materials offer a completely new approach to the structural design of acoustic metamaterials. In addition, many researchers have introduced fractal geometry into phononic crystals to obtain better dynamic properties, such as Hilbert fractal [29, 30], Koch fractal [31, 32]. However, the related acoustic metamaterials mentioned above are all passive metamaterials, and the structural invariance of passive metamaterials limits their performance, function, and tunability. An increasing number of researchers are beginning to incorporate active elements, tunable and/or programmable devices into metamaterial designs, enabling active control of materials [30–32]. However, there are few studies reported in related fields, mainly not showing the characteristics of active feedback control. It is expected that there will be more related studies in the future.
In this paper, the related researches on acoustic metamaterials in recent years are collected and analyzed. And the future prospects of acoustic metamaterials are prospected. The rest of this paper is organized as follows. In Section 2, the current related research on passive acoustic metamaterials is mainly introduced, and it is divided into three parts for comparative analysis of phononic crystals topology optimization, bioinspired acoustic metamaterials and acoustic metamaterials based on fractal geometry. In Section 3, the related research on active acoustic metamaterials is mainly introduced. Finally, the research progress of acoustic metamaterials is summarized and its prospects are prospected. It can be seen that with the promotion of additive manufacturing methods, acoustic metamaterials have great application prospects in the fields of vibration and noise control.
2 Passive metamaterials
2.1 Phononic crystals
Bragg scattering crystals [33–35] is an earlier phononic crystal type. In order to generate the Bragg band gap in the phononic crystal, the size of the lattice should be at least equal to 1/2 of the wavelength of the elastic wave. It can be seen that the center frequency of the band gap is limited by the lattice constant, and the elastic wave at low frequencies cannot be controlled. Liu et al. [14] proposed the local resonance theory. By using this theory, they made acoustic crystals based on local resonance structures. Its lattice constant is two orders of magnitude smaller than the spectral gap of the relevant wavelength, breaking through the predicament of Bragg scattering crystals at low frequencies.
Figure 1 shows the local resonance structure and its frequency characteristics of a kind of phononic crystal. The materials have a simple microstructural unit consisting of a relatively high-density solid material and a coating of elastically soft material. And using a centimeter-sized lead ball as the core material, a 2.5 mm thick layer of silicone rubber was applied (Figure 1A). The coated spheres are arranged in an 8 × 8 × 8 simple cubic crystal with a lattice constant of 1.55 cm (Figure 1B) and the hard matrix is epoxy resin. Disordered composites made from such locally resonant structures possess effective negative elastic constants and full-wave reflectors over a certain tunable range of acoustic frequencies.
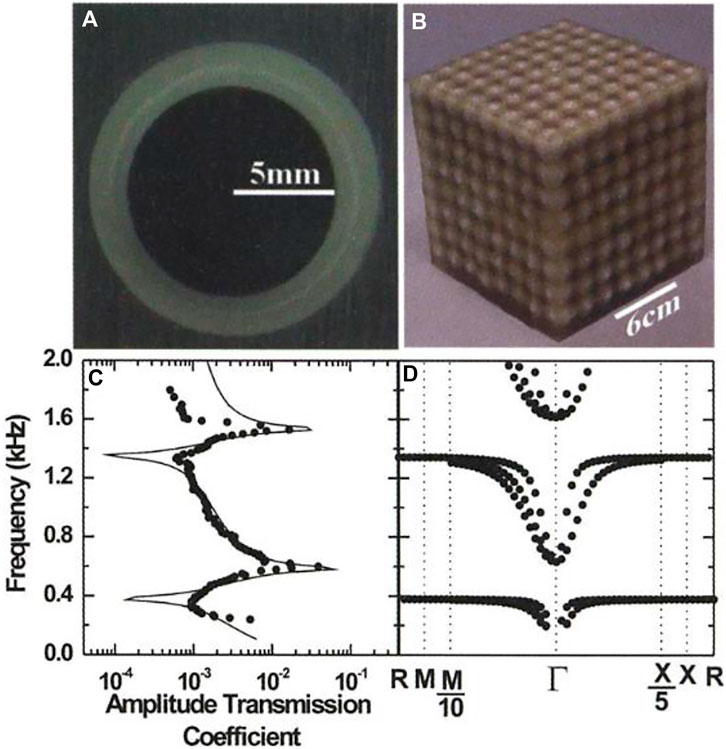
FIGURE 1. (A) The cross-section of the coated lead ball of the basic structural unit; (B) is an 8 × 8 × 8 sonic crystal; (C) Calculated (solid line) and measured (circle) amplitude transfer coefficients as a function of frequency; (D) Comparison of the observed transmission properties with the calculated band structure. Reprinted from [14] with permission.
The local resonance mechanism is different from the Bragg scattering mechanism, which emphasizes the influence of the periodic structure on the wave propagation [36–38]. It emphasizes the interaction between the resonance characteristics of a single scatterer and the long-wave traveling waves in the matrix. For the phononic crystal of the single-sided column type, the band gap of the phononic crystal can be transformed from Bragg scattering type to local resonance type by adjusting the quality of the additional column, which belongs to the composite phononic crystal. Zhang et al. [39] designed a novel hybrid phononic crystal composed of a rubber plate with periodic holes and lead pillars to obtain a wide low frequency band gap, as shown in Figure 2. Compared with the phononic crystals without periodic holes, the newly designed phononic crystals have wider band gaps and better vibration damping properties. The wider band gap can be attributed to the interaction of local resonance and Bragg scattering.
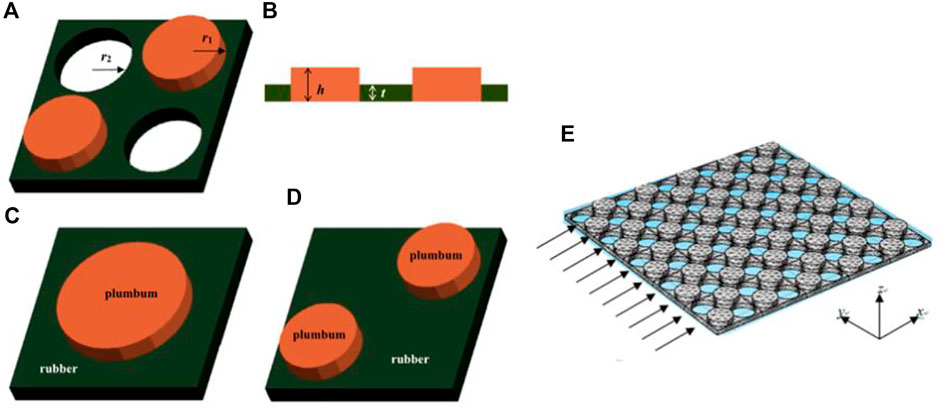
FIGURE 2. Unit cell of phononic crystal: (A) Novel PC plate; (B) Section of new PC plate; (C) Single short plate; (D) Thick plate with double short piles; (E) Incident situation of PCS. Reprinted from [39] with permission.
Nowadays, the three more traditional and mature types of phononic crystals are Bragg type, local scattering type and composite type. The three types of levels are progressive. A common problem in all three types of phononic crystals is the optimal design of the crystal structure. The most commonly used for the optimal design of phononic crystals is topology optimization, a method for calculating material distributions that creates structural layouts without prior shape information [40]. It is used to iteratively search for innovative material distributions within a prescribed design domain for optimal structural performance [41, 42]. Over the past decade, topology optimization methods have made great strides. These methods include density-based [43], level sets [44], phase fields [45, 46], topological derivatives [47], evolutionary methods [48], topology and geometry optimization [21–23, 49], etc. However, due to the high dimensionality of the engineering design space, topology optimization cannot solve the problem of precise manipulation of acoustic waves [50].
Hosseinkhani, Younesian, Krushynska, et. al [21]. studied the structural noise and vibration response of concave hexagonal honeycomb core plates by using topological optimization method and full gradient two-dimensional geometric optimization method. The results shown in Figure 3 indicate that the interaction between structural vibration and induced noise is more complex in the low frequency range, and the best noise reduction effect can be obtained by properly combining the enhanced and non-enhanced characteristics of a single structure. Under various random loads, the sound power level can be reduced by about 20%, but the total mass increases slightly (<5%). In addition, the structural eigenfrequency is transferred to a lower value, which is ideal for applications in the aerospace industry.
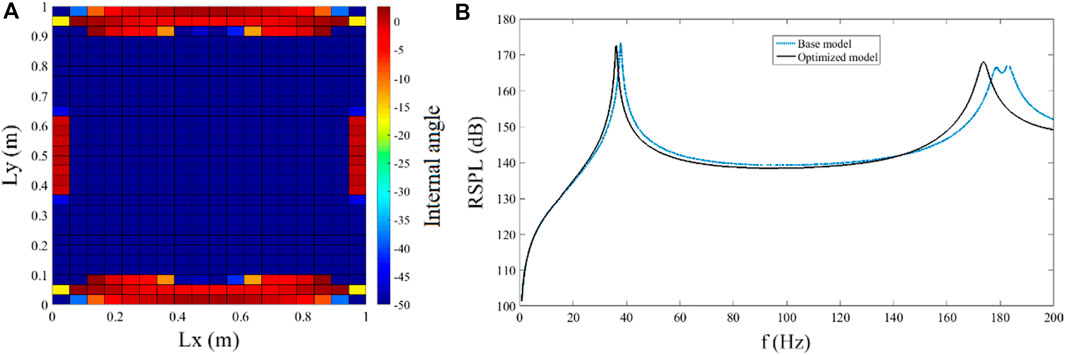
FIGURE 3. (A) Structure of the optimum core for the Violet noise excitation; (B) The RSPL of the optimized configuration in comparison with the base model. Reprinted from [21] with permission.
Mazloomi, Ranjbar and Hosseinkhani [22, 23] optimized the parameters of the distribution by identifying local internal resonators to enhance the vibration-acoustic performance of the sandwich panels with four-chiral resistance. The sandwich panel and its reinforced core were simulated using the full-scale finite element method. The equivalent homogenization model is used to reduce the calculation time of the optimization problem. The results shown in Figure 4 indicate compared with the calculated results of the accurate full size sandwich structure finite element model, and the radiated sound power levels of different geometric parameters of the sandwich structure and the minimized sandwich structure in the 0–200 Hz band are calculated. A hybrid optimization design method combining moving asymptote method and genetic algorithm is adopted. Compared with the baseline sandwich panel configuration, the optimized 2D gradient configuration significantly reduces the standardized radiated sound power level by 78% and increases the fundamental frequency by 15%.
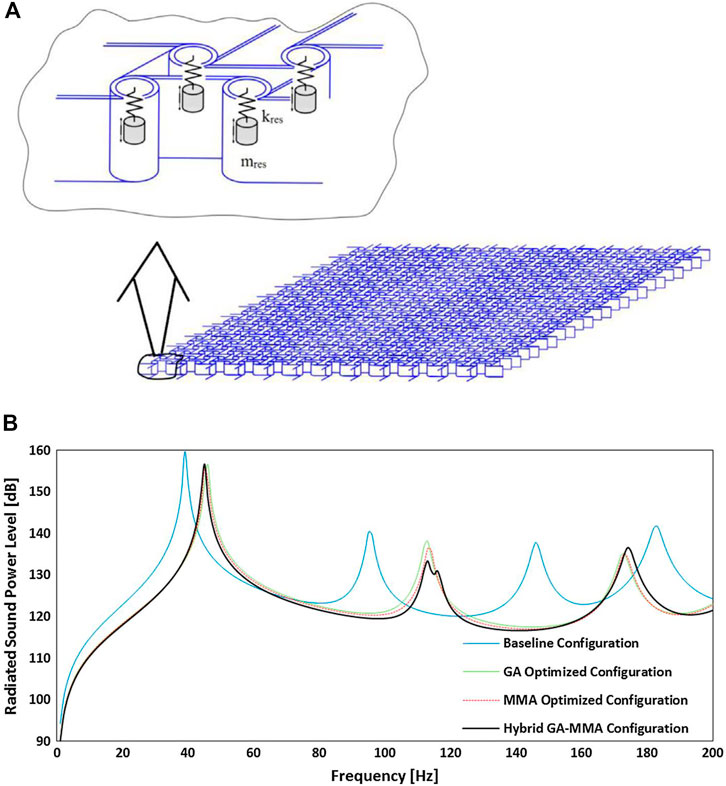
FIGURE 4. (A) Schematic of localized resonators in the auxetic core structure. Reprinted from [23] with permission. (B) RSPL vs. frequency, different anti-tetrachiral configurations. Reprinted from [22] with permission.
Aided by image-based finite element analysis and deep learning, Li et al. [51] proposed a data-driven phononic crystal design method in this study, and the workflow is shown in Figure 5. Train an autoencoder to extract topological features from sample images. The band gap of the samples was studied by finite element analysis. A multilayer perceptron is trained to establish the intrinsic relationship between the band gap and topological features. The trained model was finally used to design phononic crystals with the expected band gaps.
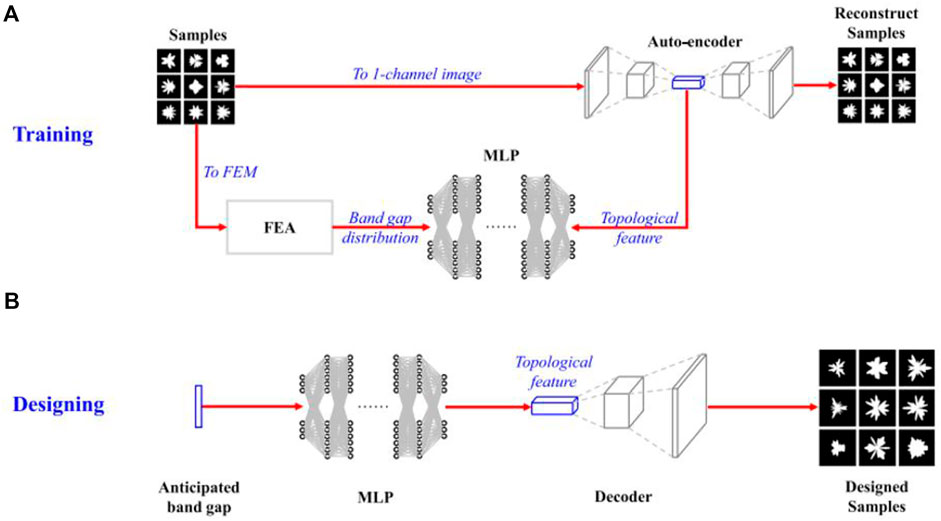
FIGURE 5. Workflow for designing a prospective bandgap phononic crystal. Reprinted from [51] with permission. (A) phononic crystal training, (B) Phononic crystal design.
In contrast to topology optimization methods, this method does not require real-time computations for specific optimization applications. The deep learning model in this method learns the implicit relationship between the input and output data. To a certain extent, the learned knowledge can accurately handle data outside the training set. In addition, deep learning models are able to self-evolve in the background by continuously providing training data. The method is not only applicable to this material, but can be further applied to design various structured mechanical materials with specific functions.
2.2 Bioinspired acoustic metamaterials
In addition to the design methods mentioned above, it is worth noting recently that many studies have begun to combine biology with mechanics, taking inspiration from biological systems to create new knots [24–28]. These new structural metamaterials have superior mechanical properties, better designability and tunability, and are new ideas for future structural design of acoustic metamaterials.
Microtubules are biopolymer hollow tubes that form an entangled radial network from the nucleus to the cell membrane. They are a major component of the cytoskeleton, providing mechanical stiffness, organization, and shape to the cytoplasm of eukaryotic cells. It plays an important role in the processes of division, intercellular transport, and internal organization of cellular components. Jafari et al. [27] investigated the propagation of elastic waves in periodic networks of various 2D microtubule bio-nanostructures, and analyzed their dynamic properties, providing the possibility for further applications. Figure 6 depicts a single microtubule and the method by which it builds its architectural structure. Microtubules themselves are composed of α-tubulin and β-tubulin (a), and a square unit cell composed of two vertical microtubules is shown in (b, c). By repeating cells in the x and y directions, two-dimensional periodic architectures can be formed (d).
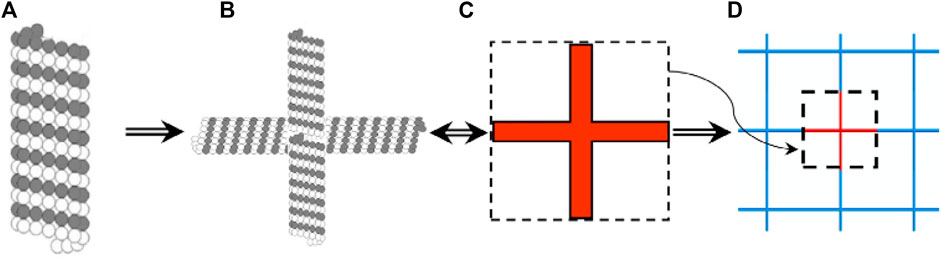
FIGURE 6. From single microtubule to periodic architected structure. Reprinted from [27] with permission. (A) Microtubule structure, (B) Two perpendicular microtubule structure, (C) Square unit cell microtubule, (D) 2-D periodic architected structure.
The research starts with the selection of a suitable single-microtubule beam model and experimentally demonstrates that ten widely used periodic structures are established. The finite element models of individual microtubules and network microtubules are established respectively, and the phonon band structure is calculated according to Bloch’s theorem. The results show that depending on the chosen topology of the unit cell and the periodicity considered, the low and high frequency band gaps of the biological filter can be designed within a specific range. This application could help researchers use architectural periodic structures to control some unwanted or harmful vibrations, and the network could be applied to next-generation nanobiomechanical instruments due to its higher biocompatibility due to its biomaterial origin, such as implantable biosensors.
Panahi, Hosseinkhani, Khansanami et al. [49] carried out numerical and experimental studies on the dispersion characteristics of elastic waves of a new Maltese cross shaped element and a triangular element instead of a lateral ligament element. Based on Bloch theorem of infinite element structure, the eigenfrequency problem of element is solved by finite element method. The results as shown in Figure 7 indicate that these new cells can provide more than 200% phonon band gap coverage factor (BGCF) in the low frequency range of 0–12 kHz. The results are compared with the band gap obtained from the periodic Bloch theorem. This study provides a practical application of a new phononic crystal as a frequency tool to prevent the propagation of elastic waves and adjust the position of the band gap according to the topology of the unit cell.
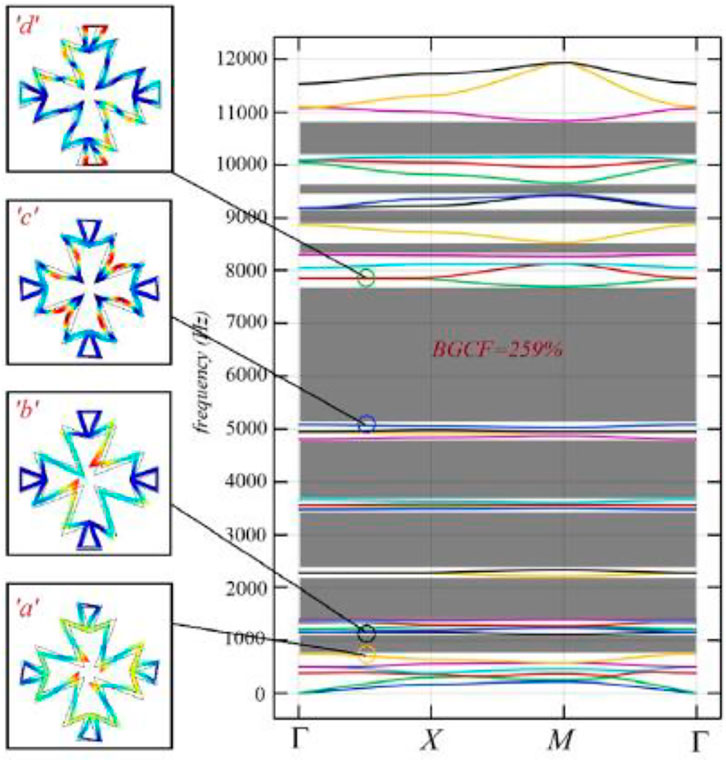
FIGURE 7. The dispersion curves along the borderline of the first irreducible Brillouin zone and vibration mode shapes. Reprinted from [49] with permission.
2.3 Acoustic metamaterials based on fractal geometry
There are also many researchers using fractal structures to realize elastic wave band gaps. It has been demonstrated that optimized fractal techniques can be used to create wider band gaps and that fractal geometries have significant advantages in band gap generation [51–53]. The most commonly used fractal technique is the Hilbert fractal. Man et al. [29, 30] designed the topology of Hilbert fractal acoustic metamaterials (HFAMs) with negative mass density and bulk modulus at the subwavelength scale by introducing the Hilbert curve channel. As shown in Figure 6. HFAM can enable applications ranging from acoustic blocking, quarter-bending, acoustic stealth to acoustic tunneling, and may further offer the possibility of engineering guidance for exotic properties at subwavelength scales.
Figure 8 shows the first-order, second-order, and third-order two-dimensional cells of HFAM, respectively. In the design of HFAM, a square with side length a/2 is divided into 21-by-21 sections. The centers of the 21-by-21 sections are connected in a clockwise direction from the lower left and lower right to form the K-Hilbert curve channel width, as shown in Figure 6A. As the fractal order increases, the square of a/2 is divided into sections of 22-by-22 and 23-by-23, respectively, as shown in Figures 8B,C. Figures 8D–F represent the first to third order cells of HFAM. The proposed structure consists of a square frame and is divided into four sectors with independent curved channels connected in the center. The total Euclidean length of a fractal waveguide can be simply calculated as
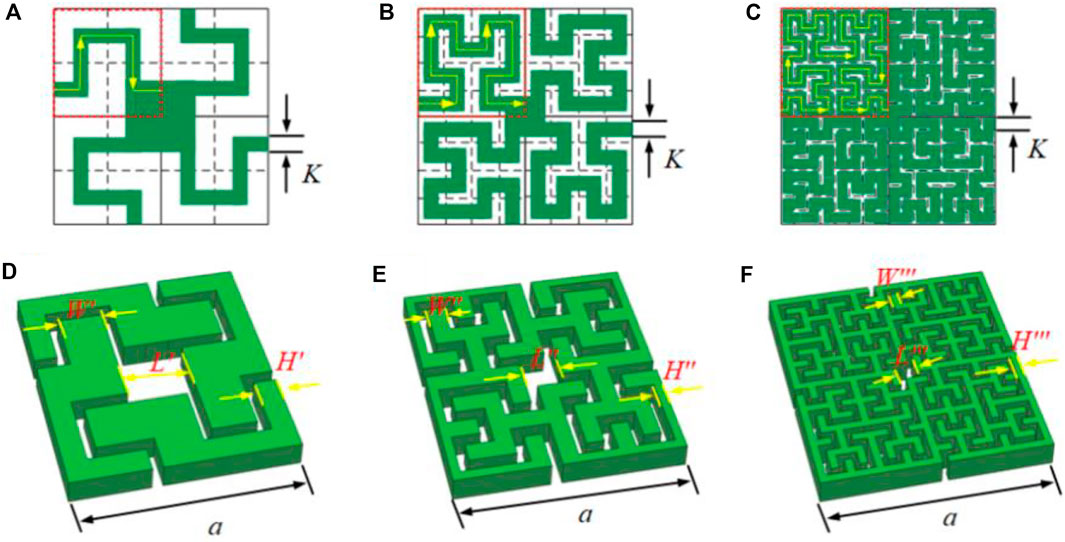
FIGURE 8. Schematic cross-sectional illustrations of three types of unit cells of HFAM: (A–C) The Hilbert curve channel of the first to third order HFAM with fluid. (D–F) The oblique drawing of unit cells of the first to third order HFAM. The material of HFAM applied is epoxy resin. The geometric and property parameters of HFAM are listed: a = 105 mm, K = 5 mm; H' = 10.625 mm, H" = 4.0625 mm, H" = 0.7812 mm: W' = 21.25 mm, W" = 8.125 mm, W"' = 1.5625 mm: p = 1,050 kg/m, c = 2,500 m/s and po = 1.25 kg/m, co = 343 m/s. Reprinted from [29] with permission.
What’s more, Zhao et al. [32] found that there are multiple low energy band gaps in lattice materials with different Koch fractal geometric parameters, and the position of the lowest energy band gap decreases with the increase of the number of iterations. Lattice metamaterials with Koch fractals have potential applications in vibration isolation and multifunctional design.
3 Active metamaterials and metadevices
The mechanism of active control is the introduction of loads from electrical and/or mechanical devices. It reduces vibration amplitudes and absorbs energy associated with dynamic structures. Active control actions have superior characteristics and engineering applications due to the ability to receive external information and respond in a timely manner. Huang et al. [54] changed the effective stiffness of metamaterials by applying normal initial stress and bias electric field, so that the position of the band gap was shifted. And they calculated the band structure under the initial shear normal stress and the initial electric field by using the theory of the small field superimposed on the bias field and the plane wave expansion method. But the application of this method is difficult because large values are required to show its impact. Malinovsky and Donskoy [35] proposed and discussed the design of an actively controlled metamaterial consisting of layers of charged nano- or micro-particles exposed to an external magnetic field. As shown in Figure 9, the particles are attached to the mechanically compliant layer. These particles are in a magnetic field created by a permanent magnet. Such structures can be used to reduce acoustic radiation from structures (due to structural support vibrations) or to protect structures from incident acoustic waves.
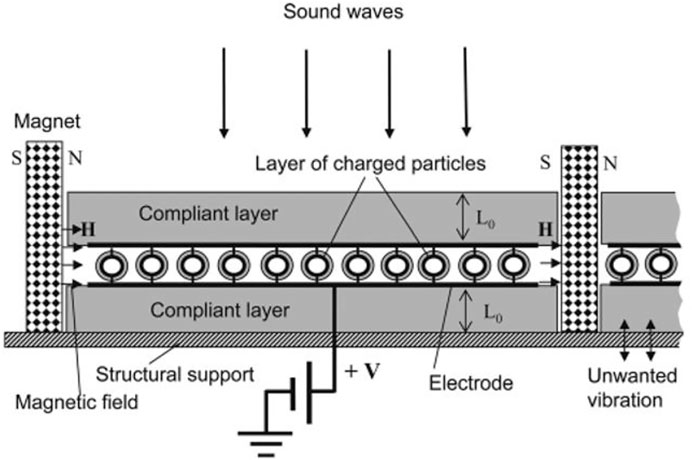
FIGURE 9. Schematic diagram of the implementation example. Reprinted from [35] with permission.
This study highlights that the proposed method of combining electromagnetic cyclotron resonance with mechanical resonance offers many opportunities for innovative design of acoustic metamaterials. It acts as a superior sound and vibration suppressor over a very wide frequency range. Applied voltages and magnetic fields may enable more advanced capabilities such as reprogrammable material acoustic properties, metalens and stealth. In addition, Wang [55] et al. proposed a novel elastic wave metamaterial and its automatic control system, as shown in Figure 10. The propagation properties of elastic waves are discussed. To verify the effectiveness of active feedback control, the stop-band characteristics of the system, the tunability of negative effective mass and the stability of the control system are considered.
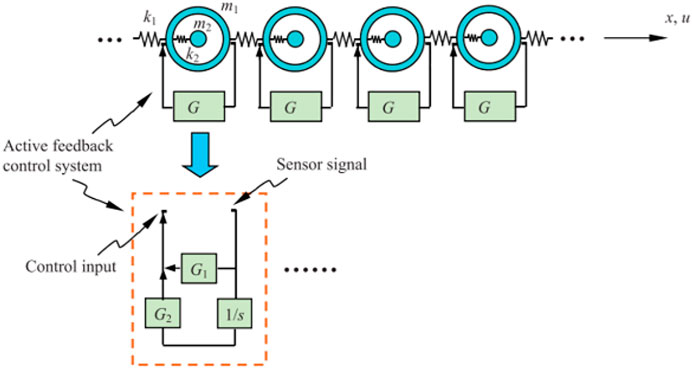
FIGURE 10. Elastic wave metamaterials with active feedback control system. Reprinted from [55] with permission.
Numerical results in the study show that positive acceleration and velocity feedback control actions can reduce the stopping bandwidth. The frequency region of the negative effective mass increases as the negative acceleration control effect increases, which is the opposite of the positive case. In addition, stable characteristics can be achieved by both positive and negative feedback control actions. This will provide a possible approach for the application of elastic wave metamaterials.
4 Conclusion and research prospect
In this paper, the related literatures on acoustic metamaterials are sorted and analyzed, and the acoustic metamaterials are divided into passive acoustic metamaterials and active acoustic metamaterials according to the response mode and compared and analyzed.
Passive acoustic metamaterial is an early and relatively mature metamaterial, which can achieve the required elastic wave gap through a specially designed material structure. The most well-known passive acoustic metamaterials are phononic crystals, which are a new type of functional material formed by periodic arrangement of elastic solids in another solid or fluid medium. In this paper, Bragg scattering and local resonance phononic crystals are introduced. The former is mainly because the periodicity of the structure plays a leading role, so the central frequency of the band gap is limited by the lattice constant, and the low-frequency elastic wave cannot be controlled. The latter is mainly dominated by the resonance characteristics of a single scatterer, whose lattice constant is several orders of magnitude smaller than the spectral gap of the relevant wavelength, which can effectively solve the predicament of Bragg scattering crystals at low frequencies. The structural design of phononic crystals mainly adopts topological structure. Mazloomi, Ranjbar and Hosseinkhani et. al. have solved the problem of precise control of sound waves in topological optimization design. The research on crystal structure design based on machine learning can also effectively solve these problems. Also noteworthy for structural design methods of passive acoustic metamaterials are bio-inspired and fractal geometry-based structural design methods. Acoustic metamaterials based on bio-inspired designs combine biology and mechanics to create new structures inspired by biological systems. The designed metamaterials have better mechanical properties, better designability and tunability. There are multiple low-energy band gaps in the acoustic metamaterial based on fractal geometry design, and the position of the lowest energy band gap decreases with the increase of fractal iterations, which has potential applications in vibration isolation and multi-functional design. Both of these design methods have great research potential.
However, the structural immutability of passive metamaterials limits their performance, functionality, and tunability. To address this conundrum, researchers have begun to incorporate active elements, tunable and/or programmable devices into metamaterial designs, making it possible to control the function of active acoustic metamaterials by external stimuli. Compared with passive acoustic metamaterials, active acoustic metamaterials can control external stimuli more freely and conveniently, and there are fewer related studies, so they have great research potential. The method of applying initial stress and bias electric field to change the material properties is feasible, but it is less practical due to the large value of the applied field. Other methods, such as magnetic field-based control, are also enumerated in this paper. Some researchers have also established automatic control systems to analyze actively controlled metamaterials more comprehensively and systematically. Active metamaterials are still less researched so far and more research is needed.
In addition, with the continuous development of additive manufacturing technology, the development process of metamaterials has been accelerated. Additive manufacturing techniques can create custom polymer, metal, ceramic and composite structures. Therefore, designing and fabricating programmable metamaterials with additive manufacturing techniques could enable a large number of metamaterial devices for practical applications. It can be seen that the manufacturing potential and application prospects of acoustic metamaterials in the future are huge.
Author contributions
Conceptualization, HD and YZ; methodology, XZ and YZ; formal analysis, WP and RZ; investigation, YZ and YG; data curation, HD; writing—original draft preparation, HD and YZ; writing—review and editing, XZ and YZ; supervision, XZ and RL; project administration, RZ; funding acquisition, RZ All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Sichuan Science and Technology Program (No.2022YFG0274), the Key Research and Development Program of Zhejiang Province (Grant No.2021C01399), National Natural Science Foundation of China (Grant No.51875146).
Acknowledgments
We thank Junyi Wu for many helpful conversations and meetings, and Wenxin Li for highly fruitful discussions and comments.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
1. Veselago VG. Electrodynamics of substances with simultaneously negative and. Usp fiz nauk (1967) 92(7):790. doi:10.3367/ufnr.0173.200307m.0790
2. Bliokh KY, Bliokh YP. What are the left-handed media and what is interesting about them? Phys -Usp (2004) 47(4):393–400. doi:10.1070/pu2004v047n04abeh001728
3. Vendik I, Vendik O. Metamaterials and their application in microwaves: A review. Tech Phys (2013) 58(1):1–24. doi:10.1134/s1063784213010234
4. Sellami K, Ketata H, Ben Ghozlen MH. Locally resonant phononic crystals band-gap analysis on a two dimensional phononic crystal with a square and a triangular lattice. Opt Quan Electron (2019) 51(9):311–4. doi:10.1007/s11082-019-2028-0
5. Miniaci M, Gliozzi AS, Morvan B, Krushynska A, Bosia F, Scalerandi M, et al. Proof of concept for an ultrasensitive technique to detect and localize sources of elastic nonlinearity using phononic crystals. Phys Rev Lett (2017) 118(21):214301. doi:10.1103/physrevlett.118.214301
6. Darinskii A, Shuvalov A. Surface acoustic waves on one-dimensional phononic crystals of general anisotropy: Existence considerations. Phys Rev B (2018) 98(2):024309. doi:10.1103/physrevb.98.024309
7. Liu Y, Chang Z, Feng XQ. Stable elastic wave band-gaps of phononic crystals with hyperelastic transformation materials. Extreme Mech Lett (2017) 11:37–41. doi:10.1016/j.eml.2016.11.007
8. Fomenko S, Golub M, Zhang C, Bui T, Wang Y-S. In-plane elastic wave propagation and band-gaps in layered functionally graded phononic crystals. Int J Sol Structures (2014) 51(13):2491–503. doi:10.1016/j.ijsolstr.2014.03.017
9. Zheng M, Wei PJ. Band gaps of elastic waves in 1-D phononic crystals with imperfect interfaces. Int J Minerals, Metall Mater (2009) 16(5):608–14. doi:10.1016/s1674-4799(09)60105-9
10. Li F-L, Wang Y-S, Zhang C. A BEM for band structure and elastic wave transmission analysis of 2D phononic crystals with different interface conditions. Int J Mech Sci (2018) 144:110–7. doi:10.1016/j.ijmecsci.2018.05.042
11. Sun Y, Yu Y, Zuo Y, Qiu L, Dong M, Ye J, et al. Band gap and experimental study in phononic crystals with super-cell structure. Results Phys (2019) 13:102200. doi:10.1016/j.rinp.2019.102200
12. Engheta N, Ziolkowski RW. Metamaterials: Physics and engineering explorations. New York: John Wiley & Sons (2006).
13. Marqués R, Martin F, Sorolla M. Metamaterials with negative parameters: Theory, design, and microwave applications. New York: John Wiley & Sons (2011).
14. Liu Z, Zhang X, Mao Y, Zhu Y, Yang Z, Chan CT, et al. Locally resonant sonic materials. science (2000) 289(5485):1734–6. doi:10.1126/science.289.5485.1734
15. Wang P, Casadei F, Kang SH, Bertoldi K. Locally resonant band gaps in periodic beam lattices by tuning connectivity. Phys Rev B (2015) 91(2):020103. doi:10.1103/physrevb.91.020103
16. Chen Y, Li T, Scarpa F, Wang L. Lattice metamaterials with mechanically tunable Poisson’s ratio for vibration control. Phys Rev Appl (2017) 7(2):024012. doi:10.1103/physrevapplied.7.024012
17. Hosseinkhani A, Younesian D, Ranjbar M. Vibro-acoustic analysis and topology optimization of anti-tetra chiral auxetic lattices driven by different colored noises. Int J Str Stab Dyn (2020) 20:2050113. doi:10.1142/s0219455420501138
18. Trainiti G, Rimoli JJ, Ruzzene M. Wave propagation in undulated structural lattices. Int J Sol Structures (2016) 97:431–44. doi:10.1016/j.ijsolstr.2016.07.006
19. Fan H, Xia B, Tong L, Zheng S, Yu D. Elastic higher-order topological insulator with topologically protected corner states. Phys Rev Lett (2019) 122(20):204301. doi:10.1103/physrevlett.122.204301
20. Xia B, Wang G, Zheng S. Robust edge states of planar phononic crystals beyond high-symmetry points of Brillouin zones. J Mech Phys Sol (2019) 124:471–88. doi:10.1016/j.jmps.2018.11.001
21. Hosseinkhani A, Younesian D, Krushynska AO, Ranjbar M, Scarpa F. Full-gradient optimization of the vibroacoustic performance of (Non-)auxetic sandwich panels. Transp Porous Media (2022) 142:139–56. doi:10.1007/s11242-021-01693-0
22. Mazloomi MS, Ranjbar M. Hybrid design optimization of sandwich panels with gradient shape anti-tetrachiral auxetic core for vibroacoustic applications. Transp Porous Media (2022) 142:5–22. doi:10.1007/s11242-021-01646-7
23. Hosseinkhani A, Younesian D, Ranjbar M, Scarpa F. Enhancement of the vibro-acoustic performance of anti-tetra-chiral auxetic sandwich panels using topologically optimized local resonators. Appl Acoust (2021) 177:107930. doi:10.1016/j.apacoust.2021.107930
24. Chen Y, Wang L. Bio-inspired heterogeneous composites for broadband vibration mitigation. Sci Rep (2015) 5(1):17865–11. doi:10.1038/srep17865
25. Miniaci M, Krushynska A, Movchan AB, Bosia F, Pugno NM. Spider web-inspired acoustic metamaterials. Appl Phys Lett (2016) 109(7):071905. doi:10.1063/1.4961307
26. Zheng B, Xu J. Mechanical logic switches based on DNA-inspired acoustic metamaterials with ultrabroad low-frequency band gaps. J Phys D Appl Phys (2017) 50(46):465601. doi:10.1088/1361-6463/aa8b08
27. Jafari H, Yazdi MRH, Fakhrabadi MMS. Wave propagation in microtubule-based bio-nano-architected networks: A lesson from nature. Int J Mech Sci (2019) 164:105175. doi:10.1016/j.ijmecsci.2019.105175
28. Zhu Z, Deng Z, Du J. Elastic wave propagation in hierarchical honeycombs with woodpile-like vertexes. J Vibration Acoust (2019) 141(4). doi:10.1115/1.4043352
29. Man X, Luo Z, Liu J, Xia B. Hilbert fractal acoustic metamaterials with negative mass density and bulk modulus on subwavelength scale. Mater Des (2019) 180:107911. doi:10.1016/j.matdes.2019.107911
30. Man XF, Xia BZ, Luo Z, Liu J. 3D Hilbert fractal acoustic metamaterials: Low-frequency and multi-band sound insulation. J Phys D Appl Phys (2019) 52(19):195302. doi:10.1088/1361-6463/ab092a
31. Khoshhesab MM, Li Y. Mechanical behavior of 3D printed biomimetic Koch fractal contact and interlocking. Extreme Mech Lett (2018) 24:58–65. doi:10.1016/j.eml.2018.09.003
32. Zhao P, Zhang K, Deng Z. Elastic wave propagation in lattice metamaterials with Koch fractal. Acta Mech Solida Sin (2020) 33(5):600–11. doi:10.1007/s10338-020-00177-w
33. Asiri S, Baz A, Pines D. Active periodic struts for a gearbox support system. Smart Mater Struct (2006) 15(6):1707–14. doi:10.1088/0964-1726/15/6/024
34. Chen Y, Hu J, Huang G. A design of active elastic metamaterials for control of flexural waves using the transformation method. J Intell Mater Syst Structures (2016) 27(10):1337–47. doi:10.1177/1045389x15590273
35. Malinovsky VS, Donskoy DM. Electro-magnetically controlled acoustic metamaterials with adaptive properties. The J Acoust Soc America (2012) 132(4):2866–72. doi:10.1121/1.4744943
36. Zhang Z, Han X. A new hybrid phononic crystal in low frequencies. Phys Lett A (2016) 380(45):3766–72. doi:10.1016/j.physleta.2016.09.019
37. Sigalas MM, Economou EN. Elastic and acoustic wave band structure. J sound vibration (1992) 158(2):377–82. doi:10.1016/0022-460x(92)90059-7
38. Kushwaha MS, Halevi P, Dobrzynski L, Djafari-Rouhani B. Acoustic band structure of periodic elastic composites. Phys Rev Lett (1993) 71(13):2022–5. doi:10.1103/physrevlett.71.2022
39. Martínez-Sala R, Sancho J, Sánchez JV, Gómez V, Llinares J, Meseguer F. Sound attenuation by sculpture. nature (1995) 378(6554):241. doi:10.1038/378241a0
40. Liu K, Tovar A. An efficient 3D topology optimization code written in Matlab. Struct Multidiscipl Optim (2014) 50(6):1175–96. doi:10.1007/s00158-014-1107-x
41. Bendsøe MP. Optimal shape design as a material distribution problem. Struct optimization (1989) 1(4):193–202. doi:10.1007/bf01650949
42. Sigmund O, Maute K. Topology optimization approaches. Struct Multidiscipl Optim (2013) 48(6):1031–55. doi:10.1007/s00158-013-0978-6
43. Andreassen E, Clausen A, Schevenels M, Lazarov BS, Sigmund O. Efficient topology optimization in MATLAB using 88 lines of code. Struct Multidiscipl Optim (2011) 43(1):1–16. doi:10.1007/s00158-010-0594-7
44. Allaire G, Jouve F, Toader A-M. Structural optimization using sensitivity analysis and a level-set method. J Comput Phys (2004) 194(1):363–93. doi:10.1016/j.jcp.2003.09.032
45. Bourdin B, Chambolle A. Design-dependent loads in topology optimization. ESAIM: Control, Optimisation and Calculus of Variations (2003) 9:19–48. doi:10.1051/cocv:2002070
46. Takezawa A, Nishiwaki S, Kitamura M. Shape and topology optimization based on the phase field method and sensitivity analysis. J Comput Phys (2010) 229(7):2697–718. doi:10.1016/j.jcp.2009.12.017
47. Norato JA, Bendsøe MP, Haber RB, Tortorelli DA. A topological derivative method for topology optimization. Struct Multidiscipl Optim (2007) 33(4):375–86. doi:10.1007/s00158-007-0094-6
48. Mattheck C, Burkhardt S. A new method of structural shape optimization based on biological growth. Int J Fatigue (1990) 12(3):185–90. doi:10.1016/0142-1123(90)90094-u
49. Panahi E, Hosseinkhani A, Khansanami MF, Younesian D, Ranjbar M. Novel cross shape phononic crystals with broadband vibration wave attenuation characteristic: Design, modeling and testing. Thin-Walled Structures (2021) 163:107665. doi:10.1016/j.tws.2021.107665
50. Bessa MA, Bostanabad R, Liu Z, Hu A, Apley DW, Brinson C, et al. A framework for data-driven analysis of materials under uncertainty: Countering the curse of dimensionality. Comp Methods Appl Mech Eng (2017) 320:633–67. doi:10.1016/j.cma.2017.03.037
51. Li X, Ning S, Liu Z, Yan Z, Luo C, Zhuang Z. Designing phononic crystal with anticipated band gap through a deep learning based data-driven method. Comp Methods Appl Mech Eng (2020) 361:112737. doi:10.1016/j.cma.2019.112737
52. Puente-Baliarda C, Romeu J, Pous R, Cardama A. On the behavior of the Sierpinski multiband fractal antenna. IEEE Trans Antennas Propag (1998) 46(4):517–24. doi:10.1109/8.664115
53. Castiñeira-Ibáñez S, Rubio C, Redondo J, Sánchez-Pérez JV. Quantitative characterization of bandgap properties of sets of isolated acoustic scatterers arranged using fractal geometries. Appl Phys Express (2014) 7(4):042201. doi:10.7567/apex.7.042201
54. Huang Y, Zhang C, Chen W. Tuning band structures of two-dimensional phononic crystals with biasing fields. J Appl Mech (2014) 81(9). doi:10.1115/1.4027915
Keywords: acoustic metamaterial, elastic wave control, material structure design, fractal geometry-based approaches, bio-inspired approaches
Citation: Dai H, Zhang X, Zheng Y, Pei W, Zhou R, Liu R and Gong Y (2022) Review and prospects of metamaterials used to control elastic waves and vibrations. Front. Phys. 10:1069454. doi: 10.3389/fphy.2022.1069454
Received: 13 October 2022; Accepted: 03 November 2022;
Published: 18 November 2022.
Edited by:
Lingyun Yao, Southwest University, ChinaReviewed by:
Mostafa Ranjbar, Ankara Yıldırım Beyazıt University, TurkeyCopyright © 2022 Dai, Zhang, Zheng, Pei, Zhou, Liu and Gong. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Xueting Zhang, enh0QGhkdS5lZHUuY24=; Rougang Zhou, NDIxNDFAaGR1LmVkdS5jbg==; Youping Gong, am9hbnkwMjA0QDE2My5jb20=
 Huajie Dai1,2
Huajie Dai1,2 Yongju Zheng
Yongju Zheng Wanrong Pei
Wanrong Pei