- 1Department of Physics, The Hong Kong University of Science and Technology, Hong Kong, Hong Kong SAR, China
- 2HKUST Shenzhen Research Institute, Shenzhen, China
- 3Center for Spintronics and Quantum Systems, State Key Laboratory for Mechanical Behavior of Materials, Xi’an Jiaotong University, Xi’an, Shaanxi, China
Butterfly magnetoresistance (BMR) and antisymmetric magnetoresistance (ASMR) are about a butterfly-cross curve and a curve with one peak and one valley when a magnetic field is swept up and down along a fixed direction. Other than the parallelogram-shaped magnetoresistance-curve (MR-curve) often observed in magnetic memory devices, BMR and ASMR are two ubiquitous types of MR-curves observed in diversified magnetic systems, including van der Waals materials, strongly correlated systems, and traditional magnets. Here, we reveal the general principles and the picture behind the BMR and the ASMR that do not depend on the detailed mechanisms of magnetoresistance: 1) The systems exhibit hysteresis loops, common for most magnetic materials with coercivities. 2) The magnetoresistance of the magnetic structures in a large positive magnetic field and in a large negative magnetic field is approximately the same. With the generalized Ohm’s law in magnetic materials, these principles explain why most BMR appears in the longitudinal resistance measurements and is very rare in the Hall resistance measurements. Simple toy models, in which the Landau-Lifshitz-Gilbert equation governs magnetization, are used to demonstrate the principles and explain the appearance and disappearance of BMR in various experiments. Our finding provides a simple picture to understand magnetoresistance-related experiments.
1 Introduction
Magnetoresistance (MR) is an important quantity that is often used to probe and to understand the electronic properties of a condensed matter [1]. Weak field MRs at a low temperature are a standard probe for extracting quantum coherence length and time of metals [2], and high field MRs are a powerful tool for measuring the Fermi surfaces of metals [1]. In magnetic materials with magnetic hysteresis, MR-curves can be classified into several types. One commonly-observed curve in magnetic memory devices is the parallelogram shape as shown in Figure 1. As an example, let us consider one type of memory devices shown in Figure 1B with a magnetic fixed layer, whose magnetization is pinned by either an exchange bias from another antiferromagnetic layer or by its bulky volume, a magnetic free layer, whose magnetization can be changed by an external force such as a magnetic field, and a spacer layer of either metal or insulator separating two magnetic layers. No matter what is the source of resistance and MR in particular, the device has a higher and a lower resistive states, respectively, when two magnetizations are antiparallel or parallel to each other [3–5]. Due to the coercivity of magnetic materials, when a magnetic field parallel to the magnetization of the fixed layer is swept up and down, a magnetic hysteresis loop is formed as the device moves between the two resistive states. This results in a parallelogram MR-curve. Other commonly-observed MR-curves are a butterfly-cross called butterfly magnetoresistance (BMR) of either upward (A) and downward (B) ones [6–9] as shown in Figures 2A,B, and an MR-curve with one peak and one valley, called antisymmetric magnetoresistance (ASMR), as shown in Figures 2C,D [10]. BMR was found in various magnetic materials, including van der Waals layered magnetic materials and strongly correlated materials, as well as many traditional magnetic materials [6–9, 11–35], at both high and low temperatures, in strong and weak magnetic fields, while people observed less common ASMR in topological Hall effect materials [36–39], antiferromagnetic topological insulators [40], magnetic multilayers [41, 42] and FeGeTe heterostructures [10]. The observation of BMR can date back to the 1950s [34, 35]. Although both BMR and ASMR were widely observed, the explanations in the literature, often involving detailed microscopic MR mechanisms, are different for different systems. For layered films such as metallic multilayers [Fe/Cr]n [Co/Cu]n, and van der Waals ClI3 layers [27, 30–32], complicated strong or weak electron scatterings involved magnetizations of adjacent layers were used to explain all kinds of MR-curves. In magnetic nanowires [23], FeO film [11], Co/HfO2/Pt sandwich structures [18], etc., BMR was attributed to the anisotropic MR effects that depend on the relative current and magnetization orientation. Electron-magnon scattering in systems like Fe5GeTe van der Waal nanostructures [6], FePt films and nanowires [16, 19], and 2D layers of Ag2CrO2 antiferromagnetic films [7], where resistance depends not only on magnetization but also on the applied fields and the temperature, is associated with BMR observation. In traditional magnets like Fe3O4 films, the electron scattering, and tunnelling at the interfaces of nanograins [33] or scattering by the magnetization structures induced by fields and anti-phase boundaries [9] were claimed to be responsible to the observed BMR. In many 2D materials, BMR in ρxx is believed to be due to the quantum anomalous Hall effect (QAHE) [20, 21]. The transverse BMR is reported in some planar Hall effects [11, 24, 25]. In summary, both BMR and ASMR were attributed to very detailed microscopic interactions in the literature so far. The explanations lead to an impression that microscopic interactions are essential for these universal curves. People did relate the BMR to magnetization reversal and hysteresis. Magnetization reversal undoubtedly occurs in all magnetic materials, but BMR sometimes occurs, and other time does not. A simple universal route leading to their observation is lacking.
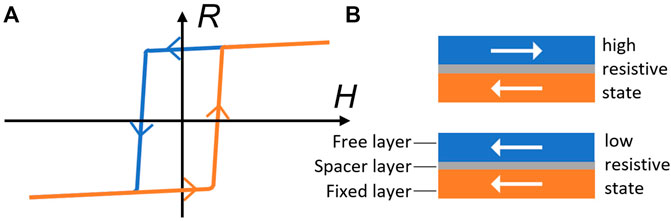
FIGURE 1. (A) Schematics of parallelogram MR-curves when a device moves between a higher resistive state and a lower one in a field sweeping-up and sweeping-down process. (B) Illustration of a memory device with two stable resistive states. The device is in a lower (higher) resistive state when the magnetization of the free-layer is parallel (antiparallel) with that of the fixed layer.

FIGURE 2. Illustration of butterfly magnetoresistance (BMR) and antisymmetric magnetoresistance (ASMR) curves. The orange and blue curves indicate resistance in the sweeping-up and sweeping-down processes, respectively. (A,B) Upward (A) and downward (B) butterfly MR-curves that display a butterfly cross. (C,D) Two possible ASMR-curves that have the feature of one peak and one valley.
Here we would like to ask whether the universal BMR and ASMR have a simple general route independent of the origins of MR. This is a sensible question because most MR-curves of all magnetic materials with magnetic hysteresis, if not all, can be grouped into one of the above three types or their variations: Parallelogram-shape, BMR, and ASMR. Since the parallelogram-shaped MR-curves have a simple picture mentioned above, there is no reason to believe that BMR and ASMR would be different.
2 The physics of BMR and ASMR
The resistance is a state function. For a magnetic system of a given magnetization distribution (magnetic/spin structure) and given external conditions such as the temperature, strains, external magnetic fields, etc., the resistance is fixed. Under a given magnetic field, a system may have one or more than one possible stable/metastable magnetic structure. If a system has only one stable magnetic structure, then the MR curve, no matter how complicated it might be, has no hysteresis. Otherwise, the MR curve has hysteresis when an external magnetic field is swept up and down in a fixed direction. Of course, hysteresis is a general feature of magnetic materials due to its coercivity.
An MR curve reflects the evolution path of the magnetic structure of a system. Whether an MR-curve is a parallelogram, a BMR, or an ASMR depends on whether the resistance of magnetic structures in a large positive magnetic field and in a large negative magnetic field are similar or different. When the resistances of large positive and negative magnetic fields are not too different, an MR-curve will be either a BMR or an ASMR, independent of the specific origin of the resistance. If the MR passes through two higher (lower) resistance states in sweeping-up and sweeping-down processes, the MR-curve displays two crossed peaks (valleys) and results in an upward (downward) BMR, as shown in Figures 2A,B. However, if the MR passes through one higher and one lower resistance state in sweeping-up and sweeping-down processes, respectively, the MR-curve displays one peak and one valley and becomes ASMR, as shown in Figures 2C,D. This simple picture is behind various magnetoresistance-related experiments on microscopic mechanisms although MR-curves can have different shapes from system to system. The coercivity field largely determines their locations of MR-loops while microscopic details modify their shapes, not their overall features.
Furthermore, with the generalized Ohm’s law in magnetic material, these principles can explain why most BMRs occur in longitudinal resistance measurements and are very rare in Hall resistance measurements. For a given magnetic material, its resistance, in general, depends on the magnetization when all other material parameters and their environment are fixed. Without losing any generality, let us define the current direction along the x-axis and transverse voltage measurement along the y-direction. The longitudinal and transverse resistance can be expressed as
3 Demonstration of principles with toy models
Whether a BMR or an ASMR appears depends only on whether the evolution of the magnetization has a hysteresis, and whether the resistances in two extreme states in large positive and negative magnetic fields are similar. In experiments, various factors can affect the appearance of BMRs, including anisotropy, thickness, temperature, etc. [6, 7, 9, 18, 27]. A BMR appears usually in a system with a strong anisotropy and at a low temperature. It appears sometimes in a thicker sample [9] and sometimes in a thinner one [6]. People knew that all these factors somehow affect the magnetization reversal through which system changes facilitate or prohibit the presence of a BMR, but a universal simple picture showing how and why a BMR occurs and does not occur in a specific system is lacking. Here, with the simple principles mentioned above, we use toy models to show these factors actually influence BMRs by changing the easy-axis and hysteresis, which are essential for BMRs and ASMRs.
Our toy model is for a ferromagnetic sample whose magnetic energy is
where m, A, Ku, μ0, Ms, H and Hd are the magnetization unit vector, the Heisenberg exchange stiffness, the perpendicular magneto-crystalline anisotropy, the vacuum permeability, the saturation magnetization, the external magnetic field, and the dipolar field, respectively. If not stated otherwise, the sample size is 100 × 20 × 2 nm3, and model parameters are A = 3 pJ/m, Ms = 0.86 MA/m, and Ku = 0.3 MJ/m3, around typical values of common magnetic materials. We also consider a weak disorder to mimic a realistic situation. Random granular sample of average 10 nm grains are generated in films by Voronoi tessellation. Anisotropies of grains vary randomly by 10% around its mean value. The non-linear Landau-Lifshitz-Gilbert (LLG) equation governs the spin dynamics of the model,
where γ, α and Heff are respectively the gyromagnetic ratio, Gilbert damping constant, and the effective field.
where V is the total sample volume [23, 29, 47].
It is known that the magnetization dynamical path relies on the angle between the applied field and the easy-axis [48]. Hysteresis loops appear only when the field is not perpendicular to the easy-axis. Otherwise, the system has only one stable structure, and magnetization is reversible such that no BMRs and ASMRs are possible. Since a field was swept in all directions in all kinds of experiments and the easy-axis is sensitive to many factors such as thickness, temperature, etc., it is not surprising to see the appearance and disappearance of a BMR in similar measurements on similar samples, but with different details. To mimic the phenomenon, we consider a sample of Ku = 0 for simplicity. The demagnetization factors of
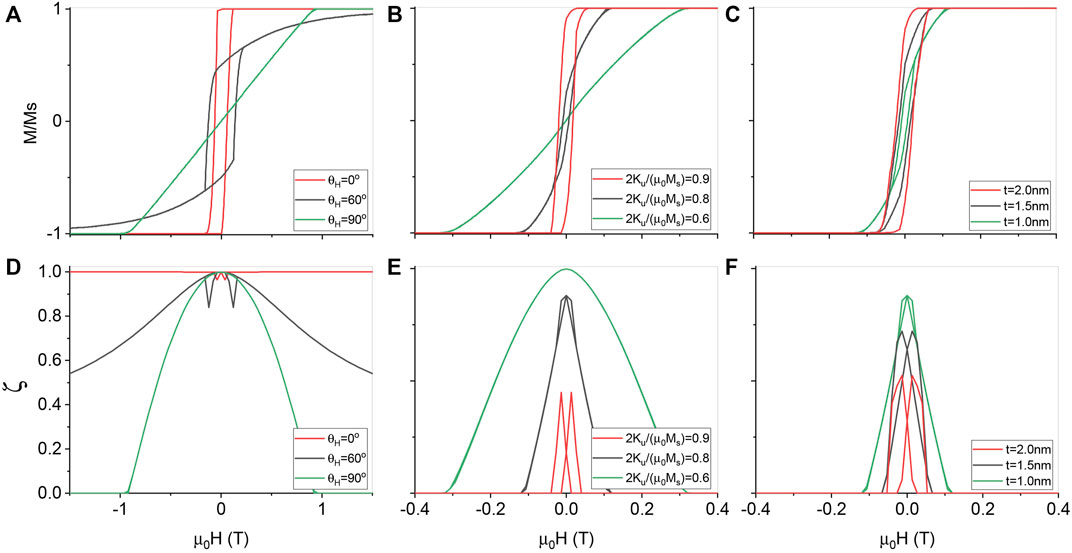
FIGURE 3. MH-curves and MR-curves for various field directions, crystalline anisotropy, and sample thickness. (A) mz vs. H along various directions. MH-curves display hysteresis when the field is not perpendicular to the easy-axis
Crystalline anisotropy varies from sample to sample and leads to the appearance and the disappearance of the BMR and the ASMR. Perpendicular magnetic anisotropy can both increase and decrease [49] with film thickness. For materials whose perpendicular anisotropy decreases or even vanishes as sample thickness increases, increase of thickness may result in vanishing BMR in the perpendicular field-sweeping. For thin films of perpendicular crystalline anisotropy that is insensitive to film thickness, the opposite behaviour can occur: Easy-axis changes from perpendicular to in-plane directions as sample thickness decreases. With the toy model, our theory can explain disappearance of a BMR when a sample thickness both increases [6, 27] or decreases. Figure 3B is the MH-curves for the field along the
The change of crystalline anisotropy can come from other sources. For example, anisotropy Ku of some materials decreases with a power of M(T) [50], which is sensitive to the temperature near the Curie temperature. The change of Ku can be substantial. For example, the magnetic anisotropy of 1.2 nm CoFeB film could drop by 50% as the temperature increases from 300 K to 400 K [51]. As the temperature increases, perpendicular magnetic anisotropy gets smaller, and the easy-axis changes from out-of-plane to in-plane. Hysteresis, as well as BMR, thus no longer exists. In contrast to our universal picture of the BMR, the disappearance of the BMR at higher temperatures was attributed to the variation of electron scattering, which, in turn, was attributed to the vanish of partially disordered states [6, 7, 9, 18].
The resistance is a state function. BMR or ASMR curves are the manifestations of magnetic hysteresis. BMR and ASMR shapes and loop positions depend on resistance mechanisms and detailed magnetic properties such as coercivity fields. To further demonstrate this point, we use various configurations and resistance mechanisms to generate all kinds of BMR’s and ASMR’s with our toy models. First, we consider the in-plane fields. A smaller Ku = 0.3 MJ/m3 is used such that the easy-axis aligns with the
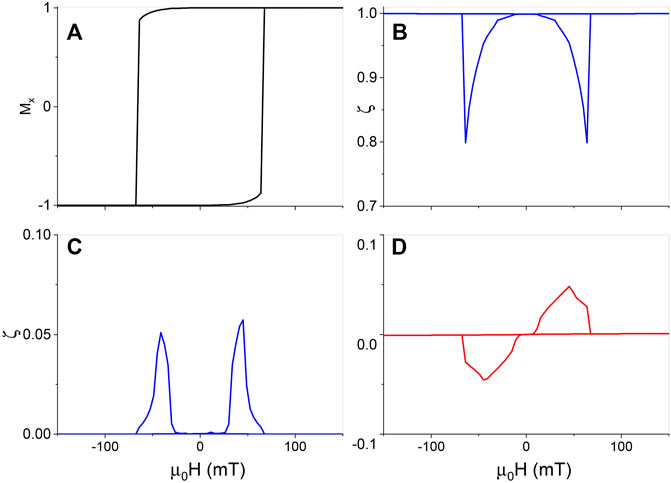
FIGURE 4. A BMR and an ASMR model for field-sweeping in the plane. The fields are swept along the direction that is 0.1° tilted from
To demonstrate the same BMR principles in the field sweeping along the perpendicular direction of a film, a larger Ku = 4.8 MJ/m3 is used in order to maintain
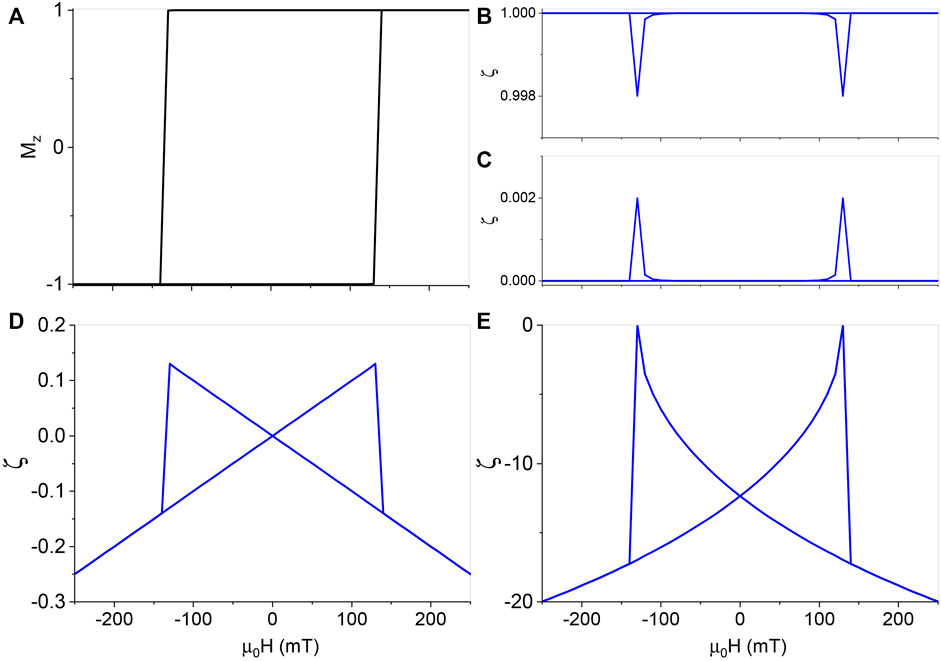
FIGURE 5. A BMR model for a field along 0.1° from
4 Discussions and conclusion
We used toy models governed by the LLG equation to demonstrate BMR and ASMR in various systems, because it is compatible with experiments involving incoherent magnetization reversal such as those in Refs. [16, 19, 23]. Other models could also be used in different scenarios. For example, BMR has also been observed in systems described by coherent-rotational models [52, 53], and other special reversal processes such as domain wall nucleation and motion described by the Kondorsky model [23]. Between two states at large positive and negative fields, there is a hysteresis in these systems, also consistent with the general picture here. If one uses the similar procedure as that in the third section, BMR or ASMR can also appear as long as the resistances is a function of magnetization, and the resistance of two states at high fields are not too different, see Supplementary Information for details.
The rules of BMR and ASMR revealed by the toy models are general. For example, in a sample of two free layers, in contrast to a memory cell where only one is free, as sketched in Figure 1B, the system has a lower resistive state of two magnetizations parallel to each other and a higher resistive state of two antiparallel magnetization. When the magnetic field is swept along the z-direction, the system moves between two stable low resistive states of magnetizations along
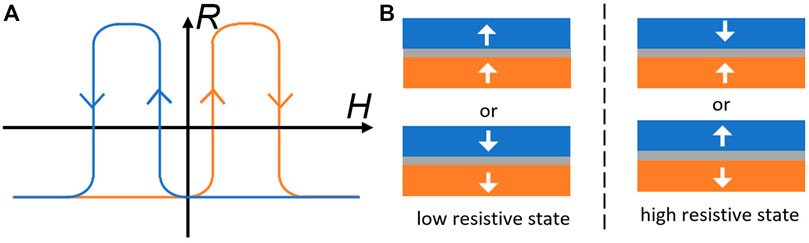
FIGURE 6. (A) Schematics of BMR in a bilayer. The system moves between two similar low resistive states by passing through a high resistive state during the field sweeping. (B) Illustration of resistive states. The device is in a higher (lower) resistive state when the magnetization of two layers are parallel (antiparallel) with each other.
It may be important to emphasize that the exact shapes and locations in a BMR and ASMR are not our concerns here. The hysteresis loop of BMR and ASMR could be very irregular in different systems. Their general features do not rely on any symmetries, as shown in the toy models of Figures 4, 5. When the resistance mechanism has inversion symmetry, the system is more likely to display ASMR as the toy model shown in Figure 4D. In general, any curve can always be decomposed into symmetric and antisymmetric components, as was usually done in experiments. Nevertheless, this kind of decomposition is not meaningful unless one can attribute each of them to a specific source. This is, of course, an interesting question but not the aim of this paper.
ASMR is less common than BMR in both Rxx and Rxy. In many experiments, the magnetic field is swept perpendicular to the currents. For the former, Mx(H) reverses between
In conclusion, similar to parallelogram MR, BMR and ASMR are universal MR behavior independent of the resistance origins. They appear as long as a system exhibits a hysteresis loop under sweeping-up and sweeping-down of a magnetic field, and its MR is approximately the same when the magnetization direction is reversed. From the generalized Ohm’s law in magnetic materials, BMR should be very common in longitudinal resistance and could also occur in transverse resistance when the magnetic field is in the plane of applied current and voltage measurement. The coercivity fields and microscopic details are encoded in the positions and shapes of a BMR and an ASMR. Although there is no inconsistency with the universal BMR/ASMR theory presented here, the explanations of many BMR and ASMR in literature [6, 7, 9–11, 18, 27, 29–32] are not the same as ours.
Data availability statement
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
Author contributions
XW planned the project. XW and HW wrote the manuscript. HW performed numerical simulations and prepared the figures. ZG and TM contributed to the result analysis and manuscript revision.
Funding
This work is supported by the Ministry of Science and Technology through grant 2020YFA0309600, the NSFC Grants (No. 12074301, 11974296), and Hong Kong RGC Grants (No. 16300522, 16302321, 16301518, and 16301619).
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Supplementary material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2022.1068605/full#supplementary-material
References
2. Huckestein B. Scaling theory of the integer quantum hall effect. Rev Mod Phys (1995) 67:357–96. doi:10.1103/RevModPhys.67.357
3. Kundt A. On the hall effect in ferromagnetic materials. Ann Phys (1893) 49:257–71. doi:10.1002/andp.18932850603
4. Smith AW, Sears RW. The hall effect in permalloy. Phys Rev (1929) 34:1466–73. doi:10.1103/PhysRev.34.1466
5. Pugh EM, Lippert TW. Hall e.m.f. and intensity of magnetization. Phys Rev (1932) 42:709–13. doi:10.1103/PhysRev.42.709
6. Ohta T, Tokuda M, Iwakiri S, Sakai K, Driesen B, Okada Y, et al. Butterfly-shaped magnetoresistance in van der waals ferromagnet Fe5GeTe2. AIP Adv (2021) 11:025014. doi:10.1063/9.0000067
7. Taniguchi H, Watanabe M, Tokuda M, Suzuki S, Imada E, Ibe T, et al. Butterfly-shaped magnetoresistance in triangular-lattice antiferromagnet ag2cro2. Sci Rep (2020) 10:2525. doi:10.1038/s41598-020-59578-z
8. Mukherjee K, Das SD, Mohapatra N, Iyer KK, Sampathkumaran EV. Anomalous butterfly-shaped magnetoresistance loops in the alloy Tb4LuSi3. Phys Rev B (2010) 81:184434. doi:10.1103/PhysRevB.81.184434
9. Li P, Zhang LT, Mi WB, Jiang EY, Bai HL. Origin of the butterfly-shaped magnetoresistance in reactive sputtered epitaxial fe3o4 films. J Appl Phys (2009) 106:033908. doi:10.1063/1.3187537
10. Hu G, Zhu Y, Xiang J, Yang TY, Huang M, Wang Z, et al. Antisymmetric magnetoresistance in a van der waals antiferromagnetic/ferromagnetic layered MnPS3/Fe3GeTe2 stacking heterostructure. ACS Nano (2020) 14:12037–44. doi:10.1021/acsnano.0c05252
11. Stankiewicz J, Jiménez-Villacorta F, Prieto C. Magnetotransport properties of oxidized iron thin films. Phys Rev B (2006) 73:014429. doi:10.1103/PhysRevB.73.014429
12. Zhou L, Song H, Liu K, Luan Z, Wang P, Sun L, et al. Observation of spin-orbit magnetoresistance in metallic thin films on magnetic insulators. Sci Adv (2018) 4:eaao3318. eaao3318. doi:10.1126/sciadv.aao3318
13. Gilbert DA, Maranville BB, Balk AL, Kirby BJ, Fischer P, Pierce DT, et al. Realization of ground-state artificial skyrmion lattices at room temperature. Nat Commun (2015) 6:8462. doi:10.1038/ncomms9462
14. Chen W, Qian L, Xiao G. Resistance of domain-wall states in half-metallic CrO2. Phys Rev B (2018) 98:174402. doi:10.1103/PhysRevB.98.174402
15. Ennen I, Kappe D, Rempel T, Glenske C, Hütten A. Giant magnetoresistance: Basic concepts, microstructure, magnetic interactions and applications. Sensors (2016) 16:904. doi:10.3390/s16060904
16. Mihai AP, Attané JP, Marty A, Warin P, Samson Y. Electron-magnon diffusion and magnetization reversal detection inFePtthin films. Phys Rev B (2008) 77:060401. doi:10.1103/PhysRevB.77.060401
17. Liu C, Wang Y, Yang M, Mao J, Li H, Li Y, et al. Magnetic-field-induced robust zero hall plateau state in MnBi2Te4 chern insulator. Nat Commun (2021) 12:4647. doi:10.1038/s41467-021-25002-x
18. Li L, Liu Y, Teng J, Long S, Guo Q, Zhang M, et al. Anisotropic magnetoresistance of nano-conductive filament in co/hfo2/pt resistive switching memory. Nanoscale Res Lett (2017) 12:210. doi:10.1186/s11671-017-1983-2
19. Nguyen VD, Vila L, Laczkowski P, Marty A, Faivre T, Attané JP. Detection of domain-wall position and magnetization reversal in nanostructures using the magnon contribution to the resistivity. Phys Rev Lett (2011) 107:136605. doi:10.1103/PhysRevLett.107.136605
20. Deng Y, Yu Y, Shi MZ, Guo Z, Xu Z, Wang J, et al. Quantum anomalous hall effect in intrinsic magnetic topological insulator mnbi2te4 Science (2020) 367:895–900. doi:10.1126/science.aax8156
21. Chang CZ, Zhang J, Feng X, Shen J, Zhang Z, Guo M, et al. Experimental observation of the quantum anomalous hall effect in a magnetic topological insulator. Science (2013) 340:167–70. doi:10.1126/science.1234414
22. Huang B, McGuire MA, May AF, Xiao D, Jarillo-Herrero P, Xu X. Emergent phenomena and proximity effects in two-dimensional magnets and heterostructures. Nat Mater (2020) 19:1276–89. doi:10.1038/s41563-020-0791-8
23. Lu J, Wang X. Magnetization reversal of single domain permalloy nanowires. J Magnetism Magn Mater (2009) 321:2916–9. doi:10.1016/j.jmmm.2009.04.057
24. Li X, Collignon C, Xu L, Zuo H, Cavanna A, Gennser U, et al. Chiral domain walls of mn3sn and their memory. Nat Commun (2019) 10:3021. doi:10.1038/s41467-019-10815-8
25. Tang HX, Kawakami RK, Awschalom DD, Roukes ML. Giant planar hall effect in epitaxial (Ga,Mn)As devices. Phys Rev Lett (2003) 90:107201. doi:10.1103/PhysRevLett.90.107201
26. Miao YQ, Guo JJ, Luo ZY, Zhong MZ, Li B, Wang XG, et al. Anisotropic magnetoresistance effect of intercalated ferromagnet FeTa3S6. Front Phys (2022) 10. doi:10.3389/fphy.2022.847402
27. Klein DR, MacNeill D, Lado JL, Soriano D, Navarro-Moratalla E, Watanabe K, et al. Probing magnetism in 2d van der waals crystalline insulators via electron tunneling. Science (2018) 360:1218–22. doi:10.1126/science.aar3617
28. Zhang Z, Feng X, Guo M, Li K, Zhang J, Ou Y, et al. Electrically tuned magnetic order and magnetoresistance in a topological insulator. Nat Commun (2014) 5:4915. doi:10.1038/ncomms5915
29. Wegrowe JE, Kelly D, Franck A, Gilbert SE, Ansermet JP. Magnetoresistance of ferromagnetic nanowires. Phys Rev Lett (1999) 82:3681–4. doi:10.1103/PhysRevLett.82.3681
30. Bass J, Pratt W. Current-perpendicular (cpp) magnetoresistance in magnetic metallic multilayers. J Magnetism Magn Mater (1999) 200:274–89. doi:10.1016/S0304-8853(99)00316-9
31. Miyazaki T, Tezuka N. Giant magnetic tunneling effect in Fe/Al2O3/Fe junction. J Magnetism Magn Mater (1995) 139:L231–4. doi:10.1016/0304-8853(95)90001-2
32. Binasch G, Grünberg P, Saurenbach F, Zinn W. Enhanced magnetoresistance in layered magnetic structures with antiferromagnetic interlayer exchange. Phys Rev B (1989) 39:4828–30. doi:10.1103/PhysRevB.39.4828
33. Lu ZL, Xu MX, Zou WQ, Wang S, Liu XC, Lin YB, et al. Large low field magnetoresistance in ultrathin nanocrystalline magnetite Fe3O4 films at room temperature. Appl Phys Lett (2007) 91:102508. doi:10.1063/1.2783191
34. Hirsch A. Influence of a magnetic field on the electrical resistance of thin ferromagnetic layers at low temperatures. Physica (1959) 25:581–9. doi:10.1016/s0031-8914(59)96020-3
35. Tatsumoto E, Kuwahara K, Goto M. Magnetoresistance effect in the magnetization reversal of permalloy films. J Phys Soc Jpn (1960) 15:1703. doi:10.1143/jpsj.15.1703
36. Wang L, Feng Q, Kim Y, Kim R, Lee KH, Pollard SD, et al. Ferroelectrically tunable magnetic skyrmions in ultrathin oxide heterostructures. Nat Mater (2018) 17:1087–94. doi:10.1038/s41563-018-0204-4
37. Zhang X, Ambhire SC, Lu Q, Niu W, Cook J, Jiang JS, et al. Giant topological hall effect in van der waals heterostructures of CrTe2/Bi2Te3. ACS Nano (2021) 15:15710–9. doi:10.1021/acsnano.1c05519
38. Qin Q, Liu L, Lin W, Shu X, Xie Q, Lim Z, et al. Emergence of topological hall effect in a srruo3 single layer. Adv Mater (2019) 31:1807008. doi:10.1002/adma.201807008
39. Niu W, Cao Z, Wang Y, Wu Z, Zhang X, Han W, et al. Antisymmetric magnetoresistance in Fe3GeTe2 nanodevices of inhomogeneous thickness. Phys Rev B (2021) 104:125429. doi:10.1103/PhysRevB.104.125429
40. He QL, Yin G, Yu L, Grutter AJ, Pan L, Chen CZ, et al. Topological transitions induced by antiferromagnetism in a thin-film topological insulator. Phys Rev Lett (2018) 121:096802. doi:10.1103/PhysRevLett.121.096802
41. Cheng XM, Urazhdin S, Tchernyshyov O, Chien CL, Nikitenko VI, Shapiro AJ, et al. Antisymmetric magnetoresistance in magnetic multilayers with perpendicular anisotropy. Phys Rev Lett (2005) 94:017203. doi:10.1103/PhysRevLett.94.017203
42. Lin W. Magnetization reversal, and generation and detection of pure spin-current. Nanjing, China: Ph.D. thesis (2007).
43. Zhang Y, Wang XS, Yuan HY, Kang SS, Zhang HW, Wang XR. Dynamic magnetic susceptibility and electrical detection of ferromagnetic resonance. J Phys : Condens Matter (2017) 29:095806. doi:10.1088/1361-648x/aa547e
44. Zhang Y, Wang XR, Zhang HW. Extraordinary galvanomagnetic effects in polycrystalline magnetic films. Europhysics Lett (2016) 113:47003. doi:10.1209/0295-5075/113/47003
45. Wang XR. A theory for anisotropic magnetoresistance in materials with two vector order parameters. Chin Phys Lett (2022) 39:027301. doi:10.1088/0256-307X/39/2/027301
46. Vansteenkiste A, Leliaert J, Dvornik M, Helsen M, Garcia-Sanchez F, Van Waeyenberge B. The design and verification of Mumax3. AIP Adv (2014) 4:107133. doi:10.1063/1.4899186
47. Chung TY, Hsu SY. Magnetization reversal in single domain permalloy wires probed by magnetotransport. J Appl Phys (2008) 103:07C506. doi:10.1063/1.2834709
48. Sun ZZ, Wang XR. Fast magnetization switching of stoner particles: A nonlinear dynamics picture. Phys Rev B (2005) 71:174430. doi:10.1103/PhysRevB.71.174430
49. Carcia PF, Meinhaldt AD, Suna A. Perpendicular magnetic anisotropy in Pd/Co thin film layered structures. Appl Phys Lett (1985) 47:178–80. doi:10.1063/1.96254
50. Schlickeiser F, Ritzmann U, Hinzke D, Nowak U. Role of entropy in domain wall motion in thermal gradients. Phys Rev Lett (2014) 113:097201. doi:10.1103/PhysRevLett.113.097201
51. Lee KM, Choi JW, Sok J, Min BC. Temperature dependence of the interfacial magnetic anisotropy in W/CoFeB/MgO. AIP Adv (2017) 7:065107. doi:10.1063/1.4985720
52. Zhao G, Wang X, Feng Y, Huang C. Coherent rotation and effective anisotropy. IEEE Trans Magn (2007) 43:2908–10. doi:10.1109/tmag.2007.893629
Keywords: butterfly magnetoresistance, antisymmetric magnetoresistance, hysteresis, landau-lifshitz-gilbert equation, generalized Ohm’s law
Citation: Wu HT, Min T, Guo ZX and Wang XR (2022) On universal butterfly and antisymmetric magnetoresistances. Front. Phys. 10:1068605. doi: 10.3389/fphy.2022.1068605
Received: 13 October 2022; Accepted: 14 November 2022;
Published: 02 December 2022.
Edited by:
Peng Yan, University of Electronic Science and Technology of China, ChinaCopyright © 2022 Wu, Min, Guo and Wang. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: X. R. Wang, cGh4d2FuQHVzdC5oaw==
 H. T. Wu
H. T. Wu Tai Min
Tai Min Z. X. Guo3
Z. X. Guo3 X. R. Wang
X. R. Wang