
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Phys., 02 December 2022
Sec. Optics and Photonics
Volume 10 - 2022 | https://doi.org/10.3389/fphy.2022.1067825
This article is part of the Research TopicLaser Field Manipulation and Its Advanced ApplicationsView all 8 articles
Engineering the chiral field is crucial for the flexible manipulation of chiral particles. Some complex optical setups for constructing spin-structured fields have been well developed to sort particles with opposite chiralities toward opposite transversal directions. In this work, we demonstrate the robust construction of a class of focal fields that possess laterally variant optical spin angular momentum by using the monolayer dielectric metalens. By utilizing the simultaneous modulation capacity of the phase and polarization of the dielectric metalens, we can establish a line focus with laterally tailored gradient optical helicity. The focusing property of this metalens and the polarization structure of the focal field are theoretically analyzed using a hybrid vector-focusing model and experimentally demonstrated by NA = 0.2 and 0.5 samples. We illustrate that this type of gradient helicity offers opportunities to induce a chirality-sensitive lateral force for chiral particles.
Chirality is a research topic of longstanding interest in light–matter interactions [1–3]. Circularly polarized light is a typical chiral light field with left- and right-handed helicities [4] which have been widely used in biological science and pharmacies for chiral-elective interactions and sensing of biomolecules [5], e.g., DNA/RNA, protein amino acids, etc. [6]. On the other hand, as the contactless and label-free advantages, lateral optical forces (non-conservative forces perpendicular to the direction of light propagation) arising from the helicity gradient of light fields with non-uniform spin angular momentum (SAM), namely, spin-structured light fields, have been demonstrated as a remarkable tool to sort chiral objects [7–11], e.g., the chiral-sensitive separation force of chiral particles in light fields with one-dimensional variant helicity [12–14].
Many efforts have been devoted to the construction of such light fields with laterally modulated helicity by manipulating the superposition of two orthogonally polarized components with elaborate phase structures [12–15]. In free space, these kinds of synthetic light fields are realized by optical setups composed of traditional polarization and phase modulators with high efficiencies, while those bulky devices have disadvantages in miniaturization and integration [14, 15]. To overcome this issue, evanescent waves such as surface plasmonic polaritons (SPPs) have been utilized to engineer the surface chirality structures [16–18] which exhibited significantly enhanced light–matter interaction effects and spatial frequency of the chirality structure [19, 20]. On the other hand, the near-field local characteristic, however, greatly limits the practical application [21, 22]. Anisotropic metasurfaces, which work as nanoscale birefringent phase retarders, provide an elegant solution to these difficulties [23]. These artificially ultra-thin materials consist of two-dimensional arrays that enable the simultaneous control of polarization, amplitude, and the phase of the wavefront in a sub-wavelength scale [24–27], facilitating the development of functional nanodevices such as lenses [28], wave plates [29], holograms [30], polarization detectors [31], and multiplexers [32, 33]. Importantly, elaborate metasurfaces have been developed in typical applications such as three-dimensional polarization modulation [33–36] and polarization-encoding vectorial holography [37, 38].
In this paper, we show that spin-structured focal fields with laterally variant helicities can be conveniently generated by a minimalist metalens. The metalens is designed according to a developed hybrid vector-focusing model based on the combined control of the polarization and phase of the wavefront [39, 40]. It consists of two segments with orthogonal polarization modulations and two-dimensional hybrid-focusing phases, which enable polarization-dependent field focusing and mixing to generate laterally oscillating SAM in the focal plane. Under the illumination of linear polarizations, the optical helicity gradient is valid to induce chirality-sensitive lateral forces for the sorting of chiral particles. Our scheme might supply an integrated and compact platform for the application of optical tweezers.
Figure 1A illustrates the basic principle of the metalens. This device consists of two segments divided by the y axis, which transforms the uniform incident polarization into two orthogonal states with two-dimensional hybrid phase retardations, of which on-axis distributions are shown in Figure 1B. The phase retardation function is defined as φ(x,y) = -k0(-f ) -k0xsinα. Here, k0 is the wave number, f denotes the focal length corresponding to the cylindrical lens along the y axis, α = tan−1 (R/2f) denotes the gradient of the phase along the x axis, and R depicts the aperture of the metalens. The hyperbolic and linear phases exhibit focusing properties as cylindrical and conical lenses along the y and x directions, respectively.
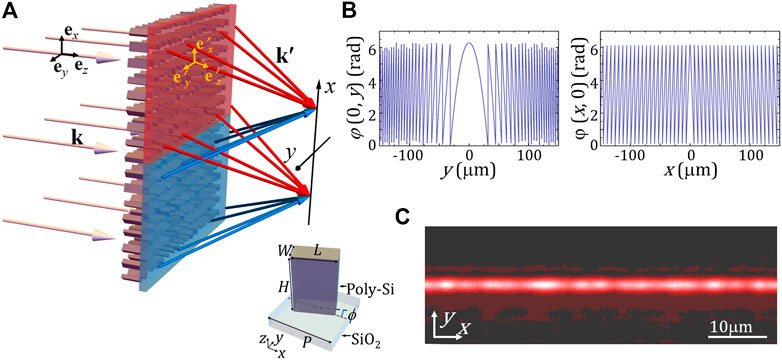
FIGURE 1. (A) Vector-focusing model of the metalens. The colored arrows indicate the local wave vectors. Inset: Schematic diagram of metalens’ meta-atom. The meta-atom is composed of a SiO2 substrate and a polycrystalline silicon (Poly-Si) rectangular nanopillar. (B) Phase retardation distributions on the two axes. (C) Intensity distribution in the focal plane of an NA = 0.2 metalens.
We study the focusing dynamics of two segments by using the vectorial diffraction integration theory, which is valid beyond the paraxial approximation [41]. Supposing that the metalens is illuminated by a normally incident plane wave and the transmitted field is expressed as E0 = [Ex Ey]T, with Ex and Ey depicting the complex amplitudes of two basic states, considering the x < 0 segment, the focal field can be written as [41, 42]
where
We first consider that the transmitted field has normalized intensity in a paraxial condition so that polarization is expressed as E0 = [cosχ sinχeiδ]T, with χ and δ determining the polarization. The electric component of the focal field can, thus, be appropriately rewritten as
where the sinc (∙) function depicts the focal profile generated from the y-axis-focusing angle and L is the aperture size of the metalens. Eq. 2 indicates that the focal field presents a sinc2 function profile along the y axis but a uniform intensity along the x axis, as the experimental result shown in Figure 1C. Likewise, the focal field corresponding to the x > 0 segment presents an identical intensity profile but the opposite wave vector in the lateral plane.
By engineering the polarization and phase modulation of the two segments, one can flexibly control the superposition state. Here, we lock the y-axis focal length with the x-axis-tilted phase. As a result, two focal components completely overlap with each other and thereby present a uniform intensity along the x axis. However, the diffraction arising from the knife edge between the two segments decreases the uniformity of the total focal field. Furthermore, in a tightly focusing case, an intriguing polarization state such as lateral SAM would be constructed because of the strong coupling from the transverse component to the longitudinal component.
We then select polycrystalline silicon (Poly-Si) to design the metalens, of which the meta-atom is schematically shown in the inset of Figure 1A. It consists of a SiO2 substrate and a Poly-Si rectangular nanopillar [40]. According to the effective waveguide theory, the Jones matrix corresponding to the equivalent birefringence effect of a meta-atom can be expressed as
where δ = φx-φy, φ0 = (φx+φy)/2, and T = Tx = Ty, with Tx, y and φx,y being the transmission amplitudes and phases of the two eigenstates; ϕ depicts the rotation angle of the rectangular nanopillar.
As a proof of principle, we select the |H⟩ and |V⟩ states on the Poincaré sphere as basic states. In this case, we set the input polarization as Ein = [1 1]T, and δ = π, ϕ1 = 22.5°, and ϕ2 = 67.5°, with ϕ1,2 depicting the rotation angles of the meta-atom in the x < 0 and x > 0 regions. The transmitted fields can thus be correspondingly expressed as E1 = Texp (iφ01)[1 0]T and E2 = Texp (iφ02)[0 1]T. Substituting two transmitted fields into Eq. 2, the normalized distributions of Stokes parameters in the focal plane are approximately expressed as S1 = −sin2α/2, S2 = cosαcos (2kxsinα), and S3 = -cosαsin (2kxsinα). Under a paraxial condition, the superposition field presents oscillating helicity (quantitatively expressed by S3) along the x axis with a spatial frequency of fx = ksinα/π, of which the polarization variation trajectory is shown as the blue meridian on the Poincaré sphere in Figure 2A. The two-dimensional HSV image in Figure 2B gives the normalized intensity and optical helicity density distributions of the focal field, i.e., S0 and S3. Therein, the brightness and color values correspond to S0 and S3, respectively. Obviously, the focal field presents a bright linear focus with the one-dimensional gradient of optical helicity.
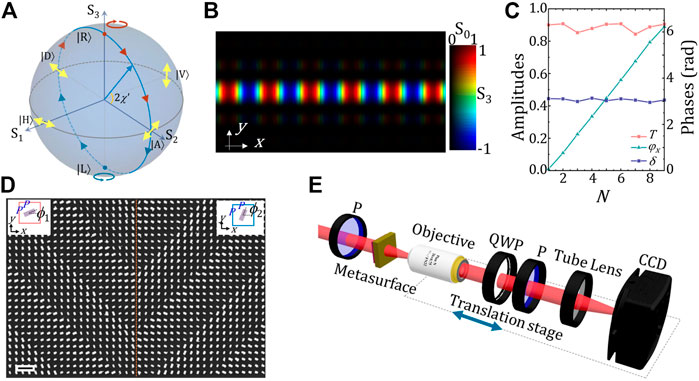
FIGURE 2. (A) Poincaré sphere and oscillating helicity trajectory based on the superposition of |H⟩ and |V⟩ states. (B) Numerically simulated local intensity S0 and helicity density S3 distributions in the focal plane. In the two-dimensional HSV colorbar, brightness and color values correspond to the intensity S0 and polarization ellipticity S3, respectively. (C) Transmission amplitude T, propagation phase φx, and phase retardation δ of selected geometries. (D) Local scanning electron microscopic (SEM) image near the y axis. The scale bar is 1 μm. ϕ1,2 depict the rotation angles of the meta-atom in the x < 0 and x > 0 regions. (E) Experimental setup. P, polarizer; QWP, quarter wave plate; CCD, charge-coupled device.
We design an all-dielectric metalens by using the electron beam exposure and plasma-etching process [40]. It should be noted that since the propagation phase φ0 actually works as the modulation phase, we select eight geometries with similar transmission amplitudes but linearly variant propagation phases to design the metalens, according to the meta-atom libraries of polarization and phase modulation in Note 2 of Supplementary Material. The transmission amplitude T, propagation phase φx, and phase retardation δ of selected geometries are shown in Figure 2C in conditions of λ = 670nm, p = 450nm, and H = 550 nm. The complex refractive index of Poly-Si is n = 3.25710 + i0.0107. Figure 2D gives a local scanning electron microscope (SEM) image near the y axis. This metalens has 1,000 × 1,000 nanopillars. Figure 2E depicts the experimental setup. The λ = 670 nm laser output from a supercontinuum laser (SC-Pro, YSL Photonics) after acoustic-optic filtering is transformed into 45° polarization, which then normally illuminates the metalens. A microscope composed by an objective (×20), tube lens, and CCD is employed to observe the focal field. This system is located on a translation stage to observe the focusing dynamics. A quarter wave plate and polarizer are used to measure the Stokes parameters.
Figure 3 displays the experimental results of NA = 0.2 and 0.5 metalenses. Here, NA is defined by the focusing phase along the y axis, so the focusing parameters of the two metalenses are f1 = 1.1mm, α1 = 5.83°, and f2 = 0.39mm, α2 = 16.1°, respectively. As shown in Figures 3A, D, the focal fields present a bright line focus with the oscillating helicity density along the x axis. The generation efficiency of this type of metalens is about 71%, which is obtained by measuring the power ratio between the focal field and input field. Figures 3B, E illustrate the measured Stokes parameter distributions in a period, where the red curves and points depict the theoretical trajectories and experimental results, respectively. Figures 3C, F show the experimentally measured focusing process of metalens in the y–z plane, and the insets are the numerically calculated results. As shown, the experimental results are consistent with the theory. Clearly, these optical helicity intensities in the focal plane oscillate in the form of sinusoidal functions with periods of about 3.2 μm and 1.2 μm, which are consistent with the theoretical predictions.
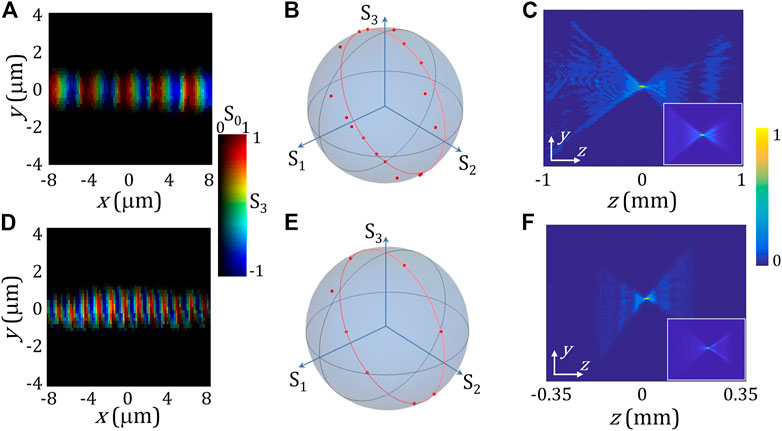
FIGURE 3. (A,D) Intensity S0 and helicity density S3 distributions near the focal point. (B,E) Measured Stokes parameters in a period. (C,F) Focusing dynamics in the y–z plane. NA = 0.2 (top) and 0.5 (bottom).
We remark that the optical helicity structure is insensitive to the input polarization orientation, namely, the oscillating property of the optical helicity intensity is invariant for the incidence of arbitrary linear polarization. According to Eq. 3, for the incidence of a linear polarization, the transmitted polarizations are always orthogonal, i.e., E01⋅E02≡0. This means that the variational trajectory of the x-dependent superposition state is locked by a meridian. On the other hand, the x-dependent phase difference is invariable for a constant NA. Therefore, the optical helicity density and its gradient of the superposition field are robust under the illumination of linear polarization. This stability is extremely important for related applications of particle manipulation.
This metalens platform is also suitable for the generation of other polarization oscillating light fields. We next design another metalens by choosing two spin states as bases. In this case, the transmitted polarizations consequently are E01 = [1 i]T and E02 = [1 -i]T, respectively. Substituting these two states into Eqs. 1, 2, one obtains the Stokes parameters of the focal field as S1 = [−2sin2α+(1 + cos2α) sin (2kxsinα)]/2, S2 = cosαcos (2kxsinα), and S3 = 0. Under the paraxial condition, S1 = sin (2kxsinα) and S2 = cos (2kxsinα); this means that the superposition state oscillates along the equator of the Poincaré sphere, as per the red trajectory shown in Figure 4A. Since the polarization azimuthal angle is 2ϕ' = tan−1(S2/S1); therefore, the polarization orientation varies as ϕ' = π/4-kxsinα along the x direction. As a proof-of-principle, we fabricate an NA = 0.2 metalens with f = 1.1 mm and α = 5.83°. The meta-atom has parameters δ = π/2, ϕ1 = 0°, and ϕ2 = 90°. Figure 4B shows the transmission properties of the selected geometries, of which the geometric sizes are shown in Note 2 and Supplementary Table S2 of Supplementary Material. The SEM image of the metalens is shown in Figure 4C. Figures 4D, E give the experimentally measured polarization orientation and Stokes parameters under the illumination of an 808-nm laser with [1 1]T polarization. Because of the challenge on selecting a nanopillar with suitable phase retardation, we fabricate and operate the experiment at a wavelength of 808 nm (the refractive index of Poly-Si at this wavelength is n = 3.23479 + i0.00102); the efficiency of this type of metalens is about 78% at this wavelength. As shown, the experimental result is consistent with the theory that the polarization orientation oscillates along the x direction with a period of 3.9 μm.
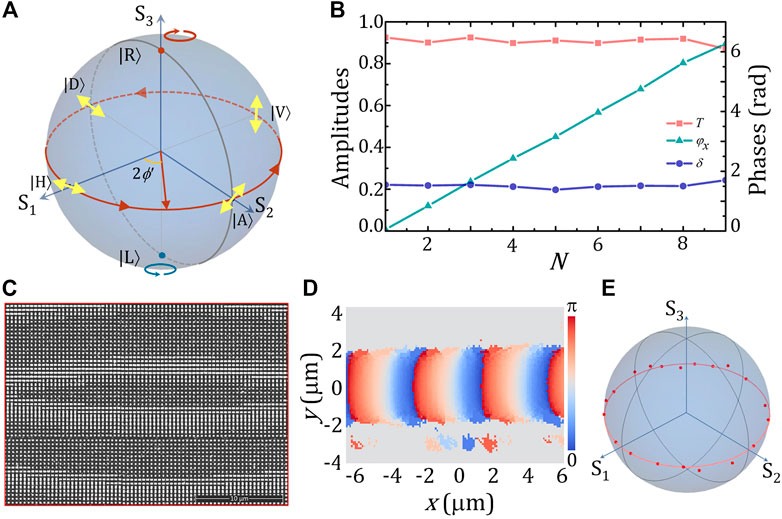
FIGURE 4. (A) Polarization variation trajectory on the Poincaré sphere when two spin states are selected as bases. (B) Transmission amplitude T, propagation phase φx, and phase retardation δ of the selected geometries. (C) Local SEM image of an NA = 0.2 metalens. This metalens has 1,000 × 1,000 nanopillars. The height and period of the meta-atom are 570 nm and 450 nm, respectively. (D) Measured polarization orientation of the focal field in the lateral plane, for the incidence of the [1 1]T state. (E) Measured Stokes parameters in a period.
We further analyze the optical force induced by this intriguing optical helicity gradient, which exhibited promising application potential in chirality-related deflection [12, 13]. We use the scattering property of a spherical chiral particle to analyze this typical force [9, 13], which has been derived as
where U=(Re [αee]|E|2 + Re [αmm]|E|2-2Re [αem]Im|H∙E*|)/4 is the term due to the light–matter interaction; ⟨S⟩ = Re [E×H*]/2 is the time-averaged Poynting vector; ⟨Le⟩ = ε0 Im [E×E*]/(4ωi) and ⟨Lm⟩ = μ0 Im [H×H*]/(4ωi) are the time-averaged spin densities; σe = k0Im [αee]/ε0, σm = k0Im [αmm]/μ0, and σ = σe+σm-c2k4 0(Re[αeeα*mm]+αemα*em); γe = -2ωIm [αem]+ ck4 0Re [αeeα*em]/(3πε0), and γe = -2ωIm [αem]+ ck4 0Re [αmmα*em]/(3πμ0); αee, αmm, and αem denote the polarizability of the particle.
In the focal plane, because of the uniform intensity distribution along the x direction, the lateral component associated with the gradient force, that is, the first term on the right side of Eq. 4, only presents the y component, i.e., Fgy. However, the radiation pressure, vortex forces, and the second and third terms in Eq. 4 are neglectable because of the uniform phase distributions. Moreover, the last term of Eq. 4 is about 10–6 smaller than that of the spin density force [9]. We, hence, focus on the terms related to the SAM density ⟨L⟩. In this case, we calculated the lateral forces on a spherical dipolar chiral particle (r = 50 nm) characterized by εr = 2.53, μr = 1, and chirality parameter κ = 1, when a |A⟩ polarized laser with λ = 670 wavelength illuminates an NA = 0.5 metalens [9, 13]. The force distributions along the x axis are shown in Figures 5A, B. Since the polarization conversion, the enhanced z-polarized component induces curl-spin (the fourth and fifth terms) and spin-density (the sixth and seventh terms) forces along the y and x directions, i.e., Fc and Fs, respectively. Because of the cylindrical focusing, the gradient force Fg dominates the y component of the lateral force, as shown in Figure 5C. The lateral forces Fx and Fy exerted on the dipole chiral particle in the focal plane are shown in Figure 5D. The gradient force Fgy acts as always as the restoring force toward y = 0. In the presence of the helicity gradient, the spatially modulated Fx component induces chiral-selective transverse motion along the x axis, that is, this transverse force derives particles with chirality of κ > 0 from the unstable equilibrium points indicated by the blue cross to stable equilibrium points indicated by the red cross. However, this force derives the particles with opposite chirality (κ < 0) along the direction depicted by the dotted line to their stable equilibrium points indicated by the blue cross.
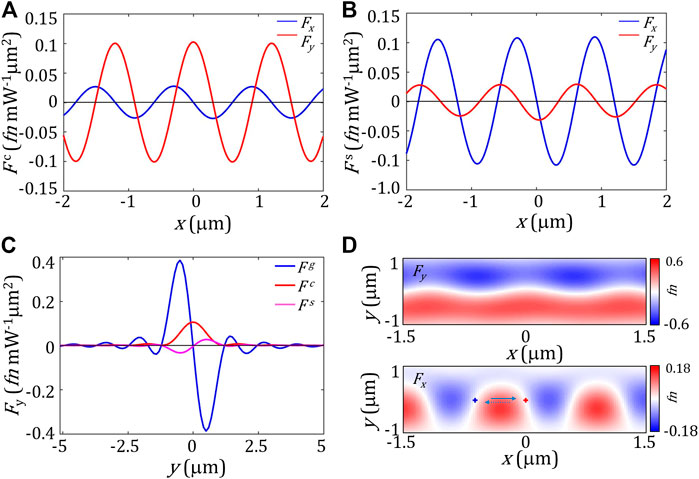
FIGURE 5. Numerical results of the lateral forces acting on the chiral sphere placed in the focal plane. (A) Curl-spin forces. (B) Spin density forces. (C) Lateral force Fy. (D) Fx and Fy distributions. The NA and chiral coefficient are set as NA = 0.5 and κ = 1, respectively.
In conclusion, we reported a monolayer dielectric metalens that can generate focal fields with oscillating optical SAM to induce a chiral-sensitive lateral optical force. We introduced a hybrid vector model to construct the focal field with a laterally tailored polarization structure and to design the metalens. Under the illuminations of linearly polarized light fields, we experimentally demonstrated the capability of constructing light fields with one-dimensional oscillating optical helicity and analyzed the lateral force induced by the gradient optical helicity affecting chiral particles. This work provides a platform for the design of integrated and compact devices to conveniently control the polarization structure of light fields for optical trapping and manipulation.
The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.
All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.
This work was supported by the National Key Research and Development Program of China (2022YFA1404800), the National Science Foundation of China (NSFC) (12174309, 11634010, 91850118, and 11774289), the Natural Science Basic Research Program of Shaanxi (2021JQ-895 and 2020JM-104), the Fundamental Research Funds for the Central Universities (3102019JC008), and the Innovation Foundation for Doctor Dissertation of Northwestern Polytechnical University (CX202046, CX202047, and CX202048).
The authors acknowledge the contributions of specific colleagues, institutions, or agencies that aided the study.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2022.1067825/full#supplementary-material
1. Hendry E, Carpy T, Johnston J, Popland M, Mikhaylovskiy RV, Lapthorn AJ, et al. Ultrasensitive detection and characterization of biomolecules using superchiral fields. Nat Nanotech (2010) 5:783–7. doi:10.1038/nnano.2010.209
2. Bliokh KY, Bekshaev AY, Nori F. Extraordinary momentum and spin in evanescent waves. Nat Commun (2014) 5:3300. doi:10.1038/ncomms4300
3. Collins JT, Kuppe C, Hooper DC, Sibilia C, Centini M, Valev VK. Chirality and chiroptical effects in metal nanostructures: Fundamentals and current trends. Adv Opt Mater (2017) 5:1700182. doi:10.1002/adom.201700182
4. Bliokh KY, Nori F. Transverse and longitudinal angular momenta of light. Phys Rep (2015) 592:1–38. doi:10.1016/j.physrep.2015.06.003
5. Tang Y, Cohen AE. Enhanced enantioselectivity in excitation of chiral molecules by superchiral light. Science (2011) 332:333–6. doi:10.1126/science.1202817
6. Mun J, Kim M, Yang Y, Badloe T, Ni J, Chen Y, et al. Electromagnetic chirality: From fundamentals to nontraditional chiroptical phenomena. Light Sci Appl (2020) 9:139. doi:10.1038/s41377-020-00367-8
7. Wang SB, Chan CT. Lateral optical force on chiral particles near a surface. Nat Commun (2014) 5:3307. doi:10.1038/ncomms4307
8. Micali N, Engelkamp H, Rhee PG, Christianen PCM, Scolaro LM, Maan JC. Selection of supramolecular chirality by application of rotational and magnetic forces. Nat Chem (2012) 4:201–7. doi:10.1038/nchem.1264
9. Hayat A, Mueller JPB, Capasso F. Lateral chirality-sorting optical forces. Proc Natl Acad Sci U S A (2015) 112:13190–4. doi:10.1073/pnas.1516704112
10. Canaguier-Durand A, Hutchison JA, Genet C, Ebbesen TW. Mechanical separation of chiral dipoles by chiral light. New J Phys (2013) 15:123037. doi:10.1088/1367-2630/15/12/123037
11. Cameron RP, Barnett SM, Yao AM. Discriminatory optical force for chiral molecules. New J Phys (2014) 16:013020. doi:10.1088/1367-2630/16/1/013020
12. Chen H, Liang C, Liu S, Lin Z. Chirality sorting using two-wave-interference-induced lateral optical force. Phys Rev A (2016) 93:053833. doi:10.1103/physreva.93.053833
13. Zhang T, Mahdy MRC, Liu Y, Teng JH, Lim CT, Wang Z, et al. All-optical chirality-sensitive sorting via reversible lateral forces in interference fields. ACS Nano (2017) 11:4292–300. doi:10.1021/acsnano.7b01428
14. Kravets N, Aleksanyan A, Brasselet E. Chiral optical Stern-Gerlach Newtonian experiment. Phys Rev Lett (2019) 122:024301. doi:10.1103/physrevlett.122.024301
15. Shi Y, Zhu T, Zhang T, Mazzulla A, Tsai DP, Ding W, et al. Chirality-assisted lateral momentum transfer for bidirectional enantioselective separation. Light Sci Appl (2020) 9:62. doi:10.1038/s41377-020-0293-0
16. Stauber T, Low T, Gómez-Santos G. Plasmon-enhanced near-field chirality in twisted van der waals heterostructures. Nano Lett (2020) 20:8711–8. doi:10.1021/acs.nanolett.0c03519
17. Zhao Y, Askarpour AN, Sun L, Shi J, Li X, Alù A. Chirality detection of enantiomers using twisted optical metamaterials. Nat Commun (2017) 8:14180. doi:10.1038/ncomms14180
18. Valev VK, Baumberg JJ, Sibilia C, Verbiest T. Chirality and chiroptical effects in plasmonic nanostructures: Fundamentals, recent progress, and outlook. Adv Mater (2013) 25:2517–34. doi:10.1002/adma.201205178
19. Hentschel M, Schäferling M, Duan X, Giessen H, Liu N. Chiral plasmonics. Sci Adv (2017) 3:e1602735. doi:10.1126/sciadv.1602735
20. Zhang S, Wei H, Bao K, Håkanson U, Halas NJ, Nordlander P, et al. Chiral surface plasmon polaritons on metallic nanowires. Phys Rev Lett (2011) 107:096801. doi:10.1103/physrevlett.107.096801
21. Gao D, Ding W, Nieto-Vesperinas M, Ding X, Rahman M, Zhang T, et al. Optical manipulation from the microscale to the nanoscale: Fundamentals, advances and prospects. Light: Sci Appl (2017) 6:e17039. doi:10.1038/lsa.2017.39
22. Kakkanattu EN, Ghamari S, Vollmer F. Review of optical sensing and manipulation of chiral molecules and nanostructures with the focus on plasmonic enhancements [Invited]. Opt Express (2021) 29:12543–79. doi:10.1364/oe.421839
23. Chen HT, Taylor AJ, Yu N. A review of metasurfaces: Physics and applications. Rep Prog Phys (2016) 79:076401. doi:10.1088/0034-4885/79/7/076401
24. Kamali SM, Arbabi E, Arbabi A, Faraon A. A review of dielectric optical metasurfaces for wavefront control. Nanophotonics (2018) 7:1041–68. doi:10.1515/nanoph-2017-0129
25. Overvig C, Shrestha S, Malek SC, Lu M, Stein A, Zheng C, et al. Dielectric metasurfaces for complete and independent control of the optical amplitude and phase. Light Sci Appl (2019) 8:92–12. doi:10.1038/s41377-019-0201-7
26. Guo X, Zhong J, Li B, Qi S, Li Y, Li P, et al. Full-color holographic display and encryption with full-polarization degree of freedom. Adv Mater (2021) 34:2103192. doi:10.1002/adma.202103192
27. Arbabi A, Horie Y, Bagheri M, Faraon A. Dielectric metasurfaces for complete control of phase and polarization with subwavelength spatial resolution and high transmission. Nat Nanotech (2015) 10:937–43. doi:10.1038/nnano.2015.186
28. Khorasaninejad M, Capasso F. Metalenses: Versatile multifunctional photonic components. Science (2017) 358:eaam8100. doi:10.1126/science.aam8100
29. Bao Y, Ni J, Qiu CW. A minimalist single-layer metasurface for arbitrary and full control of vector vortex beams. Adv Mater (2020) 32:1905659. doi:10.1002/adma.201905659
30. Deng ZL, Li G. Metasurface optical holography. Mater Today Phys (2017) 3:16–32. doi:10.1016/j.mtphys.2017.11.001
31. Rubin NA, Aversa GD, Chevalier P, Shi Z, Chen WT, Capasso F. Matrix Fourier optics enables a compact full-Stokes polarization camera. Science (2019) 365:eaax1839. doi:10.1126/science.aax1839
32. Chen S, Liu W, Li Z, Cheng H, Tian J. Metasurfaces: Metasurface-Empowered optical multiplexing and multifunction (adv. Mater. 3/2020). Adv Mater (2020) 32:2070022. doi:10.1002/adma.202070022
33. Li Z, Cheng H, Liu Z, Chen S, Tian J. Plasmonic Airy beam generation by both phase and amplitude modulation with metasurfaces. Adv Opt Mater (2016) 4:1230–5. doi:10.1002/adom.201600108
34. Dorrah AH, Rubin NA, Zaidi A, Tamagnone M, Capasso F. Metasurface optics for on-demand polarization transformations along the optical path. Nat Photon (2021) 15:287–96. doi:10.1038/s41566-020-00750-2
35. Shi Z, Zhu AY, Li Z, Huang YW, Chen WT, Qiu CW, et al. Continuous angle-tunable birefringence with freeform metasurfaces for arbitrary polarization conversion. Sci Adv (2020) 6:eaba3367. doi:10.1126/sciadv.aba3367
36. Arbabi E, Kamali SM, Arbabi A, Faraon A. Vectorial holograms with a dielectric metasurface: Ultimate polarization pattern generation. ACS Photon (2019) 6:2712–8. doi:10.1021/acsphotonics.9b00678
37. Guo X, Li P, Zhong J, Wen D, Wei B, Liu S, et al. Stokes meta-hologram toward optical cryptography. Nat Commun (2022) 13:6687. doi:10.1038/s41467-022-34542-9
38. Deng Z, Jin M, Ye X, Wang S, Shi T, Deng J, et al. Vectorial holograms: Full-color complex-amplitude vectorial holograms based on multi-freedom metasurfaces (adv. Funct. Mater. 21/2020). Adv Funct Mater (2020) 30:2070131. doi:10.1002/adfm.202070131
39. Mueller JB, Rubin NA, Devlin RC, Groever B, Capasso F. Metasurface polarization optics: Independent phase control of arbitrary orthogonal states of polarization. Phys Rev Lett (2017) 118:113901. doi:10.1103/physrevlett.118.113901
40. Guo X, Li P, Zhong J, Liu S, Wei B, Zhu W, et al. Tying polarization-switchable optical vortex knots and links via holographic all-dielectric metasurfaces. Laser Photon Rev (2020) 14:1900366. doi:10.1002/lpor.201900366
41. Wolf E. Electromagnetic diffraction in optical systems. II. an integral representation of the image field. Proc R Soc Lond Ser A (1959) 253:349–57.
Keywords: polarization, spin angular momentum, metalens, focusing, optical trapping
Citation: Li B, Xin Y, Guo X, Fan X, Liu S, Zhao J and Li P (2022) Constructing spin-structured focal fields for chiral-sensitive trapping with dielectric metalens. Front. Phys. 10:1067825. doi: 10.3389/fphy.2022.1067825
Received: 12 October 2022; Accepted: 17 November 2022;
Published: 02 December 2022.
Edited by:
Carmelo Rosales-Guzmán, Centro de Investigaciones en Optica, MexicoReviewed by:
Yongyuan Jiang, Harbin Institute of Technology, ChinaCopyright © 2022 Li, Xin, Guo, Fan, Liu, Zhao and Li. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Peng Li, cGVuZ2xpQG53cHUuZWR1LmNu
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.