- 1Department of Engineering and Computer Science, National University of Modern Languages, Islamabad, Pakistan
- 2School of Electrical and Electronic Engineering, The University of Adelaide, Adelaide, NT, Australia
- 3Department of Mathematics, University of Management and Technology Lahore, Rawalpindi, Pakistan
- 4Department of Mathematics, National University of Modern Languages, Rawalpindi, Pakistan
- 5Center of Research, Faculty of Engineering, Future University in Egypt, New Cairo, Egypt
The heat transport mechanism has an engrossing application in effective heat management for the automobile industry and the biomedical industry. The analysis of the MHD graphene−carboxymethyl cellulose (CMC) solution−water nanofluid past a stretchable wall with Joule heating and velocity slip impact is performed in this regard. A graphene-based nanofluid is considered. The dynamic model is used to simplify the complicated ordinary differential equations into non-dimensional forms, which are then evaluated analytically. Numerical data and graphs are produced to analyze the consequences of a physical entity with the aid of Maple 17. Moreover, the velocity field is decreased, while the magnitude of the magnetic parameter is increased. A decrease in θ(η) is observed as a result of an increase in ϕ. It is noted that a rise in the magnetic parameter causes a fall in the temperature distribution. It is perceived that −f′′(0) is decreased with an augmentation in βs, and an opposite trend is shown for ϕ. The velocity profile is the growing function of Mgn, βs, and Kve, with the reversed mode shown in case of ϕ. The temperature profile is the declining function of Pr, Ecrt, ϕ, and χ, with a contradictory trend observed for Mgn and βs. The flow regime is displayed against the viscoelastic parameter.
1 Introduction
In recent times, numerous fascinating energy applications have made use of nanotechnology to provide more effective and eco-friendly products and services. Moreover, one crucial aspect that is necessary to bring down the cost of maintenance or installation is the effective heat transport distribution across a power network. The optimal transmission of thermal qualities, such as density, specific heat, viscosity, and thermal conductivity, is essential for the optimum thermal efficiency. In this context, we consider the graphene nanoparticles to improve the thermal characteristics of the host fluid (CMC−water). In order to increase the rate of heat exchange, the flow patterns of nanofluids across thermal energy technologies are crucial. Several nanofluids have very engrossing applications in several fields, such as electronics cooling, automotive engine cooling, heat exchangers, boiling heat transport, solar collectors, medicine, and nuclear system cooling [1]. For the first time, [2] introduced the idea of nanofluids and empirically supported his concept. Gamachu and Ibrahim [3] investigated the mixed convection hybrid viscoelastic nanofluid. The heat exchange of the viscoelastic nanofluid past the stretched surface with many impacts was studied by [4]. In [5], a corrugated channel was considered to study the heat transport of the graphene nanofluid. [6] examined the influence of viscous dissipation on the viscoelastic nanofluid due to a circular cylinder. Numerical examination of the graphene nanofluid because of the stretchable wall was conducted by [7]. [8] directed the enhanced thermal progress of the graphene hybrid nanofluid past a stretched sheet. The impact of zero nanoparticle flux and hall current regarding the movement of the nanofluid above a stretched wall was discussed by [9]. Several other researchers studied the graphene nanofluid in [10–15]. Recently, [16] examined the MHD nanofluid past a convectively heated Riga plate placed horizontally, embedded in the porous (Darcy−Forchheimer) medium. The EMHD flow of a heterogeneous micropolar mixture with different concentrations of water, ethylene glycol, and copper oxide nanoparticles was discussed by [17]. Due to the distributions of the polymer/CNT structure nanocomposite material, morphological nanolayers have an influence on the movement of hybrid nanofluids which was studied by [18]. [19] analyzed the tetragonal nanoparticles with a variety of density and conductivity characteristics flowing in 3D using non-linear Boussinesq and Rosseland estimations. Recent research investigates how the presence of nanoparticles can significantly improve heat exchange in a variety of physical geometries [20–22]. [23] examined the analytical answers for a thermal conductor force peristaltic flow to temperature-dependent nanofluid viscosity. Utilizing two distinct methods for nanofluid analysis, the silver−water nanofluid electro-osmotic movement that is controlled by peristalsis was investigated by [24]. [25] studied the electro-osmotically assisted peristaltic pressurization of the MoS2 Rabinowitsch nanofluid and produced randomness. The use of novel nanofluids throughout clinical isolates to fight Staphylococcus aureus was investigated by [26]. Many researchers talked about boundary layer problems in various media [27–29].
The investigation of the convective boundary layer flows across a stretched surface has a broad range of uses in the polymer production sector. For example, it is employed in manufacturing fibers, polymeric extruder, and fiber glass, sheet manufacturing, condensing of aqueous films, food production, growth of crystals, and fabrication of artificial films [4]. The idea of a boundary layer flow above a stretching sheet was promoted by [30]. [31] examined the velocity slip impact on the MHD nanofluid because of the stretched sheet. The study of the magnetite nanofluid provoked by a stretching wall was observed by [32]. [33] introduced the system disorder inside the nanofluid past a stretchable wall. The MHD nanofluid with two different nanoparticles due to a heated stretched wall was analyzed by [34]. [35] revealed the linearly stretched sheet-induced double-diffusive time-dependent magnetohydrodynamic flow of the nanofluid involving convection boundary constraints. Optimizing entropy production with an unstable stagnating Casson nanofluid flow having dual chemical changes across a stretched surface was discussed by [36]. The investigation of the nanofluid with many effects above a stretching sheet was presented in [37–39].
From the potential applications mentioned previously, we analyzed the MHD graphene−CMC−water nanofluid past a stretchable wall with Joule heating and velocity slip impact. The closed-form solutions were derived analytically. To understand the behavior of various physical parameters on the fluid temperature, Nusselt number, velocity, and skin friction, the numeric tables and graphs were portrayed.
2 Problem statement
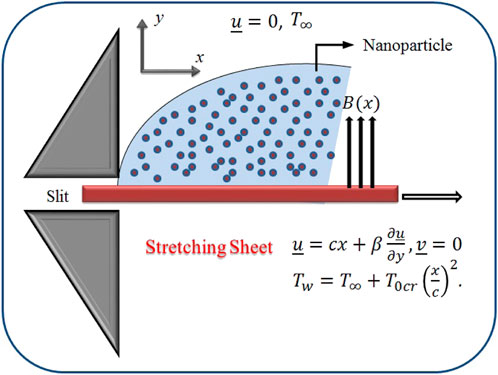
In framing the model, the flow of an incompressible and steady MHD viscoelastic nanofluid (Walter’s liquid B type) across a stretchable sheet in two dimensions is investigated. The graphene and carboxymethyl cellulose (CMC) solution−water are taken as nanoparticles and host fluid, respectively. The fluid is made up of the region y > 0, where the x-axis runs alongside the stretched surface in a flow pattern and the y-axis runs perpendicular to the flow. With a velocity of
The problem’s appropriate boundary criteria are as follows [40]:
where c is the stretching rate, β is the slip factor, νgnf is the kinematic viscosity, k0in is the initial relaxation time distribution function, ρgnf is the density, B(x) is the magnetic parameter,
In Eq. 4, ρfc is the density,
Applying Eqs 5, 2 and Eq. 3 become as:
Here, the slip parameter is βs = β(c/ν)1/2, τ1 = (1 − ϕ)2.5,
Using Eq. 7, we determine the answer to Eq. 6, as shown as follows:
Applying Eq. 6 and Eq. 9 together, we gain
where
where γ1, γ2, and ϒ are the constants.
3 Heat transfer analysis
This section describes the heat exchange investigation under the influence of Joule heating and thermal radiation phenomenon. The following is the elementary equation [42]:
where
Putting Eq. 19 into Eq. 18, we acquire the following:
and the boundary restrictions are as follows:
Here, T is the temperature field, c is the characteristic length, T0cr is the constant reference temperature, αgnf is the thermal diffusivity,
where
Here, χ is the radiation entity, Ecrt is the Eckert number, and Pr is the Prandtl number. The modified boundary constraints are as follows:
Consequently, it is simple to obtain by entering Eq. 9 into Eq. 24, expressed as
To convert Eq. 26 into Kummer’s ordinary differential equation, a latest expression is established:
As a consequence, Eq. 26 is converted into Kummer’s ordinary differential equation, which is as follows:
where κ = (1 − κ1) and
With respect to Kummer’s functions [43], the closed-form solution of Eq. 28 accompanying Eq. 29 is:
where
Here, M is the confluent hypergeometric function. The solution of the energy equation is as follows:
where
where
4 Skin friction and the local Nusselt number
The expression for the local skin friction is as follows:
where
The local Nusselt number is defined as follows:
It is obtained as follows in the present study:
5 Results and discussion
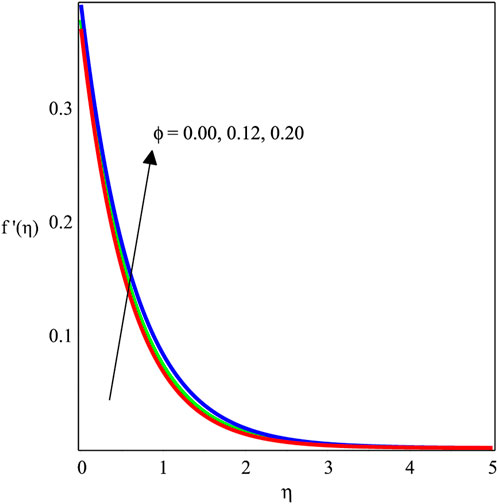
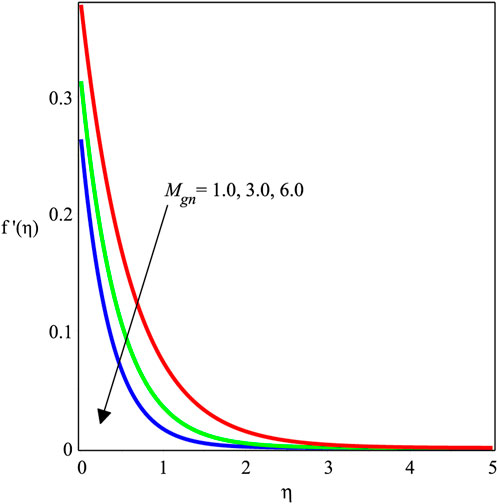
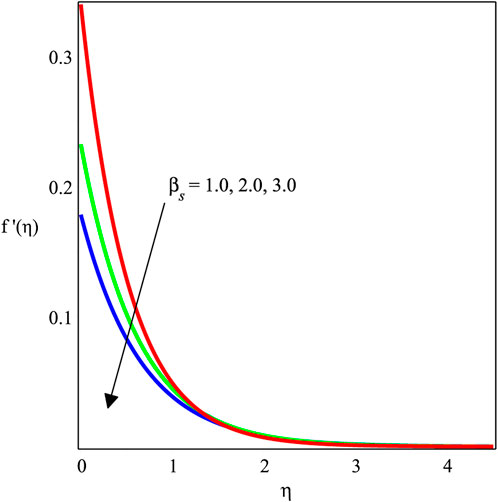
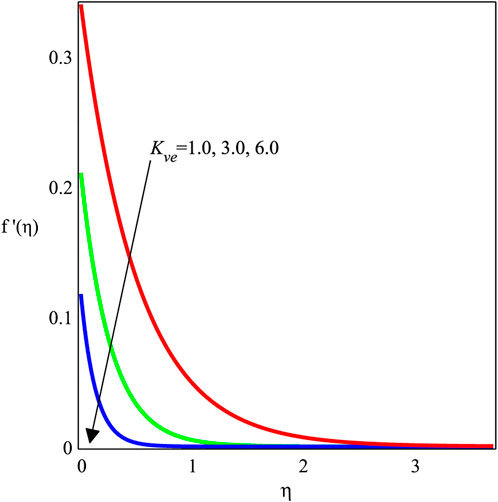
We have analyzed the fluid flow and energy transport of the MHD viscoelastic nanofluid past a stretching surface with the effects of velocity slip and thermal radiation entity. The influence of several emerging parameters such as ϕ, Mgn, βs, Kve, Ecrt, Pr, and χ on f′(η), θ(η), −f′′(0), and −θ′(0) is shown. In this connection, we have drawn the graphs and the corresponding numerical tables. The physical perspective of the considered model is depicted in Figure 1. Figures 2–5 are created to discuss the influence of these parameters on the velocity field. In Figure 2, the variation in ϕ above the velocity field is illustrated. It is noted that the magnitude of the velocity distribution is enhanced by an increment in the values of ϕ. Figure 3 depicts the variation in Mgn with βs, Kve, and ϕ. The velocity field diminishes as the Mgn increases. Physically, the Lorentz forces are dominant, which causes the velocity field to de-escalate while increasing the magnitude of Mgn. The influence of βs on f′(η) is portrayed in Figure 4. It is perceived that increasing the amount of βs causes the velocity distribution to drop rapidly. Actually, when the velocity slip occurs, the stretching surface velocity is faster than the fluid velocity, resulting in a decrease in the velocity of the nanofluid. The influence of Kve on the velocity field is delineated in Figure 5. Physically, viscoelasticity creates a tensile force that opposes fluid movement. Due to viscous and elastic factors, escalating values of Kve cause a reduction in the flow velocity.
Figures 6–11 investigate the effects of ϕ, Mgn, βs, Ecrt, Pr, and χ on θ(η). Figure 6 shows the temperature field against the nanoparticle ratio. It implies that the temperature field is enhanced with an enlargement in the magnitude of ϕ. Physically, the thermal conductivity of the fluid is enhanced by adding nanoparticles. Consequently, the temperature decreases. The behavior of the temperature field against Mgn is studied in Figure 7. It is revealed that a rise in Mgn causes the fall in temperature distribution. It is due to friction between the fluid and nanoparticles by Lorentz forces that leads to an increase in the temperature field. The development of Pr on θ(η) is shown in Figure 8. The temperature field is observed to rise, increasing the magnitude of Pr. The Prandtl number, in terms of physics, is the fraction of momentum diffusivity to thermal diffusivity. Thermal diffusivity is enhanced by adding nanoparticles, which causes a decrement in temperature distribution. Figure 9 illustrates the impact of Eert over θ(η). It is discovered that increasing Eert increases the magnitude of θ(η). The influence of the thermal radiation parameter on θ(η) is depicted in Figure 10. It demonstrates that the magnitude of θ(η) de-escalates, while the magnitude of χ increases. Figure 11 shows how decreasing the amount of χ increases the value of θ(η).
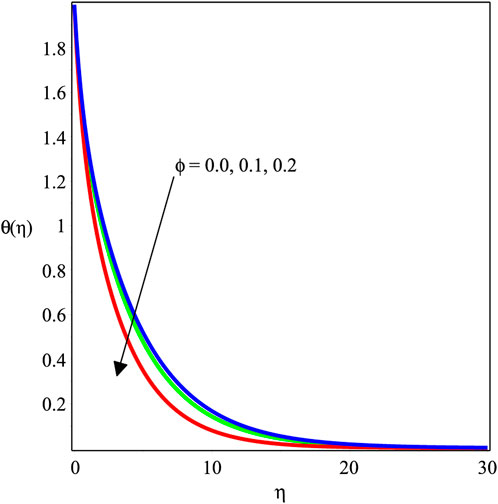
FIGURE 6. Impact of ϕ with Mgn = 1, βs = 1, Kve = 1, Ecrt = 0.3, Pr = 6.2, and χ = 0.3 on the temperature profile.
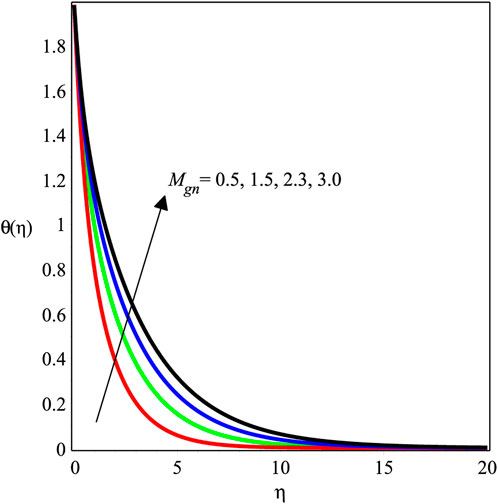
FIGURE 7. Impact of Mgn with ϕ = 0.1, βs = 1, Kve = 1, Ecrt = 0.1, Pr = 6.2, and χ = 0.3 on the temperature profile.
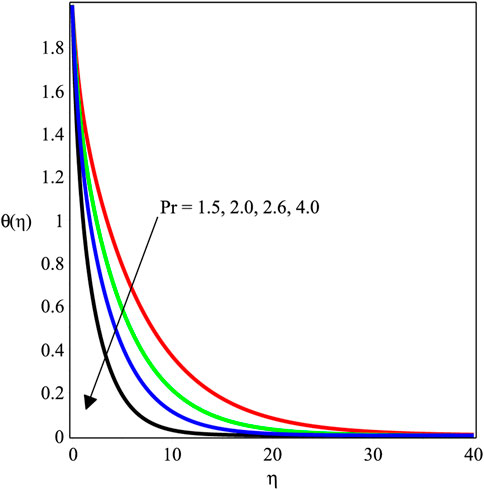
FIGURE 8. Impact of Pr with ϕ = 0.1, βs = 1, Kve = 1, Ecrt = 0.1, Mgn = 0.5, and χ = 1 on the temperature profile.
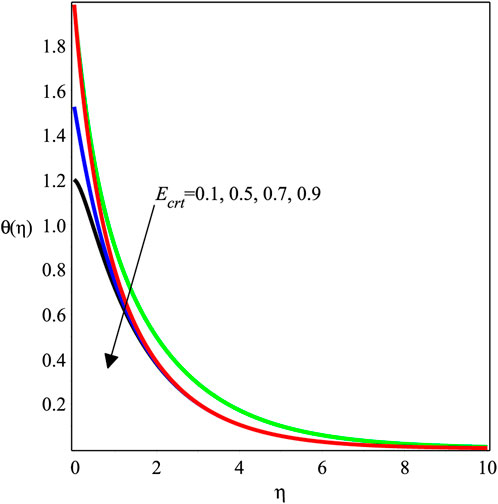
FIGURE 9. Impact of Ecrt with ϕ = 0.1, βs = 1, Kve = 1, Pr = 6.2, Mgn = 0.5, and χ = 1 on the temperature profile.
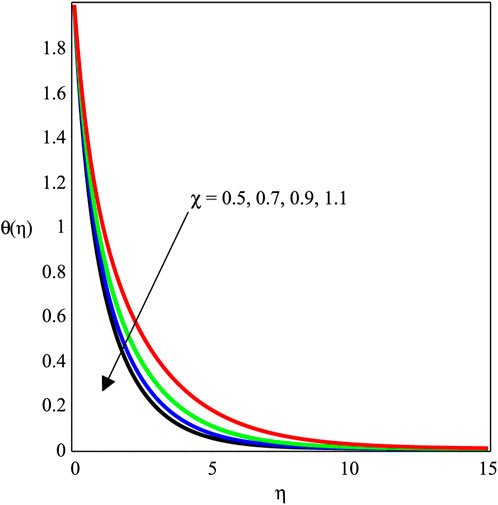
FIGURE 10. Impact of χ with ϕ = 0.1, βs = 1, Kve = 1, Pr = 6.2, Mgn = 0.5, and Ecrt = 0.1 on the temperature profile.
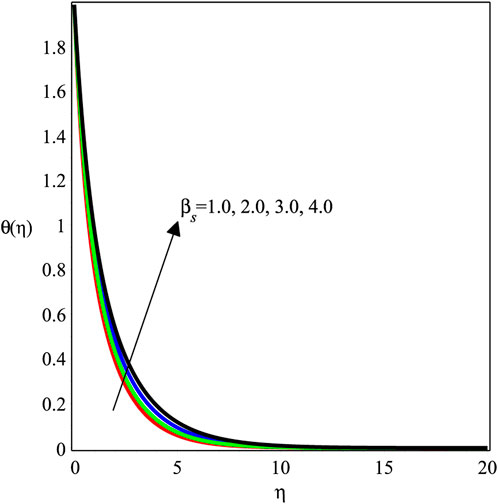
FIGURE 11. Impact of βs with ϕ = 0.1, χ = 1, Kve = 1, Pr = 6.2, Mgn = 0.5, and Ecrt = 0.1 on the temperature profile.
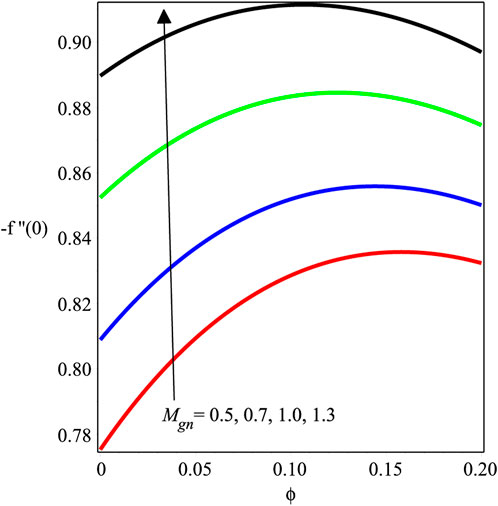
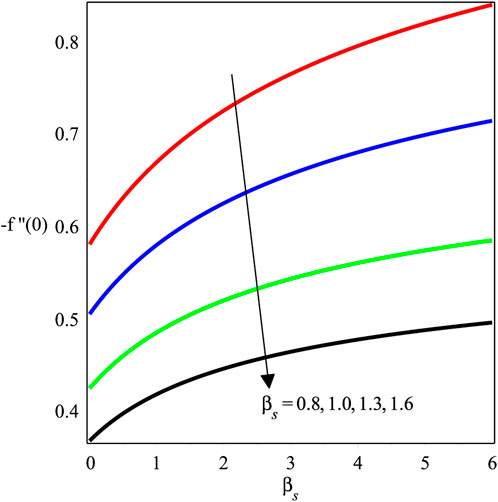
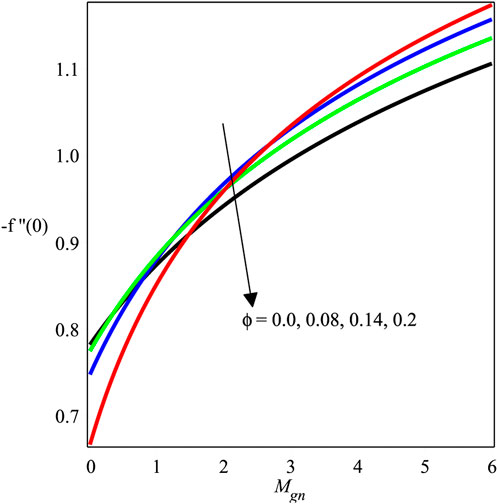
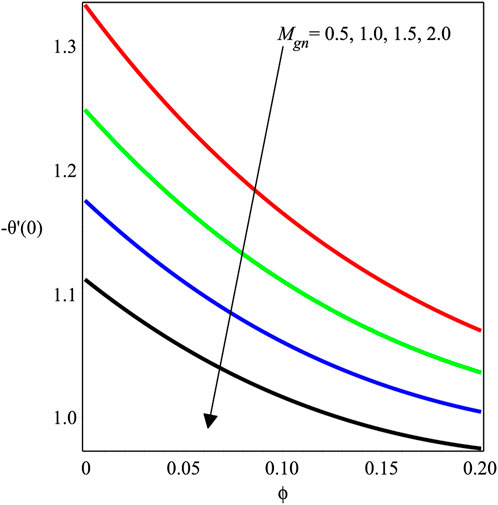
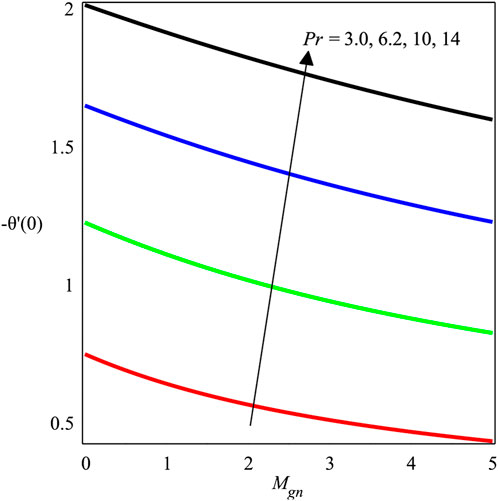
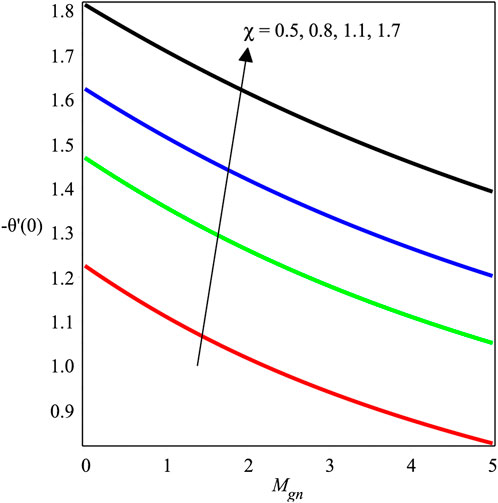
Figures 12–14 investigate the change in Mgn, βs, and ϕ over −f′′(0). The local skin friction factor is decreased with the growing magnitude of Mgn as shown in Figure 12. Physically, magnetic fields and electric forces produce Lorentz forces that create resistance forces because of which the skin friction on the wall increases. Figure 13 and Figure 14 show a plot of −f′′(0) versus βs and ϕ, respectively. It is perceived that the local skin friction field is decreased with an augmentation in βs, and an opposite trend is shown for ϕ. Figures 15–18 scrutinize the variation in Mgn, Ecrt, Pr, and χ over −θ′(0). The impact of Mgn on −θ′(0) against ϕ is presented in Figure 15, which shows a decrement in the amount of −θ′(0). Figure 16 depicts the effects of the Eckert number on the dimensionless temperature variation, −θ′(0). It can be seen that when the Eckert number increases, −θ′(0) also increases. The Eckert number Ecrt is expressed as the ratio of advective transmission to energy-dissipated capability in physical terms. Furthermore, a rise in the rate of heat transport suggests that the energy loss is accompanied by a fall in the Eckert number. Figure 17 and Figure 18 express the influence of Pr and χ on the heat exchange ratio. It is discovered that θ′(0) is augmented while the strengths of Pr and χ are increased.
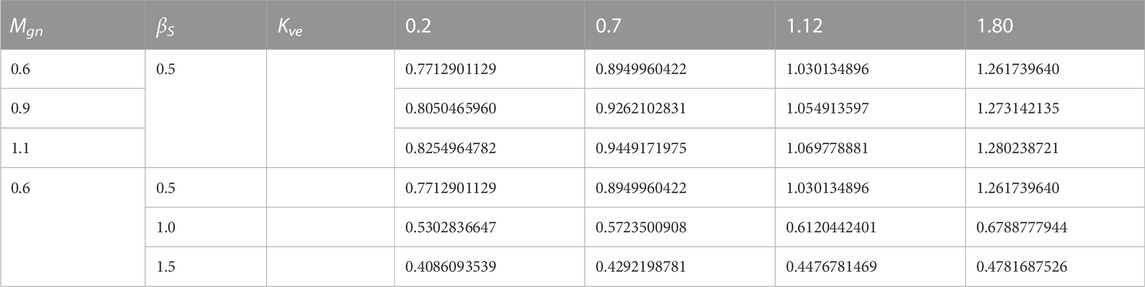
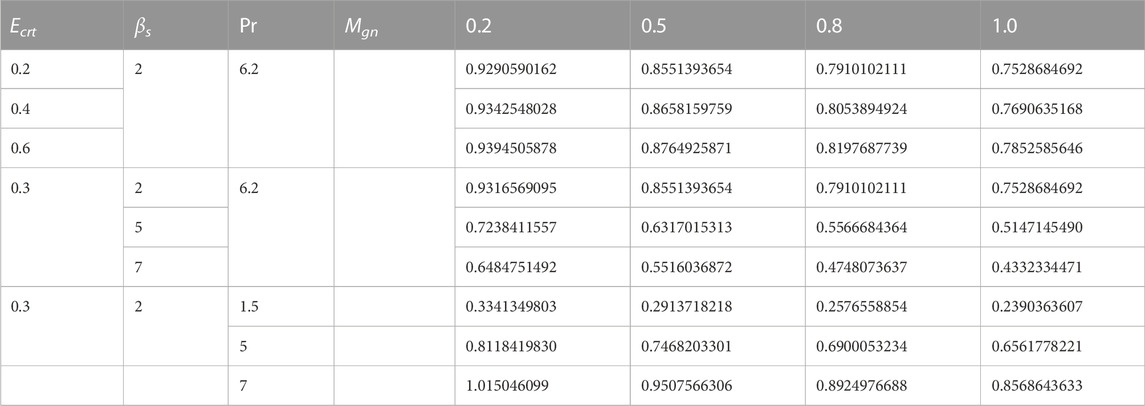
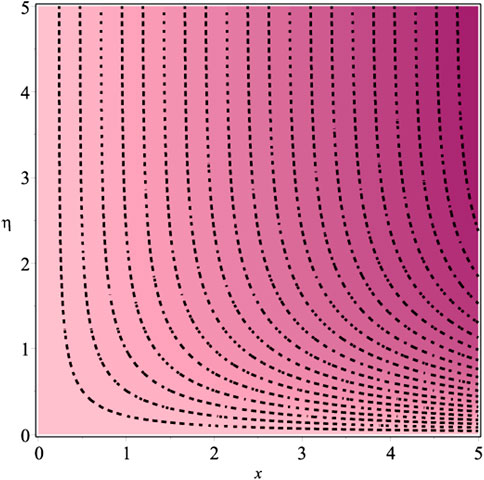
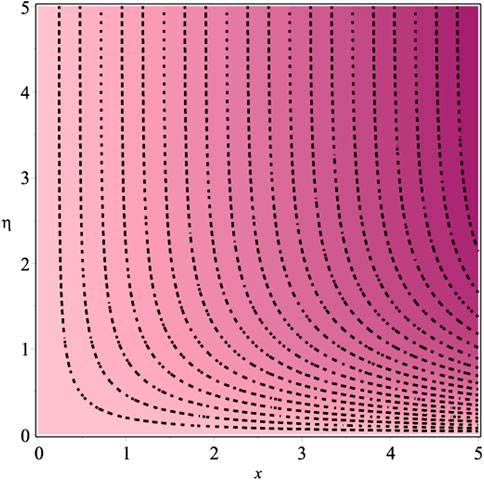
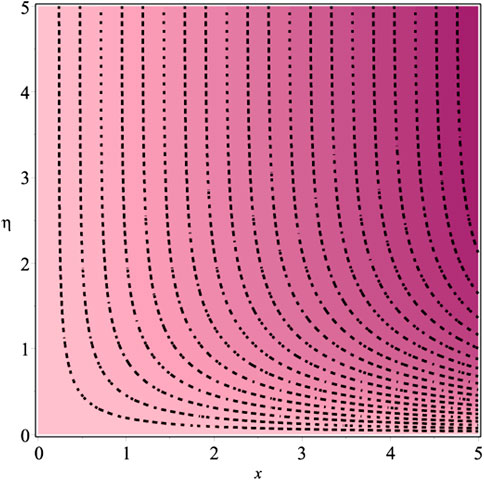
The thermophysical characteristics of graphene and CMC−water are displayed in Table 1. Tables 2, 3 show the numerical values of local skin friction coefficient and local Nusselt number respectively. Figures 19–24 indicate the streamline characteristics. It has been shown that the boundary-layer thickness dramatically shrinks when Kve is increased.
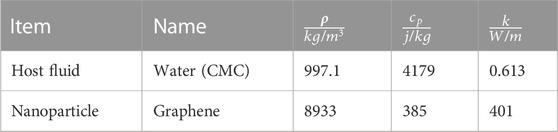
TABLE 1. Host fluid (carboxymethyl cellulose−water) and nanoparticle (graphene) thermophysical characteristics [5].
6 Conclusion
In this study, the analysis of the MHD graphene−CMC−water nanofluid past a stretchable wall with Joule heating and velocity slip impact was performed. We arrived at the following conclusions:
• The velocity profile is the growing function of Mgn, βs, and Kve, with the reversed mode shown in case of ϕ.
• The temperature profile is the declining function of Pr, Ecrt, ϕ, and χ, while a contradictory trend is observed for Mgn and βs.
• Increasing the magnitude of Mgn increases local skin friction, while βs and ϕ reveal an opposing trend.
• An increase in Ecrt, Pr, and χ is shown to be accountable for an increase in the fraction of heat exchange. As Mgn increases, the heat transmission rate decreases.
• An enhancement in Kve decreases the boundary-layer thickness which is examined in the flow regime.
Data availability statement
The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding authors.
Author contributions
IR initiated the fluid model and methodology. TZ and IR produced numerical data and graphs using software. SI completed the write-up. MA and SE assisted in numerical data and write up.
Acknowledgments
The authors are grateful to the University of Management and Technology of Lahore, and HEC Pakistan for facilitating this research under research project No 15911 (NRPU).
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
1. Arshad A, Jabbal M, Yan Y, Reay D. A review on graphene based nanofluids: Preparation, characterization and applications. J Mol Liquids (2019) 279:444–84. doi:10.1016/j.molliq.2019.01.153
2. Choi SU, Eastman JA. Enhancing thermal conductivity of fluids with nanoparticles. Argonne, IL (United States): Argonne National Lab. (1995).
3. Gamachu D, Ibrahim W. Mixed convection flow of viscoelastic Ag-Al2O3/water hybrid nanofluid past a rotating disk. Phys Scr (2021) 96(12):125205. doi:10.1088/1402-4896/ac1a89
4. Ishak N, Hussanan A, Mohamed MKA, Rosli N, Salleh MZ. Heat and mass transfer flow of a viscoelastic nanofluid over a stretching/shrinking sheet with slip condition. In: AIP conference proceedings, 2059. Kuantan, Malaysia: AIP Publishing LLC (2019). p. 020011.
5. Keklikcioglu O, Dagdevir T, Ozceyhan V. Numerical investigation on heat transfer enhancement of graphene oxide-water nanofluids in a corrugated channel. Int J Nat Eng Sci (2016) 10(2):10–4.
6. Mahat R, Rawi NA, Kasim ARM, Shafie S. Mixed convection flow of viscoelastic nanofluid past a horizontal circular cylinder with viscous dissipation. Sains Malays (2018) 47(7):1617–23. doi:10.17576/jsm-2018-4707-33
7. Sharma R, Hussain S, Raju C, Seth G, Chamkha AJ. Study of graphene maxwell nanofluid flow past a linearly stretched sheet: A numerical and statistical approach. Chin J Phys (2020) 68:671–83. doi:10.1016/j.cjph.2020.10.013
8. Ahmad F, Abdal S, Ayed H, Hussain S, Salim S, Almatroud AO. The improved thermal efficiency of Maxwell hybrid nanofluid comprising of graphene oxide plus silver/kerosene oil over stretching sheet. Case Stud Therm Eng (2021) 27:101257. doi:10.1016/j.csite.2021.101257
9. Das K, Giri SS, Kundu PK. Influence of Hall current effect on hybrid nanofluid flow over a slender stretching sheet with zero nanoparticle flux. Heat Transfer (2021) 50(7):7232–50. doi:10.1002/htj.22226
10. Sandeep N. Effect of aligned magnetic field on liquid thin film flow of magnetic-nanofluids embedded with graphene nanoparticles. Adv Powder Tech (2017) 28(3):865–75. doi:10.1016/j.apt.2016.12.012
11. Revathi G, Sajja VS, Raju C, Babu MJ. Numerical simulation for Arrhenius activation energy on the nanofluid dissipative flow by a curved stretching sheet. Eur Phys J Spec Top (2021) 230(5):1283–92. doi:10.1140/epjs/s11734-021-00048-6
12. Aly EH. Dual exact solutions of graphene–water nanofluid flow over stretching/shrinking sheet with suction/injection and heat source/sink: Critical values and regions with stability. Powder Tech (2019) 342:528–44. doi:10.1016/j.powtec.2018.09.093
13. Bhattacharyya A, Sharma R, Mishra M, Chamkha AJ, Mamatha E. Numerical and statistical analysis of dissipative and heat absorbing graphene maxwell nanofluid flow over a stretching sheet. j nanofluids (2021) 10(4):600–7. doi:10.1166/jon.2021.1808
14. Bhattacharyya A, Sharma R, Hussain S, Chamkha A, Mamatha E. A numerical and statistical approach to capture the flow characteristics of Maxwell hybrid nanofluid containing copper and graphene nanoparticles. Chin J Phys (2022) 77:1278–90. doi:10.1016/j.cjph.2021.09.015
15. Devi SSU, Devi SA. Numerical investigation of three-dimensional hybrid Cu–Al2O3/water nanofluid flow over a stretching sheet with effecting Lorentz force subject to Newtonian heating. Can J Phys (2016) 94(5):490–6. doi:10.1139/cjp-2015-0799
16. Rasool G, Shah NA, El-Zahar ER, Wakif A. Numerical investigation of EMHD nanofluid flows over a convectively heated riga pattern positioned horizontally in a Darcy-forchheimer porous medium: Application of passive control strategy and generalized transfer laws. Waves in Random and Complex Media (2022) 1–20. doi:10.1080/17455030.2022.2074571
17. Shah NA, Wakif A, El-Zahar ER, Ahmad S, Yook SJ. Numerical simulation of a thermally enhanced EMHD flow of a heterogeneous micropolar mixture comprising (60%)-ethylene glycol (EG), (40%)-water (W), and copper oxide nanomaterials (CuO). Case Stud Therm Eng (2022) 35:102046. doi:10.1016/j.csite.2022.102046
18. Qureshi MZA, Faisal M, Raza Q, Ali B, Botmart T, Shah NA. Morphological nanolayer impact on hybrid nanofluids flow due to dispersion of polymer/CNT matrix nanocomposite material. AIMS Math (2023) 8(1):633–56. doi:10.3934/math.2023030
19. Sajjan K, Shah NA, Ahammad NA, Raju C, Kumar MD, Weera W. Nonlinear Boussinesq and Rosseland approximations on 3D flow in an interruption of Ternary nanoparticles with various shapes of densities and conductivity properties. AIMS Math (2022) 7(10):18416–49. doi:10.3934/math.20221014
20. Rauf A, Shah NA, Mushtaq A, Botmart T. Heat transport and magnetohydrodynamic hybrid micropolar ferrofluid flow over a non-linearly stretching sheet. AIMS Math (2023) 8(1):164–93. doi:10.3934/math.2023008
21. Rehman SU, Fatima N, Ali B, Imran M, Ali L, Shah NA, et al. The Casson dusty nanofluid: Significance of Darcy–forchheimer law, magnetic field, and non-Fourier heat flux model subject to stretch surface. Mathematics (2022) 10(16):2877. doi:10.3390/math10162877
22. Ramesh G, Madhukesh J, Shah NA, Yook SJ. Flow of hybrid CNTs past a rotating sphere subjected to thermal radiation and thermophoretic particle deposition. Alexandria Eng J (2022) 969–979. doi:10.1016/j.aej.2022.09.026
23. Akbar NS, Maraj E, Noor N, Habib MB. Exact solutions of an unsteady thermal conductive pressure driven peristaltic transport with temperature-dependent nanofluid viscosity. Case Stud Therm Eng (2022) 35:102124. doi:10.1016/j.csite.2022.102124
24. Akram J, Akbar NS, Tripathi D. Analysis of electroosmotic flow of silver-water nanofluid regulated by peristalsis using two different approaches for nanofluid. J Comput Sci (2022) 62:101696. doi:10.1016/j.jocs.2022.101696
25. Akram J, Akbar NS, Tripathi D. Entropy generation in electroosmotically aided peristaltic pumping of MoS2 Rabinowitsch nanofluid. Fluid Dyn Res (2022) 54(1):015507. doi:10.1088/1873-7005/ac4e7b
26. Habib MB, Akbar NS. New trends of nanofluids to combat Staphylococcus aureus in clinical isolates. J Therm Anal Calorim (2021) 143(3):1893–9. doi:10.1007/s10973-020-09502-4
27. Akram J, Akbar NS, Tripathi D. Thermal analysis on MHD flow of ethylene glycol-based BNNTs nanofluids via peristaltically induced electroosmotic pumping in a curved microchannel. Arab J Sci Eng (2022) 47(6):7487–503. doi:10.1007/s13369-021-06173-7
28. Akram J, Akbar NS, Tripathi D. Electroosmosis augmented MHD peristaltic transport of SWCNTs suspension in aqueous media. J Therm Anal Calorim (2022) 147(3):2509–26. doi:10.1007/s10973-021-10562-3
29. Akram J, Akbar NS, Alansari M, Tripathi D. Electroosmotically modulated peristaltic propulsion of TiO2/10W40 nanofluid in curved microchannel. Int Commun Heat Mass Transfer (2022) 136:106208. doi:10.1016/j.icheatmasstransfer.2022.106208
30. Crane LJ. Flow past a stretching plate. J Appl Math Phys (1970) 21(4):645–7. doi:10.1007/bf01587695
31. Rashid I, Sagheer M, Hussain S. Magnetohdrodnamics nanofluid flow of shaped nanoparticles over a porous stretching wall and slip effect. Numer Methods Partial Differ Equ (2021) 1–24. doi:10.1002/num.22780
32. Gowda RP, Kumar RN, Prasannakumara B, Nagaraja B, Gireesha B. Exploring magnetic dipole contribution on ferromagnetic nanofluid flow over a stretching sheet: An application of Stefan blowing. J Mol Liquids (2021) 335:116215. doi:10.1016/j.molliq.2021.116215
33. Alazwari MA, Abu-Hamdeh NH, Goodarzi M. Entropy optimization of first-grade viscoelastic nanofluid flow over a stretching sheet by using classical Keller-box scheme. Mathematics (2021) 9(20):2563. doi:10.3390/math9202563
34. Nandi S, Kumbhakar B, Sarkar S. MHD stagnation point flow of Fe3O4/Cu/Ag-CH3OH nanofluid along a convectively heated stretching sheet with partial slip and activation energy: Numerical and statistical approach. Int Commun Heat Mass Transfer (2022) 130:105791. doi:10.1016/j.icheatmasstransfer.2021.105791
35. Patil AB, Patil VS, Humane PP, Shamshuddin M, Jadhav MA. Double diffusive time-dependent MHD Prandtl nanofluid flow due to linear stretching sheet with convective boundary conditions. Int J Model Simulation (2022) 1–15. doi:10.1080/02286203.2022.2033499
36. Oyelakin I, Mthethwa HS, Kameswaran PK, Shaw S, Sibanda P. Entropy generation optimisation for unsteady stagnation Casson nanofluid flow over a stretching sheet with binary chemical reaction and Arrhenius activation energy using the bivariate spectral quasi-linearisation method. Int J Ambient Energ (2022) 43:6489–501. doi:10.1080/01430750.2021.2023038
37. Hussanan A, Khan I, Gorji MR, Khan WA. CNTS-water–based nanofluid over a stretching sheet. BioNanoScience (2019) 9(1):21–9. doi:10.1007/s12668-018-0592-6
38. Khan SA, Nie Y, Ali B. Multiple slip effects on magnetohydrodynamic axisymmetric buoyant nanofluid flow above a stretching sheet with radiation and chemical reaction. Symmetry (2019) 11(9):1171. doi:10.3390/sym11091171
39. Hosseinzadeh K, Afsharpanah F, Zamani S, Gholinia M, Ganji D. A numerical investigation on ethylene glycol-titanium dioxide nanofluid convective flow over a stretching sheet in presence of heat generation/absorption. Case Stud Therm Eng (2018) 12:228–36. doi:10.1016/j.csite.2018.04.008
40. Haq RU, Rashid I, Khan Z. Effects of aligned magnetic field and CNTs in two different base fluids over a moving slip surface. J Mol Liquids (2017) 243:682–8. doi:10.1016/j.molliq.2017.08.084
41. Rashid I, Sagheer M, Hussain S. Entropy formation analysis of MHD boundary layer flow of nanofluid over a porous shrinking wall. Physica A: Stat Mech its Appl (2019) 536:122608. doi:10.1016/j.physa.2019.122608
42. Rashid I, Haq RU, Al-Mdallal QM. Aligned magnetic field effects on water based metallic nanoparticles over a stretching sheet with PST and thermal radiation effects. Physica E: Low-dimensional Syst Nanostructures (2017) 89:33–42. doi:10.1016/j.physe.2017.01.029
Keywords: graphene nanoparticles, slip effect, thermal radiations, magnetic field, closed-form solution
Citation: Rashid I, Zubair T, Asjad MI, Irshad S and Eldin SM (2023) The MHD graphene−CMC−water nanofluid past a stretchable wall with Joule heating and velocity slip impact: Coolant application. Front. Phys. 10:1065982. doi: 10.3389/fphy.2022.1065982
Received: 10 October 2022; Accepted: 25 November 2022;
Published: 30 January 2023.
Edited by:
Andrea Scagliarini, Institute for Calculation Applications Mauro Picone (CNR), ItalyReviewed by:
Nehad Ali Shah, Sejong University, South KoreaNoreen Sher Akbar, National University of Sciences and Technology (NUST), Pakistan
Copyright © 2023 Rashid, Zubair, Asjad, Irshad and Eldin. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: I. Rashid, bWVoYXIuaXJmYW4wMTRAZ21haWwuY29t; M. I. Asjad, aW1yYW4uYXNqYWRAdW10LmVkdS5waw==
 I. Rashid
I. Rashid T. Zubair
T. Zubair M. I. Asjad3*
M. I. Asjad3*