- GISC Departamento de Física de Materiales, Universidad Complutense, Madrid, Spain
We study the electronic states in topological nanowires of narrow-gap semiconductors, such as PbTe or SnTe, with rough surfaces, using a continuous two-band model. We calculate the subband structure and identify topological conducting states located at the surface of the nanowire. In addition, a novel approach to study a nanowire with rough surface demonstrates that the topological surface states are mostly confined in the widest areas of the nanowire. This effect leads to a flattening of the subbands, thus raising the effective mass of carriers. Finally, we analyze the thermoelectric properties of the topological nanowires. The reduction of the radius causes a noticeable enhancement of the thermoelectric efficiency due surface phonon scattering, as expected. However, we also observe that the appearance of topological surface states can play a detrimental role, reducing the thermoelectric efficiency. We conclude that, in addition to nanostructuring, the modulation of the radius of the nanowires, which partially suppress the conduction of the surface states, may be a potential strategy to improve the thermoelectric response of narrow-gap semiconductor nanowires.
1 Introduction
Thermoelectric materials offer the possibility to transform waste heat from industry and home hardware into electricity, thus making devices less energy-consuming. In the context of thermoelectricity, the efficiency of materials and devices is assessed by the so-called dimensionless figure of merit, defined as ZT = σS2T/κ [1, 2]. Here S stands for the Seebeck coefficient (thermopower), and σ and κ are the electrical and thermal conductivities at absolute temperature T, respectively. In general, electrons (el) and phonons (ph) may contribute to heat transport and consequently the thermal conductivity splits as κ = κel+κph. Approaches to designing materials for efficient heat-to-electricity conversion need to put forward strategies to increase S and σ simultaneously while keeping κ as lower as possible. However, the unfavorable interdependence of S, σ and κ in bulk materials hinders progress to achieve efficient thermoelectric materials and devices for real applications. For instance, the classical Wiedemann-Franz law [3] establishes an universal upper limit to the ratio σT/κel in conventional bulk metals.
After the pioneering work by Hicks and Dresselhaus at the beginning of the nineties on the thermoelectric efficiency of quantum-well structures [4] and one-dimensional conductors [5], nanostructured materials have been envisioned as a promising route to achieve efficient and scalable thermoelectric devices without moving parts. The reason relies on the key observation that, very often, electron mean-free-path is shorter than that of phonons. Therefore, nanostructures display enhanced surface phonon scattering, provided that their size is smaller than the phonon mean-free-path, while electric conductivity is affected to a lesser extent if the electron mean-free-path is smaller than the size. Now, it is well established that nanostructured materials may exhibit thermoelectric efficiency unachievable with their bulk counterparts [6–11].
Although several nanostructures with potential application in thermoelectricity have been proposed, nanowires (NWs) have recently attracted a lot of attention. A number of newly developed techniques facilitate the production of NWs of various materials with different sizes, cross sections, crystal orientations, surface roughness, doping and core-shell structures [12–15]. Precise control and manipulation of the physical and chemical properties of the NWs enables achieving ZT one or two orders of magnitude larger than their bulk counterparts (see Ref. [16] for a recent review). The enhancement of ZT is also observed in other nanostructures, such as quantum wells, superlattices and nanocomposites (see Ref. [17] for a comprehensive review). However, the improvement compared to the efficiency in bulk is usually lower than NWs. For instance, ZT = 2.4 in Bi2Te3–Sb2Te3 superlattices with a periodicity of 6nm, while the highest ZT value for the bulk counterparts is ZT = 1.1 [11].
Several highly efficient thermoelectric semiconductor NWs are based on topological insulators (TIs) such as Bi2Te3 [18–21], Bi2Se3 [22] (Bi1−xSbx)2Te3 [23, 24] and SnSe [25]. TIs are materials that support gapless electron states at the surface whilst the bulk remains an insulator [26–30]. The presence of heavy elements usually makes TIs to behave as high-efficient thermoelectric materials at room temperature [31]. On one hand, electrons in heavy atoms undergo strong relativistic corrections (high spin-orbit interaction and Darwin correction), yielding the band inversion that favours the occurrence of conducting states at the surface. On the other side, relativistic effects lead to narrow gaps (band shrinkage) which are favorable for room-temperature thermoelectricity [32]. In addition, heavy atoms tend to reduce the lattice thermal conductivity of the material. The combination of all these features results in a remarkable enhancement of the thermoelectric efficiency of NWs based on TIs [33].
As already mentioned, the surface plays a crucial role in the thermoelectric response of TI semiconducting NWs. Surface phonon scattering reduces κph (see Ref. [34] and references therein) and the occurrence of conducting states at the boundary that are topologically protected may increase σ. Although these features tend to improve the thermoelectric efficiency of NWs, there are other factors that need to be taken into account as well. For instance, a decrease of the diameter below the decay length of the topological surface states can prevent their appearance and opens a gap. Changes of the geometry can flatten the density of states at the Fermi level, resulting in a marked decrease of the Seebeck coefficient by virtue of Mott’s formula [3, 35]. In particular, surface roughness affects the way electrons are spatially distributed along the NW, and this will have an impact on the electric conductivity and the Seebeck coefficient. While the dependence of the electric conductivity on the surface roughness in NWs based on conventional semiconductors, such as Si and InAs, is relatively well understood [36, 37], the influence of surface roughness on the conduction properties of topologically protected surface channels is still an open question. In this work, we present a thorough study of the vertical electron transport along NWs with rough surfaces based on TIs. To gain insight into how surface roughness alters the topological states of the NWs while keeping the analysis rigorous and straightforward, we use a continuous two-band model with isotropic parameters that has been proven very accurate for bulk TIs such as PbTe and SnTe. However, it will be apparent that the results could be extended to highly anisotropic TIs such as Bi2Se3 and Bi2Te3 by setting the appropriate electron Hamiltonian. As a major result, we observe that topological surface states can reduce the thermoelectric efficiency and conclude roughness is a promising way to improve the thermoelectric response of narrow-gap semiconductor NWs.
2 Spinfull two-band model
Electron states of IV-VI compounds near the band extrema at the
Here α = (αx, αy, αz) and β denote the usual 4 × 4 Dirac matrices, αi = σx ⊗ σi and
We consider a NW oriented along the [001] direction for the sake of concreteness. Due to the axial symmetry of the system, the total angular momentum of the electron is conserved. Hence, in cylindrical coordinates (r, φ, z), the envelope function can be factorized as follows.
with j = ±1/2, ±3/2, … and
where T stands for transpose, the superscripts C and V refers to conduction and valence bands, respectively, and ↑, ↓ indicates the electron spin. It is understood that the four components depend on (r, z) as well. Inserting this ansatz in the Schrödinger equation for the Dirac-like Hamiltonian (1) we get
The envelope function is continuous at the surface of the NW. Assuming that the embedding medium is the vacuum (EG → −∞) for simplicity, boundary conditions then read
where R(z) is the z-dependent radius of the NW.
3 Uniform nanowire
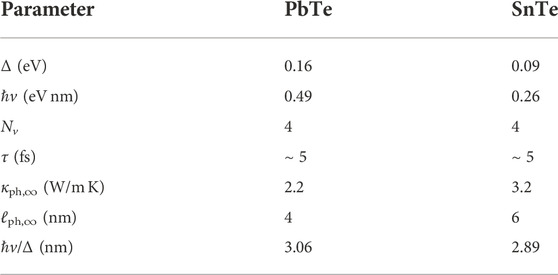
In this section, we consider a uniform NW with radius R oriented along the [001] direction and gap EG = 2Δ > 0, as depicted in Figure 1A. In addition to the total angular momentum, the z component of the wavevector, kz, is conserved as well. Therefore, ϕj(r, z) ∼ exp(ikzz) in Eq. 2. The resulting equation can be solved analytically, and the dispersion relation is found to be
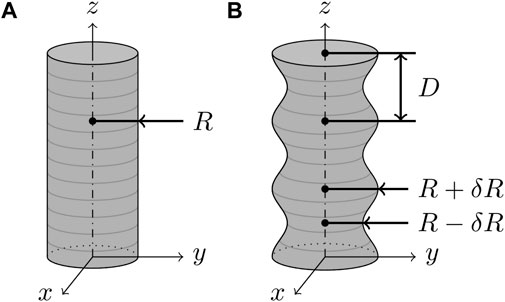
FIGURE 1. Sketch of (A) uniform and (B) rough nanowires. δR measures the surface roughness and D is the correlation length.
where En0 is the energy of the n-th subband in the conduction band at kz = 0. Dispersion Eq. 5 is the same for both bulk and surface states. However, the energy of a surface state at kz = 0 lies within the bulk gap. In other words, subbands of surface states satisfy the condition En0 < Δ. The corresponding subband edge is obtained as
being Iμ(y) the modified Bessel function of the first kind [44]. Real solutions for the energy En0 requires that |j| + 1/2 < RΔ/ℏv, implying that the number of surface subbands is the integer part of the quotient RΔ/ℏv. Remarkably, when RΔ/ℏv ≫ 1, subband edges are approximately equally spaced En0 ≃|j|ℏv/R, resembling the spectrum of the harmonic oscillator with frequency v/R.
Similarly to the previous discussion, bulk states are obtained when En0 > Δ and their energy lies in the bulk bands. In this case, one gets
with
After solving Eqs. 6, 7, subband dispersion is straightforwardly obtained from Eq. 5. As an example, Figure 2 presents the valence and conduction bands of uniform NWs with two different radii. Notice that the dispersion is symmetric with respect to the center of the gap and consists of several well-defined subbands, as mentioned before. On one side, bulk-state subbands (see shadowed area) are identified as those located outside the gap, i.e., En0 > Δ. On the other side, surface-state subbands lie within the energy gap when kz = 0. Most importantly, the variation of the radius affects surface-state subbands to a large extend while the bulk ones are remain almost unchanged. Indeed, after comparing both panels in Figure 2, we can see that the gap between conduction and valence surface-state bands is reduced on increasing the radius and the dispersion resembles the Dirac cones observed in Dirac materials. This is consistent with the flattening of the NM surface that occurs when R → ∞.
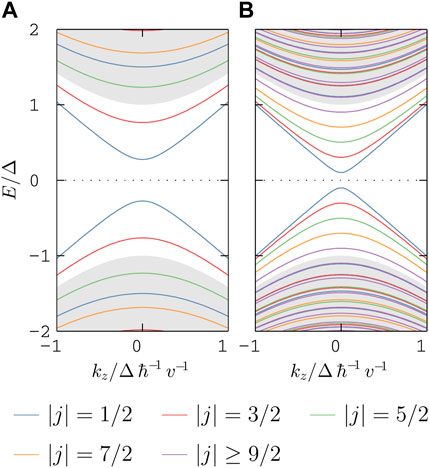
FIGURE 2. Energy spectrum labeled by the quantum number |j| of two uniform nanowires of (A) R = 2.5ℏv/Δ and (B) R = 5.5ℏv/Δ. Bulk subbands are indicated within the shadowed region while surface bands lie within the energy gap of the bulk material.
By calculating the radial probability
FIGURE 3. Radial probability density of a surface state of |j| = 1/2 in two uniform nanowires of (A) R = 2.5ℏv/Δ and (B) R = 5.5ℏv/Δ. The estimated radial localization length is indicated in both panels as r*/ℏvΔ−1.
We come to the conclusion that the decay length depends only on material parameters if R ≫ ℏv/Δ. Using the model parameters for PbTe and SnTe given in Table 1, the decay length is about r* ≃ 1.5nm in both semiconductors.
4 Rough nanowire
We now turn our attention to rough NWs. We model the ripples of the rough surface by setting the radius to be dependent on the position along the NW axis. To be specific, we take R(z) = R+δR cos(2πz/D), where δR and D are the amplitude and the characteristic length of the ripples, respectively. Figure 1B shows a schematic view of the rough NW. Due to the breaking of the translational symmetry along the [001] direction, the z component of the wave vector is no longer a good quantum number. To tackle the problem numerically, we expand ϕj (r, z) in Eq. 2a as follows
and solve the resulting equations for the four components of the unknown vectors aj (n, m). The integer numbers M and N are chosen to ensure numerical accuracy. Notice that the envelope function χ(r, φ, z) is then expressed as a linear combination of plane waves along the [001] direction with momenta kz+2πm/D.
Figure 4 shows the obtained subband structure when δR = ℏv/Δ and D = 5ℏv/Δ for two different values of the radius, namely R = 2.5ℏv/Δ and R = 5.5ℏv/Δ. For comparison, the subband structure for the uniform NW with the same radii is also shown. While bulk dispersion (not shown in the figure) are essentially the same in both uniform and rough NWs, the dispersion of surface states is noticeably modified, as seen in Figure 4. First, we observe that gaps open at wavenumber ± π/D (higher order gaps are not shown in the plot), as expected from the periodicity induced by the ripples. Second, subbands are flatter compared to the uniform NW, signaling an increase of the electron effective mass and, consequently, a reduction of the electric conductivity due to surface electrons. And third, the effective gap of the NW at kz = 0 increases, as clearly observed in Figure 4.
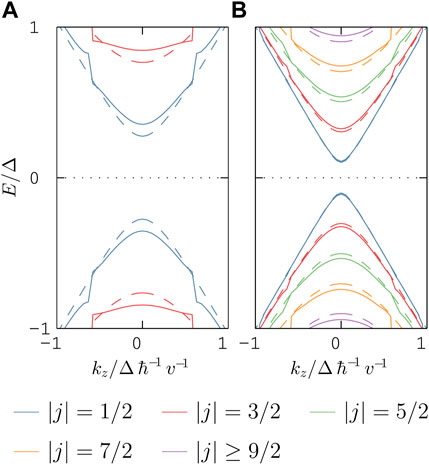
FIGURE 4. Energy spectrum labeled by the quantum number |j| of two rough nanowires of (A) R = 2.5ℏv/Δ and (B) R = 5.5ℏv/Δ and roughness parameters δR = ℏv/Δ and D = 5ℏv/Δ. For comparison energy spectra for the corresponding uniform nanowire is presented in every panel with dashed lines.
Ripples largely affect the spatial distribution of surface states. Figure 5 displays the probability density of surface states along the axial and the radial direction in rough NWs. Panels (a) and (b) compare such density for two NWs with a well-differentiated roughness, as shown in the sketches of Figure 5. On each panel, the probability density of the surface state is represented as a function of the axial z and radial r coordinates, as well as a combined representation of the former in a color map. For comparison, in both panels the radial probability density of the uniform NW of R = 2.5ℏv/Δ is shown in dashed line (see Figure 3A). On the one hand, the modulation of the radius gives rise to a radial probability whose maximum values are shifted to the outermost region of the NW. On the other hand, a careful inspection of the axial dependence of the probability density shows that surface states are mostly confined in the bumps of the surface. The size of the longitudinal region where the probability to find the particle reaches 50% is estimated by the distance D*. Indeed, spatial localization strongly increases with the amplitude of the ripples and, therefore, is expected to be quite noticeable even for relative small roughness. In the end, both features give rise to the existence of surface states strongly localized at the bumps with a zero probability density between them. Thus, as a good approximation, the NW can be envisioned as a tight-binding chain where the overlap between neighbouring sites (bumps) strongly decreases with the amplitude of the ripples. This would eventually lead to a flattening of the subbands when surface roughness is reduced, as already seen in Figure 4A.
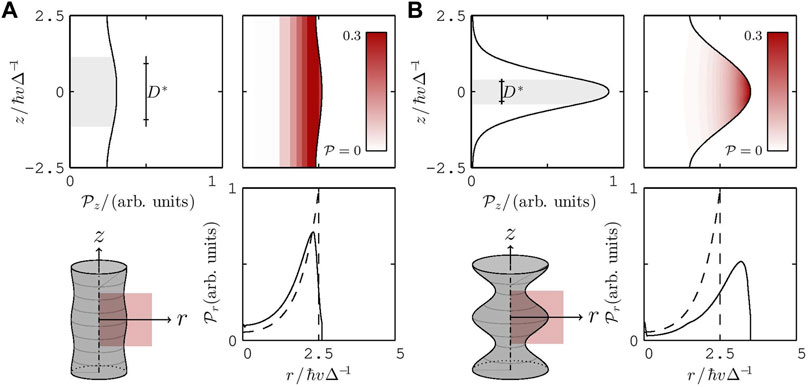
FIGURE 5. Probability density of a surface state of |j| = 1/2 in two rough nanowires of R = 2.5ℏv/Δ and D = 5ℏv/Δ. Panel (A) shows results for a slightly modulated nanowire with δR = 0.1ℏv/Δ. Panel (B) shows results for a strongly modulated nanowire with δR = ℏv/Δ. Within each panel, the subpanels presents the probability density as a function of the axial coordinate z, as a function of the radial coordinate r and a combined representation in a 2D color map. For comparison, the dashed line indicates the radial probability density of a uniform nanowire with R = 2.5ℏv/Δ. The shadowed area of size Δz = D*ℏv/Δ represents the longitudinal region where the confinement probability is 50%.
5 Thermoelectric properties
Once the electronic structure of a rough NW is known, the thermoelectric properties can be obtained within the linear response theory, using the Boltzmann transport equation within the relaxation-time approximation [47]. Let us define the following integrals
where En (kz) is the dispersion relation of the n-th subband [see Eqs 5], f ≡ f [En (kz), μ, T] is the Fermi distribution function for an electron gas with chemical potential μ, Nv is the number of valleys (see Table 1) and τ is the relaxation time. The relaxation time has been taken to be independent of the electron momentum for simplicity, and it is given in Table 1 for PbTe and SnTe. In terms of
The reduction of the lattice thermal conductivity observed in NWs, as compared to their bulk counterparts [45, 48], can be accounted for by the phonon diffusion model introduced in Ref. [49], which allows us to express κph and the phonon mean-free-path ℓph in terms of the corresponding bulk values κph,∞ and ℓph,∞, given in Table 1.
Figure 6 collects the results for a uniform PbTe NW at T = 300K. The thermoelectric response of SnTe NWs is similar and it will not be reported here. Three different radii (R = 1.5ℏv/Δ, R = 2.5ℏv/Δ, and R = 5.5ℏv/Δ) are considered, and the various magnitudes are compared to those obtained in bulk PbTe (R → ∞). We observe an overall enhancement of the electric conductivity on decreasing R. The relative increase is more pronounced when the chemical potential lies within the gap (|μ| < Δ). The increment of the electric conductivity is attributed to a larger contribution of surface states on decreasing the radius. Regarding the thermal conductivity κ = κel+κph, we find that it is dominated by the lattice contribution κph. This overarching conclusion emerges from the fact that the values of κ observed in Figure 6 agrees well with κph,∞ given in Table 1. According to the discussion of the preceding section, κph decreases upon decreasing the radius of the NW due to a stronger phonon scattering at the surface. This is easily understood by heeding that κph for the wider NW (R = 5.5ℏv/Δ) reaches the value of the bulk PbTe but is noticeably smaller if R = 1.5ℏv/Δ, i.e., when the radius is of the order of the phonon mean-free-path ℓph,∞ = 4nm.
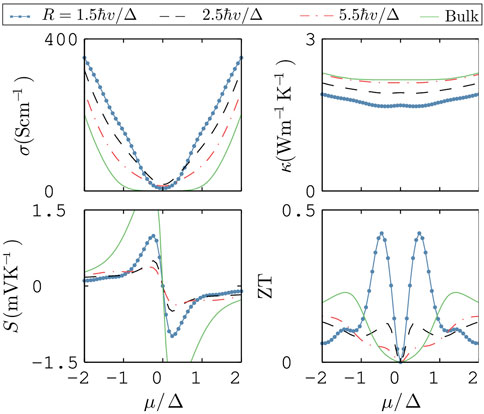
FIGURE 6. Electric conductivity σ, thermal conductivity κ = κph+κel, Seebeck coefficient S and figure of merit ZT as a function of the chemical potential at 300 K. Results for two values of the NW radius are shown and compared to bulk PbTe.
The Seebeck coefficient S displayed in Figure 6 shows a marked dependence on the chemical potential and the radius of the NW. Since the dependence of the electric and thermal conductivities on the chemical potential is rather smooth, the behavior of the Seebeck coefficient dictates the thermoelectric properties of the NW. This is clearly observed in the non-monotonous trend of ZT upon changing the chemical potential of the sample. For some particular values of μ (e.g., μ ∼Δ/2), the narrowest NW displays higher values of ZT due to the simultaneous increase of both σ and S and decrease of κ. But, admittedly, the enhancement of the thermoelectric efficiency is only achieved with narrow NWs after finely tuning the chemical potential. Unfortunately, this is not always doable in experiments. Remarkably, the Seebeck coefficient is higher in bulk PbTe than in NWs. Hence, we can conclude that the occurrence of topological surface states plays an overall detrimental role in the Seebeck coefficient displayed by NWs, although ZT can still be larger than that of the bulk material for certain values of the radius and the chemical potential. Regarding NWs with rough surface, ripples partially suppress the contribution of surface electrons, as discussed in the previous section. Hence, this provides strong evidence that rough NWs are good candidates to achieve better heat-to-electricity conversion by increasing the Seebeck coefficient.
Finally, let us stress that we have found that the thermoelectric efficiency can be enhanced in NWs when the chemical potential lies within the gap. Unfortunately, native vacancies are common point defects in PbTe and SnTe that behave as acceptor centers, leading to p-type doping (μ ≪ − Δ). However, the chemical potential gets closer to the valence band edge by partial compensation after calcium and indium co-doping [46], opening an additional route to improve the thermoelectric efficiency.
6 Conclusion
The two-band model introduced in this work allows us to relate, in a simple way, the thermoelectric efficiency with the parameters that characterize the NW, offering qualitatively correct results. From a general point of view, the development of new methods with which to solve the two-band Hamiltonian has made it possible to obtain a number of novel results, which contribute to improving our understanding of these NWs. This work is also of practical interest since two strategies have been devised to be followed to improve ZT in PbTe and SnTe NWs, namely the modulation of their radius and the creation of surface defects. The generalization of our results to highly anisotropic materials such as Bi2Te3 may help in understanding the interplay between topologically protected states and spatial modulation of surface potential reported in Ref. [20].
Data availability statement
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.
Author contributions
ED and FD-A. conceived and supervised the research. JE carried out the calculations and the numerical work. All authors were involved in the discussion of the results. The article was written through contribution of all authors.
Funding
This work was supported by the Spanish Ministry of Science and Innovation under Grant PID2019-106820RB-C21.
Acknowledgments
The authors are grateful to A. Díaz-Fernández, M. Martín-González y O. Caballero-Calero for helpful discussions.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
2. Kim HS, Liu W, Chen G, Chu CW, Ren Z. Relationship between thermoelectric figure of merit and energy conversion efficiency. Proc Natl Acad Sci U S A (2015) 112:8205–10. doi:10.1073/pnas.1510231112
3. Jonson M, Mahan GD. Mott’s formula for the thermopower and the Wiedemann-Franz law. Phys Rev B (1980) 21:4223–9. doi:10.1103/physrevb.21.4223
4. Hicks LD, Dresselhaus MS. Effect of quantum-well structures on the thermoelectric figure of merit. Phys Rev B (1993) 47:12727–31. doi:10.1103/physrevb.47.12727
5. Hicks LD, Dresselhaus MS. Thermoelectric figure of merit of a one-dimensional conductor. Phys Rev B (1993) 47:16631–4. doi:10.1103/physrevb.47.16631
6. Balandin AA, Lazarenkova OL. Mechanism for thermoelectric figure-of-merit enhancement in regimented quantum dot superlattices. Appl Phys Lett (2003) 82:415–7. doi:10.1063/1.1539905
7. Boukai AI, Bunimovich Y, Tahir-Kheli J, Yu JK, Goddard WA, Heath JR. Silicon nanowires as efficient thermoelectric materials. Nature (2008) 451:168–71. doi:10.1038/nature06458
8. Harman TC, Taylor PJ, Walsh MP, LaForge BE. Quantum dot superlattice thermoelectric materials and devices. Science (2002) 297:2229–32. doi:10.1126/science.1072886
9. Hochbaum AI, Chen R, Delgado RD, Garnett EC, Najarian M, et al. Enhanced thermoelectric performance of rough silicon nanowires. Nature (2008) 451:163–7. doi:10.1038/nature06381
10. Khitun A, Balandin A, Liu JL, Wang KL. In-plane lattice thermal conductivity of a quantum-dot superlattice. J Appl Phys (2000) 88:696–9. doi:10.1063/1.373723
11. Venkatasubramanian R, Siivola E, Colpitts T, O’Quinn B. Thin-film thermoelectric devices with high room-temperature figures of merit. Nature (2001) 413:597–602. doi:10.1038/35098012
12.ZL Wang, editor. Nanowires and nanobelts: Materials, properties and devices.In: Metal and semiconductor nanowires, Vol. I. Berlin: Springer (2006).
13. Meyyappan M, Sunkara MK. Inorganic nanowires: Applications, properties, and characterization. Boca Raton: CRC Press (2009).
14. Cao G, Wang Y. Nanostructures and nanomaterials: Synthesis, Properties and applications (Singapore: World scientific). 2nd ed. (2011).
15.W Lu, and J Xiang, editors. Semiconductor nanowires: From next-generation electronics to sustainable energy. Cambridge: Royal Society of Chemistry (2014).
16. Domínguez-Adame F, Martín-González M, Sánchez D, Cantarero A. Nanowires: A route to efficient thermoelectric devices. Physica E: Low-dimensional Syst Nanostructures (2019) 113:213–25. doi:10.1016/j.physe.2019.03.021
17. Chen ZG, Han G, Yang L, Cheng L, Zou J. Nanostructured thermoelectric materials: Current research and future challenge. Prog Nat Sci Mater Int (2012) 22:535–49. doi:10.1016/j.pnsc.2012.11.011
18. Zhang G, Kirk B, Jauregui LA, Yang H, Xu X, Chen YP, et al. Rational synthesis of ultrathin n-type Bi2Te3 nanowires with enhanced thermoelectric properties. Nano Lett (2012) 12:56–60. doi:10.1021/nl202935k
19. Zhang G, Fang H, Yang H, Jauregui LA, Chen YP, Wu Y. Design principle of telluride-based nanowire heterostructures for potential thermoelectric applications. Nano Lett (2012) 12:3627–33. doi:10.1021/nl301327d
20. Muñoz Rojo M, Zhang Y, Manzano CV, Alvaro R, Gooth J, Salmeron M, et al. Spatial potential ripples of azimuthal surface modes in topological insulator Bi2Te3 nanowires. Sci Rep (2016) 6:19014. doi:10.1038/srep19014
21. Song E, Baranovskiy A, Xu E, Busani T, Swartzentruber B, Zhang S, et al. Manipulating thermal and electronic transports in thermoelectric Bi2Te3 nanowires by porphyrin adsorption. AIP Adv (2018) 8:105010. doi:10.1063/1.5046385
22. Kong D, Randel JC, Peng H, Cha JJ, Meister S, Lai K, et al. Topological insulator nanowires and nanoribbons. Nano Lett (2010) 10:329–33. doi:10.1021/nl903663a
23. Münning F, Breunig O, Legg HF, Roitsch S, Fan D, Rößler M, et al. Quantum confinement of the Dirac surface states in topological-insulator nanowires. Nat Commun (2021) 12:1038. doi:10.1038/s41467-021-21230-3
24. Huang Y, Shklovskii BI. Disorder effects in topological insulator nanowires. Phys Rev B (2021) 104:054205. doi:10.1103/physrevb.104.054205
25. Hernandez JA, Ruiz A, Fonseca LF, Pettes MT, Jose-Yacaman M, Benitez A. Thermoelectric properties of SnSe nanowires with different diameters. Sci Rep (2018) 8:11966. doi:10.1038/s41598-018-30450-5
26. Xu SY, Liu C, Alidoust N, Neupane M, Qian D, Belopolski I, et al. Observation of a topological crystalline insulator phase and topological phase transition in Pb1−xSnxTe. Nat Commun (2012) 7:12505. doi:10.1038/ncomms12505
27. Hsieh TH, Lin H, Li J, Duan W, Bansil A, Fu L. Topological crystalline insulators in the SnTe material class. Nat Commun (2012) 3:982. doi:10.1038/ncomms1969
28. Ando Y, Fu L. Topological crystalline insulators and topological superconductors: From concepts to materials. Annu Rev Condens Matter Phys (2015) 6:361–81. doi:10.1146/annurev-conmatphys-031214-014501
29. Tchoumakov S, Jouffrey V, Inhofer A, Bocquillon E, Plaçais B, Carpentier D, et al. Volkov-Pankratov states in topological heterojunctions. Phys Rev B (2017) 96:201302. doi:10.1103/physrevb.96.201302
30. Inhofer A, Tchoumakov S, Assaf BA, Fève G, Berroir JM, Jouffrey V, et al. Observation of Volkov-Pankratov states in topological HgTe heterojunctions using high-frequency compressibility. Phys Rev B (2017) 96:195104. doi:10.1103/physrevb.96.195104
31. Xu N, Xu Y, Zhu J. Topological insulators for thermoelectrics. Npj Quan Mater (2017) 2:51. doi:10.1038/s41535-017-0054-3
32. Hinsche NF, Zastrow S, Gooth J, Pudewill L, Zierold R, Rittweger F, et al. Impact of the topological surface state on the thermoelectric transport in Sb2Te3 thin films. ACS Nano (2015) 9:4406–11. doi:10.1021/acsnano.5b00896
33. Yang J. Prospective thermoelectrics among topological insulators. In: C Uher, editor. Materials aspect of thermoelectricity. Boca Raton: CRC Press (2017). p. 583–97. chap. 21.
34. Lim J, Hippalgaonkar K, Andrews SC, Majumdar A, Yang P. Quantifying surface roughness effects on phonon transport in silicon nanowires. Nano Lett (2012) 12:2475–82. doi:10.1021/nl3005868
36. Wang J, Polizzi E, Ghosh A, Datta S, Lundstrom M. Theoretical investigation of surface roughness scattering in silicon nanowire transistors. Appl Phys Lett (2005) 87:043101. doi:10.1063/1.2001158
37. Wang F, Yip S, Han N, Fok K, Lin H, Hou JJ, et al. Surface roughness induced electron mobility degradation in inas nanowires. Nanotechnology (2013) 24:375202. doi:10.1088/0957-4484/24/37/375202
38. Kriechbaum M. Envelope function calculations for superlattices. In: Two-dimensional systems: Physics and new devices. G Bauer, F Kuchar, and H Heinrich, editors, 67. Berlin: Springer (1986). p. 120.
39. Dimmock JO, Wright GB. Band Edge Structure of PbS, PbSe, and PbTe. Phys Rev (1964) 135:A821–30. doi:10.1103/physrev.135.a821
40. Mitchell DL, Wallis RF. Theoretical energy-band parameters for the lead salts. Phys Rev (1966) 151:581–95. doi:10.1103/physrev.151.581
41. Assaf BA, Phuphachong T, Volobuev VV, Inhofer A, Bauer G, Springholz G, et al. Massive and massless Dirac fermions in Pb1−xSnxTe topological crystalline insulator probed by magneto-optical absorption. Sci Rep (2016) 6:20323. doi:10.1038/srep20323
42. Agassi D, Korenman V. Interface states in band-inverted semiconductor heterojunctions. Phys Rev B (1988) 37:10095–106. doi:10.1103/physrevb.37.10095
43. Pankratov OA. Electronic properties of band-inverted heterojunctions: Supersymmetry in narrow-gap semiconductors. Semicond Sci Technol (1990) 5:S204–9. doi:10.1088/0268-1242/5/3s/045
44. Abramowitz M, Stegun IA. Handbook of mathematical functions with formulas, graphs, and mathematical tables. New York: Dover (1964).
45. Qiu B, Bao H, Zhang G, Wu Y, Ruan X. Molecular dynamics simulations of lattice thermal conductivity and spectral phonon mean free path of PbTe: Bulk and nanostructures. Comput Mater Sci (2012) 53:278–85. doi:10.1016/j.commatsci.2011.08.016
46. Bhat DK, Shenoy US. Enhanced thermoelectric performance of bulk tin telluride: Synergistic effect of calcium and indium co-doping. Mater Today Phys (2018) 4:12–8. doi:10.1016/j.mtphys.2018.02.001
47. Lin YM, Dresselhaus MS. Thermoelectric properties of superlattice nanowires. Phys Rev B (2003) 68:075304. doi:10.1103/physrevb.68.075304
48. Muñoz Rojo M, Abad B, Manzano CV, Torres P, Cartoixà X, Alvarez FX, et al. Thermal conductivity of Bi2Te3 nanowires: How size affects phonon scattering. Nanoscale (2017) 9:6741–7. doi:10.1039/c7nr02173a
Keywords: thermoelectricity, nanowires, topological insulator, electron states, rough surface
Citation: Estrada J, Díaz E and Domínguez-Adame F (2022) Electronic properties of topological rough nanowires for thermoelectrical performance. Front. Phys. 10:1062038. doi: 10.3389/fphy.2022.1062038
Received: 05 October 2022; Accepted: 25 November 2022;
Published: 14 December 2022.
Edited by:
Judith Helena Ojeda Silva, Universidad Pedagógica y Tecnológica de Colombia, ColombiaReviewed by:
Roberto D’Agosta, University of the Basque Country, SpainSomnath Acharya, Yonsei University, South Korea
Copyright © 2022 Estrada, Díaz and Domínguez-Adame. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: E. Díaz, ZWxlbmFkZ0B1Y20uZXM=
 J. Estrada
J. Estrada E. Díaz
E. Díaz F. Domínguez-Adame
F. Domínguez-Adame