Optical phase singularities: Physical nature, manifestations and applications

Over the past 30 years, physical optics has been enriched by the appearance of singular optics as a new branch approved in scientific classifiers. This review briefly outlines the main concepts of the singular optics, their role in physical research and applications, and prospects of further development. The wave singularities are considered as a sort of structured-light elements and analyzed based on the generic example of screw wavefront dislocation (optical vortex). Their specific topological and mechanical properties associated with the transverse energy circulation are discussed. Peculiar features of the non-linear optical phenomena with singular fields are exhibited, with the special attention to generation of multidimensional entangled quantum states of photons. Optical fields with multiple singularities, especially, the stochastic speckle fields, are discussed in the context of optical diagnostics of random scattering objects. The exact and approximate correspondences between characteristic parameters of the optical-field intensity and phase distributions are analyzed with the aim of recovering phase information from the intensity measurements (“phase problem” solution). Rational singularity-based approaches to informative measurements of the scattered-field distribution are discussed, as well as their employment for the objects’ diagnostics. In particular, the practical instruments are described for the high-precision rough-surface testing. Possible enhancements of the singular-optics ideas and concepts in a wider context, including the transformation optics, near-field optics (surface waves), partially-coherent fields, and wave fields of other physical nature, are briefly exposed.

1 Introduction

During the past years, a special attention of the research and technology community has been paid to the structured light fields characterized by highly developed inhomogeneity of the amplitude, phase, polarization and spectral characteristics. This vibrant activity resulted in establishment of “structured light” as a new fruitful paradigm of physical optics [1–6]. The structured optical fields find interesting and productive applications in various branches of optical technologies, optical manipulations, optical communications and data processing as well as in optical diagnostics [7, 8].

Maybe, the most impressive feature of structured light fields is the existence of “singular” points (lines, surfaces, etc.) in space where certain parameters characterizing the field spatial structure (phase, ellipticity or helicity of polarization) are indeterminate. Despite the variability of types and sorts of optical singularities [9–22], they possess many similar features and are inherently interrelated (for example, the polarization singularities can be treated as phase singularities of separate orthogonal components of vector light beams [8, 16, 23]). The main common feature of optical singularities is their topological nature which makes the singularity stable with respect to small perturbations [24] and determines that each singularity qualitatively “organizes” the whole field in its vicinity, and different singularities combine and interact according to general laws. As a consequence, the “singular skeleton” (set of the field singularities with their positions and morphological characteristics [25–27]) represents a succinct characterization of the whole field [14, 15], which enables, for example, the economy encoding and representation of optical information [3]. In particular, the “singular” approach appears to be fruitful in the description and analysis of stochastic speckle fields [28] which frequently occur in problems of optical diagnostics of scattering objects and random surfaces [29].

The unique physical properties, great application potential as well as the vital interest of the community have inspired a series of consistent review publications treating various fundamental or applied aspects of the optical singularities (for example, Refs. [3–9, 13, 14, 17–20, 25, 30]). In this context, the present work pursues two main goals. The first one is to show how the optical singularities, even in their simplest scalar forms, illustrate the spectacular interrelations between the classical optics, non-linear optics, and quantum physics, up to the most fundamental ideas of quantum superpositions and multidimensional quantum states, and thus disclose the unity of the physical picture of the world. This task is quite compatible with the second goal, apparently much more utilitarian: description of some practical possibilities, offered by singular optics in analysis of chaotic speckle fields, and their use for reconstruction of scattering objects generating these fields. By the general approach, this paper adjoins our previous reviews on the adjacent topics [7, 8], and may be considered their further development and addition.

Due to their physical affinity, the main features of the optical singularities can be understood by considering the generic example of the point-like phase singularity; this is the topic of Section 2. The associated physical features: the wavefront dislocation, transverse energy circulation, specific mechanical properties (orbital angular momentum) are briefly analyzed, as well as the typical singularity-related manifestations in the non-linear optical phenomena (Section 3). Section 4 describes the singular photons in the context of quantum superpositions and quantum entanglement. Section 5 presents the concepts and approaches relevant for the stochastic speckle fields and their usage for the rough-object diagnostics. In Section 6, we briefly outline some interesting and important (in our opinion) features of singular optical fields and prospects of their studies and applications. The review contents are accomplished and summarized in Section 7.

2 Screw wavefront dislocations, also known as optical vortices

Let us consider a scalar light field (properly, a paraxial beam with the spatially homogeneous polarization [3, 15]). The electric field of such a beam is described by the function

$\epsilon \left(r,\varphi ,z,t\right)=\mathrm{R}\mathrm{e}\left[E\left(r,\varphi ,z\right)\exp \left(ikz-i\omega t\right)\right](1)$

where (r, ϕ, z) is a cylindrical frame, ω is the radiation frequency, and k = 2π/λ is the wave number (λ is the wavelength). In the paraxial approximation [3, 15, 31], the complex amplitude E (r, ϕ, z) obeys the equation

$\frac{1}{r}\frac{\partial }{\partial r}\left(r\frac{\partial E}{\partial r}\right)+\frac{1}{r^2}\frac{{\partial }^{2}E}{\partial {\varphi }^2}+2ik\frac{\partial E}{\partial z}=0(2)$

whose solutions can be represented in the form of azimuthal harmonics [9].

$E\left(r,\varphi ,z\right)=A\left(r,z\right)\exp \left(il\varphi \right)(3)$

where the coefficient l is called azimuthal mode index. The characteristic feature of the field (3) is the helical wavefront (WF) shape illustrated by Figure 1A (whence the term “screw WF dislocation” originates): after the round trip near the z-axis, the phase does not return to its initial value but changes by 2πl. Hence, the mode index l acquires the sense of the topological charge (TC) of the azimuthal mode (3) [9]. As the solution (3) of Eq. 2 should be unambiguous, once l ≠ 0, the wave amplitude A(r, z) = 0 at the axis, and only integer values of l are admissible (in practice, especially in cases of deliberate optical-field formation, beams of the form (3) with non-integer l can occur [32, 33] but these are “non-generic” and unstable: only exist in the initial cross section but destroy, with formation of a set of single-charge singularities, upon the beam propagation [34, 35].

FIGURE 1

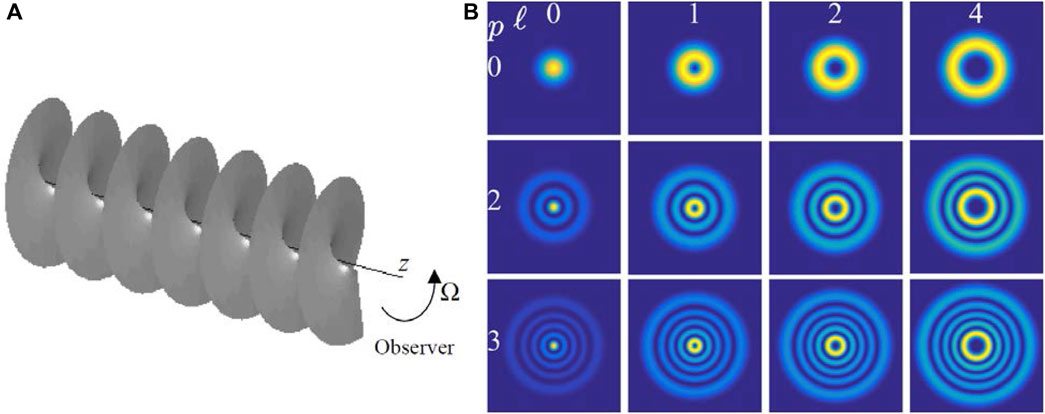
FIGURE 1. (A) The helical WF of the azimuthal harmonic (3) propagating along axis z; (B) the intensity profiles of the LG_p^l beams for different values of l and p [38]; further explanations see in the text.

The helical WF stipulates another important property of the azimuthal harmonics (3). In light beams, local directions of the energy flow are known to coincide with the WF normals [9, 15], which, for a helical WF, form 3D spiral lines; consequently, the energy propagates along the spiral-like trajectories skewed with respect to the beam axis [36]. Accordingly, there exists the transverse energy circulation near the phase singularity, which is the source of the orbital angular momentum (OAM) of light [3, 9, 15] and justifies the term “optical vortex” (OV) widely used for such singular structures [37].

A well-known example of solution to Equation 1 in the form of azimuthal harmonic is the family of Laguerre–Gaussian (LG) modes LG_p^l of a stable laser cavity [31]. The LG modes are circularly symmetric, their intensity distribution consists of dark and bright rings centered at the axis of propagation z (Figure 1B [38]). The radial index p specifies the number of dark rings in the beam cross section, and does not affect the singular properties; so the condition p = 0 will be assumed below (upper row of Figure 1B). For the LG₀^l mode, the distribution of the complex amplitude has the form

$E_{\mathit{LG}}\left(r,\varphi ,z\right)=E_s\frac{w_0}{w\left(z\right)}{\left(\frac{r}{w\left(z\right)}\right)}^{\left|l\right|}\exp \left(-\frac{r^2}{w^2\left(z\right)}\right)\times \exp \left[\mathrm{i}\left(kz+\frac{k{r}^2}{2R\left(z\right)}+l\varphi -\left(\left|l\right|+1\right)\arctan \left(\frac{z}{z_R}\right)\right)\right](4)$

where

$z_R=\frac{k{w}_0^2}{2},w^2\left(z\right)=w_0^2\left(1+\frac{z^2}{z_R^2}\right),R\left(z\right)=\frac{z^2+z_R^2}{z}.(5)$

The mechanical OAM L of such circularly-symmetric OV beams is described by the universal relation [39].

$L=l\frac{W}{\omega }(6)$

where W is the light energy, i.e. each photon with the energy $W=\mathrm{\hslash }\omega$ carries the OAM $L_p=l\mathrm{\hslash }$, ħ being the reduced Planck constant.

The spiral energy flows near the screw WF dislocation manifest themselves in many physical phenomena, for example, in photoinduced rotation of particles [40, 41]. But their direct observations in the OV edge-diffraction phenomena are especially simple and impressive [42–44] (Figures 2, 3). A spectacular picture of the intensity-profile evolution is shown in Figure 2 [43]. Here, the beam parameters and the observation plane are chosen such that the usual diffraction fringes are almost unnoticeable while the change of the beam transverse profile can be easily traced from the initial section immediately behind the screen (a) to the observation plane distanced from the screen by z = z_R (b). It can be seen that the initial pattern actually rotates in accordance with the direction of the transverse energy circulation, and one of the “edges” of the bright semi-ring penetrates into the shadow region behind the obstacle, while the other moves away from it. One might expect that the magnitude of the rotation increases with |l|, but in fact this is not the case; the larger initial slope of the vortex trajectories is compensated by an increase in the diffraction divergence, and beams with different |l| generally rotate the same way. However, in the case of large TCs, the bright semi-ring is located farther from the axis and is less distorted by diffraction, so the rotation itself is more noticeable.

FIGURE 2

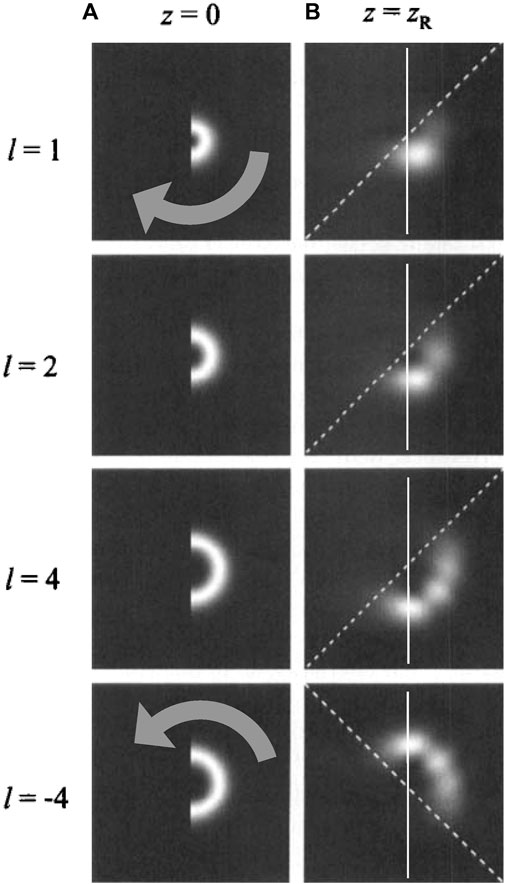
FIGURE 2. Intensity distribution of diffracted LG beams with different azimuthal indices l (beam waist coincides with the screen plane, the screen with the rectilinear vertical edge covers exactly half of the incident beam cross section) [43]: (A) immediately behind the screen and (B) at a distance z = z_R behind the screen. Grey arrows show the direction of transverse energy circulation, dashed lines correspond to a rotation angle of 45°, solid vertical lines are projections of the screen edge (the shadow-area border).

FIGURE 3

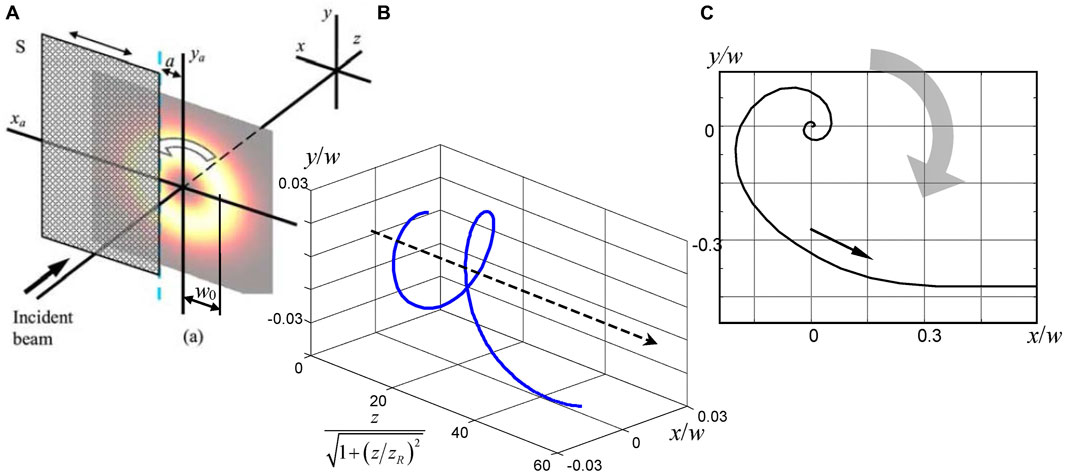
FIGURE 3. (A) Scheme of the OV beam diffraction: an opaque screen S is located in the transverse plane z = 0, where the WF of the incident beam is flat; the distance a between the screen edge and the beam axis is adjustable, the diffraction pattern is observed in the z plane furnished with the coordinate frame (x, y); (B) 3D trajectory of the amplitude zero in the diffracted LG₀⁻¹ beam (l = –1) at a fixed screen position a = 1.4w₀ (see Equation 5 and comments thereto); (C) the trajectory described by the OV core of the same beam in a fixed observation plane z = 0.57z_R when the screen is translated in the diffraction plane from a = 2.1w₀ to a = 0.14w₀ (view from the positive end of the z-axis). Broad arrows on (A) and (C) show the direction of energy circulation in the incident beam, all transverse dimensions are given in units of the current radius $w=w_0\sqrt{1+{\left(z/z_R\right)}^2}$, the longitudinal distance on (B) is shown in normalized units, in which the value of the longitudinal coordinate 54 corresponds to the far field (z = ∞).

Subsequent works [45–48] have shown that the usual edge diffraction offers rather informative and picturesque evidence of internal energy flows in beams with OV. Of particular interest is the behavior of the diffraction pattern when the screen covers an insignificant part of the beam “ring”, retaining the pattern of internal circulation as a whole (Figure 3A). The diffraction perturbation of the beam causes a shift of the amplitude zero (singularity “core”) relative to its initial axial location (in the case of the initial l-charged OV, |l| single-charged OVs are formed near the axis). Then, as the diffracted beam propagates, the displaced OVs migrate inside the beam “body” along helical trajectories that unwind in the direction opposite to the direction of energy circulation in the incident beam. At small distances behind the screen, the spirals unwind at a high rate, but with further propagation, the rotation slows down and stops in the far-field (Figure 3B). A similar OV migration occurs in a fixed section of the diffracted beam, when the edge of the screen moves perpendicular to its axis (Figures 3A, C)—a very spectacular illustration of the rotational properties of the field singularity.

The topological nature of the screw WF dislocation opens impressive possibilities for the data encoding and the information transfer [49–51]. The specific pattern of the transverse energy flows is responsible for another interesting phenomenon—rotational Doppler effect [52–59]. Indeed, the visible phase of the azimuthal harmonic (3) depends on the mutual angular positions of an observer and the beam with respect to the axis z (see Figure 1A). As a result, when the beam (or observer) rotates with the angular velocity Ω, the visible frequency changes by $\Delta \omega =l\mathrm{\Omega }$. This effect finds fruitful applications for the spectral analysis of light beams and the distant detection of the rotational motion of various objects [55, 58, 59], which are described in detail by recent reviews [59, 60]. For this reason, we do not dwell further upon the rotational Doppler shifts but proceed to some impressive non-linear effects involving the optical singularities.

3 Non-linear phenomena with optical vortices

Naturally, the study of phase singularities was extended to nonlinear optics, primarily to active schemes, e.g. in photorefractive laser oscillators. When the angular aperture of the cavity was compressed to the level of modes with the lowest transverse indices, a dynamic pattern of nucleation of pairs (dipoles) of OVs was observed in the output radiation [61]. The effect was then considered in the passive scheme of an induced nonlinear lens, where it was accompanied by the appearance of a closed spatial dislocation line in the form of a “seam on a tennis ball” and a quadrupole of vortices in the beam cross section [62]. In the stationary case, such closed and open (going into the far-field zone) “dark lines” of dislocations wrap around regions with the field intensity maxima, forming three-dimensional cells, and in the non-stationary case of dynamic light scattering processes, they create a “light boiling” structure, up to optical turbulence [63–65].

A number of new effects accompany the singular beams’ propagation in non-linear media. As was shown in [66], the non-linear medium asymmetry (astigmatism) destroys the OV with |l| > 1 (this effect is in parallel to the high-order OV decomposition in linear astigmatic systems [67, 68]); however, the instability of the cubic non-linear medium influences the first-order singularity also. Evidently, each singularity contains an inevitable amplitude zero, and the results of the beam self-focusing in the medium with cubic nonlinearity (positive non-linear refractive index) was unclear. A series of research works was undertaken that established the azimuthal instability of the bright ring of an OV beam and its decomposition into separate solitons [69].

On the other hand, a defocusing cubic medium also creates conditions for the OV instability and generation of “vortex” solitons [70, 71]. In the work [72], a beam with the edge WF dislocation is considered. As is shown in Figure 4, with growing non-linearity the initial edge dislocation (black line) acquires waviness and ultimately breaks up into separate “dark” solitons.

FIGURE 4

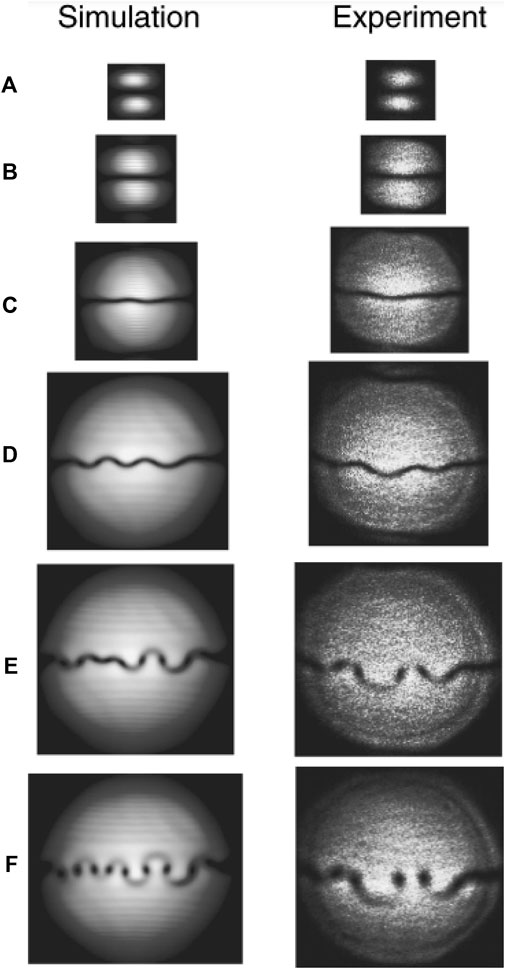
FIGURE 4. Transverse beam profile at the exit of a nonlinear defocusing medium (a cell filled with gas), showing the instability of the edge WF dislocation (dark line) with an increase in the nonlinearity parameter (gas concentration) (A-F) (left column) theoretical calculation, (right column) experimental results. The concentration of cesium vapor increases from negligible values with non-linearity absent (A) to approximately 10¹³ cm⁻³ (F).

Obviously, the nature of the screw WF dislocation determines the pattern of the second-harmonic generation with pumping by an OV beam in a medium with quadratic nonlinearity. In the case of an initial TC l, a vortex with a TC of 2l should appear in the second-harmonic wave. However, the emergence of two spatially separated intensity zeros was experimentally recorded when the frequency of the OV beam with the TC l = 1 is doubled, which means the influence of the “irrotational” component in the beam (possibly, as a consequence of astigmatism) [73].

Further detailed analysis of the second-harmonic generation has shown that, as the intensity increases, the ring profile of the OV beam (like those shown in Figure 1B, top row) becomes unstable in a medium with quadratic nonlinearity, and the bright ring breaks up into several soliton-like beams of doubled optical frequency; moreover, the initial OV beam of a unit TC generates three separate beams [74]. The OAM conservation law “works” in this situation too, forcing the “combined” intensity profile of three beams to rotate as a whole in the transverse plane as they propagate.

4 Optical vortices and quantum entanglement

A particularly interesting manifestation of nonlinear optical interactions involving OV beams is the generation of singular vortex fields in the process of spontaneous parametric scattering (SPS) [75–79, 82]. In the first experiments [75], azimuthal harmonics in the form of Bessel beams arose as a result of the amplification of quantum noise in a lithium triborate (LBO) crystal 15 mm long under pulse pumping (1 ps, 30 GW/cm², 527 nm, a focused Gaussian beam with a half-maximum diameter of 61 μm). Under these conditions, signal beams were observed with a wavelength of 960 nm; in 45% of cases they had a profile described by the zero-order Bessel function (non-vortex), and in 36% vortex Bessel beams with TCs $l=\pm 1$ appeared. In other cases, the signal wave had a complex speckle structure without apparent regularity. Unfortunately, in [75], the result of the parametric amplification depended decisively on the random pattern of “seed” noises, and it was not possible to achieve stable and reproducible generation of vortex modes.

Another approach was realized in [76–79, 82] where the SPS process was used for creation and investigation of multidimensional entangled states of vortex photons. Therewith, the structures of the idle and signal beams were not studied immediately but the stress was made on the non-local connection between them. In these experiments [79], the pump radiation from an Ar laser (λ = 351 nm) entered the anisotropic crystal BBO (barium beta-borate) where the signal and idle waves with equal wavelengths 702 nm were generated, propagating at angles 4° with respect to the pump beam (see Figure 5). Herewith, each pump photon generates two scattered ones which are in the single entangled quantum state. Denoting the photon state described by the LG₀^l mode (4) as $|l\rangle$, and if the pump wave is a Gaussian beam with zero OAM (Equation 4 with l = 0), this entangled state can be represented as

$|\psi \rangle =C_{\mathrm{0,0}}{|0\rangle }_1{|0\rangle }_2+C_{1,-1}{|1\rangle }_1|-1\rangle +C_{-\mathrm{1,1}}{|-1\rangle }_1{|1\rangle }_2+C_{2,-2}{|2\rangle }_1{|-2\rangle }_2+C_{-\mathrm{2,2}}{|-2\rangle }_1{|2\rangle }_2+...(7)$

where ${|l_1\rangle }_1{|l_2\rangle }_2$ is the two-photon state in which the idle wave (channel 1 in Figure 5) is described by the ${\mathrm{LG}}_0^{l_1}$ mode, and the signal wave (channel 2)—by the ${\mathrm{LG}}_0^{l_2}$ mode (strictly speaking, in the expansion (7), modes with non-zero radial indices p should also be present but their contribution is relatively small).

FIGURE 5

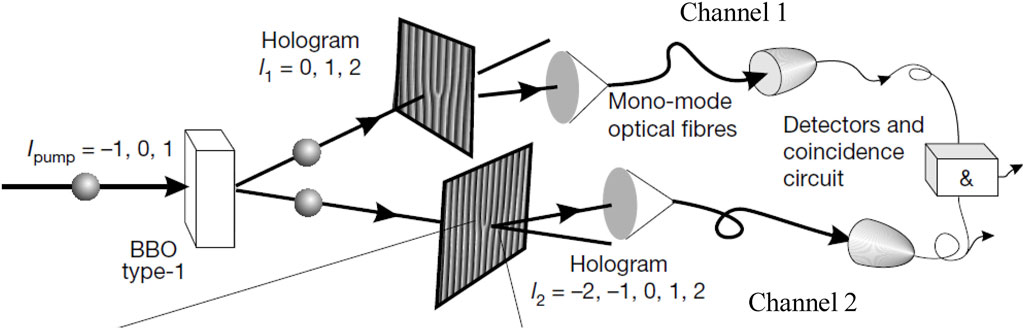
FIGURE 5. Experimental scheme for detection of multidimensional entangled states of photons obtained in the SPS process [79].

Thus, the photons obtained after the parametric conversion have no definite OAM and no definite TC; however, the subsequent measurement of the TC of one of them, which gave, for example, the value l₁ = 1 for an idle wave, leads to the reduction of state (7): from the entire infinite sum, only the term remains with ${|1\rangle }_1{|-1\rangle }_2$. Consequently, the signal photon also acquires a definite TC l₂ = −1, and this occurs instantly (“teleportation”), despite the fact that at the moment of measurement it can be spatially removed from the idle one by a macroscopic distance (“non-locality”). Without going into details, we can see here how quantum mechanical effects “work” with OV states obtained from a completely classical pump field.

In the setup of Figure 5, each of the photons enters the mode detector, which consists of a hologram with the groove bifurcation (“fork”) and a single-mode optical fiber. Such holograms are generally used for the generation of optical singularities [9, 25, 83, 84]; here they operate in the “reverse mode.” The fact is that the hologram, which is designed to generate an OV beam with azimuthal index l from the initial Gaussian beam with a smooth WF, will create the same Gaussian beam if it is illuminated (while maintaining the other conditions) by an OV beam with index − l. In its turn, the next element of the mode detector, a single-mode fiber, has selective sensitivity specifically to a Gaussian beam: only a Gaussian beam obtained after a hologram can “penetrate” a single-mode fiber (in other cases, higher LG modes are obtained at the hologram output, whose size of the spatial distribution does not satisfy the fiber excitation conditions). Therefore, the appropriate choice of the hologram in the signal or idle channel allows one to purposefully “check” the presence of a photon state with one or another TC value in the superposition (7).

The connection between photons in channels 1 and 2 is detected via analyzing the coincidences of the detector signals in both channels in the photon counting mode. Figure 6A convincingly demonstrates that when measurements show the presence of a photon with TC l₁ in channel 1, then a photon with l₂ = –l₁ is formed in channel 2.

FIGURE 6

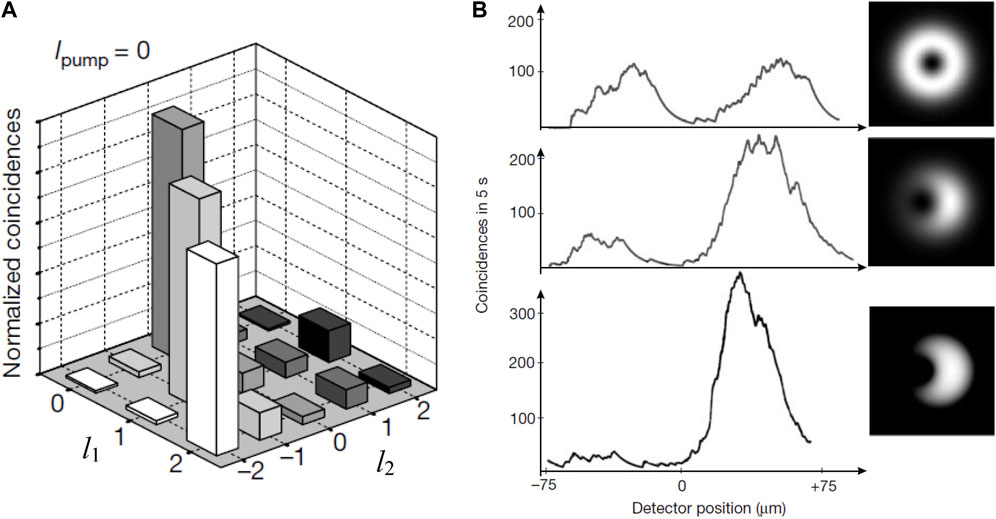
FIGURE 6. (A) Diagrams of the relative numbers of coincidences in channels 1 and 2; (B) experimental confirmation of entanglement of the photon states in channels 1 and 2 [79] (cf. Figure 5).

The most convincing evidence for the entanglement of photon states is obtained when not “pure” LG modes are detected in the channels, but their superpositions. For example, state (7) can be represented in the form

$|\psi \rangle =\left(a_0{|0\rangle }_1+a_1{|1\rangle }_1\right)\left(a_0{C}_{\mathrm{0,0}}{|0\rangle }_2+a_1{C}_{1,-1}{|-1\rangle }_2\right)+\left(a_1{|0\rangle }_1-a_0{|1\rangle }_1\right)\left(a_1{C}_{\mathrm{0,0}}{|0\rangle }_2-a_0{C}_{1,-1}{|-1\rangle }_2\right)$

$+C_{-\mathrm{1,1}}{|-1\rangle }_1{|1\rangle }_2+C_{2,-2}{|2\rangle }_1{|-2\rangle }_2+C_{-\mathrm{2,2}}{|-2\rangle }_1{|2\rangle }_2+...,(8)$

where a₀ and a₁ are real numbers, and the normalization condition $a_0^2+a_1^2=1$ is required (here only the two first summands of (7) are transformed, the rest of the terms remain unchanged). The expression $\left(a_0{|0\rangle }_1+a_1{|1\rangle }_1\right)$ in the first summand represents the superposition of a Gaussian and ${\mathrm{LG}}_0^1$ beams, for which the intensity distribution possesses the shape of a ring with the amplitude zero displaced from the axis [9], see Figure 6B.

Such a superposition is realized in channel 1 when the hologram center slightly shifts from the propagation axis of photon 1 (in Figure 6B, from top to bottom, three stages of such a shift are shown: with growing shift, the “ring” transforms into “crescent”). After passing the hologram, the state (8) reduces to the first summand, i.e. the photon 2 appears in the superposition state too, $\left(a_0{C}_{\mathrm{0,0}}{|0\rangle }_2+a_1{C}_{1,-1}{|-1\rangle }_2\right)$, but here a Gaussian beam is combined with the mode ${\mathrm{LG}}_0^{-1}$. For detection of this superposition, the hologram is removed in channel 2, and the mode detector scans the transverse intensity distribution, in order to determine the position of the second-photon amplitude zero with respect to the beam center. The coincidence calculation shows that, indeed, the photon in channel 2 is also in the state of superposition of the LG and Gaussian modes (Figure 6B).

Classical correlation would give a pattern of coincidences that is simply a mixture of Gaussian and LG modes: the intensity minimum would remain at the beam center, but would be smeared, and the intensity would be everywhere greater than zero.

Multidimensional entangled quantum states are of interest for fundamental research of the quantum physics foundations, in particular, for testing Bell’s inequalities [77–79, 82]. On the other hand, they make it possible to create quantum memory cells with more than two states, which leads to an increase in the speed and reliability of information processing, and thus are promising for numerous applications in the field of quantum cryptography, encoding, quantum communication networks, and quantum computers [80–82]. Pioneering experiments with entangled OV photons [79, 80, 82] were awarded the 2022 Nobel Prize.

A curious modification of the concept of entangled vortex photons was realized in the “non-local OV” [85, 86]. In this case, the OV is observed via the correlations of photons produced from SPS, and the phase singularity appears in a nonlocal coordinate plane where one dimension is the usual coordinate of one photon whereas the second dimension corresponds to the transverse momentum of the second photon. This idea demonstrates the power and flexibility of the quantum-mechanical concepts and supplies their pictorial realization with intuitively clear macroscopic objects.

We hope that the above sections supply a representative exposition of some not very well known properties of beams with screw WF dislocations. Their contents illustrate a relatively small part of the huge massive of facts and concepts accumulated since the OV discovery [21, 22, 37], and the works in this direction are still growing like an avalanche up to the present time. Some additional aspects will be presented in further sections; a representative picture of current development of this fascinating and productive field of research can be traced with the help of periodic special issues [87–90] and in other reviews, for example Refs. [5, 6, 30, 33].

Meantime, we proceed to the next step of the present review, which addresses the fields with multiple singularities formed by the coherent light scattering by various random objects, and their applications for the optical-diagnostic purposes.

5 Singularities in speckle fields

5.1 Statistical characteristics of random objects and speckle fields

The speckle structure is a characteristic feature of laser light scattered by any diffuse object, and its analysis can be used for diagnostics of scattering object’s properties [28, 91]. At the dawn of the singular-optics age, it was recognized that the speckle structure actually represents a network of optical singularities [21, 22, 92–97], and this fact opens new possibilities in optical diagnostics and information processing. Actually, any optical field formed due to transmission of coherent light through a diffuse transparency, or reflected by a rough surface, can be treated as a system of OVs, so that, on the average, each bright spot in the speckle structure is associated with the adjacent screw WF dislocation. In 3D space, the phase dislocations form “zero lines” which do not intersect and constitute the 3D singular skeleton of the field [14, 97].

It was mentioned above that the singular skeleton supplies essential characteristics of the scattering object and, as such, carries specific information of its properties. Accordingly, the problem of singularities’ detection and evaluation arises. In the usual way, it is solved imposing an off-axis coherent reference wave and observing its interference with the speckle field of interest (the interference technique) [9, 21, 22]. In the vicinity of the amplitude zeros, the interference fringes bifurcate and form so-called interference “forklets” (like those presented in Figure 5) which are easily detected visually. Yet, the accuracy of this approach is generally limited by the period of interference pattern, and the precise location of amplitude zeros in speckle fields is of high importance.

A fruitful approach to this problem involves the optical correlation technique, and is further applied for studying the fields scattered by random and fractal rough surfaces [29, 98]. In general, a rough surface is an example of a specific scattering object with a highly irregular structure. Normally, it is described by the profilogram—a real function h(r), r = (x, y), expressing the surface “height” with respect to a certain nominal plane. For simplicity (and in compliance with practical needs), we suppose the field h(r) to be statistically homogeneous, i.e. the statistical properties of functions h(r) and h (r + ρ) are identical for any relevant shift ρ, and the same assumption will be kept for other stochastic fields considered in this paper. Then, the function h(r) is characterized by the usual statistical parameters: autocorrelation function

$F\left(\mathbf{\rho }\right)=\frac{\langle h\left(\mathbf{r}\right)h\left(\mathbf{r}+\mathbf{\rho }\right)\rangle }{\langle h^2\left(\mathbf{r}\right)\rangle }=\frac{\int h\left(\mathbf{r}\right)h\left(\mathbf{r}+\mathbf{\rho }\right)d^2\mathbf{r}}{\int h^2\left(\mathbf{r}\right)d^2\mathbf{r}}(9)$

(⟨…⟩ mean statistical average), angular power spectrum

$S\left(\mathbf{f}\right)=k^2\int F\left(\mathbf{\rho }\right)e^{ik\mathbf{f}\mathbf{\rho }}\frac{d^2\mathbf{\rho }}{{\left(2\pi \right)}^2}(10)$

(k is the wavenumber, f = (f_x, f_y) is the angular frequency), and their statistical moments such as the correlation length

${\rho }_{cor}={\left[\frac{\int {\mathbf{\rho }}^{2}F\left(\mathbf{\rho }\right)d^2\mathbf{\rho }}{\int F\left(\mathbf{\rho }\right)d^2\mathbf{\rho }}\right]}^{1/2},(11)$

root mean square (RMS) roughness

$R_q=\sqrt{\langle h^2\left(\mathbf{r}\right)\rangle }={\left[\frac{1}{A}\int h^2\left(\mathbf{r}\right)d^2\mathbf{r}\right]}^{1/2},(12)$

as well as other higher-order parameters of statistical distributions (skewness Sk, kurtosis Ku, etc. [98, 101]). In Eq. 12 A is the surface area, and, for simplicity, the reference plane h = 0 is chosen such that the mean surface height $\langle h\left(\mathbf{r}\right)\rangle =\left(1/A\right)\int h\left(\mathbf{r}\right)d^2\mathbf{r}=0$. Note that in practice, the correlation length can be defined alternatively as the distance at which the correlation function falls to 1/2 of its maximum,

$F\left({\mathbf{\rho }}_{cor}\right)=0.5F\left(0\right)(13)$

Statistical description of random fields differs from the above-presented description of rough surfaces in two important aspects: the field is an essentially 3D object, and, in contrast to the real function h (x, y), it is characterized by the complex amplitude (1). The first difference is not crucial if we consider the fields that can be treated as paraxial [3], and the distributions in fixed cross sections z = const are of main interest. In such situations, statistical properties of random fields are generally characterized by the complex degree of coherence [107], which is defined similarly to Eq. 9 but applied to the complex amplitude (1):

$F_E\left(\mathbf{\rho }\right)=\frac{\langle E\left(\mathbf{r}\right)E^{*}\left(\mathbf{r}+\mathbf{\rho }\right)\rangle }{\langle {\left|E\left(\mathbf{r}\right)\right|}^2\rangle }=\frac{\int E\left(\mathbf{r}\right)E^{*}\left(\mathbf{r}+\mathbf{\rho }\right)d^2\mathbf{r}}{\int {\left|E\left(\mathbf{r}\right)\right|}^2{d}^2\mathbf{r}}.(14)$

Since in this definition the longitudinal coordinate z is supposed constant, the function $F_E\left(\mathbf{\rho }\right)$ characterizes the “transverse” correlations, which will be implied further in this review. Together with the correlation function of amplitude (14), the important characteristic of wave fields is the correlation function of intensity $I={\left|E\right|}^2$. As $I\left(\mathbf{r}\right)$ is a real-valued function, its expression is, essentially, quite similar to (9):

$F_I\left(\mathbf{\rho }\right)=\frac{\int I\left(\mathbf{r}\right)I\left(\mathbf{r}+\mathbf{\rho }\right)d^2\mathbf{r}}{\int I^2\left(\mathbf{r}\right)d^2\mathbf{r}}.(15)$

According to the two correlation functions, (14) and (15), the two transverse correlation lengths, ${\rho }_{cor}^E$ and ${\rho }_{cor}^I$, can be introduced; for determinacy, let them be defined, like in Eq. 13, by relations

$F_E\left({\rho }_{cor}^E\right)=0.5F_E\left(0\right),F_I\left({\rho }_{cor}^I\right)=0.5F_I\left(0\right).(16)$

For any physical field, the functions $F_E\left(\mathbf{\rho }\right)$ and $F_I\left(\mathbf{\rho }\right)$ are mutually related, and their comparative analysis discloses meaningful information on the optical field properties (see Section 5.3).

5.2 Fractal objects and fractal properties of scattered fields

However, real surfaces (or, equivalently, transparent phase screens which introduce the phase modulations k(n—1)h(r) where n is the refractive index) may contain various fractures, sharp peaks, and crevasses. Sometimes it is impossible to characterize it exhaustively by a single characteristic scale or correlation length of inhomogeneities like (11). Some of such structures can be classified as fractals [99–103]. In particular, the fractal-like surface nature is manifested by the fact that the correlation length of inhomogeneities grows with an increase in the surface area under investigation [104, 105]. This fact can be explained as a consequence of the surface-structure self-similarity, when a part of the surface of a greater scale is of identical statistical structure as the parts of the surface with smaller scales. A characteristic feature of fractal objects is that their power spectra (10) obey an inverse power law of the form

$S\left(f_x\right)=\frac{K_{\nu }}{f_x^{\nu }},1<v<3(17)$

(see Figure 10). The spectral strength K_ν and the spectral index ν supply an alternative fractal-surface characterization often more consistent than the correlation length (11) or the RMS roughness (12). In particular, there exists a direct correspondence with the Hearst index H (ν = 2H + 1) and the fractal dimension (Hausdorff—Besicovitch dimension) D_f = (5—ν)/2 [98, 101].

Relief-height probability density function and the statistical parameters of random and fractal surfaces are illustrated in Figure 7 as follows: the arithmetic-mean deviation of the profile from the nominal surface line, R_a = ⟨|h (x,y)|⟩, RMS deviation R_q (12), the asymmetry coefficient of the distribution (skewness) Sk, and the excess coefficient (kurtosis) Ku. This example is obtained by simulation with the maximal interval of the surface inhomogeneity heights (the difference between the maximal and minimal heights) assumed to be Δh_max = 2 μm.

FIGURE 7

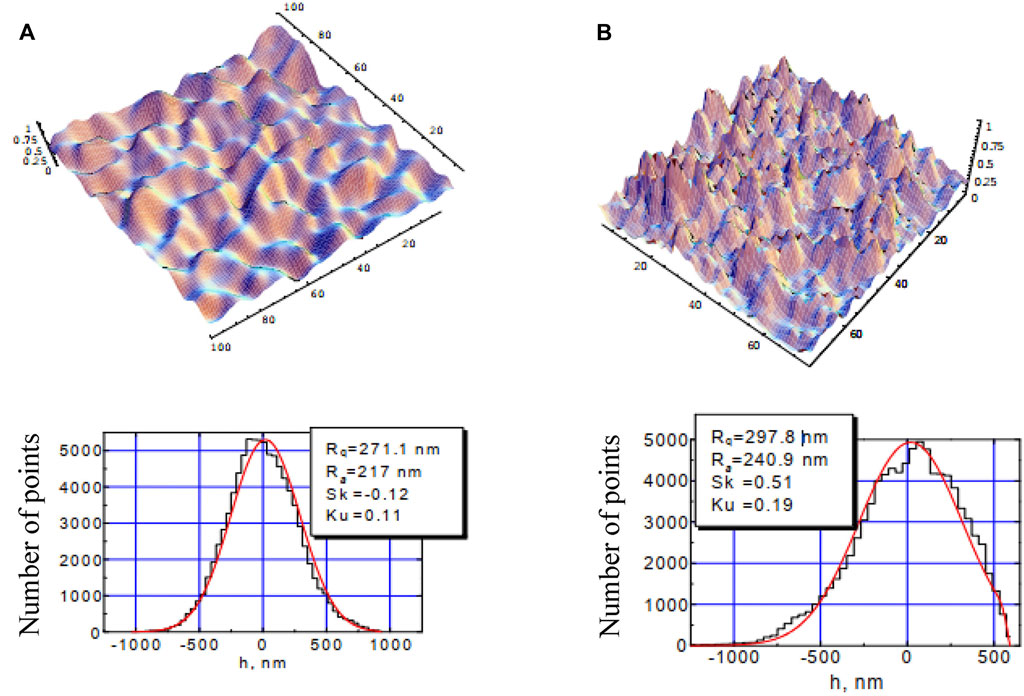
FIGURE 7. Relief, height distribution function and statistical parameters of (A) random non-fractal and (B) fractal surfaces. Sizes in the upper-row images are indicated in micrometers.

The statistical parameters are obtained via the discrete approximation of the function h (x, y) for which the surface is covered by the rectangular network (x_i, y_j), (i, j) = 1, 2, … N, with the step δ = x_i+1 –x_i = y_j+1 –y_j, and the values h_ij = h (x_i, y_j) are taken, for example,

$\mathrm{S}\mathrm{k}\simeq \frac{1}{R_q^3}\frac{1}{N^2}{\displaystyle \sum }_{i,j=1}^N{h}_{ij}^3,\mathrm{K}\mathrm{u}\simeq \frac{1}{R_q^4}\frac{1}{N^2}{\displaystyle \sum }_{i,j=1}^N{h}_{ij}^4-3,(18)$

$F\left({\rho }_x,{\rho }_y\right)\simeq \frac{{\displaystyle \sum }_{i,j=1}^N{h}_{ij}{h}_{i+m_x,j+m_y}}{{\displaystyle \sum }_{i,j=1}^N{h}_{ij}^2}.(19)$

Formally, the latter expression defines $F\left({\rho }_x,{\rho }_y\right)$ only in points where (ρ_x/δ) = m_x and (ρ_y/δ) = m_y are integer numbers but the values of $F\left({\rho }_x,{\rho }_y\right)$ at the intermediate points can be found via interpolation. Note that the kurtosis definition of Eq. 18 differs from the common one by the second summand, for which reason it expresses, in fact, the kurtosis “excess” above 3 [101].

The next step is to study peculiar features of light fields scattered by surfaces of different types [98]. An example of the field scattered from a non-fractal rough surface observed at an off-surface distance z = 100 μm is shown in Figure 8. In this example, the surface parameters were as follows: maximum height deviation h_max = 8 μm; total object size 400 × 400 μm²; the number of pixels 1,200 × 1,200 (which corresponds to N = 1,200, δ = 0.33 μm, see (Eq. 18)). Figure 8 demonstrates the field region of the size 5 × 5 μm², with the resolution determined by the number of pixels 1,000 × 1,000.

FIGURE 8

FIGURE 8. Example of the field scattered off a rough surface: (A) intensity distribution, (B) phase distribution.

The phase discontinuities are clearly seen in Figure 8B as the sharp boundaries between black (phase–π) and white (phase +π) areas; the phase singularities (screw WF dislocations) are at the ends of the discontinuity lines. In 3D space, the phase singularities form a set of continuous lines (singular skeleton of the scattered field) illustrated by Figure 9A (the pattern of Figure 8 represents the cross section of the same field at z = 100 μm). The phase singularities (amplitude zeros) in a fixed cross section z = const appear as the points where the singular lines cross the plane z = const. In Figure 9A, the singularities’ positions are shown in the cross sections z = 10, 40 and 70 μm (green points), z = 20 and 50 μm (blue points), z = 30 and 60 μm (red points). The singular lines are continuous; sometimes they go to z = ∞, sometimes closed loops are formed. In the latter case, numbers of singularities observed in different cross sections vary: the topological events of the dislocation birth and/or annihilation occur [14, 106].

FIGURE 9

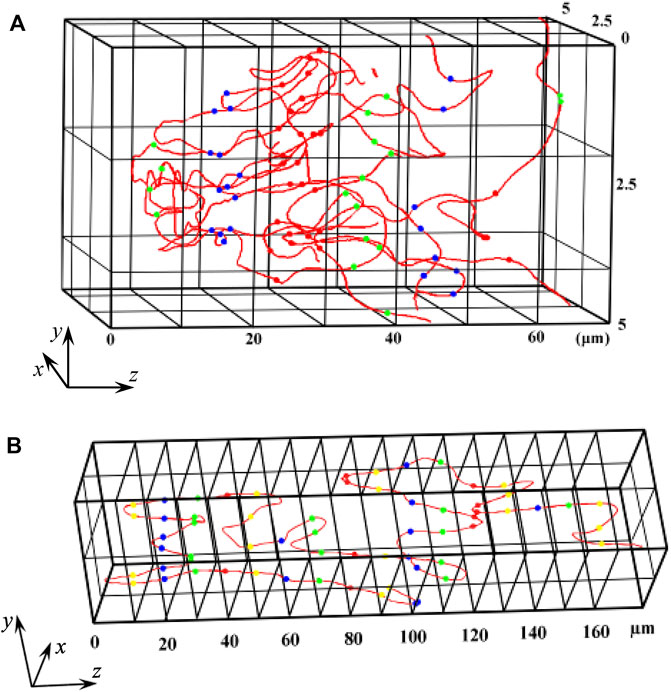
FIGURE 9. Examples of the singular lines forming the skeleton of a field scattered by a rough (A) non-fractal and (B) fractal surface.

Figure 9B illustrates the singular skeleton of the field scattered by a fractal surface with the same h_max, N, δ, object size 400 × 400 μm² and the field size 5 × 5 μm² as were accepted for the non-fractal object in Figures 8, 9A. Locations of the phase singularities in the cross sections chosen from z = 10 μm to z = 160 μm with the step 10 μm are shown by points of alternating colors (yellow—green—blue—red) discriminating the consecutive cross sections. It was found [98] that the field scattered by a fractal source shows statistical characteristics different from those typical for random surfaces. In particular, the fractal properties are inherent in 3D singularity lines, which can be seen from the power spectra (17) (Figure 10): in the double-logarithmic scale, the S(f) dependence is close to linear. For the function ρ_s(z), where ρ_s is the transverse shift of the dislocation line, the power spectrum (Figure 10A) obeys the relation S(f) = K_ν f^–ν. In the fields scattered by fractal surfaces with small height intervals (h_max = 2—5 μm), the spectral index is close to ν = 2, and the Hearst index H = (ν –1)/2 = 0.5, which is typical for generalized Brownian motion. The corresponding fractal dimension of different singularity lines varies in close vicinity of D_f = 2—H = 1.5 (see Eq. 17 and the comments thereby).

FIGURE 10

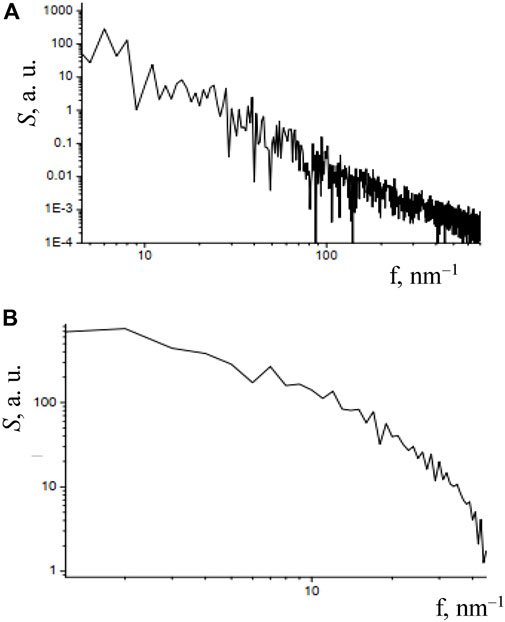
FIGURE 10. Power spectra of the singularity lines observed in the fields scattered by (A) fractal (see Figure 9B) and (B) random non-fractal (see Figure 9A) objects.

Increasing the height interval leads to larger phase delays between the waves scattered by different points of the surface and, as a consequence, to stronger chaotization of the phase fluctuations. This results in a decrease of the Hearst index, H < 0.5, and, correspondingly, the fractal dimension increases, D_f > 1.5.

5.3 Correlation-optics approach for diagnostics of phase singularities

Optical fields with phase singularities possess an interesting general property: for them, the amplitude correlation length ${\rho }_{cor}^E$ is higher than the intensity correlation length ${\rho }_{cor}^I$ (see (Eq. 16) and Figure 11A), and the difference essentially depends on the presence or absence of amplitude zeros within the observed field fragment [98]. This fact can be used for experimental detection of phase singularities as well as for the scattering object characterization.

FIGURE 11

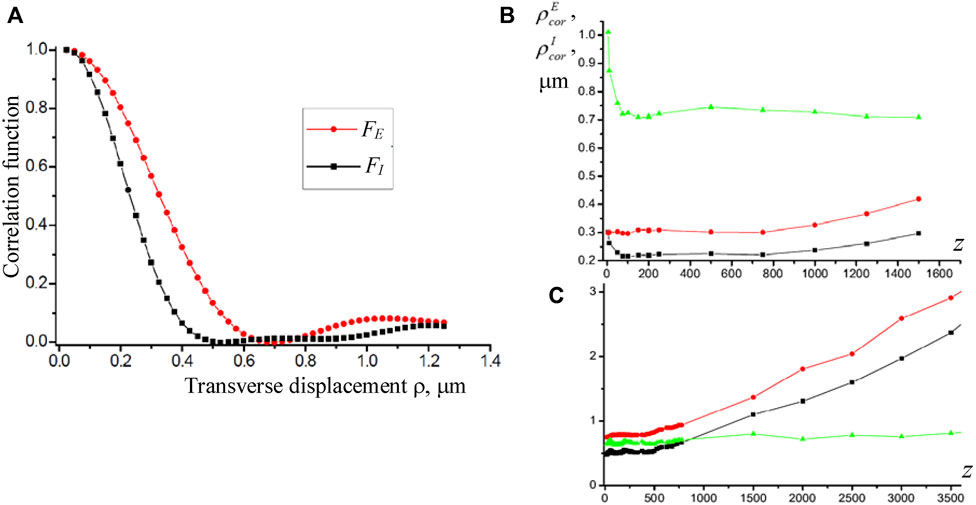
FIGURE 11. (A) Correlation functions of amplitude F_E(r) (14) and intensity F_I(r) (15) probed at a distance z = 100 μm from the object; z-dependencies of the correlation lengths of amplitude ${\rho }_{cor}^E$ (red) and of intensity ${\rho }_{cor}^I$ (black) of the field scattered by a (B) random rough surface and (C) fractal rough surface with h_max = 20 μm.

In particular, in the field scattered by a rough surface, the ratio of the correlation lengths $a={\rho }_{cor}^I/{\rho }_{cor}^E$ gradually saturates near 0.66–0.7 with growing propagation distance z (green curves in Figures 11B,C). In case of a random non-fractal surface, the saturation occurs after the rapid change in the near-field zone, whereas for a fractal surface, the ratio is approximately constant on the whole propagation distance. In the far field, both correlation lengths gradually increase due to spatial-frequency filtering. For the field scattered by a fractal surface, the correlation lengths are higher and grow more articulately than in the non-fractal situation. These features can be used in experimental practice for estimation of the number of speckles and the number of singularities (amplitude zeros) in the observed field area [98]. But the most interesting is their application for practical detection and diagnostics of OVs.

The fact is that in the immediately observable intensity patterns (for example, see Figure 8A or Figure 12A), the amplitude zeros are hardly distinguishable from the local intensity minima. Although the physical difference between these points is significant, it can only be seen via the phase distribution (i.e. Figure 8B or Figure 12C), whose visualization requires complex interference techniques and obeys some limitations in spatial resolution. The problem of the OV recognition can be solved if, after the preliminary selection of a small dark area L where the amplitude zero is suspected, the correlation analysis of the field inside this small area is performed (Figure 12). In this procedure, the local analogs of the correlation functions (14) and (15) are experimentally determined:

${\left[F_E\left(\mathbf{\rho }\right)\right]}_L=\frac{{\int }_{L}E\left(\mathbf{r}\right)E^{*}\left(\mathbf{r}+\mathbf{\rho }\right)d^2\mathbf{r}}{{\int }_{L}I\left(\mathbf{r}\right)d^2\mathbf{r}},{\left[F_I\left(\mathbf{\rho }\right)\right]}_L=\frac{{\int }_{L}I\left(\mathbf{r}\right)I\left(\mathbf{r}+\mathbf{\rho }\right)d^2\mathbf{r}}{{\int }_L{I}^2\left(\mathbf{r}\right)d^2\mathbf{r}}.(20)$

FIGURE 12

FIGURE 12. Localization of the amplitude zeros in the field scattered by a rough surface: (A) intensity distribution $I\left(\mathbf{r}\right)$; (B) preliminary locations of the intensity minima (shown by bright spots); (C) phase distribution; (D) locations of the amplitude zeros. Red contours in (B) indicate “false” zeros which are filtered out due to the correlation-length analysis.

In practice, the integrals are replaced by sums (as in Eqs 18 and 19), and for the statistical reliability, the number of pixels in the local area must be sufficient, which implies a high resolution of the field registration. Note that the shift magnitude |ρ| can, generally, exceed the size of the area L, provided that it does not reach the similar local area near another dark point. Then, the correlation lengths of amplitude ${\rho }_{cor}^E$ and of intensity ${\rho }_{cor}^I$ for functions (20) are evaluated similarly to (16):

${\left[F_E\left({\rho }_{cor}^E\right)\right]}_L=0.5{\left[F_E\left(0\right)\right]}_L,{\left[F_I\left({\mathit{\rho }}_{cor}^I\right)\right]}_L=0.5{\left[F_I\left(0\right)\right]}_L(21)$

and if the ratio $a_L={\left({\rho }_{cor}^I/{\rho }_{cor}^E\right)}_L$ appears to be less than a certain critical value (0.8 is recommended in [98]), the decision is made that the OV is present within the analyzed area. The whole procedure is illustrated by Figure 12. In this way, the singular skeleton of an arbitrary speckle field can be detected and localized with a high accuracy [98].

5.4 Practical schemes for the correlation analysis of speckle fields

The specific properties of the transverse correlation functions of random wave fields, and their peculiar features in fields scattered by surfaces with different structural inhomogeneities, served as the basis for the development of special instruments for the rough-surfaces’ diagnostics [29, 108–111]. The general scheme of such devices is presented in Figure 13.

FIGURE 13

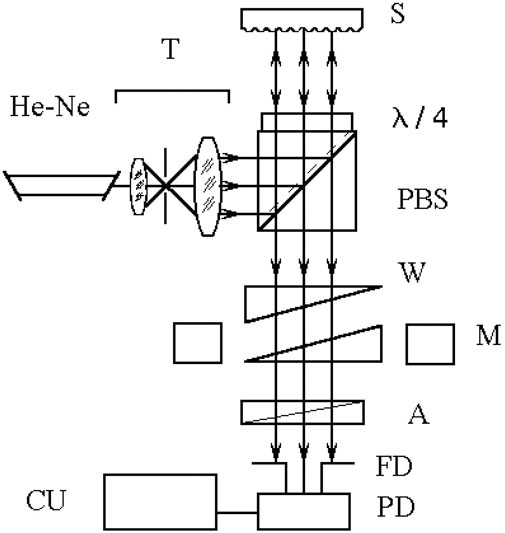
FIGURE 13. Experimental arrangement for measuring the surface roughness: (He-Ne) laser, (T) telescope, (PBS) polarizing beam-splitter, (S) sample, (W) calcite wedges, (M) electromechanical modulator, (A) analyzer, (FD) field-of-view diaphragm, (PD) photodetector, (CU) calculation unit.

A plane wave (632.8 nm) produced by the laser source and telescope T (microscope objective + pinhole diaphragm + objective lens), undergoes a total reflection in the polarizer cube PBS, and passes through the quarter-wave plate λ/4, after which it hits the surface S to be measured. The double pass of the plane wave through the quarter-wave plate results in a 90° rotation of the polarization plane. Thus, almost 100% of the reflected light passes through the polarizer cube. The wedges W (one of which is stationary, the other movable) are made of calcyte (birefringent material) in such a way that their main axis is oriented at 45° with respect to the polarization of the light wave exiting the PBS. Accordingly, the ordinary and extraordinary beams are formed with identical transverse profiles but mutually shifted in the transverse plane; the shift value is regulated by the movable wedge’s position. In turn, the main axis of the analyzer A is oriented at 45° to the polarization planes of the ordinary and extraordinary beams outgoing the wedges, and both of them obtain the same polarization and equal amplitudes at the analyzer output. As a result, the light power reaching the photodetector PD is proportional to

${\int }_{L}I\left(\mathbf{r}\right)d^2\mathbf{r}+{\int }_{L}I\left(\mathbf{r}+\mathbf{\rho }\right)d^2\mathbf{r}+2\mathrm{R}\mathrm{e}{\left[F_E\left(\mathbf{\rho }\right)\right]}_L\cdot {\int }_{L}I\left(\mathbf{r}\right)d^2\mathbf{r}(22)$

where the area of integration L is determined by the diaphragm FD, I(r) and F_E(ρ) are the intensity distribution and the correlation function (14) or (20) (regarding the diaphragm shape and position) of the wave scattered by the sample S, observed in the FD plane. Analysis of the function (22) may give meaningful information on the correlation functions (14) or (20) of the field. To this end, the measurement procedure is repeated for different displacements of the movable wedge, and the corresponding electric signals are processed by the electronic processor unit CU, which reconstructs the correlation properties of the scattered field, e.g., the correlation length, magnitudes of the amplitude and phase fluctuations, etc. In particular, the RMS surface-height deviation (12) can be estimated via relation

$R_q=\frac{\lambda }{4\pi }\sqrt{-\ln \frac{U_{\max }-U_{\min }}{U_{\max }+U_{\min }}}$

where U_max and U_min are the maximum and minimum of the signal registered by the photodetector when the beams’ mutual displacement changes due to the wedge translation.

The stationary and portable versions of the device for the surface roughness control based on measuring the scattered field’s coherence function were realized [29]. They are intended for diagnosing the slightly rough surfaces and enable measurements of the R_q values over the range 0.002 μm–0.10 μm with the measurement accuracy 0.002 μm; indication rate is one measurement per second. The device can be used for arbitrarily shaped surfaces with the radius of curvature larger than 0.3 m, which specifies its applicability areas: the photochemical industry to monitor the quality of crankshaft; space industry to monitor the quality of mirrors fabricated by diamond micro-sharpening; polishing machine tools where this device was used for the surface-quality on-line control.

Another approach for the surface roughness control was developed based on measuring a phase variance of the boundary object field (Figure 14). A telescope consisting of two objective lenses transforms a light beam from a single-mode laser source into a plane wave, which then undergoes amplitude splitting into a reference wave and an object wave using a beam splitter BS1. The object wave is focused by an objective lens O1 onto the rough surface of a sample S. The radiation reflected off the sample (object wave) is used to form the sample surface image in the plane of a 2 × 2 position-sensitive photodetector array PD. The radiation reflected by the mirror M forms a coaxial reference wave to interfere with the object wave, forming an interference pattern with fringes localized at infinity. The zero-order interference fringe is automatically kept within the photodetector array PD active area by means of a transverse displacement of the microobjective O2 in the reference arm using two electric motors EM, together with a longitudinal displacement of the mirror M using a piezoceramic modulator PM. In this manner, the amplitude modulation of the resulting light beam is simultaneously performed.

FIGURE 14

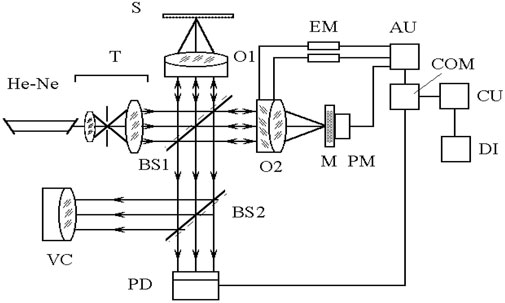
FIGURE 14. Experimental arrangement for measuring the roughness of low-reflectance surface, with the components: (He-Ne) laser, (T) telescope, (BS1, BS2) beam-splitters, (O1, O2) objective lenses, (S) sample, (M) mirror, (PM) piezoceramic modulator, (PD) 2×2 position-sensitive photodetector array, (VC) visualization channel, (EM) electric motors, (AU) automatic zero fringe adjustment unit, (COM) comparator, (CU) analogue calculation unit, (DI) digital indicator.

The output signal from the photodetector array PD is fed to the phase comparators, which generate control signals for the motors and piezoceramic modulator. The net signal is then transformed into the R_q value using the analog processing unit CU, and is displayed on the indicator DI.

The main technical parameters of the device described by Figure 14 are as follows: the measurable RMS height range 0.002–0.08 μm, the measurement accuracy 0.001 μm, indication rate is one measurement per 5 s. The device enables testing the plane and spherical surfaces with the radius of curvature larger than 0.2 m, and can be used in polishing machine tool for the surface quality control during the detail fabrication. Its characteristic feature is the possibility to analyze rough surface in the wide range of reflectivities (∼2%–100%), which is favorable for transparent optical surfaces of glass, quartz, etc. This device can be made as a stationary instrument.

Note that all devices described in this Section 5.4 are based on the following principal conditions:

- heights of surface micro-irregularities are less than the probing radiation wavelength, and their transverse scale is larger than the wavelength, so that the specular component of the reflected radiation is present;

- the phase variance is measured in the “boundary” scattered field, which is formed immediately near the sample surface (the sample surface is imaged at the plane of analysis, so that the effective propagation length z = 0); the transverse coherence function of a field can be measured for arbitrary cross section;

- statistical parameters of the scattered field are measured in interferometric arrangements, within the zero (infinitely extended) interference fringe.

5.5 Indirect reconstruction of the singular skeleton of speckle fields

The physical relevance of the optical-field phase information stimulates the continuous search for efficient means for its extraction from the immediately available intensity profiles [112–118]. Still, most of approaches are complicated and do not warrant appropriate results in real noisy conditions. Here we describe a general approximate method for reconstructing the phase skeleton of complex optical fields from the measured two-dimensional intensity distribution [119]. The core of the algorithm consists in locating the saddle points of the intensity distribution and connecting such points into nets by the “gradient lines” (GL)—lines of the steepest descent [120] of intensity. According to [119], the GL are closely associated with the equi-phase lines of the field, and their network provides a partial solution to the inverse problem in optics commonly referred to as the phase problem [97, 112].

The idea of the method is grounded on the empirical fact that, in stochastic fields, the regions of small intensity gradients (smooth spatial changes of intensity) are the regions with rapid change of phase [9]. That is why the GLs, that unite the saddle points and the minima of intensity, to a high degree (95%–98%) correlate with the characteristic lines of the phase distribution. The situation is illustrated by Figures 15A, B. It represents the simulated speckle-field cross section where the GL (yellow lines), saddle points (cyan triangles), intensity maxima (cyan rhombs), amplitude zeros (red and blue squares, discriminating the phase singularities with positive or negative TC), and the non-singular intensity minima (green squares) are shown together with the blue lines ImE (x,y) = 0 and red lines ReE (x,y) = 0. The phase map (Figure 15B) indicates the regions with relative phase 0 to π/2 (white), π/2 to π (light-grey), π to 3π/2 (dark-grey), and 3π/2 to 2π (black).

FIGURE 15

FIGURE 15. Top row: (A) Intensity and (B) phase distribution of a speckle field with the marked peculiar points of the intensity and phase profiles [119] (explanations in text). Bottom row: Views of the luminescent nanoparticles in the tested speckle field [121]: (C) At the moment of speckle field switching; (D) Recorded tracks of the particles during their field-induced motion; (E) The particles’ positions after their redistribution to the low-intensity regions (observation time 5 s).

Figures 15A, B illustrate two peculiarities of the GLs: 1) nonintersecting lines passing the saddle point connect phase singularities of opposite signs; 2) the most of the GLs approximately reproduce the equi-phase boundaries between the different-color areas of Figure 15B. Perhaps, the pattern of Figure 15B is not absolutely convincing but an accurate statistical analysis of the phase variations along the GLs has indicated 95% coincidence [119]. Note that the choice of boundary phases is conventional and, with different choice, the mentioned coincidence between the yellow lines and the equi-phase lines can be made still more impressive.

Supported by the proper interpolation techniques, the described approach [119] offers a simple and efficient algorithm for estimation of the phase distribution of complex stochastic fields, which are of the main interest in practical situations (despite that it is not applicable to some special cases, and one can easily find the corresponding examples). However, its further implementation needs additional means for recognition of the significant points and lines of the intensity distributions, and this task can be fulfilled with the help of new facilities supplied by the specially designed nanoprobes. To this purpose, the synthesized carbon nanoparticles [121] of the size about λ/10 with strong absorption in the yellow-green region (405 nm), weak absorption at the speckle-field wavelength (633 nm), and showing the luminescence at 530 nm were proposed.

According to the method presented in [121], the speckle field image is projected into the cuvette filled with water, in which the carbon nanoparticles are suspended (see the microscopic image of the selected field area 30 × 30 μm² in Figure 15C; the “green” particles are seen due to luminescence). Inside the inhomogeneous optical field, the particles experience mechanical influences of different natures [122–124]; normally, their optical properties determine that the main effect is produced by the gradient force. Under its action, the particles, being initially at random positions, start to move, predominantly in the directions of local transverse gradient of the field intensity (Figure 15D) and tend to the low-intensity regions (Figure 15E shows the picture observable 5 s after the speckle field is switched on), and ultimately concentrate in local intensity minima (the whole observation time is 30 s).

As a result, observing the nanoparticles and their motion in the field, one obtains the map of the intensity gradients and intensity minima. Not always the local intensity minima coincide with the “true” amplitude zeros (phase singularities) but the latter can be distinguished qualitatively by higher concentration of the “trapped” particles. The measurement errors in this method are caused by the Brownian motion, and to avoid the undesirable temperature effects, the temperature regime and the exposure time are controlled. In experiments of [121], the luminescence-exciting beam power was limited by 5 mW whereas the speckle-beam radiation (633 nm) is weakly absorbed, and its power can be chosen with some freedom.

Finally, the phase map and the full speckle-field pattern can be restored from the gradient lines and the phase singularities’ positions using the principles described above. Processing the optical field scattered by a stochastic object is recorded in real time and takes several minutes.

The approaches involving the fluorescent probe nanoparticles are expected to have many applications. First of all, we mention the recent proposition where the single fluorescent particle is controllably translated along the probed surface and is excited by a strongly focused beam [124]. The lateral position of the particle is dictated by a special optical tweezer connected to the atomic-force microscope, and can be controlled with 50–70 nm resolution; in turn, the particle “vertical” position on the surface is detected via the luminescence intensity with the accuracy of 3–5 nm, thus exceeding the usual limitations of the optical-field measurements by the wavelength order.

Other versions of the probe-particle approach may be developed which involve the particles of special properties enabling efficient luminescence excitation and quenching, depending on the particle position. These special properties can be attained, for example, by using plasmonic (highly conductive) particles of a certain size or morphology, coated by a dielectric layer with embedded fluorophore clusters, provided that the geometry of the particle is compatible with the characteristics of its excitation [125–127]. In such particles, radiation with a fluorophore-excitation wavelength will excite luminescence, and radiation with a plasmon-resonance wavelength will quench it. For example, if the particle is composed of a highly-conductive nanorod core and a fluorophore shell, the external light, polarized along the nanorod axis will excite the fluorescence, whereas when the light is polarized orthogonally, the transverse plasmon resonance will be excited, which leads to the luminescence quenching [125]. When such particles are used as the probe particles, their uniform orientation can be achieved due to their anisotropic polarizability and intrinsic dipole moments [128–132], e.g., by means of a properly oriented static electric field.

Light-matter interactions can be essentially enhanced at the nanoscale [133]. This is of particular benefit for light interactions with single nanoparticles, such as colloidal quantum dots, viruses, DNA fragments and proteins. To achieve structured light at the nanoscale, many researchers have used nanoplasmonics, shaping metals at the nanoscale to control the electromagnetic energy concentration. In such cases, additional degrees of freedom are offered by the light polarization: e.g., in a strongly focused beam, the electric field contains a strong longitudinal (z-) component [2, 3, 15], which can be used for controllable excitation or quenching of properly oriented anisotropic nanoparticles. Remarkably, due to the chemical and biological compatibility of the carbon nanoparticles, the above-discussed ideas and methods can be relevant for the diagnostics of biological tissues and media, for example, in the studies of non-stationary processes in cells.

To finalize Section 5.5, exposing the singularity-based rough-surface profilometry principles, we should add that in the past paragraphs we have touched on the subject of using the structured light for the precise profilometry. The associated concepts and approaches are promising and even inevitable in many situations where the use of interference methods is impossible: in the study of sharply focused beams [134]; in the analysis of dynamic liquid media, including the restoration of the size distribution function of micro and nanoparticles in dynamic light scattering technologies [135]; in the studies of turbulent gaseous media [136], as well as for the solution of problems of digital holographic interference in the analysis of non-stationary objects and scenes. Additionally to the approaches presented, in such cases the use of structured light with discrete spatial modes appears to be helpful [2, 137]. The corresponding technique is based on the projection (in the functional meaning) of the beam reflected by the sample onto a properly tailored spatial mode, which essentially enhances the signal-to noise ratio. The authors of [137] demonstrate the measurement of a step height smaller than 10 nm, i.e., (1/80) of the wavelength with a standard error in the picometer scale, and substantiate the feasibility of the proposed technique to the detection of subnanometer layer thicknesses.

6 Ubiquitous phase singularities in optics and matter waves

In this Section, we consider some additional examples illustrating the physical productivity and practical relevance of the ideas and concepts of singular optics. As the first such example we mention the group of phenomena explicitly demonstrating the peculiar internal energy flows in the beams with OV [138–147]. In Section 2, we discussed such manifestations in the edge-diffraction phenomena but really, the OV-caused “disbalance” of energy flows comes to light in every situation where its symmetry is broken [68, 148]. This is the case, for example, if an “oblique” section of the OV beam is important. This “orbital” analogue of the geometric spin Hall effect [149] manifests itself in the deformations of the transverse beam profile and in the corresponding shifts of the beam “center of gravity” when the beam experiences reflection or refraction at a plane interface [140–146]. The effect is especially expressive in case of non-specular reflection near the critical angle of total reflection [145], or when the beam undergoes a grating diffraction into a highly non-geometric order [138, 139]. This “orbital” Hall effect expresses the interaction between the “intrinsic” and “extrinsic” degrees of freedom of a singular light beam, which are discussed in much detail in a series of topical reviews (see, e.g., Ref. [150]).

Another important enhancement of the phase-singularity concepts is coupled with their penetration into the near-field optics, especially, into the vibrant domain of near-surface evanescent waves [151–156]. In works [151, 152], the singular evanescent wave is excited during the total internal reflection of an OV-carrying LG mode (4). The resulting field in the low-index region possesses vortex properties: it has well-defined OAM, residing in an azimuthal phase relative to the propagation direction of the internally reflected light. Such surface modes are characterized by a small mode volume, they can strongly couple to atomic or molecular systems in the vicinity of the surface. In case of counter-propagating, symmetrically incident LG_p^l modes, efficient 3D optical traps with parameters adjustable via the LG mode indices, can be realized.

Similar singular structures can be realized in the surface plasmon-polariton (SPP) waves supported by a metal-dielectric interface [2, 3]; in particular, this situation offers advantages of remarkably higher light intensity due to plasmonic enhancement [133]. In [153, 154], the radially propagating vortex SPP was excited due to coupling of a circularly polarized laser beam via a coaxial ring-like aperture in the gold film. As a result, near the metal-vacuum interface, the surface wave appears with the electric field components

$E_{\mathit{pr}}\left(r\right)=0,E_{p\varphi }\left(r\right)=i\sigma u_p\left(r\right)e^{i\sigma \varphi },E_{pz}\left(r\right)=-u_p\left(r\right)e^{i\sigma \varphi }(23)$

(r and ϕ are the polar coordinates in the interface plane, z-axis is directed along its normal) where

$u_p\left(r\right)=A{e}^{-\kappa z}\frac{H_1^{\left(1\right)}\left(kr\right)}{H_1^{\left(1\right)}\left(k{r}_0\right)},r\ge r_0,(24)$

r₀ is the aperture radius, σ = ±1 is the incident wave helicity, κ specifies the SPP near-interface confinement, and $H_1^{\left(1\right)}$ is the Hankel function [157]; the constants κ and A are determined by the incident laser beam and by the excitation geometry. The field (23), (24) is characterized by the helical phase but, in contrast to the usual OVs (3), where the helicity “evolves” in the cross-section plane, now the plane (r, ϕ) is the propagation plane. The phase dislocation “strength” (TC) is determined by the incident field polarization helicity σ. In the field (23), (24), the energy flow propagates within the (r, ϕ) plane along the spiral lines; the helical structure can be easily observed in the near field by means of interference, which is especially evident when multiple vortex SPPs are formed simultaneously [155, 156]. The phase terms σϕ in Eq. 22 are analogous to the spiral phase acquired by electron waves scattered by a cylinder containing a magnetic flux (optical analog of the Aharonov—Bohm effect [153, 158]). The formation of such surface waves can be treated as a sort of spin-orbital interaction, highly sensitive to the incident beam polarization, which offers a perfect quantum weak-measurement tool with a built-in post-selection in the SPP mode [154]. The vortex SPPs of this type show valuable abilities in observation fine light-matter interaction effects and characterizing the SPP-supporting interface topology. At this point, we should note that, generally, the SPP fields serve as efficient instruments for ultra-sensitive testing the surface properties, up to detection of single molecules or atomic-size defects [159, 160], as well as the surface roughness [161–163]. In this context, the unique properties of the singular SPPs similar to those described by Eqs 23, 24 may open new prospects due to their specific topological nature and peculiar polarization features.

Very interesting possibilities arise from the ideas of “coherence vortices” (CV)—“hidden” phase singularities which exist in the correlation function rather than in the immediately observable field distribution (1) [164–183]. Generally, usual partially-coherent paraxial fields are spatially inhomogeneous and are characterized by the two-point correlation function

$F\left({\mathbf{r}}_1,{\mathbf{r}}_2\right)=\frac{\langle E^{*}\left({\mathbf{r}}_1\right)E\left({\mathbf{r}}_2\right)\rangle }{{\langle I\left({\mathbf{r}}_1\right)\rangle }^{1/2}{\langle I\left({\mathbf{r}}_2\right)\rangle }^{1/2}}(25)$

where $I\left(\mathbf{r}\right)={\left|E\left(\mathbf{r}\right)\right|}^2$ is the local intensity, and angular brackets denote the ensemble average (this formula can be reduced to (14) if the field statistical properties in points r₁ and r₂ are identical, and $F\left({\mathbf{r}}_1,{\mathbf{r}}_2\right)$ depends only on the difference ρ = r₁—r₂). Actually, the coherence function (25) is four-dimensional [166, 167] but it can be characterized via its 2D projections. The most common situations are the following: 1) one point (say, r₁) is fixed and the correlation function (25) depends only on r₂ [165, 174–176], and 2) points r₁ and r₂ are interrelated such that r₁ =—r₂ [166, 167, 176]. The CVs are the singularities of the “reduced” 2D correlation functions $F\left(\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{s}\mathrm{t},{\mathbf{r}}_2\right)$ and $F\left({\mathbf{r}}_2,-{\mathbf{r}}_2\right)$ which may show the typical singular behavior in the r₂-plane while the observable complex amplitude distribution ⟨E (r₂)⟩ is everywhere regular at any moment of time.

For example, in the “wandering beam” model, the propagation of a LG₀^l beam (4) is considered while its axis position in the transverse plane is a random function, and the cross-correlation function of Eq. 25 can be determined as

$\langle E^{*}\left({\mathbf{r}}_1\right)E\left({\mathbf{r}}_2\right)\rangle =\int E^{*}\left({\mathbf{r}}_1-{\mathbf{r}}^{\prime }\right)E\left({\mathbf{r}}_2-{\mathbf{r}}^{\prime }\right)q\left({\mathbf{r}}^{\prime }\right)d^2{\mathbf{r}}^{\prime },q\left(\mathbf{r}\right)=\frac{1}{\pi {\rho }_c^2}\exp \left(-\frac{r^2}{{\rho }_c^2}\right)(26)$

where ρ_c is the measure of the transverse coherence. With the help of this model, it is demonstrated for a time-invariant linear optical system that there exists a definite connection between the usual OVs (phase singularities of the field amplitude), which appear when the system is illuminated by spatially coherent light, and the CVs of the function $F\left(\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{s}\mathrm{t},{\mathbf{r}}_2\right)$ which appear when it is illuminated by partially coherent light [173–176]. Usual OV beams can evolve into CVs when the degree of coherence falls down (ρ_c → 0): according to the conservation laws, the TC, associated with the phase singularity, “moves” from the field to the coherence function, as well as the OAM does.

When the projection 2) is used, the correlation function (25) $F\left({\mathbf{r}}_2,-{\mathbf{r}}_2\right)$ contains annular ring-like edge phase dislocations [9] with the configurations depending on the input partially-coherent LG_p^l beam characteristics [176–179]. The singularity of the function $F\left({\mathbf{r}}_2,-{\mathbf{r}}_2\right)$ may exist even in a non-vortex beam (l = 0) due to the non-zero radial index [178]. Interestingly, the number of ring dislocations in the far-field correlation function equals to 2p + |l| for the low-coherence cases. This fact may offer efficient means for measuring the magnitude and sign of TC of partially coherent OVs [178, 182], which would be particularly useful in atmospheric laser communication.

Based on the beam-wander model, investigations of the partially coherent LG beam propagation for any radial and azimuthal indices and at any propagation distance have been performed in [183]. It was shown that, as the coherence decreases, the correlation function acquires increasing number of the single-charged vortex-type singularities, and this effect depends on the radial index of the input LG beam. These observations indicate that a proper choice of randomization is favorable for the CVs’ detection and open new possibilities to sort photons not only by their TC but also by radial indices. During the beam propagation, the CVs exhibit “self-healing” properties, which are interpreted as a van Cittert–Zernike-style [28] evolution that depends strongly on the manner in which the beam is randomized. Though the total OAM of the beam is conserved, different distributions of the OAM density can be realized by adjusting the input radial index and propagation distance. These features can be applied in optical communications employing both azimuthal and radial orders of the OV beams as well as for the fine tuning of the rotation of particles trapped in OV beams [183].

Besides the beam-wander conditions, the CVs can be generated when an OV beam passes a random scatterer (e.g., rotating ground-glass disc) [179, 180], or due to special randomization of multiple partially-coherent “source” beams regularly arranged over the input plane [181]. In the arrangement of [179], the “regular” large-scale singularity is “hidden” inside the visually chaotic speckle structure but can be recovered via the correlation analysis. Notably, such CV structures are “robust”: After the beam passes through an obstacle which apparently blocks a noticeable part of the beam profile, its coherence function experiences essential changes but with further beam propagation, these changes disappear and the CV is restored [179, 180]. Together with the self-healing properties mentioned in the above paragraph [183], this fact is illustration of the important general feature of the CV structures: their high stability and low sensitivity to external perturbations, even when compared with the usual OVs. Remarkably, this stability can be enhanced by additional randomization and/or decrease of coherence of the input laser radiation [179, 181, 183].

All these facts illustrate the exclusive features of CVs as specific topological entities carrying information in the correlation degree of freedom, and testify for their bright prospects in applications for the data encoding, optical communication as well as in formation of structured fields with special configurations for optical trapping and manipulation. Remarkably, despite the impressive and sometimes counter-intuitive properties, the CVs are not so exotic as it seems at first glance: the correlation functions of black-body radiation are known to possess an infinite number of phase singularities (related to the zeros of the spherical Bessel functions [184]).

Since the early days of the “singular era” in optics, optical communications and data processing remain among the most important fields of application [49–51]. In the recent years, employment of the structured-light concepts opens up new possibilities in fundamental applications, including image visualization, increasing the throughput of communication systems through mode-separation multiplexing, high-dimensional quantum cryptography and the creation of multidimensional quantum encryption systems [80, 81, 185–188]. However, the usual optical encryption protocols have been primarily based on the first-order field characteristics, which are strongly affected by interference effects and make the systems unstable because of light–matter interaction. This defect is avoided in an alternative optical-encryption protocol [189] whereby the information is encoded into the second-order spatial coherence distribution of a structured random light beam via a generalized van Cittert–Zernike theorem. The new approach has two key advantages over its conventional counterparts: 1) the complexity of measuring the spatial coherence distribution of light enhances the encryption protocol security, and 2) the relative insensitivity of the second-order statistical characteristics of light to environmental noise makes the protocol robust against the environmental fluctuations, e.g., the atmospheric turbulence.

Optical singularities are essential elements of multiple applications of structured light for precision material handling. Manipulating the amplitude, intensity, phase or polarization leads to new fundamental implementations for solving a significant range of problems, such as optical communication technology, data security in information optics, material nanotechnology, etc. The main principles of optical manipulation [152, 190–192] are the same as were outlined in Section 5.5, see Figures 15C–E (a particle is “kept” inside the light-intensity minimum or maximum) but, due to the implementation facility and flexibility of control, specially tailored structured light fields [193–195] realize the “smart” optical-trapping technologies enabling the material engineering at the atomic level. The modern optical traps minimize the photon-scattering and thermal effects and use the coherence as an additional control channel. They find applications in the control of cold atoms, manipulation of the quantum states of the degenerate gases, generation of non-conventional states of the matter waves, etc.

The need for new ultra-compact structured-light sources gave impetus to the development of artificial optical materials, including metamaterials and metasurfaces, which determined the great enhancement of the means for purposeful light-field engineering [196–201]. The discovery of toroidal optical dipole traps made it possible to realize the conditions for confining a super-fluid Bose–Einstein condensate by introducing a weak radial barrier with tunable coupling [202]. The natural next step is associated with the possibility of manipulating de Broglie atomic waves by analogy with the manipulation of light waves in optics. Accordingly, the singular-optics ideas can be generalized to the matter-wave optics [203], as a complex of concepts and tools for manipulating the amplitude and phase of the atomic and electron waves.

We cannot exhaustively describe this fascinating emerging field within the limited frame of this review but merely mention that it opens new and very promising ways in the material science and optics. The central concept of the singular atom optics is the “electron vortex” [204–210] being the electron-wave analog of the usual screw WF dislocation (azimuthal harmonic (3)). With all the precautions caused by the different physical nature (electric charge instead of neutrality, half-integer spin, obeying the Dirac equation [211] instead of the Helmholtz one (2)), the electron vortex carries distinct characteristic features of the wave singularity stipulated by its topological nature. Just like an OV, an electron vortex is a spiral de Broglie wave carrying a quantized OAM. However, unlike the photon OAM, electronic OAM can directly excite dipole transitions in atoms due to the Coulomb interaction, thereby realizing new applications in nanooptics also, as well as participate in specific electromagnetic interactions [209, 210]. Waves of electronic matter have the ability of coherent transformation, with the possibility of creating elements analogous to holographic diffractive optics. Following the optical analogy, electron vortices are promising candidate for the data encoding and qubits-based quantum memory elements.

To sum up, the principles of the wave diagnostic and engineering capabilities, worked out on the example of optical singularities, are intensively transferring to the wave fields of other physical nature [30, 212, 213]. In these new fields, they form powerful grounds and promising prospects for impressive applications in the huge area of science and technology, from the subatomic scales to the biological cells and to the world of galaxies [30, 214, 215].

7 Conclusion

In this review, we tried to expose some selected features of singular optics which seem to us the most relevant and interesting in both fundamental and applied aspects. To this purpose, the generic properties of point-like phase singularities in scalar fields (OVs) are discussed in detail. This example is especially useful and demonstrative as it enables, via simple and intuitively clear models, to show the common features of vortex motions in different physical systems, from light fields to tornado storms and spiral galaxies [7, 25] and thus effectively exposes the unity of physical world and the general character of physical laws. In particular, the OV diffraction properties are discussed which reveal the singularity-related energy circulation in light beams (Section 2). The peculiarities of the OV-beams’ non-linear behavior, associated with their specific intensity profiles, are described in Section 3. On the other hand, the spontaneous parametric down-conversion with participation of the OV photons (Section 4) supplies a picturesque and instructive illustration of quantum entanglement but also opens impressive possibilities in advanced data encoding, quantum encryption, communication and computing.

In Section 5, the main attention is paid to the stochastic speckle fields that are known [92–97] to contain multiple optical singularities, which, due to their topological nature, form coherent and interrelated networks (“singular skeletons”) and characterize the optical field “as a whole”. In this Section, the principles of the statistical characterization of random singular fields are outlined; the specific features of the fields produced by fractal and non-fractal random scatterers are discussed, as well as the possibilities for their recognition via optical diagnostic means. Simultaneously, the methods of the singular-skeleton detection, and of the combined employment of correlation-optics and singular-optics approaches for the practical field diagnostics are presented in Section 5.3 and Section 5.5. In particular, they supply new solutions to the famous “phase problem” in optics [112, 114]: non-interference recovering the “full” field information from the immediately observed intensity distribution.

Section 6 offers a brief outlook of the singularity-associated problems and knowledges that are the subjects of continuing discussions and investigations. In particular, it describes the singularity-induced beam shifts, stipulated by the internal energy flows [138, 140, 145]; phase singularities and vortex-like structures in the surface evanescent waves [151, 153]; “coherence vortices” inherent in the field coherence function rather than in the complex amplitude distribution “per se” [175]. Advanced applications of the singular optical fields in optical communication systems and optical manipulation techniques are discussed. Finally, possible extrapolations of the singular-optics ideas and concepts on wave fields of other physical nature, such as acoustic waves, and, especially, matter waves and electron beams in quantum mechanics, are characterized in brief.

As a concluding remark, we should emphasize that it is impossible to exhaustively describe the development of concepts and applications associated with optical singularities, even restricted to the simplest case of phase dislocations in scalar fields, within the framework of one review. We believe that the data and knowledges, presented above, fairly reflect the current state of the art in singular optics but these are inevitably restricted by the experiences and interests of the authors. Many further impressive results and ideas can be found in other collections, for example, in topical special issues [87–90], recent reviews [5, 6, 30, 33], etc.

Author contributions

OA, CZ and PM contributed to conception and design of the study; CZ and JZ wrote the first draft of the manuscript; AB and JZ wrote Introduction and Conclusion; MV wrote Section 2 and Section 3; AB and MV wrote Section 4; OA, PM and CZ wrote Section 5, AB and MV wrote Section 6. All authors contributed to manuscript revision, read and approved the submitted version.

Funding

Research Institute of Zhejiang University—Taizhou, Center for Modern Optical Technology, China; Ministry of Education and Science of Ukraine (project 610/22, #0122U001830).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Andrews DL. Structured light and its applications: An introduction to phase-structured beams and nanoscale optical forces. Amsterdam: Academic Press (2011).

Google Scholar

2. Rubinsztein-Dunlop H, Forbes A, Berry MV, Dennis MR, Andrews DL, Mansuripur M, et al. Roadmap on structured light. J Opt (2017) 19:013001. doi:10.1088/2040-8978/19/1/013001

CrossRef Full Text | Google Scholar

3. Angelsky OV, Bekshaev AY, Hanson SG, Zenkova CY, Mokhun II, Zheng J. Structured light: Ideas and concepts. Front Phys (2020) 8:114. doi:10.3389/fphy.2020.00114

CrossRef Full Text | Google Scholar

4. Shen Y, Pidishety S, Nape IM, Dudley A. Self-healing of structured light: A review. J Opt (2022) 24:103001. doi:10.1088/2040-8986/ac8888

CrossRef Full Text | Google Scholar

5. Forbes A, de Oliveira M, Dennis MR. Structured light. Nat Photon (2021) 15(4):253–62. doi:10.1038/s41566-021-00780-4

CrossRef Full Text | Google Scholar

6. Dorrah AH, Capasso F. Tunable structured light with flat optics. Science (2022) 376:eabi6860. doi:10.1126/science.abi6860

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Angelsky OV, Bekshaev AY, Mokhun II, Vasnetsov MV, Zenkova CY, Hanson SG, et al. Review on the structured light properties: Rotational features and singularities. Opto-Electronics Rev (2022) 30:e140860. doi:10.24425/opelre.2022.140860

CrossRef Full Text | Google Scholar

8. Angelsky OV, Bekshaev AY, Zenkova CY, Ivansky DI, Zheng J. Correlation optics, coherence and optical singularities: Basic concepts and practical applications. Front Phys (2022) 10:924508. doi:10.3389/fphy.2022.924508

CrossRef Full Text | Google Scholar

9. Soskin MS, Vasnetsov MV. Singular optics. Prog Opt (2001) 42:219–76. doi:10.1016/S0079-6638(01)80018-4

CrossRef Full Text | Google Scholar

10. Nye JF, Berry MV. Dislocations in wave trains. Proc R Soc Lond A (1974) 336:165–90. doi:10.1098/rspa.1974.0012

CrossRef Full Text | Google Scholar

11. Berry MV. Singularities in waves and rays. In: R Balian, M Klaeman, and JP Poirier, editors. Physics of defects. Les houches lecture series session XXXV. Amsterdam: North Holland (1981). p. 453–549.

Google Scholar

12. Nye JF. Natural focusing and fine structure of light. Caustics and wave dislocations. Bristol: Institute of Physics Publishing (1999).

Google Scholar

13. Mokhun II. Introduction to linear singular optics. In: O Angelsky, editor. Optical correlation: Techniques and applications. Bellingham, Washington: SPIE Press (2007). p. 1–131. doi:10.1117/3.714999

CrossRef Full Text | Google Scholar

14. Dennis MR, O’Holleran K, Padgett MJ. Chapter 5 singular optics: Optical vortices and polarization singularities. Prog Opt (2009) 53:293–363. doi:10.1016/S0079-6638(08)00205-9

CrossRef Full Text | Google Scholar

15. Bekshaev A, Bliokh K, Soskin M. Internal flows and energy circulation in light beams. J Opt (2011) 13(5):053001. doi:10.1088/2040-8978/13/5/053001

CrossRef Full Text | Google Scholar

16. Bekshaev AY, Soskin MS. Transverse energy flows in vectorial fields of paraxial beams with singularities. Opt Commun (2007) 271:332–48. doi:10.1016/j.optcom.2006.10.057

CrossRef Full Text | Google Scholar

17. Gbur GJ. Singular optics. Boca Raton: CRC Press (2016). doi:10.1201/9781315374260

CrossRef Full Text | Google Scholar

18. Senthilkumaran P. Singularities in physics and engineering: Properties, methods, and applications. Bristol, UK: IOP Publishing (2018). doi:10.1088/978-0-7503-1698-9

CrossRef Full Text | Google Scholar

19.OV Angelsky, editor. Introduction to singular correlation optics. Bellingham: SPIE Press (2019).

Google Scholar

20. Ruchi, Senthilkumaran P, Pal SK. Phase singularities to polarization singularities. Int J Opt (2020) 2020:1–33. doi:10.1155/2020/2812803

CrossRef Full Text | Google Scholar

21. Baranova NB, Zel’dovich BY, Mamaev AV, Philipetskii NF, Shkunov VV. Dislocations of the wavefront of a speckle-inhomogeneous field (theory and experiment). JETP Lett (1981) 33:195–9.

Google Scholar

22. Baranova NB, Mamaev AV, Pilipetskii NV, Shkunov VV, Zel’dovich BY. Wave-front dislocations: Topological limitations for adaptive systems with phase conjugation. J Opt Soc Am (1983) 73:525–8. doi:10.1364/JOSA.73.000525

CrossRef Full Text | Google Scholar

23. Freund I, Soskin MS, Mokhun AI. Elliptic critical points in paraxial optical fields. Opt Commun (2002) 208(4-6):223–53. doi:10.1016/S0030-4018(02)01585-7

CrossRef Full Text | Google Scholar

24. Gbur G, Tyson RK. Vortex beam propagation through atmospheric turbulence and topological charge conservation. J Opt Soc Am A (2008) 25(1):225–30. doi:10.1364/JOSAA.25.000225

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Bekshaev A, Soskin M, Vasnetsov M. Paraxial light beams with angular momentum. New York: Nova Science Publishers (2008). p. 112.

Google Scholar

26. Roux FS. Distribution of angular momentum and vortex morphology in optical beams. Opt Commun (2004) 242:45–55. doi:10.1016/j.optcom.2004.08.006

CrossRef Full Text | Google Scholar

27. Bekshaev A, Orlinska O, Vasnetsov M. Optical vortex generation with a “fork” hologram under conditions of high-angle diffraction. Opt Commun (2010) 283:2006–16. –16. doi:10.1016/j.optcom.2010.01.012

CrossRef Full Text | Google Scholar

28. Francon M. Laser speckle and applications in optics. Academic Press (1979).

Google Scholar

29. Angelsky OV, Maksimyak PP. Optical correlation approaches in rough surface characterization. In: O Angelsky, editor. Optical correlation techniques and applications. Bellingham, Washington: SPIE Press (2007). p. 167–211. doi:10.1117/3.714999

CrossRef Full Text | Google Scholar

30. Shen Y, Wang X, Xie Z, Min C, Fu X, Liu Q, et al. Optical vortices 30 years on: OAM manipulation from topological charge to multiple singularities. Light Sci Appl (2019) 8:90. doi:10.1038/s41377-019-0194-2

PubMed Abstract | CrossRef Full Text | Google Scholar

31. Anan’ev YA. Laser resonators and the beam divergence problem. Bristol, Philadelphia & New York: Adam Hilger (1992).

Google Scholar

32. Berry MV. Optical vortices evolving from helicoidal integer and fractional phase steps. J Opt A: Pure Appl Opt (2004) 6:259–68. doi:10.1088/1464-4258/6/2/018

CrossRef Full Text | Google Scholar

33. Zhang H, Zeng J, Lu X, Wang Z, Zhao C, Cai Y. Review on fractional vortex beam. Nanophotonics (2022) 11(2):241–73. doi:10.1515/nanoph-2021-0616

CrossRef Full Text | Google Scholar

34. Basistiy IV, Pas’ko VA, Slyusar VV, Soskin MS, Vasnetsov MV. Synthesis and analysis of optical vortices with fractional topological charges. J Opt A: Pure Appl Opt (2004) 6:S166–9. doi:10.1088/1464-4258/6/5/003

CrossRef Full Text | Google Scholar

35. Gbur G. Fractional vortex Hilbert’s hotel. Optica (2016) 3(3):222–5. doi:10.1364/OPTICA.3.000222

CrossRef Full Text | Google Scholar

36. Allen L, Padgett MJ. The Poynting vector in Laguerre–Gaussian beams and the interpretation of their angular momentum density. Opt Commun (2000) 184(1-4):67–71. doi:10.1016/S0030-4018(00)00960-3

CrossRef Full Text | Google Scholar

37. Coullet P. Optical vortices. Opt Commun (1989) 73:403–8. doi:10.1016/0030-4018(89)90180-6

CrossRef Full Text | Google Scholar

38. Rosales-Guzmán C, Bhebhe N, Mahonis N, Forbes A. Multiplexing 200 spatial modes with a single hologram. J Opt (2017) 19(11):113501. doi:10.1088/2040-8986/aa8b8e

CrossRef Full Text | Google Scholar

39. Allen L, Beijersbergen MV, Spreeuw RJC, Woerdman JP. Orbital angular momentum of light and the transformation of Laguerre-Gaussian laser modes. Phys Rev A (1992) 45:8185–9. doi:10.1103/PhysRevA.45.8185

PubMed Abstract | CrossRef Full Text | Google Scholar

40. Friese MEJ, Enger J, Rubinsztein-Dunlop H, Heckenberg NR. Optical angular-momentum transfer to trapped absorbing particles. Phys Rev A (Coll Park) (1996) 54:1593–6. doi:10.1103/PhysRevA.54.1593

PubMed Abstract | CrossRef Full Text | Google Scholar

41. MacDonald MP, Paterson L, Volke-Sepulveda K, Arlt J, Sibbett W, Dholakia K. Creation and manipulation of three-dimensional optically trapped structures. Science (2002) 296:1101–3. doi:10.1126/science.1069571

PubMed Abstract | CrossRef Full Text | Google Scholar

42. Vasnetsov MV, Marienko IG, Soskin MS. Self-reconstruction of an optical vortex. JETP Lett (2000) 71:130–3. doi:10.1134/1.568297

CrossRef Full Text | Google Scholar

43. Arlt J. Handedness and azimuthal energy flow of optical vortex beams. J Mod Opt (2003) 50:1573–80. doi:10.1080/09500340308235231

CrossRef Full Text | Google Scholar

44. Bekshaev A, Mohammed KA, Kurka IA. Transverse energy circulation and the edge diffraction of an optical-vortex beam. Appl Opt (2014) 53:B27–37. doi:10.1364/AO.53.000B27

PubMed Abstract | CrossRef Full Text | Google Scholar

45. Bekshaev A, Chernykh A, Khoroshun A, Mikhaylovskaya L. Localization and migration of phase singularities in the edge-diffracted optical-vortex beams. J Opt (2016) 18:024011. doi:10.1088/2040-8978/18/2/024011

CrossRef Full Text | Google Scholar

46. Bekshaev A, Chernykh A, Khoroshun A, Mikhaylovskaya L. Displacements and evolution of optical vortices in edge-diffracted Laguerre-Gaussian beams. J Opt (2017) 19:055605. doi:10.1088/2040-8986/aa6352

CrossRef Full Text | Google Scholar

47. Bekshaev A, Chernykh A, Khoroshun A, Mikhaylovskaya L. Singular skeleton evolution and topological reactions in edge-diffracted circular optical-vortex beams. Opt Commun (2017) 397:72–83. doi:10.1016/j.optcom.2017.03.062

CrossRef Full Text | Google Scholar

48. Bekshaev A, Angelsky O, Hanson SG. Transformations and evolution of phase singularities in diffracted optical vortices. In. Advances in optics: Reviews, book series: SY Yurish, editor, 1. Barcelona, Spain: International Frequency Sensor Association (2018). p. 345–89.

Google Scholar

49. Gibson G, Courtial J, Padgett MJ, Vasnetsov M, Pas’ko V, Barnett SM, et al. Free-space information transfer using light beams carrying orbital angular momentum. Opt Express (2004) 12:5448–56. doi:10.1364/OPEX.12.005448

PubMed Abstract | CrossRef Full Text | Google Scholar

50. Martelli P, Gatto A, Boffi P, Martinelli M. Free-space optical transmission with orbital angular momentum division multiplexing. Electron Lett (2011) 47:972–3. doi:10.1049/el.2011.1766

CrossRef Full Text | Google Scholar

51. Willner AE, Ren Y, Xie G, Yan Y, Li L, Zhao Z, et al. Recent advances in high-capacity free-space optical and radio-frequency communications using orbital angular momentum multiplexing. Phil Trans R Soc A (2017) 375:20150439. doi:10.1098/rsta.2015.0439

PubMed Abstract | CrossRef Full Text | Google Scholar

52. Basistiy IV, Slyusar VV, Soskin MS, Vasnetsov MV, Bekshaev AY. Manifestation of the rotational Doppler effect by use of an off-axis optical vortex beam. Opt Lett (2003) 28:1185–7. doi:10.1364/OL.28.001185

PubMed Abstract | CrossRef Full Text | Google Scholar

53. Courtial J, Dholakia K, Robertson DA, Allen L, Padgett MJ. Measurement of the rotational frequency shift imparted to a rotating light beam possessing orbital angular momentum. Phys Rev Lett (1998) 80:3217–9. doi:10.1103/PhysRevLett.80.3217

CrossRef Full Text | Google Scholar

54. Courtial J, Robertson DA, Dholakia K, Allen L, Padgett MJ. Rotational frequency shift of a light beam. Phys Rev Lett (1998) 81:4828–30. doi:10.1103/PhysRevLett.81.4828

CrossRef Full Text | Google Scholar

55. Vasnetsov MV, Torres JP, Petrov DV, Torner L. Observation of the orbital angular momentum spectrum of a light beam. Opt Lett (2003) 28:2285–7. doi:10.1364/OL.28.002285

PubMed Abstract | CrossRef Full Text | Google Scholar

56. Bekshaev AY, Soskin MS, Vasnetsov MV. Rotation of arbitrary optical image and the rotational Doppler effect. Ukr J Phys (2004) 49:490–5.

Google Scholar

57. Bekshaev A, Popov A. Noncollinear rotational Doppler effect. Proc SPIE (2004) 5477:55–66. doi:10.1117/12.558759

CrossRef Full Text | Google Scholar

58. Zhou HL, Fu DZ, Dong JJ, Zhang P, Chen DX, Cai XL, et al. Orbital angular momentum complex spectrum analyzer for vortex light based on the rotational Doppler effect. Light Sci Appl (2017) 6(4):e16251. doi:10.1038/lsa.2016.251

PubMed Abstract | CrossRef Full Text | Google Scholar

59. Cheng TY, Wang WY, Li JS, Guo JX, Liu S, Lü JQ. Rotational Doppler effect in vortex light and its applications for detection of the rotational motion. Photonics (2022) 9:441. doi:10.3390/photonics9070441

CrossRef Full Text | Google Scholar

60. Fang L, Padgett MJ, Wang J. Sharing a common origin between the rotational and linear Doppler effects. Laser Photon Rev (2017) 11(6):1700183. doi:10.1002/lpor.201700183

CrossRef Full Text | Google Scholar

61. Balzer G, Matamontero S, Vasnetsov M, Tschudi T. Phase defects in a phase-conjugate photorefractive-gain oscillator. J Mod Opt (1994) 41(4):807–16. doi:10.1080/09500349414550811

CrossRef Full Text | Google Scholar

62. Ilyenkov AV, Khiznyak AI, Kreminskaya LV, Soskin MS, Vasnetsov MV. Birth and evolution of wave-front dislocations in a laser beam passed through a photorefractive LiNbO3: Fe crystal. Appl Phys B (1996) 62(5):465–71. doi:10.1007/BF01081045

CrossRef Full Text | Google Scholar

63. Arecchi FT, Giacomelli G, Ramazza PL, Residori S. Vortices and defect statistics in two-dimensional optical chaos. Phys Rev Lett (1991) 67(27):3749–52. doi:10.1103/PhysRevLett.67.3749

PubMed Abstract | CrossRef Full Text | Google Scholar

64. Weiss CO. Spatio-temporal structures. Part II. Vortices and defects in lasers. Phys Rep (1992) 219(3-6):311–38. doi:10.1016/0370-1573(92)90145-P

CrossRef Full Text | Google Scholar

65. Staliunas K. Vortices and dark solitons in the two-dimensional nonlinear Schrödinger equation. Chaos, Solitons & Fractals (1994) 4(8-9):1783–96. doi:10.1016/0960-0779(94)90111-2

CrossRef Full Text | Google Scholar

66. Mamaev AV, Saffman M, Zozulya AA. Decay of high order optical vortices in anisotropic nonlinear optical media. Phys Rev Lett (1997) 78:2108–11. doi:10.1103/PhysRevLett.78.2108

CrossRef Full Text | Google Scholar

67. Bekshaev AY, Soskin MS, Vasnetsov MV. Transformation of higher-order optical vortices upon focusing by an astigmatic lens. Opt Commun (2004) 241(4-6):237–47. doi:10.1016/j.optcom.2004.07.023

CrossRef Full Text | Google Scholar

68. Bekshaev AY, Karamoch AI. Astigmatic telescopic transformation of a high-order optical vortex. Opt Commun (2008) 281:5687–96. doi:10.1016/j.optcom.2008.09.017

CrossRef Full Text | Google Scholar

69. Desyatnikov AS, Kivshar YS, Torner L. Optical vortices and vortex solitons. Prog Opt (2005) 47:291–391. doi:10.1016/S0079-6638(05)47006-7

CrossRef Full Text | Google Scholar

70. Swartzlander GA, Anderson DR, Regan JJ, Yin H, Kaplan AE. Spatial dark-soliton stripes and grids in self-defocusing materials. Phys Rev Lett (1991) 66:1583–6. doi:10.1103/PhysRevLett.66.1583

PubMed Abstract | CrossRef Full Text | Google Scholar

71. McDonald GS, Syed KS, Firth WJ. Optical vortices in beam propagation through a self-defocussing medium. Opt Commun (1992) 94:469–76. doi:10.1016/0030-4018(92)90589-J

CrossRef Full Text | Google Scholar

72. Luther-Davies B, Christou J, Tikhonenko V, Kivshar YS. Optical vortex solitons: Experiment versus theory. J Opt Soc Am B (1997) 14:3045–53. doi:10.1364/JOSAB.14.003045

CrossRef Full Text | Google Scholar

73. Soskin MS, Vasnetsov MV. Nonlinear singular optics. Pure Appl Opt (1998) 7:301–11. doi:10.1088/0963-9659/7/2/019

CrossRef Full Text | Google Scholar

74. Petrov DV, Torner L, Martorell J, Vilaseca R, Torres JP, Cojocaru C. Observation of azimuthal modulational instability and formation of patterns of optical solitons in a quadratic nonlinear crystal. Opt Lett (1998) 23:1444–6. doi:10.1364/OL.23.001444

PubMed Abstract | CrossRef Full Text | Google Scholar

75. Di Trapani P, Beržanskis A, Minardi S, Sapone S, Chinaglia W. Observation of optical vortices and J₀ Bessel-like beams in quantum-noise parametric amplification. Phys Rev Lett (1998) 81(23):5133–6. doi:10.1103/PhysRevLett.81.5133

CrossRef Full Text | Google Scholar

76. Arlt J, Dholakia K, Allen L, Padgett M. Parametric down-conversion for light beams possessing orbital angular momentum. Phys Rev A (1999) 59:3950–2. doi:10.1103/PhysRevA.59.3950

CrossRef Full Text | Google Scholar

77. Arnaut HH, Barbosa GA. Orbital and intrinsic angular momentum of single photons and entangled pairs of photons generated by parametric down-conversion. Phys Rev Lett (2000) 85:286–9. doi:10.1103/PhysRevLett.85.286

PubMed Abstract | CrossRef Full Text | Google Scholar

78. Franke-Arnold S, Barnett SM, Padgett MJ, Allen L. Two-photon entanglement of orbital angular momentum states. Phys Rev A (2002) 65(3):033823. doi:10.1103/PhysRevA.65.033823

CrossRef Full Text | Google Scholar

79. Mair A, Vaziri A, Weichs G, Zeilinger A. Entanglement of the orbital angular momentum states of photons. Nature (2001) 412(6844):313–6. doi:10.1038/35085529

PubMed Abstract | CrossRef Full Text | Google Scholar

80. Krenn M, Handsteiner J, Fink M, Fickler R, Zeilinger A. Twisted photon entanglement through turbulent air across Vienna. Proc Natl Acad Sci U S A (2015) 112:14197–201. doi:10.1073/pnas.1517574112

PubMed Abstract | CrossRef Full Text | Google Scholar

81. Mirhosseini M, Magaña-Loaiza OS, O’Sullivan MN, Rodenburg B, Malik M, Lavery MP, et al. High-dimensional quantum cryptography with twisted light. New J Phys (2015) 17:033033. doi:10.1088/1367-2630/17/3/033033

CrossRef Full Text | Google Scholar

82. Krenn M, Malik M, Erhard M, Zeilinger A. Orbital angular momentum of photons and the entanglement of Laguerre–Gaussian modes. Phil Trans R Soc A (2017) 375(2087):20150442. doi:10.1098/rsta.2015.0442

PubMed Abstract | CrossRef Full Text | Google Scholar

83. Bazhenov VY, Vasnetsov MV, Soskin MS. Laser beams with screw dislocations in their wavefronts. JETP Lett (1990) 52:429–31.

Google Scholar

84. Heckenberg NR, McDuff R, Smith CP, White AG. Generation of optical phase singularities by computer-generated holograms. Opt Lett (1992) 17:221–3. doi:10.1364/OL.17.000221

PubMed Abstract | CrossRef Full Text | Google Scholar

85. Gomes RM, Salles A, Toscano F, Ribeiro PS, Walborn SP. Observation of a nonlocal optical vortex. Phys Rev Lett (2009) 103(3):033602. doi:10.1103/PhysRevLett.103.033602

PubMed Abstract | CrossRef Full Text | Google Scholar

86. Gomes RM, Salles A, Toscano F, Ribeiro PS, Walborn SP. Production of optical phase space vortices with non-locally distributed mode converters. J Opt (2011) 13(6):064020. doi:10.1088/2040-8978/13/6/064020

CrossRef Full Text | Google Scholar

87. Berry MV, Dennis MR, Soskin MS. The plurality of optical singularities. J Opt A: Pure Appl Opt (2004) 6(5):S155–6. doi:10.1088/1464-4258/6/5/E01

CrossRef Full Text | Google Scholar

88. Molina-Terriza G, Padgett M. Special issue on optical angular momentum. J Opt (2011) 13(6):060201. doi:10.1088/0240-8978/13/6/060201

CrossRef Full Text | Google Scholar

89. Desyatnikov AS, Fadeyeva TA, Dennis MR. Special issue on singular optics. J Opt (2013) 15(4):040201. doi:10.1088/2040-8978/15/4/040201

CrossRef Full Text | Google Scholar

90. Soskin M, Boriskina SV, Chong Y, Dennis MR, Desyatnikov A. Singular optics and topological photonics. J Opt (2017) 19(1):010401. doi:10.1088/2040-8986/19/1/010401

CrossRef Full Text | Google Scholar

91. Angelsky OV, Maksimyak PP, Magun II, Perun TO. On the spatial stochastisation of optical fields and possibilities of optical diagnostics of objects with large-scale phase inhomogeneities. Opt Spectrosc (1991) 71(1):123–8.

Google Scholar

92. Freund I, Shvartsman N. Wave-field phase singularities: The sign principle. Phys Rev A (1994) 50(6):5164–72. doi:10.1103/PhysRevA.50.5164

PubMed Abstract | CrossRef Full Text | Google Scholar

93. Freund I, Shvartsman N, Freilikher V. Optical dislocation networks in highly random media. Opt Commun (1993) 101(3–4):247–64. doi:10.1016/0030-4018(93)90375-F

CrossRef Full Text | Google Scholar

94. Berry MV, Dennis MR. Phase singularities in isotropic random waves. Proc R Soc Lond A (2000) 456:2059–79. doi:10.1098/rspa.2000.0602

CrossRef Full Text | Google Scholar

95. Berry MV, Dennis MR. Polarization singularities in isotropic random vector waves. Proc R Soc Lond A (2001) 457:141–55. doi:10.1098/rspa.2000.0660

CrossRef Full Text | Google Scholar

96. Berry MV, Dennis MR. Knotted and linked phase singularities in monochromatic waves. Proc R Soc Lond A (2001) 457:2251–63. doi:10.1098/rspa.2001.0826

CrossRef Full Text | Google Scholar

97. Galushko Y, Mokhun I. Characteristics of scalar random field and its vortex networks. Recovery of the optical phase. J Opt A: Pure Appl Opt (2009) 11:094017. doi:10.1088/1464-4258/11/9/094017

CrossRef Full Text | Google Scholar

98. Angelsky OV, Maksimyak AP, Maksimyak PP, Hanson SG. Spatial behaviour of singularities in fractal- and Gaussian speckle fields. Open Opt J (2009) 3:29–43. doi:10.2174/1874328500903010029

CrossRef Full Text | Google Scholar

99. Mandelbrot BB. The fractal geometry of nature. New York: Freeman (1982).

Google Scholar

100. Falconer KJ. Fractal geometry. New York: Wiley (1990).

Google Scholar

101. Angelsky OV, Maksimyak PP, Ryukhtin VV, Hanson SG. New feasibilities for characterizing rough surfaces by optical-correlation techniques. Appl Opt (2001) 40:5693–707. doi:10.1364/AO.40.005693

PubMed Abstract | CrossRef Full Text | Google Scholar

102. Angelsky OV, Burkovets DN, Kovalchuk AV, Hanson SG. Fractal description of rough surfaces. Appl Opt (2002) 41:4620–9. doi:10.1364/AO.41.004620

PubMed Abstract | CrossRef Full Text | Google Scholar

103. Angelsky OV, Burkovets DN, Maksimyak PP, Hanson SG. Applicability of the singular-optics concept for diagnostics of random and fractal rough surfaces. Appl Opt (2003) 42:4529–40. doi:10.1364/AO.42.004529

PubMed Abstract | CrossRef Full Text | Google Scholar

104. Church EL. Fractal surface finish. Appl Opt (1998) 27:1518–26. doi:10.1364/AO.27.001518

PubMed Abstract | CrossRef Full Text | Google Scholar

105. Church EL. Comments on the correlation length. Proc SPIE (1986) 0680102–11. doi:10.1117/12.939599

CrossRef Full Text | Google Scholar

106. O'Holleran K, Dennis MR, Padgett MJ. Illustrations of optical vortices in three dimensions. J Eur Opt Soc Rap Public (2006) 1:06008. doi:10.2971/jeos.2006.06008

CrossRef Full Text | Google Scholar

107. Soroko LM. Holography and coherent optics. NY, London: Plenum Press (1980).

Google Scholar

108. Angelsky OV, Maksimyak PP. Optical correlation diagnostics of surface roughness in coherent-domain optical methods. In: VV Tuchin, editor. Coherent-domain optical methods: Biomedical diagnostics, environmental and material science. Boston: Kluwer Academic Publishers (2004). p. 67–119.

Google Scholar

109. Angelsky OV, Hanson SG, Maksimyak AP, Maksimyak PP. On the feasibility for determining the amplitude zeroes in polychromatic fields. Opt Express (2005) 13:4396–405. doi:10.1364/OPEX.13.004396

PubMed Abstract | CrossRef Full Text | Google Scholar

110. Angelsky OV, Maksimyak PP. Optical diagnostics of slightly rough surfaces. Appl Opt (1992) 31, 140–3. doi:10.1364/AO.31.000140

PubMed Abstract | CrossRef Full Text | Google Scholar

111. Angelsky OV, Maksimyak PP, Hanson S. Use of optical-correlation techniques for characterizing scattering object and media. Bellingham: SPIE Press PM71 (1999).

Google Scholar

112.HP Baltes, editor. Inverse source problems in optics. Berlin, Heidelberg: Springer-Verlag (1978).

Google Scholar

113. Nakajima N, Asakura T. Two-dimensional phase retrieval using the logarithmic Hilbert transform and the estimation technique of zero information. J Phys D: Appl Phys (1986) 19(3):319–31. doi:10.1088/0022-3727/19/3/005

CrossRef Full Text | Google Scholar

114. Gerchberg RW, Saxton WO. A practical algorithm for the determination of the phase from image and diffraction plane pictures. Optik (1972) 35:237–46.

Google Scholar

115. Wang K, Xiao P, Feng X, Wu G. Image feature detection from phase congruency based on two-dimensional Hilbert transform. Pattern Recognition Lett (2011) 32(15):2015–24. doi:10.1016/j.patrec.2011.08.013

CrossRef Full Text | Google Scholar

116. Latychevskaia T. Iterative phase retrieval for digital holography: Tutorial. J Opt Soc Am A (2019) 36(12):D31–40. doi:10.1364/JOSAA.36.000D31

PubMed Abstract | CrossRef Full Text | Google Scholar

117. Zenkova CY, Gorsky MP, Ryabiy PA. Phase retrieval of speckle fields based on 2D Hilbert transform. Opt Mem Neural Networks (2015) 24(4):303–8. doi:10.3103/S1060992X15040074

CrossRef Full Text | Google Scholar

118. Zenkova CY, Gorsky MP, Ryabiy PA, Angelskaya AO. Additional approaches to solving the phase problem in optics. Appl Opt (2016) 55(12):B78–84. doi:10.1364/AO.55.000B78

PubMed Abstract | CrossRef Full Text | Google Scholar

119. Angelsky OV, Gorsky MP, Hanson SG, Lukin VP, Mokhun , Polyanskii PV, et al. Optical correlation algorithm for reconstructing phase skeleton of complex optical fields for solving the phase problem. Opt Express (2014) 22:6186–93. doi:10.1364/OE.22.006186

PubMed Abstract | CrossRef Full Text | Google Scholar

120.Wikipedia. 2022 Gradient descent. Available at: https://en.wikipedia.org/wiki/Gradient_descent (Accessed November 04, 2022).

Google Scholar

121. Angelsky OV, Zenkova CY, Hanson SG, Ivansky DI, Tkachuk VM, Zheng J. Random object optical field diagnostics by using carbon nanoparticles. Opt Express (2021) 29:916–28. doi:10.1364/OE.411118

PubMed Abstract | CrossRef Full Text | Google Scholar

122. Bekshaev AY. Subwavelength particles in an inhomogeneous light field: Optical forces associated with the spin and orbital energy flows. J Opt (2013) 15:044004. doi:10.1088/2040-8978/15/4/044004

CrossRef Full Text | Google Scholar

123. Bekshaev AY, Angelsky OV, Hanson SG, Zenkova CY. Scattering of inhomogeneous circularly polarized optical field and mechanical manifestation of the internal energy flows. Phys Rev A (2012) 86(2):023847. doi:10.1103/PhysRevA.86.023847

CrossRef Full Text | Google Scholar

124. Angelsky OV, Bekshaev AY, Zenkova CY, Ivansky DI, Zheng J, Tkachuk VM. Fluorescence record diagnostics of 3D rough-surface landscapes with nano-scale inhomogeneities. Front Phys (2022) 9:787821. doi:10.3389/fphy.2021.787821

CrossRef Full Text | Google Scholar

125. Ming T, Zhao L, Yang Z, Chen H, Sun L, Wang J, et al. Strong polarization dependence of plasmon-enhanced fluorescence on single gold nanorods. Nano Lett (2009) 9(11):3896–903. doi:10.1021/nl902095q

PubMed Abstract | CrossRef Full Text | Google Scholar

126. Demchenko A. Excitons in carbonic nanostructures. C (2019) 55(4):71. doi:10.3390/c5040071

CrossRef Full Text | Google Scholar

127. Kamanina NV, Shurpo NA, Likhomanova SV, Timonin DN, Serov SV, Barinov OV, et al. Features of the nanostructured composites. In: Tenth international conference on material technologies and modeling. Ariel, Israel: Ariel University (2011). p. 77–85. Avaliable at: https://www.ariel.ac.il/sites/conf/mmt/ws2011/service%20files/papers/77-85.pdf (Accessed November 04, 2022).

Google Scholar

128. Otani M, Okada S, Okamoto Y. Intrinsic dipole moment on the capped carbon nanotubes. Phys Rev B (2009) 80:153413. doi:10.1103/PhysRevB.80.153413

CrossRef Full Text | Google Scholar

129. Martin JW, Slavchov RI, Yapp EKY, Akroyd J, Mosbach S, Kraft M. The polarization of polycyclic aromatic hydrocarbons curved by pentagon incorporation: The role of the flexoelectric dipole. J Phys Chem C (2017) 121:27154–63. doi:10.1021/acs.jpcc.7b09044

CrossRef Full Text | Google Scholar

130. Kutrovskaya S, Chestnov I, Osipov A, Samyshkin V, Sapegina I, Kavokin A, et al. Electric field assisted alignment of monoatomic carbon chains. Sci Rep (2020) 10:9709. doi:10.1038/s41598-020-65356-8

PubMed Abstract | CrossRef Full Text | Google Scholar

131. Lethiec C, Laverdant J, Vallon H, Javaux C, Dubertret B, Frigerio J-M, et al. Measurement of three-dimensional dipole orientation of a single fluorescent nanoemitter by emission polarization analysis. Phys Rev X (2014) 4:021037. doi:10.1103/physrevx.4.021037

CrossRef Full Text | Google Scholar

132. Lotito V, Sennhauser U, Hafner CV, Bona G-L. Interaction of an asymmetric scanning near field optical microscopy probe with fluorescent molecules. Prog Electromagn Res (2011) 121:281–99. doi:10.2528/PIER11091703

CrossRef Full Text | Google Scholar

133. Ciraci C, Pendry JB, Smith DR. Hydrodynamic model for plasmonics: A macroscopic approach to a microscopic problem. ChemPhysChem (2013) 14:1109–16. doi:10.1002/cphc.201200992

PubMed Abstract | CrossRef Full Text | Google Scholar

134. Brown TG, Alonso MA, Vella A, Theisen MJ, Head ST, Gillmer SR, et al. Focused beam scatterometry for deep subwavelength metrology. Proc SPIE (2014) 894989490Y. doi:10.1117/12.2045651

CrossRef Full Text | Google Scholar

135. Stetefeld J, McKenna SA, Patel TR. Dynamic light scattering: A practical guide and applications in biomedical sciences. Biophys Rev (2016) 8(4):409–27. doi:10.1007/s12551-016-0218-6

PubMed Abstract | CrossRef Full Text | Google Scholar

136. Lukin VP, Fortes BV. Phase-correction of turbulent distortions of an optical wave propagating under conditions of strong intensity fluctuations. Appl Opt (2002) 41(27):5616–24. doi:10.1364/AO.41.005616

PubMed Abstract | CrossRef Full Text | Google Scholar

137. Hermosa N, Rosales-Guzmán C, Pereira SF, Torres JP. Nanostep height measurement via spatial mode projection. Opt Lett (2014) 2:299–302. doi:10.1364/OL.39.000299

PubMed Abstract | CrossRef Full Text | Google Scholar

138. Bekshaev AY. Oblique section of a paraxial light beam: Criteria for azimuthal energy flow and orbital angular momentum. J Opt A: Pure Appl Opt (2009) 11:094003. doi:10.1088/1464-4258/11/9/094003

CrossRef Full Text | Google Scholar

139. Bekshaev AY, Popov AY. Method of light beam orbital angular momentum evaluation by means of space-angle intensity moments. Ukr J Phys Opt (2002) 3:249–57. doi:10.3116/16091833/3/4/249/2002

CrossRef Full Text | Google Scholar

140. Fedoseyev VG. Spin-independent transverse shift of the centre of gravity of a reflected and of a refracted light beam. Opt Commun (2001) 193:9–18. doi:10.1016/S0030-4018(01)01262-7

CrossRef Full Text | Google Scholar

141. Dasgupta R, Gupta PK. Experimental observation of spin-independent transverse shift of the centre of gravity of a reflected Laguerre–Gaussian light beam. Opt Commun (2006) 257(1):91–6. doi:10.1016/j.optcom.2005.07.033

CrossRef Full Text | Google Scholar

142. Fedoseyev VG. Reflection of the light beam carrying orbital angular momentum from a lossy medium. Phys Lett A (2008) 372(14):2527–33. doi:10.1016/j.physleta.2007.11.059

CrossRef Full Text | Google Scholar

143. Fedoseyev VG. The mechanisms of the specific effects accompanying the reflection and transmission of a light beam carrying the orbital angular momentum. J Opt (2011) 13(6):064025. doi:10.1088/2040-8978/13/6/064025

CrossRef Full Text | Google Scholar

144. Fedoseyev VG. Surface transverse linear momenta accompanying the reflection and refraction of a paraxial light beam. Phys Rev A (2019) 99(5):053827. doi:10.1103/PhysRevA.99.053827

CrossRef Full Text | Google Scholar

145. Okuda H, Sasada H. Huge transverse deformation in nonspecular reflection of a light beam possessing orbital angular momentum near critical incidence. Opt Express (2006) 14(18):8393–402. doi:10.1364/OE.14.008393

PubMed Abstract | CrossRef Full Text | Google Scholar

146. Okuda H, Sasada H. Significant deformations and propagation variations of Laguerre-Gaussian beams reflected and transmitted at a dielectric interface. J Opt Soc Am A (2008) 25:881–90. doi:10.1364/JOSAA.25.000881

PubMed Abstract | CrossRef Full Text | Google Scholar

147. Long W, Pan J, Guo X, Liu X, Lin H, Zheng H, et al. Optimized weak measurement of orbital angular momentum-induced beam shifts in optical reflection. Photon Res (2019) 7(11):1273–8. doi:10.1364/PRJ.7.001273

CrossRef Full Text | Google Scholar

148. Bekshaev AY, Soskin MS, Vasnetsov MV. Optical vortex symmetry breakdown and decomposition of the orbital angular momentum of light beams. J Opt Soc Am A (2003) 20:1635–43. doi:10.1364/JOSAA.20.001635

PubMed Abstract | CrossRef Full Text | Google Scholar

149. Aiello A, Lindlein N, Marquardt C, Leuchs G. Transverse angular momentum and geometric spin Hall effect of light. Phys Rev Lett (2009) 103(10):100401. doi:10.1103/PhysRevLett.103.100401

PubMed Abstract | CrossRef Full Text | Google Scholar

150. Bliokh KY, Aiello A. Goos–Hänchen and Imbert–Fedorov beam shifts: An overview. J Opt (2013) 15(1):014001. doi:10.1088/2040-8978/15/1/014001

CrossRef Full Text | Google Scholar

151. Lembessis VE, Babiker M, Andrews DL. Surface optical vortices. Phys Rev A (2009) 79(1):011806. doi:10.1103/PhysRevA.79.011806

CrossRef Full Text | Google Scholar

152. Lembessis VE, Al-Awfi S, Babiker M, Andrews DL. Surface plasmon optical vortices and their influence on atoms. J Opt (2011) 13:064002. doi:10.1088/2040-8978/13/6/064002

CrossRef Full Text | Google Scholar

153. Gorodetski Y, Nechayev S, Kleiner V, Hasman E. Plasmonic Aharonov-Bohm effect: Optical spin as the magnetic flux parameter. Phys Rev B (2010) 82:125433. doi:10.1103/PhysRevB.82.125433

CrossRef Full Text | Google Scholar

154. Gorodetski Y, Bliokh KY, Stein B, Genet C, Shitrit N, Kleiner V, et al. Weak measurements of light chirality with a plasmonic slit. Phys Rev Lett (2012) 109(1):013901. doi:10.1103/PhysRevLett.109.013901

PubMed Abstract | CrossRef Full Text | Google Scholar

155. Shitrit N, Nechayev S, Kleiner V, Hasman E. Spin-dependent plasmonics based on interfering topological defects. Nano Lett (2012) 12(3):1620–3. doi:10.1021/nl204556r

PubMed Abstract | CrossRef Full Text | Google Scholar

156. Shitrit N, Bretner I, Gorodetski Y, Kleiner V, Hasman E. Optical spin Hall effects in plasmonic chains. Nano Lett (2011) 11(5):2038–42. doi:10.1021/nl2004835

PubMed Abstract | CrossRef Full Text | Google Scholar

157. Abramovitz M, Stegun I. Handbook of mathematical functions. Gaithersburg, MD: National Bureau of Standards (1964).

Google Scholar

158. Peshkin M, Tonomura A The Aharonov-Bohm Effect (Lecture Notes in Physics, Vol. 340. Berlin-Heidelberg-New York-London-Paris-Tokyo-Hong Kong: Springer-Verlag (1989).

Google Scholar

159. Jatschka J, Dathe A, Csáki A, Fritzsche W, Stranik O. Propagating and localized surface plasmon resonance sensing — a critical comparison based on measurements and theory. Sensing Bio-Sensing Res (2016) 7:62–70. doi:10.1016/j.sbsr.2016.01.003

CrossRef Full Text | Google Scholar

160. Hu ZJ, Tan PS, Zhu SW, Yuan X-C. Structured light for focusing surface plasmon polaritons. Opt Express (2010) 18(10):10864–70. doi:10.1364/OE.18.010864

PubMed Abstract | CrossRef Full Text | Google Scholar

161. Durach M, Noginova N. On the nature of the plasmon drag effect. Phys Rev B (2016) 93(16):161406. doi:10.1103/PhysRevB.93.161406

CrossRef Full Text | Google Scholar

162. Noginova N, LePain M, Rono V, Mashhadi S, Hussain R, Durach M. Plasmonic pressure in profile-modulated and rough surfaces. New J Phys (2016) 18(9):093036. doi:10.1088/1367-2630/18/9/093036

CrossRef Full Text | Google Scholar

163. Noginova N, Ronurpraful T, Jerop N, Keene D, Durach M. Plasmon drag effect and opportunities for sensing applications. In: CLEO: QELS_Fundamental science 2018. San Jose, CA: Optica Publishing Group (2018). p. FF2F.2. doi:10.1364/CLEO_QELS.2018.FF2F.2

CrossRef Full Text | Google Scholar

164. Gori F, Santarsiero M, Borghi R, Vicalvi S. Partially coherent sources with helicoidal modes. J Mod Opt (1997) 45:539–54. doi:10.1080/09500349808231913

CrossRef Full Text | Google Scholar

165. Bogatyryova GV, Fel'de CV, Polyanskii PV, Ponomarenko SA, Soskin MS, Wolf E. Partially coherent vortex beams with a separable phase. Opt Lett (2003) 28:878–80. doi:10.1364/OL.28.000878

PubMed Abstract | CrossRef Full Text | Google Scholar

166. Palacios DM, Maleev ID, Marathay AS, Swartzlander GA. Spatial correlation singularity of a vortex field. Phys Rev Lett (2004) 92(14):143905. doi:10.1103/PhysRevLett.92.143905

PubMed Abstract | CrossRef Full Text | Google Scholar

167. Maleev ID, Palacios DM, Marathay AS, Swartzlander GA. Spatial correlation vortices in partially coherent light: Theory. J Opt Soc Am B (2004) 21(11):1895–900. doi:10.1364/JOSAB.21.001895

CrossRef Full Text | Google Scholar

168. Maleev ID, Swartzlander GA. Propagation of spatial correlation vortices. J Opt Soc Am B (2008) 25:915–22. doi:10.1364/JOSAB.25.000915

CrossRef Full Text | Google Scholar

169. Motsek K, Kivshar YS, Shih M-F, Swartzlander GA. Spatial coherence singularities and incoherent vortex solitons. J Opt Soc Am B (2005) 22:1437–42. doi:10.1364/JOSAB.22.001437

CrossRef Full Text | Google Scholar

170. Wang W, Takeda M. Coherence current, coherence vortex, and the conservation law of coherence. Phys Rev Lett (2006) 96(22):223904. doi:10.1103/PhysRevLett.96.223904

PubMed Abstract | CrossRef Full Text | Google Scholar

171. Wang W, Duan Z, Hanson SG, Miyamoto Y, Takeda M. Experimental study of coherence vortices: Local properties of phase singularities in a spatial coherence function. Phys Rev Lett (2006) 96(7):073902. doi:10.1103/PhysRevLett.96.073902

PubMed Abstract | CrossRef Full Text | Google Scholar

172. Visser TD, Wolf E. Spectral anomalies near phase singularities in partially coherent focused wavefields. J Opt A: Pure Appl Opt (2003) 5(4):371–3. doi:10.1088/1464-4258/5/4/311

CrossRef Full Text | Google Scholar

173. Gbur G, Visser TD. Coherence vortices in partially coherent beams. Opt Commun (2003) 222(1-6):117–25. doi:10.1016/S0030-4018(03)01606-7

CrossRef Full Text | Google Scholar

174. Gbur G, Visser TD, Wolf E. ‘Hidden’singularities in partially coherent wavefields. J Opt A: Pure Appl Opt (2004) 6(5):S239–42. doi:10.1088/1464-4258/6/5/017

CrossRef Full Text | Google Scholar

175. Gbur G, Visser TD. Phase singularities and coherence vortices in linear optical systems. Opt Commun (2006) 259(2):428–35. doi:10.1016/j.optcom.2005.08.074

CrossRef Full Text | Google Scholar

176. Gbur G, Visser TD. The structure of partially coherent fields. Prog Opt (2010) 55:285–341. doi:10.1016/B978-0-444-53705-8.00005-9

CrossRef Full Text | Google Scholar

177. Yang YJ, Mazilu M, Dholakia K. Measuring the orbital angular momentum of partially coherent optical vortices through singularities in their cross-spectral density functions. Opt Lett (2012) 37:4949–51. doi:10.1364/OL.37.004949

PubMed Abstract | CrossRef Full Text | Google Scholar

178. Yang YJ, Chen MZ, Mazilu M, Mourka A, Liu YD, Dholakia K. Effect of the radial and azimuthal mode indices of a partially coherent vortex field upon a spatial correlation singularity. New J Phys (2013) 15:113053. doi:10.1088/1367-2630/15/11/113053

CrossRef Full Text | Google Scholar

179. Alves CR, Jesus-Silva AJ, Fonseca EJ. Robustness of a coherence vortex. Appl Opt (2016) 55:7544–9. doi:10.1364/AO.55.007544

PubMed Abstract | CrossRef Full Text | Google Scholar

180. Alves CR, Amaral JP, Neto APS, Neto JGMN, Jesus-Silva AJ. Measuring the topological charge of coherence vortices through the geometry of the far-field cross-correlation function. Appl Opt (2020) 59:1553–7. doi:10.1364/AO.381556

PubMed Abstract | CrossRef Full Text | Google Scholar

181. Liu MJ, Chen J, Zhang Y, Shi Y, Zhao CL, Jin SZ. Generation of coherence vortex by modulating the correlation structure of random lights. Photon Res (2019) 7(12):1485–92. doi:10.1364/PRJ.7.001485

CrossRef Full Text | Google Scholar

182. Lu X, Zhao C, Shao Y, Zeng J, Konijnenberg S, Zhu X, et al. Phase detection of coherence singularities and determination of the topological charge of a partially coherent vortex beam. Appl Phys Lett (2019) 114:201106. doi:10.1063/1.5095713

CrossRef Full Text | Google Scholar

183. Zhang Y, Cai Y, Gbur G. Partially coherent vortex beams of arbitrary radial order and a van Cittert–Zernike theorem for vortices. Phys Rev A (2020) 101(4):043812. doi:10.1103/PhysRevA.101.043812

CrossRef Full Text | Google Scholar

184. Mehta CL, Wolf E. Coherence properties of blackbody radiation. III. Cross-spectral tensors. Phys Rev (1967) 161(5):1328–34. doi:10.1103/PhysRev.161.1328

CrossRef Full Text | Google Scholar

185. Wang J. Advances in communications using optical vortices. Photon Res (2016) 4(5):B14–28. doi:10.1364/PRJ.4.000B14

CrossRef Full Text | Google Scholar

186. Willner AE, Huang H, Yan Y, Ren Y, Ahmed N, Xie G, et al. Optical communications using orbital angular momentum beams. Adv Opt Photon (2015) 7(1):66–106. doi:10.1364/AOP.7.000066

CrossRef Full Text | Google Scholar

187. Willner AE, Pang K, Song H, Zou K, Zhou H. Orbital angular momentum of light for communications. Appl Phys Rev (2021) 8(4):041312. doi:10.1063/5.0054885

CrossRef Full Text | Google Scholar

188. Feng F, Hu J, Guo Z, Gan JA, Chen PF, Chen G, et al. Deep learning-enabled orbital angular momentum-based information encryption transmission. ACS Photon (2022) 9(3):820–9. doi:10.1021/acsphotonics.1c01303

CrossRef Full Text | Google Scholar

189. Peng D, Huang Z, Liu Y, Chen Y, Wang F, Ponomarenko SA, et al. Optical coherence encryption with structured random light. PhotoniX (2021) 2:6. doi:10.1186/s43074-021-00027-z

PubMed Abstract | CrossRef Full Text | Google Scholar

190. Grier DG. A revolution in optical manipulation. Nature (2003) 424(6950):810–6. doi:10.1038/nature01935

PubMed Abstract | CrossRef Full Text | Google Scholar

191. Dienerowitz M, Mazilu M, Dholakia K. Optical manipulation of nanoparticles: A review. J Nanophoton (2008) 2(1):021875. doi:10.1117/1.2992045

CrossRef Full Text | Google Scholar

192. Gao D, Ding W, Nieto-Vesperinas M, Ding X, Rahman M, Zhang T, et al. Optical manipulation from the microscale to the nanoscale: Fundamentals, advances and prospects. Light Sci Appl (2017) 6(9):e17039. doi:10.1038/lsa.2017.39

PubMed Abstract | CrossRef Full Text | Google Scholar

193. Arnold AS. Extending dark optical trapping geometries. Opt Lett (2012) 37:2505–7. doi:10.1364/OL.37.002505

PubMed Abstract | CrossRef Full Text | Google Scholar

194. Zhang Y, Min C, Dou X, Wang X, Urbach HP, Somekh MG, et al. Plasmonic tweezers: For nanoscale optical trapping and beyond. Light Sci Appl (2021) 10(1):59–41. doi:10.1038/s41377-021-00474-0

PubMed Abstract | CrossRef Full Text | Google Scholar

195. Radwell N, Walker G, Franke-Arnold S. Cold-atom densities of more than 10¹² cm^–3 in a holographically shaped dark spontaneous-force optical trap. Phys Rev A (2013) 88:043409. doi:10.1103/PhysRevA.88.043409

CrossRef Full Text | Google Scholar

196. Niv A, Biener G, Kleiner V, Hasman E. Spiral phase elements obtained by use of discrete space-variant subwavelength gratings. Opt Commun (2005) 251:306–14. doi:10.1016/j.optcom.2005.03.002

CrossRef Full Text | Google Scholar

197. Knöner G, Parkin S, Nieminen TA, Loke VLY, Heckenberg NR, Rubinsztein-Dunlop H. Integrated optomechanical microelements. Opt Express (2007) 15:5521–30. doi:10.1364/OE.15.005521

PubMed Abstract | CrossRef Full Text | Google Scholar

198. Yu N, Genevet P, Kats MK, Aieta F, Tetienne JP, Capasso F, et al. Light propagation with phase discontinuities: Generalized laws of reflection and refraction. Science (2011) 334:333–7. doi:10.1126/science.1210713

PubMed Abstract | CrossRef Full Text | Google Scholar

199. Zhao Z, Wang J, Li S, Wilner AE. Metamaterials-based broadband generation of orbital angular momentum carrying vector beams. Opt Lett (2013) 38:932–4. doi:10.1364/OL.38.000932

PubMed Abstract | CrossRef Full Text | Google Scholar

200. Sun J, Zeng J, Litchinitser NM. Twisting light with hyperbolic metamaterials. Opt Express (2013) 21:14975–81. doi:10.1364/OE.21.014975

PubMed Abstract | CrossRef Full Text | Google Scholar

201. Sun J, Wang X, Xu T, Kudyshev ZA, Cartwright AN, Litchinitser NM. Spinning light on the nanoscale. Nano Lett (2014) 14:2726–9. doi:10.1021/nl500658n

PubMed Abstract | CrossRef Full Text | Google Scholar

202. Ramanathan A, Wright KC, Muniz SR, Zelan M, Hill WT, Lobb CJ, et al. Superflow in a toroidal bose-einstein condensate: An atom circuit with a tunable weak link. Phys Rev Lett (2011) 106:130401. doi:10.1103/PhysRevLett.106.130401

PubMed Abstract | CrossRef Full Text | Google Scholar

203. Hansen A, Schultz JT, Bigelow NP. Singular atom optics with spinor Bose–Einstein condensates. Optica (2016) 3:355–61. doi:10.1364/OPTICA.3.000355

CrossRef Full Text | Google Scholar

204. Lloyd SM, Babiker M, Thirunavukkarasu G, Yuan J. Electron vortices: Beams with orbital angular momentum. Rev Mod Phys (2017) 89:035004. doi:10.1103/RevModPhys.89.035004

CrossRef Full Text | Google Scholar

205. Bliokh KY, Ivanov IP, Guzzinati G, Clark L, Van Boxem R, Béché A, et al. Theory and applications of free-electron vortex states. Phys Rep (2017) 690:1–70. doi:10.1016/j.physrep.2017.05.006

CrossRef Full Text | Google Scholar

206. Verbeeck J, Tian H, Schattschneider P. Production and application of electron vortex beams. Nature (2010) 467:301–4. doi:10.1038/nature09366

PubMed Abstract | CrossRef Full Text | Google Scholar

207. Handali J, Shakya P, Barwick B. Creating electron vortex beams with light. Opt Express (2015) 23:5236–43. doi:10.1364/OE.23.005236

PubMed Abstract | CrossRef Full Text | Google Scholar

208. Kozák M. Electron vortex beam generation via chiral light-induced inelastic ponderomotive scattering. ACS Photon (2021) 8(2):431–5. doi:10.1021/acsphotonics.0c01650

CrossRef Full Text | Google Scholar

209. Bliokh KY, Dennis MR, Nori F. Relativistic electron vortex beams: Angular momentum and spin-orbit interaction. Phys Rev Lett (2011) 107(17):174802. doi:10.1103/PhysRevLett.107.174802

PubMed Abstract | CrossRef Full Text | Google Scholar

210. Bliokh KY, Schattschneider P, Verbeeck J, Nori F. Electron vortex beams in a magnetic field: A new twist on landau levels and Aharonov-Bohm states. Phys Rev X (2012) 2(4):041011. doi:10.1103/PhysRevX.2.041011

CrossRef Full Text | Google Scholar

211. Thaller B. The Dirac equation. Springer Science & Business Media (2013).

Google Scholar

212. Hefner BT, Marston PL. An acoustical helicoidal wave transducer with applications for the alignment of ultrasonic and underwater systems. J Acoust Soc Am (1999) 106:3313–6. doi:10.1121/1.428184

CrossRef Full Text | Google Scholar

213. Zhang LK, Marston PL. Angular momentum flux of nonparaxial acoustic vortex beams and torques on axisymmetric objects. Phys Rev E (2011) 84:065601. doi:10.1103/PhysRevE.84.065601

PubMed Abstract | CrossRef Full Text | Google Scholar

214. Anzolin G, Tamburini F, Bianchini A, Umbriaco G, Barbieri C. Optical vortices with starlight. Astron Astrophys (2008) 488(3):1159–65. doi:10.1051/0004-6361:200810469

CrossRef Full Text | Google Scholar

215. Berkhout GC, Beijersbergen MW. Method for probing the orbital angular momentum of optical vortices in electromagnetic waves from astronomical objects. Phys Rev Lett (2008) 101(10):100801. doi:10.1103/PhysRevLett.101.100801

PubMed Abstract | CrossRef Full Text | Google Scholar