Triaxial closed-loop measurement based on a single-beam zero-field optically pumped magnetometer

In this study, we propose an approach for the simultaneous measurement of triaxial magnetic fields using a single-beam zero-field optically pumped atomic magnetometer, in which a rotational high-frequency (ω₁) and another high-frequency (ω₂) modulated magnetic field magnetic fields are applied along the transverse directions and the longitudinal direction, respectively. Theoretical analysis, numerical simulation, and experiments are conducted to demonstrate this method. Experimental sensitivities of 18 fT/Hz^1/2 along the two transverse directions and 140 fT/Hz^1/2 along the longitudinal direction are simultaneously achieved. On this basis, we operate the magnetometer in closed-loop mode to expand the bandwidth and dynamic range, and to keep the triaxial magnetic field sensed by the magnetometer at zero. The triaxial bandwidths are increased from below 100 Hz to over 1.6 kHz. The triaxial dynamic ranges are all extended to ±150 nT. Plus, we verify the ±1,000 nT dynamic range of the triaxial magnetometer through increasing the triaxial coil constants. The synchronization of triaxial closed-loop measurement, simplicity of magnetometer structure, and closed-loop detection with high sensitivities make it applicable and attractive for biomagnetism imaging in challenging environments.

1 Introduction

In the past couple of years, zero-field optically pumped atomic magnetometers (OPMs), especially those operating in the spin-exchange relaxation-free (SERF) regime, have been developed rapidly and have a profound impact on the detection of extremely weak magnetic fields [1–5]. In particular, it has attracted enormous interest in magnetoencephalography (MEG) and magnetocardiography (MCG) due to its advantages, including cryogenic-free condition, ultra-high sensitivity, low cost, and the convenience of miniaturization [6–8].

Vector magnetic field measurement can provide more complete information than scalar one. Conventional zero-field OPMs measure the magnetic field along the transverse one or two directions perpendicular to the pump direction and are difficult to realize the simultaneous and independent measurement of the triaxial magnetic fields [1, 9, 10]. To achieve triaxial measurement, some research groups adopted a dual-beam configuration, either pump-probe [11, 12], or dual-pump/probe scheme [13, 14]. This scheme complicates the structure of the magnetometer, which in turn increases the sensor’s volume and complexity, and is not beneficial for its development into an arrayed wearable system.

Currently the most suitable configuration for miniaturization is the single-beam scheme [15, 16]. Hence, triaxial measurement based on the single-beam configuration is attracts a lot of attention [9, 10, 16], and some attempts have been made. For instance, Dong et al. demonstrated that magnetic fields along the three axes could be demodulated by applying three low-frequency (below 210 Hz) modulation fields with different frequencies [17]. Huang et al. proposed a method using the combination of one transverse low-frequency rotating field (90 Hz) and one longitudinal modulation field (130 Hz), which could implement simultaneous three-axis magnetic-field measurement [18]. However, these schemes both rely on low-frequency modulation, and the low-frequency system noise limits the detection sensitivity to be over 100 fT/Hz^1/2. Xiao et al. reflected pump laser beam behind two bonded vapor cells for triaxial magnetic field information [19], yet this configuration was complex in combined cell design. Tang et al. imposed the DC-offset field along different axes to measure triaxial field, but the measurement could only be conducted with a time-sharing scheme [20]. For practical applications, simultaneous triaxial measurement method based on simple single-beam configuration is urgently needed.

In addition, the dynamic range and bandwidth of zero-field OPMs operating in conventional open-loop mode are limited to several nanoteslas and below 100 Hz, respectively [1, 9]. The small dynamic range and low bandwidth restrict many possible applications, especially in challenging environments with magnetic interferences. For instances, frequency of some neuromagnetic signals is over 1 kHz [21, 22]. And certain biomagnetism measurement needs to be conducted inside weakened magnetic shields [23]. These problems mentioned above can be mitigated through closed-loop mode of the magnetometer. For current zero-field OPMs with pump-probe, dual-pump/probe scheme, or single-beam configuration, researchers have proposed closed-loop operation methods, which have been verified by experiment [11,14,24,25,26,27].

In this study, a novel simultaneous triaxial measurement method based on conventional single-beam configuration is proposed, and three-axis closed-loop operation is conducted on this basis. Thereby, we achieve triaxial magnetic field measurement with large dynamic range and high bandwidth, without substantially modifying the current single-beam magnetometer design.

A group of high-frequency longitudinal and transverse rotational modulation fields are applied to the magnetometer. Triaxial measurement is achieved through simultaneously demodulating three different observables. The transverse and longitudinal magnetic sensitivities are 18 fT/Hz^1/2 and 140 fT/Hz^1/2, respectively. On this basis, we conduct closed-loop operation of the proposed method to expand both the bandwidth and dynamic range of the magnetometer, and to keep the triaxial magnetic field sensed by the magnetometer at zero. The triaxial bandwidths of our magnetometer are increased from below 100 Hz to over 1.6 kHz, and the triaxial dynamic ranges of our magnetometer are all expanded from less than 40 nT to ±150 nT. Plus, we verify the ±1,000 nT dynamic range of the triaxial magnetometer through increasing the triaxial coil constants. Operating with closed loop, the magnetic field sensitivity keeps superior to 22 fT/Hz^1/2 in the transverse directions, and 230 fT/Hz^1/2 in the longitudinal direction. The high dynamic range and high bandwidth, synchronization of measurement, and closed-loop operation enable this method to perform in various applications.

2 Materials and methods

2.1 Principles

The evolution dynamics of electron spin polarization vector P of alkali atomic ensemble in our zero-field OPM can be well-described by the Bloch equation [28]:

$\begin{array}{c}\frac{d\mathbf{P}}{dt}=\frac{1}{q\left(P\right)}\left[{\gamma }^e\mathbf{B}\times \mathbf{P}+R_{\mathrm{o}\mathrm{p}}\left(s\widehat{z}-\mathbf{P}\right)-R_{\mathrm{r}\mathrm{e}\mathrm{l}}\mathbf{P}\right]\end{array}(1)$

where q(P) is the nuclear slowing-down factor which is a function of the magnitude of P [29], ${\gamma }^e\approx 2\pi \times 28\mathrm{H}\mathrm{z}/\mathrm{n}\mathrm{T}$ is the gyromagnetic ratio of electron, B is the magnetic field vector, ${\left[B_x,B_y,B_z\right]}^T$, R_op is the optical pumping rate along z-axis, R_rel is the spin-relaxation rate, and s is the polarization degree of pump light.

Single-beam zero-field OPMs perform magnetic field measurements by detecting the transmitted light intensity of pump beam, which only reflects the longitudinal polarization P_z [17, 28]. According to Ref. [17], the approximated relationship between the output of the magnetometer R_out and P_z is

$\begin{array}{c}{R}_{out}=R_0\bullet \exp \left[-OD\left(\nu \right)\left(1-P_z\right)\right]\end{array}(2)$

where R₀ is the original signal before the vapor cell, and $OD\left(\nu \right)=nL\sigma \left(\nu \right)$ is the optical depth of the vapor cell. And n is the number density of the alkali vapor, σ(ν) is the absorption cross-section as a function of light frequency ν, and L is the length of the vapor cell. Thus, we focus on the response of P_z to magnetic field. The P_z component of the stable-state solution to (1) is

$\begin{array}{c}{P}_z^{stable}=P_0\frac{B_z^2+{\left[\left(R_{\mathrm{o}\mathrm{p}}+R_{\mathrm{r}\mathrm{e}\mathrm{l}}\right)/{\gamma }^e\right]}^2}{B_x^2+B_y^2+B_z^2+{\left[\left(R_{\mathrm{o}\mathrm{p}}+R_{\mathrm{r}\mathrm{e}\mathrm{l}}\right)/{\gamma }^e\right]}^2}\end{array}(3)$

For low-frequency system noise suppression and magnetic field sensitivity improvement, single-beam zero-field OPMs are usually modulated with high-frequency magnetic field. Conventionally, only one transverse axis is modulated, in which way only magnetic field measurement of the modulated axis is achieved [10, 30]. For dual-axis measurement, using the transverse rotationally modulated magnetic field results in the output signal being orthogonally demodulated to obtain the in-phase and out-of-phase terms, realizing the simultaneous measurement of both transverse directions [26, 31, 32]. According to Ref. [26], the response of P_z with dual-axis measurement containing both information about B_x0 and B_y0 is

$\begin{array}{c}{P}_z^{dual}\propto \frac{R_{o\mathrm{p}}{J}_0^3\left(u\right)J_1\left(u\right)\left[B_{x0}\sin \left({\omega }_{1}t\right)+B_{x0}\cos \left({\omega }_{1}t\right)\right]}{{\mathrm{\Gamma }}_1^2+J_0^2\left(u\right)B_{x0}^2+J_0^2\left(u\right)B_{y0}^2+J_0^4\left(u\right)B_{z0}^4}\end{array}(4)$

where ${\Gamma }_1=\left(R_{\mathrm{o}\mathrm{p}}{J}_0^2\left(u\right)+R_{\mathrm{r}\mathrm{e}\mathrm{l}}\right)/{\gamma }^e$ represents the zero-field resonance linewidth, and $J_n\left(u\right)$ represents the nth order Bessel function of the first kind. Variable $u={\gamma }^e{B}_{xym}/\left[q\left(P\right){\omega }_1\right]$ is the modulation index. B_xym is the modulated magnetic field amplitude along the transverse directions. Emitting the quadratic terms in the denominator of (4), the $P_z^{dual}$ response to B_x0 and B_y0 are orthogonal in phase, which means that orthogonal demodulation can offer dual-axis measurement from $P_z^{dual}$.

For measurement scheme mentioned above, optical pumping aligns the atomic spin polarization along the z-axis, resulting in the insensitivity of spin polarization precession to a small magnetic field along the same z-axis. Hence, we made an attempt to apply another modulated magnetic field with different frequency along the longitudinal direction.

In summary, our combined modulated magnetic field are expressed as

$B_x=B_{xym}\sin \left({\omega }_{1}t\right)+B_{x0}$

$\begin{array}{c}{B}_y=B_{xym}\cos \left({\omega }_{1}t\right)+B_{y0}\end{array}(5)$

$B_z=B_{zm}\sin \left({\omega }_{2}t\right)+B_{z0}$

where B_xym and B_zm are the amplitudes of the transverse rotational and longitudinal modulated magnetic field, respectively, and B_×0, B_y0, and B_z0 are the magnetic fields to be detected along the three orthogonal directions. The combined modulated magnetic field results in an amalgamated precession of atomic spin polarization, which can be sensitive to magnetic field along all the three orthogonal directions. From Equation 3, it could be found that P_z has naturally contained information of B_z0. Through employing the modulated magnetic field along the z-axis, the scale factor of the magnetometer to B_z0 is enhanced, and its sensitivity to B_z0 presents. This conclusion is drawn mostly from numerical simulation, for that analytical solution to Bloch Equation 1 under combined modulated magnetic field (5) is difficult to obtain. Specifically, the mathematical operation of cross product $\mathbf{B}\times \mathbf{P}$ in (1) can be transformed into matrix and vector multiplication:

$\begin{array}{c}\mathbf{B}\times \mathbf{P}=\left[\begin{array}{c}{B}_x\\ B_y\\ B_z\end{array}\right]\times \left[\begin{array}{c}{P}_x\\ P_y\\ P_z\end{array}\right]=\left[\begin{array}{ccc}0& -B_z& B_y\\ B_z& 0& -B_x\\ -B_y& B_x& 0\end{array}\right]\bullet \left[\begin{array}{c}{P}_x\\ P_y\\ P_z\end{array}\right]={\mathbf{B}}_t\bullet \mathbf{P}\end{array}(6)$

When the third modulated magnetic field is applied, the time-varying cross terms with trigonometric functions of B_t complicate the analytical solution to (1).

Besides, it is worth noticing that with combined modulated magnetic field for triaxial measurement, the response of P_z to transverse magnetic field did not change substantially due to different modulation frequency. We rely on response characteristics at transverse modulation frequency (Figure 1A) through demodulating with lock-in amplifiers, which are not different from that in dual-axis measurement scheme. Therefore, Equation 4 can still be used in our triaxial measurement scheme.

FIGURE 1

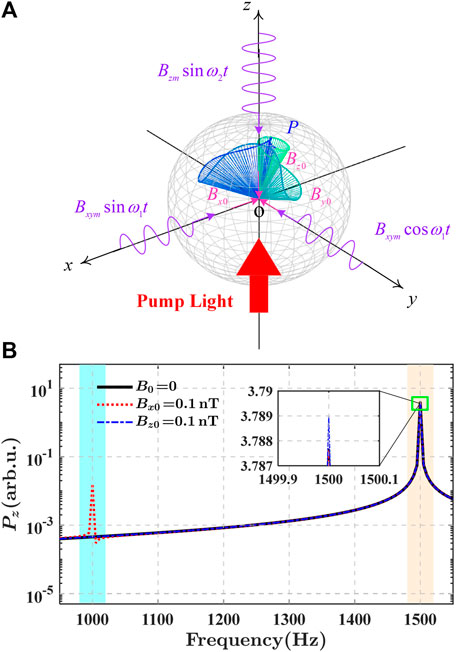
FIGURE 1. Simulation results. (A) The evolution of P subjected to the combined triaxial modulated magnetic field. The meshed sphere is illustrated as a guide for eyes. (B) The frequency-domain response spectrum of P_z between 800 Hz and 1700 Hz. The black solid line represents the condition of ${\mathit{B}}_{\mathit{x}\mathbf{0}}={\mathit{B}}_{\mathit{y}\mathbf{0}}={\mathit{B}}_{\mathit{z}\mathbf{0}}=\mathbf{0}\mathbf{n}\mathbf{T}$, the red dotted line represents the condition of ${\mathit{B}}_{\mathit{x}\mathbf{0}}=\mathbf{0.1}\mathbf{n}\mathbf{T}$ and ${\mathit{B}}_{\mathit{y}\mathbf{0}}={\mathit{B}}_{\mathit{z}\mathbf{0}}=\mathbf{0}\mathbf{n}\mathbf{T}$, the blue dot-dashed line represents the condition of ${\mathit{B}}_{\mathit{z}\mathbf{0}}=\mathbf{0.1}\mathbf{n}\mathbf{T}$ and ${\mathit{B}}_{\mathit{x}\mathbf{0}}={\mathit{B}}_{\mathit{y}\mathbf{0}}=\mathbf{0}\mathbf{n}\mathbf{T}$. The inset shows the detailed zoom-in around the peaks of 1,500 Hz.

We performed numerical simulation based on 1) and 5) to study the response characteristics of P_z. It is crucial to investigate three independent demodulated observables which only depend on the changes of B_x0, B_y0, or B_z0 from the response signal, respectively. We distinguish the observables by frequency and phase, and in particular, the response of frequency ω₁ and ω₂, i.e., P_zω1 (R_zω1) and P_zω2 (R_zω2), are the quantities of interest.

The numerical simulation is executed with typical parameters of $R_{\mathrm{o}\mathrm{p}}=R_{\mathrm{r}\mathrm{e}\mathrm{l}}=150{\mathrm{s}}^{-1}$, $B_{xym}=B_{zm}=140\mathrm{n}\mathrm{T}$, ${\omega }_1=2\pi \times 1000\mathrm{H}\mathrm{z}$, ${\omega }_2=2\pi \times 1500\mathrm{H}\mathrm{z}$,. The simulated 3D trajectory of P subjected to the combined modulated magnetic fields is depicted in Figure 1A, showing an apparent time-domain variation of P_z. This variation could finally be detected to sense the triaxial magnetic fields, on condition that it needs to be transformed into the frequency domain. Therefore, we made a preliminary exploration to observe the dependence of P_zω1 and P_zω2 on B_x0 and B_z0 (B_x0 as an example of transverse directions). As shown in Figure 1B, P_zω1 responses markedly to a change of 0.1 nT in B_x0, and by contrast it hardly responses to a change of B_z0. Moreover, under the condition of zero magnetic field, P_zω2 is not zero but has a remarkable peak value. And it is only sensitive to the variation of B_z0, which is detailed in the inset.

Based on the above investigation, a systematic analysis within the typical dynamic range of zero-field OPMs (especially SERF magnetometers), [-20, 20] nT, was carried out and presented in Figure 2. Figure 2A shows that the in-phase signal of P_zω1 are linearly dependent on B_x0 near B_x0 = 0, and Figure 2B indicates that the out-of-phase signal of P_zω1 linearly response to B_y0 near B_y0 = 0. And these two signals are zero when magnetic field along their corresponding direction is zero, respectively. These features are the same with dual-axis measurement scheme. Besides, in Figure 2A and Figure 2B, the amplitude of P_zω2 presents stable response near B_x0 = 0 or B_y0 = 0. Comparatively, Figure 2C shows that P_zω1 hardly responds to the variation of B_z0, while the amplitude of P_zω2, exhibits an observable approximately linear dependence on B_z0, although P_zω2 has a large offset when B_z0 = 0. Note that the steepness of the distinct response to B_z0 over the offset is about an order of magnitude smaller than that of the in-phase signal of P_zω1 replying to B_x0 (or the out-of-phase signal of P_zω1 replying to B_y0), which implies that the sensitivity of the transverse directions is better than the longitudinal one. Therefore, we can conclude that B_x0, B_y0, and B_z0 can be independently and simultaneously measured in the vicinity of zero magnetic field just by demodulating the in-phase signal of P_zω1, the out-of-phase signal of P_zω1 and the amplitude of P_zω2 respectively from the response signal of P_z. This analysis through numerical simulation has verified our aforementioned investigation.

FIGURE 2

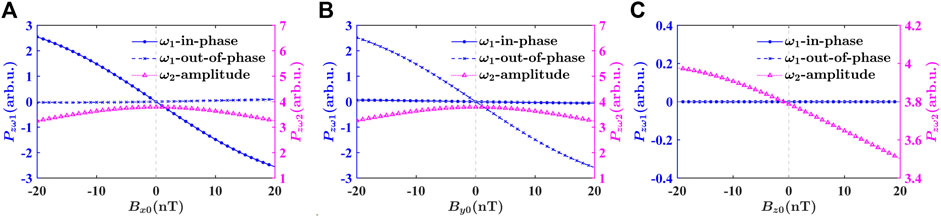
FIGURE 2. Simulated dependence of the in-phase and out-of-phase signal of P_zω1 and the amplitude of P_zω2 on: (A) the variation of B_x0 within the range of [-20,20] nT; (B) the variation of B_y0 within the range of [-20,20] nT. (C) The variation of B_z0 within the range of [-20,20] nT.

For zero-field OPMs, the frequency response of the input-output relationship could be described as [1, 9].

$\begin{array}{c}R\left(f\right)=\frac{A}{\sqrt{{\left(2\pi f\right)}^2+{BW}^2}}\end{array}(7)$

where A is a constant related to the scale factor of the magnetometer, BW represents the bandwidth of the magnetometer. The transfer function corresponding to (7) is

$\begin{array}{c}{G}_{open}\left(s\right)=\frac{A}{s+BW}\end{array}(8)$

The transfer function of PI controllers is

$\begin{array}{c}{G}_c\left(s\right)=K_p+\frac{K_i}{s}\end{array}(9)$

where K_p and K_i denote the proportional and integral gains, respectively.

When the atomic magnetometer works in the closed-loop mode, the triaxial magnetic information is extracted and fed into three separate proportional and integral controllers (PI controllers). The outputs of three controllers are converted into feedback current and applied to the triaxial coils to keep magnetic field along each direction locked at zero. At the moment, the magnetic field generated by the coil is the magnetic field to be measured. Each single axis closed loop is operated independently, as depicted in Figure 3. The transfer function of the closed-loop magnetometer is

$\begin{array}{c}{G}_{closed}\left(s\right)=\frac{G_{open}\left(s\right)}{1+{G_c\left(s\right)\bullet K_{coil}\bullet G}_{open}\left(s\right)}=\frac{As}{s^2+\left(K_p{K}_{coil}A+BW\right)s+K_i{K}_{coil}A}\end{array}(10)$

FIGURE 3

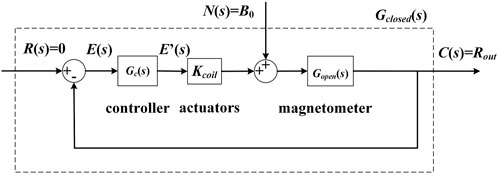
FIGURE 3. The schematic of negative feedback with PI controller and actuators (waveform generator, resistor, and coil) of the closed-loop magnetometer in a single axis.

Comparing (8) with (10), it could be found that the system characteristics of the closed-loop magnetometer are different from that of the open-loop magnetometer. For instances, the closed-loop magnetometer is regarded as a second-order system. By comparison, the open-loop magnetometer can be simply considered as a first-order system. Through adjusting the controller parameters, the frequency responses of the closed-loop magnetometer can be altered to enlarge the bandwidth.

2.2 Experimental setup and procedure

2The experimental system of our single-beam closed-loop triaxial zero-field OPM is depicted in Figure 4. The cubic vapor cell, made of borosilicate glass, has an internal size of 8 mm × 8 mm × 8 mm, which is filled with a droplet of ⁸⁷Rb and about 600 torr N₂. The vapor cell is heated to 433 K for working using 200 kHz alternating current generated by an electric heater. The laser beam generated by a distributed-feedback (DFB) laser is first transmitted to the zero-field OPM via a polarization-maintaining fiber, and then is transformed into circularly polarized light by a quarter-wave plate before illuminating the vapor cell. It plays the dual roles as both optical pumping and probing, whose wavelength is set to about 794.98 nm, near the center of the D1 line of ⁸⁷Rb. The transmitted light through the vapor cell is sensed and converted into current signal by the photodiode and finally transformed to voltage signal by the trans-impedance amplifier (PDA200C, Thorlabs). Then, the two channels of one lock-in amplifier (MFLI, Zurich Instruments) are used as quadrature demodulator for the in-phase and the out-of-phase signal of R_zω1. Another lock-in amplifier (MFLI, Zurich Instruments) is used to demodulate the amplitude of R_zω2. Afterward, all the three different signals are sent into built-in PI controllers of LIAs to generate negative feedback signals. The feedback signals are utilized to control the waveform generators (33522B, Keysight) which drive the coil via selected resistors, keeping the triaxial magnetic field sensed by the zero-field OPM locked at zero. Finally, all signals are acquired by the data-acquisition system (PXIe-4464, National Instruments).

FIGURE 4

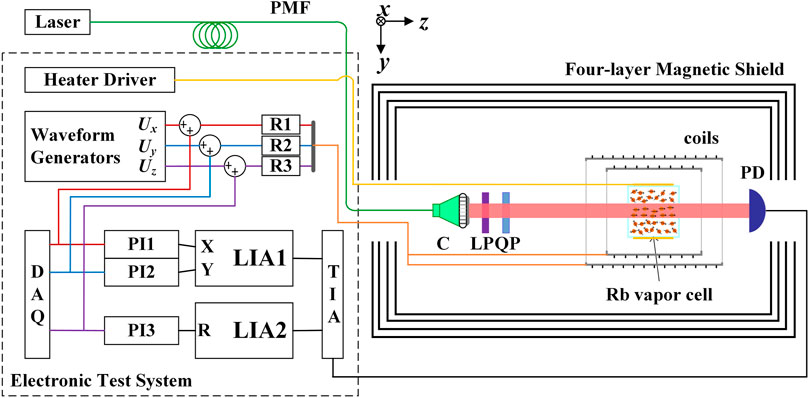
FIGURE 4. The experimental system schematic of our single-beam closed-loop triaxial zero-field OPM. PMF: polarization maintaining fiber; C: collimating lens; LP: linear polarizer; QP: quarter-wave plate; PD: photodiode; TIA: transimpedance amplifier; LIA1 and LIA2: lock-in amplifiers; PI1, PI2, and PI3: proportional and integral controllers; DAQ: data-acquisition; R1, R2, and R3: resistors.

The near-zero magnetic field environment of the atomic magnetometer is created by four-layer μ-metal magnetic shield. Then, inside the shield a group of triaxial coils is used for active magnetic field compensation and generation of modulated magnetic fields. The coil group is composed of a nested saddle coil [33] for radial magnetic field and a Lee-Whiting coil [34] for axial magnetic field.

Our experiments are conducted by two steps. At the first step, the triaxial measurement is conducted, including the magnetic field sweeps along the three axes as a verification of the simulation results. And we offer the triaxial sensitivity test result. Then, negative feedbacks are adopted to build a closed-loop magnetometer. Plus, comparison is made between sensitivity, bandwidth, and dynamic range of open-loop mode and those of closed-loop mode.

3 Results and discussion

3.1 Triaxial measurement

To confirm the validity of triaxial measurement with the proposed method, we sweep the DC magnetic fields B_×0, B_y0 and B_z0 around the zero magnetic field respectively, and simultaneously record the variation of the in-phase and the out-of-phase signal of R_zω1, and the amplitude of R_zω2. The sweep range of B_x0, B_y0 and B_z0are all set to [-20, 20] nT.

As shown in Figures 5A–C, the experimental results are in good agreement with the simulation results. By observing and comparing the dependence of the three observables on B_x0, B_y0 and B_z0, respectively, major conclusions can be drawn below. Within the range of [-20, 20] nT, the in-phase and the out-of-phase signal of R_zω1 are orthogonally dependent on B_x0 and B_y0, whose dependence features show a dispersion curve. And the relationship between the amplitude of R_zω2 and B_x0 (B_y0) presents an absorption curve. Specifically, in the vicinity of zero field ([-2, 2] nT), as shown in Figure 5D inset, the in-phase signal of R_zω1 is linearly dependent on B_x0, while the out-of-phase signal of R_zω1 and the amplitude of R_zω2 are not sensitive to B_x0. Similar features reproduce in Figure 5E inset. As shown in Figure 5C, only the amplitude of R_zω2 shows a linear dependence on B_z0 within the range of [-20, 20] nT, while the signals of R_zω1 do not change substantially when B_z0 varies. These characteristics are more pronounced in the vicinity of zero field ([-2, 2] nT), which is shown in Figure 5F inset. The interference between the transverse and longitudinal signals is probably caused by non-orthogonal angles of the beams and triaxial coils [35].

FIGURE 5

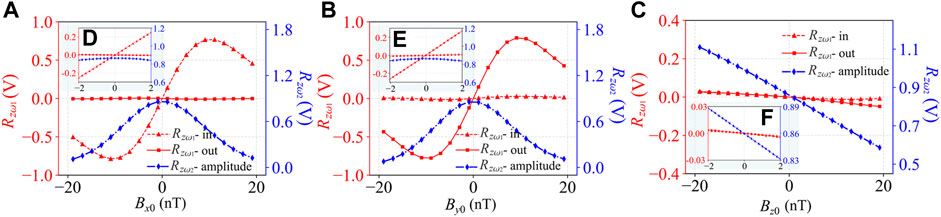
FIGURE 5. Experimental results. Comparison of the dependence properties of the three observables, the in-phase (red triangles) and out-of-phase (red squares) signals of R_zω1 and the amplitude of R_zω2 (blue diamonds), on (A) B_x0, (B) B_y0, and (C) B_z0 within the range of [-20, 20] nT, respectively. Insets (D–F) show the detailed zoom-in in the vicinity of zero field within the range of [-2, 2] nT.

Moreover, triaxial scale factors, which is defined as k=ΔR/ΔB, are also evaluated. ΔR is the magnetometer response in voltage when sensing magnetic field variation ΔB. The results show that x and y directions have scale factors of 0.128 V/nT and 0.136 V/nT, respectively. In contrast, the scale factor of longitudinal direction is -0.0148 V/nT, whose absolute value is about one-ninth of that of transverse directions. This scale factor difference among transverse directions and the longitudinal direction is basically consistent with that in numerical simulation mentioned before in Section 2.1. The response of R_zω2 to magnetic field along the longitudinal direction is over its offset, and the response is about one order smaller than that of R_zω1 to magnetic field along transverse directions.

The triaxial magnetic field sensitivities are analyzed by acquiring the noise spectra of the output signals of magnetometer. A 100 pT_rms magnetic calibration signal at 30.5 Hz is employed along the three axes in turn. At each turn, the voltage output signal was firstly acquired and collected for 60s. We conduct noise spectra analysis towards the voltage output signal. And then the voltage noise spectra are divided by the amplitude frequency responses (Figure 7) to obtain the sensitivities of our magnetometer.

The triaxial sensitivities in our experiments is given in Figure 6A, in which the maximum peak in each noise spectrum represents the calibration signal. The triaxial magnetic field sensitivities are 18 fT/Hz^1/2 along the x-axis, 18 fT/Hz^1/2 along the y-axis, and 140 fT/Hz^1/2 along the z-axis. The transverse sensitivities are excellent, in line with expectations. And we achieve measurement of magnetic field along the longitudinal direction without modifying conventional single-beam configuration. The fact that the sensitivity of longitudinal direction is inferior to that of transverse directions is mainly due to small response amplitude over the large offset of R_zω2 when B_z0 varies around zero-field, while the response amplitudes of R_zω1 to magnetic field along transverse directions are strong, which have zero offset at zero field. A qualitative description is given below: the spin polarization vector P is basically along the z-axis, and the angle between B_z0 and P is small, so the magnetometer signal representing precession variation of P is small as well. By comparison, B_x0 (B_y0) and P approaches perpendicular, so the precession variation of P is distinct leading to the strong magnetometer signal.

FIGURE 6

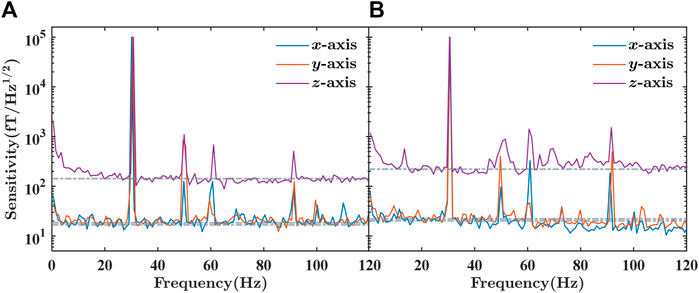
FIGURE 6. The magnetic measurement sensitivity spectra along the three axes on different conditions. The maximum peak in each spectrum is the 100 pT_rms magnetic calibration signal at 30.5 Hz. (A) The magnetic measurement sensitivity spectra with the same parameters as that in simulation. The magnetic field sensitivity is 18 fT/Hz^1/2 along x-axis, 18 fT/Hz^1/2 along y-axis, and 140 fT/Hz^1/2 along z-axis. (B) The magnetic measurement sensitivity spectra on condition of closed-loop high bandwidth and large dynamic range configuration. The triaxial sensitivities are 22 fT/Hz^1/2 along x-axis, 22 fT/Hz^1/2 along y-axis, and 230 fT/Hz^1/2 along z-axis, maintaining at the high level.

3.2 Closed-loop operation

When the triaxial measurement is completed, as depicted in Figure 3, we adopt the closed-loop operation based on PI controllers to enlarge the bandwidth of the magnetometer and the dynamic range of the magnetometer, and to keep the triaxial magnetic field sensed by the magnetometer locked at zero. The closed loops of three axes are operating independently of each other, with three separate PI controller.

We firstly alter the open-loop magnetic modulation parameters for extending bandwidth, as a basis for bandwidth expansion in closed-loop mode. With operating parameters same as above simulation conditions, the bandwidths of triaxial magnetic detection are 92 Hz, 92 Hz, and 100 Hz, as Figure 7 shows. According to our previous research [14, 25, 26], high-frequency and large amplitude modulated magnetic field would bring about high bandwidth of the zero-field OPM. Thus, we set transverse rotationally modulated magnetic field at 6 kHz, with 2000 nT_pp amplitude, and longitudinal modulated magnetic field at 9 kHz, with the same 2000 nT_pp amplitude. The ratio of frequencies in this group is the same as that in simulation parameters for better performance. In this condition, the bandwidths of open-loop triaxial magnetic detection are 809 Hz, 757 Hz, and 270 Hz.

FIGURE 7

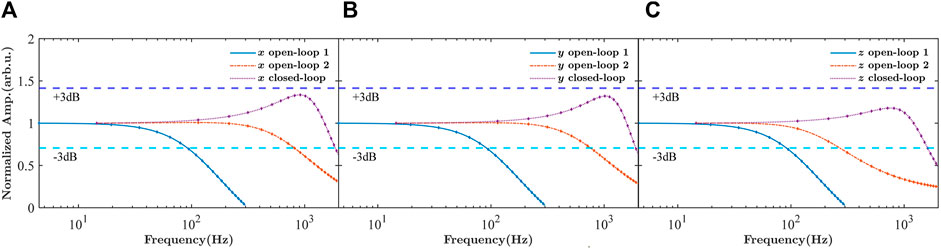
FIGURE 7. The amplitude-frequency response of the triaxial magnetometer to magnetic field detected along x-axis (A), y-axis (B) and z-axis (C), when the magnetometer is operating with open-loop parameters consistent with the simulation in Section 2.1 (“open-loop 1”), open-loop high-frequency measurement parameters (“open-loop 2”), or closed-loop control. “Normalized Amp.” is the abbreviation for normalized amplitude, with low-frequency triaxial field gains regarded as unit.

Finally, the closed-loop operation is conducted with optimized parameters as in Figure 3 to further expand the triaxial detection bandwidths to 1.86 kHz, 1.90 kHz, and 1.61 kHz. The feedback bandwidth is 2.5 kHz, which is larger than the current triaxial bandwidths of the closed-loop magnetometer, and would not affects the bandwidths.

The response curves in Figure 8 indicate that the triaxial dynamic ranges of the open-loop magnetometer with operating parameters same as simulation ones are restricted to below 20 nT for the transverse directions, and less than 40 nT for the longitudinal direction. Operating in closed-loop mode, the triaxial dynamic ranges of the magnetometer are enhanced to ±150 nT. Furthermore, closed-loop operation with increased triaxial coil constants enlarges the triaxial dynamic ranges of the magnetometer to over ±1,000 nT.

FIGURE 8

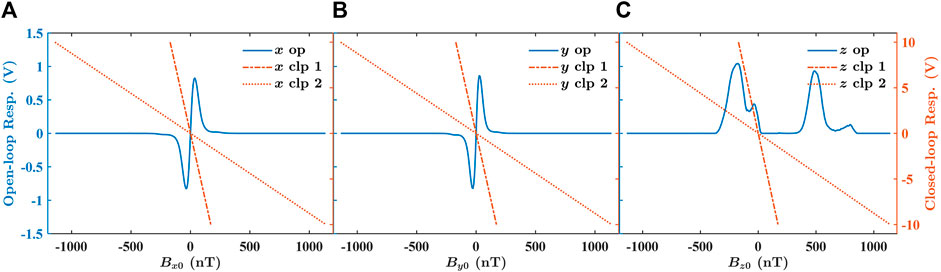
FIGURE 8. Responses of the triaxial magnetometer to magnetic field offset sweep, when the magnetometer is operating in open-loop mode (“op”), when the magnetometer is operating in closed-loop mode without changing coil constants (“clp 1”), and when the magnetometer is operating in closed-loop mode with increased coil constants (“clp 2”). (A) The sweep is along x-axis. (B) The sweep is along y-axis. (C) The sweep is along z-axis. “Resp.” is the abbreviation for response. The open-loop dynamic range of the three axes: 18 nT along x axis; 13 nT along y axis; 35 nT along z axis.

We achieve the high-bandwidth and large dynamic range of the magnetometer, and meanwhile keep its ultra-high triaxial sensitivities, which are presented below in Figure 6B. The triaxial sensitivities are 22 fT/Hz^1/2 along x-axis, 22 fT/Hz^1/2 along y-axis, and 230 fT/Hz^1/2 along z-axis. The sensitivities degrade performance may result from two reasons: the first reason is the large relaxation rate caused by large modulation amplitude, and the second reason is stronger system noise from closed-loop controller and actuators.

In addition, to evaluate the stability of the triaxial closed loop, we lock the triaxial magnetic field sensed by the magnetometer at zero. By contrast, working in open loop, the magnetometer signal may drift along with either the drift of environmental magnetic field or the drift of magnetometer itself (including the drift of light, cell temperature, etc.). We conduct experiment to record the variation of the triaxial sensed magnetic field, and make comparison between the magnetic field variation record with magnetometer operating in open loop and that with magnetometer operating in closed loop. Records in Figure 9 indicate that in 30 min triaxial magnetic field variations with closed loop are less than 1% of that with open loop. This result has confirmed that with triaxial closed loop, we could keep the magnetometer operating in zero field effectively.

FIGURE 9

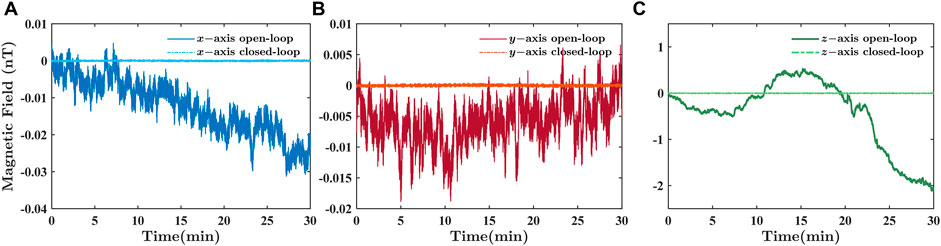
FIGURE 9. The triaxial magnetic field sensed by the magnetometer when it is operating in open loop or in closed loop for 30 min recording time. (A) The field sensed along x-axis. (B) The field sensed along y-axis. (C) The field sensed along z-axis. With closed-loop control, the triaxial sensed magnetic fields are kept locked at zero, with variations less than 1% of that with open loop.

4 Conclusion

In this study, we propose a method to measure triaxial field simultaneously based on a single-beam zero-field OPM, through applying a high-frequency (ω₁) rotational modulation field along the transverse directions and another high-frequency (ω₂) modulation field along the longitudinal direction. The in-phase and out-of-phase of signals demodulated at ω₁ (R_zω1) are considered as signals indicating B_x0 and B_y0; the amplitude of signals demodulated at ω₂ (R_zω2) is regarded as signal representing B_z0.

Theoretical analysis, numerical simulation, and experiments are conducted to demonstrate this method. In experiments, the transverse and longitudinal magnetic sensitivities are 18 fT/Hz^1/2 and 140 fT/Hz^1/2, respectively. Then negative feedback is adopted for closed-loop operation of the magnetometer to expand both the bandwidth and dynamic range, and to keep the triaxial magnetic field sensed by the magnetometer locked at zero. The triaxial bandwidths of our magnetometer are all increased to over 1.6 kHz, and the triaxial dynamic ranges of our magnetometer are expanded to ±150 nT. And we verify that the triaxial dynamic ranges of the magnetometer can be extended to over ±1,000 nT, when the triaxial coil constants are increased. The closed-loop magnetic field sensitivity is superior to 22 fT/Hz^1/2 in the transverse directions, and 230 fT/Hz^1/2 in the longitudinal direction. Based on the most simple and common single-beam configuration, we achieve magnetic field measurement along the third longitudinal direction and triaxial closed-loop operation without extra hardware and structure reconstruction.

Data availability statement

The data presented in this study are available on reasonable request from the corresponding author.

Author contributions

Conceptualization, KW, KZ and BZ; methodology, KW, KZ, and BZ; validation, KW and KZ; formal analysis, KW, KZ, WW, and JL; investigation, KW, KZ, FL, SZ, and JL; data curation, KW, KZ, YY and WW; writing—original draft preparation, KW; writing—review and editing, KW, KZ and JL; supervision, BZ and JL; project administration, JL; funding acquisition, J.L. All authors have approved this study for publication.

Funding

This work was supported by the National Natural Science Foundation of China (No. 61903013).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Kominis IK, Kornack TW, Allred JC, Romalis MV. A subfemtotesla multichannel atomic magnetometer. Nature (2003) 422:596–9. doi:10.1038/nature01484

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Allred JC, Lyman RN, Kornack TW, Romalis MV. High-sensitivity atomic magnetometer unaffected by spin-exchange relaxation. Phys Rev Lett (2002) 89:130801. doi:10.1103/PhysRevLett.89.130801

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Dang HB, Maloof AC, Romalis MV. Ultrahigh sensitivity magnetic field and magnetization measurements with an atomic magnetometer. Appl Phys Lett (2010) 97:151110. doi:10.1063/1.3491215

CrossRef Full Text | Google Scholar

4. Le Gal G, Lieb G, Beato F, Jager T, Gilles H, Palacios-Laloy A. Dual-Axis hanle magnetometer based on atomic alignment with a single optical access. Phys Rev Appl (2019) 12:064010. doi:10.1103/PhysRevApplied.12.064010

CrossRef Full Text | Google Scholar

5. Colombo AP, Carter TR, Borna A, Jau Y-Y, Johnson CN, Dagel AL, et al. Four-channel optically pumped atomic magnetometer for magnetoencephalography. Opt Express (2016) 24:15403. doi:10.1364/oe.24.015403

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Boto E, Holmes N, Leggett J, Roberts G, Shah V, Meyer SS, et al. Moving magnetoencephalography towards real-world applications with a wearable system. Nature (2018) 555:657–61. doi:10.1038/nature26147

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Iivanainen J, Zetter R, Parkkonen L. Potential of on-scalp MEG: Robust detection of human visual gamma-band responses. Hum Brain Mapp (2003) 41:150–61. doi:10.1002/hbm.24795

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Wyllie R, Kauer M, Wakai RT, Walker TG. Optical magnetometer array for fetal magnetocardiography. Opt Lett (2012) 37:2247. doi:10.1364/OL.37.002247

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Shah VK, Wakai RT. A compact, high performance atomic magnetometer for biomedical applications. Phys Med Biol (2013) 58:8153–61. doi:10.1088/0031-9155/58/22/8153

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Mhaskar R, Knappe S, Kitching J. A low-power, high-sensitivity micromachined optical magnetometer. Appl Phys Lett (2012) 101:241105. doi:10.1063/1.4770361

CrossRef Full Text | Google Scholar

11. Seltzer SJ, Romalis MV. Unshielded three-axis vector operation of a spin-exchange-relaxation-free atomic magnetometer. Appl Phys Lett (2004) 85:4804–6. doi:10.1063/1.1814434

CrossRef Full Text | Google Scholar

12. Huang HC, Dong HF, Hu XY, Chen L, Gao Y. Three-axis atomic magnetometer based on spin precession modulation. Appl Phys Lett (2015) 107:182403. doi:10.1063/1.4935096

CrossRef Full Text | Google Scholar

13. Boto E, Shah V, Hill RM, Rhodes N, Osborne J, Doyle C, et al. Triaxial detection of the neuromagnetic field using optically-pumped magnetometry: Feasibility and application in children. NeuroImage (2022) 252:119027. doi:10.1016/j.neuroimage.2022.119027

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Yan Y, Lu J, Zhang S, Lu F, Yin K, Wang K, et al. Three-axis closed-loop optically pumped magnetometer operated in the SERF regime. Opt Express (2022) 30:18300. doi:10.1364/OE.458367

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Shah V, Knappe S, Schwindt PDD, Kitching J. Subpicotesla atomic magnetometry with a microfabricated vapour cell. Nat Photon (2007) 1:649–52. doi:10.1038/nphoton.2007.201

CrossRef Full Text | Google Scholar

16. Osborne J, Orton J, Alem O, Shah V. Fully integrated, standalone zero field optically pumped magnetometer for biomagnetism. In: SM Shahriar, and J Scheuer, editors. Proc. SPIE 10548, steep dispersion engineering and opto-atomic precision metrology XI. San Francisco, CA, USA: SPIE) SPIE (1054). 10.1117/12.2299197.

Google Scholar

17. Dong HF, Fang JC, Zhou BQ, Tang XB, Qin J. Three-dimensional atomic magnetometry. Eur Phys J Appl Phys (2012) 57:21004. doi:10.1051/epjap/2011110392

CrossRef Full Text | Google Scholar

18. Huang H, Dong H, Chen L, Gao Y. Single-beam three-axis atomic magnetometer. Appl Phys Lett (2016) 109:062404. doi:10.1063/1.4960971

CrossRef Full Text | Google Scholar

19. Xiao W, Wu Y, Zhang X, Feng Y, Sun C, Wu T, et al. Single-beam three-axis optically pumped magnetometers with sub-100 femtotesla sensitivity. Appl Phys Express (2021) 14:066002. doi:10.35848/1882-0786/ac00d9

CrossRef Full Text | Google Scholar

20. Tang J, Zhai Y, Cao L, Zhang Y, Li L, Zhao B, et al. High-sensitivity operation of a single-beam atomic magnetometer for three-axis magnetic field measurement. Opt Express (2021) 29:15641. doi:10.1364/OE.425851

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Fedele T, Scheer HJ, Burghoff M, Curio G, Körber R. Ultra-low-noise EEG/MEG systems enable bimodal non-invasive detection of spike-like human somatosensory evoked responses at 1 kHz. Physiol Meas (2015) 36:357–68. doi:10.1088/0967-3334/36/2/357

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Dash D, Ferrari P, Malik S, Wang J. Overt speech retrieval from neuromagnetic signals using wavelets and artificial neural networks, Proceedings of the 2018 IEEE Global Conference on Signal and Information Processing (GlobalSIP), November 2018 IEEE. p. 489–93. doi:10.1109/GlobalSIP.2018.8646401Anaheim, CA, USA

CrossRef Full Text | Google Scholar

23. Fu K-MC, Iwata GZ, Wickenbrock A, Budker D. Sensitive magnetometry in challenging environments. AVS Quan Sci (2020) 2:044702. doi:10.1116/5.0025186

CrossRef Full Text | Google Scholar

24. Guo Q, Hu T, Chen C, Feng X, Wu Z, Zhang Y, et al. A high sensitivity closed-loop spin-exchange relaxation-free atomic magnetometer with broad bandwidth. IEEE Sensors J (2021) 21:21425–31. doi:10.1109/jsen.2021.3102146

CrossRef Full Text | Google Scholar

25. Wang K, Lu J, Yan Y, Tang J, Ye M, Yin K, et al. Bandwidth expansion through large-amplitude modulation and proportional feedback for single-beam atomic magnetometers. IEEE Sensors J (2022) 22:2016–23. doi:10.1109/jsen.2021.3136213

CrossRef Full Text | Google Scholar

26. Tang J, Zhai Y, Zhou B, Han B, Liu G. Dual-Axis closed loop of a single-beam atomic magnetometer: Toward high bandwidth and high sensitivity. IEEE Trans Instrum Meas (2021) 70:1–8. doi:10.1109/tim.2021.3112797

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Robinson SE, Andonegui AB, Holroyd T, Hughes KJ, Alem O, Knappe S, et al. Cross-Axis dynamic field compensation of optically pumped magnetometer arrays for MEG. NeuroImage (2022) 262:119559. doi:10.1016/j.neuroimage.2022.119559

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Seltzer SJ. Developments in alkali-metal atomic magnetometry Princeton university Priceton, NJ, USA (2008).

Google Scholar

29. Appelt S, Baranga AB-A, Erickson CJ, Romalis MV, Young AR, Happer W. Theory of spin-exchange optical pumping of ³He and ¹²⁹Xe. Phys Rev A (1998) 58:1412–39. doi:10.1103/PhysRevA.58.1412

CrossRef Full Text | Google Scholar

30. Shah V, Romalis MV. Spin-exchange-relaxation-free magnetometry using elliptically-polarized light. Phys Rev A (Coll Park) (2009) 80:013416. doi:10.1103/physreva.80.013416

CrossRef Full Text | Google Scholar

31. Dupont-Roc J. Détermination par des méthodes optiques des trois composantes d’un champ magnétique très faible. Rev Phys Appl (Paris) (1970) 5:853–64. doi:10.1051/rphysap:0197000506085300

CrossRef Full Text | Google Scholar

32. Dupont-Roc J. Étude théorique de diverses résonances observables en champ nul sur des atomes «habillés» par des photons de radiofréquence. J Phys France (1971) 32:135–44. doi:10.1051/jphys:01971003202-3013500

CrossRef Full Text | Google Scholar

33. Wu W, Zhou B, Liu G, Chen L, Wang J, Fang J. Novel nested saddle coils used in miniature atomic sensors. AIP Adv (2018) 8:075126. doi:10.1063/1.5036605

CrossRef Full Text | Google Scholar

34. Wang J, Zhou B, Wu W, Chen L, Fang J. Uniform field coil design based on the target-field method in miniature atomic sensors. IEEE Sensors J (2019) 19:2895–901. doi:10.1109/JSEN.2018.2881760

CrossRef Full Text | Google Scholar

35. Li S, Lu J, Ma D, Wang K, Gao Y, Sun C, et al. In situ measurement of nonorthogonal angles of a three-Axis vector optically pumped magnetometer. IEEE Trans Instrum Meas (2022) 71:1–9. doi:10.1109/TIM.2022.3144737

CrossRef Full Text | Google Scholar