Ying Yang- College of Physics and Electronic Engineering, Chongqing Normal University, Chongqing, China
A recent study reported the enhancement of thermoelectric response due to the presence of triple point phonons [Phys. Rev. Mater 2, 114204 (2018)]. Because the topological triple point phonons field is still at its early stage, it is necessary to search for realistic materials with ideal triple point phonons. In this work, we show that cubic Ca3I3P is an excellent material to host the ideal charge-two triple points at high-symmetry points
Introduction
The study of topological behaviors in condensed matter systems [1–10] has generated much interest in solid-state physics over the past 10 years. Emergent low-energy quasiparticles in solid states, derived from the intrinsic topological order of the crystalline, can serve as exotic analogs of the elementary particles in high-energy physics and thus serve as a valuable platform to examine the related fundamental physics. Significant accomplishments have been made thanks to ongoing work and development, mainly since the topological band theory was established. Beyond the conventional Weyl, Dirac, and Majorana particles under the Poincare symmetry, many more unconventional topological quasiparticles [11–20] have been predicted thus far. In solid states, these quasiparticles can exhibit a variety of topological charges, dispersion types, and pseudospin structures.
The current study of crystal topology has even been further extended to bosons, including phonons, photons, and magnons. Phonons [21–40] can be a perfect platform for realizing these quasiparticles owing to their unique device applications and the advantages of whole frequency range observation. For example, in the phonon dispersion of three-dimensional-SiO2, Wang et al. [40] proposed a topological triangular Weyl complex made up of one double Weyl point and two single Weyl points. In realistic three-dimensional materials with space group numbers 195–199, and 207–214, Liu et al. reported charge-four Weyl point phonons. Xie et al. [24] reported that sixfold degenerate nodal-point phonons could appear in three-dimensional materials C3N4, Sc4C3, Y4Sb3, and K8Si46. Chen et al. [39] systematically studied three-dimensional Dirac phonons in 2021. As potential candidates for materials with Dirac point phonons, some realistic three-dimensional materials are also put forth in their work. In 2022, Ding et al. [32] reported that three-dimensional BaZnO2 has a type-III charge-two Weyl point phonon and double-helicoid phonon surface states. Experimentally, inelastic x-ray scattering was used to identify the double Weyl points in three-dimensional FeSi [36, 38], which was a significant driving force for the field.
According to a recent study by Singh et al. [41], the presence of triple point phonons enhances the thermoelectric response. However, only a handful of candidate materials are proposed to host triple-point phonons. At the very least, the material should meet the following criteria to qualify as a good candidate for triple nodal point phonons. First, there must be no nearby extraneous phonon bands at a particular frequency, as such a situation may make it more challenging to interpret the measured properties. Second, candidate materials with triple nodal point phonons should have more evident arc-shaped surface modes (i.e., not covered by the bulk phonon modes). It is still urgently necessary to search for realistic material systems with ideal triple nodal point phonons due to these limitations on potential materials.
In this work, we selected a realistic material, cubic Ca3I3P with space group 214 [42], to be the ideal material candidate with two charge-two triple nodal points at points
Computational methods
We perform the first-principle calculations based on the density functional theory (DFT) [43]. The generalized gradient approximation (GGA) [44] with Perdew–Burke–Ernzerhof (PBE) [45] realization was adopted for the exchanged correlation potential. The phonon spectra of cubic Ca3I3P is calculated by using the Phonopy code. The pre-process and post-process were performed in the PHONOPY package using density functional perturbation theory (DFPT) [46]. The cutoff energy for the plane wave was 600 eV, and the Brillouin zone is sampled using converged 5 × 5 × 5 Γ-centered k-mesh grids. To study the topological properties of nontrivial band crossings in the phonon spectrum, we calculate its corresponding surface states and constant frequency slices using the WANNIERTOOLS package [47]. In this work, the phononic surface spectrums were simulated by the following steps: 1) by calculating the phonon dispersion of a slab system; 2) First, we used the phonopyTB tool, installed in the root folder of WannierTools [47], to generate the phononic tight-binding Hamiltonian with the FORCE−CONSTANTS. Then, we used the iterative Green’s function method to calculate the surface states of phonons in the software package WannierTools [47].
Results and discussion
The crystal structure of cubic Ca3I3P with space group I4132 is shown in Figure 1A. Ca3I3P is a colorless insulator [48], as expected from the closed-shell electronic configuration of (Ca2+)3(I−)3P3−. The obtained lattice constants for cubic Ca3I3P are a = b = c = 10.779 Å, agreeing well with the experimental lattice constants a = b = c = 10.665 Å [42]. The Ca, I, and P atoms locate at 48i (−0.26853, −0.98147, 0.03706), 24i (0.74736, –0.75000, −0.24736), 8f (–0.25 –0.75000 0.250000) Wyckoff positions, respectively. Ca2+ is bonded to two equivalent P³– and four equivalent I1- atoms to form a mixture of edge and corner-sharing CaP₂I₄ octahedra. P³⁻ is bonded to six equivalent Ca2+ atoms to form edge-sharing PCa6 octahedra. I1− is bonded in a distorted rectangular see-saw-like geometry to four equivalent Ca2+ atoms.
FIGURE 1. (A) The crystal structure for cubic Ca3I3P and (B) 3D BZ and selected symmetry paths.
The phonon dispersion for cubic Ca3I3P along G -P-H- G -N-H-N-P (see Figure 1B) is exhibited in Figure 2A. At first glance, the cubic Ca3I3P is dynamically stable due to the absence of imaginary frequencies. We only focus on the R1 region, where two obvious triple nodal points appear at high-symmetry points. The enlarged figure of the phonon bands in R1 regions is exhibited in Figure 2B. From Figure 2B, two charge-two triple nodal points with a topological charge |C| = 2 can be found at high-symmetry points
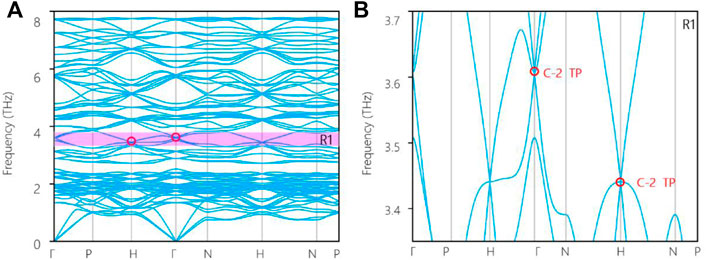
FIGURE 2. (A) Phonon dispersion for cubic Ca3I3P and (B) enlarged phonon bands in R1 of (A). Red circles mark the charge-two triple nodal point (C-2 TP).
The three-dimensional plots of the phonon bands around these two charge-two triple nodal points are shown in Figures 3A,B. Obviously, the charge-two triple nodal point (C-2 TP) is a zero-dimensional threefold band degeneracy and features a linear energy splitting along any direction in momentum space. Note that the charge-two triple nodal point can only appear at a high-symmetry point in three-dimensional BZ.
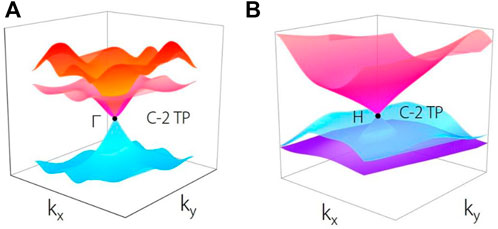
FIGURE 3. (A) and (B) three-dimensional plots of the phonon bands around the charge-two triple nodal points (C-2 TPs) at high-symmetry points
Nontrivial surface states can characterize these charge-two triple nodal points. To obtain the surface states for cubic Ca3I3P, a surface slab model has been constructed along the (010) surface. The calculated phononic local density of the surface states for cubic Ca3I3P is shown in Figure 4B, and the corresponding surface path can be referred to in Figure 4A. The surface spectra of cubic Ca3I3P are very clean and arise from the projections of the two charge-two triple nodal points.
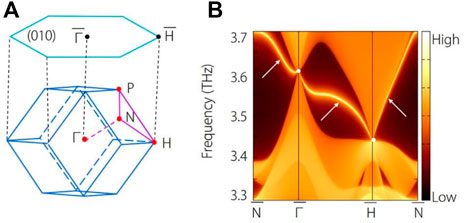
FIGURE 4. (A) Two-dimensional (010) surface BZ and selected surface paths. (B) The calculated phononic surface states on the (010) surface for cubic Ca3I3P using the iterative Greens function method based on a phononic tight-binding Hamiltonian. White arrows highlight the nontrivial surface states.
Interestingly, the phononic arc state around the projected point of the nodal point shows chirality-dependent properties [49]. Because the charge-two triple nodal point has a topological charge of |C| = 2, two phononic arcs would be observed in cubic Ca3I3P. Surface states on the (010) surface at 3.60 THz and 3.45 THz are shown in Figure 5A and Figure 5B, respectively. Indeed, one could observe that two arcs emanate from the projections of the two charge-two triple nodal points, as shown in Figure 5.
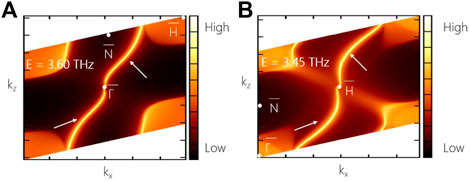
FIGURE 5. (A) and (B) the corresponding constant frequency slices at 3.60 THz and 3.45 THz, respectively. White arrows highlight the double arc surface states.
Examining the distinctive physical characteristics of the topological phonon states will be a crucial objective of upcoming research. Inelastic x-ray scattering has been used in topological phonon experiments thus far to visualize the topological band degeneracy. We need to look for other measurable effects from the topological phonons and to propose sound material systems. In order to detect these effects experimentally, new methods must be developed, precisely ways to separate the signal from topological modes. In an experiment, the surface phonon modes can be verified by high-resolution electron energy loss spectroscopy, helium-atom scattering, or THz spectroscopy.
Summary
With the help of first principle calculations, the phononic charge-two triple nodal points are reported to appear at high-symmetry points in cubic Ca3I3P. In addition, we also studied the phononic surface states and the isofrequency arcs on the (010) surface. Such clean and visible double surface arcs confirm the topological charge of |C| = 2 for the two triple nodal points in cubic Ca3I3P. Moreover, the nontrivial surface states are long and clean, benefiting the experimental detections soon. Our work not only determines the ideal charge-two triple nodal point states but also confirms the clean and long double phononic surface arcs in cubic Ca3I3P.
Data availability statement
The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.
Author contributions
YY-investigations and writing.
Acknowledgments
YY is grateful for support from the key project of education planning supported by the Chongqing municipal education commission (No. 2021-GX-013), National Natural Science Foundation of China (No. 12175027), and the Basic Research and Frontier Exploration Project of Chongqing Municipality (cstc2018jcyjAX0820).
Conflict of interest
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
2. Lv BQ, Qian T, Ding H. Experimental perspective on three-dimensional topological semimetals. Rev Mod Phys (2021) 93(2):025002. doi:10.1103/revmodphys.93.025002
3. Gao H, Venderbos JW, Kim Y, Rappe AM. Topological semimetals from first principles. Annu Rev Mater Res (2019) 49:153–83. doi:10.1146/annurev-matsci-070218-010049
4. Weng H, Dai X, Fang Z. Topological semimetals predicted from first-principles calculations. J Phys : Condens Matter (2016) 28(30):303001. doi:10.1088/0953-8984/28/30/303001
5. Bernevig A, Weng H, Fang Z, Dai X. Recent progress in the study of topological semimetals. J Phys Soc Jpn (2018) 87(4):041001. doi:10.7566/jpsj.87.041001
6. Hu J, Xu SY, Ni N, Mao Z. Electronic transport and quantum oscillation of topological semimetals (2019).
7. Fang C, Lu L, Liu J, Fu L. Topological semimetals with helicoid surface states. Nat Phys (2016) 12(10):936–41. doi:10.1038/nphys3782
8. Schoop LM, Pielnhofer F, Lotsch BV. Chemical principles of topological semimetals. Chem Mater (2018) 30(10):3155–76. doi:10.1021/acs.chemmater.7b05133
9. Klemenz S, Lei S, Schoop LM. Topological semimetals in square-net materials. Annu Rev Mater Res (2019) 49:185–206. doi:10.1146/annurev-matsci-070218-010114
10. Fang C, Gilbert MJ, Dai X, Bernevig BA. Multi-Weyl topological semimetals stabilized by point group symmetry. Phys Rev Lett (2012) 108(26):266802. doi:10.1103/physrevlett.108.266802
11. Jin L, Zhang XM, Dai XF, Wang LY, Liu HY, Liu GD. Screening topological materials with a CsCl-type structure in crystallographic databases. IUCrJ (2019) 6(4):688–94. doi:10.1107/s2052252519007383
12. Jin L, Zhang X, He T, Meng W, Dai X, Liu G. Topological nodal line state in superconducting NaAlSi compound. J Mater Chem C Mater (2019) 7(34):10694–9. doi:10.1039/c9tc03464a
13. He T, Zhang X, Wang L, Liu Y, Dai X, Wang L, et al. Theoretical realization of fully spin-polarized nodal box with traversing Brillouin zone surface state. Phys Rev B (2022) 106(7):075155. doi:10.1103/physrevb.106.075155
14. Zhang H, Zhang X, He T, Dai X, Liu Y, Liu G, et al. Three-dimensional Weyl hourglass networks in the nonsymmorphic half-metal Mg2VO4. Phys Rev B (2020) 102(15):155116. doi:10.1103/physrevb.102.155116
15. He T, Liu Y, Tian L, Zhang X, Meng W, Dai X, et al. Coexistence of fully spin-polarized Weyl nodal loop, nodal surface, and Dirac point in a family of quasi-one-dimensional half-metals. Phys Rev B (2021) 103(8):085135. doi:10.1103/physrevb.103.085135
16. Jin L, Zhang X, Liu Y, Dai X, Liu G. Theoretical realization of two-dimensional half-metallicity and fully spin-polarized multiple nodal-line fermions in monolayer PrOBr. Phys Rev B (2022) 105(7):075414. doi:10.1103/physrevb.105.075414
17. He T, Zhang X, Liu Y, Dai X, Liu G, Yu ZM, et al. Ferromagnetic hybrid nodal loop and switchable type-I and type-II Weyl fermions in two dimensions. Phys Rev B (2020) 102(7):075133. doi:10.1103/physrevb.102.075133
18. He T, Zhang X, Liu Y, Dai X, Wang L, Liu G. Potential antiferromagnetic Weyl nodal line state in LiTi2O4 material. Phys Rev B (2021) 104(4):045143. doi:10.1103/physrevb.104.045143
19. Meng W, Zhang X, Liu Y, Dai X, Liu G. Lorentz-violating type-II Dirac fermions in full-Heusler compounds XMg2Ag (X= Pr, Nd, Sm). New J Phys (2020) 22(7):073061. doi:10.1088/1367-2630/ab9d55
20. Zhang H, Zhang X, Liu Y, Dai X, Chen G, Liu G. Possibility of fully spin-polarized nodal chain state in several spinel half metals. Phys Rev B (2020) 102(19):195124. doi:10.1103/physrevb.102.195124
21. Wang X, Zhou F, Yang T, Kuang M, Yu ZM, Zhang G. Symmetry-enforced ideal lanternlike phonons in the ternary nitride Li6WN4. Phys Rev B (2021) 104(4):L041104. doi:10.1103/physrevb.104.l041104
22. Zhou F, Chen H, Yu ZM, Zhang Z, Wang X. Realistic cesium fluogermanate: An ideal platform to realize the topologically nodal-box and nodal-chain phonons. Phys Rev B (2021) 104(21):214310. doi:10.1103/physrevb.104.214310
23. Zhou F, Zhang Z, Chen H, Kuang M, Yang T, Wang X. Hybrid-type nodal ring phonons and coexistence of higher-order quadratic nodal line phonons in an AgZr alloy. Phys Rev B (2021) 104(17):174108. doi:10.1103/physrevb.104.174108
24. Xie C, Liu Y, Zhang Z, Zhou F, Yang T, Kuang M, et al. Sixfold degenerate nodal-point phonons: Symmetry analysis and materials realization. Phys Rev B (2021) 104(4):045148. doi:10.1103/physrevb.104.045148
25. Zhong M, Han Y, Wang J, Liu Y, Wang X, Zhang G. Material realization of double-Weyl phonons and phononic double-helicoid surface arcs with P213 space group. Phys Rev Mater (2022) 6(8):084201. doi:10.1103/physrevmaterials.6.084201
26. Wang J, Yuan H, Yu ZM, Zhang Z, Wang X. Coexistence of symmetry-enforced phononic Dirac nodal-line net and three-nodal surfaces phonons in solid-state materials: Theory and materials realization. Phys Rev Mater (2021) 5(12):124203. doi:10.1103/physrevmaterials.5.124203
27. Ding G, Sun T, Surucu G, Surucu O, Gencer A, Wang X. Complex nodal structure phonons formed by open and closed nodal lines in CoAsS and Na2CuP solids. Phys Chem Chem Phys (2022) 24(28):17210–6. doi:10.1039/d2cp01992b
28. Wang J, Yuan H, Liu Y, Zhou F, Wang X, Zhang G. Hourglass Weyl and Dirac nodal line phonons, and drumhead-like and torus phonon surface states in orthorhombic-type KCuS. Phys Chem Chem Phys (2022) 24(5):2752–7. doi:10.1039/d1cp05217a
29. Xie C, Yuan H, Liu Y, Wang X, Zhang G. Three-nodal surface phonons in solid-state materials: Theory and material realization. Phys Rev B (2021) 104(13):134303. doi:10.1103/physrevb.104.134303
30. Wang J, Yuan H, Kuang M, Yang T, Yu ZM, Zhang Z, et al. Coexistence of zero-one-and two-dimensional degeneracy in tetragonal SnO2 phonons. Phys Rev B (2021) 104(4):L041107. doi:10.1103/physrevb.104.l041107
31. Ding G, Sun T, Wang X. Ideal nodal-net, nodal-chain, and nodal-cage phonons in some realistic materials. Phys Chem Chem Phys (2022) 24(18):11175–82. doi:10.1039/d2cp00731b
32. Ding G, Zhou F, Zhang Z, Yu ZM, Wang X. Charge-two Weyl phonons with type-III dispersion. Phys Rev B (2022) 105(13):134303. doi:10.1103/physrevb.105.134303
33. Zhong M, Liu Y, Zhou F, Kuang M, Yang T, Wang X, et al. Coexistence of phononic sixfold, fourfold, and threefold excitations in the ternary antimonide Zr3Ni3Sb4. Phys Rev B (2021) 104(8):085118. doi:10.1103/physrevb.104.085118
34. Yang T, Xie C, Chen H, Wang X, Zhang G. Phononic nodal points with quadratic dispersion and multifold degeneracy in the cubic compound Ta3Sn. Phys Rev B (2022) 105(9):094310. doi:10.1103/physrevb.105.094310
35. Xie C, Yuan H, Liu Y, Wang X. Two-nodal surface phonons in solid-state materials. Phys Rev B (2022) 105(5):054307. doi:10.1103/physrevb.105.054307
36. Miao H, Zhang TT, Wang L, Meyers D, Said AH, Wang YL, et al. Observation of double Weyl phonons in parity-breaking FeSi. Phys Rev Lett (2018) 121(3):035302. doi:10.1103/physrevlett.121.035302
37. Li J, Liu J, Baronett SA, Liu M, Wang L, Li R, et al. Computation and data driven discovery of topological phononic materials. Nat Commun (2021) 12(1):1204–12. doi:10.1038/s41467-021-21293-2
38. Zhang T, Song Z, Alexandradinata A, Weng H, Fang C, Lu L, et al. Double-Weyl phonons in transition-metal monosilicides. Phys Rev Lett (2018) 120(1):016401. doi:10.1103/physrevlett.120.016401
39. Chen ZJ, Wang R, Xia BW, Zheng BB, Jin YJ, Zhao YJ, et al. Three-dimensional Dirac phonons with inversion symmetry. Phys Rev Lett (2021) 126(18):185301. doi:10.1103/physrevlett.126.185301
40. Wang R, Xia BW, Chen ZJ, Zheng BB, Zhao YJ, Xu H. Symmetry-protected topological triangular Weyl complex. Phys Rev Lett (2020) 124(10):105303. doi:10.1103/physrevlett.124.105303
41. Singh S, Wu Q, Yue C, Romero AH, Soluyanov AA. Topological phonons and thermoelectricity in triple-point metals. Phys Rev Mater (2018) 2(11):114204. doi:10.1103/physrevmaterials.2.114204
42. Jensen EA, Hoistad LM, Corbett JD. Lanthanum and praseodymium bromide pnictides. A convergence of interstitial chemistry in cluster halides and intermetallic pnictides. J Solid State Chem (1999) 144(1):175–80. doi:10.1006/jssc.1999.8143
43. Parr RG. Density functional theory. Annu Rev Phys Chem (1983) 34(1):631–56. doi:10.1146/annurev.pc.34.100183.003215
44. Perdew JP, Burke K, Ernzerhof M. Generalized gradient approximation made simple. Phys Rev Lett (1996) 77(18):3865–8. doi:10.1103/physrevlett.77.3865
45. Perdew JP, Burke K, Ernzerhof M. Perdew, burke, and ernzerhof reply. Phys Rev Lett (1998) 80(4):891. doi:10.1103/physrevlett.80.891
46. Baroni S, De Gironcoli S, Dal Corso A, Giannozzi P. Phonons and related crystal properties from density-functional perturbation theory. Rev Mod Phys (2001) 73(2):515–62. doi:10.1103/revmodphys.73.515
47. Wu Q, Zhang S, Song HF, Troyer M, Soluyanov AA. WannierTools: An open-source software package for novel topological materials. Comp Phys Commun (2018) 224:405–16. doi:10.1016/j.cpc.2017.09.033
48. Hamon C, Marchand R, Laurent Y, Lang J. Étude d'halogénopnictures. III. Structure de Ca2PI et Ca3PI3. Surstructures de type NaCl. bulmi (1974) 97:6–12. doi:10.3406/bulmi.1974.6909
Keywords: triple point, topological phonons, phonon band crossings, topological charge, arc-shaped surface states
Citation: Yang Y (2022) Cubic Ca3I3P with ideal charge-two triple point. Front. Phys. 10:1058242. doi: 10.3389/fphy.2022.1058242
Received: 30 September 2022; Accepted: 10 October 2022;
Published: 19 October 2022.
Edited by:
Yong Fang, Changshu Institute of Technology, ChinaReviewed by:
Jiangchao Han, Beihang University, ChinaHaopeng Zhang, Chongqing University of Posts and Telecommunications, China
Copyright © 2022 Yang. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Ying Yang, 20131184@cqnu.edu.cn