Combining beams in different locations for aerospace defense in a turbulent atmosphere

A fixed high-power laser system used as an aerospace defense weapon has limitations such as the transmitter size, serious thermal blooming during propagation, rapid motion, and the variation of the location of the target. In the present paper, we propose a method by arranging many high-power systems with adequate distance in a defense area. The intensity distribution and the energy irradiated on the target are studied and compared with a fixed laser system. Results show that adequate arrangement of many high-power laser systems can reply to the arbitrary and rapid motion of the target.

Introduction

In today’s world, aerospace defense has become more important and complex accompanied by the development of hypersonic missiles [1, 2]. High-power lasers are considered one of the most promising methods due to the energy travels with the speed of light [2, 3]. However, the output power of the laser and the effect of the atmosphere are the major barriers of high-power lasers used as the aerospace defense weapon [4, 5].

Since coherent beam combining (CBC) is more complex and expensive, incoherent beam combining (IBC) is regarded as the major method to increase the output power of the transmitter in the application of the laser weapon [6–11]. There are two factors that will hinder the application of IBC in aerospace defense. One factor is the size of the transmitter. When we use a transmitter to send the combined beams, the size of the aperture will limit the channels of the beam. Another factor is that further increasing the output power of the combined beams will result in serious nonlinear effects [12–14].

In the present paper, we propose a new aerospace defense method by combining laser beams apart from a long distance.

Concept of incoherent combination of different location beams

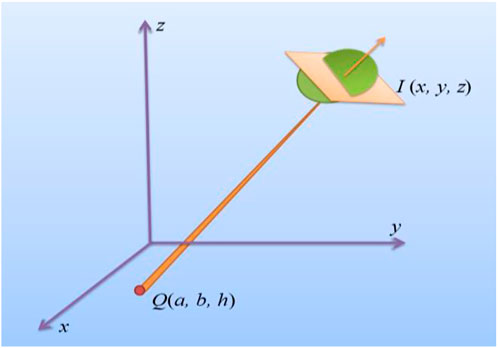
The propagation of incoherent combination of different location beams is shown in Figure 1. There are many laser beams located in different locations. All the laser beams are transmitted to the same target.

FIGURE 1

FIGURE 1. Propagation schematic representation of the incoherent beams by combining different location beams.

There are many factors that will affect the propagation, such as the wavelength, size of the transmitter, the distance between each laser, and the propagation distance [4, 15]. In practice, the target moves in a very high speed which will cause the change of the propagation distance, as shown in Figure 2. P denotes the location of the target which moves in a velocity v. Q is the location of one laser source.

FIGURE 2

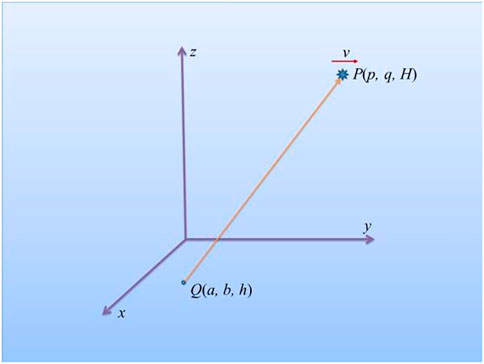
FIGURE 2. Variation of the distance between the target and the beams due to the motion of the target.

We can see from Figure 2 that the distance between the beam and the target is

$L=\sqrt{{\left(p-a\right)}^2+{\left(q-b\right)}^2+{\left(H-h\right)}^2,}(1)$

where (a, b, h) and (p, q, H) are the coordinates of the beam and the target, respectively. In addition to the propagation distance, the zenith angle of propagation also affects the destructive effect, as shown in Figure 3.

FIGURE 3

FIGURE 3. Variation of the direction of the irradiation for the beam and the surface of the target.

From Figures 2, 3 we can see that the direction of beam is

$\left[\begin{array}{l}\cos \left(\alpha \right)\\ \cos \left(\beta \right)\\ \cos \left(\gamma \right)\end{array}\right]=\frac{1}{L}\left(\begin{array}{l}p-a\\ q-b\\ H-h\end{array}\right),(2)$

where (α, β, γ) are the direction angles of the beam. If we assume that the surface irradiated by the laser is $\overrightarrow{S}=S\widehat{n}$, where $S$ is the area and $\widehat{n}$ is the normal direction, the flux of the beam on an area can be described as

$\mathrm{\Phi }=\iint I\left(x,y,z\right)\left[\cos \left(\alpha \right)\widehat{i}+\cos \left(\beta \right)\widehat{j}+\cos \left(\gamma \right)\widehat{k}\right]·d\overrightarrow{S,}(3)$

where $I\left(x,y,z\right)$ is the intensity arriving at the target and γ also is the zenith angle.

In practice, laser beams need a period of time to damage the target. The energy of the laser irradiating on the target can be expressed as

$E={\int }_0^T\mathrm{\Phi }dt,(4)$

where T is the time of the irradiation of the laser on the target. From Eqs 3, 4, we can see that $\mathrm{\Phi }$ and E are the power and energy of the laser radiating on the area S, respectively.

Laser beam propagating in the atmosphere

Absorption, scattering, turbulence, and thermal blooming of the atmosphere will affect the propagation of the laser beam in free space [16]. In the present paper, only the effect of turbulence is considered. For simplicity, we assume that the beam has a Gaussian intensity distribution. Thus, the initial optical field at the arbitrary location is denoted as [17]

$U_m\left(x_0,y_0\right)=\sqrt{\frac{2P}{\pi w_0^2}}\exp \left[-\frac{{\left(x_0-a_m\right)}^2+{\left(y_0-b_m\right)}^2}{w_0^2}\right],(5)$

where P is the power of the beam, w₀, the waist width, (a_m, b_m), the location of the laser beam, and (x₀, y₀), the coordinates of the initial plane perpendicular to the propagation direction. The intensity distribution at the target can be calculated by [18]

$\langle I_m\left(\mathit{r},z\right)\rangle ={\left(\frac{1}{\lambda L}\right)}^2{\int }_{-\infty }^{\infty }{\int }_{-\infty }^{\infty }{H}_m\left({\mathit{s}}_d\right)M\left({\mathit{s}}_d\right)\exp \left(\frac{ik}{L}\mathit{r}\cdot {\mathit{s}}_d\right)d^2{\mathit{s}}_d,(6)$

where

$\left(\begin{array}{l}\mathit{s}\\ {\mathit{s}}_d\end{array}\right)=\left(\begin{array}{l}\left({\mathit{r}}_{01}+{\mathit{r}}_{02}\right)/2\\ {\mathit{r}}_{01}-{\mathit{r}}_{02}\end{array}\right)(7)$

is the coordinate conversion, and $\mathit{r}=\left(x,y\right)$ is the position vector at the receiver. When the propagation distance is equal to the focal length, also at the focal plane

$H_m\left({\mathit{s}}_d\right)={\int }_{-\infty }^{\infty }{\int }_{-\infty }^{\infty }{U}_m\left(\mathit{s}+\frac{{\mathit{s}}_d}{2}\right)U_m^{*}\left(\mathit{s}-\frac{{\mathit{s}}_d}{2}\right)d^2\mathit{s}(8)$

and $M\left({\mathit{s}}_d\right)=\exp \left(-{\mathit{s}}_{\mathit{d}}^2/{\rho }_0^2\right)$ is the transfer function of turbulence, where * denotes the conjugate and ${\rho }_0$ is the coherence length of a spherical wave and can be found by [19]

${\rho }_0={\cos }^{3/5}\left(\gamma \right){\rho }_H(9)$

where

${\rho }_H={\left[1.46k^2{\int }_{h_0}^H{C}_n^2\left(h\right){\left(1-\frac{h}{H-h_0}\right)}^{5/3}dh\right]}^{-3/5}(10)$

is the coherence length vertical from the ground to the altitude H [20], and $C_n^2\left(h\right)$ is the vertical index structure constant function. From Eqs 5–10, we can obtain the intensity distribution of one laser at the focal plane as

$\langle I_m\left(\mathit{r},z\right)\rangle =\frac{2P}{\pi {\tau }^2{w}_0^2}\exp \left[-\frac{2}{{\tau }^2{w}_0^2}\left(x^2+y^2\right)\right],(11)$

where $\tau =\sqrt{{\tau }_2^2+{\tau }_3^2}$, ${\tau }_2$, and ${\tau }_3$ are the factors of the beam spread due to diffraction and the turbulence effect, respectively. The non-dimensional quantities are introduced as [17]

${\tau }_2=\frac{2L}{k{w}_0^2};{\tau }_3=\frac{2\sqrt{2}L}{k{w}_0{\rho }_0}(12)$

The total average intensity of the incoherent combining beam at the target is the sum of the average intensity of each laser radiating on the target.

Special cases and discussion

To analyze the performance of the aerospace defense method, the special case is given as follows.

To compare the damage effect of the incoherent beams, the power levels are evaluated by using the total average intensity of the incoherent combining beam at the target, which is the sum of the average intensity of each laser radiating on the target. The average intensity of each laser is expressed in Eq. 11, where P is a constant.

For simplicity, we assume h = 0, namely, all of the laser sources are located at the ground, as shown in (Figure 4). The coordinates of the laser sources are Q₁₁ (-a, -a), Q₁₂ (0, -a), Q₁₃ (a, -a), Q₂₁ (-a, 0), Q₂₂ (0, 0), Q₂₃ (a, 0), Q₃₁ (-a, a), Q₃₂ (0, a), and Q₃₃ (a, a). The coordinate of the target is p = p₀ + vt and q = 0, and the altitude is H. For calculation, we set a = 10 km, p₀ = –50 km, v = 300 m/s, and H = 10 km.

In this paper, we select the ITU-R model presented in 2001 to describe the model of the altitude-dependent structure constant.

$C_n^2\left(h\right)=8.148\times {10}^{-56}{V}^2{h}^{10}\exp \left(-h/1000\right)+2.7\times {10}^{-16}\exp \left(-h/1500\right)+C_0\exp \left(-h/100\right),(13)$

where $V={\left(v_g^2+30.69v_g+348.91\right)}^{1/2}$ is the wind speed along the vertical path and v_g is the ground wind speed. C₀ is the nominal value of at the ground level (the typical value is 1.7 × 10⁻¹⁴m^−2/3). For the convenience of the study, we set v_g = 0 in this paper.

For comparison, we assume that the power of each laser is P when all of the nine lasers are sent to the target together. Even though, the spot of the laser maybe an ellipse, in practice, we only concern a certain area. We assume the area is a circle with the radius R = 0.1 m. If only one laser is sent to the area, we assume the output power of the laser is 9P. Figure 5 shows the variation of the energy in the area of the circle with the irradiated time. It should be noted that the ratio of energy to power expresses the damage ability of the incoherent beam on the area S of the target and has the unit of time when the power of these lasers is a constant.

FIGURE 4

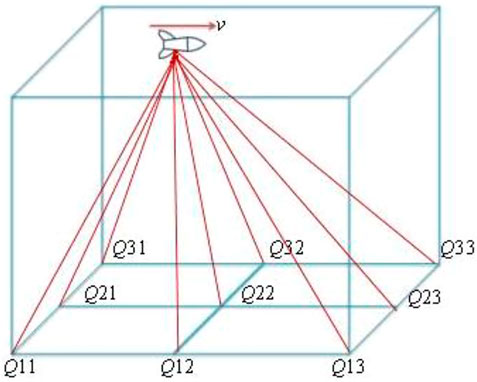
FIGURE 4. Special case for analyzing the performance of the aerospace defense method, where Q₁₁ to Q₃₃ denote nine laser sources and the target moves horizontally in a uniform velocity.

FIGURE 5

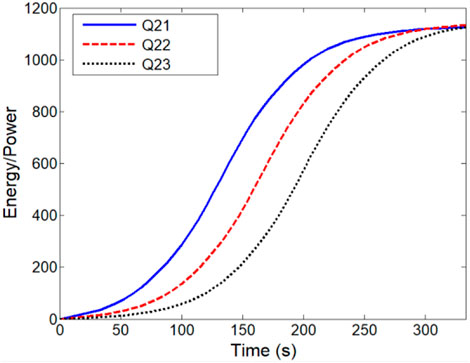
FIGURE 5. Variation of the energy in the irradiated area with the irradiated time for lasers Q₂₁, Q₂₂, and Q₂₃, respectively.

Because Q₂₁ is in the front of the three lasers, the energy increases fast at the start. The energy increases slowly when the target is far apart from the laser. With the increase in the angle of elevation, the growth rate of the energy becomes fast and keeps a period of time. This period of time is the optimum irradiated time. The energy irradiated by Q₂₂ and Q₂₃ has the same variation. Figure 6 gives the variation of the energy in the area irradiated by lasers Q₁₁, Q₁₂, and Q₁₃, respectively.

FIGURE 6

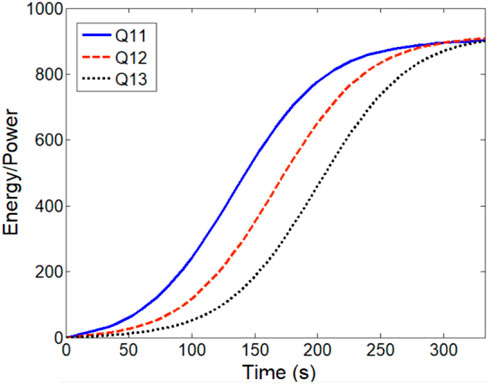
FIGURE 6. Variation of the energy in the irradiated area with the irradiated time for lasers Q₁₁, Q₁₂, and Q₁₃, respectively.

Comparing with Figure 5, we can see that the variation of the energy irradiated by lasers Q₁₁, Q₁₂, and Q₁₃ has the same trend as in Figure 5. Because the trajectory of the target is just above the line determined by Q₂₁, Q₂₂, and Q₂₃, namely, the angle of elevation for Q₂₁, Q₂₂, and Q₂₃ is larger than that for Q₁₁, Q₁₂, and Q₁₃, the total energy irradiated by Q₂₁, Q₂₂, and Q₂₃ at the same time is larger than that by Q₁₁, Q₁₂, and Q₁₃, respectively.

In application, it is difficult for letting a laser just under the trajectory of the target. Arrays of many lasers can solve the problem of the target moving in the arbitrary trajectory. Figure 7 shows the comparison between variation of the energy irradiated by one laser or by all of the lasers. We assume the power of each laser is P when all of the lasers irradiate the target together. Thus, the total power of all the lasers also is 9P. The energy irradiated on the target is expressed by Q. The power of one laser is 9P if only one laser irradiates the target.

FIGURE 7

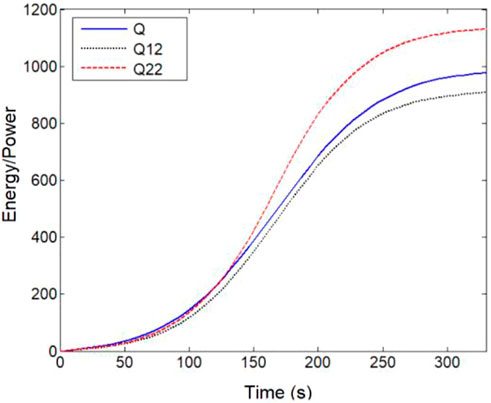
FIGURE 7. Comparison between the variation of the energy irradiated by only one laser and all of the lasers, where Q denotes the energy irradiated on the target by all lasers.

It can be seen that the effect of irradiation by the laser array is better than that only by Q₁₂ and is worse than that only by Q₂₂. When the target is far from the laser, namely, the angle of elevation is small, the effect of the irradiation has little difference between the lasers Q, Q₁₂, and Q₂₂.

Conclusion

It is important and difficult for the aerospace defense duo to the complex trajectory and very fast velocity of the target. Not only the power of one laser system is hard to satisfy the requirement but also its propagation distance and the variation of the angle of elevation will hinder the performance, even though the laser system is fixed in a moving device.

Arranging the laser system with an adequate distance can solve the problem of aerospace defense by using high-power laser systems. No matter what location the targets come from, there are several high-power laser systems with effective operating distance. Results show that these arrangements of laser systems take many advantages over a fixed laser.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

XC developed the concept, and KL and ZL performed the numerical simulations.

Funding

This research was supported by the State Key Laboratory of Pulsed Power Laser Technology Foundation (SKL2021KF02).

Conflict of interest

Authors KL and ZW were employed by the companies China Electronics Technology Information Industry Co., Ltd., and The 27th Research Institute of China Electronics Technology Group Corporation.

The remaining author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Bankman IN, Rogala EW, Pavek RE. Laser radar in ballistic missile defense. Johns Hopkins Apl Tech Dig (2001) 22:379–93.

Google Scholar

2. Syed AA, Mohsin M, Ali S. Survey and technological analysis of laser and its defense applications. Defence Tech (2021) 17:583–92. doi:10.1016/j.dt.2020.02.012

CrossRef Full Text | Google Scholar

3. Jung M, Riesbeck T, Schmitz J, Baumgärtel T, Ludewigt K, Graf A. High energy laser demonstrators for defense applications. In: Proc. SPIE 10254, XXI International Symposium on High Power Laser Systems and Applications 1025416 (2016).

Google Scholar

4. Burlamacchi P, Consortini A, Ronchi L, Francia GTD. Laser beam propagation in the atmosphere. IEEE J Quan Electron (1967) 3:259. doi:10.1109/jqe.1967.1074506

CrossRef Full Text | Google Scholar

5. Li X, Cheng Z, Jiang J, Xu G, Shi H, Zhao Q. Focus characteristics of laser beam for long distance propagation in atmosphere. Acta Optica Sinica (2001) 03:324–9.

Google Scholar

6. Sprangle P, Ting A, Penano J, Fischer R, Hafizi B. Incoherent combining and atmospheric propagation of high-power fiber lasers for directed-energy applications. IEEE J Quan Electron (2008) 45:138–48. doi:10.1109/jqe.2008.2002501

CrossRef Full Text | Google Scholar

7. Fan TY. Laser beam combining for high-power, high-radiance sources. IEEE J Sel Top Quan Electron (2005) 11:567–77. doi:10.1109/jstqe.2005.850241

CrossRef Full Text | Google Scholar

8. Leger JR, "Fundamentals of coherent and incoherent beam combining," In Proceedings of SPIE - The International Society for Optical Engineering (2006).

Google Scholar

9. Pu Z, Liu Z, Wang X, Ma Y, Ma H, Xu X. Coherent beam combining of two fiber amplifiers using stochastic parallel gradient descent algorithm. Opt Laser Tech (2009) 41:853–6. doi:10.1016/j.optlastec.2009.03.002

CrossRef Full Text | Google Scholar

10. Wirth C, Schmidt O, Tsybin I, Schreiber T, Jung M, Bruckner F, et al. 2 kW incoherent beam combining of four narrow-linewidth photonic crystal fiber amplifiers. Opt Express (2009) 17:1178–83. doi:10.1364/oe.17.001178

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Ma P, Zhou P, Ma Y, Su R, Liu Z. Coherent polarization beam combining of four fiber amplifiers in 100 ns pulsed-regime. Opt Laser Tech (2013) 47:336–40. doi:10.1016/j.optlastec.2012.08.030

CrossRef Full Text | Google Scholar

12. Gebhardt FG. Twenty-five years of thermal blooming - an overview. Proc SPIE - Int Soc Opt Eng (1990) 2–25.

CrossRef Full Text | Google Scholar

13. Sheldon SJ, Knight LV, Thorne JM. Laser-induced thermal lens effect: A new theoretical model. Appl Opt (1982) 21:1663–9. doi:10.1364/ao.21.001663

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Ding Z, Li X, Cao J, Ji X. Influence of thermal blooming on the beam quality of an array of Hermite–Gaussian beams propagating in the atmosphere. Appl Opt (2020) 59:10944. doi:10.1364/ao.405980

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Chu X, Sun Q, Wang J, Lu P, Xie W, Xu X. Generating a Bessel-Gaussian beam for the application in optical engineering. Sci Rep (2016) 5:18665. doi:10.1038/srep18665

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Ishimaru A. Wave propagation and scattering in random media”. New York: Academic Press (1978).

Google Scholar

17. Chu X, Liu Z, Wu Y. Propagation of a general multi-Gaussian beam in turbulent atmosphere in a slant path. J Opt Soc Am A (2008) 25:74–9. doi:10.1364/josaa.25.000074

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Yura HT, Hanson SG. Optical beam wave propagation through complex optical systems. J Opt Soc Am A (1987) 4:1931–48. doi:10.1364/josaa.4.001931

CrossRef Full Text | Google Scholar

19. Tyson RK, Wizinowich PL. Principles of adaptive optics. Phys Today (1992) 45:100. doi:10.1063/1.2809540

CrossRef Full Text | Google Scholar

20. Tyson R, Frazier B. Field guide to adaptive Optics. Washington, USA: SPIE (2012).

Google Scholar