Ying Yang- College of Physics and Electronic Engineering, Chongqing Normal University, Chongqing, China
In recent decades, nodal point states in electronic systems have attracted significant interest in current research. Recently, the conceptual framework of nodal point states has been extended to bosonic systems, especially the phononic one. It is well known that the nodal point states may exist much more universally in materials other than topological electronic systems. Fortunately, a series of nodal point phonons are reported in three-dimensional realistic materials, and some are certified in experiments. However, to our knowledge, the study of phononic 2D nodal points is still relatively primitive. Hence, a highlight of research in the emerging area covering approximately the last two-three years is necessary. This mini-review will summary the recent advances in the phononic nodal point in two dimensions. Some typical examples, including graphene, CrI3 monolayer, YGaI monolayer, TiB4 monolayer, Ti2P monolayer, and Cu2Si monolayer, are concluded in this mini-review. The topological properties and possible applications of these material candidates are also summarized.
Introduction
To this date, various topological quasiparticles in three-dimensional (3D) crystalline solids, such as nodal points [1–10], nodal lines [11–20], and nodal surfaces [21–27], have attracted widespread attention because of their unique physical properties and potential applications. As prominent examples, Dirac/Weyl nodal point materials refer to a class of solid materials that feature topology-/symmetry-protected band degeneracies around the Fermi level, such that the Dirac/Weyl equations can describe the low-energy fermionic excitations around the band crossings in high-energy region.
Recently, the searching of nodal point states has been extended to spinless phonon systems [28–45]. Phonons can be viewed as a perfect platform for realizing the nodal point states [46–58] due to their unique device applications and the advantages of whole frequency range observation. For example, Wang et al. [53] proposed a topological triangular Weyl complex composed of one double Weyl point and two single Weyl points in the phonon dispersion of three-dimensional α-SiO2. Liu et al. [52] reported charge-four Weyl point phonons in three-dimensional realistic materials with space group numbers 195–199, and 207–214. Xie et al. [46] reported sixfold degenerate nodal-point phonons in three-dimensional materials, including C3N4, Sc4C3, Y4Sb3, and K8Si46. In 2021, Chen et al. [51] systematically investigated three-dimensional Dirac phonons in all space groups with inversion symmetry. Some realistic three-dimensional materials are also proposed in their work [22] to be candidate materials with Dirac point phonons. In 2022, Ding et al. [54] reported that three-dimensional BaZnO2 has a type-III charge-two Weyl point phonon and double-helicoid phonon surface states. In the same year, Yang et al. [47] proposed the appearance of phononic nodal points with quadratic dispersion and multifold degeneracy in the three-dimensional Ta3Sn. Experimentally, the double Weyl points in three-dimensional FeSi [56] were detected by inelastic x-ray scattering, which provided a strong driving force for the field.
However, to our knowledge, studying phononic nodal points in two dimensions is still relatively primitive. Only a handful of two-dimensional materials have been predicted to host phononic nodal points [59–61]. Hence, a highlight or summary of research in the emerging area of phononic nodal points in two dimensions covering approximately the last two-three year is highly desired. This mini-review highlights recent and vital developments in the phononic nodal points in two dimensions. The proposed phononic Dirac point and higher-order nodal point in two dimensions will be summarized, and some typical material candidates, including graphene, CrI3 monolayer, YGaI monolayer, TiB4 monolayer, Ti2P monolayer, and Cu2Si monolayer, are concluded in this mini-review. The author will also summarize these material candidates’ related topological properties and possible applications in this mini-review.
Phononic dirac point in two dimensions
In 2020, Li et al. [61] proposed the topological phonons in graphene based on the first-principle calculation and symmetry analysis. The phonon dispersion of graphene is collected in Figure 1A, one finds that there exist four types of Dirac points (DPs), named DP1-DP4, respectively. From Figure 1A, the DP1 and DP2 locate at K and K′ high-symmetry points. The DP3 appears on Γ-M path and the DP4 appears on Γ-M surface path, respectively. Moreover, Li et al. [61] examined the topological signatures for these DPs by calculating the Berry phases of the DP1-DP4. The Berry phases of DP1-DP4 are highlighted by “+” and “-“ for π and -π, respectively. Hence, DP1-DP4 appear in pairs and are topologically nontrivial.
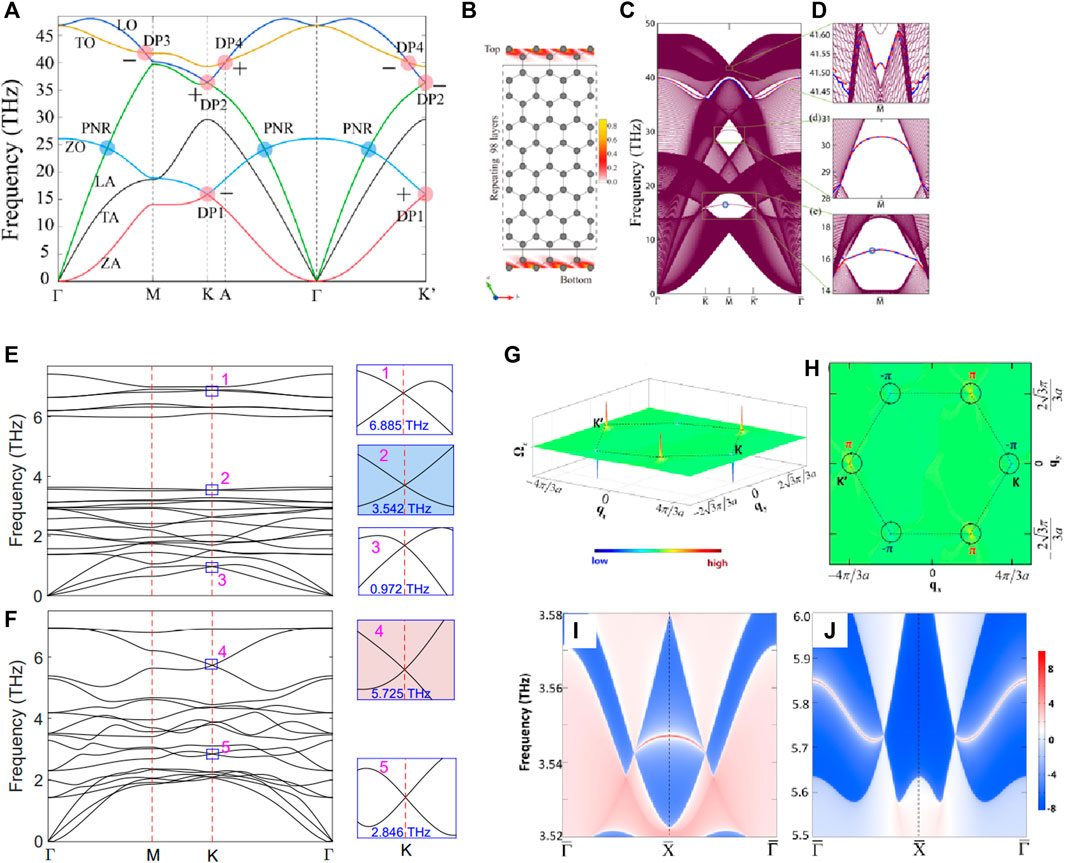
FIGURE 1. (A) phonon dispersion for graphene along
Moreover, two phononic band crossing points around 24 THz are obvious along Γ-K and Γ-K′ paths (see Figure 1A). These two points are not isolated and should form a closed ring (i.e., phononic nodal ring (PNR)). Li et al. [61] also investigated the edge states for the two-dimensional graphene with the help of Green’s function iteration method. The results of the edge states are collected in Figures 1C,D. The top figure of Figure 1D shows the edge states arising from the projections of DP3 phonons. The middle figure of Figure 1D shows the edge states arising from the projections of PNR phonons, and the bottom figure of Figure 1D shows the edge states arising from the projections of DP1 phonons. The appearance of the phononic nodal points is essential for graphenes, providing an excellent direction to investigate the interesting topological phonons in two dimensions. Moreover, the predictions of the phononic nodal point in two dimensions can pave a new way to study the related topological properties, such as destructive interference and quantum (anomalous/spin) Hall-like topological effects.
Interestingly, Jin, Wang, and Xu [60] proposed a method to generate Dirac phonon states with a quantized valley Berry phase in a two-dimensional hexagonal lattice. Using this method, they [60] proved that candidates with C3 symmetry at corners of the hexagonal Brillouin zone could host robust valley Dirac phonons. With the help of first-principle calculations, the phonon dispersions of two typical examples, i.e., CrI3 monolayer and YGaI monolayer, are calculated by Jin, Wang, and Xu [60]. The results are collected in Figures 1E, F, in which multiple Dirac points can be observed at K and K′ high-symmetry points. Note that the CrI3 monolayer is a magnetic semiconductor with a Curie temperature of 42.8 K. In 2018, Jiang et al. [62] proposed that the magnetism of two-dimensional CrI3 can be controlled by electrostatic doping. Hence, Jin, Wang, and Xu [60] paved a new way to study topological phonons in two-dimensional magnetic materials. Similar to the DP1 and DP2 located at K and K′ high-symmetry points in graphene, the Dirac point phonons appear at K and K′ in the CrI3 monolayer and YGaI monolayer. As shown in Figures 1G,H, the quantized Berry phase of π and -π are verified at K′ and K valleys by calculating the Berry curvature distributions. The edge states for the CrI3 monolayer are visibly terminated at the projections of the Dirac points at K and K'. Their work not only provides a broad application of topological phonons in two dimensions but also extends the aspect of valley physics.
Phononic higher-order nodal point in two dimensions
In 2022, Yu et al. [59] searched through 80-layer groups and found that the phononic higher-order nodal point can appear in two dimensions. The appearance of the phononic higher-order nodal points is protected by rotation (except the twofold one) and time-reversal symmetries. They also stated that the highest order of momentum in a two-dimensional system is the second order, named quadratic order. From Figure 2A, Yu et al. [59] pointed out that the phononic higher-order nodal points can appear in layer groups of 49–80. The high-symmetry points where the phononic higher-order nodal points appear, the PG, and the Generators are also exhibited in Figure 2A.
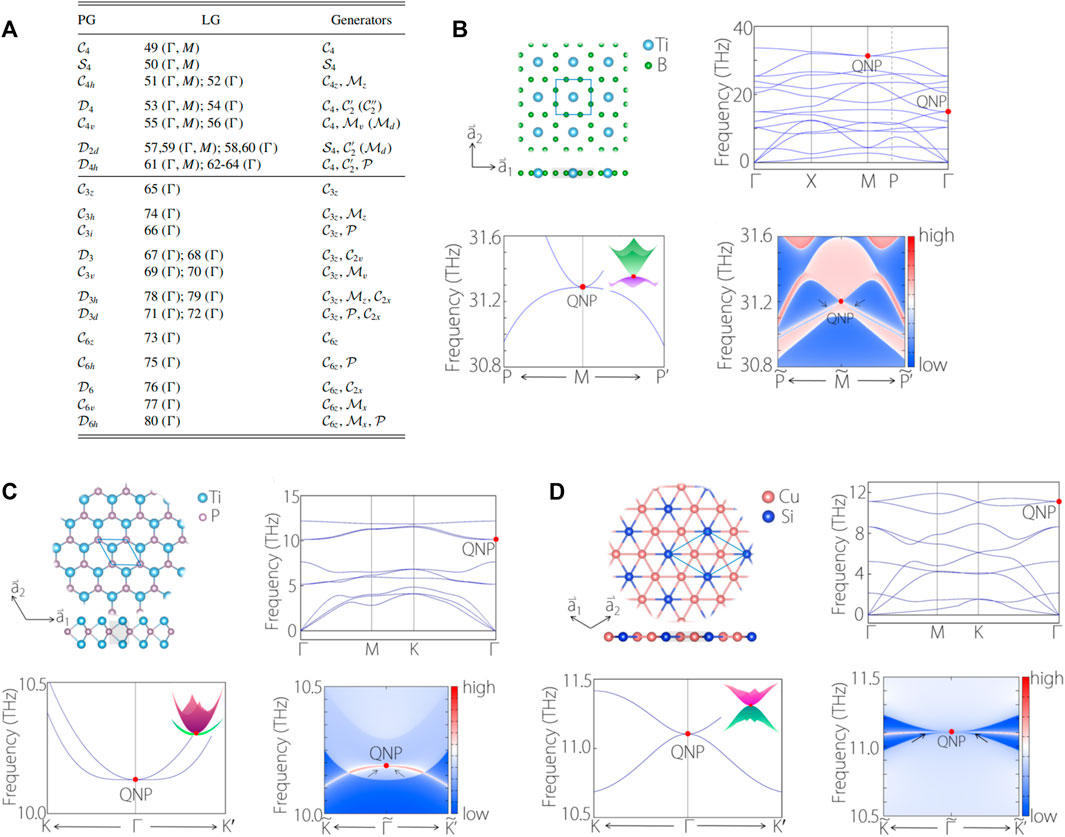
FIGURE 2. (A) Lists of PG, LG, and Generators related to the phononic quadratic nodal points at high-symmetry points. (B–D) structural models, calculated phonon dispersions, enlarged phonon bands around the quadratic nodal points (QNPs), and the calculated edge states for TiB4, Ti2P, and Cu2Si monolayers, respectively. Reproduced from Ref. [59] with permissions.
As shown in Figures 2B–D, they [59] proposed some two-dimensional material candidates, including TiB4, Ti2P, and Cu2Si monolayers, hosting the quadratic nodal point phonons at high-symmetry points. The structural models and the calculated phonon dispersions for these three monolayers are collected in Figures 2B–D, respectively.
Summary
In this mini-review, the author summarized the recent advances in the phononic nodal point in two dimensions covering approximately the last two-three years. Typical two-dimensional material candidates, such as the CrI3 monolayer, YGaI monolayer, TiB4 monolayer, Ti2P monolayer, and Cu2Si monolayer, are concluded in this mini-review. Their topological signatures and possible properties are also summarized. This mini-review is hoped to help study phononic nodal point phonons in two dimensions.
Author contributions
YY- investigations and writing.
Funding
YY is grateful for support from the key project of education planning supported by Chongqing municipal education commission (No. 2021-GX-013), the National Natural Science Foundation of China (No. 12175027), and the Basic Research and Frontier Exploration Project of Chongqing Municipality (cstc2018jcyjAX0820).
Conflict of interest
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
1 Young SM, Kane CL. Dirac semimetals in two dimensions. Phys Rev Lett (2015) 115(12):126803. doi:10.1103/physrevlett.115.126803
2 Liu ZK, Zhou B, Zhang Y, Wang ZJ, Weng HM, Prabhakaran D, et al. Discovery of a three-dimensional topological Dirac semimetal, Na3Bi. Science (2014) 343(6173):864–7. doi:10.1126/science.1245085
3 Armitage NP, Mele EJ, Vishwanath A. Weyl and Dirac semimetals in three-dimensional solids. Rev Mod Phys (2018) 90(1):015001. doi:10.1103/revmodphys.90.015001
4 Gibson QD, Schoop LM, Muechler L, Xie LS, Hirschberger M, Ong NP, et al. Three-dimensional Dirac semimetals: Design principles and predictions of new materials. Phys Rev B (2015) 91(20):205128. doi:10.1103/physrevb.91.205128
5 Wieder BJ, Kim Y, Rappe AM, Kane CL. Double Dirac semimetals in three dimensions. Phys Rev Lett (2016) 116(18):186402. doi:10.1103/physrevlett.116.186402
6 Yang BJ, Nagaosa N. Classification of stable three-dimensional Dirac semimetals with nontrivial topology. Nat Commun (2014) 5(1):4898–10. doi:10.1038/ncomms5898
7 Yan B, Felser C. Topological materials: Weyl semimetals. Annu Rev Condens Matter Phys (2017) 8:337–54. doi:10.1146/annurev-conmatphys-031016-025458
8 Lv BQ, Weng HM, Fu BB, Wang XP, Miao H, Ma J, et al. Experimental discovery of weyl semimetal TaAs. Phys Rev X (2015) 5(3):031013. doi:10.1103/physrevx.5.031013
9 Soluyanov AA, Gresch D, Wang Z, Wu Q, Troyer M, Dai X, et al. Type-ii weyl semimetals. Nature (2015) 527(7579):495–8. doi:10.1038/nature15768
10 Hosur P, Parameswaran SA, Vishwanath A. Charge transport in Weyl semimetals. Phys Rev Lett (2012) 108(4):046602. doi:10.1103/physrevlett.108.046602
11 Wang X, Ding G, Cheng Z, Surucu G, Wang XL, Yang T. Rich topological nodal line bulk states together with drum-head-like surface states in NaAlGe with anti-PbFCl type structure. J Adv Res (2020) 23:95–100. doi:10.1016/j.jare.2020.01.017
12 Wang X, Ding G, Khandy SA, Cheng Z, Zhang G, Wang XL, et al. Unique topological nodal line states and associated exceptional thermoelectric power factor platform in Nb 3 GeTe 6 monolayer and bulk. Nanoscale (2020) 12(32):16910–6. doi:10.1039/d0nr03704d
13 Wang X, Ding G, Cheng Z, Surucu G, Wang XL, Yang T. Novel topological nodal lines and exotic drum-head-like surface states in synthesized CsCl-type binary alloy TiOs. J Adv Res (2020) 22:137–44. doi:10.1016/j.jare.2019.12.001
14 Zhou F, Liu Y, Kuang M, Wang P, Wang J, Yang T, et al. Time-reversal-breaking Weyl nodal lines in two-dimensional A 3 C 2 (A= Ti, Zr, and Hf) intrinsically ferromagnetic materials with high Curie temperature. Nanoscale (2021) 13(17):8235–41. doi:10.1039/d1nr00139f
15 Zhou F, Cui C, Wang J, Kuang M, Yang T, Yu ZM, et al. Perovskite-type YRh3B with multiple types of nodal point and nodal line states. Phys Rev B (2021) 103(24):245126. doi:10.1103/physrevb.103.245126
16 Fang C, Weng H, Dai X, Fang Z. Topological nodal line semimetals. Chin Phys B (2016) 25(11):117106. doi:10.1088/1674-1056/25/11/117106
17 Yang SY, Yang H, Derunova E, Parkin SS, Yan B, Ali MN. Symmetry demanded topological nodal-line materials. Adv Phys X (2018) 3(1):1414631. doi:10.1080/23746149.2017.1414631
18 Hu J, Tang Z, Liu J, Liu X, Zhu Y, Graf D, et al. Evidence of topological nodal-line fermions in ZrSiSe and ZrSiTe. Phys Rev Lett (2016) 117(1):016602. doi:10.1103/physrevlett.117.016602
19 Bian G, Chang TR, Sankar R, Xu SY, Zheng H, Neupert T, et al. Topological nodal-line fermions in spin-orbit metal PbTaSe2. Nat Commun (2016) 7(1):10556–8. doi:10.1038/ncomms10556
20 Yu R, Fang Z, Dai X, Weng H. Topological nodal line semimetals predicted from first-principles calculations. Front Phys (Beijing) (2017) 12(3):127202–14. doi:10.1007/s11467-016-0630-1
21 Wu W, Liu Y, Li S, Zhong C, Yu ZM, Sheng XL, et al. Nodal surface semimetals: Theory and material realization. Phys Rev B (2018) 97(11):115125. doi:10.1103/physrevb.97.115125
22 Zhang X, Yu ZM, Zhu Z, Wu W, Wang SS, Sheng XL, et al. Nodal loop and nodal surface states in the Ti3Al family of materials. Phys Rev B (2018) 97(23):235150. doi:10.1103/physrevb.97.235150
23 Yang Y, Xia JP, Sun HX, Ge Y, Jia D, Yuan SQ, et al. Observation of a topological nodal surface and its surface-state arcs in an artificial acoustic crystal. Nat Commun (2019) 10(1):5185–7. doi:10.1038/s41467-019-13258-3
24 Qie Y, Liu J, Wang S, Sun Q, Jena P. Tetragonal C 24: A topological nodal-surface semimetal with potential as an anode material for sodium ion batteries. J Mater Chem A Mater (2019) 7(10):5733–9. doi:10.1039/c8ta11276b
25 Xiao M, Ye L, Qiu C, He H, Liu Z, Fan S. Experimental demonstration of acoustic semimetal with topologically charged nodal surface. Sci Adv (2020) 6(8):eaav2360. doi:10.1126/sciadv.aav2360
26 Yang T, Jin L, Liu Y, Zhang X, Wang X. Spin-polarized type-II nodal loop and nodal surface states in hexagonal compounds XTiO2 (X = Li, Na, K, Rb). Phys Rev B (2021) 103(23):235140. doi:10.1103/physrevb.103.235140
27 Xiao M, Fan S (2017). Topologically charged nodal surface. Available at: https://arxiv.org/abs/1709.02363
28 Liu Y, Chen X, Xu Y. Topological phononics: From fundamental models to real materials. Adv Funct Mater (2020) 30(8):1904784. doi:10.1002/adfm.201904784
29 Prodan E, Prodan C. Topological phonon modes and their role in dynamic instability of microtubules. Phys Rev Lett (2009) 103(24):248101. doi:10.1103/physrevlett.103.248101
30 Stenull O, Lubensky TC. Signatures of topological phonons in superisostatic lattices. Phys Rev Lett (2019) 122(24):248002. doi:10.1103/physrevlett.122.248002
31 Liu G, Jin Y, Chen Z, Xu H. Symmetry-enforced straight nodal-line phonons. Phys Rev B (2021) 104(2):024304. doi:10.1103/physrevb.104.024304
32 Zhou F, Zhang Z, Chen H, Kuang M, Yang T, Wang X. Hybrid-type nodal ring phonons and coexistence of higher-order quadratic nodal line phonons in an AgZr alloy. Phys Rev B (2021) 104(17):174108. doi:10.1103/physrevb.104.174108
33 Wang J, Yuan H, Liu Y, Zhou F, Wang X, Zhang G. Hourglass Weyl and Dirac nodal line phonons, and drumhead-like and torus phonon surface states in orthorhombic-type KCuS. Phys Chem Chem Phys (2022) 24(5):2752–7. doi:10.1039/d1cp05217a
34 Wang J, Yuan H, Yu ZM, Zhang Z, Wang X. Coexistence of symmetry-enforced phononic Dirac nodal-line net and three-nodal surfaces phonons in solid-state materials: Theory and materials realization. Phys Rev Mater (2021) 5(12):124203. doi:10.1103/physrevmaterials.5.124203
35 Zhou F, Chen H, Yu ZM, Zhang Z, Wang X. Realistic cesium fluogermanate: An ideal platform to realize the topologically nodal-box and nodal-chain phonons. Phys Rev B (2021) 104(21):214310. doi:10.1103/physrevb.104.214310
36 Ding G, Sun T, Wang X. Ideal nodal-net, nodal-chain, and nodal-cage phonons in some realistic materials. Phys Chem Chem Phys (2022) 24(18):11175–82. doi:10.1039/d2cp00731b
37 Liu QB, Fu HH, Wu R. Topological phononic nodal hexahedron net and nodal links in the high-pressure phase of the semiconductor CuCl. Phys Rev B (2021) 104(4):045409. doi:10.1103/physrevb.104.045409
38 Zheng B, Zhan F, Wu X, Wang R, Fan J. Hourglass phonons jointly protected by symmorphic and nonsymmorphic symmetries. Phys Rev B (2021) 104(6):L060301. doi:10.1103/physrevb.104.l060301
39 Zhang TT, Miao H, Wang Q, Lin JQ, Cao Y, Fabbris G, et al. Phononic helical nodal lines with PT protection in MoB2. Phys Rev Lett (2019) 123(24):245302. doi:10.1103/physrevlett.123.245302
40 Wang M, Wang Y, Yang Z, Fan J, Zheng B, Wang R, et al. Symmetry-enforced nodal cage phonons in Th2BC2. Phys Rev B (2022) 105(17):174309. doi:10.1103/physrevb.105.174309
41 Chen ZJ, Xie ZJ, Jin YJ, Liu G, Xu H. Hybrid nodal-ring phonons with hourglass dispersion in AgAlO2. Phys Rev Mater (2022) 6(3):034202. doi:10.1103/physrevmaterials.6.034202
42 Xie C, Yuan H, Liu Y, Wang X, Zhang G. Three-nodal surface phonons in solid-state materials: Theory and material realization. Phys Rev B (2021) 104(13):134303. doi:10.1103/physrevb.104.134303
43 Liu Y, Zou N, Zhao S, Chen X, Xu Y, Duan W. Ubiquitous topological states of phonons in solids: Silicon as a model material. Nano Lett (2022) 22(5):2120–6. doi:10.1021/acs.nanolett.1c04299
44 Jin YJ, Chen ZJ, Xia BW, Zhao YJ, Wang R, Xu H. Ideal intersecting nodal-ring phonons in bcc C8. Phys Rev B (2018) 98(22):220103. doi:10.1103/physrevb.98.220103
45 Yang T, Gu Q, Wang P, Wu Z, Zhang Z. Phononic quadratic nodal lines of different types in Li2NaN. Appl Phys Lett (2022) 121(5):053102. doi:10.1063/5.0102217
46 Xie C, Liu Y, Zhang Z, Zhou F, Yang T, Kuang M, et al. Sixfold degenerate nodal-point phonons: Symmetry analysis and materials realization. Phys Rev B (2021) 104(4):045148. doi:10.1103/physrevb.104.045148
47 Yang T, Xie C, Chen H, Wang X, Zhang G. Phononic nodal points with quadratic dispersion and multifold degeneracy in the cubic compound Ta3Sn. Phys Rev B (2022) 105(9):094310. doi:10.1103/physrevb.105.094310
48 Sreeparvathy PC, Mondal C, Barman CK, Alam A. Coexistence of multifold and multidimensional topological phonons in KMgBO3. Phys Rev B (2022) 106(8):085102. doi:10.1103/physrevb.106.085102
49 Li J, Xie Q, Ullah S, Li R, Ma H, Li D, et al. Coexistent three-component and two-component Weyl phonons in TiS, ZrSe, and HfTe. Phys Rev B (2018) 97(5):054305. doi:10.1103/physrevb.97.054305
50 Wang J, Yuan H, Kuang M, Yang T, Yu ZM, Zhang Z, et al. Coexistence of zero-one-and two-dimensional degeneracy in tetragonal SnO2 phonons. Phys Rev B (2021) 104(4):L041107. doi:10.1103/physrevb.104.l041107
51 Chen ZJ, Wang R, Xia BW, Zheng BB, Jin YJ, Zhao YJ, et al. Three-dimensional Dirac phonons with inversion symmetry. Phys Rev Lett (2021) 126(18):185301. doi:10.1103/physrevlett.126.185301
52 Liu QB, Wang Z, Fu HH. Charge-four weyl phonons. Phys Rev B (2021) 103(16):L161303. doi:10.1103/physrevb.103.l161303
53 Wang R, Xia BW, Chen ZJ, Zheng BB, Zhao YJ, Xu H. Symmetry-protected topological triangular Weyl complex. Phys Rev Lett (2020) 124(10):105303. doi:10.1103/physrevlett.124.105303
54 Ding G, Zhou F, Zhang Z, Yu ZM, Wang X. Charge-two Weyl phonons with type-III dispersion. Phys Rev B (2022) 105(13):134303. doi:10.1103/physrevb.105.134303
55 Jin YJ, Chen ZJ, Xiao XL, Xu H. Tunable double Weyl phonons driven by chiral point group symmetry. Phys Rev B (2021) 103(10):104101. doi:10.1103/physrevb.103.104101
56 Miao H, Zhang TT, Wang L, Meyers D, Said AH, Wang YL, et al. Observation of double Weyl phonons in parity-breaking FeSi. Phys Rev Lett (2018) 121(3):035302. doi:10.1103/physrevlett.121.035302
57 Zhang T, Song Z, Alexandradinata A, Weng H, Fang C, Lu L, et al. Double-Weyl phonons in transition-metal monosilicides. Phys Rev Lett (2018) 120(1):016401. doi:10.1103/physrevlett.120.016401
58 Zhong M, Han Y, Wang J, Liu Y, Wang X, Zhang G. Material realization of double-Weyl phonons and phononic double-helicoid surface arcs with P213 space group. Phys Rev Mater (2022) 6(8):084201. doi:10.1103/physrevmaterials.6.084201
59 Yu WW, Liu Y, Meng W, Liu H, Gao J, Zhang X, et al. Phononic higher-order nodal point in two dimensions. Phys Rev B (2022) 105(3):035429. doi:10.1103/physrevb.105.035429
60 Jin Y, Wang R, Xu H. Recipe for Dirac phonon states with a quantized valley berry phase in two-dimensional hexagonal lattices. Nano Lett (2018) 18(12):7755–60. doi:10.1021/acs.nanolett.8b03492
61 Li J, Wang L, Liu J, Li R, Zhang Z, Chen XQ. Topological phonons in graphene. Phys Rev B (2020) 101(8):081403. doi:10.1103/physrevb.101.081403
Keywords: nodal point, Dirac point, Weyl point, phonons, 2D monolayer
Citation: Yang Y (2022) Phononic nodal point in two dimensions: A mini-review. Front. Phys. 10:1057520. doi: 10.3389/fphy.2022.1057520
Received: 29 September 2022; Accepted: 05 October 2022;
Published: 17 October 2022.
Edited by:
Xiaoming Zhang, Hebei University of Technology, ChinaReviewed by:
Guangqian Ding, Chongqing University of Posts and Telecommunications, ChinaMingmin Zhong, Southwest University, China
Copyright © 2022 Yang. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Ying Yang, MjAxMzExODRAY3FudS5lZHUuY24=