Design of an ellipsoidal mirror assisted oblique plane microscopy

Using one objective for excitation and detection simultaneously, oblique plane microscopy (OPM) provides a mounting-friendly approach for optical sectioning. Unfortunately, the original OPM has three major defects: the mechanical constraints when placing the objectives, the phase loss and the resulting anisotropy of the point spread function (PSF). In order to alleviate the above defects, an ellipsoidal mirror assisted oblique plane microscopy (EM-OPM) was proposed. By inserting an ellipsoidal mirror into the optical path to help collect the light beam, the problem of placing the objectives was solved. The numerical calculation results showed that EM-OPM can obtain higher relative light intensity and larger effective area of exit pupil than OPM when the tilt angle of the light sheet becomes larger. The imaging simulation results showed that EM-OPM effectively solves the problem of resolution reduction in the Y direction of OPM. In addition, optimization of the higher-order terms of the ellipsoidal mirror further improved the imaging ability of EM-OPM in large field of view (FOV).

1 Introduction

In order to achieve high-speed, high-resolution, low damage and large FOV imaging simultaneously, light sheet fluorescence microscopy (LSFM) came into being [1–3]. The biggest difference between light sheet microscopy and wide field microscopy comes from different illuminating methods. In classical configuration of LSFM, there are two orthogonally placed objective lenses with the sample at the common focal point. One objective lens, also known as the illumination objective, focus laser light to a thin sheet which is always perpendicular to the optical axis of the other objective also known as the detection objective. The key point of LSFM is that only the sample located in the focal plane of the detection objective lens is illuminated, while the upper and lower samples are not affected. Therefore, LSFM can be used for long-term biological studies with high axial resolution and minimal phototoxicity.

Although LSFM has the above advantages, it has some limitations. The dual objective geometry and the need for side-on illumination restricts the type of sample that can be mounted between the objectives. In addition, in a high-resolution LSFM system, the sample has to directly contact the non-sterile optical surface to ensure the high numerical aperture of the immersion objective lens. These challenges have led to innovative strategies for optical path design, including LSFM that uses the same objective lens for illumination and detection [4, 5].

In 2008, Dunsby proposed oblique plane microscopy (OPM) to enable LSFM using a single objective to illuminate the specimen and collect the resulting fluorescence at the same time [6]. As shown in Figure 1A, the light sheet emitted from the edge of O₁ illuminate the sample obliquely. The fluorescence illuminated by the light sheet is also captured by O₁ but cannot be imaged by it directly because of the severe optical aberrations. The solution in OPM is to employ a one-to-one magnification system which simultaneously follow both the sine and Herschel condition by introducing O₂ [7]. The oblique intermediate real image is then brought to lie perpendicular to the optical axis of O₃ and can be imaged in a conventional way by a camera. Due to the improvement of illumination path, OPM can be assembled based on standard inverted microscopes, and is suitable for traditional sample placement and laser based auto focusing. However, there are three main defects in the original OPM: 1, mechanical constraint between O₂ and O₃; 2, Loss of phase information on pupil plane (Short for Phase Loss); 3. Anisotropy of PSF [8, 9]. For the first defect, in addition to sacrificing the numerical aperture of O₃ for working distance, installing a micro mirror after O₂ can also eliminate the mechanical size limitation between O₂ and O₃ [10–12]. However, the fine fabrication and accurately installation of a micro mirror is technically challenging. Using a diffractive grating can achieve the same goal, but the intensity will be dispersed by the diffractive element [13]. To mitigate the impact of the second defect, Yang et al introduced a small special water container at the rear focus to change the refractive index of the light beam on both sides, so that almost all beams from O₂ can be collected by O₃ [14]. Although the phase loss of the system is effectively reduced, the addition of the water container increases the difficulty of focusing the system and intensifies the mechanical constraint between O₂ and O₃. A similar idea was also put forward later [15], while facing the same challenge. For the third defect, Kim et al introduced a polarizer to change the polarization state of the beam thus improve the anisotropy of the overall PSF [16]. However, the improvement is unstable and the polarized beam splitter (PBS) in the optical path makes the phase loss more serious. To sum up, OPM and its existing improved system cannot solve the three defects mentioned above at the same time.

FIGURE 1

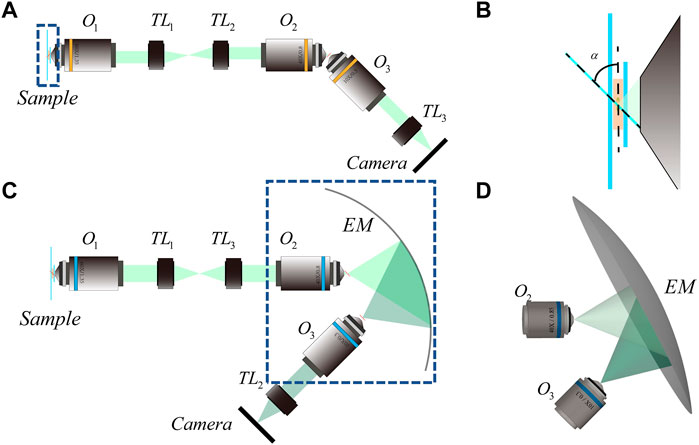
FIGURE 1. Schematic diagram of OPM system and EM-OPM system (A) 2D optical path diagram of OPM system (B) Enlarged view of the part bounded by dotted lines in Figure (A–C) 2D optical path diagram of EM-OPM system (D) The three-dimensional schematic diagram of the dotted line in Figure (B).

In this paper, inspired by the optical property of ellipse, we proposed an ellipsoidal mirror assisted oblique plane microscopy (EM-OPM), which provides some advantages over the original OPM and other OPMs. In this configuration, the light beam emitted by O₂ is collected by O₃ after being reflected by the ellipsoidal mirror, thus avoiding the top-to-top placement of O₂ and O₃. Numerical results demonstrate the advantages of EM-OPM in terms of relative light intensity and relative effective pupil area. Imaging simulation results prove that the resolution of EM-OPM in Y direction is improved. In addition, the optimization of ellipsoidal mirror further improves the large FOV imaging capability of EM-OPM.

2 Materials and methods

2.1 EM-OPM

As mentioned above, the original OPM has three defects. In order to solve these three problems, we proposed a new optical configuration, namely EM-OPM, which is expected to solve these three defects simultaneously. Except for the introduction of an ellipsoidal mirror (EM) between O₂ and O₃, EM-OPM uses elements similar to the original OPM. The expression of the EM is:

$z=\frac{c{r}^2}{1+\sqrt{1-\left(1+k\right)c^2{r}^2}}(1)$

where c represents the curvature, k represents the conic coefficient. In our design, c = 0.01 and k = 0.01. $r$ is the unit radial coordinate and $z$ is the height of ellipsoidal mirror.

The way the sample is illuminated is depicted in Figure 1B. The inclined light sheet used for illuminating the sample in OPM is formed by scanning an inclined beam with an angle of α to the focal plane. The layout of EM-OPM is shown in Figure 1C. The back focus of O₂ is coincident with one of the focuses of EM when back focus of O₃ is coincident with the other. By adjusting the tilting angle of each element, the major axis of EM is parallel to the light sheet and perpendicular to the optical axis of O₃ at the same time. Although the real image of the sample is still inclined to the focal plane of O₁, it lies parallel to the focal plane of O_3, thus make the ordinary flat field imaging using O₃ possible. Our design can be understood as an extension of the remote focusing (RF) system [17], because the information of the sample is further copied from the back focal plane of O₂ to a more flexible space by an EM.

2.2 Mechanical constraint

The mechanical constraint of O₂ and O₃ is mainly due to the fact that the working distances of the two objective lenses is far less than their mechanical dimensions. To make sure that the objectives will not grind against each other, the working distance (WD₂ for O₂ and WD₃ for O₃) and the radius of the glass cover plate (r_CG2 for O₂ and r_CG3 for O₃) should meet at least one of the following requirements:

$\{\begin{array}{l}W{D}_2+W{D}_3\cdot \tan \alpha >r_{CG2}\cdot \tan \alpha \\ W{D}_2\cdot \cos \alpha +r_{CG2}\cdot \sin \alpha >r_{CG3}\end{array}(2)$

In the system proposed by Dunsby, O₂ is a 40×/0.85 air objective with r_CG2 = 3.750 mm and WD₂ = 0.200 mm. To meet the requirements above when α = 45 for example, WD₃ must be greater than 2.510mm, otherwise r_CG3 must be less than 2.793 mm. We can use d, the distance between the vertices of O₂ and O₃, to indicate the severity of the mechanical constraint. In OPM:

$d=\sqrt{W{D}_2^2+W{D}_3^2+2\cdot W{D}_2\cdot W{D}_3\cdot \sin \alpha }(3)$

In EM-OPM, d is determined by the parameters of the EM, which can be calculated as:

$d=2\cdot \sqrt{\frac{k}{c^2{\left(1-k\right)}^2}}(4)$

2.3 Phase loss

The phase loss mainly occurs between O₂ and O₃ (Some OPM using a planar micro mirror lose extra 50% intensity due to the introduction of PBS). To make it clear, it is the reduction in NA and the tilting placement of O₃ that result in the phase loss. In order to calculate the phase loss, it is necessary to calculate the initial pupil ignoring O₃ and the effective pupil of the complete system. The calculation of the initial and effective pupil can be based on either the strict analytic geometry method [18] or the Monte Carlo algorithm. In this paper, the three-dimensional point clouds representing the pupils of OPM and EM-OPM are obtained after ray tracing using Monte Carlo algorithm. The Delaunay triangulation algorithm is used to convert the three-dimensional point cloud into a triangular mesh [19]. Then, all the meshes are traversed, and the area of each triangular mesh is calculated separately. After accumulation, the approximate effective pupil area can be obtained. Based on the theory above, we compared the effective pupil of OPM and EM-OPM.

2.4 Point spread function

The third defect of OPM is the anisotropy of PSF. Because objective lenses with large numerical aperture are used, the paraxial approximation scalar diffraction theory is no longer applicable [20]. Based on the vector diffraction theory [21], the electromagnetic field distribution at any point p (x, y, z) in the focus area of the objective lens can be regarded as the superposition of all diffracted plane waves that can pass through the pupil of the objective lens within the solid angle (determined by NA).

$\begin{array}{l}E\left(x,y,z\right)=-\frac{i}{\lambda }{\int }_0^{\beta }{\int }_0^{2\pi }\sin \theta \cos \theta A\left(\theta ,\phi \right)P\left(\theta ,\phi \right)\\ \times \exp \left[ikn\left(z\cos \theta +x\sin \theta \cos \phi +y\sin \theta \sin \phi \right)\right]d\theta d\phi \end{array}(5)$

With 0<θ<β, where β is the maximum focus angle of the objective lens. φ represents the azimuth angle in the object plane, λ represents the wavelength. A (θ, φ) is the amplitude of the incident beam. p (θ, φ) indicates the polarization state of the EM field in the focal region.

The effective pupil can be cut into a large number of sub regions by using the Monte Carlo algorithm to trace a large number of rays. The position of each sub region can be approximately determined by one of the points u_i (θ_i, φ_i, r_i). It is approximately considered that the plane wave from each sub region to the pointp has a unique direction vector. Then Eq. (5) can be written by a discretely way as:

$\begin{array}{l}E\left(x,y,z\right)={\displaystyle \sum }_{\left(u_i({\theta }_i,{\phi }_i,r_i\right)\in R)}\sin {\theta }_i\cos \theta A\left({\theta }_i,{\phi }_i\right)P\left({\theta }_i,{\phi }_i\right)\\ \times \exp \left[ikn\left(z\cos {\theta }_i+x\sin {\theta }_i\cos {\phi }_i+y\sin {\theta }_i\sin {\phi }_i\right)\right]\end{array}(6)$

In this study, the numerical calculation is programmed by a personal code script based on Matlab software. The code allows to simulate PSFs for OPM and EM-OPM under different conditions, such as different NA, different light sheet angles, etc.

3 Results and discussion

As a single-objective LSFM methods, OPM offers a convenient approach for optical sectioning using a conventional epi-fluorescence microscope. The trade-offs it has to make in order to achieve the convenience of sample mounting sacrifice the imaging quality. Unfortunately, all of the improved configurations up to now have failed to reduce the three defects mentioned above simultaneously. By inserting an ellipsoidal mirror into the space near the focal region of O₂ and titling the following elements accordingly, we reconstructed OPM into EM-OPM. EM-OPM has obvious progress compared with OPM, especially in the alleviation of the three defects. We used numerical calculations to illustrate these advances.

We proved the alleviation of the first defect by comparing the space between O₂ and O₃ in EM-OPM and OPM. Except for some extremely high NA objectives for special purposes, only a series of small NA objectives with ×10 magnification can meet the requirements in Eq. (5). Therefore, O₃ is a 10×/0.3 air objective which has a working distance of 3.100 mm in original OPM. Even it is very easy to align and the working distance is plenty, the distance between the two vertices is only 3.241 mm (Figure 2A). In contrast, in EM-OPM, the distance between the two vertices is relaxed to 20.202 mm (Figure 2B). It significantly eased the mechanical constraint and therefore increased the flexibility of O₃ selection.

FIGURE 2

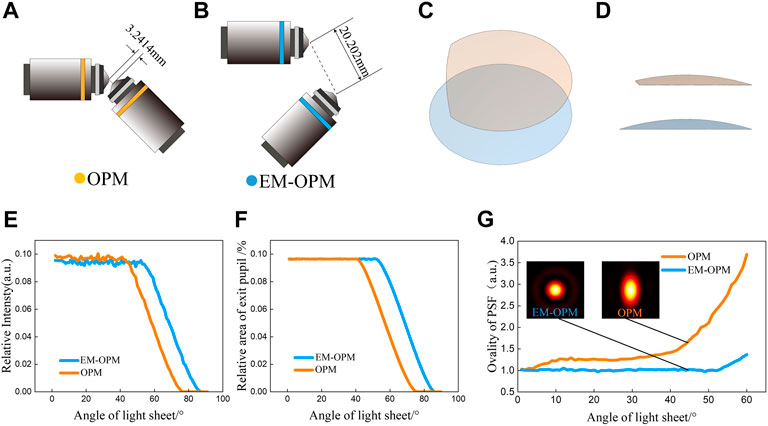
FIGURE 2. Comparison between OPM system and EM-OPM system (A) In OPM system, the distance between two objective lens vertices is 3.241 mm (B) In the EM-OPM system, the distance between the two objective lens vertices is 20.202 mm (C) Comparison of effective pupil of OPM system and EM-OPM system (45 top view) (D) Comparison of effective pupil of OPM system and EM-OPM system (front view) (E) The relative intensity of the two systems varies with α from 0 to 90 (F) The relative effective exit pupil area of the two systems varies with α from 0 to 90 (G) The ellipticity of the PSF of the two systems with different α and the PSF distribution of the two systems when α = 45.

The effective pupil of OPM and EM-OPM when α = 45 are shown in Figures 2C,D. Both remaining a small part of the spherical shell, the effective pupil of OPM is cut out while the effective pupil of the EM-OPM is still complete. Due to the reduction of NA of objective lens, the pupil of both systems becomes smaller. Effective pupil of EM-OPM faithfully reflects the reduction of NA but avoids the influence of the inclined placement of O₂ and O₃. When α < 42, the relative light intensity and the relative effective pupil area of OPM and EM-OPM are approximately the same (Figure 2E). However, EM-OPM system has higher relative light intensity and larger effective pupil area when α ≥ 42 (Figure 2F). When α is too large, both systems are unable to collect the light from O₂. For OPM, α should be smaller than 75, while for EM-OPM, α should be smaller than 85. Calculation result shows that EM-OPM can make more effective use of fluorescence. This is exactly the goal of researchers to reduce phase loss when improving OPM.

The third defect of OPM system, namely the anisotropy of PSF, can also be understood as the loss of resolution in Y direction. Generally, the more complete the effective pupil, the more complete the high-frequency information contained in the optical system, which means that the resolution of the system in each direction is not lost. According to the results in the previous section, the PSF of EM-OPM is predicted to be more isotropic. The numerical calculation results also agree with this idea. In Figure 2G, the anisotropy of PSF is measured by a defined parameter, μ calculated as:

$\mu =\frac{\mathrm{F}\mathrm{W}\mathrm{H}\mathrm{M}\mathrm{y}\mathrm{o}\mathrm{f}\mathrm{P}\mathrm{S}\mathrm{F}}{\mathrm{F}\mathrm{W}\mathrm{H}\mathrm{M}\mathrm{x}\mathrm{o}\mathrm{f}\mathrm{P}\mathrm{S}\mathrm{F}}(7)$

With the increase of α, μ of the OPM increases, while μ of EM-OPM is relatively stable. For example, when α = 45, the PSF of EM-OPM presents a perfect quasi-Gaussian distribution, while the PSF of OPM is elongated along the y-direction. In other words, EM-OPM can recover the Y direction loss of resolution in OPM.

We then demonstrate the power of EM-OPM by presenting the imaging simulation of OPM and EM-OPM. We focus on the imaging performance of Fluorescence conjugated to the focal plane of O₃, therefore the simulation results are 2D images. Firstly, we generate the ground truth pattern used for simulation. Here to highlight the difference in resolution, we choose hollow circular structure to be the sample pattern which is aimed to model nuclear pore complexes (NPCs). This pattern consists of octagons labelled at their vertices for the convenience of calculation. The positions of the centers of octagons randomly distributed within an active area of 81.92 × 81.92 μm2 and the octagon radius is randomly distributed between 400 nm and 1200 nm. Secondly, we simulate the imaging process. In most algorithms used for single molecule localization microscopy (SMLM) simulation [22, 23], PSF is usually space-invariant. In order to accurately study the imaging results under different FOV, we have established the communication between our imaging simulation algorithm and Zemax/OpticStudio^™. Because the built-in ray tracing package of Zemax can easily calculate the PSF at different FOVs. Therefore, the PSF of different areas in the FOV can be obtained and then convolved with the ground truth image. Figure 3A is the simulation result obtained using the OPM system, and Figure 3B is the one obtained using the EM-OPM system. The improvement of EM-OPM can be found by comparing the imaging results of the entire FOV or ROI area delineated by white solid lines. OPM will significantly reduce the Y resolution of the image, while EM-OPM can achieve higher resolution in both directions.

FIGURE 3

FIGURE 3. Simulated image obtained by imaging with OPM and EM-OPM (A) Simulation image of OPM (B) Simulation image of EM-OPM.

EM-OPM has significant advantages over OPM, but the ellipsoidal mirror will introduce serious coma, which limits the use of EM-OPM in large FOV. It is also illustrated by the severe degradation of imaging quality in the large FOV area in Figure 3B (note the two octagons marked with arrows). In order to improve the imaging capability in large FOV, we designed an optimization function to comprehensively evaluate the imaging ability of each vertex in the field of 60 × 60 μm2, and optimized the high-order terms in the expression of EM. The optimization results are shown in Figure 4A,B. It can be seen that the normalized Strehl ratio of the optimized EM-OPM at each FOV point is higher than that of the pre-optimized EM-OPM. The optimization result indicates that the imaging contrast of the system at each position in the large FOV is improved.

FIGURE 4

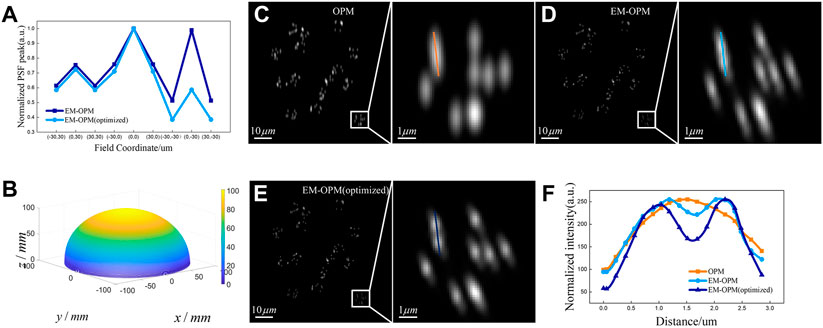
FIGURE 4. Optimization results and imaging simulation comparison of OPM, EM-OPM and EM-OPM (optimized) (A) Normalized Strehl ratio of EM-OPM and EM-OPM (optimized) at each FOV point (B) 3D profile of the optimized ellipsoidal mirror (C) Simulation imaging results of OPM (D) Simulation imaging results of EM-OPM before optimization (E) Simulation imaging results of optimized EM-OPM (F) Resolution comparison of three systems.

The imaging simulations of OPM, EM-OPM and EM-OPM (optimized) were then carried out respectively. To compare the resolution and edge distortion of these three systems at the same time, fluorescence beads distributed randomly are chosen to be the ground truth pattern. Several fluorescent beads are set to be in a group, and the center of each group are still randomly distributed within an active area of 81.92 × 81.92 μm2. We also define that the fluorescent beads of each group are randomly distributed in a circle with a radius of 3000 nm. The simulation results of the three systems are shown in Figures 4C–E respectively. The simulation results prove again that the original OPM system has the problem of reduced resolution in the Y direction, which makes it impossible to distinguish some fluorescent spheres with close distance using OPM. In EM-OPM, the problem of PSF anisotropy has been significantly alleviated. However, the decrease of image contrast and serious side lobe indicate that the imaging capability in large FOV is still unsatisfying. Fortunately, the optimized EM-OPM make some change. A line segment is used to extract the intensity distribution in the ROI regions in Figures 4C–E and the resolution comparison of the three systems is shown in Figure 4F. It can be seen that OPM is unable to distinguish the two fluorescent beads that are close to each other, EM-OPM can barely distinguish them, and the optimized EM-OPM further improves the resolution.

4 Conclusion

EM-OPM proposed in this paper is an improvement based on OPM. An ellipsoidal mirror is inserted into the space between O₂ and O₃. The optical property of the ellipse is used to collect the beam so that the mechanical constraint between O₂ and O₃ can be solved. The change of relative intensity and the change of relative effective pupil area under different tilt angles of the light sheet are studied and compared by numerical calculation method. The results prove that: the relative light intensity and the relative effective pupil area of OPM and EM-OPM are approximately the same when α < 42, and the relative light intensity and the relative effective pupil area of EM-OPM are larger than that of OPM when α ≥ 42. This means EMOPM can make more effective use of fluorescence and retain as much optical high-frequency information as possible. The alleviation in phase loss is also the basis for the improvement of PSF anisotropy. Compared to OPM, EM-OPM has higher resolution in Y direction for any tilt angle of the light sheet.

Due to the complexity of the actual imaging system, image simulation based on space-variant PSFs is carried out. Simulation results show that OPM loses resolution in Y direction, while EM-OPM can achieve higher resolution in both directions. The simulation results of imaging also reveal the weakness of EM-OPM in the large FOV imaging. In order to improve the imaging ability in large FOV, we carried out optimization for high order terms of the ellipsoidal mirror. The optimization improved the normalized Strehl ratio of the system at each vertex within the field of 60 × 60 μm2. The later imaging simulation proves that the optimized EM-OPM further improves the resolution and contrast in large FOV. With the development of ultra-precision machining capability of free-form surface, the optimized EM-OPM is expected to replace OPM in low and medium resolution applications.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation

Author contributions

YL and JM conceived the project; YL performed the experiments; YL wrote the manuscript and performed simulation and data analysis; QC, YF, LM, and JM revised the manuscript.

Funding

This work was financially supported by the National Key R&D Program of China (2021YFF0502900), National Natural Science Foundation of China (62175034, 62175036ml, 82030106fyy, 32271510), Shanghai Natural Science Foundation (grant No. 20ZR1405100, 20ZR1403700fyy), Science and Technology Research Program of Shanghai (grant No. 19DZ2282100), Shanghai key discipline construction plan (2020–2022) (grant No. GWV-10.1-XK01), Shanghai Engineering Technology Research Center of Hair Medicine (19DZ2250500), Medical Engineering Fund of Fudan University (yg2021-022), Pioneering Project of Academy for Engineering and Technology, Fudan University (gyy2018-001, gyy2018-002), Yantai Returned Scholars’ Pioneering Park.

Acknowledgments

The authors wish to thank JW for help with the use of Zemax, MJ, YC for help in revising the manuscript.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Stelzer EH, Strobl F, Chang BJ, Preusser F, Preibisch S, McDole K, et al. Light sheet fluorescence microscopy. Nat Rev Methods Primers (2021) 1(1):73–25. doi:10.1038/s43586-021-00069-4

CrossRef Full Text | Google Scholar

2. Olarte OE, Andilla J, Gualda EJ, Loza-Alvarez P. Light-sheet microscopy: A tutorial. Adv Opt Photon (2018) 10:111–79. doi:10.1364/AOP.10.000111

CrossRef Full Text | Google Scholar

3. Weber M, Huisken J. Light sheet microscopy for real-time developmental biology. Curr Opin Genet Dev (2011) 21:566–72. doi:10.1016/j.gde.2011.09.009

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Gagliano G, Nelson T, Saliba N, Vargas-Hernández S, Gustavsson AK. Light sheet illumination for 3D single-molecule super-resolution imaging of neuronal synapses. Front Synaptic Neurosci (2021) 13:761530. doi:10.3389/fnsyn.2021.761530

PubMed Abstract | CrossRef Full Text | Google Scholar

5. You R, McGorty R. Light sheet fluorescence microscopy illuminating soft matter. Front Phys (2021) 9:760834. doi:10.3389/fphy.2021.760834

CrossRef Full Text | Google Scholar

6. Dunsby C. Optically sectioned imaging by oblique plane microscopy. Opt Express (2008) 16(25):20306–16. doi:10.1364/OE.16.020306

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Botcherby EJ, Juskaitis R, Booth MJ, Wilson T. Aberration-free optical refocusing in high numerical aperture microscopy. Opt Lett (2007) 32:2007–9. doi:10.1364/OL.32.002007

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Theer P, Dragneva D, Knop M. πSPIM: High NA high resolution isotropic light-sheet imaging in cell culture dishes. Sci Rep (2016) 6:32880. doi:10.1038/srep32880

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Smith CW, Botcherby EJ, Wilson T. Resolution of oblique-plane images in sectioning microscopy. Opt Express (2011) 19(3):2662–9. doi:10.1364/OE.19.002662

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Bouchard MB, Voleti V, Mendes CS, Lacefield C, Grueber WB, Mann RS, et al. Swept confocally-aligned planar excitation (SCAPE) microscopy for high-speed volumetric imaging of behaving organisms. Nat Photon (2015) 9(2):113–9. doi:10.1038/nphoton.2014.323

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Anselmia F, Ventalon C, Begue A, Ogden D, Emiliani V. Three-dimensional imaging and photostimulation by remote-focusing and holographic light patterning. Proc Natl Acad Sci U S A (2011) 108(49):19504–9. doi:10.1073/pnas.1109111108

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Li T, Ota S, Kim J, Wong ZJ, Wang Y, Yin X, et al. Axial plane optical microscopy. Sci Rep (2015) 4:7253. doi:10.1038/SREP07253

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Hoffmann M, Judkewitz B. Diffractive oblique plane microscopy. Optica (2019) 6(9):1166–70. doi:10.1364/OPTICA.6.001166

CrossRef Full Text | Google Scholar

14. Yang B, Chen X, Wang Y, Feng S, Pessino V, Stuurman N, et al. Epi-illumination SPIM for volumetric imaging with high spatial-temporal resolution. Nat Methods (2019) 16(6):501–4. doi:10.1038/s41592-019-0401-3

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Sapoznik E, Chang BJ, Huh J, Ju RJ, Azarova EV, Pohlkamp TA versatile oblique plane microscope for large-scale and high-resolution imaging of subcellular dynamics. Elife (2020) 9:e57681. doi:10.7554/eLife.57681

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Kim J, Li T, Wang Y, Zhang X. Vectorial point spread function and optical transfer function in oblique plane imaging. Opt Express (2014) 22(9):11140. doi:10.1364/OE.22.011140

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Botcherby EJ, Juškaitis R, Booth MJ, Wilson T. An optical technique for remote focusing in microscopy. Opt Commun (2008) 281(4):880–7. doi:10.1016/j.optcom.2007.10.007

CrossRef Full Text | Google Scholar

18. Kim J, Wojcik M, Wang Y, Moon S, Zin EA, Marnani N, et al. Oblique-plane single-molecule localization microscopy for tissues and small intact animals. Nat Methods (2019) 16:853–7. doi:10.1038/s41592-019-0510-z

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Barber CB, Dobkin DP, Huhdanpaa H. The quickhull algorithm for convex hulls. ACM Trans Math Softw (1993) 22(4):469–83. doi:10.1145/235815.235821

CrossRef Full Text | Google Scholar

20. Gu M. Advanced optical imaging theory. Berlin; Heidelberg: Springer-Verlag (2000).

Google Scholar

21. Richards B, Wolf E. Electromagnetic diffraction in optical systems. II. Structure of the image field in an aplanatic system. Proc R Soc A. Math Phys Eng Sci (1959) 253(1274):358. doi:10.1098/rspa.1959.0200

CrossRef Full Text | Google Scholar

22. Sinkó J, Kákonyi R, Rees E, Metcalf D, Knight AE, Kaminski CF, et al. TestSTORM: Simulator for optimizing sample labeling and image acquisition in localization based super-resolution microscopy. Biomed Opt Express (2014) 5(3):778–87. doi:10.1364/BOE.5.000778

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Venkataramani V, Herrmannsdörfer F, Heilemann M, Kuner T. SuReSim: Simulating localization microscopy experiments from ground truth models. Nat Methods (2016) 13(4):319–21. doi:10.1038/nmeth.3775

PubMed Abstract | CrossRef Full Text | Google Scholar