Shedding light on the 239Pu fission source term with new high-precision experiments and advanced fission modeling

In the last decade, there has been a renaissance of fission research resulting in new high-precision experiments and advanced fission modeling. For instance, the Chi-Nu and CEA teams supplied, for the first time, the ²³⁹Pu prompt fission neutron spectrum (PFNS) for broad ranges of incident and outgoing neutron energies. The CEA team also measured ²³⁹Pu average prompt neutron multiplicities, ${\bar{\nu }}_p$, with lower statistical uncertainties and a technique significantly different than the one used in the past. The NIFFTE collaboration provided ²³⁹Pu(n,f)/²³⁵U(n,f) cross section shape ratios with uncertainties below 1% utilizing a novel detector type. Advanced fission event generators were developed, among them CGMF, FIFRELIN, FREYA, and GEF, which calculate post-scission fission observables in a correlated manner. These new experimental data and more consistent fission models change the evaluated PFNS, ${\bar{\nu }}_p$, and (n,f) cross sections, some only modestly, compared to ENDF/B-VIII.0. In turn, the individual new nuclear data distinctly change simulated effective neutron multiplication factors of fast critical assemblies, but their combined impact is small, while affecting the prediction of LLNL pulsed sphere neutron leakage spectra and reaction rates only within experimental uncertainties. Also, the parameters obtained from fitting to ${\bar{\nu }}_p$ reproduce various post-scission fission observables within the uncertainties of experimental data. This indicates that new differential experiments and consistent fission modeling reduce compensating errors present in ENDF/B-VIII.0.

1 Introduction

The process of prompt emission after fission has been investigated experimentally and theoretically since the 1940s [1], but open questions remain. For instance, the average number of prompt fission neutrons emitted, ${\bar{\nu }}_p$, has been measured repeatedly with uncertainties as low as 0.75% for ²³⁹Pu [2–5], but experimenters almost always employed the liquid scintillator technique [6–9]. The ²³⁹Pu(n,f) cross sections were primarily measured with fission chambers with uncertainties ranging typically from 1.2% to 1.5% [10–12]. Until now, no precise and reliable data existed for incident neutron energies above 2 MeV for ²³⁹Pu energy spectra of prompt fission neutrons, PFNS [13]. Typical PFNS measurements reach uncertainties of 3%–5% near the peak but systematic effects such as multiple scattering of neutrons and background led to questioning all but two ²³⁹Pu data sets [14]. Until the early 2000s, fission models [15–18] predicted ${\bar{\nu }}_p$, PFNS, and (n,f) cross section independently from each other and post-scission fission observables such as pre-neutron emission fragment yields as a function of mass, spectra, and multiplicities of prompt fission γ rays, although they stem from the same physics process.

An accurate description of fission is key to performing reliable simulations of applications in reactor physics and nuclear criticality safety, for instance. Simulations are performed with neutron transport codes. These rely on nuclear data to compute the probability of particle interactions with matter. Nuclear data incorporate information from differential experiments and theory. Combinations of nuclear data of several observables are jointly validated with respect to integral experiments [19]. These experiments represent an application of interest. For instance, the effective neutron multiplication factor, k_eff, of ICSBEP critical assemblies [20], describes the number of neutrons lost versus produced in a critical assembly from one generation to the next in a chain reaction. Its simulation relies on nuclear data such as scattering and the fission source term [PFNS, ${\bar{\nu }}_p$, and (n,f) cross sections]. Discrepancies between simulated and experimental k_eff values cannot uniquely identify an issue in a specific nuclear data value, but differential experimental data can. However, the uncertainties mentioned above in the latter result in nuclear data uncertainties that in turn cause large simulated k_eff uncertainties, namely 1,025 pcm for the Jezebel critical assembly (Table VIII of [21]); this is about 5–10 larger than the experimental uncertainties published for various versions of Jezebel in Ref. [20]. This unconstrained physics space spanned between differential and integral information allows for several different combinations of PFNS, ${\bar{\nu }}_p$, and (n,f) cross sections that agree with available experimental data. Therefore, compensating errors between nuclear data of different observables occur. Such compensating errors adversely impact the predictive power of application simulations if an application goes beyond the physics described by validation experiments.

Here, we implement new high-precision measurements and consistent fission modeling, which are described in Section 2, into evaluations of PFNS, ${\bar{\nu }}_p$, and (n,f) cross sections. This new information addresses the questions mentioned above on fission and thus better constrains nuclear data. The measurements decisively inform the evaluations either by covering for the first time for broad incident and outoing neutron energy ranges the ²³⁹Pu PFNS with high precision [22–24], or by utilizing novel methods or detectors to obtain high-precision (n,f) cross sections and ${\bar{\nu }}_p$ [25–27]. We also use the post-scission fission event generator CGMF [28]. It enables, like others of its kind [29–31], constraining nuclear data by consistently predicting several fission quantities (distributions in mass, charge and total kinetic energy, PFNS, ${\bar{\nu }}_p$, etc.), and, thus, eliminating unphysical combinations between them. The evaluated results in Section 3 for ${\bar{\nu }}_p$, PFNS and (n,f) cross section above 14 MeV differ noticeably from ENDF/B-VIII.0 but are within ENDF/B-VIII.0 and new evaluated uncertainties. The evaluated PFNS and model parameters fitted to ${\bar{\nu }}_p$ predict other fission observables within associated experimental data (Section 3) providing consistency checks of nuclear data that were not feasible before. The effect of this new ²³⁹Pu fission source term on k_eff, LLNL pulsed spheres neutron leakage spectra [32], and reaction rates in critical assemblies, was assessed, and found to be small on all three integral responses, even though the changes in k_eff due to swapping out one nuclear data observable at a time are large. This good agreement with differential and integral data indicates a possible reduction of compensating errors fueled by new high-precision experiments and advanced fission modeling.

2 Evaluation input and methodology

2.1 New high-precision prompt fission neutron spectrum measurements

The Chi-Nu experiment was built over the last ∼15 years to produce high-precision PFNS for major actinides, with a well-documented experimental setup and detailed covariance analysis. Incident neutrons for these experiments are produced via proton spallation reactions on a tungsten target at the Weapons Neutron Research (WNR) facility at the Los Alamos Neutron Science Center (LANSCE). The resulting incident neutron spectrum available for Chi-Nu is E_inc = ≈0.7–700 MeV, with neutrons up to 20 MeV utilized for this measurement. The flight path located 15° to the left of the incident proton beam direction was used for Chi-Nu measurements; it has a “get-lost basement” (2 m of empty space beneath an Al floor) to significantly reduce environmental neutron scattering. Neutron-induced fission events are measured using a parallel-plate avalanche counter (PPAC) target [33]. Neutrons are detected with two detector arrays in two separate experiments: a twenty-two detector Li-glass array to measure PFNS neutrons from ∼0.01–1.5 MeV and the other a fifty-four detector liquid scintillator array for neutrons from ∼0.8–10.0 MeV. Data from both neutron detection arrays are combined to form a single PFNS shape result for outgoing neutron energies E_out = 0.01–10.0 MeV, at twenty contiguous E_inc ranges from 1.0 to 20.0 MeV. Covariances for each PFNS are calculated including statistical and all systematic uncertainties from, e.g., input nuclear data for MCNP simulations, fission detection efficiency, and more [22] for PFNS across all E_out and E_inc. Results from various target isotopes (e.g., ²³⁹Pu [22, 34], ²³⁵U [35], ²³⁸U, etc.) are correlated as well, allowing for accurate results for PFNS ratios to be calculated [36], of which there were only two measurements of the ²³⁹Pu/²³⁵U PFNS ratio at or near 1.5 MeV incident neutron energy prior to Chi-Nu results.

Also at WNR, another experimental campaign to measure the PFNS has taken place over recent years led by the French Atomic and Alternative Energy Commission (CEA)/DAM [23]. The differences and similarities between the Chi-Nu and CEA PFNS experimental approaches and ²³⁹Pu PFNS results are reviewed in detail in Ref. [24]. Briefly, both measurements share the same fifty-four liquid scintillator array, experimental flight path, and incident neutron flux shape. While Chi-Nu uses the Li-glass array for measurements of lower PFNS energies, CEA measurements utilize only the liquid scintillator array with a lower PFNS energy limit (200 keV) from this array compared with Chi-Nu. The other most notable difference between these experiments is the use of a CEA-made fission chamber [37] as opposed to a PPAC. The third most notable difference is that, while Kelly et al. simulated the neutron detector efficiency, the CEA team measured it with respect to a ²⁵²Cf source. Despite these differences, results from these two experiments for ²³⁹Pu are in overall agreement across the overlapping E_inc of 1.0–20.0 MeV within uncertainties for nearly all data points. Lastly, while there appear to be some systematic shape differences between these two data sets, comparisons of results from each experiment shown as ratios to data at the lowest E_inc (thereby canceling or reducing many systematic effects in the analysis) show near perfect agreement between the two results for all E_inc and E_out. Previously, high-precision experimental ²³⁹Pu PFNS existed for E_inc ≤ 2 MeV, whereas CEA and Chi-Nu measurements have now decisively mapped out the ²³⁹Pu PFNS across broad E_inc and E_out ranges.

2.2 New high-precision ${\bar{\nu }}_p$ measurement with the double time-of-flight technique

An accurate and precise measurement of ²³⁹Pu(n,f) ${\bar{\nu }}_p$ is a challenge; it requires 1) exact identification of fission events despite an intense α-decay background, and 2) a high-efficiency neutron detector with excellent neutron-γ discrimination. The majority of ²³⁹Pu ${\bar{\nu }}_p$ measurements in the MeV range were carried out more than 30 years ago; all employed the liquid-scintillator technique, where neutrons are detected with a close-to-4π scintillator in coincidence with fission events, e.g., [2–8, 38, 39]. Contrary to these measurements, Marini et al. [27] collected for the first time high-precision ²³⁹Pu ${\bar{\nu }}_p$ with the double time-of-flight technique that integrates neutrons over the PFNS; this setup couples a high-efficiency fast-timing fission chamber [37] to a segmented liquid scintillator array [40].¹ This measurement was performed at the WNR facility of LANSCE at LANL for 1–700 MeV incident neutron energies, thus extending the energy range of available experimental data from 30 to 700 MeV. The resulting experimental data agree within 0.3% with a trend predicted by a statistical analysis of all previous experimental data listed in Table 1 up to 7 MeV, thus validating the bulk of previous data obtained with an independent technique. Above 7 MeV, structures arise related to the opening of second and higher-chance fission. Such structures were clearly visible for the first time in Marini et al. data. In addition to that, the Marini measurement benefits from a better understanding of the fission process compared to 30 years ago that allowed, for instance, for better-informed corrections for the angular distributions of fission fragments. Hence, these new data provide valuable validation of past data below 7 MeV, and improved experimental input for evaluations.

2.3 New high-precision (n,f) cross section measurement with a time projection chamber

New measurements of the shape of the ²³⁹Pu(n,f)/²³⁵U(n,f) cross section ratio were performed by the NIFFTE TPC (Neutron Induced Fission Fragment Tracking Experiment Time Projection Chamber) collaboration to address concerns regarding the spread in the previous data relative to the Neutron Data Standard evaluation uncertainty [25]. The bulk of past measurements were undertaken using fission chambers which could be subject to several potential sources of systematic uncertainty [10, 11, 45]. The similar design of previous measurements also means they are often highly correlated with one another. The NIFFTE TPC tackled that by using a new type of detector, the fission Time Projection Chamber (fissionTPC) [46] that allows for full 3D reconstruction of charged-particle tracks ranging from protons to fission fragments. This type of measurement is in contrast to fission chambers which usually only provide a pulse height or energy and, depending on the configuration, some angular information on the fission fragments. With 3D track reconstruction, the fissionTPC benefits from a direct measurement of several quantities needed to adequately correct cross section ratios, including beam and target uniformity and detector efficiency, eliminating the need to make certain assumptions or auxiliary measurements. A detailed and carefully documented analysis was conducted to understand all the relevant uncertainty sources and validate the analysis results [25]. In short, the fissionTPC produced a precision shape measurement that is largely uncorrelated with previous measurements and has some different systematic uncertainties. The shape of previous measurements and the ENDF/B-VIII.0 evaluation was generally verified, however, valuablel information was provided above 14 MeV, where several data sets are discrepant [10, 47–50].

2.4 Correlated fission modeling

CGMF is a Hauser-Feshbach fission fragment decay code [28] that calculates prompt fission observables and their correlations through the event-by-event de-excitation of fission fragments. As input for this de-excitation, information about the compound nucleus is needed, e.g., multi-chance fission probabilities and pre-fission neutron energies. The initial distributions of the primary fission fragments, prior to neutron emission, have to be sampled in mass, charge, total kinetic energy, spin, and parity—Y(A, Z, TKE, J, π).

The mass distribution is written as a sum of three Gaussians,

$Y\left(A|E_{\text{inc}}\right)=G_0\left(A|E_{\text{inc}}\right)+G_1\left(A|E_{\text{inc}}\right)+G_2\left(A|E_{\text{inc}}\right)(1)$

defined as

$G_{\mathrm{1,2}}\left(A|E_{\text{inc}}\right)=\frac{W_{\mathrm{1,2}}}{\sqrt{2\pi {\sigma }_{\mathrm{1,2}}^2}}\left\{\exp \left[-\frac{{\left(A-{\mu }_{\mathrm{1,2}}\right)}^2}{2{\sigma }_{\mathrm{1,2}}^2}\right]+\exp \left[-\frac{{\left(A-\left(A_c-{\mu }_{\mathrm{1,2}}\right)\right)}^2}{2{\sigma }_{\mathrm{1,2}}^2}\right]\right\},(2)$

and

$G_0\left(A|E_{\text{inc}}\right)=\frac{W_0}{\sqrt{2\pi {\sigma }_0^2}}\exp \left[-\frac{{\left(A-A_c/2\right)}^2}{2{\sigma }_0^2}\right],(3)$

where A_c is the mass of the compound nucleus that undergoes fission, and the weights, means, and standard deviations of each Gaussian are energy dependent with $W_i={\{1+\exp \left[(E_{\text{inc}}-w_i^a)/w_i^b\right]\}}^{-1}$, ${\mu }_i={\mu }_i^a+{\mu }_i^b{E}_{\text{inc}}$, and ${\sigma }_i={\sigma }_i^a+{\sigma }_i^b{E}_{\text{inc}}$. The charge distribution of fission fragments before neutron emission, Y(Z|A), is defined by the Wahl systematics [51]. The total kinetic energy, TKE, as a function of incident energy is linear, but allows for a slope change as indicated by some experimental data, e.g., [52],

$\mathrm{T}\mathrm{K}\mathrm{E}\left(E_{\text{inc}}\right)=\left\{\begin{array}{cc}a+b{E}_{\text{inc}},\hfill & \text{if\hspace{0.17em}}{E}_{\text{inc}}\le E_0\hfill \\ c+d{E}_{\text{inc}},\hfill & \text{if\hspace{0.17em}}{E}_{\text{inc}}\ge E_0\hfill \end{array}\right.,(4)$

where c is defined by equating those two equations at E = E₀. For ²³⁹Pu(n,f), TKE has no slope change, and E₀ = b = 0 and a = c. For each mass, TKE(A) is defined as a Gaussian, with high-order polynomials for the mean and width, $\overline{\mathrm{T}\mathrm{K}\mathrm{E}}(A)=\sum _{i=0}^4{a}_i{(A-A_m(\mathrm{T}\mathrm{K}\mathrm{E}))}^i$ and ${\sigma }_{\text{TKE}}(A)=\sum _{i=0}^3{b}_i{(A-A_m(\mathrm{s}\mathrm{T}\mathrm{K}\mathrm{E}))}^i$. Each of these polynomials also has a maximum mass for which they are defined, A_max beyond which, $\overline{\mathrm{T}\mathrm{K}\mathrm{E}}(A)$ and σ_TKE(A) become constant. The spin-parity distribution is Gaussian-like, $P(J,\pi )=(1/2)(2J+1)\exp \left[-\frac{J(J+1)}{2B^2(A,Z,T)}\right]$, where B² is defined in terms of the fragment mass, charge, temperature, and moment of inertia, ${\mathcal{I}}_0(A,Z)$ as $B=\alpha {\mathcal{I}}_0(A,Z)T/{\hslash }^2$. α = α₀ + α₁E_inc is an adjustable, energy-dependent parameter that controls the competition between neutron and γ-ray emission.

For the optimization to the prompt neutron multiplicity, we consider the parameters in Table 2, for first-, second-, and third-chance fission. The initial parameters, p₀, are the default CGMF parameters [28]. To calculate the model parameter uncertainties, δp₀, we sample the Y(A|E_inc), TKE(E_inc), $\overline{\mathrm{T}\mathrm{K}\mathrm{E}}(A)$, and σ_TKE(A) distributions and accept those parameter sets that keep the χ² of the experimental data consistent. We then calculate the sensitivity of ${\bar{\nu }}_p$ to each of the CGMF parameters,

$S_{ij}=\frac{{\bar{\nu }}_p\left(E_{\text{inc}}^j|p_i^{+}\right)-{\bar{\nu }}_p\left(E_{\text{inc}}^j|p_i^{-}\right)}{p_i^{+}-p_i^{-}},(5)$

where $p_i^{\pm }=p_0\pm 0.01p_0$, for each i parameter in Table 2. By performing the evaluation in the parameter space of CGMF, we calculate not only the evaluated ${\bar{\nu }}_p$ but also the evaluated parameters that link back to other fission observables in CGMF, potentially allowing us to remove unphysical parameter space.

2.5 Other evaluation input

2.5.1 Prompt fission neutron spectrum evaluation

The ²³⁹Pu PFNS evaluation for incident-neutron energies, E_inc, 0.5–30 MeV differs from an earlier one of [53] by 1) the inclusion of Chi-Nu and CEA experimental data [22–24], 2) considering ²³⁹Pu PFNS at E_inc = 2 MeV [54] that were extracted by Lestone similarly to [55], and 3) assumptions on the prior for E_inc < 3 MeV. In general, the same prior as for [52] was used to obtain evaluated PFNS; the Los Alamos model [15] was paired with the exciton model [56] as well as the average total kinetic energy and energy release parametrizations based on [57, 58]. The only difference between the prior used for the evaluation of [53] and the one here is that the model correlation across E_inc are set to zero for evaluating PFNS at E_inc < 3 MeV—effectively evaluating PFNS one E_inc at a time for this energy range. This choice was taken, as otherwise evaluated PFNS for E_inc < 3 MeV are systematically lower than the experimental data for E_out > 8 MeV. This too low trend is caused by a rigid prior across E_inc paired with a parameterization that is too far from Chi-Nu and CEA PFNS at the second-chance fission threshold.

2.5.1.1 ${\bar{\nu }}_p$

In addition to the new Marini ²³⁹Pu ${\bar{\nu }}_p$, all experimental data in the EXFOR database [59] were analyzed by studying their EXFOR entries and literature. Only those data sets listed in Table 1 were adopted for the evaluation; reasons for rejecting other data sets are documented in [60].

TABLE 1

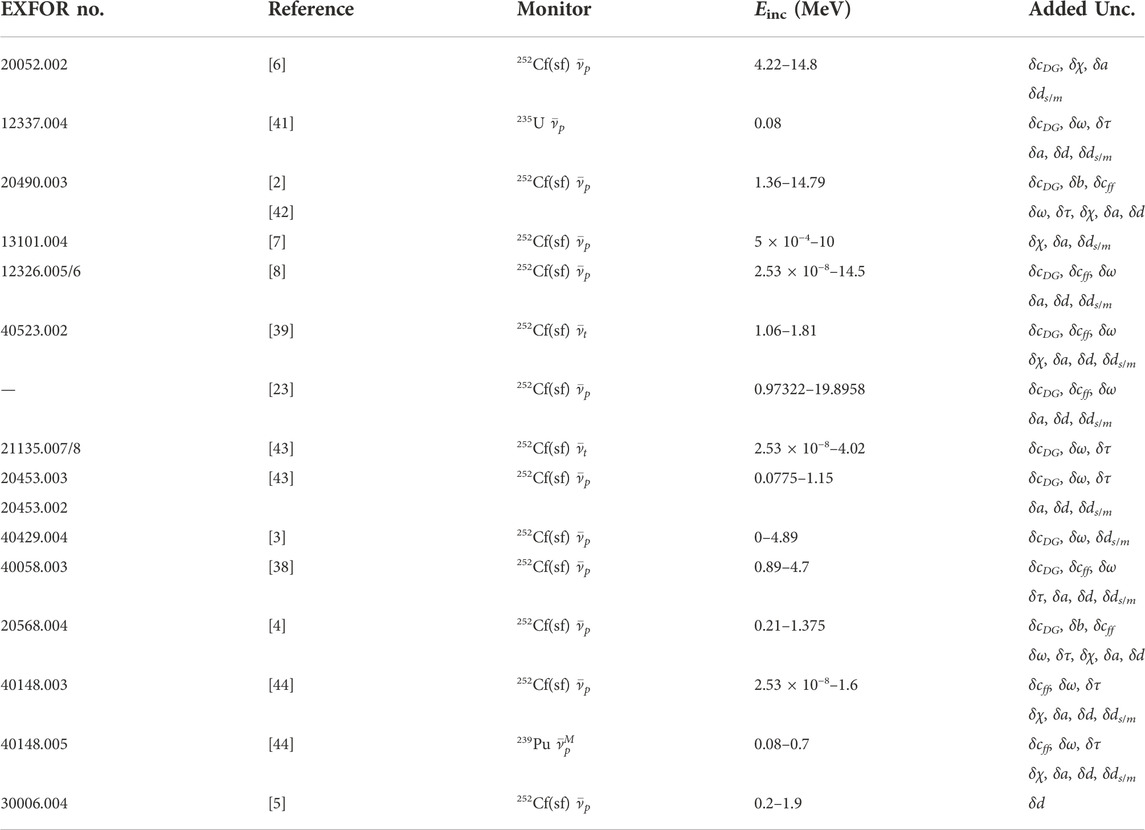
TABLE 1. Experimental ²³⁹Pu ${\bar{\nu }}_p$ included in the evaluation are listed with their EXFOR No., first author, year of publication, main reference and E_inc. The last column tabulates uncertainty sources that were added to those found in the literature. The variable names define the following uncertainty sources: δc_DG for delayed γ rays, δχ and δa for PFNS and angular distribution of fission neutrons corrections, δd_s/m for sample displacement, δω and δb for correcting impurities and random background, δτ for deadtime, δd for sample thickness, and δc_ff for false fission corrections.

Total covariances, ${\mathrm{C}\mathrm{o}\mathrm{v}}_{i,j}^{\mathit{tot}}$, were estimated by ${\mathrm{C}\mathrm{o}\mathrm{v}}_{i,j}^{\mathit{tot}}={\sum }_k{\delta }_i^k{\mathrm{C}\mathrm{o}\mathrm{r}}_{i,j}^k{\delta }_j^k$, for each and between experiments using a new module in the code ARIADNE [61]. This procedure accounts for uncertainty values, ${\delta }_i^k$, and correlation coefficients, ${\mathrm{C}\mathrm{o}\mathrm{r}}_{i,j}^k$, for an independent uncertainty source k at E_inc i or j. Special care was taken to estimate uncertainties consistently across all data sets in the database by accounting for uncertainty sources typically encountered in ${\bar{\nu }}_p$ liquid scintillator ratio measurement. If no uncertainty values were reported in the literature for a specific source, these missing values were estimated based on templates of expected uncertainties for this measurement type [9]. While systematic uncertainties were missing for at least one source per measurement (Table 1), statistical uncertainties, δs, dominate the total ones. δs ranges from 1% to 2% contrary to total systematic uncertainties with values of 0.5%–0.9%, where the common usage of the Neutron Data Standards ²⁵²Cf(sf) ${\bar{\nu }}_t$ significantly contributes with 0.42% [10].

Nearly the same data as for the ENDF/B-VIII.0 evaluation of ²³⁹Pu ${\bar{\nu }}_p$ [62] were adopted with the exception of the data of Huanqiao, Nesterov, Johnstone, Smirenkin and Leroy. The latter three data sets are too uncertain to influence the evaluation, while the former two were down-weighted in the evaluation of [62] by doubling their uncertainties compared to those in EXFOR. The experimental uncertainties also differ in as far as the evaluation of [62] adopted most uncertainties as reported in the EXFOR database, while here a detailed uncertainty estimate was undertaken.

2.5.1.2 (n,f) cross sections

The ²³⁹Pu(n,f) cross section is evaluated as part of the Neutron Data Standards project with the code GMAP [63, 63]. We build here upon the data file related to the work of [11]. In this paper, all covariances of experimental ²³⁹Pu(n,f) cross sections were updated with templates of expected measurement uncertainties for this observable [11, 12]. Given that, all experimental data for the ²³⁹Pu(n,f) cross section should have a consistent weight compared to NIFFTE data. The only difference between this evaluation and the one used here is the inclusion of NIFFTE ²³⁹Pu/²³⁵U(n,f) and ²³⁸U/²³⁵U(n,f) cross section ratios [65, 66].

2.6 Evaluation methodology

The generalized least squares (GLS) algorithm [67], and the Kalman filter method [68] were employed to evaluate mean values, N, and covariances, Cov^N. Both algorithms are encoded in the same set of equations,

$\begin{array}{ll}\hfill \mathit{N}& =\mathit{p}+{\mathbf{C}\mathbf{o}\mathbf{v}}^N{\mathit{S}}^t{\left({\mathbf{C}\mathbf{o}\mathbf{v}}^e\right)}^{-1}\left(\mathit{e}-\mathit{S}\mathit{p}\right),\hfill \\ \hfill {\mathbf{C}\mathbf{o}\mathbf{v}}^N& ={\mathbf{C}\mathbf{o}\mathbf{v}}^p-{\mathbf{C}\mathbf{o}\mathbf{v}}^p{\mathit{S}}^t{Q}^{-1}\mathit{S}{\mathbf{C}\mathbf{o}\mathbf{v}}^p,\hfill \\ \hfill Q& =\mathit{S}{\mathbf{C}\mathbf{o}\mathbf{v}}^p{\mathit{S}}^t+{\mathbf{C}\mathbf{o}\mathbf{v}}^e,\hfill \end{array}(6)$

where the main difference lies in how the prior mean values, p, prior covariances, Cov^p, and sensitivities, S, are defined. The variables e and Cov^e encode all experimental data used for the evaluation and their covariances. The code GMAP [63, 64] is used for evaluating the (n,f) cross section via GLS; PFNS and ${\bar{\nu }}_p$ are evaluated with ARIADNE [61] which encompasses both GLS and Kalman filter methodologies.

If the equations are applied for GLS, p and Cov^p are in the same physical space as for the observable to be evaluated. In GMAP, the previous standard values are used as p with a diagonal covariance matrix of 100%, i.e., an uninformative prior. The same approach is taken in ARIADNE to evaluate ${\bar{\nu }}_p$ based on only experimental data (ENDF/B-VIII.0 ${\bar{\nu }}_p$ mean values are used for the prior along with uncertainties of 100%), while prior PFNS and covariances from the LAM in PFNS space [53] are taken for PFNS evaluations. The variable S is a design matrix that linearly interpolates in Ref. [53] experimental data onto the E_inc grid of the prior data. The variable S^t is the transpose of S. The evaluated mean values N and Cov^N correspond in this case to evaluated ${\bar{\nu }}_p$, PFNS, or (n,f) cross sections and their covariances.

The CGMF model was included into the ${\bar{\nu }}_p$ evaluation by applying Eq. 6 as a Kalman filter; p are model-parameter values and Cov^p their covariances in this case. The variable S corresponds then to sensitivities of the CGMF-calculated ${\bar{\nu }}_p$ to the model parameters. Due to that, N and Cov^N are in the case of the Kalman filter evaluated model parameters of CGMF and their covariances. The mean values are fed into CGMF to obtain what is presented as an evaluated ${\bar{\nu }}_p$ based on this code.

The experimental covariances were corrected for an effect termed “Peelle’s Pertinent Puzzle” (PPP) [69], where the mean value computed from strongly correlated data lies outside of the range of the input data due to an improperly formulated covariance matrix [70]. Both GMAP and ARIADNE use iterative linear least squares [71, 72] to mitigate the impact of PPP.

3 Discussion of evaluation and validation results

3.1 Evaluated results

3.1.1 Prompt fission neutron spectrum

The new evaluated PFNS in Figures 1, 2 interpolate between the high-precision ²³⁹Pu PFNS of CEA and Chi-Nu for all E_inc, and closely follow Lestone data. In doing so, the evaluation differs noticeably from ENDF/B-VIII.0 highlighting that CEA and Chi-Nu PFNS provide decisive input. This is especially true for E_inc > 2 MeV where past PFNS [73] were too uncertain to guide the evaluation. To be more specific, the evaluated PFNS are softer than ENDF/B-VIII.0 for E_inc < 12 MeV. At E_inc = 14 MeV, the new evaluation, distinctly different from ENDF/B-VIII.0, follows closely structures and shapes shown in CEA and Chi-Nu data. In fact, CEA and Chi-Nu data resolve for the first time physics expected structures expected at second and third-chance fission thresholds of the ²³⁹Pu PFNS: Characteristic structures from second-chance fission present themselves at E_inc = 6–7 MeV as an increase in the PFNS for E_out = 0.1–0.8 MeV. Third-chance fission structures are less pronounced but are visible for E_inc = 10–12 MeV for E_out = 0.1–0.8 MeV. In addition to that, the pre-equilibrium peak starts to emerge for E_inc = 12 MeV at E_out > 5 MeV. While ENDF/B-VIII.0 correctly predicted the E_inc and E_out of these structures, it incorrectly estimated their magnitude and the shape. Only CEA and Chi-Nu data enabled an accurate description of the PFNS physics there.

FIGURE 1

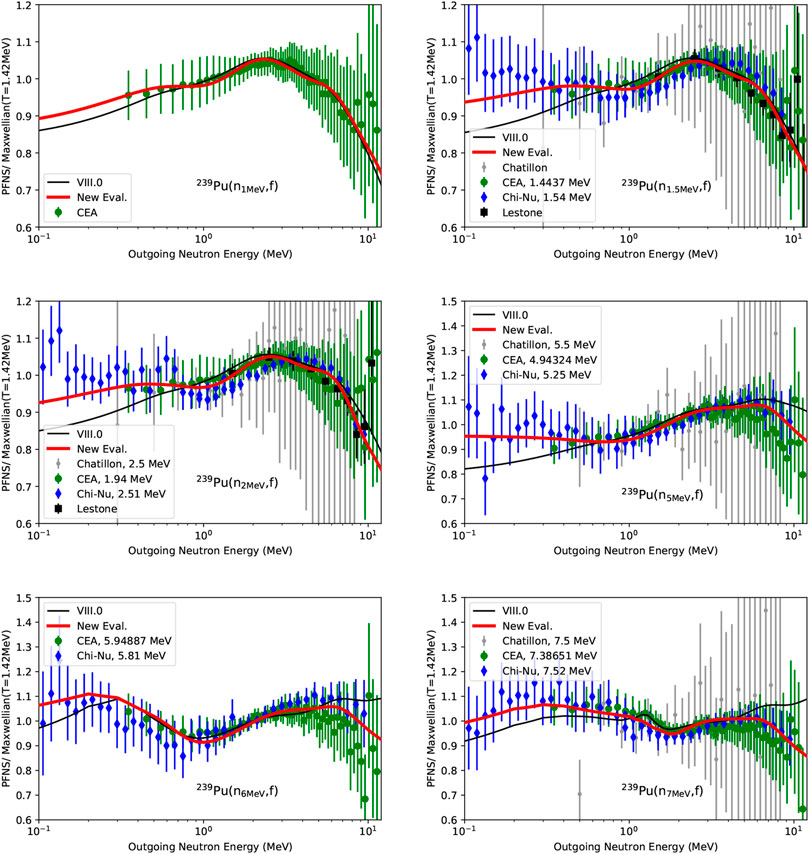
FIGURE 1. Evaluated ²³⁹Pu PFNS are shown in comparison to ENDF/B-VIII.0 and experimental data that were used for the evaluation, for incident neutron energies from 1 to 7 MeV.

FIGURE 2

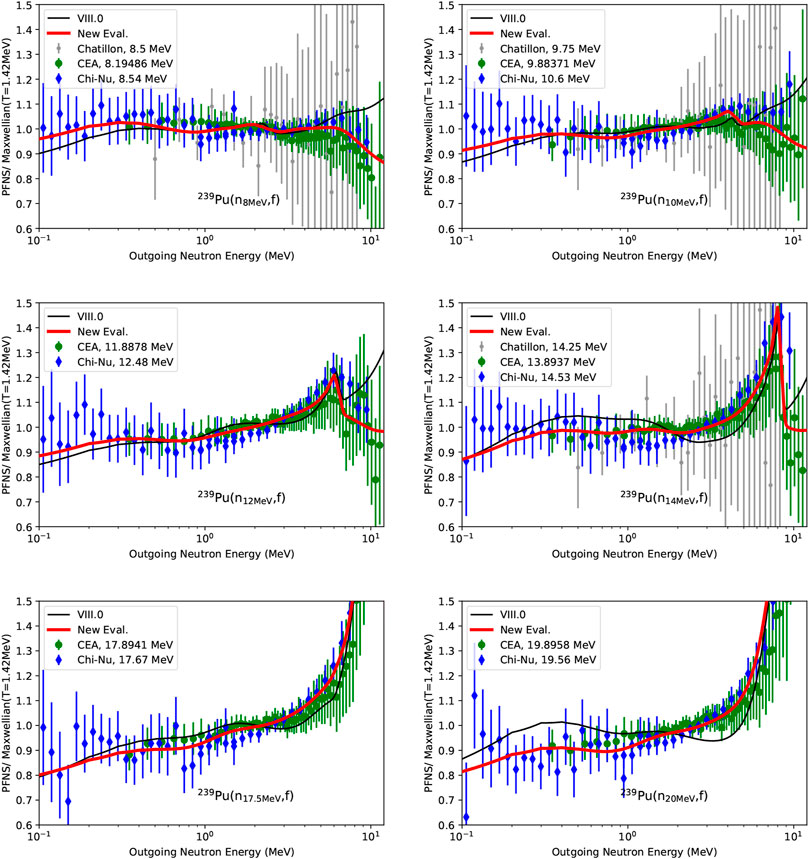
FIGURE 2. Same as Figure 1 for incident neutron energies from 8 to 20 MeV.

The changes in the PFNS can be also observed in the first two plots of Figure 3 showing the mean energy of the PFNS—that is the first moment of the PFNS—as a function of E_inc. The new evaluated mean energy integrated for E_out = 0.01–10 MeV follows CEA and Chi-Nu data closely but is softer (by approximately 20 keV) than ENDF/B-VIII.0 up to 5 MeV. ENDF/B-VIII.0 also did not capture the mean energy close to second-and third-chance fission thresholds due to lack of experimental information. Non-linear behavior in the average mean energy in Figure 3 from thermal (calculated from INDEN PFNS [13]; [73]) to 1 MeV can be observed. The challenge we faced was that evaluated PFNS at E_inc = 1, 1.5 and 2 MeV in Figure 1, based on the CEA, Chi-Nu, and Lestone data, gave evaluated mean energies in Figure 3. On the other hand, the INDEN PFNS at thermal [13]; [73], based on stringently-reviewed data at thermal [14], decreased mean energies versus ENDF/B-VIIII.0. If we had prioritized a smooth trend in the mean energy for E_inc from thermal to 2.5 MeV, this would have been in contradiction to the aforementioned PFNS; i.e., we might have had to have a hotter spectrum at thermal or a softer spectrum at E_inc = 1 MeV than the data called for. Our decision was to not under-value the 1 MeV PFNS data, while adopting also the new thermal assessment, and this led to the non-linear structures in the mean energies from thermal to 1 MeV. While the true E_inc dependence of the mean energy is expected to be smooth from 0 to 2.5 MeV, it reflects our priorities to accurately represent the CEA and Chi-Nu PFNS in this fast range. Over time, we hope future measurements will better inform this evaluation decision, but such experiments typically take many years.

FIGURE 3

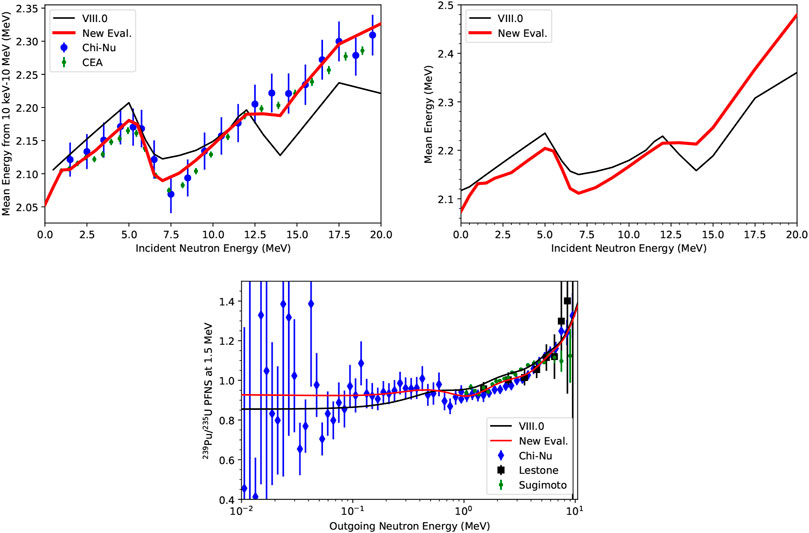
FIGURE 3. Further validation of evaluated PFNS is shown: (Top, right) Mean energies calculated from the PFNS from 100 keV to 10 MeV are compared for this evaluation, ENDF/B-VIII.0 and those from CEA and Chi-Nu experimental data. At thermal, the PFNS from INDEN is adopted [13, 73]. (Top, left) The same as the first plot but calculated mean energies are shown integrated over all E_out. (Bottom) Ratio of ²³⁹Pu/²³⁵U PFNS at E_inc = 1.5 are shown for ENDF/B-VIII.0, this evaluation and one for ²³⁵U including Chi-Nu PFNS, Chi-Nu, Lestone and Sugimoto experimental data.

Further evidence on the consistency of the evaluated PFNS across isotopes is provided in the bottom of Figure 3 where the ratio of this evaluated PFNS to a new ²³⁵U PFNS [75], which also includes new Chi-Nu data [35], at E_inc = 1.5 MeV compares well to experimental ratio data by [22, 24, 35, 55, 76].

3.1.2 Average prompt fission neutron multiplicity, ${\bar{\nu }}_p$

Three ${\bar{\nu }}_p$ evaluations are compared in Figures 4, 5: Two ${\bar{\nu }}_p$ evaluations are obtained via GLS based on only experimental data, (1) for the database without Marini, and (2) with Marini data. In evaluation (3), the Kalman filter method is used to bring in the CGMF model. This three-evaluation approach allows us to assess the impact of Marini data and CGMF. Also, evaluation (1) is expected to differ little from ENDF/B-VIII.0.

FIGURE 4

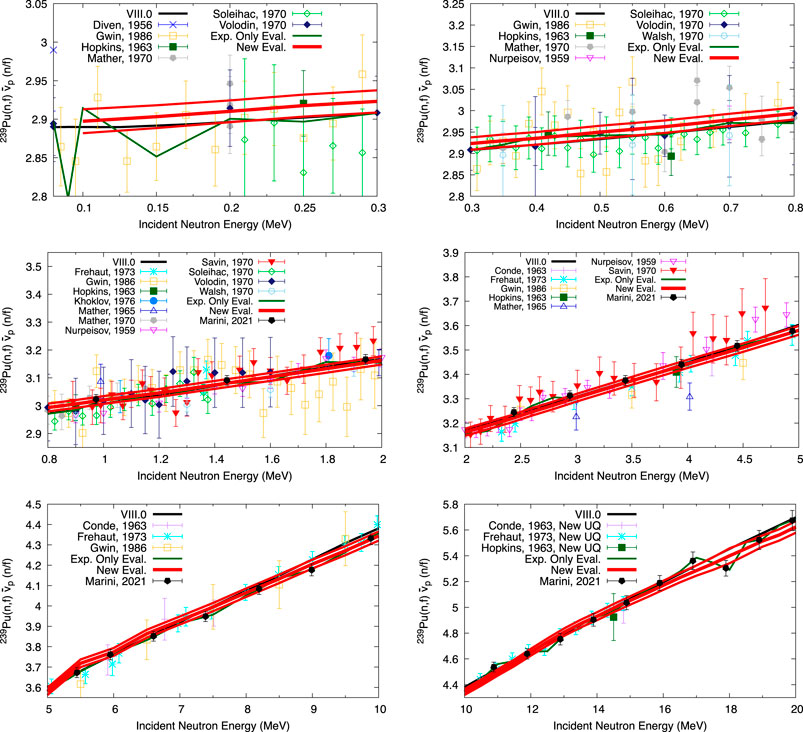
FIGURE 4. Evaluated ²³⁹Pu ${\bar{\nu }}_p$ of evaluations (2, only experimental data) and (3, including CGMF) are shown in comparison to ENDF/B-VIII.0 and experimental data that were used for the evaluation.

FIGURE 5

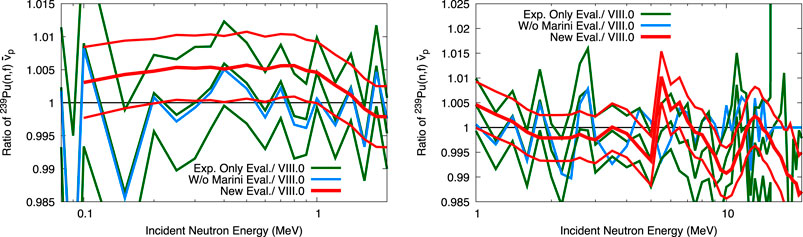
FIGURE 5. ²³⁹Pu ${\bar{\nu }}_p$ evaluations 1–3 [evaluation (1) is based on only experimental data without Marini data, evaluation (2) builds upon (1) but includes Marini data, while (3) includes on top of (2) CGMF] are shown in ratio to ENDF/B-VIII.0.

For ENDF/B-VIII.0 ²³⁹Pu ${\bar{\nu }}_p$, GLS was applied to experimental data and covariances with an uninformative prior, similarly to how ARIADNE was used to evaluate ${\bar{\nu }}_p$ based on only experimental data. The resulting evaluated ${\bar{\nu }}_p$ were smoothed for ENDF/B-VIII.0. The new GLS results for ${\bar{\nu }}_p$ without Marini data meander around ENDF/B-VIII.0 (see Figure 4) as is expected since no smoothing algorithm was applied to the GLS result. These random structures stem from statistical scatter in experimental data. The rejection of five data sets (first-authored by Huanqiao, Nesterov, Smirenkin, Johnstone, and Leroy) had little impact given their large uncertainties. The impact of adding missing systematic uncertainties via templates is also minor as total uncertainties are dominated by statistical ones which are included in both evaluations. A larger difference can be observed from 0.1 to 0.5 MeV where experimental ${\bar{\nu }}_p$ are less plentiful and more scattered. The scatter in experimental data below 0.5 MeV stems from counting statistics, beam background, and thickness effects from either the sample or the backing material. Counting statistics uncertainties are large (up to 2%) as it is a challenge to get neutron beams in the hundreds of keV range with modest energy spread all the while having a high enough flux. Incident beam neutrons could also be downgraded in energy by multiple scattering in the surrounding materials. If neutrons are assumed to be measured at higher E_inc than they actually are, fewer neutrons per fission will be appropriated to that energy. Parasitic scattering cross sections of ¹⁶O, ²⁷Al, and ¹H show either resonances or have high scattering cross sections (¹H) in this energy range, and could be responsible for downgrading neutron-beam energies.

If Marini data are included, ${\bar{\nu }}_p$ slightly rises below 1 MeV because of correlations between data sets arising from the common ²⁵²Cf(sf) ${\bar{\nu }}_t$ monitor. Starting with 1 MeV, Marini data change the shape of the evaluation, most notably above 4 MeV. First, the evaluated data decrease around 4 MeV and then are slightly higher, only to decrease again below ENDF/B-VIII.0 for 7–12 MeV. The second evaluation with Marini is higher from 12 to 14 MeV and then lower again. These structures appear at the second and third-chance fission thresholds and have a plausible physics basis. Historic data sets did not show this effect as large statistical uncertainties wash out these subtle structures. Applying smoothing algorithms to evaluated data without the physics information of second and third chance fission removed any remnants of this effect from the ENDF/B-VIII.0 ${\bar{\nu }}_p$. Marini data are able to resolve these structures for the first time and thus lead to small changes in evaluated data above 4 MeV, while remaining minimal below 4 MeV. Thus, the Marini data, which measured ²³⁹Pu ${\bar{\nu }}_p$ for the first time with the double time-of-flight technique, validate the trend seen from historic data that were all measured with the liquid-scintillator ratio method.

Including the CGMF prior via the Kalman filter smooths the evaluated ${\bar{\nu }}_p$ and further enhances second- and third-chance fission structures from 4.5 to 6 MeV and 9–12 MeV, in agreement with the structures present in Marini data. Below 1 MeV, the evaluation (3) including Marini data and CGMF is systematically higher (on average 0.5%) than ENDF/B-VIII.0: Compared to evaluation (2), CGMF gives a smooth ${\bar{\nu }}_p$ close to the higher points of the second evaluation. This difference from ENDF/B-VIII.0 is within the 1-σ evaluated uncertainties and the scatter of experimental data. While the evaluated uncertainties realistically assess the spread in evaluations, this difference will merit future continued studies given the importance of this observable. On the model side, these higher values could be caused by uncertainties in the energy dependence parametrizations, particularly in the mass distribution, Y(A|E_inc). Also, ${\bar{\nu }}_p$ based on only experimental data is uncertain to 0.6%–0.8% in Figure 6 given the issues affecting the accuracy and precision of experimental data detailed above. Hence, new high-precision experimental ${\bar{\nu }}_p$ below 1 MeV would be of importance. A comparison to fission experimental data beyond ${\bar{\nu }}_p$ and usage in simulations validation experiments might yield more insight.

FIGURE 6

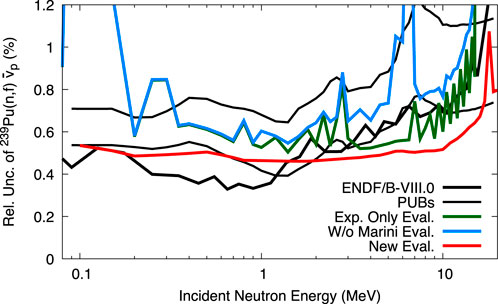
FIGURE 6. Evaluated uncertainties with and without Marini, and including CGMF are compared to ENDF/B-VIII.0 uncertainties and PUBs bounds.

The uncertainties of evaluation (1) are larger than those of ENDF/B-VIII.0 in Figure 6 from up to 15 MeV. It was shown via the Physical Uncertainty Bounds (PUBs) method [45, 77, 78] that ENDF/B-VIII.0 ${\bar{\nu }}_p$ uncertainties are underestimated considering the experimental data used for this evaluation. This is illustrated in Figure 6, where ENDF/B-VIII.0 uncertainties are below the minimal realistic bound estimated via PUBs below 1 MeV and on the lower end above. Contrary to that, the uncertainties of evaluation (1) lie within PUBs bounds indicating them to be more realistic. Adding Marini data into evaluation (2) decreases evaluated uncertainties, showcasing clearly the impact of the small uncertainties reported by Marini et al. Adding the CGMF model via evaluation (3) decreases uncertainties by an average factor of 0.8 from 0.5 to 15 MeV. Evaluated uncertainties are decreased more below 0.5 and above 15 MeV where experimental data are scarce. These new evaluated uncertainties of evaluation (3) are now below PUBs bounds but that is justified as PUBs bounds were estimated without taking Marini and CGMF model parameterization into account which both credibly reduce uncertainties due to their low experiment uncertainties or physics content.

3.1.3 (n,f) cross section

Three evaluations are discussed: 1) The 2018 standards evaluation (Std. 2018) that is in ENDF/B-VIII.0 from 0.04 to 20 MeV [10], (2) an evaluation building upon (1) from [11] differing in ²³⁹Pu(n,f) cross section experimental covariances updated by templates of expected measurement uncertainties, and (3) evaluation (2) updated with NIFFTE TPC data. These evaluations differ by a maximum of 0.5% until 14 MeV, as shown in the bottom of Figure 7. However, most of the previous data were measured with fission chambers, while NIFFTE TPC shape data were obtained with a time-projection chamber which allows accurate tracking of charged particles in three dimensions. Hence, this small difference up to 14 MeV in the shape of evaluations (2) and (3) indicates that the TPC confirms the shape obtained from a bulk of data measured with fission chambers.

FIGURE 7

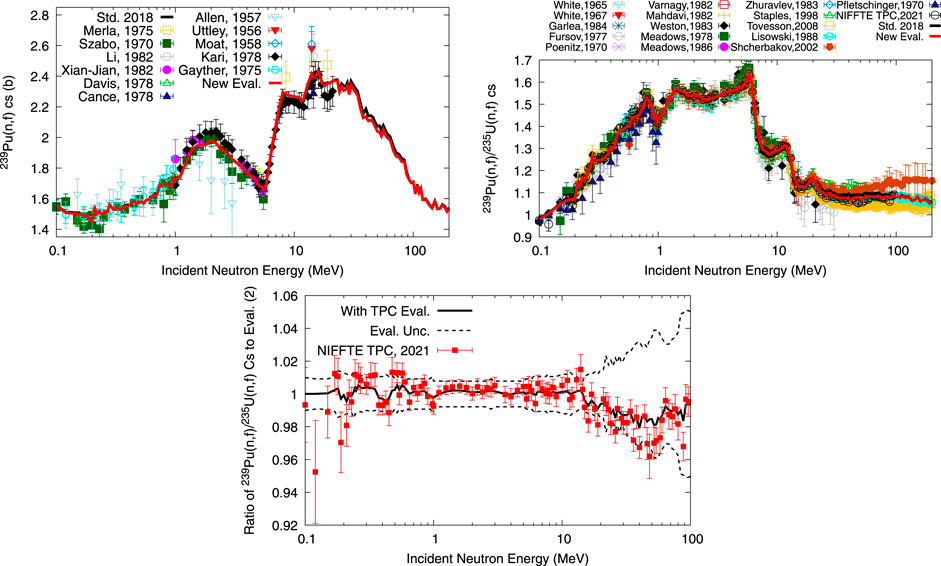
FIGURE 7. The ²³⁹Pu(n,f) cross section and ²³⁹Pu(n,f)/²³⁵U(n,f) cross section ratio obtained in the nuclear data evaluations (1) and (3) are compared to experimental data in the top two plots. In the bottom plot, NIFFTE TPC data are compared to evaluated data with and without NIFFTE TPC data [evaluations (2) and (3)].

Above 14 MeV, the evaluated (n,f) cross section of evaluation (3), with NIFFTE TPC data, is systematically lower by 2% than without, evaluation (2), but within the GMAP uncertainties. In this energy range, the exact value of the (n,f) cross section was not well defined [10] given discrepancies in previous data sets [47–50]. NIFFTE TPC data support the shape of Lisowski [47] data rather than the higher ones of Shcherbakov [49] and Staples [50]. No integral experiments exist that allow to conclusively validate whether evaluations (1) or (3) of the (n,f) cross section are more realistic from 10 to 15 MeV. While LLNL pulsed spheres [32] are sensitive to nuclear data from 5 to 15 MeV, changes in the ²³⁹Pu(n,f) cross section of less than 5% were shown in [79] to have minimal impact on their simulation. Hence, the new NIFFTE TPC measurement is an important clue to accurately define the (n,f) cross section above 14 MeV.

3.2 Validation with respect to various fission quantities

The evaluated parameters listed in Table 2 were used not only to calculate the evaluated ${\bar{\nu }}_p$, but also to predict various prompt fission observables enabling us, for the first time, to consistently compute additional fission observables with the evaluation of ${\bar{\nu }}_p$. The evaluated parameters ${\mu }_1^a$, ${\mu }_2^a$ and a for first-chance fission change very little compared to their prior values in Table 2 as they were fit in the default version of CGMF to available experimental Y(A) data, as a function of E_inc, while a was fit to TKE(E_inc) data but adjusted by hand to better reproduce experimental ²³⁹Pu ${\bar{\nu }}_p$ data for first-chance fission. Instead, we see changes in the widths of the Gaussian parametrizations of Y(A), the TKE(A) distributions, and the spin-parity distributions which have a significantly lower impact on the determination of ${\bar{\nu }}_p$ and are likely poorly constrained by this observable alone.

TABLE 2

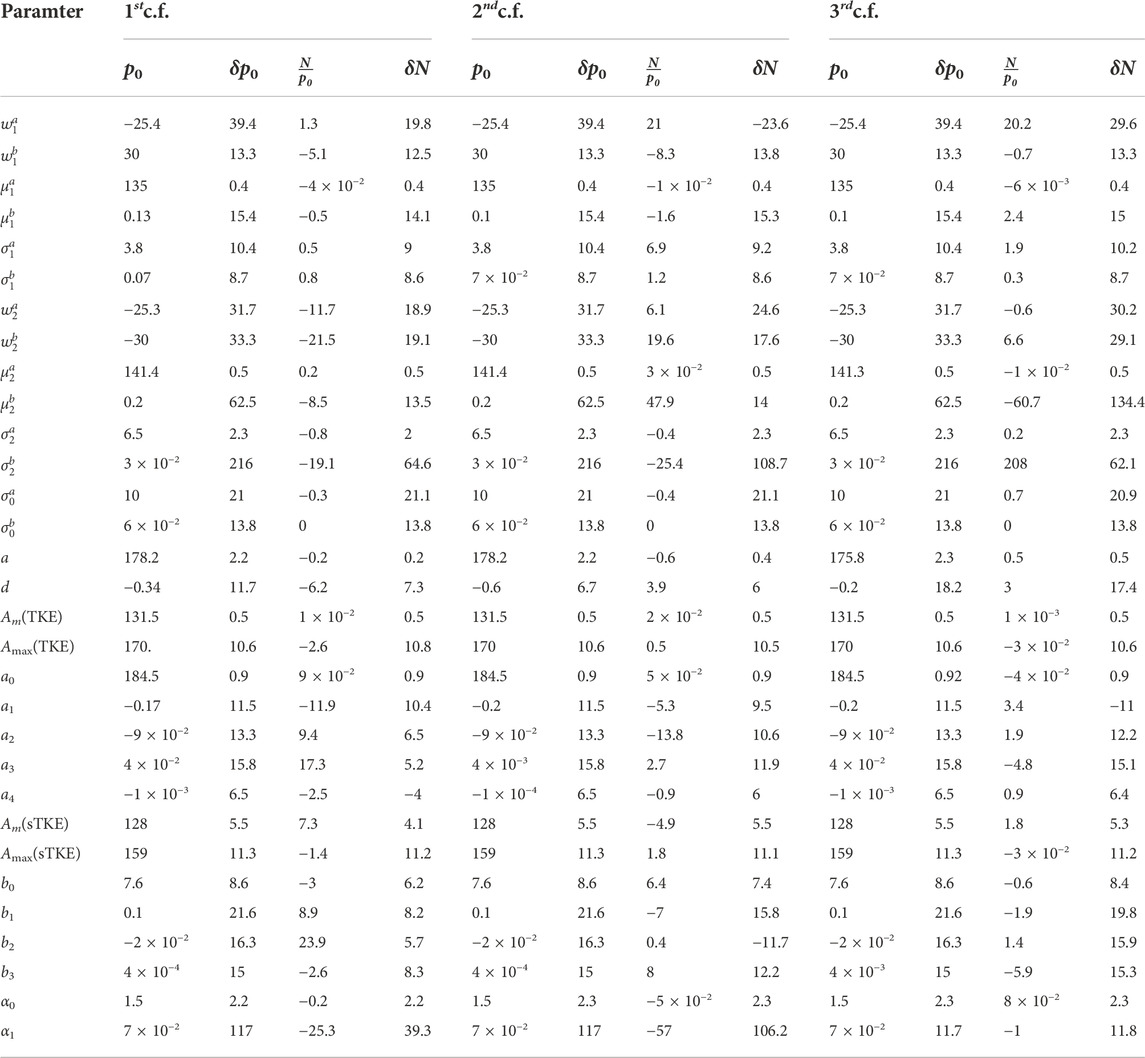
TABLE 2. Prior CGMF parameter values, p₀, for the ${\bar{\nu }}_p$ evaluation are given along with their uncertainties in %, δp₀. The variable N signifies one of the evaluated parameters. The change in evaluated parameters as a ratio to the prior, $\frac{N}{p_0}$, is compared to p₀ in %, and the evaluated parameter uncertainties, δN, are given in %.

As these are potentially large parameter changes, we use the evaluated parameters to calculate other fission observables in CGMF to ensure their consistency. The mass distributions in the first chance energy range, shown in Figure 8, differ only little from prior estimates despite changes of 10%–20% in parameter values. However, seemingly small changes $(<5\%)$ in the a and d parameters used to determine the total kinetic energy as a function of E_inc distinctly impact TKE(E_inc) in Figure 9. The evaluated parameters lead to a TKE that is more similar to the bulk of the experimental data below 5 MeV. Finally, small differences between the baseline CGMF calculations and the ones with the evaluated parameters can be observed for the average neutron and γ-ray energies as a function of incident neutron energy in Figure 9. Although there is no γ-ray information included in the fit, γ-ray average energies remain reasonable. The mean energies computed from predicted PFNS are systematically low compared to experimental data, which is a well-known but not fully understood defect of existing Hauser-Feshbach fission fragment decay models. Due to this defect, the LAM, not CGMF, was used to evaluated PFNS for this work. The evaluated parameters do not impact this result very much.

FIGURE 8

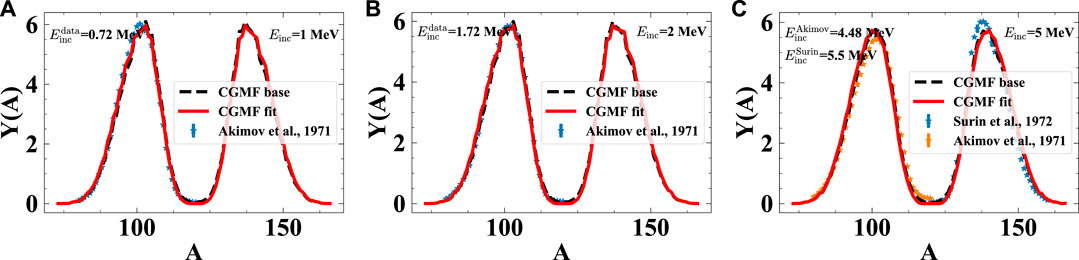
FIGURE 8. Comparison of the baseline CGMF calculation (black dashed), evaluated CGMF calculation (red solid) and experimental data (filled symbols) for the pre-neutron emission mass distributions, Y(A), at incident neutron energies of 1, 2, and 5 MeV.

FIGURE 9

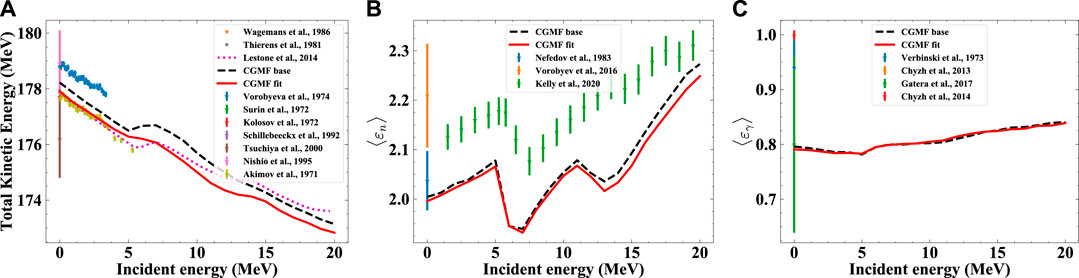
FIGURE 9. CGMF baseline calculation, evaluated CGMF calculation, and experimental data are compared for several observables: (Left) Total kinetic energy, TKE, as a function of incident neutron energy. The curve of Lestone et al. is a phenomenological model calculation informed by experimental data. (Center) Average outgoing energies of the prompt neutrons and (right) γ rays as a function of incident neutron energy.

The predicted prompt fission observables are all well in line with experimental data except for the known discrepancies in the mean energies of the PFNS. This close agreement of fission data beyond ${\bar{\nu }}_p$, supports the trend we see in the evaluation with CGMF and thus adds additional insight for ${\bar{\nu }}_p$.

3.3 Validation with respect to integral experiments

The evaluated ²³⁹Pu ${\bar{\nu }}_p$, PFNS, and (n,f) cross section of this work are assessed with effective neutron multiplication factors, k_eff, of ICSBEP critical assemblies [20], LLNL pulsed-sphere neutron-leakage spectra [32], and fission reaction rates measured in the center of ICSBEP critical assemblies in Figure 10 and Tables 3, 4 using MCNP-6.2 [80]. To this end, the new PFNS, ${\bar{\nu }}_p$, and (n,f) cross section were folded into the ²³⁹Pu ENDF/B-VIII.0 file. This file also differs from ENDF/B-VIII.0 in ${\bar{\nu }}_t$ and (n,el) cross section that absorb changes in ${\bar{\nu }}_p$ and (n,f) cross section to satisfy sum rules. Also, the INDEN PFNS was adopted at thermal [13].

FIGURE 10

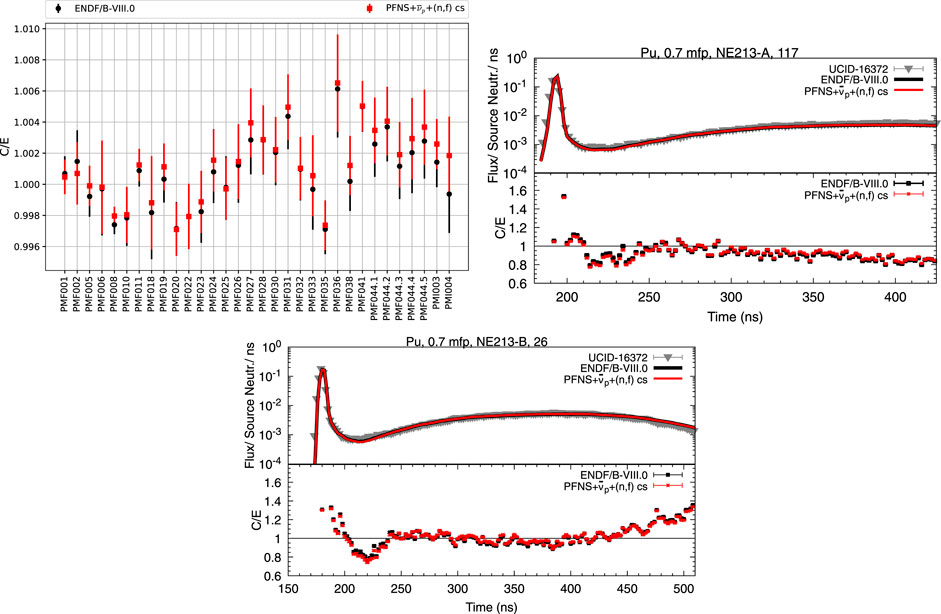
FIGURE 10. Simulated values (“C”) for k_eff of PMF and PMI assemblies (left) and two Pu LLNL pulsed sphere neutron leakage spectra (other two plots) are depicted for ENDF/B-VIII.0 versus the new fission source term. Experimental data (“E”) are shown for comparison.

TABLE 3

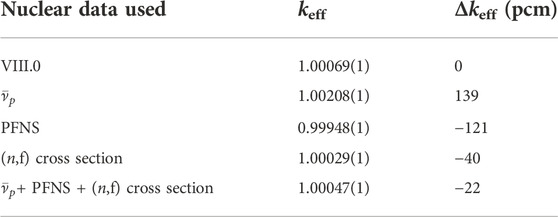
TABLE 3. Calculated values of PMF-001rev.4 k_eff are shown for ENDF/B-VIII.0 and ENDF/B-VIII.0 with different combinations of nuclear data. Δk_eff is the difference between k_eff using new nuclear data identified with the same row and ENDF/B-VIII.0.

TABLE 4

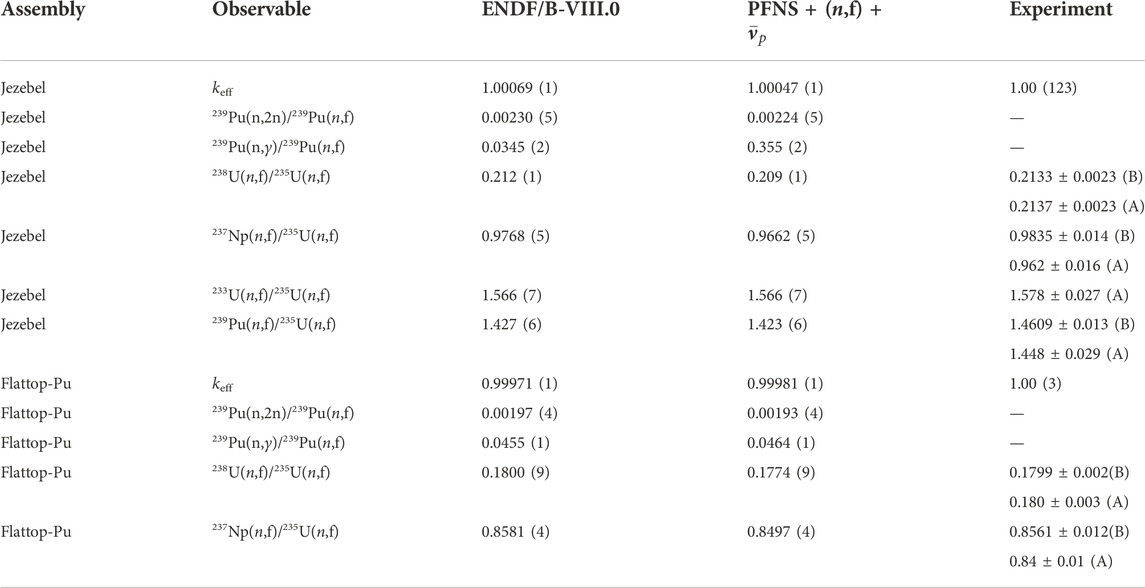
TABLE 4. Calculated values are shown for reaction rates of various reactions in Jezebel and Flattop-Pu critical assemblies. Calculated values are given for ENDF/B-VIII.0 as well as the ²³⁹Pu fission source term. Experimental values were taken from Table XXXIX of Ref. [85].

We have assessed the impact of changing each fission source term observable on simulated k_eff values of PMF001v.4 (Jezebel) by swapping them into ENDF/B-VIII.0 and comparing them to ENDF/B-VIII.0 simulated results in Table 3. The simulated k_eff values change distinctly: k_eff decreases by 121 pcm if the new PFNS is used. This large change, largely driven by including CEA and Chi-Nu data, is counterbalanced by the new ${\bar{\nu }}_p$ guided by Marini experimental data and CGMF modeling that increases k_eff by 139 pcm. The impact of the (n,f) cross section change is modest with 40 pcm as NIFFTE TPC shape data confirmed the general trend of ENDF/B-VIII.0 data. The overall effect of updating all three observables is modest, −22 pcm, and well within the currently documented experimental uncertainties of 123 pcm; it decreases the bias slightly compared to ENDF/B-VIII.0.

Similarly to what was seen for changing the fission source term for predicting PMF001.v4, k_eff values of several PU-MET-FAST (PMF) and PU-MET-INT (PMI) assemblies simulated with new nuclear data are close to ones predicted with ENDF/B-VIII.0: the mean bias calculated from ENDF/B-VIII.0 C/E, calculated over experimental, values is 18 pcm, and increases to only 58 pcm for the file including the new nuclear data. The k_eff value of benchmarks with harder spectra are predicted slightly better than with ENDF/B-VIII.0. For instance, Jezebel (PMF001v.4), dirty Jezebel (PMF002), and Flattop-Pu (PMF006) k_eff values predicted with the new fission source term are closer to experimental values, while PMI and PMF assemblies with a softer spectrum (011, 018, 019, 021.1, 021.2, 024, 027, 031, 032, 033, 036, 038, and all cases of 044) have worse C/E for the new file than when simulated with ENDF/B-VIII.0. This difference could point to the need for a lowering of the ${\bar{\nu }}_p$, or for better describing the unresolved energy range of the ²³⁹Pu(n,f) cross section, if one would concentrate on only fission source term observables. However, ²³⁹Pu elastic and capture cross sections should also be studied along with nuclear data of isotopes often appearing in PMI assemblies and PMF ones with softer spectra.

The differences in using ENDF/B-VIII.0 and the new fission source term for simulating plutonium LLNL pulsed spheres [32] are modest. These experiments validate ²³⁹Pu fission and neutron scattering nuclear data from approximately 5–15 MeV, but little impact was expected from changes in the (n,f) cross section and ${\bar{\nu }}_p$, as these would lead mostly to a constant offset of the simulated neutron leakage spectra that is lost as these spectra are treated as shape data [81]. The new PFNS also leads to minimal changes. Better prediction of the valley of the pulsed sphere neutron leakage spectra can only be achieved by improving ²³⁹Pu inelastic cross sections and angular distributions, and such changes have been indeed included in recent studies by the INDEN project, and at LLNL and LANL [82–84]. Changes in simulated reaction rates in PMF001.v4 and PMF006 compared to ENDF/B-VIII.0 beyond their Monte Carlo statistics uncertainties are observed for the ²³⁹Pu(n,γ)/²³⁹Pu(n,f) and ²³⁷Np(n,f)/²³⁵U(n,f) cross section reaction rate for PMF001.v4 and the ²³⁹Pu(n,γ)/²³⁹Pu(n,f) ²³⁸U(n,f)/²³⁵U(n,f) and ²³⁷Np(n,f)/²³⁵U(n,f) cross sections. The simulated values are within experimental uncertainties, where available. Overall, the simulated reaction rates in columns 3 and 4 of Table 4 are very similar. The slightly lower (2%–3%) (n,2n) reaction rate is caused by the softer PFNS of the new evaluation in the fast E_inc range.

4 Summary and outlook

Recently, new high-precision experimental fission data and detailed modeling became available that refined our understanding of ²³⁹Pu prompt fission neutron spectra, PFNS, average prompt-fission neutron multiplicity, ${\bar{\nu }}_p$, and (n,f) cross sections:

• The LANL Chi-Nu and CEA teams provided two data sets, that covered for the first time ²³⁹Pu PFNS for broad incident and outgoing energy ranges with high precision. These show that the ²³⁹Pu PFNS should be softer for E_inc < 5 MeV than in ENDF/B-VIII.0, and resolved, for the first time, predicted structures in the PFNS due to multiple chance fission and the pre-equilibrium component. While the data confirmed the incident and outgoing energies where theory predicted these structures, the experimental data led to corrections in the magnitude of these effects.

• The average prompt fission neutron multiplicity, ${\bar{\nu }}_p$, was measured and reported by the CEA team using a different technique than any previous ²³⁹Pu ${\bar{\nu }}_p$ data set. The data confirmed evaluated results obtained from a bulk of past data using the ratio liquid scintillator technique from 1 to 4 MeV, further strengthening our trust in this technique. Marini data were able to resolve for the first time expected second and third-chance fission structures that are now part of evaluated data. CGMF detailed fission modeling also predicts these structures. This fission event generator also links model parameters obtained by fitting to ${\bar{\nu }}_p$ to various fission quantities including yields as function of mass, the average total kinetic energy of fission fragment, and γ and neutron emission observables. It was shown that these predicted observables were mostly within the spread of experimental data, providing for the first time a validation of evaluated ²³⁹Pu ${\bar{\nu }}_p$ with these fission quantities.

• The NIFFTE TPC collaboration measured ²³⁹Pu(n,f)/²³⁵U(n,f) cross sections, with high precision using a new detector type, a time-projection chamber. To date, these data are recommended to be treated as shape data. These data confirmed the shape of previous evaluated data that were mostly driven by fission chamber measurements below 14 MeV. The new data resolved a question triggered by discrepant data above 14 MeV and lowered the evaluated cross section by 2%.

The detailed fission theory and new high precision experiments distinctly changed the evaluated nuclear data. These changes balance each other, without the need for tweaks, such that their combined impact on the simulated effective neutron multiplication factors of ICSBEP critical assemblies is small. Given that the new evaluations are backed by new high precision experimental data and detailed fission modeling, it is likely that compensating errors between the fission source term observables in ENDF/B-VIII.0 are reduced.

Future work could focus on predicting PFNS and ${\bar{\nu }}_p$ within the same framework, and, therefore, bringing in further consistency between fission source term observables. While CGMF would offer this possibility, model defects in the PFNS must be resolved before using it for evaluations. Also, the fission source term is only one component to simulating integral experiments. Scattering and capture cross sections as well as angular distributions for the former should be studied experimentally and theoretically to further reduce compensating effects between nuclear data.

Data availability statement

The evaluated data generated as part of this study can be found in https://www-nds.iaea.org/INDEN/ under Tab “Pu-239“. The code GMAP is available on https://github.com/IAEA-NDS/gmapy. The code CGMF is available on https://github.com/lanl/CGMF. The code ARIADNE is currently under review for release at LANL. It cannot be made available before this review is successfully finalized per LANL rules. The code containing the exciton and Los Alamos model is a code by another LANL employee and cannot be made available by the authors per LANL rules. The MCNP code is distributed to its worldwide user community by the Radiation Safety Information Computational Center (RSICC), which is based at the Oak Ridge National Laboratory in Oak Ridge, Tennessee. Because the MCNP code is export controlled, the distribution through RSICC is governed by US laws and Department of Energy regulations. Information can be found on: https://mcnp.lanl.gov/how\_to\_get\_the\_mcnp\_code.html.

Author contributions

DN undertook the evaluations, uncertainty quantification of input data, and integral-experiment analysis. AL provided the prior and fission-observable validation for the ${\bar{\nu }}_p$ evaluation. KK, PM, LS, MD, JT, and MW were involved in the analysis of new experimental data, and/ or discussions on uncertainties and past experimental data. AL, MW, PT, and MC were involved in critically discussing evaluation input and output. MC prioritized optimally matching the measured PFNS data in the fast region, even though this led to a kink in the average mean energy of the PFNS. MW and MC were involved in critical discussions and guidance on integral-experiment validation. DN wrote the first draft of the manuscript. AL, KK, PM, and LS wrote sections of the manuscript. All authors contributed to manuscript revision, read, and approved the submitted version.

Funding

Work at LANL was carried out under the auspices of the National Nuclear Security Administration (NNSA) of the U.S. Department of Energy (DOE) under contract 89233218CNA000001. Research on compensating errors mentioned in this publication was supported by the U.S. Department of Energy LDRD program at Los Alamos National Laboratory.

Acknowledgments

DN thanks N. Gibson (LANL) for his help in assembling the ²³⁹Pu file for integral-experiment validation. We gratefully acknowledge partial support of the Advanced Simulation and Computing program at LANL and the DOE Nuclear Criticality Safety Program, funded and managed by NNSA for the DOE.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Footnotes

¹The liquid scintillator array was used to measure PFNS above 200 keV, while an extrapolation was used to approximate the PFNS below (which constitutes 0.3% of the PFNS for E_inc = 1–3 MeV and, therefore, keeps the uncertainty due to the extrapolation low).

References

1. Chadwick MB. Nuclear science for the manhattan project and comparison to today’s ENDF data. Nucl Technology (2021) 207:S24–S61. doi:10.1080/00295450.2021.1901002

CrossRef Full Text | Google Scholar

2. Fréhaut J, Mosinski G, Soleilhac M. Recent results in v̄_p measurements between 1.5 and 15 MeV. In: v̄_p The average Number of Emitted Neutrons in Fission, Contributions to the EANDC Topical Conference held on Novembre 29 (1973).

Google Scholar

3. Nurpeisov B, Volodin K, Nesterov VG, Smirenkin G, Turchin Y. Dependence of \overline\nu on neutron energies up to 5 MeV for ²³³U, ²³⁸U, and ²³⁹Pu. At Energy (1975) 39:807–13. doi:10.1007/bf01122383

CrossRef Full Text | Google Scholar

4. Soleilhac M, Fréhaut J, Gauriau J, Mosinski G. Average number of prompt neutrons and relative fission cross-sections of U-235 and Pu-239 in the 0.3 to 1.4 MeV range. Nucl Data Reactors Conf (1970) 2:145–56.

Google Scholar

5. Walsh R, Boldeman J. The energy dependence of ν_p for ²³³U, ²³⁵U and ²³⁹Pu below 5⋅ 0 MeV. J Nucl Energ (1971) 25:321–30. doi:10.1016/0022-3107(71)90064-5

CrossRef Full Text | Google Scholar

6. Condé H, Hansén J, Holmberg M. Prompt ν in neutron-induced fission of ²³⁹Pu and ²⁴¹Pu. J Nucl Energ (1968) 22:53–60. doi:10.1016/0022-3107(68)90064-6

CrossRef Full Text | Google Scholar

7. Gwin R, Spencer R, Ingle R. Measurements of the energy dependence of prompt neutron emission from ²³³U, ²³⁵U, and ²³⁹Pu for e_n = 0.0005 to 10 MeV relative to emission from spontaneous fission of ²⁵²Cf. Nucl Sci Eng (1986) 94:365–79. doi:10.13182/nse86-a18347

CrossRef Full Text | Google Scholar

8. Hopkins J, Diven B. Prompt neutrons from fission. Nucl Phys (1963) 48:433–42. doi:10.1016/0029-5582(63)90182-2

CrossRef Full Text | Google Scholar

9. Neudecker D, Lewis AM, Matthew E. Templates of expected measurement uncertainties. Tech. Rep. LA-UR-19-31156. Los Alamos, MN: Los Alamos National Laboratory (2019).

Google Scholar

10. Carlson A, Pronyaev V, Capote R, Hale G, Chen Z-P, Duran I, et al. Evaluation of the Neutron Data StandardsSpecial issue on nuclear reaction data. Nucl Data Sheets (2018) 148:143–88. doi:10.1016/j.nds.2018.02.002

CrossRef Full Text | Google Scholar

11. Neudecker D, Smith D, Tovesson F, Capote R, White M, Bowden N, et al. Applying a template of expected uncertainties to updating ²³⁹Pu(n, f) cross-section covariances in the neutron data standards database. Nucl Data Sheets (2020) 163:228–48. doi:10.1016/j.nds.2019.12.005

CrossRef Full Text | Google Scholar

12. Neudecker D, Hejnal B, Tovesson F, White MC, Smith DL, Vaughan D, et al. Template for estimating uncertainties of measured neutron-induced fission cross-sections. EPJ Nucl Sci Technol (2018) 4:21. doi:10.1051/epjn/2018026

CrossRef Full Text | Google Scholar

13. Capote R, Chen Y-J, Hambsch F-J, Kornilov N, Lestone J, Litaize O, et al. Prompt fission neutron spectra of ActinidesSpecial issue on nuclear reaction data. Nucl Data Sheets (2016) 131:1–106. doi:10.1016/j.nds.2015.12.002

CrossRef Full Text | Google Scholar

14. Neudecker D, Taddeucci T, Haight R, Lee H, White M, Rising M. The need for precise and well-documented experimental data on prompt fission neutron spectra from neutron-induced fission of ²³⁹Pu. Nucl Data Sheets (2016) 131:289–318. doi:10.1016/j.nds.2015.12.005

CrossRef Full Text | Google Scholar

15. Madland D, Nix J. New calculation of prompt fission neutron spectra and average prompt neutron multiplicities. Nucl Sci Eng (1982) 81:213–71. doi:10.13182/nse82-5

CrossRef Full Text | Google Scholar

16. Kornilov N. The scale method as an approach for prompt fission neutron spectra analysis and EvaluationSpecial issue on nuclear reaction data. Nucl Data Sheets (2019) 155:75–85. doi:10.1016/j.nds.2019.01.004

CrossRef Full Text | Google Scholar

17. Kawano T. CoH₃: The coupled-channels and hauser-feshbach code. Springer Proc Phys (2021) 254:28–34. doi:10.1007/978-3-030-58082-7

CrossRef Full Text | Google Scholar

18. Vladuca G, Tudora A. Improved Los Alamos model applied to the neutron induced fission of 239Pu and 240Pu and to the spontaneous fission of Pu isotopes²³⁹Pu and ²⁴⁰Pu and to the spontaneous fission of Pu isotopes, journal = Annals of Nuclear Energy. Ann Nucl Energ (2001) 28:689–700. doi:10.1016/s0306-4549(00)00083-9

CrossRef Full Text | Google Scholar

19. Kahler A, MacFarlane R, Mosteller R, Kiedrowski B, Frankle S, Chadwick M, et al. ENDF/B-VII.1 neutron cross section data testing with critical assembly benchmarks and reactor experiments. Nucl Data Sheets (2011) 112:2997–3036. doi:10.1016/j.nds.2011.11.003

CrossRef Full Text | Google Scholar

20.ICS. International handbook of evaluated criticality safety benchmark experiments/nuclear energy agency. Tech. Rep. (NEA;7328). Paris: OECD Nuclear Energy Agency (2019).

Google Scholar

21. Chadwick M, Capote R, Trkov A, Herman M, Brown D, Hale G, et al. CIELO collaboration summary results: International evaluations of neutron reactions on uranium, plutonium, iron, oxygen and hydrogen. Nucl Data Sheets (2018) 148:189–213. doi:10.1016/j.nds.2018.02.003

CrossRef Full Text | Google Scholar

22. Kelly KJ, Devlin M, O’Donnell JM, Gomez JA, Neudecker D, Haight RC, et al. Measurement of the ²³⁹Pu(n, f) prompt fission neutron spectrum from 10 keV to 10 MeV induced by neutrons of energy 1–20 MeV. Phys Rev C (2020) 102:034615. doi:10.1103/physrevc.102.034615

CrossRef Full Text | Google Scholar

23. Marini P, Taieb J, Laurent B, Bélier G, Chatillon A, Etasse D, et al. Prompt-fission-neutron spectra in the ²³⁹Pu(n, f ) reaction. Phys Rev C (2020) 101:044614. doi:10.1103/physrevc.101.044614

CrossRef Full Text | Google Scholar

24. Kelly K, Marini P, Taieb J, Devlin M, Neudecker D, Haight R, et al. Comparison of results from recent NNSA and CEA measurements of the ²³⁹Pu(n, f) prompt fission neutron spectrum. Nucl Data Sheets (2021) 173:42–53. doi:10.1016/j.nds.2021.04.003

CrossRef Full Text | Google Scholar

25. Snyder L, Anastasiou M, Bowden N, Bundgaard J, Casperson R, Cebra D, et al. Measurement of the ²³⁹Pu(n, f)/²³⁵U(n, f) cross-section ratio with the NIFFTE fission time projection chamber. Nucl Data Sheets (2021) 178:1–40. doi:10.1016/j.nds.2021.11.001

CrossRef Full Text | Google Scholar

26. Monterial M, Schmitt K, Prokop C, Leal-Cidoncha E, Anastasiou M, Bowden N, et al. Measurement of material isotopics and atom number ratio with α-particle spectroscopy for a NIFFTE fission Time Projection Chamber actinide target. Nucl Instr Methods Phys Res Section A: Acc Spectrometers, Detectors Associated Equipment (2022) 1021:165864. doi:10.1016/j.nima.2021.165864

CrossRef Full Text | Google Scholar

27. Marini P. Energy dependence of prompt fission neutron multiplicity in the ²³⁹Pu(n,f) reaction (2021).

Google Scholar

28. Talou P. Fission fragment decay simulations with the CGMF code (2020).

Google Scholar

29. Verbeke J, Randrup J, Vogt R. Fission reaction event yield algorithm FREYA 2.0.2. Computer Phys Commun (2018) 222:263–6. doi:10.1016/j.cpc.2017.09.006

CrossRef Full Text | Google Scholar

30. Litaize O, Serot O, Berge L. Fission modelling with FIFRELIN. Eur Phys J A (2015) 51:177. doi:10.1140/epja/i2015-15177-9

CrossRef Full Text | Google Scholar

31. Schmidt K-H, Jurado B, Amouroux C, Schmitt C. General description of fission observables: GEF model code. Nucl Data Sheets (2016) 131:107–221. doi:10.1016/j.nds.2015.12.009

CrossRef Full Text | Google Scholar

32. Wong C, Anderson J, Brown P, Hansen L, Kammerdiener J, Logan C, et al. Livermore pulsed sphere program: Program summary through july 1971. LLNL Ucrl-51144 Rev (1972) 1.

Google Scholar

33. Wu CY, Henderson RA, Haight RC, Lee HY, Taddeucci TN, Bucher B, et al. A multiple parallel-plate Avalanche counter for fission-fragment detection. Nucl Instr Methods Phys Res Section A: Acc Spectrometers Detectors Associated Equipment (2015) 794:76–9. doi:10.1016/j.nima.2015.05.010

CrossRef Full Text | Google Scholar

34. Kelly KJ, Kawano T, O’Donnell JM, Gomez JA, Devlin M, Neudecker D, et al. Preequilibrium asymmetries in the ²³⁹Pu(n, f) prompt fission neutron spectrum. Phys Rev Lett (2019) 122:072503. doi:10.1103/physrevlett.122.072503

PubMed Abstract | CrossRef Full Text | Google Scholar

35. Kelly KJ, Gomez JA, Devlin M, O’Donnell JM, Neudecker D, Lovell AE, et al. Measurement of the ²³⁵U(n, f) prompt fission neutron spectrum from 10 keV to 10 MeV induced by neutrons of energy 1–20 MeV. Phys Rev C (2022) 105:044615. doi:10.1103/physrevc.105.044615

CrossRef Full Text | Google Scholar

36. Devlin M, Kelly KJ. Prompt neutron emission from fission: Recent experimental results. Front Phys (2022).

Google Scholar

37. Laurent B, Taieb J, Bélier G, Marini P, Morfouace P. New developments of a fission chamber for very high radioactivity samples. Nucl Instr Methods Phys Res Section A: Acc Spectrometers, Detectors Associated Equipment (2021) 990:164966. doi:10.1016/j.nima.2020.164966

CrossRef Full Text | Google Scholar

38. Savin M, Khokhlov Y, Zamjatnin Y, Paramonova I. The average number of prompt neutrons in fast neutron induced fission of ²³⁵U and ²³⁹Pu. Nucl Data Reactors Conf. (1970) 2:157–65.

Google Scholar

39. Savin M, Khokhlov Y, Savelév A, Paramonova I. Energy dependence of v̄ in the fission of U²³⁵ by fast neutrons. Soviet J Nucl Phys (1973) 16:638–40.

Google Scholar

40. Haight R, Lee H, Taddeucci T, O’Donnell J, Perdue B, Fotiades N, et al. Two detector arrays for fast neutrons at LANSCE. J Instrum (2012) 7:C03028. doi:10.1088/1748-0221/7/03/c03028

CrossRef Full Text | Google Scholar

41. Diven BC, Martin HC, Taschek RF, Terrell J. Multiplicities of fission neutrons. Phys Rev (1956) 101:1012–5. doi:10.1103/physrev.101.1012

CrossRef Full Text | Google Scholar

42. Soleilhac M, Frehaut J, Gauriau J. Energy dependence of ν̄p for neutron-induced fission of ²³⁵U, ²³⁸U and ²³⁹Pu from 1.3 to 15 MeV. J Nucl Energ (1969) 23:257–82. doi:10.1016/0022-3107(69)90060-4

CrossRef Full Text | Google Scholar

43. Mather D, Fieldhouse P, Moat A. Measurement of prompt ν for the neutron-induced fission of Th²³², U²³³, U²³⁴, U²³⁸ and Pu²³⁹. Nucl Phys (1965) 66:149–60. doi:10.1016/0029-5582(65)90139-2

CrossRef Full Text | Google Scholar

44. Bolodin K, Kuznetsov V, Nesterov V, Nurpeisov B, Prokhorova L, Turchin Y, et al. Average number of prompt neutrons in Pu²³⁹ fission. At Energy (1972) 33:1045–50. doi:10.1007/bf01124606

CrossRef Full Text | Google Scholar

45. Neudecker D, White M, Vaughan D, Srinivasan G. Validating nuclear data uncertainties obtained from a statistical analysis of experimental data with the ”Physical Uncertainty Bounds” method. EPJ Nucl Sci Technol (2020) 6:19. doi:10.1051/epjn/2020007

CrossRef Full Text | Google Scholar

46. Heffner M, Asner D, Baker R, Baker J, Barrett S, Brune C, et al. A time projection chamber for high accuracy and precision fission cross-section measurements. Nucl Instr Methods Phys Res Section A: Acc Spectrometers, Detectors Associated Equipment (2014) 759:50–64. doi:10.1016/j.nima.2014.05.057

CrossRef Full Text | Google Scholar

47. Lisowski P, Ullman J, Balestrini S, Carlson A, Wasson O, Hill N. Neutron induced fission cross section ratios for ²³²Th, ^{235, 238}U, ²³⁷Th and ²³⁹Pu from 1 to 400 MeV. Proc Conf Nucl Data Sci Technol Mito (1988) 1988:97–9.

Google Scholar

48. Tovesson F, Hill T. Cross sections for ²³⁹Pu(n, f) and ²⁴¹Pu(n, f) in the range e_n = 0.01 eV to 200 MeV. Nucl Sci Eng (2010) 165:224–31. doi:10.13182/nse09-41

CrossRef Full Text | Google Scholar

49. Shcherbakov O, Donets A, Evdokimov A, Fomichev A, Fukahori T, Hasegawa A, et al. Neutron-induced fission of ²³³U, ²³⁸U, ²³²Th, ²³⁹Pu, ²³⁷Np, ^natPb and ²⁰⁹Bi relative to ²³⁵U in the energy range 1–200 MeV. J Nucl Sci Technol (2002) 39:230–3. doi:10.1080/00223131.2002.10875081

CrossRef Full Text | Google Scholar

50. Staples P, Morley K. Neutron-induced fission cross-section ratios for ²³⁹Pu, ²⁴⁰Pu, ²⁴²Pu, and ²⁴⁴Pu relative to ²³⁵U from 0.5 to 400 MeV. Nucl Sci Eng (1998) 129:149–63. doi:10.13182/nse98-a1969

CrossRef Full Text | Google Scholar

51. Wahl AC. Systematics of fission-product yields. Los Alamos National Laboratory (2002).

Google Scholar

52. Duke DL. Fission fragment mass distributions and total kinetic energy release of 235-uranium and 238-uranium in neutron-induced fission at intermediate and fast neutron energies. Ph.D. thesis. Golden, CO: Colorado School of Mines (2015).

Google Scholar

53. Neudecker D, Talou P, Kawano T, Kahler A, White M, Taddeucci T, et al. Evaluations of energy spectra of neutrons emitted promptly in neutron-induced fission of ²³⁵U and ²³⁹Pu. Nucl Data Sheets (2018) 148:293–311. doi:10.1016/j.nds.2018.02.006

CrossRef Full Text | Google Scholar

54. Chadwick M, Herman M, Obložinský P, Dunn M, Danon Y, Kahler A, et al. ENDF/B-VII.1 nuclear data for science and Technology: Cross sections, covariances, fission product yields and decay DataSpecial issue on ENDF/B-VII.1 library. Nucl Data Sheets (2011) 112:2887–996. doi:10.1016/j.nds.2011.11.002

CrossRef Full Text | Google Scholar

55. Lestone J, Shores E. Uranium and plutonium average prompt-fission neutron energy spectra (PFNS) from the analysis of NTS NUEX data. Nucl Data Sheets (2014) 119:213–6. doi:10.1016/j.nds.2014.08.059

CrossRef Full Text | Google Scholar

56. Gadioli E, Hodgson P. Pre-equilibrium nuclear reactions. Oxford, UK: Clarendon Press (1992).

Google Scholar

57. Lestone J, Strother T. Energy dependence of plutonium and uranium average fragment total kinetic energies. Nucl Data Sheets (2014) 118:208–10. doi:10.1016/j.nds.2014.04.038

CrossRef Full Text | Google Scholar

58. Madland D. Total prompt energy release in the neutron-induced fission of ²³⁵U, ²³⁸U, and ²³⁹Pu. Nucl Phys A (2006) 772:113–37. doi:10.1016/j.nuclphysa.2006.03.013

CrossRef Full Text | Google Scholar

59. Otuka N, Dupont E, Semkova V, Pritychenko B, Blokhin A, Aikawa M, et al. Towards a more complete and accurate experimental nuclear reaction data library (EXFOR): International collaboration between nuclear reaction data centres (NRDC). Nucl Data Sheets (2014) 120:272–6. doi:10.1016/j.nds.2014.07.065

CrossRef Full Text | Google Scholar

60. Neudecker D, Lovell A, Talou P. Producing ENDF/B-quality Evaluations of ²³⁹Pu(n,f) and ²³⁵U(n,f) average prompt neutron Multiplicities using the CGMF model. Tech. Rep. LA-UR-21–29906. Los Alamos, MN: Los Alamos National Laboratory (2021).

Google Scholar

61. Neudecker D. ARIADNE—A program estimating covariances in detail for neutron experiments. EPJ Nucl Sci. Technol. (2018) 4:34. doi:10.1051/epjn/2018012

CrossRef Full Text | Google Scholar

62. Young P, Chadwick M, MacFarlane R, Talou P, Kawano T, Madland D, et al. Evaluation of neutron reactions for ENDF/B-vii: ^232−241U and ²³⁹Pu. Nucl Data Sheets (2007) 108:2589–654. doi:10.1016/j.nds.2007.11.002

CrossRef Full Text | Google Scholar

63. Poenitz W, Aumeier S. The simultaneous evaluation of the standards and other cross-sections of importance for Technology. Tech. Rep. ANL/NDM-139. Chicago, IL: Argonne National Laboratory Report (1997).

Google Scholar

64. Badikov S, Chen Z, Carlson A. International evaluation of neutron cross-section standards. Tech. Rep. STI/PUB/1291. Vienna, Austria: International Atomic Energy Agency (2007).

Google Scholar

65. Neudecker D, Pronyaev V, Snyder L. Including^238U(n,f)/²³⁵U(n,f) and²³⁹Pu(n,f)/²³⁵U(n,f) NIFFTE fissionTPC Cross-sections into the Neutron Data Standards Database. Los Alamos, MN: Los Alamos National Laboratory (2021). Tech. Rep. LA-UR-21–24093.

Google Scholar

66. Neudecker D, Otuka N, Casperson R, Bowden N, Snyder L, Schmitt K, et al. Information files of ²³⁸U(n,f)/²³⁵U(n,f) NIFFTE fissionTPC cross-sections for the neutron data standards project. Tech. Rep. LA-UR-18–23788. Los Alamos, MN: Los Alamos National Laboratory (2018).

Google Scholar

67. Carlson A, Pronyaev V, Smith D, Larson N, Chen Z, Hale G, et al. International evaluation of neutron cross section StandardsSpecial issue on nuclear reaction data. Nucl Data Sheets (2009) 110:3215–324. doi:10.1016/j.nds.2009.11.001

CrossRef Full Text | Google Scholar

68. Herman MW. Covariance data in the fast neutron region. Tech. Rep. NEA/NSC/WPEC/DOC(2010)427. Paris, France: Organization for Economic Co-operation and Development-Nuclear Energy Agency (2011).

Google Scholar

69. Peelle RW. Peelle’s pertinent puzzle. Oak Ridge, TN: Oak Ridge National Laboratory (1987).

Google Scholar

70. Neudecker D, Frühwirth R, Leeb H. Peelle’s pertinent puzzle: A fake due to improper analysis. Nucl Sci Eng (2012) 170:54–60. doi:10.13182/nse11-20

CrossRef Full Text | Google Scholar

71. Chiba S, Smith D. A suggested procedure for resolving an anomaly in least-squares data analysis known as ”peelle’s pertinent puzzle” and the general implications for nuclear data evaluation. Chicago, IL: Argonne National Laboratory}, (1991). doi:10.2172/10121367

CrossRef Full Text

72. Grosskopf M, Vander Wiel S. On using fully-correlated relative covariance for catpuring systematic uncertainty (2022).

Google Scholar

73. Chatillon A, Bélier G, Granier T, Laurent B, Morillon B, Taieb J, et al. Measurement of prompt neutron spectra from the ²³⁹Pu(n, f) fission reaction for incident neutron energies from 1 to 200 MeV. Phys Rev C (2014) 89:014611. doi:10.1103/physrevc.89.014611

CrossRef Full Text | Google Scholar

74. Trkov A, Capote R, Pronyaev V. (2015 current issues in nuclear data evaluation methodology: ²³⁵U prompt fission neutron spectra and multiplicity for thermal neutrons. Nucl Data Sheets (2015) 123:8–15. doi:10.1016/j.nds.2014.12.003

CrossRef Full Text | Google Scholar

75. Neudecker D, Kelly KJ. Including chi-nu ²³⁵U PFNS experimental Data into an ENDF/B-VIII. 1 release candidate evaluation. Tech. Rep. LA-UR-22–22220. Los Alamos, MN: Los Alamos National Laboratory (2022).

Google Scholar

76. Sugimoto M, Smith AB, Guenther PT. Ratio of the prompt fission neutron spectrum of 239pu to that of 235u. Nucl Sci Eng (1987) 97:235–8. doi:10.13182/nse87-a23505

CrossRef Full Text | Google Scholar

77. Vaughan DE, Preston DL. Physical uncertainty bounds (PUB). Los Alamos, MN: Los Alamos National Laboratory (2014).

Google Scholar

78. Neudecker D, White MC. Report on validating ENDF/B-VIII.0 ²³⁹Pu average prompt fission neutron multiplicity. Los Alamos, MN: Los Alamos National Laboratory (2019).

Google Scholar

79. Neudecker D, Cabellos O, Clark A, Grosskopf M, Haeck W, Herman M, et al. Informing nuclear physics via machine learning methods with differential and integral experiments. Phys Rev C (2021) 104:034611. doi:10.1103/PhysRevC.104.034611

CrossRef Full Text | Google Scholar

80. Werner C, Armstrong J, Brown F, Bull J, Casswell L, Cox L, et al. MCNP users manual - code version 6.2. Tech. Rep. LA-UR-17-29981. Los Alamos, MN: Los Alamos National Laboratory (2017).

Google Scholar

81. Neudecker D, Cabellos O, Clark A, Haeck W, Capote R, Trkov A, et al. Which nuclear data can be validated with LLNL pulsed-sphere experiments? Ann Nucl Energy (2021) 159:108345. doi:10.1016/j.anucene.2021.108345

CrossRef Full Text | Google Scholar

82. Mumpower M, Neudecker D, Kawano T, Herman M, Kleedtke N, Lovell AE, et al. The Los Alamos evaluation of ²³⁹Pu neutron-induced reactions in the fast energy range. Tech. Rep. LA-UR-22-24121. Los Alamos, MN: Los Alamos National Laboratory (2022).

Google Scholar

83. Aguilar GP, Descalle M, Kravvaris K, Ormand W, Beck B, Mattoon C, et al. LLNL Evaluation of n +239Pu. Tech. Rep. LLNL-MI-834591. Lawrence Livermore National Laboratory (2022).

Google Scholar

84. Capote R, Trkov A, Pigni M, Neudecker D, Herman M, Kelly K, et al. INDEN evaluation of neutron induced reactions on Pu-239. EPJ Web of conferences (2022).

Google Scholar

85. Brown DA, Chadwick MB, Capote R, Kahler AC, Trkov A, Herman MW, et al. ENDF/B-VIII.0: The 8th major release of the nuclear reaction data library with cielo-project cross sections, new standards and thermal scattering data. Nucl Data Sheets (2018) 148:1–142. doi:10.1016/j.nds.2018.02.001

CrossRef Full Text | Google Scholar