Ying Yang- College of Physics and Electronic Engineering, Chongqing Normal University, Chongqing, China
Recently, there has been significant interest in exploring the chiral quasiparticles in phonons, which describe the atomic lattice vibrations in solids. In this work, using first-principle calculation, we select a realistic material Na2Zn2O3 as an example to demonstrate that it is an ideal candidate with charge-two Dirac point phonons and charge-two Weyl point phonons at high-symmetry points A and Γ, respectively. The phononic charge-two nodal points in Na2Zn2O3 are visible and almost ideal. That is, there are no other phonon bands nearby. Moreover, nontrivial phononic surface arcs span the whole surface Brillouin zone. Such clean and long nontrivial arc-shaped phononic surface states benefit the experimental detection. The current work is hoped to guide the investigations of chiral nodal points in phononic systems.
Introduction
It is well known that the chiral quasiparticles could exist in spinless systems, such as the phononic system and classical elastic waves in macroscopic artificial phononic crystals. Recently, there has been great interest in exploring topological quasiparticles in phonons [1], which describe the atomic lattice vibrations in solids. So far, a number of materials hosting Weyl point phonons [2–10], Dirac point phonons [11, 12], triple degenerate nodal point phonons [13, 14], sixfold degenerate nodal point phonons [15, 16], nodal line phonons [17–30] and nodal surfaces phonons [31–33] have been discovered. Compared with chiral fermions in electronic systems, chiral phonons exist without spin-orbital coupling.
Let us come to review the recent advances in chiral nodal point phonons as follows: In 2018, Zhang et al. [2] identified a class of crystalline materials of MSi (M = Fe, Co, Mn, Re, Ru) exhibiting double Weyl phonons, and they named the topological points as ‘spin-1 Weyl point’ at the Brillouin zone (BZ) center and “charge-2 Dirac point” at the zone corner. Motivated by Zhang et al.’s recent theoretical work [2], Huang et al. [4] measured the phonon dispersion in parity-breaking FeSi using inelastic x-ray scattering and confirmed the double Weyl phonons in experiments. Moreover, based on first-principle calculation and symmetry analysis, Liu et al. [5] defined a new type of Weyl phonons with Chern numbers of ±4. They [5] also proposed that BiIrSe and Li3CuS2 are candidate materials with charge-four Weyl phonons. In 2020, Wang et al. [9] proposed a symmetry-protected topological triangular Weyl complex composed of one double Weyl point and two single Weyl points. They [9] also stated that the unique triangular Weyl complex could be observed in the phonon dispersion of α−SiO2. In 2022, Ding et al. [34] predicted that BaZnO2 is an ideal material candidate with type-III charge-two Weyl point phonons. BaZnO2 can support double-helicoid phonon surface states covering the entire Brillouin zone (001) surface. Besides trigonal BaZnO2, they [34] stated that some other candidate materials, including tetragonal MgTiO4, trigonal Li2GeF6, hexagonal CaSO4, and cubic Li10B14Cl2O25, can host the type-III charge-two Weyl point phonons.
In this work, we propose a realistic material Na2Zn2O3 [35] is an ideal system with chiral phonons, i.e., charge-two Dirac point phonons and charge-two Weyl point phonons at A and Γ high-symmetry points, respectively. More interestingly, the nontrivial phonon surface arcs are very long, clean, and span over the whole surface BZ. Na2Zn2O3 phonons should be an excellent platform to investigate the coexistence of charge-two Dirac and Weyl points in spinless systems. Also, our results can be extended to other bosonic systems.
Approach
We perform the first-principle calculations based on the density functional theory (DFT) [36]. The generalized gradient approximation (GGA) [37] with Perdew–Burke–Ernzerhof (PBE) [38] realization was adopted for the exchanged correlation potential. The phonon spectra of Na2Zn2O3 is calculated by using the 2 × 2×1 supercell as implemented in Phonopy code. The pre-process and post-process were performed in the PHONOPY package using density functional perturbation theory (DFPT) [39]. The cutoff energy for the plane wave was 600 eV, and the Brillouin zone is sampled using converged 5 × 5×3 Γ-centered k-mesh grids. To study the topological properties of nontrivial band crossings in the phonon spectrum, we calculate its corresponding surface states and constant frequency slices using the WANNIERTOOLS package [40].
Results and discussion
Figure 1A shows the crystal structure of tetragonal Na2Zn2O3 with the P43212 space group. Na1+ is bonded in a 4-coordinate geometry to four O2- atoms. Zn2+ is bonded to four O2- atoms to form a mixture of corner and edge-sharing ZnO4 tetrahedra. There are two inequivalent O2- sites. In the first O2- site, O2- is bonded in a 4-coordinate geometry to two equivalent Na1+ and two equivalent Zn2+ atoms. In the second O2- site, O2- is bonded to three equivalent Na1+ and three equivalent Zn2+ atoms to form distorted edge-sharing ONa3Zn3 octahedra. The calculated lattice constants for tetragonal Na2Zn2O3 are a = b = 6.262 Å, c = 9.507 Å, closing to the experimental data a = b = 6.181 Å, c = 9.447 Å. The Na atoms locate at 8b Wyckoff position, O atoms locate at 8b and 4a Wyckoff positions, and the Zn locates at 8b Wyckoff position.
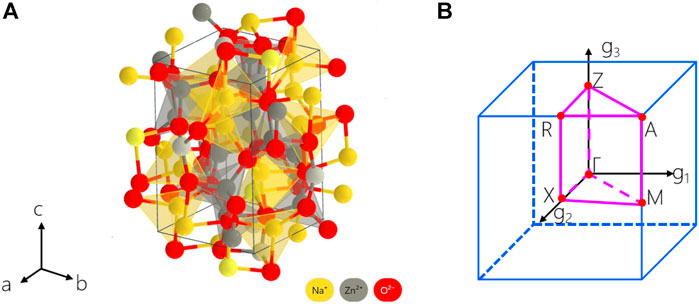
FIGURE 1. (A) Crystal structure of tetragonal Na2Zn2O3 with P43212 space group. (B) Three-dimensional BZ and selected symmetry paths.
Based the 3D BZ and the selected high-symmetry paths in Figure 1B, the phonon dispersion of Na2Zn2O3 along Γ-X-M-Γ-Z-R-A-Z-X-R-M-A high-symmetry paths are shown in Figure 2. From Figure 2, one finds that there is no imaginary frequency, demonstrating the dynamical stability of material Na2Zn2O3. Moreover, one finds that all the phonon bands along A-M-R-X-M and Z-R-A-Z paths are twofold degeneracy, and two twofold degenerate bands cross at A high-symmetry point, forming a fourfold degenerate Dirac point. Moreover, one finds that multiple Dirac points appear at high-symmetry point A with different frequencies, suggesting these Dirac points are symmetry-enforced and must appear at A high point. It is worth noting that the three-dimensional charge-two Dirac points may be hidden in rambling branches; thus, their topological features are invisible. We only focus on the Dirac point at about 16 THz (highlighted by the red circle). The three-dimensional plot of the phonon bands around the Dirac point are shown in Figure 3B. From Figure 3B, one finds that the Dirac point at A point has fourfold degeneracy. It should be noted that the Dirac point at A point is a charge-two Dirac point, which is a zero-dimensional fourfold band degeneracy with a topological charge |C| = 2. From Figure 3B, the charge-two Dirac point at A features a linear dispersion along any momentum-space direction. Dirac point can be considered as a combination of two charge-one Weyl points with opposite topological charge. Hence, the charge-two Dirac point contains two charge-one Weyl points with the same topological charge.
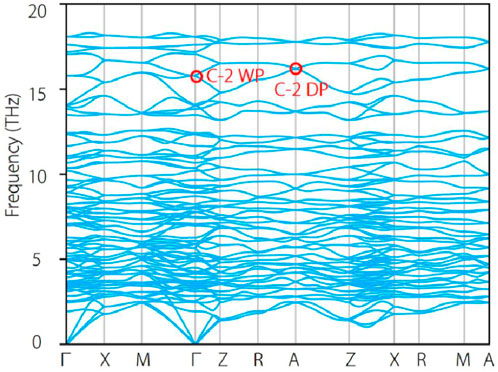
FIGURE 2. Phonon dispersion of tetragonal Na2Zn2O3 with P43212 along Γ-X-M-Γ-Z-R-A-Z-X-R-M-A high-symmetry paths. The charge-two Weyl point (C-2 WP) and charge-two Dirac point (C-2 DP) at high-symmetry points Γ and A, are highlighted by red circles.
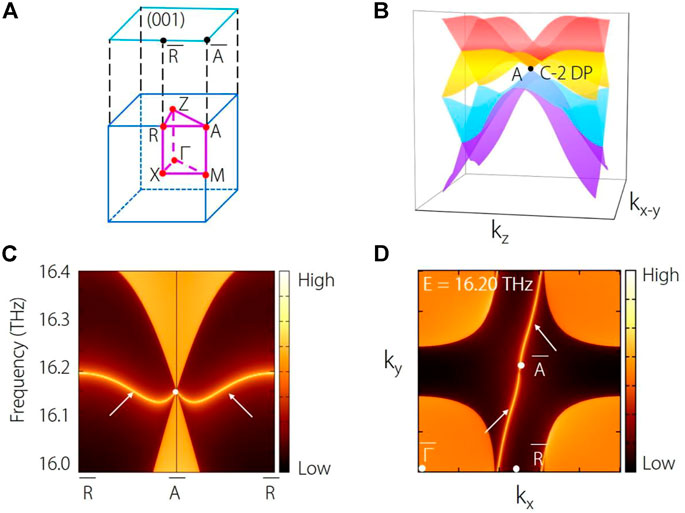
FIGURE 3. The bulk BZ and the corresponding (001) surface BZ. (B) Three-dimensional plot of the phonon bands around the charge-two Dirac point (C-2 DP) at (A). (C) Projected spectrum on the (001) surface, and (D) the corresponding constant frequency slice at 16.20 THz.
In Figure 3C, we show the projected spectrum on the (001) surface for Na2Zn2O3. Obviously, clean phononic surface states can be found from the projection of the charge-two Dirac point. Moreover, the (001) surface states further display linear dispersions of the charge-two Dirac point, showing consistency with the three-dimensional plot of the phonon band in Figure 3B. Figure 3D shows the corresponding constant frequency slice at 16.20 THz. Indeed, one could observe that two arcs emanate from the projections of each Dirac point, indicating the charge of the Dirac point should equal 2. More interestingly, the surface arcs are nontrivial due to the chirality. The surface arcs (marked by white arrows) are very long and span over the whole surface BZ.
Next, we discuss the charge-two Weyl point at Γ high-symmetry point around 15.8 THz. From Figure 2, one finds that there exists a twofold degenerate Weyl point at Γ point. Such Weyl point is a charge-two Weyl point, a zero-dimensional twofold band degeneracy with a topological charge |C| = 2. As shown in Figure 4B, one finds that the charge-two Weyl point features a linear dispersion along kz direction and a quadratic energy splitting in the plane (kx-ky plane) normal to the kz direction. Here, the phonon spectrum is plotted in Figure 4C, in which one can observe the nontrivial surface states arising from the projections of the charge-two Weyl point at point. The isofrequency (001) surfaces at 15.79 THz are exhibited in Figure 4D. We can see that two branches of surface arcs start at
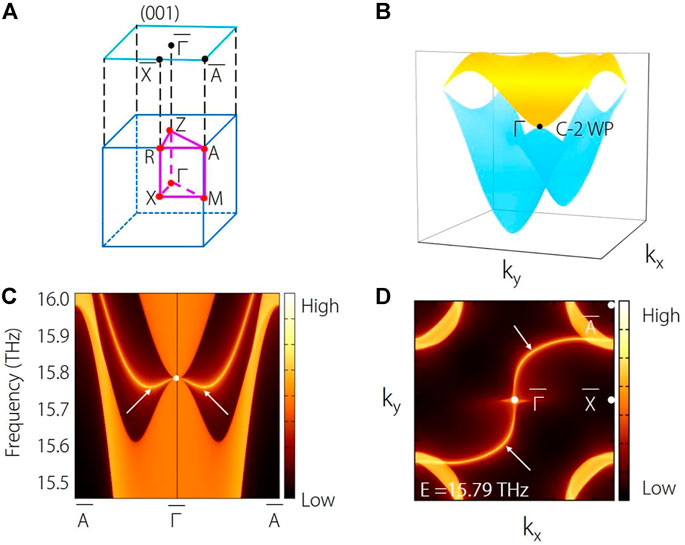
FIGURE 4. (A) The bulk BZ and the corresponding (001) surface BZ. (B) Three-dimensional plot of the phonon bands around the charge-two Weyl point (C-2 WP) at Γ. (C) Projected spectrum on the (001) surface, and (D) the corresponding constant frequency slice at 15.79 THz.
Conclusion
In summary, we propose a realistic material, tetragonal Na2Zn2O3 with P43212 space group, which hosts symmetry-enforced charge-two Dirac point phonons and charge-two Weyl point phonons with unique long and nontrivial surface arcs. Our work uncovers the appearance of the chiral Dirac and Weyl points in the spinless system. In addition, we provide an ideal candidate who possesses chiral Dirac and Weyl points at high-symmetry points, leading to the formation of long and nontrivial surface arcs. Our work provides a good idea for detecting chiral phonons in realistic materials.
Data availability statement
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
Author contributions
YY - investigations and writing.
Funding
YY is grateful for support from the key project of education planning supported by Chongqing municipal education commission (No. 2021-GX-013), the National Natural Science Foundation of China (No. 12175027), and the Basic Research and Frontier Exploration Project of Chongqing Municipality (cstc2018jcyjAX0820).
Conflict of interest
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
1. Liu Y, Chen X, Xu Y. Topological phononics: From fundamental models to real materials. Adv Funct Mater (2020) 30(8):1904784. doi:10.1002/adfm.201904784
2. Zhang T, Song Z, Alexandradinata A, Weng H, Fang C, Lu L, et al. Double-Weyl phonons in transition-metal monosilicides. Phys Rev Lett (2018) 120(1):016401. doi:10.1103/physrevlett.120.016401
3. Li J, Xie Q, Ullah S, Li R, Ma H, Li D, et al. Coexistent three-component and two-component Weyl phonons in TiS, ZrSe, and HfTe. Phys Rev B (2018) 97(5):054305. doi:10.1103/physrevb.97.054305
4. Miao H, Zhang TT, Wang L, Meyers D, Said AH, Wang YL, et al. Observation of double Weyl phonons in parity-breaking FeSi. Phys Rev Lett (2018) 121(3):035302. doi:10.1103/physrevlett.121.035302
5. Liu QB, Wang Z, Fu HH. Charge-four Weyl phonons. Phys Rev B (2021) 103(16):L161303. doi:10.1103/physrevb.103.l161303
6. Xia BW, Wang R, Chen ZJ, Zhao YJ, Xu H. Symmetry-protected ideal type-II Weyl phonons in CdTe. Phys Rev Lett (2019) 123(6):065501. doi:10.1103/physrevlett.123.065501
7. Liu QB, Qian Y, Fu HH, Wang Z. Symmetry-enforced Weyl phonons. Npj Comput Mater (2020) 6(1):95–6. doi:10.1038/s41524-020-00358-8
8. Liu J, Hou W, Wang E, Zhang S, Sun JT, Meng S. Ideal type-II Weyl phonons in wurtzite CuI. Phys Rev B (2019) 100(8):081204. doi:10.1103/physrevb.100.081204
9. Wang R, Xia BW, Chen ZJ, Zheng BB, Zhao YJ, Xu H. Symmetry-protected topological triangular Weyl complex. Phys Rev Lett (2020) 124(10):105303. doi:10.1103/physrevlett.124.105303
10. Jin YJ, Chen ZJ, Xiao XL, Xu H. Tunable double Weyl phonons driven by chiral point group symmetry. Phys Rev B (2021) 103(10):104101. doi:10.1103/physrevb.103.104101
11. Chen ZJ, Wang R, Xia BW, Zheng BB, Jin YJ, Zhao YJ, et al. Three-dimensional Dirac phonons with inversion symmetry. Phys Rev Lett (2021) 126(18):185301. doi:10.1103/physrevlett.126.185301
12. Wang J, Yuan H, Liu Y, Zhou F, Wang X, Zhang G. Hourglass Weyl and Dirac nodal line phonons, and drumhead-like and torus phonon surface states in orthorhombic-type KCuS. Phys Chem Chem Phys (2022) 24(5):2752–7. doi:10.1039/d1cp05217a
13. Singh S, Wu Q, Yue C, Romero AH, Soluyanov AA. Topological phonons and thermoelectricity in triple-point metals. Phys Rev Mater (2018) 2(11):114204. doi:10.1103/physrevmaterials.2.114204
14. Sreeparvathy PC, Mondal C, Barman CK, Alam A. Coexistence of multifold and multidimensional topological phonons in KMgBO3. Phys Rev B (2022) 106(8):085102. doi:10.1103/physrevb.106.085102
15. Xie C, Liu Y, Zhang Z, Zhou F, Yang T, Kuang M, et al. Sixfold degenerate nodal-point phonons: Symmetry analysis and materials realization. Phys Rev B (2021) 104(4):045148. doi:10.1103/physrevb.104.045148
16. Zhong M, Liu Y, Zhou F, Kuang M, Yang T, Wang X, et al. Coexistence of phononic sixfold, fourfold, and threefold excitations in the ternary antimonide Zr3Ni3Sb4. Phys Rev B (2021) 104(8):085118. doi:10.1103/physrevb.104.085118
17. Liu G, Jin Y, Chen Z, Xu H. Symmetry-enforced straight nodal-line phonons. Phys Rev B (2021) 104(2):024304. doi:10.1103/physrevb.104.024304
18. Zhou F, Zhang Z, Chen H, Kuang M, Yang T, Wang X. Hybrid-type nodal ring phonons and coexistence of higher-order quadratic nodal line phonons in an AgZr alloy. Phys Rev B (2021) 104(17):174108. doi:10.1103/physrevb.104.174108
19. Ding G, Sun T, Surucu G, Surucu O, Gencer A, Wang X. Complex nodal structure phonons formed by open and closed nodal lines in CoAsS and Na2CuP solids. Phys Chem Chem Phys (2022) 24(28):17210–6. doi:10.1039/d2cp01992b
20. Wang J, Yuan H, Yu ZM, Zhang Z, Wang X. Coexistence of symmetry-enforced phononic Dirac nodal-line net and three-nodal surfaces phonons in solid-state materials: Theory and materials realization. Phys Rev Mater (2021) 5(12):124203. doi:10.1103/physrevmaterials.5.124203
21. Zhou F, Chen H, Yu ZM, Zhang Z, Wang X. Realistic cesium fluogermanate: An ideal platform to realize the topologically nodal-box and nodal-chain phonons. Phys Rev B (2021) 104(21):214310. doi:10.1103/physrevb.104.214310
22. Ding G, Sun T, Wang X. Ideal nodal-net, nodal-chain, and nodal-cage phonons in some realistic materials. Phys Chem Chem Phys (2022) 24(18):11175–82. doi:10.1039/d2cp00731b
23. Wang X, Zhou F, Yang T, Kuang M, Yu ZM, Zhang G. Symmetry-enforced ideal lanternlike phonons in the ternary nitride Li6WN4. Phys Rev B (2021) 104(4):L041104. doi:10.1103/physrevb.104.l041104
24. Zheng B, Zhan F, Wu X, Wang R, Fan J. Hourglass phonons jointly protected by symmorphic and nonsymmorphic symmetries. Phys Rev B (2021) 104(6):L060301. doi:10.1103/physrevb.104.l060301
25. Liu QB, Fu HH, Wu R. Topological phononic nodal hexahedron net and nodal links in the high-pressure phase of the semiconductor CuCl. Phys Rev B (2021) 104(4):045409. doi:10.1103/physrevb.104.045409
26. Zhang TT, Miao H, Wang Q, Lin JQ, Cao Y, Fabbris G, et al. Phononic helical nodal lines with PT protection in MoB2. Phys Rev Lett (2019) 123(24):245302. doi:10.1103/physrevlett.123.245302
27. Wang M, Wang Y, Yang Z, Fan J, Zheng B, Wang R, et al. Symmetry-enforced nodal cage phonons in Th2BC2. Phys Rev B (2022) 105(17):174309. doi:10.1103/physrevb.105.174309
28. Wang J, Yuan H, Kuang M, Yang T, Yu ZM, Zhang Z, et al. Coexistence of zero-one-and two-dimensional degeneracy in tetragonal SnO2 phonons. Phys Rev B (2021) 104(4):L041107. doi:10.1103/physrevb.104.l041107
29. Liu Y, Zou N, Zhao S, Chen X, Xu Y, Duan W. Ubiquitous topological states of phonons in solids: Silicon as a model material. Nano Lett (2022) 22(5):2120–6. doi:10.1021/acs.nanolett.1c04299
30. Yang T, Gu Q, Wang P, Wu Z, Zhang Z. Phononic quadratic nodal lines of different types in Li2NaN. Appl Phys Lett (2022) 121(5):053102. doi:10.1063/5.0102217
31. Liu QB, Wang ZQ, Fu HH. Ideal topological nodal-surface phonons in RbTeAu-family materials. Phys Rev B (2021) 104(4):L041405. doi:10.1103/physrevb.104.l041405
32. Xie C, Yuan H, Liu Y, Wang X. Two-nodal surface phonons in solid-state materials. Phys Rev B (2022) 105(5):054307. doi:10.1103/physrevb.105.054307
33. Xie C, Yuan H, Liu Y, Wang X, Zhang G. Three-nodal surface phonons in solid-state materials: Theory and material realization. Phys Rev B (2021) 104(13):134303. doi:10.1103/physrevb.104.134303
34. Ding G, Zhou F, Zhang Z, Yu ZM, Wang X. Charge-two Weyl phonons with type-III dispersion. Phys Rev B (2022) 105(13):134303. doi:10.1103/physrevb.105.134303
35. Trinschek D, Jansen M. Eine neue modifikation von Na2Zn2O3/A new modification of Na2Zn2O3. Z für Naturforschung B (1996) 51(7):917–21. doi:10.1515/znb-1996-0703
36. Parr RG. Density functional theory. Annu Rev Phys Chem (1983) 34(1):631–56. doi:10.1146/annurev.pc.34.100183.003215
37. Perdew JP, Burke K, Ernzerhof M. Generalized gradient approximation made simple. Phys Rev Lett (1996) 77(18):3865–8. doi:10.1103/physrevlett.77.3865
38. Perdew JP, Burke K, Ernzerhof M. Perdew, burke, and ernzerhof reply. Phys Rev Lett (1998) 80(4):891. doi:10.1103/physrevlett.80.891
39. Baroni S, De Gironcoli S, Dal Corso A, Giannozzi P. Phonons and related crystal properties from density-functional perturbation theory. Rev Mod Phys (2001) 73(2):515–62. doi:10.1103/revmodphys.73.515
Keywords: topological phonons, DFPT calculation, Dirac point, weyl point, phonons
Citation: Yang Y (2022) Ideal phononic charge-two nodal point and long nontrivial surface arcs in Na2Zn2O3. Front. Phys. 10:1055981. doi: 10.3389/fphy.2022.1055981
Received: 28 September 2022; Accepted: 05 October 2022;
Published: 17 October 2022.
Edited by:
San-Dong Guo, Xi’an University of Posts and Telecommunications, ChinaCopyright © 2022 Yang. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Ying Yang, cGh5c2ljc3l5QDEyNi5jb20=