Topological structure effects of Laguerre-Gaussian laser on self-collimation acceleration mechanism

Energetic plasma beams can be generated through the interaction between a short-pulse high-intensity laser and solid target. However, obtaining collimated plasma beams with low divergence remains challenging. In this study, we devised a self-collimation scheme driven by a topologically structured Laguerre–Gaussian (LG) laser that irradiates a thin target in three-dimensional particle-in-cell simulations. It was observed that a high-density and narrow plasma beam could be formed by the intrinsic hollow intensity distribution of the LG laser. A magnetic tunnel was generated around the beam and collimated the plasma beam within a radius of hundreds of nanometers. This collimation can be enhanced by increasing the topological charge from l = 1 to l = 3 and then destroyed for a larger l. The collimation method is promising in applications requiring well-collimated energetic plasma beams, such as indirect drive inertial con-finement fusion, laboratory astrophysics, and radiation therapy.

Introduction

With the advent of the multi-petawatt laser era, the laser pulse intensity can exceed 10²² W/cm² [1, 2]. When such an intense laser irradiates a solid plasma target, a large number of energetic particles are produced. In the laser-plasma interaction, the laser firstly accelerates the electrons, then the resulting space-charge field accelerates the ions. They move together as a neutral plasma beam that can propagate over a longer distance than non-neutral particle beams [3]. These plasma beams can be used for fast ignition (FI) in inertial confinement fusion [4], tumor therapy, radiographic applications, and understanding astrophysical jet phenomena. However, all these applications require the collimation or low beam divergence of the particle beam. In the FI in inertial confinement fusion, this can significantly enhance the coupling efficiency of the beam to the compressed fusion fuel and avoid a rapid decrease in the beam intensity away from the target [5–7].

Many experiments have demonstrated that the particles (electrons and/or ions) beam has low collimation when using ultrashort high-intensity lasers [8–11]. To solve this issue, a series of simulations and experiments have been proposed to obtain an energetic particle beam with low divergence. For example, Alraddadi et al. used foam-filled resistive guide targets to achieve fast electron collimation [12]. Robinson et al. [13] used an azimuthal magnetic field pre-generated by a laser prepulse to confine the electron beam, where radially inward Lorentz forces played significant roles. Kar et al. [14] used a target with a radius of curvature to acquire a focusing ion-plasma beam. Tonican et al. [15] presented a technique for focusing ion-plasma beams using a radial electric field from a hollow microcylinder. However, these methods require rigorous target engineering or multistage acceleration schemes, which may significantly affect the stability and efficiency of most high-intensity laser-solid interactions. Therefore, a robust collimation scheme is important for various applications. In recent years, relativistic Laguerre–Gaussian (LG) lasers, which have a special structure and hollow light intensity distribution [16], have been generated experimentally [17]. A radially inward ponderomotive force can be generated from the hollow-distributed laser intensity and used to collimate the electron beam.

In this paper, we present a collimation mechanism for generating an extremely converging plasma beam. It is driven by an ultra-intense and ultrashort vortex laser with the topological charge l impinging on a solid plasma target. First, a hollow-structured plasma is formed owing to the hollow intensity distribution of the LG laser. The plasma was then concentrated toward the central axis by the radial ponderomotive force and accelerated forward by the longitudinal force. As the plasma propagates, a plasma beam with high density and current arises on the central axis. Meanwhile, the current in the plasma beam generates a strong magnetic tunnel that confines the plasma beam. Such collimation methods driven by vortex lasers can potentially be applied in a wide range of fields, such as indirect drive inertial confinement fusion, ultrafast diagnostics, and radiation therapy.

Numerical simulation and analysis

Simulation parameter

We performed 3D PIC simulations (EPOCH code [18]) to study the interaction between an ultra-intense ultrashort circularly polarized LG laser pulse and a solid plasma target. The wavelength of the laser pulse was λ₀ = 0.8 μm. The laser period is T_L = λ₀/c, where c is the speed of light in vacuum. The CP LG laser can be expressed as follows:

$E_{\mathit{\perp }}=a_0{C}_l(\sqrt{2}r/w_0{)}^l\exp (-\sqrt{2}r/2w_0){\sin }^2(\pi (x-ct)/2L)e^{i\left(kx-\omega t+l\phi \right)}\widehat{a}(1)$

where a₀ = eE₀/m_ecω, e is the electron charge, E₀ is the laser amplitude, m_e is the electron mass, ω is the laser frequency, $C_l$ = l^–l/2exp(l/2) is the normalized factor of the LG laser for each order model, $r=\sqrt{y^2+z^2}$, w₀ is the beam waist, l is the orbital angular momentum parameter, L is the pulse length in the x direction, k is the wave number, $\widehat{a}=\widehat{y}+\mathrm{i}\widehat{\mathrm{z}}$σ_z is the direction vector, and σ_z = -1 is the polarization parameter. For the simulations, we set a₀ = 30, w₀ = 4 μm, L = 9.9 μm, and l = 1, 2, and 3 for different topological structures of the LG laser.

The size of the simulation box was 80 μm (x) × 16 μm (y) × 16 μm (z), the number of cells was 800 × 320 × 320, and each cell was filled with two macro-electrons and two macro-protons. The mesh size is Δx = 1/10 μm and Δy = Δz = 1/20 μm. The front surface of the target was located at x = 30 μm and the foil thickness was 1 μm. The foil density was n = 30n_c, where $n_{\mathrm{c}}={\omega }_{\mathrm{L}}^2{m}_{\mathrm{e}}/4\pi e^2$ = 1.1 × 10²¹ cm⁻³ is the critical density. The foil was assumed to be fully ionized to protons and electrons before the laser peak arrived at the target. Notably, a micrometer plasma target can be formed by prepulse heating in the experiments [17].

Simulation analysis

The proposed self-collimation mechanism can be divided into three main stages: hole-boring, shock acceleration, and transporting stages. In the hole-boring stage [19], the laser arrives at the front surface of the target at t = 30T_L and begins to interact with the plasma target. The LG laser first pushed the electrons to the back surface of the target, leaving the heavy protons behind. Subsequently, a charged separation field between the electrons and ions is generated, accelerating the protons in the following progress [20–23]. Figure 1 shows the hollow-structured intensity distribution of an LG laser with l = 1, 2, and 3. This field profile generates a radial ponderomotive force that first pushes the electrons to the center axis. The resulting charge separation field between the electrons and protons then drags the protons together.

FIGURE 1

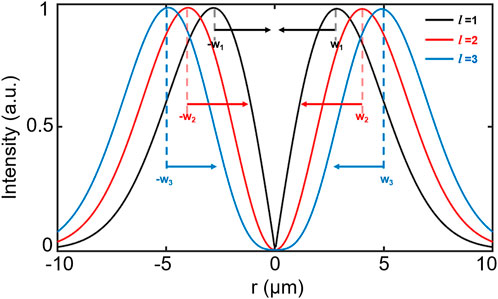
FIGURE 1. Profiles of LG laser intensity with topological l = 1, 2, and 3. The radius w₁, w₂, and w₃ correspond to the maximum light field for the topological charge of l = 1, 2, and 3.

Notably, we used the normalized factor of the LG laser C_pl (C_l=1 = 1.65, C_l=2 = 1.36, C_l=3 = 0.86 for l = 1, 2, 3) in Eq. 1 to maintain the laser intensity for research on the effects of the topological structure factor l on the plasma acceleration and collimation process. These effects are compared in Figure 1, where the maximum laser fields for l = 1, 2, 3 are at w₁ = 2.83 μm, w₂ = 4 μm, w₃ = 4.9 μm, respectively. It is assumed that the radial ponderomotive force of the LG laser plays an important role, which can be expressed as

$F_{\mathrm{r}}=\frac{-e^2}{4m_{\mathrm{e}}{w}_0^2}\partial \frac{{\left|E\right|}^2}{\partial r}(2)$

where -$\partial$|E|²/$\partial r$ = 2|E|²(2r²/lw₀²-1)/r. According to Eq. 2, the electrons can be accelerated to the central axis in the focusing region ($\left|r\right|<w_0\sqrt{\left|l\right|/2}$), which is consistent with the laser intensity distribution shown in Figure 1. In contrast, the electrons in the defocus region ($\left|r\right|>w_0\sqrt{\left|l\right|/2}$) were pushed to both sides. It was observed that a hollow-structured compressed plasma layer was formed during the hole-boring stage, where the electrons (Figures 2A–C) are first pushed toward the center axis and then drag protons (Figures 2D–F) inward by the charge separation field between the electrons and protons. As shown in Figure 2, more electrons and protons are trapped in the central region when the topological charge l increases because the size of the focusing region w₀ $w_0\sqrt{\left|l\right|/2}$ is determined by l. Notably, the laser is mostly completely reflected at t = 50T_L by the compressed plasma layer formed by the laser pressure in our case. Subsequently, the plasma layer continues to travel forward and inward in the focusing region ($\left|r\right|<w_0\sqrt{\left|l\right|/2}$). For the protons, the shock acceleration mechanism plays a major role, which can be verified by calculating the Mach number Ma = v/C_s during interactions, where v is the shock velocity, $C_s=\sqrt{Z{K}_b{T}_e/m_i}$ is the ion sound speed, Z is the charge number, $K_b{T}_e$ is the electron temperature, and m_i is the ion mass. In the case of l = 1, a shock with velocity v ≈ 0.1c was formed at x = 30.5 μm at the beginning of the interaction (t ≈ 50T_L). Figure 3A shows the features of the protons in the phase space, where the protons in front of the target are reflected by the shock. Here, the electron temperature ∼1.1 MeV can be calculated from the electron energy spectrum shown in Figure 3B. Therefore, Mach number Ma = 3 can be obtained, which satisfies the condition of electrostatic shocks (Ma > 1.5) [24], so that shock acceleration occurs.

FIGURE 2

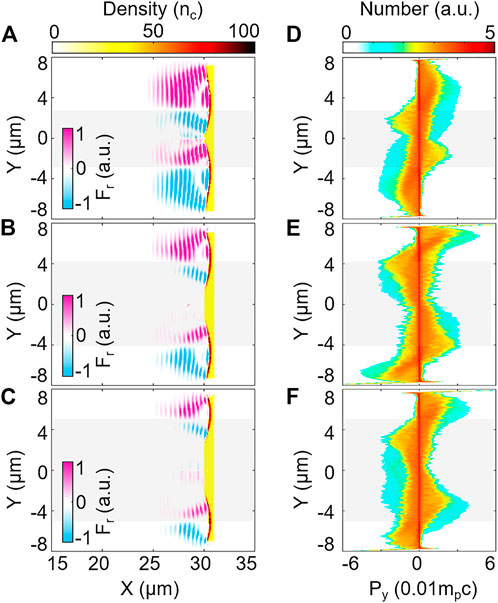
FIGURE 2. Interactions between lasers and plasma targets at t = 50T_L. The distribution of the electron density and LG laser ponderomotive force with topological charge (A) l = 1, (B) l = 2, (C) l = 3 are shown. The corresponding proton momentum distribution for the case with (D) l = 1, (E) l = 2, (F) l = 3 are compared. The gray bands represent the focusing regions.

FIGURE 3

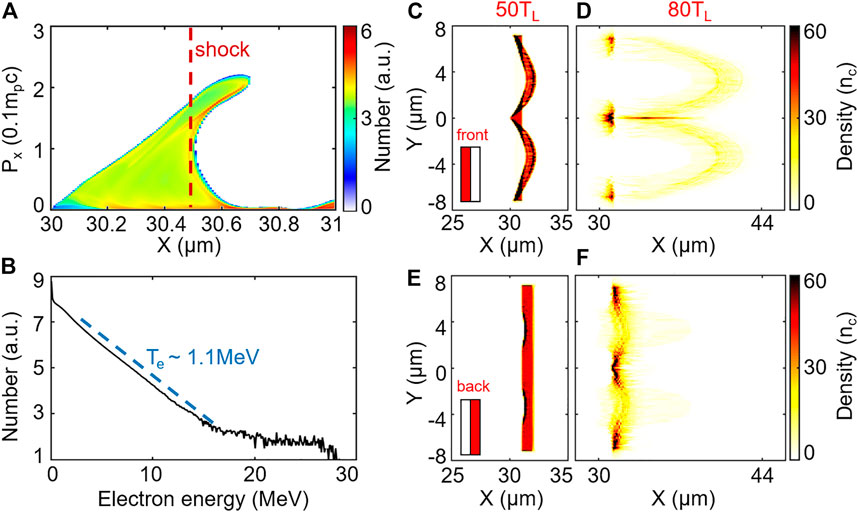
FIGURE 3. Proton acceleration in shock acceleration stage. (A) Proton phase space at t = 50T_L. The red dashed line represents the shock front. (B) Electron energy spectrum and electron temperature at t = 50T_L. Distribution of (C,D) the protons in the front of the target at t = 50T_L, 80T_L. Distribution of (E,F) the protons in the back of the target at t = 50T_L, 80T_L.

To clarify the part of the target that is collimated after the shock acceleration of the target, we divided the target into two parts: the front (30 μm $<$ x $<$ 30.5 μm) and the back (30.5 μm $<$ x $<$ 31 μm). Figures 3C,D show that the front protons are mainly reflected by the shock and accelerated forward. A striking high-density plasma beam is formed around the central axis at t = 80T_L. In contrast, the protons around the peak intensity of the LG laser are mainly accelerated, and are assumed to be partially accelerated by the target normal sheath field acceleration mechanism [25] (see Figures 3E,F). Figure 3 shows that the collimated plasma beam in our case was mainly formed from the front side of the target in the shock acceleration mechanism.

When the narrow plasma beam appears on the central axis, a negative current is formed, which can be calculated by $j={\displaystyle \sum }_i{n}_i{q}_i{v}_i$, where i indicate particle including electron and proton, n_i is number density, q_i is electric charge, v_i is velocity of particle. Figures 4A,C show the distribution of electrons and protons. Although they have similar spatial distributions, their phase spaces are entirely different (see Figures 4B,D). The average effect of the moving electron and protons caused a negative current in the beam.

FIGURE 4

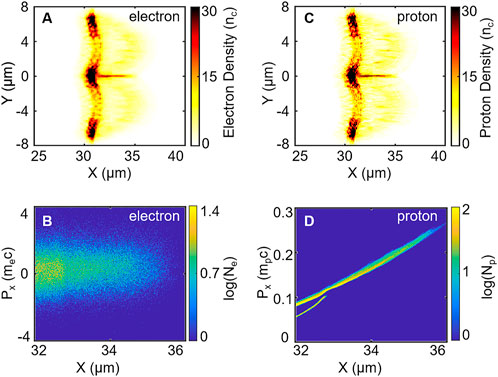
FIGURE 4. Density distribution of (A) the electrons and (B) the protons at t = 80TL. Phase spaces of (C) the electrons and (D) protons in the region (r ≤ 0.2 μm, 32 μm < × < 34 μm).

A narrow plasma beam with current is maintained for several hundred laser cycles in the transporting stage because of the self-generated magnetic field. Here, the magnetic field is assumed to be quasistatic because it is maintained for a long time, as shown in Figure 5 (right column). In the region near the target area (30 μm $<$ x $<$ 35 μm), the magnetic field is mainly caused by the Biermann battery effects $\left(\nabla n_e\times \nabla T_e\right)$ [26,27] and does not affect particle collimation in our case. In contrast, an elongated magnetic field tunnel is generated when a high-density fast electron beam with a negative current (Figures 5D–F) is transported forward and plays a main role in collimating particle beams. The main reason is that a clockwise magnetic field surrounds the plasmas beam for a long time in a long size in space (see Figures 5G–I), which can efficiently collimate electrons in center (see Figures 5A–C). Meanwhile, that the electrons are restricted in the narrow region can improve the collimation of the accelerated ions.

FIGURE 5

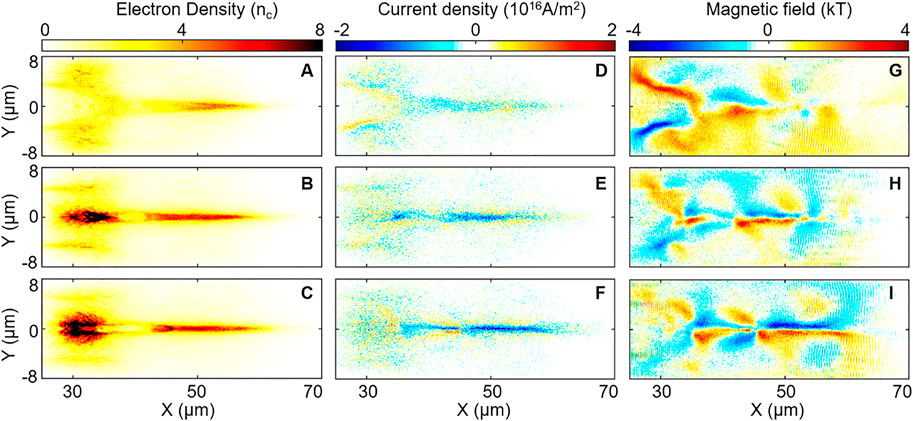
FIGURE 5. Collimation results driven by different topological structured LG lasers. Longitudinal cross sections of electron particle density ne (A–C), current density (D–F), and magnetic field (G–I) at t = 200TL for topological charge of laser l = 1 (top row), l = 2 (center row), and l = 3 (bottom row). For the current, the forward-moving electrons in the plasma beam defined here as a negative current are indicated in blue, whereas the positive current densities corresponding to the return current of the surrounding electrons are indicated in red.

Discussion

In the following section, the magnetic field effects on the collimation mechanism are described. It is well-known that the magnetic field is $\nabla \times B={\mu }_{0}j$, where ${\mu }_0$ is the vacuum permeability and j is the current density. Usually, a quantitative estimate of the relationship between the current and magnetic fields can be obtained by employing a rigid beam model [28] to estimate the magnetic field generation, where a fixed current density is considered to vary with the radius. Here, the plasma beam with current is assumed to remain static. For simplicity, we used Gaussian profiles to fit the average current densities, where j_x = j₀ exp(−r²/2R²), j₀ is the maximum current density, and R is the current radius. In our simulations, j₀ = 3 $\times$ 10¹⁵A/m² (R = 0.7 μm), 7.6 $\times$ 10¹⁵A/m² (R = 0.33 μm) and 11.5 $\times$ 10¹⁵A/m² (R = 0.32 μm) are fitted and obtained at t = 200T_L for the case of l = 1, 2, and 3, just as shown in Figure 6A. Evidently, a larger current density is generated for a larger l because more electrons are trapped by the topological intensity distributions of the LG lasers into the center region in the cases of l = 1 and 2 in the hole-boding stage. The magnetic field generation can then be obtained by integrating the current density, $B_{\phi }=\frac{{\mu }_0}{2\pi }\frac{\int j_{x}ds}{r}$. Evidently, the magnetic fields calculated by the rigid beam model were almost consistent with the simulation results, as shown in Figure 6B.

FIGURE 6

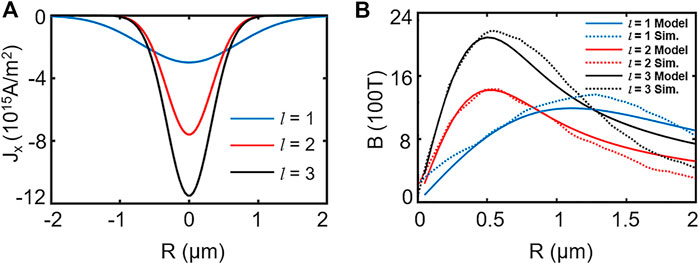
FIGURE 6. (A) Fitted current density distribution for the case of l = 1 (blue), l = 2 (red), and l = 3 (black). (B) The magnetic field in the rigid beam model calculation (solid line) and simulations (dotted line) for the case of l = 1 (blue), l = 2 (red), and l = 3 (black).

The electrons can then be collimated in a quasistatic magnetic field with intensity B and radius L_r. Electrons with divergence $\theta$, speed v, and the Lorentz factor $\gamma$ can be confined and collimated in the magnetic field when the condition $L_r\ge r_e\left(1-\cos \theta \right)$ [29] is satisfied, where r_e = γm_ev/eB is the electron Larmor radius. According to the Larmor radius, the corresponding relation can be obtained as

$\Gamma <2B{L}_{\mathrm{r}}e/m_{\mathrm{e}}(3)$

where $\Gamma =\gamma v{\theta }^2$. It is assumed that more electrons can be collimated when the strength of the magnetic field B increases according to Eq. 3. Based on the simple analysis and results, the beam collimation can be enhanced for l = 3 compared with the cases of l = 1 and 2, because B is larger in Figure 5B, which is consist with the simulation results in Figures 5A–C. It should be noted that the electrons and protons move together as a neutral plasma. Hence we just give the density distribution of electrons at t = 400T_L (see Figure 5).

The collimation of the plasma beams disappears with an increase in the topological parameter l for the LG laser. For the example of l = 5, the electrons cannot be well collimated in a long-size tunnel t = 160T_L as the case in Figure 7, although they are focused onto a spot at x = 45 μm. This is mainly because the intensity is smoothly distributed near the beam axis (r = 0), resulting in a small ponderomotive force at the center and weak concentrating effects on the plasma beam.

FIGURE 7

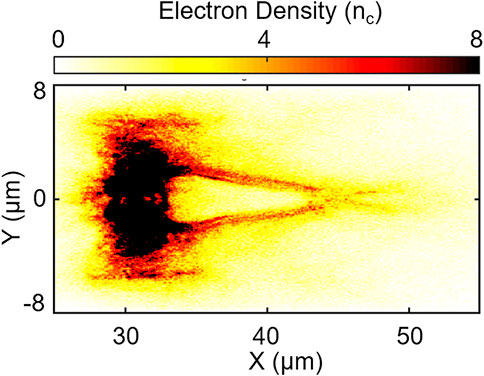
FIGURE 7. Longitudinal cross sections of electron density at t = 160T_L for topological charge of laser l = 5.

Conclusion

The self-collimation mechanism of an energetic plasma beam driven by an ultra-intense and ultrashort LG laser was demonstrated by 3D PIC simulation. A narrow plasma beam was formed and collimated to hundreds of nanometers and transported for a long time. On the one hand, the radial ponderomotive force of the LG laser can first concentrate the plasma into the center. On the other hand, such a beam can be further self-collimated by a magnetic field tunnel for a longer time. Studies have shown that better collimation can be achieved by properly choosing the topological charge l of an LG laser. It is important to achieve a better collimation effect and stable magnetic field when l = 3. The proposed scheme provides a simple and effective method for generating a collimated plasma beam and magnetic tunnel, which is useful in many applications, such as fast ignition in inertial confinement fusion, medical therapy, and astrophysics.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author contributions

HD conducted the simulations and drafted the manuscript. WW supervised the work. All authors discussed the results and reviewed the manuscript.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Tiwari G., Gaul E., Martinez M., Dyer G., Gordon J., Spinks M., et al. Beam distortion effects upon focusing an ultrashort petawatt laser pulse to greater than 10²² W/Cm². Opt Lett (2019) 44(11):2764. doi:10.1364/ol.44.002764

CrossRef Full Text | Google Scholar

2. Yoon J. W., Kim Y. G., Choi I. W., Sung J. H., Lee H. W., Lee S. K., et al. Realization of laser intensity over 20²³ W/Cm². Optica (2021) 8(5):630. doi:10.1364/optica.420520

CrossRef Full Text | Google Scholar

3. Roth M., Cowan T. E., Key M. H., Hatchett S. P., Brown C., Fountain W., et al. Fast ignition by intense laser-accelerated proton beams. Phys Rev Lett (2001) 86(3):436–9. doi:10.1103/PhysRevLett.86.436

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Xu H., Yu W., Yu M. Y., Cai H. B., Luan S. X., Yang S. H., et al. High energy density micro plasma bunch from multiple laser interaction with thin target. Appl Phys Lett (2014) 104(2):024105. doi:10.1063/1.4858956

CrossRef Full Text | Google Scholar

5. Ramakrishna B., Kar S., Robinson A. P., Adams D. J., Markey K., Quinn M. N., et al. Laser-driven fast electron collimation in targets with resistivity boundary. Phys Rev Lett (2010) 105(13):135001. doi:10.1103/PhysRevLett.105.135001

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Badziak J., Parys P., Rosiński M., Zaraś-Szydłowska A. Laser-driven accelerator of intense plasma beams for materials research. Fusion Eng Des (2017) 124:1298–301. doi:10.1016/j.fusengdes.2017.01.061

CrossRef Full Text | Google Scholar

7. Wang W. Q., Yin Y., Zou D. B., Yu T. P., Xu H., Shao F. Q. Effects of parameters on the proton focusing driven by coulomb explosion. High Energ Density Phys (2019) 32:77–81. doi:10.1016/j.hedp.2019.06.003

CrossRef Full Text | Google Scholar

8. Zhuo H. B., Chen Z. L., Sheng Z. M., Chen M., Yabuuchi T., Tampo M., et al. Collimation of energetic electrons from a laser-target interaction by a magnetized target back plasma preformed by a long-pulse laser. Phys Rev Lett (2014) 112(21):215003. doi:10.1103/PhysRevLett.112.215003

CrossRef Full Text | Google Scholar

9. Stephens R. B., Snavely R. A., Aglitskiy Y., Amiranoff F., Andersen C., Batani D., et al. Kαfluorescence measurement of relativistic electron transport in the context of fast ignition. Phys Rev E (2004) 69(6):066414. doi:10.1103/PhysRevE.69.066414

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Lancaster K. L., Green J. S., Hey D. S., Akli K. U., Davies J. R., Clarke R. J., et al. Measurements of energy transport patterns in solid density laser plasma interactions at intensities of 5×10²⁰  W cm⁻². Phys Rev Lett (2007) 98(12):125002. doi:10.1103/PhysRevLett.98.125002

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Kar S., Markey K., Simpson P. T., Bellei C., Green J. S., Nagel S. R., et al. Dynamic control of laser-produced proton beams. Phys Rev Lett (2008) 100(10):105004. doi:10.1103/PhysRevLett.100.105004

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Alraddadi R. A. B., Robinson A. P. L., Woolsey N. C. Improved fast electron transport through the use of foam guides. Phys Plasmas (2020) 27(9):092701. doi:10.1063/5.0011723

CrossRef Full Text | Google Scholar

13. Robinson A. P., Sherlock M., Norreys P. A. Artificial collimation of fast-electron beams with two laser pulses. Phys Rev Lett (2008) 100(2):025002. doi:10.1103/PhysRevLett.100.025002

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Kar S., Markey K., Borghesi M., Carroll D. C., McKenna P., Neely D., et al. Ballistic focusing of polyenergetic protons driven by petawatt laser pulses. Phys Rev Lett (2011) 106(22):225003. doi:10.1103/PhysRevLett.106.225003

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Toncian T., Borghesi M., Fuchs J., d'Humieres E., Antici P., Audebert P., et al. Ultrafast laser-driven microlens to focus and energy-select mega-electron volt protons. Science (2006) 312(5772):410–3. doi:10.1126/science.1124412

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Bacon E. F. J., King M., Wilson R., Frazer T. P., Gray R. J., McKenna P. High order modes of intense second harmonic light produced from a plasma aperture. Matter Radiat Extremes (2022) 7(5):054401. doi:10.1063/5.0097585

CrossRef Full Text | Google Scholar

17. Wang W. P., Jiang C., Dong H., Lu X. M., Li J. F., Xu R. J., et al. Hollow plasma acceleration driven by a relativistic reflected hollow laser. Phys Rev Lett (2020) 125(3):034801. doi:10.1103/PhysRevLett.125.034801

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Arber T. D., Bennett K., Brady C. S., Lawrence-Douglas A., Ramsay M. G., Sircombe N. J., et al. Contemporary particle-in-cell approach to laser-plasma modelling. Plasma Phys Control Fusion (2015) 57(11):113001. doi:10.1088/0741-3335/57/11/113001

CrossRef Full Text | Google Scholar

19. Robinson A. P. L. Production of high energy protons with hole-boring radiation pressure acceleration. Phys Plasmas (2011) 18(5):056701. doi:10.1063/1.3562551

CrossRef Full Text | Google Scholar

20. Wang W. P., Shen B. F., Zhang X. M., Ji L. L., Yu Y. H., Yi L. Q., et al. Dynamic study of a compressed electron layer during the hole-boring stage in a sharp-front laser interaction region. Phys Rev ST Accel Beams (2012) 15(8):081302. doi:10.1103/physrevstab.15.081302

CrossRef Full Text | Google Scholar

21. Wang W. P., Shen B. F., Xu Z. Z. Accelerating gradient improvement from hole-boring to light-sail stage using shape-tailored laser front. Phys Plasmas (2017) 24(1):013104. doi:10.1063/1.4973330

CrossRef Full Text | Google Scholar

22. Wang W. P., Shen B. F., Zhang X. M., Ji L. L., Wen M., Xu J. C., et al. Ultra-intense single attosecond pulse generated from circularly polarized laser interacting with overdense plasma. Phys Plasmas (2011) 18:083104. doi:10.1063/1.3623588

CrossRef Full Text | Google Scholar

23. Wang W., Jiang C., Li S., Dong H., Shen B., Leng Y., et al. Monoenergetic proton beam accelerated by single reflection mechanism only during hole-boring stage. High Pow Laser Sci Eng (2019) 7(3):e55. doi:10.1017/hpl.2019.40

CrossRef Full Text | Google Scholar

24. Forslund D. W., Shonk C. R. Formation and structure of electrostatic collisionless shocks. Phys Rev Lett (1970) 25(25):1699–702. doi:10.1103/PhysRevLett.25.1699

CrossRef Full Text | Google Scholar

25. Snavely R. A., Key M. H., Hatchett S. P., Cowan T. E., Roth M., Phillips T. W., et al. Intense high-energy proton beams from petawatt-laser irradiation of solids. Phys Rev Lett (2000) 85(14):2945–8. doi:10.1103/PhysRevLett.85.2945

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Borghesi M., MacKinnon A. J., Bell A. R., Gaillard R., Willi O. Megagauss magnetic field generation and plasma jet formation on solid targets irradiated by an ultraintense picosecond laser pulse. Phys Rev Lett (1998) 81(1):112–5. doi:10.1103/PhysRevLett.81.112

CrossRef Full Text | Google Scholar

27. Stamper J. A., Papadopoulos K., Sudan R. N., Dean S. O., McLean E. A., Dawson J. M. Spontaneous magnetic fields in laser-produced plasmas. Phys Rev Lett (1971) 26(17):1012–5. doi:10.1103/PhysRevLett.26.1012

CrossRef Full Text | Google Scholar

28. Davies J. R., Green J. S., Norreys P. A. Electron beam hollowing in laser–solid interactions. Plasma Phys Control Fusion (2006) 48(8):1181–99. doi:10.1088/0741-3335/48/8/010

CrossRef Full Text | Google Scholar

29. Robinson A. P. L., Sherlock M. Magnetic collimation of fast electrons produced by ultraintense laser irradiation by structuring the target composition. Phys Plasmas (2007) 14(8):083105. doi:10.1063/1.2768317

CrossRef Full Text | Google Scholar