Experimental study of a tunable perfect flexural wave absorber with a piezoelectric shunted resonator

1 Introduction

Recently, elastic metamaterials have gained lots of attention thanks to their extraordinary dynamic properties [1–3], such as effective negative mass density and/or stiffness [4–7], that are not directly available in natural materials. By artificially designing the microstructures at the deep subwavelength scale, elastic metamaterials have been proven to be good candidates for remarkable wave manipulation [7–12], wave attenuation [1, 13], etc. Most recently, efforts are more paid to the design of elastic metasurfaces [14–19], which are a new kind of planar metamaterials, to manipulate wavefronts via a suitable arrangement of discontinuities on a material interface or boundary. Perfect wave absorption, an exceptional wave control ability to totally absorb incoming waves, has been demonstrated in 1-dimensional (1D) or 2-dimensional (2D) acoustic and elastic metamaterials/metasurfaces using passive [20–28] or active [18, 29] approaches. Examples of the perfect absorption demonstrated in optics, acoustics, as well as elastic waves, were achieved by satisfying the critical coupling condition [23–27, 30, 31], in which the balance between the energy leakage and the inherent losses of the resonator was fulfilled. Similar to optics [31], by placing a scatterer at or near a waveguide boundary, i.e., a perfect reflecting mirror, in a one-port system, the perfect absorption is observed, through the tuning of loss. The one-port and two-port near perfect flexural wave absorbers on 1D structures have also been reported using acoustic black hole (ABH) [30], Willis coupling [27, 29, 32], coated strip-like beam [26, 28], etc. However, most of the existing passive perfect absorbers achieve perfect absorption only at a single frequency point, which hinders their practical applications. Precisely controlling the amount of damping in the scatterers also makes it difficult to design and fabricate the absorbers in experiments. To tune or broaden the absorption frequency, actively shunted piezoelectric patches [18, 29] and thermally controlled shape memory polymer resonators [33] have made it possible, whereas there are still limitations in the existing designs, such as degraded low-frequency performance and inconvenient control strategies.

Using a shunted damping concept proposed by Forward [34], one can not only accurately control the added damping but also tune the system parameters. In this work, we design and fabricate a tunable inductance-resistance (LR) shunted mechanical resonator via a bonded piezoelectric patch for the demonstration of perfect flexural wave absorption at the low-frequency range. By changing the electrical resonance, perfect absorption can be tuned to various frequencies for perfect absorption. The tunable perfect absorption performances are further validated through experiments. In the end, we further numerically demonstrate that the absorption spectrum could be enhanced to broadband absorption with an additional negative capacitance connected in parallel. The approach proposed sheds light on designs of reconfigurable dynamic control devices and enables alternative solutions for ultrasonic sensing of complex engineering structures.

2 Materials and methods

2.1 Design

The concept and a schematic of our designed LR shunted absorber are shown in Figures 1A, B, respectively. The shunted resonator is designed with a cantilever-like beam bonded with a piezoelectric patch (PZT-5H) on its top surface. The piezoelectric patch with dimensions (L_p × w_p × h_p = 10 mm × 5 mm × 1 mm) is connected to an LR-shunted circuit. For low-frequency wave absorption, a large value of inductance is required, which will largely increase the added weight and size to the overall system. To avoid this bulky design, we implement a synthetic inductor described in more detail in the next. The LR-shunted resonator is attached near a free end of a semi-infinite beam with a cross-section area (w × h = 12.7 mm × 3.1 mm) and material properties being Young’s modulus (E = 70 GPa), mass density (ρ = 2700 kg/m³), and Poisson’s ratio (ν = 0.33). A cube-shape tip mass made of stainless steel with Young’s modulus (E = 205 GPa), mass density (ρ = 7850 kg/m³), and Poisson’s ratio (ν = 0.28), is attached at the end of an aluminum strip. Another identical cube functions as a support connected to the other end but on the bottom surface of this beam strip. In our previously investigated coupled mechanical resonators on a two-port system [27], we demonstrated that the coupling distance and the mechanical damping played essential roles in achieving perfect absorption due to the scattering toward the two ports as well as the neighboring resonators. Here, in the one port system as shown in Figure 1, we consider a general case where the scatterer is placed at x = d away from the free end. The scattered waves from the resonator will interfere with the waves reflected from the free boundary and the incident waves [18]. The effect of the location of the resonator on the absorption performance is analyzed through a systematic study. In this analysis, we evaluate the absorption performance as a function of resonator location and resonator damping by considering the mechanical resonator as a damped resonator. We find that for the current chosen design the optimized location of the resonator is at d = 17 mm away from the free end of the beam, which is in the deep subwavelength of the working frequency. Other geometric parameters can be found in the Supplementary Material, and the material properties of the piezoelectric patch can be found in [19]. We use a commercially available Finite Element Method (FEM) package, COMSOL MultiPhysics, to validate our design. Both frequency domain and time domain simulations are performed and the simulation results are given in the next section.

FIGURE 1

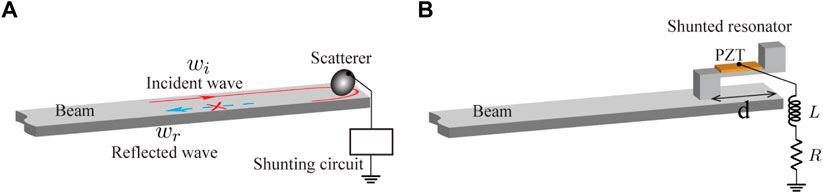
FIGURE 1. Design of an LR-shunted tunable perfect flexural wave absorber. (A) Concept of a shunted scatterer for perfect flexural wave absorption. (B) Schematic of an LR-shunted tunable perfect flexural wave absorber.

2.2 Sample fabrication and experimental setup

In what follows we fabricate our LR-shunted resonator and characterize its absorption performance through experiments. The fabricated samples and the experimental setup are illustrated in Figure 2. To fabricate the mechanical resonator, a aluminum strip (L₁ × w₁ × h₁ = 21 mm × 5 mm × 1 mm) is bonded with two identical stainless-steel cubes with side length (w_c = 5 mm) on each side of the beam strip facing each other. One of the cubes functions as a tip mass, and the other one as a support to interact with the host beam. A piezoelectric patch is glued on the top surface of the beam strip with a 1 mm gap to the tip mass. A photo of the fabricated absorber is shown in Figure 2A. The bottom electrode of the piezoelectric patch is grounded and the top one is connected to the external LR circuit. To realize a large value of inductance without adding too much weight to the system, we implement a synthetic inductor, Antoniou’s Circuit. A photo of the fabricated circuit and a schematic of the Antoniou’s circuit are shown in Figures 2C, D, respectively. The synthetic inductor consists of two operational amplifiers (OPA445), four resistors (R₁−R₄), and a capacitor (C). The inductance of the synthetic inductor is calculated as, L = R₁R₃R₄C/R₂. One can see that by simply adjusting one of the circuit parameters the inductance can be tuned. In the experiment, we use a trimmer to tune the resistor, R₁, while keeping other parameters fixed. In practical application, this trimmer could be replaced with a digital resistor programmed by a control system to realize perfect absorption at the required frequency.

FIGURE 2

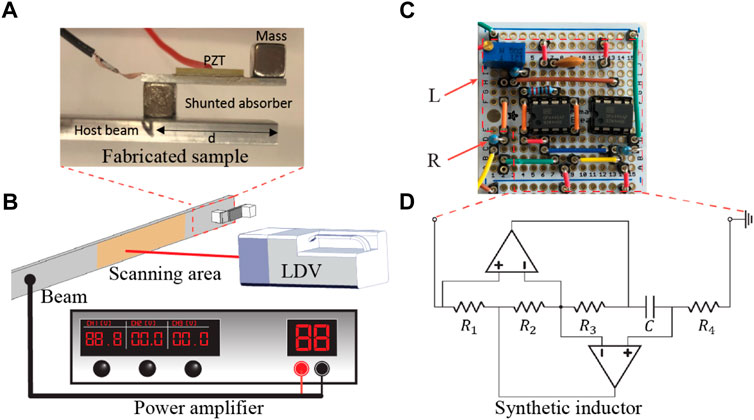
FIGURE 2. Fabricated samples and experimental setup. (A) A photo of the fabricated LR-shunted resonator attached near a free end of a beam end. (B) A schematic of the experimental setup. (C) A photo of the fabricated LR circuit. (D) Schematic of the synthetic inductor.

To test the absorption performance of the fabricated LR-shunted absorber, we carry out the experiments with the setup as demonstrated in Figure 2B. An additional piezoelectric patch attached at 0.5 m away from the right free end of the host beam functions as an actuator to generate incident waves. This distance could effectively reduce the evanescent waves generated by the actuator without affecting the measurement results. A sine-signal sweeping from 1.0 kHz to 2.5 kHz generated from a function generator is fed to the actuator via a power amplifier. An artificial absorbing layer made with high damping materials is carefully placed on the surface of the left end of the host beam to suppress the reflected waves from that boundary. A laser vibrometer is used to scan the pointwise velocity responses of the host beam in the highlighted orange region with 21 points and a point distance of 5 mm [27]. The measured responses are processed to calculate the wave reflection (r) and absorption (α = 1 − r) coefficients.

3 Results

3.1 Simulation results

3.1.1 Frequency domain simulation

To demonstrate the robustness of our tunable absorber to achieve perfect absorption at multiple frequencies, we optimize the circuit parameters, L and R, at each interested frequency. In the optimization, the Nelder-Mead method [35] is used by minimizing the wave reflection coefficient, r, as the objective function with two optimization variables, L and R. Perfect absorption peaks could be achieved from 1.5 kHz to 2.5 kHz. Here, we only plot the absorption spectra optimized at 1.5 kHz–2.5 kHz with an increment of 0.25 kHz, as illustrated in Figure 3A. Still, one could understand that perfect absorption could be achieved at other frequencies in this range, as well, by optimizing the circuit parameters. Optimized circuit parameters are listed in Supplementary Table S1. One can see that as the electrical resonances increase by decreasing the inductor values the peaks of the absorption spectra are shifted to higher frequencies.

FIGURE 3

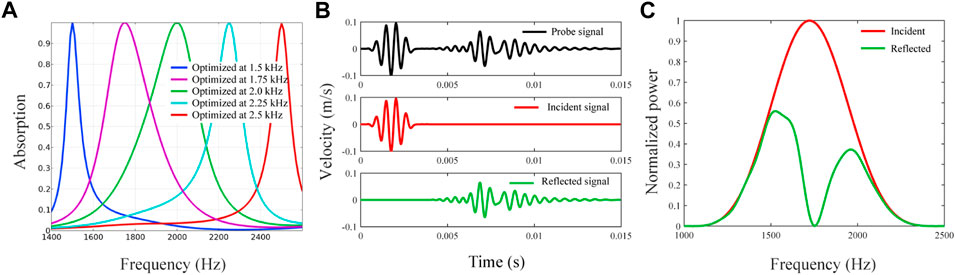
FIGURE 3. Numerical simulation results for the tunable perfect flexural wave absorber. (A) Illustration of perfect flexural wave absorption tuned to different frequencies. (B) Time domain simulation for perfect absorption at 1.75 kHz. (C) Normalized powers of the incident and reflected signals.

The simulated absorption spectra clearly show that perfect absorption could be achieved from a broadband frequency range. Note that in the simulation no damping is added to the mechanical resonator and the perfect absorption is mainly due to the strong interaction between the mechanical and electrical resonances as well as the destructive interference due to the terminal end of the host beam. Also, we notice that when the electrical and mechanical resonances are strongly coupled the absorption spectra (purple and green lines) are wider, whereas as the electric resonance is shifted away from the mechanical resonance the absorption spectra (blue and red lines) are much narrower. Here, the mechanical resonance is at about 2.0 kHz. Nevertheless, perfect absorption can be achieved at various frequencies by tuning the circuit parameters along, which demonstrates the robustness of our proposed tunable perfect absorber.

3.1.2 Transient simulation

To further show the effectiveness of our proposed absorber in flexural wave mitigation, transient analysis is performed. In the simulation, we choose the target frequency at 1.75 kHz for perfect absorption by adopting the circuit parameters listed in Supplementary Table S2. A 5-peak tone-burst signal centered at f_c = 1.75 kHz is excited at the host beam. A displacement probe is placed on the host beam to capture the out-of-plane response. The position of the probe is chosen at 1 m away from the shunted resonator so that the incident and reflected signals can be separated from each other in the time domain. The recorded signal is shown in the top panel of Figure 3B, which contains two main wave packets, the incident response from the incident waves (middle panel of Figure 3B) and the reflected response corresponding to the reflected waves (bottom panel of Figure 3B). The overall amplitude of the reflected signal is largely reduced and the largest amplitude reduction is observed near the center of the reflected wave packet, which is corresponding to the perfect absorption frequency. To further verify this, we calculate the reflected and incident powers normalized to the maximum power of the incident wave, as illustrated in Figure 3C. We can see that almost zero reflected energy is found located near the optimized frequency, f = 1.75 kHz, in the power spectra, thanks to the perfect absorption from the LR-shunted resonator.

3.2 Experimental results

Next, we carry out our experiment to characterize the absorption performance of this proposed tunable absorber. Before we evaluate the shunting circuit performance, we first test the absorption performance with an open circuit.

3.2.1 Open circuit performance

Due to the intrinsic loss in the fabricated resonator, the mechanical resonator with an open circuit might be able to dissipate part of the incident energy. Therefore, before evaluating the absorption performance, we perform a vibration test from Frequency Response Function (FRF) by exciting the fabricated mechanical resonator alone on a shaker. The loss factor is characterized as η = 0.057 from a half-power bandwidth method [27]. To quantify the absorption due to this passive damping from the resonator, the measured absorption coefficient is illustrated by red plus symbols in Figure 4A. Peak absorption of about 50% can be observed in the experiment at around 1.5 kHz. To further validate our experimental results, a 3-D numerical model is built by adopting the same loss factor measured from the experiment for the resonator. In this simulation, a 0.1 mm thin layer is also added between the supporting cube and the beam strip to consider the effect of the supper glue with material properties being Young’s modulus E = 1.1 GPa, Poisson’s ratio ν = 0.35, and mass density ρ = 1050 kg/m³. A solid blue line denotes the simulated absorption spectrum shown in Figure 4A. The experimentally measured absorption spectrum matches well with the simulated spectrum.

FIGURE 4

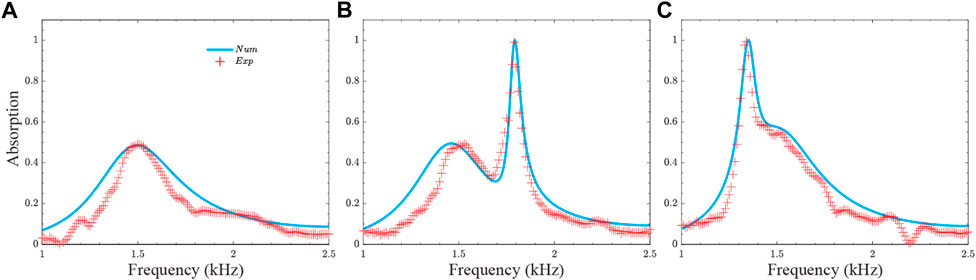
FIGURE 4. Experimentally measured absorption spectra (read plus symbols) compared to numerical simulations (blue solid lines). The absorption spectra with (A) an open circuit and an LR-shunted circuit with (B) L =5.8 H and R =1.0 kΩ (C) L =9.7 H and R =2.9 kΩ.

3.2.2 LR-shunted circuit performance

Our proposed tunable flexural wave perfect absorber is experimentally tested for its performance. For illustration purposes, we show two perfect absorption spectra in Figures 4B, C, respectively. Two absorption peaks can be observed in both of the absorption spectra. The peak at around 1.5 kHz with a wider bandwidth but a lower absorption coefficient is due to the intrinsic mechanical damping, which has a similar shape as the open circuit case. However, the second peak at about 1.8 kHz (1.32 kHz for Figure 4C) induced by the coupling between the mechanical and electrical resonances can almost reach to unit absorption. Interestingly, by varying the electrical resonance, i.e., re-programming the circuit inductance and resistance, the unit absorption peaks can be tuned to different frequencies, which can make our proposed absorber much more robust for overcoming some uncertainties in a time-varying environment. For example, by adjusting the inductance from L = 5.8 H to L = 9.7 H, and the resistance from R = 1 kΩ to R = 2.9 kΩ, the absorption peak is tuned from 1.8 kHz to 1.32 kHz. The absorption performance of the tunable absorber is compared with numerical simulations. A very good agreement can be found, as well. The tunable perfect absorber can achieve almost perfect absorption in a broad frequency range, from 1.5 kHz to 2.5 kHz, and more than 99.8% absorption is experimentally obtained at various frequencies.

4 Discussion

Negative capacitance shunting circuits have been demonstrated in acoustic and elastic metamaterials for broadband damping performance [36–38]. Here, we use a simple negative capacitor (C_NC = −C) connected with a resistor (R′) in series hybrid with an LR-shunted (NC-LR) circuit to investigate broadband absorption performance through numerical simulation. Figure 5A shows the schematic of the design of enhanced absorption with the hybrid shunting circuit. In the simulation, we optimize the inductor value (L) and two resistor values (R and R′), while keeping the value of the negative capacitor as β = C_NC/C_p = −0.8, where C_p is the capacitance of the piezoelectric patch. A color map of the absorption spectra optimized from 1.5 kHz to 2.5 kHz with a step of 0.1 kHz is shown in Figure 5B. Due to the presence of the negative capacitor, broadband absorption can be observed. The negative capacitor functions as broadband shunted damping to the mechanical resonator. Due to the compensation of the damping from the negative capacitor to the mechanical resonator, the absorption spectrum originating from the mechanical resonator starts to approach to the unit absorption. Note that by using a negative capacitor one can achieve perfect absorption as well, but the absorption spectrum is equivalent to a damped mechanical resonator showing a single absorption peak. Here, in order to show the advantage of the NC-LR shunted circuit, we combine the NC circuit with the LR-shunted circuit so that the absorption peaks are merged together to form a broadband absorption spectrum as the electrical resonance is close to the mechanical resonance. To better illustrate the effect of the hybrid circuit, two of the optimization results optimized at 1.5 kHz (blue solid line) and 1.7 kHz (red dotted line), respectively, are shown in Figure 5C compared with the absorption spectrum from an LR-shunted circuit alone (green solid line). The absorption spectrum is largely enhanced to a broad frequency range. Two absorption peaks can be seen in the case with NC-LR1, whereas the two peaks are merged into a single broadband peak by properly choosing the optimization parameters. The circuit parameters for the NC-LR1 and NC-LR2 circuits used in the simulations are provided in the Supplementary Material.

FIGURE 5

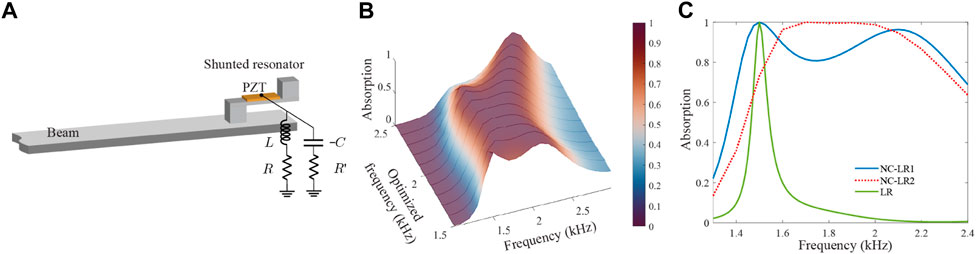
FIGURE 5. Enhanced flexural wave absorption with a hybrid shunting circuit. (A) Schematic of the enhanced flexural wave absorption with an NC-LR shunted circuit. (B) Color map of the absorption spectra optimized from 1.5 kHz to 2.5 kHz. (C) Comparison of the absorption spectra with the NC-LR shunted circuit to the LR shunted circuit.

5 Conclusion

We have designed and experimentally demonstrated a tunable absorber for perfect flexural wave absorption at a broad frequency range. The tunable absorber is composed of a mechanical resonator with a bonded piezoelectric patch and a shunted circuit. The critical coupling conditions are fulfilled through the shunted circuit damping at various frequencies by varying the circuit parameters. Therefore, unit absorption peaks are achieved at a broad frequency range, which is validated through numerical simulations and experiments. In the end, we numerically demonstrate an enhanced absorption spectrum with a hybrid NC-LR circuit for broadband absorption. Thanks to the flexible tunability and enhanced low-frequency performance, the proposed tunable absorber could set forth the basis of a markedly distinct approach toward perfect absorbers of subwavelength wave and elastic wave cloaking.

Data availability statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author contributions

XL: conceptualization, methodology, software, investigation, writing–original draft, writing–review and editing. ZY: conceptualization, investigation, validation, writing–review and editing. TL: conceptualization, investigation, validation, writing–review and editing. All authors contributed to manuscript revision, read, and approved the submitted version.

Conflict of interest

Authors XL, ZY and TL were employed by company Toyota Motor North America.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2022.1054634/full#supplementary-material

References

1. Liu Z, Zhang X, Mao Y, Zhu Y, Yang Z, Chan CT, et al. Locally resonant sonic materials. science (2000) 289:1734–6. doi:10.1126/science.289.5485.1734

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Kadic M, Milton GW, van Hecke M, Wegener M. 3D metamaterials. Nat Rev Phys (2019) 1:198–210. doi:10.1038/s42254-018-0018-y

CrossRef Full Text | Google Scholar

3. Bertoldi K, Vitelli V, Christensen J, Van Hecke M. Flexible mechanical metamaterials. Nat Rev Mater (2017) 2:17066–11. doi:10.1038/natrevmats.2017.66

CrossRef Full Text | Google Scholar

4. Wu Y, Lai Y, Zhang ZQ. Elastic metamaterials with simultaneously negative effective shear modulus and mass density. Phys Rev Lett (2011) 107:105506. doi:10.1103/physrevlett.107.105506

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Huang H, Sun C, Huang G. On the negative effective mass density in acoustic metamaterials. Int J Eng Sci (2009) 47:610–7. doi:10.1016/j.ijengsci.2008.12.007

CrossRef Full Text | Google Scholar

6. Liu XN, Hu GK, Huang GL, Sun CT. An elastic metamaterial with simultaneously negative mass density and bulk modulus. Appl Phys Lett (2011) 98:251907. doi:10.1063/1.3597651

CrossRef Full Text | Google Scholar

7. Zhu R, Liu X, Hu G, Sun C, Huang G. Negative refraction of elastic waves at the deep-subwavelength scale in a single-phase metamaterial. Nat Commun (2014) 5:5510–8. doi:10.1038/ncomms6510

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Yan X, Zhu R, Huang G, Yuan FG. Focusing guided waves using surface bonded elastic metamaterials. Appl Phys Lett (2013) 103:121901. doi:10.1063/1.4821258

CrossRef Full Text | Google Scholar

9. Chen Y, Huang G. Active elastic metamaterials for subwavelength wave propagation control. Acta Mech Sin (2015) 31:349–63. doi:10.1007/s10409-015-0402-0

CrossRef Full Text | Google Scholar

10. Mousavi SH, Khanikaev AB, Wang Z. Topologically protected elastic waves in phononic metamaterials. Nat Commun (2015) 6:8682–7. doi:10.1038/ncomms9682

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Cha J, Kim KW, Daraio C. Experimental realization of on-chip topological nanoelectromechanical metamaterials. Nature (2018) 564:229–33. doi:10.1038/s41586-018-0764-0

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Chen H, Nassar H, Huang G. A study of topological effects in 1d and 2d mechanical lattices. J Mech Phys Sol (2018) 117:22–36. doi:10.1016/j.jmps.2018.04.013

CrossRef Full Text | Google Scholar

13. Huang H, Sun C. Wave attenuation mechanism in an acoustic metamaterial with negative effective mass density. New J Phys (2009) 11:013003. doi:10.1088/1367-2630/11/1/013003

CrossRef Full Text | Google Scholar

14. Assouar B, Liang B, Wu Y, Li Y, Cheng JC, Jing Y. Acoustic metasurfaces. Nat Rev Mater (2018) 3:460–72. doi:10.1038/s41578-018-0061-4

CrossRef Full Text | Google Scholar

15. Zhu H, Semperlotti F. Anomalous refraction of acoustic guided waves in solids with geometrically tapered metasurfaces. Phys Rev Lett (2016) 117:034302. doi:10.1103/physrevlett.117.034302

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Chen Y, Li X, Nassar H, Hu G, Huang G. A programmable metasurface for real time control of broadband elastic rays. Smart Mater Struct (2018) 27:115011. doi:10.1088/1361-665x/aae27b

CrossRef Full Text | Google Scholar

17. Zhu H, Patnaik S, Walsh TF, Jared BH, Semperlotti F. Nonlocal elastic metasurfaces: Enabling broadband wave control via intentional nonlocality. Proc Natl Acad Sci U S A (2020) 117:26099–108. doi:10.1073/pnas.2004753117

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Li X, Chen Y, Zhu R, Huang G. An active meta-layer for optimal flexural wave absorption and cloaking. Mech Syst Signal Process (2021) 149:107324. doi:10.1016/j.ymssp.2020.107324

CrossRef Full Text | Google Scholar

19. Li X, Chen Y, Zhang X, Huang G. Shaping elastic wave mode conversion with a piezoelectric-based programmable meta-boundary. Extreme Mech Lett (2020) 39:100837. doi:10.1016/j.eml.2020.100837

CrossRef Full Text | Google Scholar

20. Zhang C, Hu X. Three-dimensional single-port labyrinthine acoustic metamaterial: Perfect absorption with large bandwidth and tunability. Phys Rev Appl (2016) 6:064025. doi:10.1103/physrevapplied.6.064025

CrossRef Full Text | Google Scholar

21. Wei P, Croënne C, Tak Chu S, Li J. Symmetrical and anti-symmetrical coherent perfect absorption for acoustic waves. Appl Phys Lett (2014) 104:121902. doi:10.1063/1.4869462

CrossRef Full Text | Google Scholar

22. Long H, Shao C, Liu C, Cheng Y, Liu X. Broadband near-perfect absorption of low-frequency sound by subwavelength metasurface. Appl Phys Lett (2019) 115:103503. doi:10.1063/1.5109826

CrossRef Full Text | Google Scholar

23. Lee T, Nomura T, Dede EM, Iizuka H. Asymmetric loss-induced perfect sound absorption in duct silencers. Appl Phys Lett (2020) 116:214101. doi:10.1063/5.0009631

CrossRef Full Text | Google Scholar

24. Lee T, Iizuka H. Heavily overdamped resonance structurally engineered in a grating metasurface for ultra-broadband acoustic absorption. Appl Phys Lett (2018) 113:101903. doi:10.1063/1.5047798

CrossRef Full Text | Google Scholar

25. Huang S, Fang X, Wang X, Assouar B, Cheng Q, Li Y. Acoustic perfect absorbers via spiral metasurfaces with embedded apertures. Appl Phys Lett (2018) 113:233501. doi:10.1063/1.5063289

CrossRef Full Text | Google Scholar

26. Leng J, Gautier F, Pelat A, Picó R, Groby JP, Romero-Garcia V. Limits of flexural wave absorption by open lossy resonators: Reflection and transmission problems. New J Phys (2019) 21:053003. doi:10.1088/1367-2630/ab1761

CrossRef Full Text | Google Scholar

27. Li X, Yu Z, Iizuka H, Lee T. Experimental demonstration of extremely asymmetric flexural wave absorption at the exceptional point. Extreme Mech Lett (2022) 52:101649. doi:10.1016/j.eml.2022.101649

CrossRef Full Text | Google Scholar

28. Cao L, Yang Z, Xu Y, Fan SW, Zhu Y, Chen Z, et al. Flexural wave absorption by lossy gradient elastic metasurface. J Mech Phys Sol (2020) 143:104052. doi:10.1016/j.jmps.2020.104052

CrossRef Full Text | Google Scholar

29. Chen Y, Li X, Hu G, Haberman MR, Huang G. An active mechanical willis meta-layer with asymmetric polarizabilities. Nat Commun (2020) 11:3681–8. doi:10.1038/s41467-020-17529-2

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Leng J, Romero-García V, Pelat A, Pico R, Groby JP, Gautier F. Interpretation of the acoustic black hole effect based on the concept of critical coupling. J Sound Vibration (2020) 471:115199. doi:10.1016/j.jsv.2020.115199

CrossRef Full Text | Google Scholar

31. Piper JR, Fan S. Total absorption in a graphene monolayer in the optical regime by critical coupling with a photonic crystal guided resonance. Acs Photon (2014) 1:347–53. doi:10.1021/ph400090p

CrossRef Full Text | Google Scholar

32. Norris AN, Packo P. Non-symmetric flexural wave scattering and one-way extreme absorption. The J Acoust Soc America (2019) 146:873–83. doi:10.1121/1.5087133

PubMed Abstract | CrossRef Full Text | Google Scholar

33. Raybaud G, Ouisse M, Leng J, Pelat A, Groby JP, Romero-García V, et al. Control of bending wave reflection at beam terminations by thermally tunable subwavelength resonators. J Sound Vibration (2022) 530:116918. doi:10.1016/j.jsv.2022.116918

CrossRef Full Text | Google Scholar

34. Forward RL. Electronic damping of vibrations in optical structures. Appl Opt (1979) 18:690–7. doi:10.1364/ao.18.000690

PubMed Abstract | CrossRef Full Text | Google Scholar

35. Conn AR, Scheinberg K, Vicente LN. Introduction to derivative-free optimization. Thailand: SIAM (2009).

Google Scholar

36. Fukada E, Date M, Kimura K, Okubo T, Kodama H, Mokry P, et al. Sound isolation by piezoelectric polymer films connected to negative capacitance circuits. IEEE Trans Dielectr Electr Insul (2004) 11:328–33. doi:10.1109/tdei.2004.1285904

CrossRef Full Text | Google Scholar

37. Beck BS, Cunefare KA, Collet M. The power output and efficiency of a negative capacitance shunt for vibration control of a flexural system. Smart Mater Struct (2013) 22:065009. doi:10.1088/0964-1726/22/6/065009

CrossRef Full Text | Google Scholar

38. Beck B, Cunefare KA, Ruzzene M. Broadband vibration suppression assessment of negative impedance shunts. Smart Mater Adaptive Structures Intell Syst (2008) 43314:491–500.

CrossRef Full Text | Google Scholar