Using photonic reservoirs as preprocessors for deep neural networks

Artificial neural networks are very time consuming and energy intensive to train, especially when increasing the size of the neural network in an attempt to improve the performance. In this paper, we propose to preprocess the input data of a deep neural network using a reservoir, which has originally been introduced in the framework of reservoir computing. The key idea of this paper is to use such a reservoir to transform the input data into a state in a higher dimensional state-space, which allows the deep neural network to process the data with improved performance. We focus on photonic reservoirs because of their fast computation times and low-energy consumption. Based on numerical simulations of delay-based reservoirs using a semiconductor laser, we show that using such preprocessed data results in an improved performance of deep neural networks. Furthermore, we show that we do not need to carefully fine-tune the parameters of the preprocessing reservoir.

Introduction

Deep neural networks (DNNs) are a key part of the domain of machine learning and artificial neural networks. They have shown to be widely applicable for various problems, e.g. natural language processing [1], drug discovery [2], detection of medical images [3–5], fault diagnosis in solar panels [6] and many other applications. They are able to achieve very high accuracy on these tasks because of their ability to generalise underlying patterns and features. This is achieved by training the network, which is performed by means of fitting a large dataset of input samples to a model. In order to achieve high accuracies, one often uses large and complex networks, with a large number of parameter weights [7]. However, increasing the number of layers and parameters in DNNs is computationally difficult and requires much memory, time and energy. For example, the GPT-3 autoregressive language model [8] contains 175 billion parameters which need to be optimized. Several hardware implementations have been investigated to accelerate the training of such DNNs. Examples include application specific integrated circuits (ASICs), graphics processing units (GPUs) and field programmable gate arrays (FPGAs) [9, 10]. Instead of the aforementioned electronic hardware accelerators, several different photonic hardware accelerators have also been investigated [11, 12]. Examples of this include coherent nanophotonic circuits [13], diffractive deep neural networks [14], all-optical neural networks [15] and photonic convolutional accelerators for optical neural networks [16]. The reason why photonics-based accelerators are particularly interesting is because of their high bandwidth and high power efficiency. Different from hardware accelerators, one can also look into preprocessing the input data before injecting it into the DNNs to improve their performance. For example, using a diffuser that generates speckle patterns can improve the scalability and generalization when using convolutional neural networks [17]. Additionally, hybrid data processing architectures have also been developed, such as LightOn’s optical processing unit which functions as a fast external preprocessor [18, 19]. Motivated by these photonic implementations, we look into the opportunities offered by photonic reservoir computing (RC) as preprocessor for DNNs.

Reservoir computing systems are recurrent neural networks which consist of three layers: an input layer, a reservoir and an output layer. The input layer is where the data is injected into the system and the output layer is where predictions are made using the input data, typically using a linear read-out. The reservoir contains a large amount of randomly connected nonlinear nodes. An illustration of such an RC system is shown in Figure 1A. Different from deep neural networks is that the weights of the reservoir are fixed and are not altered. Only the weights in the output layer are trained, shortening the training time of the network drastically. This also reduces the overall complexity of RCs and makes them ideally suited for hardware implementations using various physical systems [20]. They have been successfully applied for various prediction tasks, such as speech recognition [21, 22], time-series predictions [23–25] and nonlinear channel equalization tasks [26].

FIGURE 1

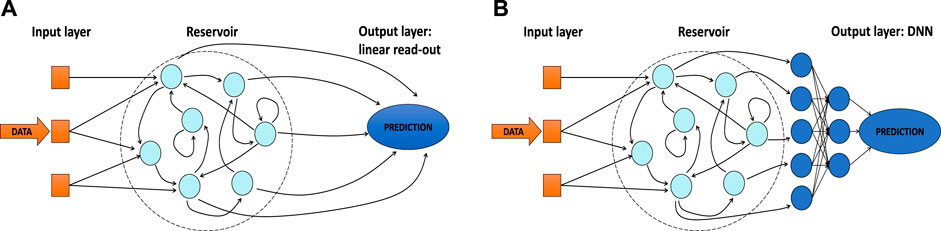
FIGURE 1. Simplified representation of a generic reservoir computing system, with the input layer, reservoir and linear read-out as output layer (A). Simplified representation of the network that uses a reservoir as preprocessor. In the output layer, we have replaced the linear read-out layer with a deep neural network (DNN) in order to make predictions (B).

The reason why RC systems perform well with a simple linear read-out layer (shown in Figure 1A) as output layer, is because the reservoirs transform the input in a high-dimensional state-space. Such a transformation, however, might also be very useful to be done at the input of a DNN such that the combined performance of a reservoir and DNN surpasses that of the DNN and/or that of the RC. In this paper, we investigate this conjecture, and we will do that based on a specific photonic reservoir by way of example.

We focus on a photonic reservoir, because of its fast information processing rate, high bandwidth and small power consumption [27, 28]. More specifically, we use a photonic delay-based reservoir based on a single-mode semiconductor laser to function as a fast, low-energy preprocessor for digital deep neural networks. This optoelectronic delay-based reservoir has already shown good performance for various tasks in previous experiments, e.g. for spoken-digit recognition, time-series prediction of the Santa Fe dataset [29], speech recognition tasks [30], and nonlinear channel equalization tasks [26].

We investigate and compare the performance of various networks. We use the photonic delay-based reservoir, combined with either a linear read-out layer such as in conventional reservoir computing, or combined with a deep neural network. In case of the combined reservoir and DNN system, we feed the output of the reservoir as input to the DNN, making the photonic reservoir in this coupled system a preprocessor. This basically means that the linear read-out layer in Figure 1A is replaced with a DNN, as shown in Figure 1B. We compare the performance of these networks with other neural networks, such as the DNN alone and a long short-term memory (LSTM) network. This latter network contains a form of memory, making it ideal to be used to make comparisons with the other networks for the specific benchmark task used in this paper. We investigate the performance of the different networks on a time-series prediction task as benchmark and give a heuristic explanation for these results making use of their memory capacity. The final goal of this paper is to investigate whether photonic reservoirs are viable to preprocess input data when coupled to DNNs, resulting in a better performance compared to DNNs without such a preprocessing network. This allows one to use a fast photonic reservoir, combined with a relatively small DNN (which needs limited training) to achieve good results on benchmark tasks.

This paper is organised as follows. Section 2 gives a short introduction on the various networks used in this paper: delay-based reservoir computing, together with the numerical model used to simulate this RC system (in Section 2.1), the deep neural network (in Section 2.2) and the long short-term memory network (in Section 2.3). The combined system, consisting of the preprocessing reservoir and DNN, which is the novel architecture, is described in Section 2.4. In these sections, we also discuss how we perform training. Additionally, we explain the benchmark task which is used (in Section 2.5) and describe a heuristic explanation of the results of the networks by their memory capacity (in Section 2.6). In Section 3, we give an overview of the performance results of the different networks. Section 4 concludes with a discussion of the results in this paper.

Materials and methods

Photonic delay-based reservoir computing

In this work, we simulate a reservoir computing system which is based on a semiconductor laser (SL) with delayed optical feedback [31]. The layout of our RC system is shown in Figure 2, where we show in detail how the different layers of Figure 1A are implemented in our system. The input layer is where the input data is optically injected into the reservoir layer using an unbalanced Mach-Zehnder modulator (MZM). Before injecting the input data samples into the reservoir, these data samples are first convoluted with a mask m(t). The reservoir is made using a single-mode semiconductor laser with delayed optical feedback. The delay time is indicated by τ. In the output layer, the intensity of the SL is measured by a photodetector and is sampled at θ time intervals to represent the response at the virtual nodes. These intensity values are then multiplied with the trained weights in order to make a prediction [27, 32].

FIGURE 2

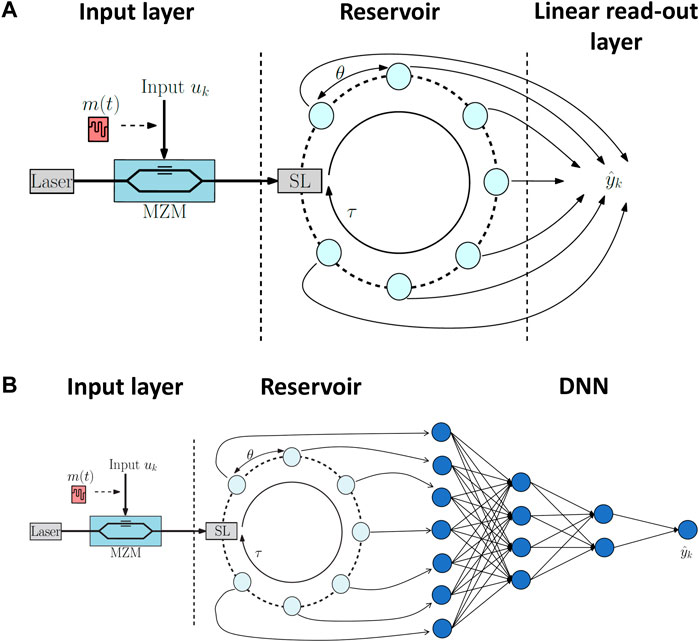
FIGURE 2. Simplified architecture of a delay-based reservoir computing system, with the input layer, reservoir and linear read-out layer. SL represents the semiconductor laser, driven by a constant pump current. In the input layer, a mask m(t) encodes the input sample u_k, which is in turn injected into the reservoir using a Mach-Zehnder modulator (MZM). In the reservoir, we have a node separation θ and a delay time τ, the virtual nodes are depicted by the cyan circles. In the linear read-out layer, we show the predicted target data ${\widehat{y}}_k$. (A). Simplified representation of the network architecture of the reservoir, functioning as preprocessor, coupled to the DNN, with its nodes depicted by blue circles (B).

The simulations for the delay-based RC system used in this paper are based on numerical integration of the following rate-equations [33].

$\frac{dE\left(t\right)}{dt}=\frac{1}{2}\left(1+i\alpha \right)\xi N\left(t\right)E\left(t\right)+\eta E\left(t-\tau \right)e^{-i{\varphi }_{FB}}+{\tilde{F}}_{\beta }\left(t\right)+\mu E_{\mathit{inj}}\left(t\right)(1)$

$\frac{dN\left(t\right)}{dt}=\frac{\mathrm{\Delta }I}{e}-\frac{N\left(t\right)}{{\tau }_c}-\left[g+\xi N\left(t\right)\right]{\left|E\left(t\right)\right|}^2,(2)$

Where E is the dimensionless complex-valued slowly-varying envelope of the electric field of the laser and N the excess amount of carriers. α is the linewidth enhancement factor, ξ the differential gain and g the threshold gain of the semiconductor laser. η and μ are the feedback and injection rates. ϕ_FB represents the phase difference between the electric field of SL in Figure 2A and the feedback term, which is delayed with the delay time τ. ${\tilde{F}}_{\beta }(t)$ represents the Gaussian distributed white noise, modelling spontaneous emissions. This noise strength is controlled by β and has following properties, $⟨{\tilde{F}}_{\beta }(t)⟩=0$ and $⟨{\tilde{F}}_{\beta }(t){\tilde{F}}_{\beta }{(t^{\prime })}^{*}⟩=\beta /{\tau }_c\delta (t-t^{\prime })$, with τ_c the carrier lifetime. ΔI/e is the excess pump current divided by the elementary charge, where ΔI = I − I_thr, with I the pump current and I_thr the threshold pump current of the SL. The injection of input data is handled by an MZM, which optically injects data into the reservoir. This injection is modeled in the simulations using E_inj, where $E_{\mathit{inj}}(t)=ϵ\left(1+e^{iB(t)}\right)$, and is performed with no frequency detuning as E_inj is injected on the same frequency as the optical frequency of the free running semiconductor laser [34]. The amplitude of the injected electric field is represented by ϵ, and the injected data signal by B(t), where B(t) = A S(t) + Φ. A and Φ are here the modulation amplitude and bias of the MZM, and S(t) the masked input signal that is defined as the convolution between the k-th input sample -from a total of n input samples- u_k, and the mask m(t),

$S\left(t\right)=m\left(t\right)\ast \sum _k{u}_k\delta \left(t-k\tau \right).(3)$

The mask m(t) is a piecewise constant function, with N values randomly selected from $\left[\mathrm{0,0.25},0.5,0.75,1\right]$, where each sublevel has a time length equal to the node separation θ. This ensures that the total length of the mask equals Nθ. In this work, we have chosen for the period of the mask Nθ being equal to the delay time τ, where τ = 4 ns. This choice is taken out of simplicity, although an improvement in performance has been observed in literature when a small mismatch in the mask length is introduced [35]. The parameters which are used in this work are summarized in Table 1, and are taken from [34] where it is shown that these parameter values lead to good RC performance.

TABLE 1

TABLE 1. Parameters used in the simulations.

To construct the linear read-out layer, the light intensity is calculated as |E(t)|², as in a practical implementation one would sample the reservoir’s output using a photodetector that measures intensities. We sample the intensity after every time interval of duration θ, and thus we calculate N samples of the intensity during every input sample u_k.

A state matrix A is then constructed with the N sampled intensities stored in the columns of this matrix, for every input data sample, stored in the rows. This state matrix has the dimensions (n × N) and is normalized between 0 and 1, by dividing it with the maximum value found in this matrix. This state matrix is used during the training phase to obtain the output weights w corresponding to the N nodes of the reservoir, via a least squares minimization procedure with the expected data y,

$\mathbf{w}={\mathbf{A}}^{†}\mathbf{y}.(4)$

where we have used the real Moore–Penrose pseudoinverse (denoted by the symbol^†). The predicted values $\widehat{\mathbf{y}}$ for the data samples are thus given by

$\widehat{\mathbf{y}}=\mathbf{A}\mathbf{w}.(5)$

Note that in Eq. 4, we actually add an additional bias node in the state matrix which can account for possible offsets in the data, so that the dimensions of A are here (n × (N + 1)). The addition of this extra bias node is only done for the linear read-out layer of the reservoir computing system. Adding an extra bias node is not performed for the other networks discussed in this paper, because they already have biases in their networks. The weights of Eq. 4 are then used in the test phase, where we apply these weights to unseen data and measure its performance.

Deep neural network

The DNN model we employ in this paper uses as input the data, with 200 features (unless stated otherwise), and returns a single value as a prediction. The reason for the specific amount of features is explained in Section 2.5. The network consists of three fully-connected layers, where the amount of nodes is decreased throughout the network. The first hidden layer in the DNN is a fully-connected layer with 100 nodes, with a ReLU activation function in each of the nodes [36]. The next hidden layer is another fully-connected layer, now with 50 nodes, and again with the ReLU activation function. This information is then injected into the final layer, which only has one node. The output of this node corresponds to the target data and results in a prediction ${\widehat{y}}_k$ for the data sample. Note that this network architecture is not necessarily the most optimal structure for the problems considered in this paper. Its architecture was chosen by a small preliminary study, where the amount of nodes is decreased with a factor of two in the next hidden layer compared to each previous layer. The optimization of this architecture, however, is not within the scope of this paper and thus we do not alter the DNN architecture itself here.

This DNN model is trained using the Adam optimizer [37], with a learning rate of 10⁻³ for 10⁴ epochs (unless stated otherwise). In order to avoid overfitting on the data, we use early stopping on a validation set, which is different from the training and test set. The loss, defined here as the mean squared error between the expected target data samples y_k and the predicted target data samples ${\widehat{y}}_k$, is calculated for every epoch for the training and validation set. If the loss for the validation set increases for a certain amount of epochs, the training is stopped. Once the model is trained after the defined epoch amount, the model weights are used on the test data and the performance of the trained model is evaluated. We implement the DNN on a standard consumer mobile CPU (Intel Core i7-10710U) using the PyTorch 1.4.0 and NumPy 1.19.2 libraries, with Python 3.8.5 as programming language.

Long short-term memory

The DNN from the previous section does not contain recurrent connections and will thus have no memory in the internal network. In the time-series forecasting task that we use as benchmark (see details in Section 2.5), such memory might be essential to achieve good performance. Therefore, and in order to further validate any performance gains by the reservoir as preprocessor, we also consider another type of neural network with recurrent connections. More specifically, we also study the performance of the long short-term memory (LSTM) networks [38, 39].

The LSTM network was first introduced in 1997 by Sepp Hochreiter and Jürgen Schmidhuber as a solution to the vanishing and exploding gradient problem of recurrent neural networks, which can occur when training an artificial neural network [40]. LSTMs are gradient-based recurrent neural networks with feedback connections and are able to introduce a lasting type of memory of recent inputs in the network during training. This is accomplished by using memory cells with gate units, where a connection is made to the neuron itself at the next time step during training. They have been proven to be very useful in many tasks, e.g. for speech recognition, natural language modeling and text classification [41, 42].

We use an LSTM network that takes input data with 200 features. The LSTM network used in this paper has a hidden dimension of 500 nodes, with the ReLU activation function and batch normalisation. Additionally, a recurrent dropout is used with a rate of 50%. The final layer consists of a single fully-connected node, and results in a prediction ${\widehat{y}}_k$ for the data sample. Note that this network architecture is not necessarily the most optimal structure of the LSTM for the problems considered in this paper. For example, the amount of nodes is found by a small preliminary study, and is most likely not the optimal amount. The optimization of this architecture, however, is not within the scope of this paper and thus we do not alter the LSTM architecture itself here.

We again train using the Adam optimizer, with a learning rate of 10⁻⁴ for 10⁴ epochs. Early stopping on a validation set is also used here to avoid overfitting. The loss, defined here as the mean squared error between the expected target data sample y_k and the predicted target data sample ${\widehat{y}}_k$, is calculated for every epoch for the training and validation set. If the loss for the validation set increases for a certain amount of epochs, the training is stopped. Once the model is trained after the defined epoch amount, the model weights are used on the test data and the performance of the trained model is evaluated. We implement the LSTM on a standard consumer mobile CPU (Intel Core i7-10710U) using the PyTorch 1.4.0 and NumPy 1.19.2 libraries, with Python 3.8.5 as programming language.

Photonic reservoir as preprocessor for deep neural networks

With the aim of achieving an improved performance when combining systems, we use the photonic delay-based reservoir from Section 2.1 as preprocessor, together with the DNN described in Section 2.2, with the same (hyper)parameters. This means that the conventional linear read-out layer from Figure 2A is now replaced with the DNN, which is shown in Figure 2B. This is done as follows: we inject the input data samples as described in Section 2.1 into the reservoir. After the reservoir, we calculate the light intensity from the simulated time traces as |E(t)|² and perform the sampling in order to construct the state matrix A. Instead of performing training using the conventional linear read-out in the output layer, we now use a DNN and train its weights.

The advantages of such a photonic reservoir is that in principle it can be very fast to run, promises a low power requirement [27, 28] and has inherently a form of memory due to the delayed feedback, making it an ideal candidate to preprocess the input data for the DNN. This means that all time-dependent information processing is done by the fast analog photonic reservoir and the DNN is used for regression.

The physical implementation of the fast photonic reservoir can be based on existing (delay-based) RC systems. An example of such an RC system is described in [43], where a semiconductor laser is coupled with a fiber-optic feedback loop. This implementation achieved good performance on several tasks such as speaker recognition, spoken digit recognition and chaotic time-series prediction, and this at data rates above 1 Gbyte/s. Such a system, however, can become quite large to physically implement with many components. Instead, integrated implementations have been proposed and tested. For example, in [31], a compact delay-based reservoir computing system is demonstrated by using a laser and delay line on an InP photonic integrated circuit. They showed in their experiment that the chip was able to operate at 0.87 GSa/s, for a reservoir which contains 23 nodes. Another example of such an integrated implementation is given in [44]. The authors demonstrate a spatially parallel delay-based photonic reservoir, where multiple integrated optical cavities are used, resulting in the possibility for a much higher amount of virtual nodes. The experimental maximum bandwidth was here only limited by the used arbitrary waveform generator oscilloscope to 20 GHz. Such compact on-chip implementations of photonic reservoirs would allow for small-scale implementations of the combined system, where the information of the light intensity of the reservoir is measured by photodetectors and then digitally sent to the DNN which is implemented on e.g. FPGAs, ASICs, etc. Where the training is performed.

The DNN again takes as input data with 200 features, due to the reservoir containing 200 nodes in our case, so that every node from the reservoir is now sent as input to the DNN for every input sample, as shown in Figure 2B.

It is important to note that we do not further optimize the architecture of the DNN itself, but rather the reservoir with which we want to couple it with. This is done because the optimization of the DNN is out of the scope of this paper and because we mainly focus on the reservoir itself as the preprocessor.

One-step ahead prediction task: Santa Fe dataset

In order to compare the performance of the different networks, we evaluate their normalized mean squared error on a one-step ahead time-series prediction task as benchmark. The used input dataset is the Santa Fe dataset which consists of 9093 data samples sampled from a far-IR laser in a chaotic regime [45]. The Santa Fe data is first normalized over the whole dataset before being used in the networks, resulting in u_k ∈ [0,1].

For the networks containing a reservoir, we inject the first 3010 data samples, which function as the training dataset. As test dataset, we inject the following 1010 data samples, with an interval of 10 samples between the training and the test dataset. For both training and test set we discard the first 210 samples to avoid transients occurring from switching datasets (10 samples) and to be able to compare with the other networks that do not contain a reservoir (200 samples). This results in a training dataset and test dataset with sizes of 2800 and 800 input samples for the networks containing a reservoir.

For the networks without a reservoir, we have to redefine the input as we do not have a state matrix here, which normally originates from the reservoir. As input for these networks, we create a matrix analogous to such a state matrix, but which features the preceding data samples, instead of the intensity response of the nodes of the reservoir. For this, we now use a sliding window over the data samples to create the input for the neural networks. The 200 data samples preceding a data sample are now used to predict the next data sample. This means that the first row of the matrix contains the first 200 Santa Fe data samples to predict the 201st data sample, the second row contains data samples 2 to 201 to predict the 202nd data sample and so on. This results in a training dataset and test dataset with dimensions (2800 × 200) and (800 × 200), which are the same dimensions as the state matrices used in the networks with reservoirs. The difference now is that the resulting matrices use the 200 previous data samples as features to predict the next data samples. Note that we will split the training dataset into a true training dataset, containing 2300 samples, and a validation set, containing 500 input samples.

The final performance of the different networks is evaluated by their normalized mean squared error (NMSE) on the test set between the expected output y and predicted output $\widehat{\mathbf{y}}$,

$NMSE\left(\widehat{\mathbf{y}},\mathbf{y}\right)=\frac{⟨{\left(\mathbf{y}-\widehat{\mathbf{y}}\right)}^2⟩}{⟨{\left(\mathbf{y}-⟨\mathbf{y}⟩\right)}^2⟩}.(6)$

The network with the lowest NMSE thus results in the best performance for this particular task. The typical state-of-the-art values for the normalized mean squared error on the Santa Fe one-step ahead predictions via RC system simulations are around 0.01 [46, 47].

Memory capacity

In order to give a heuristic explanation for the increase in performance between the delay-based reservoir computer and the DNN which uses the reservoir as preprocessor, we will calculate their task-independent memory capacities. This is done using techniques from [48] where we inject discrete input samples u_k from a uniform distribution between [−1, +1] into the reservoir and train the weights to reconstruct products of normalized Legendre polynomials via l_i-delayed past input samples u(k − l_i) [48, 49]. In this work, we will limit this delayed input to l_i ≤ 10, and we calculate the memory capacity up until degree 5 to limit the computation time.

The target data y(k) is produced by a product of Legendre polynomials P_δ(⋅), of a certain degree δ, from previous inputs. Note that there exist multiple combinations of Legendre polynomials if we consider combined degrees greater than 1. For example, if the combined degree d = 3, we have to consider product combinations of Legendre polynomials with degrees: δ ∈ {(3), (2, 1) and (1, 1, 1)}. For example, the combination δ = (2, 1) for the third degree can then be written as a product of Legendre polynomials with degree 2 and 1:

$y_{\left(\delta =\left(\mathrm{2,1}\right),\left(l_1,l_2,l_3\right)\right)}\left(k\right)=P_2\left(u\left(k-l_1\right),u\left(k-l_2\right)\right)P_1\left(u\left(k-l_3\right)\right),(7)$

where (l₁, l₂, l₃) are the set of indices of past input samples, which we have limited to l_i ≤ 10 here. This means that we also have many different possible combinations for these values, adding to the complexity when calculating the memory capacity. The mean squared error between the expected signal y(k), such as for the example given in Eq. (7), and the predicted signal $\widehat{y}(k)$ can be calculated for all input samples. The mean squared error, for a specific product combination δ and a set of specific indices of past inputs (l₁, … ), is used for calculating the memory capacity,

$C_{\left(\delta ,\left(l_1,\dots \right)\right)}=1-\frac{⟨{\left(\mathbf{y}-\widehat{\mathbf{y}}\right)}^2⟩}{⟨{\mathbf{y}}^2⟩},(8)$

where $C_{(\delta ,(l_1,\dots ))}\in [\mathrm{0,1}]$ and with the average taken over all input samples. If one then sums over all possible combinations of the delayed elements (l₁, … ), where l_i ≤ 10, for a specific combination of Legendre polynomials δ, we have

$C_{y_{\left(\delta \right)}}=\sum _{\left(l_1,\; \dots \right)}{C}_{y_{\left(\delta ,\left(l_1,\; \dots \right)\right)}}.(9)$

If we then sum $C_{y_{(\delta )}}$ over all possible Legendre combinations which give rise to the combined degree d, we have the memory capacity per degree d,

$C_d=\sum _{\delta }{C}_{y_{\left(\delta \right)}}.(10)$

The total computational capacity of the system, CC, can be calculated by summing over all memory capacities C_d, for all degrees. According to [48], its theoretical upper limit for the delay-based RC system considered in this paper is given by the amount of virtual nodes N. Since we are only using a finite amount of input data, we could potentially overestimate the value for the memory capacity C_d. To avoid this, we implement a threshold capacity C_thr, so that values below C_thr are not considered for calculating the memory capacity, as discussed in [48]. The reason for this is because memory capacities below C_thr are not statistically relevant and are thus removed for its calculation.

In order to limit the computational load when calculating the memory capacities, due to the large amount of possible combinations of Legendre polynomials and delays, we limit the amount of virtual nodes in the reservoir for this specific task to N = 25, instead of the previous N = 200 for the one-step ahead prediction task. The node separation θ remains fixed to θ = 20 ps, and the input data consists of 5 × 10⁵ uniformly distributed samples, with values between -1 and 1. For the parameters used here, we have a threshold memory capacity of approximately C_thr ≈ 2.7 × 10⁻⁴. Since we have changed the amount of virtual nodes to N = 25, we have also changed the layout of the DNN itself. It still consists of 3 fully-connected layers, but the DNN now takes input data with 25 features. The first hidden layer is a fully-connected layer with 12 nodes, followed by the ReLU activation function [36]. The next layer is another fully-connected layer, now with 6 nodes, and again with the ReLU activation function. The final layer again only has a single node for predicting ${\widehat{y}}_k$.

In case of the combined reservoir and DNN, we use the first 4 × 10⁴ data samples for training the model, while the last 10⁴ samples are used as validation dataset. This validation dataset is used for the early stopping procedure against overfitting, where the standard amount of training epochs is set at 1.5 × 10³ epochs. The DNN is trained using the Adam optimizer, with a learning rate of 10⁻³.

Results

Performance on santa Fe one-step ahead prediction task

We compare the different networks based on their performance as expressed by the NMSE on the one-step ahead prediction of the Santa Fe dataset. The final NMSE on the test dataset, together with their total training time and time per epoch are summarized in Table 2. The different times are measured on a standard consumer mobile CPU (Intel Core i7-10710U). For the parameters of the reservoir, we use the values given in Table 1, as they are the parameter values which were optimal in previous scans for the RC system [34].

TABLE 2

TABLE 2. NMSE and time used for training the different simulated network models, on the Santa Fe one-step ahead prediction task.

We have investigated the learning curves, i.e. the NMSE as a function of the epochs (not shown), of all networks which require backpropagation, i.e. containing a DNN or LSTM, for choosing the amount of epochs to train the networks. We have observed that all three networks showed a decreasing training loss with increasing epochs. For both the combined system of the reservoir and DNN and only the DNN, we have observed that the validation loss saturates to a constant loss after around 2000 epochs. As their training time per epoch is not very large for both these networks, as shown in Table 2, we have limited their amount of epochs to 10⁴, allowing for a good NMSE. For the LSTM network, we observed that the validation error still decreases with increasing epochs. Due to this network being very time-intensive to train, with a training time per epoch being 30 times that of the other two networks as shown in Table 2, we have limited its training to also 10⁴ epochs. It is important to note again that for this amount of epochs, the saturation of the validation loss is not yet reached for the LSTM.

The time required for calculating the weights of the RC network is negligible, because no backpropagation is performed here, in contrast to the other models. We can clearly see from Table 2 that the photonic reservoir coupled with the DNN as output layer outperforms all other networks, in both low training time and low NMSE. For the parameters specified in Table 1, we are able to achieve an NMSE for the reservoir combined with the DNN which is almost 4 times lower than the NMSE achieved when using a photonic RC system. The DNN has a total training time comparable to that of the photonic reservoir coupled with the DNN, and the same amount of free parameters that are being trained, but the NMSE is much larger when using only the DNN. The LSTM network, which is generally a good choice for time-series forecasting due to its recurrent nature, has an NMSE which is around 1.5 times larger than that of the photonic RC. This can be explained by the fact that the LSTM is very time-intensive to train compared to the other networks, so that we have opted to limit its amount of training epochs, and which still results in almost 1 hour of training time. We expect that if the amount of epochs is increased further (i.e. for several additional 10⁴ epochs), we are able to achieve a similar NMSE as the photonic RC. Both the DNN and LSTM networks have a higher NMSE compared to the photonic RC system, with the LSTM having the largest training time. The reason why the photonic RC system has a lower NMSE than the DNN is due to the fact that the RC system is a recurrent neural network, which is able to capture the time dependencies of sequential input data. For example, the (software) introduction of reservoir computing was partially introduced by the Echo State Network (ESN) [23], which is a recurrent neural network and which showed good performance on the Santa Fe time-series prediction task [25].

Note that the simulation of photonic reservoir itself requires a lot of time. This simulation is, however, not concluded in the training time in Table 2, because physical implementations of photonic RC can be very fast. Its computing time is approximately equal to the amount of input samples multiplied with the delay time, nτ. This is of the order of several μs and is thus negligible compared to the training times in Table 2. Note that the time required for the optimization of the (hyper)parameters of the reservoir (for the photonic RC and photonic reservoir with DNN) and the neural networks (for the DNN combined with or without the reservoir, and for the LSTM) is not shown in Table 2, as it is not actual training time. However, if one wants to achieve the best possible performance, a scan for the reservoir parameters and/or of the network hyperparameters needs to be performed, which also requires time. The advantage of the photonic reservoir is that its parameter optimization does not need to be very precise, as a good performance can already be achieved for a rather broad range of parameter values, as we will show in the following results.

The results in Table 2 show that the photonic reservoir, coupled with or without the DNN, results in a good performance. Therefore, we now investigate these two networks when varying the parameters of the reservoir instead of using only fixed reservoir parameters. We do this by varying the pump current, injection rate and feedback rate. For this, we fix the feedback rate and perform a grid scan over the pump current and injection rate in Figure 3. This is shown for both the RC system, in Figure 3A and the reservoir coupled with the DNN, in Figure 3B. The improvement factor, defined as the NMSE resulting from the RC system divided by the NMSE of the reservoir coupled with the DNN, for the same parameters of both reservoirs, is shown in Figure 3C. The same figures are shown in Figure 4, where the feedback rate and pump current are now varied, for a constant injection rate.

FIGURE 3

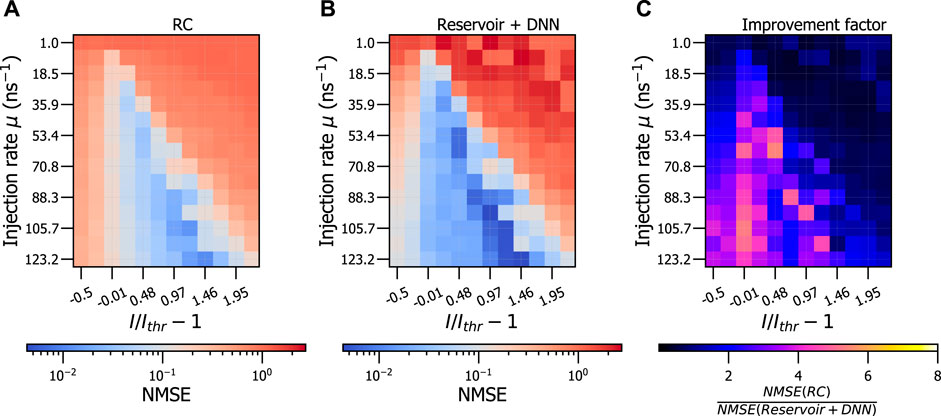
FIGURE 3. NMSE resulting from a grid search of injection rate and pump current, at constant feedback rate η =7.8 ns⁻¹, for conventional RC (A), for the photonic reservoir coupled with the DNN (trained for 1.6 ×10⁴ epochs) (B) and the improvement factor of the reservoir combined with the DNN compared to the RC system (C).

FIGURE 4

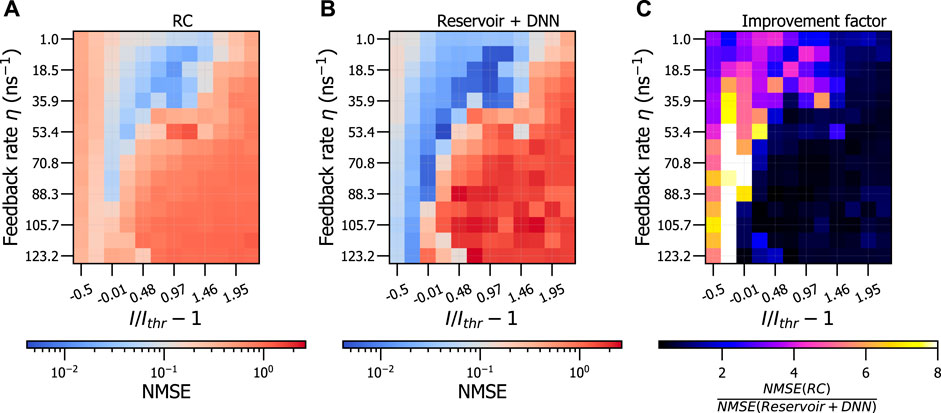
FIGURE 4. NMSE resulting from a grid search of feedback rate and pump current, at constant injection rate μ =98.1 ns⁻¹, for conventional RC (A), for the photonic reservoir coupled with the DNN (trained for 1.6 × 10⁴ epochs) (B) and the improvement factor of the reservoir combined with the DNN compared to the RC system (C).

Figure 3A shows that the RC system performs well for a broad range of pump currents and injection rates. This region can mainly be found around high pump currents and high injection rates. This is indicated by the light and dark blue regions in the figures. The darker the blue color, the better performance, indicated by a lower NMSE on the test set. Additionally, we observe that the region of good performance is broader, and with better performance, when the reservoir is combined with the DNN, as shown in Figure 3B. This improvement of the reservoir coupled with the DNN is also clearly visible in the improvement factor in Figure 3C. Values which are larger than 1 indicate an improvement in performance when using the reservoir with the DNN compared to the RC system. This figure shows that a large portion of parameter space results in an improvement, often with a factor around 2 to 5, compared to only the RC system. Notably, the region below the threshold pump current is improved when using the combined system (shown in Figure 3C where the horizontal axis is less than 0). This indicates that these reservoirs can function relatively well even when the threshold pump current is not yet reached. If one considers the region at high current and low injection rate for which the RC did not result in a good performance (indicated by the red regions in Figure 3A), we can see that the performance at these parameter combinations is not improved upon when the reservoir is combined with the DNN (also shown by the red regions in Figure 3B).

As with Figure 3, Figure 4A shows that there is a broad parameter range of pump current and feedback rate for which the RC system performs well. This region is further broadened and improved when we use a reservoir coupled with the DNN, shown in Figure 4B. This is again reflected by the light and dark blue regions in both figures, indicating a low NMSE, and thus good performance. We observe that when the pump current is increased above threshold, the feedback rate needs to be decreased in order to achieve a good performance on both networks. Analogous to Figure 3, all of the parameter combinations which were already performing well with the RC system are improved when the reservoir is coupled with the DNN at those same parameter combinations. This is shown in Figure 4C, where typical improvement factors can be found around 4 to 8 for a broad area of parameter combinations. Most notably, there are even parameter combinations which have more than 10 times improvement in performance, which can be found just below threshold pump current¹. This shows that the feedback rate and pump current play a large role when using reservoirs combined with DNNs, and can allow for large performance increases when properly adjusted.

In order to find the optimal values for the reservoir parameters, we perform an additional Bayesian search in the parameter space of pump current, injection rate and feedback rate. This Bayesian search is performed using the Gaussian Processes function gp_minimize of the scikit-optimize 0.8.1 library. Figure 5 shows the NMSE for 1653 points projected on the pump-current and injection rate axes (Figures 5A, B) and on the pump-current and feedback rate axes (Figures 5C, D). This figure shows the projections of a true three dimensional scan of the full three dimensional parameter ranges for the RC system and the reservoir coupled with the DNN. This is opposed to Figures 3, 4, where only two dimensional scans were performed, and where one value always remained fixed (either feedback rate or injection rate). In Figure 5, the parameter combinations which result in a good performance, and thus low NMSE, are represented by large, dark blue dots. If the NMSE is high, and thus a poor performance, the dots are small and red.

FIGURE 5

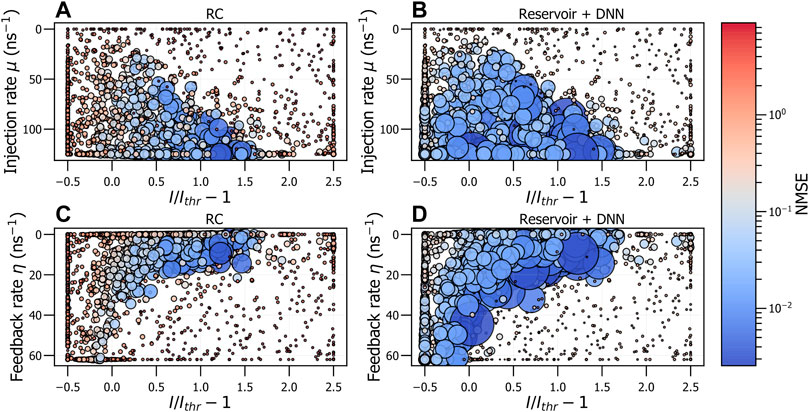
FIGURE 5. NMSE for various values for injected pump current, feedback rate and injection rate. The selection of these values was performed using a Bayesian optimisation of this three dimensional parameter space. The two left plots are the results when using only an RC system, (A,C), and the two right plots are the results of the reservoir combined with the DNN (trained for 1.6 ×10⁴ epochs), (B,D). Large and blue values for the dots indicate a low NMSE, and thus a good performance.

The results of Figure 5 show that also in this scan of parameter space the NMSE is improved when the reservoir is coupled with the DNN, as indicated by the larger and bluer dots in Figures 5B, D as compared to Figures 5A, C. This is even the case for parameter values which resulted in a poor performance for the RC systems, e.g. near the edges of the searched parameter space. This is in agreement with the results found in Figures 3, 4, where the same parameter regions with good performance can be found. The most optimal values (i.e. with the lowest NMSE) found for both systems are shown in Table 3. In this table, we see that the reservoir coupled with the DNN, at its most optimal parameter values, is able to have an NMSE which is 3.5 times better than the best NMSE found with RC, also at its most optimal parameter values. Note that these two NMSE values are found at different parameter combinations, as we are comparing the best possible performance we are able to achieve with both systems. This is in contrast to the previous two dimensional scans, where we reported the improvement factor for the same parameter combinations, where we observed higher improvement factors.

TABLE 3

TABLE 3. Optimal NMSE and reservoir parameters for the photonic RC system and the reservoir combined with the DNN (trained for 1.6 ×10⁴ epochs), on the Santa Fe one-step ahead prediction task.

Memory capacity

In the previous section, we have established that combining a photonic reservoir with a DNN works well. We now try to gain more insight as to why such systems work well by calculating their memory capacity.

Figure 6 shows the memory capacity for various degrees as colored bars. In this figure, we observe that the delay-based reservoir coupled with the DNN has for both the linear and nonlinear degrees the highest memory capacities. This results in this system having the largest total memory capacity, when compared with the conventional delay-based reservoir computing system.

FIGURE 6

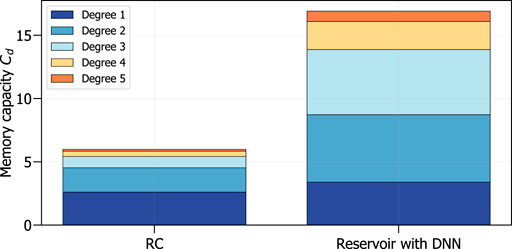
FIGURE 6. Memory capacity per degree of linearly independent basis functions for the delay-based reservoir computing system, with N =25, and the reservoir, also with N =25, coupled with the DNN.

Knowing that the total memory capacity for the RC system is bounded by N, in our case N = 25, we observe that the RC system has a low memory capacity. This is presumed to be the case due to noise inherently present in the delay-based system and due to correlations present between virtual nodes. As the output layer in such system is only a linear layer, we conjecture that this system thus has more trouble dealing with such negative effects compared to the combined reservoir with the DNN, which can minimize these effects and has much more inherent nonlinearity due to its structure. This also explains why mostly the nonlinear degrees for the memory capacity seem to benefit from adding a DNN to the reservoir, resulting in the total memory capacity being larger.

Note that it is not clear if the total memory capacity of the combined system is still bounded by the theoretical upper limit for the RC system, which is the size of the photonic reservoir (i.e. the maximum total memory capacity is equal to the number of nodes). It might be possible that the theoretical maximum of the memory capacity for the combined system is larger than the upper limit for the RC system, as additional variables are introduced in the DNN. However, an in-depth study of the theoretical maximum memory capacity of the combined system is outside the scope of the present paper.

Figure 6 shows that coupling a delay-based RC system with a DNN significantly enhances both the linear and nonlinear memory capacities. This gives a heuristic explanation as to why it is able to outperform a conventional RC on the Santa Fe prediction task. This is because the Santa Fe one-step ahead prediction task typically requires high non-linear memory capacities [50], which is the case when a preprocessor is used. This also indicates that the combination of a reservoir and a DNN can potentially outperform the RC system in other tasks, different from the time-series prediction.

Discussion

In this work, we have numerically investigated the use of photonic delay-based reservoirs as preprocessors for deep neural networks. This results in a combined system which is different from conventional reservoir computing, as the output layer now contains more parameters which can be trained. The choice for photonic reservoirs was made because of their potential to achieve fast information processing, high bandwidth and small power consumption, making such reservoirs ideal as physically implemented preprocessors. These reservoirs are able to transform the input data into a higher dimensional state-space, which improves performance of the deep neural networks. We show that using a preprocessing reservoir with a deep neural network results in an test error which is almost four times lower when compared to conventional reservoir computing, at the most optimal reservoir parameters, and around ten times lower when compared with the DNN alone for predicting the Santa Fe time-series. Additionally, the improvement in performance is valid for a broad region of reservoir parameters, making the preprocessing reservoir advantageous even when it is not properly fine-tuned. We have also investigated the memory capacity in order to provide an explanation for the improvement when using a reservoir with a deep neural network compared to the reservoir computing system. We found that the memory capacity with the combined system is much higher when compared with the reservoir computing system. Therefore, we have shown that photonic reservoirs are ideally suited as preprocessors for achieving improved performance when combined with deep neural networks.

In our simulations, we have focused on predicting the Santa Fe time-series as main learning task. This task typically requires large nonlinear memory capacities in order to result in a good performance. A reservoir computing system is able to solve this task, as it has nonlinear memory capacity. However, as shown by our study of the memory capacity, we are able to increase the linear and nonlinear memory capacities of a DNN when we combine it with a preprocessor.

Note that it is also possible to use other networks, different from the DNN, which also have intrinsic memory, such as e.g. the LSTM network. We have also investigated its performance on the Santa Fe time-series prediction task, but observed that its performance is slightly worse compared to the photonic reservoir computing system. Additionally, if we use an LSTM network with many parameters, it becomes very intesive to train. Using only a DNN for this prediction task results in the worst performance of all investigated networks. This is most likely because such networks have a lower memory capacity compared to the other networks. Note that some extra form of memory is added to both the LSTM and DNN due to the construction of the input data (i.e. using a sliding window of the input data) but it is not sufficient for this training task as reflected by their performance. This shows that first using a recurrent neural network as preprocessor for DNNs results in better performance for time-dependent prediction tasks, such as the Santa Fe task, as opposed to using recurrent DNNs. This is also supported by the fact that the memory capacity, which is a task-independent performance indicator, is higher when using a combined system consisting of a reservoir as preprocessor and a DNN when compared to using only a reservoir computing system. We conjecture that due to the increased (non)linear memory capacities, the addition of a preprocessor is also able to yield improvements for other tasks which require such memory capacities, e.g. for tasks defined in [27]. Therefore, we are convinced that additional learning tasks, such as dynamical system modelling tasks (e.g. nonlinear autoregressive moving average model, NARMA) and nonlinear channel-equalization tasks could be of great interest for future studies, due to their time-dependent nature, for the combined system of a reservoir and DNN.

Note that one does not necessarily need to use a delay-based reservoir to function as a preprocessor. The use of other reservoirs is also expected to give improvements, such as e.g. for photonic spatial reservoirs, or other types of photonic reservoirs, when coupled with DNNs. This is further supported for photonic spatial reservoirs, such as the swirl architecture, by the fact that they show good performance on the same task considered here [51], i.e. the Santa Fe one-step ahead prediction task. Therefore, we are convinced that adding such a reservoir to a DNN will also result in an improved performance. Our study thus indicates that physical reservoirs, as developed in the framework of reservoir computing, are very well suited as preprocessors for DNNs, resulting in improved performance.

Data availability statement

Data underlying the results presented in this paper are not publicly available at this time but may be obtained from the authors upon reasonable request.

Author contributions

IB performed the simulations and analyzed the data. IB, GVa, PB, and GVe discussed the results and wrote the paper.

Funding

This research was funded by the Research Foundation Flanders (FWO) under grants G028618N, G029519N and G006020N. Additional funding was provided by the EOS project “Photonic Ising Machines”. This project (EOS number 40007536) has received funding from the FWO and F.R.S.-FNRS under the Excellence of Science (EOS) programme.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Footnotes

¹Note that this is not visible in Figure 4C due to the maximum scale set here.

References

1. Chowdhary K. Natural language processing. New Delhi: Fundamentals of artificial intelligence (2020). p. 603–49.

CrossRef Full Text | Google Scholar

2. Jiménez-Luna J, Grisoni F, Schneider G. Drug discovery with explainable artificial intelligence. Nat Mach Intell (2020) 2:573–84. doi:10.1038/s42256-020-00236-4

CrossRef Full Text | Google Scholar

3. Esteva A, Kuprel B, Novoa RA, Ko J, Swetter SM, Blau HM, et al. Dermatologist-level classification of skin cancer with deep neural networks. nature (2017) 542:115–8. doi:10.1038/nature21056

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Jermyn M, Desroches J, Mercier J, Tremblay MA, St-Arnaud K, Guiot MC, et al. Neural networks improve brain cancer detection with Raman spectroscopy in the presence of operating room light artifacts. J Biomed Opt (2016) 21:094002. doi:10.1117/1.jbo.21.9.094002

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Wang D, Khosla A, Gargeya R, Irshad H, Beck AH. Deep learning for identifying metastatic breast cancer. arXiv preprint arXiv:1606.05718 (2016).

Google Scholar

6. Van Gompel J, Spina D, Develder C. Satellite based fault diagnosis of photovoltaic systems using recurrent neural networks. Appl Energ (2022) 305:117874. doi:10.1016/j.apenergy.2021.117874

CrossRef Full Text | Google Scholar

7. Xu X, Ding Y, Hu SX, Niemier M, Cong J, Hu Y, et al. Scaling for edge inference of deep neural networks. Nat Electron (2018) 1:216–22. doi:10.1038/s41928-018-0059-3

CrossRef Full Text | Google Scholar

8. Brown T, Mann B, Ryder N, Subbiah M, Kaplan JD, Dhariwal P, et al. Language models are few-shot learners. Adv Neural Inf Process Syst (2020) 33:1877–901.

Google Scholar

9. Sze V, Chen YH, Yang TJ, Emer JS. Efficient processing of deep neural networks: A tutorial and survey. Proc IEEE (2017) 105:2295–329. doi:10.1109/jproc.2017.2761740

CrossRef Full Text | Google Scholar

10. Baischer L, Wess M, TaheriNejad N. Learning on hardware: A tutorial on neural network accelerators and co-processors (2021). arXiv preprint arXiv:2104.09252.

Google Scholar

11. Huang C, Sorger VJ, Miscuglio M, Al-Qadasi M, Mukherjee A, Lampe L, et al. Prospects and applications of photonic neural networks. Adv Phys X (2022) 7:1981155. doi:10.1080/23746149.2021.1981155

CrossRef Full Text | Google Scholar

12. Wu J, Lin X, Guo Y, Liu J, Fang L, Jiao S, et al. Analog optical computing for artificial intelligence. Engineering (2021) 10:133–45. doi:10.1016/j.eng.2021.06.021

CrossRef Full Text | Google Scholar

13. Shen Y, Harris NC, Skirlo S, Prabhu M, Baehr-Jones T, Hochberg M, et al. Deep learning with coherent nanophotonic circuits. Nat Photon (2017) 11:441–6. doi:10.1038/nphoton.2017.93

CrossRef Full Text | Google Scholar

14. Lin X, Rivenson Y, Yardimci NT, Veli M, Luo Y, Jarrahi M, et al. All-optical machine learning using diffractive deep neural networks. Science (2018) 361:1004–8. doi:10.1126/science.aat8084

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Zuo Y, Li B, Zhao Y, Jiang Y, Chen YC, Chen P, et al. All-optical neural network with nonlinear activation functions. Optica (2019) 6:1132–7. doi:10.1364/optica.6.001132

CrossRef Full Text | Google Scholar

16. Xu X, Tan M, Corcoran B, Wu J, Boes A, Nguyen TG, et al. 11 TOPS photonic convolutional accelerator for optical neural networks. Nature (2021) 589:44–51. doi:10.1038/s41586-020-03063-0

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Li Y, Xue Y, Tian L. Deep speckle correlation: A deep learning approach toward scalable imaging through scattering media. Optica (2018) 5:1181–90. doi:10.1364/optica.5.001181

CrossRef Full Text | Google Scholar

18. Brossollet C, Cappelli A, Carron I, Chaintoutis C, Chatelain A, Daudet L, et al. LightOn optical processing unit: Scaling-up AI and HPC with a non von Neumann co-processor (2021). arXiv preprint arXiv:2107.11814.

Google Scholar

19. Launay J, Poli I, Müller K, Carron I, Daudet L, Krzakala F, et al. Light-in-the-loop: Using a photonics co-processor for scalable training of neural networks. arXiv preprint arXiv:2006.01475 (2020).

Google Scholar

20. Tanaka G, Yamane T, Héroux JB, Nakane R, Kanazawa N, Takeda S, et al. Recent advances in physical reservoir computing: A review. Neural Networks (2019) 115:100–23. doi:10.1016/j.neunet.2019.03.005

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Verstraeten D, Schrauwen B, Stroobandt D, Van Campenhout J. Isolated word recognition with the liquid state machine: A case study. Inf Process Lett (2005) 95:521–8. doi:10.1016/j.ipl.2005.05.019

CrossRef Full Text | Google Scholar

22. Verstraeten D, Schrauwen B, Stroobandt D. IEEE international joint conference on neural network proceedings. IEEE (2006). p. 1050–3.Reservoir-based techniques for speech recognitionThe.

CrossRef Full Text | Google Scholar

23. Jaeger H, Haas H. Harnessing nonlinearity: Predicting chaotic systems and saving energy in wireless communication. Science (2004) 304:78–80. doi:10.1126/science.1091277

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Skibinsky-Gitlin ES, Alomar ML, Isern E, Roca M, Canals V, Rossello JL. Reservoir computing hardware for time series forecasting. In: 2018 28th international symposium on power and timing modeling, optimization and simulation (PATMOS). IEEE (2018). p. 133–9.

CrossRef Full Text | Google Scholar

25. Canaday D, Griffith A, Gauthier DJ. Rapid time series prediction with a hardware-based reservoir computer. Chaos (2018) 28:123119. doi:10.1063/1.5048199

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Paquot Y, Duport F, Smerieri A, Dambre J, Schrauwen B, Haelterman M, et al. Optoelectronic reservoir computing. Sci Rep (2012) 2:287–6. doi:10.1038/srep00287

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Van der Sande G, Brunner D, Soriano MC. Advances in photonic reservoir computing. Nanophotonics (2017) 6:561–76. doi:10.1515/nanoph-2016-0132

CrossRef Full Text | Google Scholar

28. De Lima TF, Shastri BJ, Tait AN, Nahmias MA, Prucnal PR. Progress in neuromorphic photonics. Nanophotonics (2017) 6:577–99. doi:10.1515/nanoph-2016-0139

CrossRef Full Text | Google Scholar

29. Larger L, Soriano MC, Brunner D, Appeltant L, Gutiérrez JM, Pesquera L, et al. Photonic information processing beyond turing: An optoelectronic implementation of reservoir computing. Opt Express (2012) 20:3241–9. doi:10.1364/oe.20.003241

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Salehi MR, Abiri E, Dehyadegari L. An analytical approach to photonic reservoir computing–a network of SOA’s–for noisy speech recognition. Opt Commun (2013) 306:135–9. doi:10.1016/j.optcom.2013.05.036

CrossRef Full Text | Google Scholar

31. Harkhoe K, Verschaffelt G, Katumba A, Bienstman P, Van der Sande G. Demonstrating delay-based reservoir computing using a compact photonic integrated chip. Opt Express (2020) 28:3086–96. doi:10.1364/oe.382556

PubMed Abstract | CrossRef Full Text | Google Scholar

32. Appeltant L, Soriano MC, Van der Sande G, Danckaert J, Massar S, Dambre J, et al. Information processing using a single dynamical node as complex system. Nat Commun (2011) 2:468–6. doi:10.1038/ncomms1476

PubMed Abstract | CrossRef Full Text | Google Scholar

33. Lenstra D, Yousefi M. Rate-equation model for multi-mode semiconductor lasers with spatial hole burning. Opt Express (2014) 22:8143–9. doi:10.1364/oe.22.008143

PubMed Abstract | CrossRef Full Text | Google Scholar

34. Harkhoe K, Van der Sande G. Delay-based reservoir computing using multimode semiconductor lasers: Exploiting the rich carrier dynamics. IEEE J Sel Top Quan Electron (2019) 25:1–9. doi:10.1109/jstqe.2019.2952594

CrossRef Full Text | Google Scholar

35. Stelzer F, Röhm A, Lüdge K, Yanchuk S. Performance boost of time-delay reservoir computing by non-resonant clock cycle. Neural Networks (2020) 124:158–69. doi:10.1016/j.neunet.2020.01.010

PubMed Abstract | CrossRef Full Text | Google Scholar

36. Nair V, Hinton GE. Rectified linear units improve restricted Boltzmann machines. Toronto: Icml (2010).

Google Scholar

37. Kingma DP, Ba J. Adam: A method for stochastic optimization (2014). arXiv preprint arXiv:1412.6980.

Google Scholar

38. Sagheer A, Kotb M. Time series forecasting of petroleum production using deep LSTM recurrent networks. Neurocomputing (2019) 323:203–13. doi:10.1016/j.neucom.2018.09.082

CrossRef Full Text | Google Scholar

39. Chimmula VKR, Zhang L. Time series forecasting of COVID-19 transmission in Canada using LSTM networks. Chaos, Solitons & Fractals (2020) 135:109864. doi:10.1016/j.chaos.2020.109864

PubMed Abstract | CrossRef Full Text | Google Scholar

40. Hochreiter S, Schmidhuber J. Long short-term memory. Neural Comput (1997) 9:1735–80. doi:10.1162/neco.1997.9.8.1735

PubMed Abstract | CrossRef Full Text | Google Scholar

41. LeCun Y, Bengio Y, Hinton G. Deep learning. nature (2015) 521:436–44. doi:10.1038/nature14539

PubMed Abstract | CrossRef Full Text | Google Scholar

42. Voulodimos A, Doulamis N, Doulamis A, Protopapadakis E. Deep learning for computer vision: A brief review (2018). p. 2018.Comput intelligence Neurosci.

43. Brunner D, Soriano MC, Mirasso CR, Fischer I. Parallel photonic information processing at gigabyte per second data rates using transient states. Nat Commun (2013) 4:1364–7. doi:10.1038/ncomms2368

PubMed Abstract | CrossRef Full Text | Google Scholar

44. Nakajima M, Tanaka K, Hashimoto T. Scalable reservoir computing on coherent linear photonic processor. Commun Phys (2021) 4:20–12. doi:10.1038/s42005-021-00519-1

CrossRef Full Text | Google Scholar

45. Weigend AS, Gershenfeld NA. Results of the time series prediction competition at the Santa Fe Institute. In IEEE international conference on neural networks (IEEE) (1993) 1786–93.

Google Scholar

46. Nguimdo RM, Verschaffelt G, Danckaert J, Van der Sande G. Fast photonic information processing using semiconductor lasers with delayed optical feedback: Role of phase dynamics. Opt Express (2014) 22:8672–86. doi:10.1364/oe.22.008672

PubMed Abstract | CrossRef Full Text | Google Scholar

47. Soriano MC, Ortín S, Brunner D, Larger L, Mirasso CR, Fischer I, et al. Optoelectronic reservoir computing: Tackling noise-induced performance degradation. Opt Express (2013) 21:12–20. doi:10.1364/oe.21.000012

PubMed Abstract | CrossRef Full Text | Google Scholar

48. Dambre J, Verstraeten D, Schrauwen B, Massar S. Information processing capacity of dynamical systems. Sci Rep (2012) 2:514–7. doi:10.1038/srep00514

PubMed Abstract | CrossRef Full Text | Google Scholar

49. Harkhoe K, Van der Sande G. Task-independent computational abilities of semiconductor lasers with delayed optical feedback for reservoir computing. In: Photonics, 6. Basel: Multidisciplinary Digital Publishing Institute (2019). p. 124.

CrossRef Full Text | Google Scholar

50. Inubushi M, Yoshimura K. Reservoir computing beyond memory-nonlinearity trade-off. Sci Rep (2017) 7:10199–10. doi:10.1038/s41598-017-10257-6

PubMed Abstract | CrossRef Full Text | Google Scholar

51. Freiberger M, Sackesyn S, Ma C, Katumba A, Bienstman P, Dambre J. Improving time series recognition and prediction with networks and ensembles of passive photonic reservoirs. IEEE J Sel Top Quan Electron (2019) 26:1–11. doi:10.1109/jstqe.2019.2929699

CrossRef Full Text | Google Scholar