
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Phys., 14 December 2022
Sec. Low-Temperature Plasma Physics
Volume 10 - 2022 | https://doi.org/10.3389/fphy.2022.1049218
This article is part of the Research TopicEditor’s Challenge in Low-Temperature Plasma Physics: Atmospheric Pressure Nonequilibrium PlasmaView all 4 articles
Electron–hole pairs in semiconductors can be stimulated by a laser beam with energy larger than the energy gap of the semiconductor. The interaction between an electron–hole plasma with a laser beam can be a source of instability. The dependence of the instability on the electron and hole temperatures and the unperturbed potential of the incident laser are examined. Using Maxwell’s equations along with electron–hole fluid equations, an evolution equation describing the system is obtained. The latter is reduced to an energy equation that characterizes localized pulse propagation.
Laser pulses are a powerful tool to produce modifications in different materials [1, 2]. Laser pulses can be used to locally modify inside the material’s bulk, the chemical structure, the index of refraction, the density of color centers, and surface nanostructures. Under a laser-induced strong field, bound electrons transit from the valence band to the conduction band, leaving a hole in the valence band. Pairs of the electron–hole plasma are accelerated in the laser field, which results in the multiplication of the free carrier density via impact ionization and potentially in the creation of a dense electron–hole plasma. Plasma provides a promising medium because it is capable of tolerating very high powers and shows strong non-linear effects. On the other hand, electrons and their corresponding holes exist as free carriers that are created as pairs in inter-band transitions [3]. Particles of the electron–hole plasma are accelerated in the laser field, which results in the multiplication of the free carrier density via impact ionization and potentially in the creation of a dense electron–hole plasma. Finally, at timescales much larger than several picoseconds, thermal and structural events take place inside the material [1]. Semiconductors provide a compact and less expensive medium to model non-linear phenomena encountered in laser-produced plasmas. When a laser beam propagates through plasmas, the shape of the pulse changes in the form of a steeped front and broad tail due to plasma-based non-linearities [4, 5]. The produced non-linear waves can experience amplitude modulation because of the coupling between the propagating laser and non-linear plasma environment.
Various studies of the laser–plasma interaction were carried out theoretically and experimentally, such as Kruer [6] introduced a theoretical study with evidence that the experiment on laser light could heat an electron plasma wave. Later, Manes et al. [7] introduced an experimental work on how the electron plasma absorbs energy from a high laser intensity that led to plasma heating. Ripin et al. [8] carried out an experiment to illustrate that the long and low-irradiance laser pulses are very efficient in the absorption process with non-thermal electron heating. They studied the mechanisms of the absorption process, plasma formation, plasma heating, and plasma expansion by experimental treatment. Shukla et al. [9] theoretically investigated the wave equation for the laser beam propagating in ion plasma. They derived an effective potential energy and non-linear frequency shift, taking into account the linear and non-linear motions of plasma under the effect of ponderomotive electromagnetic force. Kruer [10] introduced the main ideas about the laser–plasma interaction, such as describing the linear and non-linear interactions and the plasma instabilities. The effects of the laser interaction and semiconductor materials appear on many mechanisms such as the recombination process, increased current flow, decreased energy gap, load diffusion, decreased carrier mobility, increased collision rate, increased conductivity, and decreased conductivity. Yeom et al. [11] conducted a theoretical study about the interaction of laser beams and electrons in a semiconductor material (silicon) by using the Monte Carlo method, which led to the electron motion of oscillation and the creation of electron–hole pairs. Shukla et al. [12] investigated electron–positron pairs by introducing an analytical solution of the wave equation that describes the interaction between the laser beam and pair plasma. Rubano et al. [13] introduced an experimental excitation with the non-radiative recombination process by intense laser pulses. Dyukin et al. [14] studied the interaction of femtosecond laser pulses with solids. They found that the kinetic energy of electrons increased by pulse absorption, and energy distribution became non-equilibrium. The interaction of intensive laser fields and relativistic electron–positron–ion plasma was investigated by [15]. Bogachev et al. [16] generated an electron–hole pair by the laser beam acting on the material surfaces, which could be used as a dipole antenna. Tsatrafyllis et al. [17] conducted an experiment about the interaction of a strong laser pulse with the semiconductor. They could measure the absorption coefficient in the presence of strong laser fields. Shcherbakov et al. [18] studied the interaction of the semiconductor with a short laser pulse. They introduced experimental and theoretical development and studied the non-linear effects of semiconductors with the laser. Gupta and Suk [19] considered the beating of two co-propagating laser beams that can resonantly excite a large amplitude plasma wave in a narrow-gap semiconductor. The higher ponderomotive force on the electrons due to the plasma beat wave makes the medium highly non-linear. As a result, the incident laser beams become self-focused due to the non-linearity by the ponderomotive force. They showed the self-focusing and spot size evolution of the laser beams in semiconductor plasmas. From the last, plasma provides a promising medium since it is eligible for tolerating very high powers and shows strong non-linear effects. The motivation of the present work is to examine the interaction between the laser pulse and semiconductor (such as GaAs and GaSb). This interaction gives rise to the generation of non-linear localized structures. We used Maxwell’s equation along with electron and hole relativistic momentum equations. These equations are reduced to one evolution equation called the modified non-linear Schrödinger (mNLS) equation. Furthermore, the instability regions are examined. The mNLS equation is reduced to an energy equation, which characterizes the propagating localized pulses.
The dynamics of the electromagnetic wave (EMW) in e–h pair semiconductor plasma is introduced by Maxwell’s Ref. [20]
where A is the vector potential of the laser, c is the light speed, and J is the current between the carriers, and it is given by
where e is the magnitude of the electron charge, ne(nh) is the electron (hole) number density, and ve(vh) is the electron (hole) velocity in the electromagnetic field.
According to the Coulomb gauge, (the vector potential has no divergence), ∇ ⋅A = 0, then Eq. 1 can be written as
Poisson’s equation presents the electric potential ϕ, which is given by
where ϕ is the ambipolar potential associated with the plasma slow motion.
The electron and hole momentum conservation equation gives the relativistic electron and hole velocities as
where m0(mh) is the mass of electron (hole), and
Given a large amount of activity in this field, we only highlighted the applications, focusing on intensities greater than 1018 W/cm2, where relativistic effects dominate phenomena (see [21, 22]) that cover applications in the intensity range 1014–1018 W/cm2. At intensities greater than 1018 W/cm2, the field of the laser is much larger than the Coulomb field binding the ground state electron in the hydrogen atom, Eat = 5 × 109 V/cm. At 1019 W/cm2, the laser electric field is close to 1011 V/cm, 20 times Eat. At these intensities, the electrons have a relativistic characteristic. They acquire cycle-average oscillatory energy (quiver energy) Eosc = moc2(l + 2Up/moc2 − 1) greater than the electron rest energy, where mo is the electron rest mass. For example, at 1019 W/cm2, for λ = 1 μm, this quiver energy is on the order of 1 MeV or twice the electron rest energy moc2 = 0.5 MeV. The relativistic nature of the electron motion requires the use of the full Lorentz force, F = q(E + v/cB), where q is the charge of the electron; E and B are the vector electric and magnetic fields of the laser, respectively; v is the quiver velocity; and c is the speed of light. It should be noted that in linear and non-linear optics (of the bound electron), the force due to the magnetic field is always neglected because the quiver velocity of the electron is small compared to c. Above 1018 W/cm2, the magnetic and electric forces applied to the electron become equal and responsible for extremely large light pressure, P = I/c. At 1019 W/cm2, the light pressure reaches the respectable value of 0.3 Gbar. It has a profound implicate.
Now, we define the expressions of the densities of the electrons and holes ne,h in terms of potentials. The momentum equation in the presence of the relativistic effect [23] is given as
where j = e, h and the pressure Pj takes the form
where Tj is the electron and hole thermal temperature in electron volt.
The interaction of electromagnetic waves with charged particles is of practical interest in the study of the laboratory and astrophysical plasma. Linear theory shows that electromagnetic waves with frequencies less than the electron plasma frequency cannot propagate in unmagnetized plasma. In addition to the electron mass variation non-linearity, the self-interaction of large amplitude waves also leads to a time-averaged low-frequency non-linear force, namely, the ponderomotive force. Because of the large mass of the ions, acting mainly on the electrons, expelling them from regions of high field intensity, the ambipolar field thus created pulls away the ions. The local plasma density is, therefore, reduced by the ponderomotive force. The combined effect of the ponderomotive force and the relativistic electron mass variation on the modulational instability, soliton formation, self-focusing, and profile modification has been investigated. The low-frequency electrostatic potential is balanced by the relativistic ponderomotive potential that relativistic effects can modify the plasma flow speed in the outer and inner density shelves quantitatively [23].
Substituting the relativistic velocity vj from Eq. 5 and the expressions
where ne0(nh0) is the unperturbed electron (hole) number density. Here, we assume that the number density is homogeneous for high frequency near the absorption peak. The homogeneity increases with increasing temperature as in the case at hand [24].
Non-linear interactions between intense electromagnetic waves and the plasma slow motion produce a slowly varying envelope of circularly polarized electromagnetic waves. The interaction of the intense electromagnetic waves and the slow plasma motion is expressed as a vector potential, which takes the form [15]
where a and b are constants, k is the wave vector, r is the radial space coordinate, ω is the frequency of the electromagnetic field, and t is the time of the interaction. Applying Eq. 9 into Eq. 3, we have
Applying the following scaling
The dispersion relation of our plasma model between the field and the particles takes the form [23, 25]
For
where
Substituting the dispersion relation (Eq. 13) into Eq. 11, we have
where M = me/mh is the mass ratio of the electron to hole. Eq. 14 is a final evolution equation in the form of the modified non-linear Schrödinger (mNLS) equation.
It is important to find a relation between the densities Ne,h and the potential a. From Eqs. 7, 8, we have
and
where βe = m0c2/Te, βh = mhc2/Th,
To get a relation between the potential Φ and vector potential a, we compare Eqs. 7, 15 to have
Furthermore, from Eqs 8, 16, we get
In the quasi-neutral limit of the plasma Ne = Nh, from Eqs 17, 18, we obtain
where E = βe/(βe + Mβh) and H = βh/(βe + Mβh).
We expand Ne and Nh using Taylor’s expansion and substitute into Eq. 14 to obtain the NLS equation as
for λ, given in Appendix A.
To obtain the dispersion relation for the instability, we assume that the vector potential takes the expression [25]
where a0 is an unperturbed potential, a1 is a perturbed potential, and δ is the non-linear frequency shift. Substituting Eq. 21 into Eq. 14, we obtain the non-linear frequency shift as
To discuss the non-linear dispersion relation for our purposes, we linearize Eq. 14 with respect to a1 as
where Ω(k) is the frequency (wave number) of the low-frequency modulation.
Substituting the expression of a1, its conjugate, and the expansions for the last term in Eq. 14, then the linear differential equation in terms a1 takes the form
where β and β* are given in Appendix A. The non-linear dispersion relation of our model reads
which gives the modulational instability growth rate Γ = −iΩ [26, 27], and
We have studied the non-linear propagation of arbitrary large-amplitude light pulses in an electron–hole plasma, taking into account the relativistic electron and hole mass increase in the electromagnetic fields, as well as the plasma density profile modification by the relativistic ponderomotive force of light. The combined action and non-linear coupling between these two non-linear effects produce a modulational instability of an intense light pulse, leading to light localization and intensification.
Now, we discuss the localized non-linear solution of Eq. 14 using the separation of the variables, we assume that a is given by the relation
Substituting Eq. 27 into Eq. 14, we get the energy equation
where Ψ takes the form of the Sagdeev-like potential as
where A, B, and C are given in Appendix A.
There are many types of semiconductor plasmas that can interact with the laser, such as gallium antimonide (GaSb) and gallium arsenide (GaAs). We apply our mathematical model of the laser–plasma interaction using the physical properties of GaAs and GaSb [28, 29]. It is well known that GaAs and GaSb are two examples of extrinsic semiconductors since they include some impurities, so they are not chemically pure, such as those termed intrinsic semiconductors. In extrinsic semiconductors, the number of holes and electrons is not similar; therefore, it is determined by the properties of the impurities. Even then, in the present study to simplify the analysis, we assumed a homogeneous distribution for a quasi-neutral concept. The interaction between the laser and plasma wave follow the Raman interaction, which demands the unperturbed potential of the incident laser a0, which must satisfy the condition 0 ≤ a0 ≤ 1 [30]. The plasma parameters for GaSb are
The NLS Eq. 20 has two solutions called bright and dark solutions. Each solution depends on the sign of the product of the coefficients of non-linear and dispersion terms. The coefficient of the dispersion term is always positive, but the coefficient of the non-linear term λ should be examined as depicted in Figure 1. We have used the data from both types of semiconductors, namely, GaSb and GaAs. It is seen that the coefficient of the non-linear term λ is always negative. Therefore, a dark or stable wave packet exists, and a bright or unstable pulse cannot propagate [32, 33].
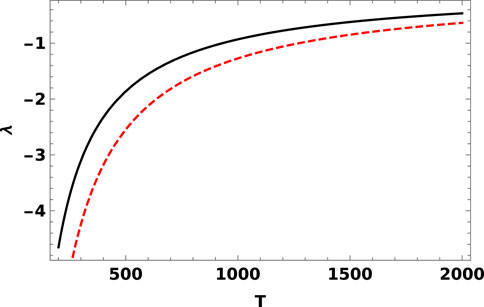
FIGURE 1. Coefficient of the non-linear term vs. electron–hole temperature for GaSb and GaAs semiconductors. The black curve stands for GaSb, where
The existence of finite amplitude solitons of circularly polarized electromagnetic waves has been considered by several authors in recent years. Using the quasi-neutrality assumption for the low-frequency response of the plasma, the researchers showed the existence of rarefaction and compressional electromagnetic solitons. On the other hand, they have given a numerical treatment of the problem including departures from the quasi-neutrality condition. Their results indicate that in addition to the symmetric solutions for the high-frequency field amplitude, there also exist antisymmetric electromagnetic solitons. A general analytical treatment of the problem is given, accounting simultaneously for the non-linearities due to the relativistic ponderomotive force and the electron mass variation including full ion dynamics together with the Poisson equation. It has obtained analytically the symmetric compression and rarefaction solitons that are found in the quasi-neutral case, and also, the antisymmetric solution was numerically obtained in the non-neutral limit. Parameter space analysis of symmetric and antisymmetric solutions has been considered. On the other hand, for quasi-stationary density modulations, only symmetric solitons have been obtained. Modulational instability and soliton formation are possible if the non-linear frequency shift is the frequency of the electromagnetic field [20]
The growth rate represented by Eq. 26 is depicted against the wave number k for different electron and hole thermal temperatures for GaSb and GaAs semiconductors. From Figure 2, it is seen that the growth rate increases up to a threshold wave number k ≡ kc; then, it decreases until it vanishes for both kinds of semiconductors. The critical wave number kc can be determined as follows. At kc, the slope of the curve in the γ − k plan vanishes. Thus, we calculate dΓ/dk, solve it for dΓ/dk = 0, and then we obtain a threshold value of kc, at which the system tends to have less instability. From the calculations, we found that the value of kc for the GaSb semiconductor is kc = 9.91, 8.58, 7.68 for the black, red, and blue curves, respectively. However, the value of kc for the GaAs semiconductor is kc = 12, 10.39, 9.29 for the black, red, and blue curves, respectively. Indeed, increasing the electron–hole temperature at a constant value of the unperturbed potential of the incident laser a0 would lead to reduce the instability to lower k. This is attributed to the constant a0, and the plasma does not gain energy from outside the system (i.e., from the laser source). Thus, increasing the particle temperature will be consumed from the moving wave, and hence, the wave suffers from deprivation from a source of energy that tends to have less instability.
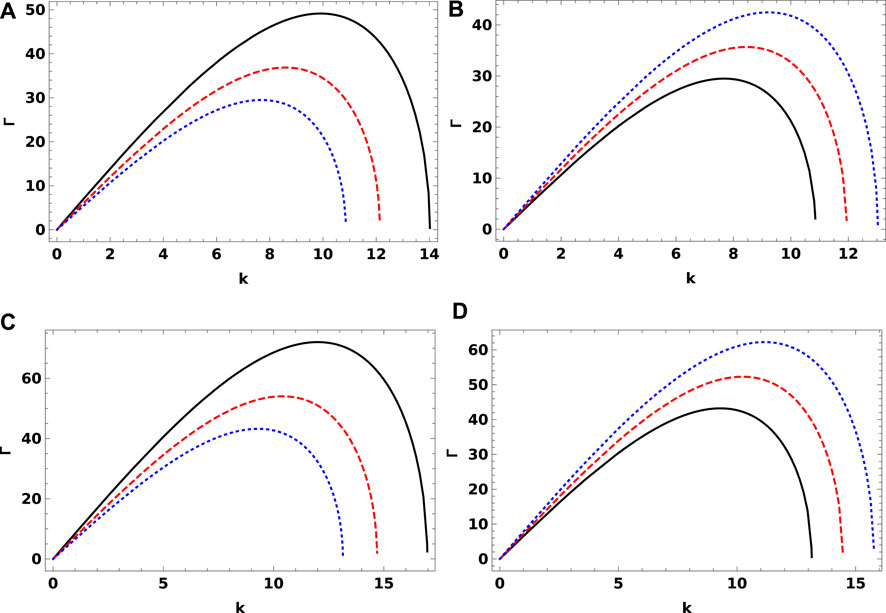
FIGURE 2. Growth rate vs. the wave number k for GaSb (upper panel) and GaAs (lower panel) semiconductors. (A) and (C) for T = 300 K (solid black curve), T = 400 K (dashed red curve), and T = 500 K (dotted blue curve); (B) and (D) for a0 = 0.01 K (solid black curve), a0 = 0.011 K (dashed red curve), and a0 = 0.012 K (dotted blue curve).
The growth rate is plotted against the wave number k for different values of the unperturbed potential of the incident laser a0 for GaSb and GaAs semiconductors. The plasma instability increases with the wave number and achieves the maximum, and thereafter, it falls rapidly. It is observed that for a powerful unperturbed potential of the incident laser (i.e., higher values of a0), the growth rate increases and the system tends to have more instability. This is speculated to that increasing the unperturbed potential of the incident laser pump additional energy in the e–h semiconductor, which produces instability in the system.
The dependence of Sagdeev pseudo-potential (Ψ(w)) represented by Eq. 29 with the potential w is depicted in Figure 3. Physically, the potential Ψ(w) is interpreted by a quasi-particle oscillating periodically back and forth between two real zeros. On the other hand, the quasi-particle oscillates in the potential well Ψ(w), which is corresponding to the solitary wave or localized structure. It is important to mention that the potential profile contains essential information about the solitary structure such as the width of the potential well refers to the amplitude of the solitary wave and the depth of the potential measures the steepness of the solitary pulse.
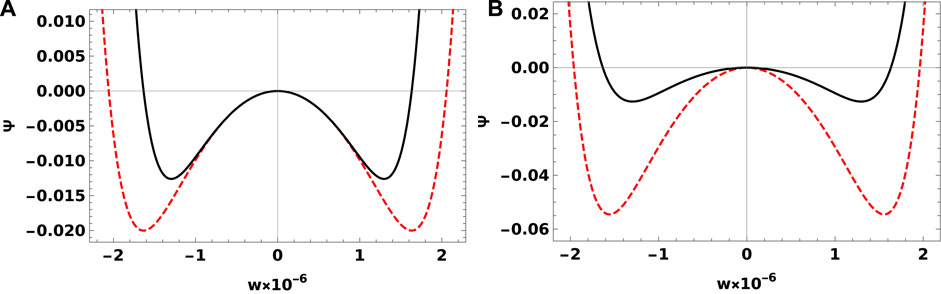
FIGURE 3. Sagdeev pseudo-potential (Ψ(w)) vs. the potential w for the GaSb semiconductor. (A) for T = 300 K (solid black curve), and T = 350 K (dashed red curve). (B) for Ω = −1010 (black solid curve) and Ω = −3 × 1010 (red-dashed curve).
To determine the stability or the properties of the instability associated with a given plasma equilibrium, we use a method based on energy considerations [34]. According to this method, it is necessary to calculate the change in the potential energy of the plasma as a result of a given perturbation. Thus, we use Sagdeev potential in Eq. 29. A necessary condition for the existence of the localized (solitary) wave is
Equation 31 shows that stable localized pulses exist when Ω < 0; otherwise, stable pulses cannot exist in the plasma. Typical values of the electron plasma period are of the order of a picosecond. The corresponding frequency of localized pulses is chosen for excitation of 100 THz. Now, we examine the behavior of localized pulses with the corresponding frequency Ω. It is seen that both positive (compressive) and negative (rarefactive) solitary waves can exist simultaneously. This may be attributed to that both electrons and holes have different masses. For the electron–positron plasma system (with equal masses), we get only a positive (compressive) solitary wave such as in [12]. Also, increasing Ω enhances the pulse amplitude and decreases the pulse width, i.e., the depth of the Sagdeev potential is inversely proportional with the pulse width. On the other hand, for higher Ω, the solitary pulse becomes taller and narrower. From the terminology of solitary waves, taller and narrower pulses are faster. In Figure 3B, the solid curve for Te = Th = T = 300 K, while the dashed curve for Te = Th = T = 350 K for the GaSb semiconductor. For higher temperature, the solitary pulses become towering, thinning, and then speeder.
The interaction between an electron–hole semiconductor plasma with a laser beam is a source of instability. Using Maxwell’s equations along with electron–hole fluid equations, the interaction between the laser beam and non-linear density perturbations of the electrons and holes gives rise to a localized electric field envelope, whose dynamics is described by the non-linear Schrödinger equation. The latter provides dark envelope solutions, representing the electric field wave packet. We have investigated the conditions for the existence of localized solitary waves by using a pseudo-potential formalism. The variation of the solitary wave profile with e–h temperature and frequency is examined. It is found that both compressive and rarefactive solitary pulses exist simultaneously.
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
1. Gattass R, Mazur E. Femtosecond laser micromachining in transparent materials. Nat Photon (2008) 2:219–25. doi:10.1038/nphoton.2008.47
2. Sugioka K, Cheng Y. Ultrafast lasers-reliable tools for advanced materials processing. Light Sci Appl (2014) 3:e149. doi:10.1038/lsa.2014.30
3. Afify MS, Moslem WM, Tolba RE, Hassouba MA. Generation of soliton, cnoidal, and periodic waves during pumping GaAs by an electron beam. Chaos, Solitons & Fractals (2019) 124:18–25. doi:10.1016/j.chaos.2019.04.032
4. Gurjar MC, Gopal K, Gupta DN, Kulagin VV. Terahertz radiation generation from short-pulse laser interaction with electron-hole plasmas. Europhys Lett (2021) 133:14001. doi:10.1209/0295-5075/133/14001
5. Morel B, Giust R, Ardaneh K, Courvoisier F. Two-fluid plasma model for ultrashort laser-induced electron-hole nanoplasmas. Phys Rev B (2022) 106:035207. doi:10.1103/PhysRevB.106.035207
6. Kursunoglu B, Perlmutter A, WidmayerKruer SM. Progress in lasers and laser fusion. In: Chapter: Theoretical interpretations of enhanced laser light absorption by Kruer WL. Florida: Springer (1975).
7. Manes K, Ahlstrom H, Haas R, Holzrichter J. Light–plasma interaction studies with high-power glass laser. J Opt Soc Am (1977) 67:717–26. doi:10.1364/josa.67.000717
8. Ripin B, Whitlock R, Young F, Obenschain S, McLean E, Decoste R. Long-pulse laser-plasma interactions at 1012-1015 W/cm2. Phys Rev Lett (1979) 43:350–3. doi:10.1103/physrevlett.43.350
9. Shukla PK, Yu MY, Tsintsadze NL. Intense solitary laser pulse propagation in a plasma. Phys Fluids (1984) 27:327–8. doi:10.1063/1.864628
11. Yeom K, Jiang H, Singh J. High power laser semiconductor interactions: A Monte Carlo study for silicon. J Appl Phys (1997) 81:1807–12. doi:10.1063/1.364037
12. Shukla PK, Marklund M, Eliasson B. Nonlinear dynamics of intense laser pulses in a pair plasma. Phys Lett A (2004) 324:193–7. doi:10.1016/j.physleta.2004.02.065
13. Rubano A, Paparo D, Miletto F, di Uccio US, Marrucci L. Recombination kinetics of a dense electron-hole plasma in strontium titanate. Phys Rev B (2007) 76:125115. doi:10.1103/PhysRevB.76.125115
14.I Peshko, editor. Laser pulses - theory, Technology, and applications. Chapter: Interaction of femtosecond laser pulses with solids: Electron/phonon/plasmon dynamics by dyukin rv, martsinovskiy ga, sergaeva on, shandybina gd, svirina VV, yakovlev eb, 10. London: IntechOpen (2012). p. 5772.
15. Cheng LH, Tang RA, Zhang AX, Xue JK. Nonlinear interaction of intense laser pulses and an inhomogeneous electron-positron-ion plasma. Phys Rev E (2013) 87:025101. doi:10.1103/PhysRevE.87.025101
16. Bogachev N, Gusein-zade N, Zhluktova I, Kazantsev SY, Kamynin V, Podlesnykh S, et al. Semiconductor plasma antennas formed by laser radiation. Tech Phys Lett (2019) 45:1223–5. doi:10.1134/s1063785019120174
17. Tsatrafyllis N, Kühn S, Dumergue M, Foldi P, Kahaly S, Cormier E, et al. Quantum optical signatures in a strong laser pulse after interaction with semiconductors. Phys Rev Lett (2019) 122:193602. doi:10.1103/PhysRevLett.122.193602
18. Shcherbakov M, Eilenberger F, Staude I. Interaction of semiconductor metasurfaces with short laser pulses: From nonlinear-optical response toward spatiotemporal shaping. J Appl Phys (2019) 126:085705. doi:10.1063/1.5108630
19. Gupta DN, Suk H. Enhanced focusing of laser beams in semiconductor plasmas. J Appl Phys (2007) 101:043109. doi:10.1063/1.2654873
21. Chandrashekhar J, Paul C. Interactions of ultra-intense laser light with matter. Phys Today (1995) 48(1):36–43. doi:10.1063/1.881451
22. Mourou GA, Barty CP, Perry MD. Ultrahigh-intensity laser: Physics of the extreme on a tabletop. Phys Today (1997) 51:22. doi:10.1063/1.882131
23. Shukla PK, Rao NN, Yu MY. Relativistic nonlinear effects in plasmas. Phys Rep (1986) 138:1–149. doi:10.1016/0370-1573(86)90157-2
24. Miller RC, Kleinman DA. Excitons in GaAs quantum wells. J Lumin (1985) 30(1-4):520–40. doi:10.1016/0022-2313(85)90075-4
26. Moslem WM. Langmuir rogue waves in electron-positron plasmas. Phys Plasmas (2011) 18:032301. doi:10.1063/1.3559486
27. Shukla PK, Bharuthram R, Tsintsadze N. Modulational instability of strong electromagnetic waves in plasmas. Phys Rev A (1987) 35:4889–91. doi:10.1103/PhysRevA.35.4889
28. Zeba I, Yahia ME, Shukla PK, Moslem WM. Electron–hole two-stream instability in a quantum semiconductor plasma with exchange-correlation effects. Phys Lett A (2012) 376:2309–13. doi:10.1016/j.physleta.2012.05.049
29. Abdelsalam UM, Allehiany FM, Moslem WM. Nonlinear waves in GaAs semiconductor. Acta Phys Pol A (2016) 129:472–7. doi:10.12693/APhysPolA.129.472
30. Jokar F, Eslami E. Study on the effect of laser parameters on wakefield excitation in femtosecond pulsed laser–plasma interaction using PIC method. Optik (2012) 12321:1947–51. doi:10.1016/j.ijleo.2011.09.022
31. Shukla PK, Bharuthram R, Tsintsadze NL. Fully relativistic filamentation instability of strong electromagnetic radiation in unmagnetized plasmas. Phys Scr (1988) 38:578–83. doi:10.1088/0031-8949/38/4/014
32. Afanasyev VV, Kivshar YS, Konotop VV, Serkin VN. Dynamics of coupled dark and bright optical solitons. Opt Lett (1989) 14:805–7. doi:10.1364/ol.14.000805
33. Kumar H, Chand F. Dark and bright solitary wave solutions of the higher order nonlinear Schrödinger equation with self-steepening and self-frequency shift effects. J Nonlinear Optic Phys Mat (2013) 22:1350001. doi:10.1142/S021886351350001X
34. Moslem WM, Sabry R. Zakharov–Kuznetsov–Burgers equation for dust ion acoustic waves. Chaos Solitons Fractals (2008) 36:628–34. doi:10.1016/j.chaos.2006.06.097
Keywords: laser interaction with an electron hole, modified non-linear Schrödinger equation, localized pulse propagation, solitons, plasma instability
Citation: Elgarawany AZ, Gamal YEE-D, El-Hafeez SA and Moslem WM (2022) Dynamics of laser-bumped electron–hole semiconductor plasma. Front. Phys. 10:1049218. doi: 10.3389/fphy.2022.1049218
Received: 20 September 2022; Accepted: 22 November 2022;
Published: 14 December 2022.
Edited by:
XinPei Lu, Huazhong University of Science and Technology, ChinaReviewed by:
DN Gupta, University of Delhi, IndiaCopyright © 2022 Elgarawany, Gamal, El-Hafeez and Moslem. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Waleed M. Moslem, d21tb3NsZW1AaG90bWFpbC5jb20=
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.