Adaptive iterative learning control method for finite-time tracking of an aircraft track angle system based on a neural network

Based on a neural network, this paper presents a new adaptive iterative learning control method for the finite-time tracking control problem of an uncertain aircraft track angle system, which can control the aircraft track inclination through the designed control input rudder deflection angle, so that it can track the preset trajectory in a finite time interval. First, the flight path angle system of the aircraft is abstractly modeled by variable substitution to obtain a triangular model in the form of strict feedback. Second, radial basis function neural network approximation is used to model the uncertain part of the system, aiming at the abstract strict feedback model, and two virtual quantities are designed through the three-layer inversion design method, and then, Lyapunov functions are designed for each subsystem to derive virtual control laws, the actual control law, and the neural network weight adaptive laws. Through Lyapunov stability analysis, it can be seen that the designed controller and adaptive laws can make the whole closed-loop system tend to be stable and realize the tracking of a target trajectory in a finite time interval. Finally, the feasibility and effectiveness of the theory are verified by a simulation example.

1 Introduction

Today, aircraft has become an important tool for the human society. People are constantly considering the flight safety of an aircraft, which is followed by the rapid development of aircraft technology. In order to ensure the flight safety of the aircraft, it is necessary to find the optimal flight trajectory that satisfies the trajectory constraints. Therefore, a careful study of aircraft trajectories is required. With the continuous development of the technological era, the control process of the aircraft has become more and more complex [1, 2]. This has led to a new upsurge in the research on aircrafts. However, due to the strong coupling and highly non-linear characteristics of the aircraft dynamics model, the design of the aircraft control law has certain challenges. This paper mainly studies the flight path angle of the aircraft, designs the control law of the aircraft in the finite time interval, and ensures the safety and stability of the flight process of the aircraft.

Under the current boom in aircraft research, many scholars who study aircraft trajectory planning have emerged. Up to now, it can be roughly divided into four categories: the online real-time trajectory search algorithm based on a large environment [3], target route planning for motion [4], aircraft planning method for multiple tracks, and path planning method for coordinated multiple aircraft working at the same time. For the research on the aircraft track angle system, it is generally adopted to abstract the aircraft track angle model into the aircraft longitudinal model for research [5–7].

Adaptive iterative learning control combines adaptive control and iterative learning control. In the iterative learning control, the characteristics of an adaptive control that can deal with systems with uncertain terms are introduced. Thus, the problem that the adaptive control [8, 9] cannot achieve the desired control effect in a given time is improved. Therefore, many scholars have joined in the theoretical research on the adaptive iterative learning control. For example, in [10], the method of adaptive iterative learning control combined with fuzzy control is introduced into the high-speed train model, which solves the problem that the system has a random varying iteration length and speed and input force constraints and realizes the tracking control of the non-linear and uncertain high-speed train motion system. In [11], a barrier adaptive iterative learning control scheme is proposed, which uses adaptive iterative learning control technology and robust control technology to compensate for parametric and non-parametric uncertainties and asymmetric dead zone non-linearity. The trajectory tracking problem of the tank gun control system under the condition of a non-zero initial error is solved.

A neural network [12–15] is an algorithm mathematical model for distributed parallel information processing by simulating the network behavior characteristics of a biological neural network using bionics ideas. The radial basis function (RBF) neural network is a neural network with RBF as the activation function. The existence of the RBF makes the neural network structure have the characteristics of a local response. Later, people found that a better system accuracy, system robustness, and adaptability can be obtained by using the RBF neural network to approximate. Therefore, they have been paid more attention in the field of non-linear control, which has triggered a large number of scholars’ research. As in [16], self-organizing recursive radial basis function neural networks are studied, and a non-linear model predictive control scheme is designed to predict the future dynamic behavior of non-novel systems. In [17], an adaptive gradient multi-objective particle swarm optimization algorithm was designed, the AGMOPSO algorithm was proposed, and it was used in the RBF neural network so as to solve the problem that the RBF neural network converges to the local minimum value.

The neural network was combined with adaptive iterative learning control to design the controller. The combined application of the neural network and the adaptive iterative learning control system [18, 19] greatly improves the information processing ability and adaptability of the system and has a great impact on the intelligence level of the system. In [20], an adaptive iterative learning control strategy is proposed by using the RBF neural network, which solves the non-uniform trajectory tracking problem of a class of non-linear pure feedback systems with initial state errors. In [21], an iterative learning control algorithm based on the RBF neural network is proposed, which solves the trajectory tracking control up to the rehabilitation robot.

According to the aforementioned discussion, this paper uses the RBF neural network algorithm and the adaptive iterative learning control method to control the longitudinal uncertainty model of the aircraft. Using the characteristics of the RBF neural network approximation model, the uncertainty function in the aircraft is approximated. Using the adaptive iterative learning control to design the control law, on the basis that the closed-loop system tends to converge and stabilize, the system output can better track the desired trajectory within a limited time. Finally, the reliability and stability of the modified method are verified by an example simulation.

2 Model building and a controller design

In this paper, the research on the flight path angle system of the aircraft takes the longitudinal model of the uncertain aircraft as the object, converts it into a strict feedback system with model uncertainty, and then, applies the designed neural network adaptive iterative learning controller to the system to complete the tracking of the ideal trajectory of the aircraft.

2.1 System specification

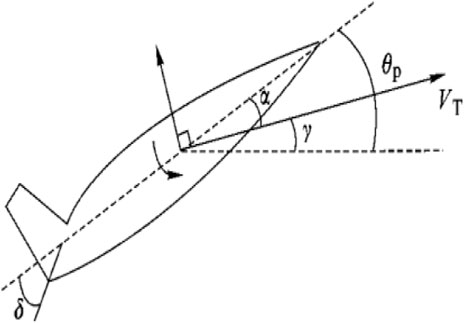
Due to the strong coupling and highly non-linear characteristics of the dynamic model of the aircraft, this paper considers controlling the inclination of the aircraft track by inputting the ideal inclination of the rudder surface of the aircraft.

The simplified longitudinal model of the aircraft is shown in Figure 1:

FIGURE 1

FIGURE 1. Longitudinal model of the aircraft.

The simplified model is

$\left\{\begin{array}{l}\dot{\gamma }={\overline{L}}_{\alpha }\alpha -\frac{g}{V_T}\cos \gamma +{\overline{L}}_o,\\ \dot{\alpha }=q+\frac{g}{V_T}\cos \gamma -{\overline{L}}_{\alpha }\alpha -{\overline{L}}_o,\\ {\dot{\theta }}_p=q,\\ \dot{q}=M_o+M_{\delta }\delta ,\end{array}\right.(1)$

where we see ${\overline{L}}_o=\frac{L_o}{m{V}_T}$ and ${\overline{L}}_{\alpha }=\frac{L_{\alpha }}{m{V}_T}$, where $\gamma$ is the inclination of the aircraft track. $\alpha$ is the angle of attack of the aircraft. ${\theta }_p$ is the pitch angle of the aircraft. $q$ is the change speed of the pitch angle. $V_T$ is the flight speed. $m$ is the mass of the aircraft. $g$ is the acceleration of gravity. ${\overline{L}}_{\alpha }$ is the slope of the lift curve. ${\overline{L}}_o$ is the other influencing factor of the lift. $M_{\delta }$ is the control pitch moment. $M_o$ is the moment from other sources, which is approximately replaced by $M_o=M_{\alpha }+M_{\delta }\delta$. $\delta$ is the deflection angle of the rudder surface. At any time, the slope of the lift curve, other influencing factors of the lift, control pitch moment, other source moment, and other values are all unknown constants.

By defining the states $x_{1,k}=\gamma$, $x_{2,k}=\alpha$, and $x_{3,k}=q$, the control input is the declination angle of the rudder surface $u_k=\delta$; at this time, considering the uncertainty, the following triangular model under a strict feedback form is obtained:

$\left\{\begin{array}{l}{\dot{x}}_{1,k}=a_1{x}_{2,k}+W_{1,k}\left(x_{1,k},t\right),\\ {\dot{x}}_{2,k}=x_{3,k}+W_{2.k}\left(x_{1,k},x_{2,k},t\right),\\ {\dot{x}}_{3,k}=a_3{u}_k+W_{3,k}\left(x_{2,k},x_{3,k},t\right),\end{array}\right.(2)$

where $W_{1,k}=f_{1,k}\left(x_{1,k}\right)+{\Delta }_{1,k}\left(x_k,t\right)$, $W_{2,k}=f_{2,k}\left(x_{1,k},x_{2,k}\right)+{\Delta }_{2,k}\left(x_k,t\right)$, $W_{3,k}=f_{3,k}\left(x_{2,k},x_{3,k}\right)+{\Delta }_{3,k}\left(x_k,t\right)$, and ${\Delta }_{i,k}\left(x_k,t\right),i=\mathrm{1,2,3}$ are the uncertain parts, $\left|{\Delta }_{i,k}\left(x_k,t\right)\right|\le {\rho }_i$, and ${\rho }_i$ is a positive real number and

$\left\{\begin{array}{l}{f}_{1,k}\left(x_{1,k}\right)=-\frac{g}{V_T}\cos x_{1,k}+{\overline{L}}_0,\\ f_{2,k}\left(x_{1,k},x_{2,k}\right)=\frac{g}{V_T}\cos x_{1,k}-{\overline{L}}_0-{\overline{L}}_{\alpha }{x}_{2,k},\\ f_{3,k}\left(x_{2,k},x_{3,k}\right)=M_{\alpha }{x}_{2,k}+M_q{x}_{2,k}.\end{array}\right.(3)$

At the same time, $a_1={\overline{L}}_{\alpha }>0,a_3=M_{\delta }>0$.

The following assumptions about the model will be used in the controller design process.

Assumption 1 The speed $V_T$ will stabilize within a small region of the ideal value through a linear controller, which is treated as a constant.

Assumption 2 All state variables can be solved and used for feedback.

Assumption 3 The bounds of the unknown parameters are known, that is to say, for $=\mathrm{1,3}$, there are known positive numbers $a_{im}$ and $a_{iM}$ such that $a_{im}\le a_i\le a_{iM}$.

Assumption 4 The ideal trajectory is bounded, whose first and second derivatives exist, and $x_{1d}^2+{\dot{x}}_{1d}^2+{\ddot{x}}_{1d}^2\le \chi$ is satisfied for a positive real number $\chi$.The control objective is to design a neural network adaptive iterative learning controller $u_k$, which makes the output of the system $y_k\left(t\right)$ track the ideal trajectory $y_r\left(t\right)$ in a limited time $\left[0,T\right]$.

2.2 Design of a neural network adaptive iterative learning controller for the aircraft track angle system

During the design of the controller, the following definition and lemma of the convergent series sequence will be used.

Definition 1 The convergent series sequence ${\Delta }_k$ is defined as

${\Delta }_k=\frac{a}{k^l},(4)$

where $k=\mathrm{1,2},\cdots$; $a$ and $l$ are constant parameters that need to be designed, satisfying $a>0\in R$ and $l\ge 2\in N$.

Lemma 1 For a given sequence $\left\{\frac{1}{k^l}\right\}$, where $k=\mathrm{1,2},\cdots$ and the positive integer $l\ge 2$, the following inequality holds:

$\underset{k\to \infty }{\lim }{\sum }_{i=1}^k\frac{1}{i^l}\le 2.(5)$

Next, the whole process of the controller design is given.

Step 1 Define three errors.Define the error between the first actual trajectory and the ideal trajectory as

$z_{1,k}=y_k-y_r=x_{1,k}-y_r.(6)$

Define the error between the first virtual control variable $x_{2,k}$ and the first virtual controller ${\alpha }_{1,k}$ as

$z_{2,k}=x_{2,k}-{\alpha }_{1,k}.(7)$

Define the error between the second virtual control variable $x_{3,k}$ and the second virtual controller ${\alpha }_{2,k}$ as

$z_{3,k}=x_{3,k}-{\alpha }_{2,k}.(8)$

Derive and combine it with model Eq. 2 to get

${\dot{z}}_{1,k}={\dot{x}}_{1,k}-{\dot{y}}_r=a_1{x}_{2,k}+W_{1,k}-{\dot{y}}_r=a_1\left(x_{2,k}+\frac{W_{1,k}}{a_1}-\frac{1}{a_1}{\dot{y}}_r\right),(9)$

${\dot{z}}_{2,k}={\dot{x}}_{2,k}-{\dot{\alpha }}_{1,k}=x_{3,k}+W_{2,k}-{\dot{\alpha }}_{1,k},(10)$

${\dot{z}}_{3,k}={\dot{x}}_{3,k}-{\dot{\alpha }}_{2,k}=a_3{u}_k+W_{3,k}-{\dot{\alpha }}_{2,k}=a_3\left(u_k+\frac{W_{3,k}}{a_3}-\frac{1}{a_3}{\dot{\alpha }}_{2,k}\right).(11)$

Step 2 Approximate the unknown parts in step 1 with RBF neural networks.Let

$\left\{\begin{array}{l}\frac{W_{1,k}}{a_1}={\omega }_1^{*T}{\xi }_1\left(x_{1,k},t\right)+{\sigma }_{1,k}\left(t\right),\\ W_{2,k}={\omega }_2^{*T}{\xi }_2\left(x_{1,k},x_{2,k},t\right)+{\sigma }_{2,k}\left(t\right),\\ \frac{W_{3,k}}{a_3}={\omega }_3^{*T}{\xi }_3\left(x_{2,k},x_{3,k},t\right)+{\sigma }_{3,k}\left(t\right),\end{array}\right.(12)$

where ${\omega }_1^{*}$, ${\omega }_2^{*}$, and ${\omega }_3^{*}$ are the ideal weight, $‖{\omega }_1^{*}‖\le {\omega }_M$, $‖{\omega }_2^{*}‖\le {\omega }_M$, $‖{\omega }_3^{*}‖\le {\omega }_M$, and ${\omega }_1^{*},{\omega }_2^{*},{\omega }_3^{*}$ are unknown parameters, The corresponding adaptive control law needs to be designed for estimation, and the specific design will be explained later. ${\sigma }_{1,k},{\sigma }_{2,k},{and\sigma }_{3,k}$ are approximation errors, and $\left|{\sigma }_{1,k}\right|\le {\sigma }_M,\left|{\sigma }_{2,k}\right|\le {\sigma }_M,\left|{\sigma }_{3,k}\right|\le {\sigma }_M$.Simultaneously,

${\dot{z}}_{1,k}=a_1\left(x_{2,k}+{\omega }_1^{*T}{\xi }_1+{\sigma }_{1,k}-\frac{1}{a_1}{\dot{y}}_r\right),(13)$

${\dot{z}}_{2,k}=x_{3,k}+{\omega }_2^{*T}{\xi }_2+{\sigma }_{2,k}-{\dot{\alpha }}_{1,k},(14)$

${\dot{z}}_{3,k}=a_3\left(u_k+{\omega }_3^{*T}{\xi }_3+{\sigma }_{3,k}-\frac{1}{a_3}{\dot{\alpha }}_{2,k}\right).(15)$

Define

${\omega }_1^T={\omega }_1^{*T},{\omega }_2^T={\omega }_2^{*T},{\omega }_3^T={\omega }_3^{*T},(16)$

$\frac{1}{a_1}=P_1,\frac{1}{a_3}=P_2.(17)$

Step 3 Select the Lyapunov function to design the controller.According to the closed-loop system composed of the triangular model and the actual controller in the form of strict feedback, in the case of satisfying the four assumptions, it can be obtained from the second principle of Lyapunov stability in the preliminary knowledge, the set $V\left(x\right)$ must satisfy the positive definite condition, and the reciprocal satisfies the negative semidefinite condition to achieve asymptotic stability.The Lyapunov function is designed as follows:

$V_{1,k}=\frac{1}{2}{z}_{1,k}^2+\frac{a_1}{2}{\stackrel{\sim }{\omega }}_{1,k}^T{\mathrm{\Gamma }}_1^{-1}{\stackrel{\sim }{\omega }}_{1,k}+\frac{a_1}{2}{\mathrm{\Gamma }}_2^{-1}{\stackrel{\sim }{S}}_{1,k}^2+\frac{a_1}{2}{\mathrm{\Gamma }}_3^{-1}{\stackrel{\sim }{P}}_{1,k}^2,(18)$

$V_{2,k}=\frac{1}{2}{z}_{2,k}^2+\frac{1}{2}{\stackrel{\sim }{\omega }}_{2,k}^T{\mathrm{\Gamma }}_4^{-1}{\stackrel{\sim }{\omega }}_{2,k}+\frac{1}{2}{\mathrm{\Gamma }}_5^{-1}{\stackrel{\sim }{S}}_{2,k}^2+\frac{1}{a_1}{V}_{1,k},(19)$

$V_k=\frac{1}{2}{z}_{3,k}^2+\frac{a_3}{2}{\stackrel{\sim }{\omega }}_{3,k}^T{\mathrm{\Gamma }}_6^{-1}{\stackrel{\sim }{\omega }}_{3,k}+\frac{a_3}{2}{\mathrm{\Gamma }}_7^{-1}{\stackrel{\sim }{S}}_{3,k}^2+\frac{a_3}{2}{\mathrm{\Gamma }}_8^{-1}{\stackrel{\sim }{P}}_{2,k}^2+a_3{V}_{2,k},(20)$

where ${\stackrel{\sim }{\omega }}_{i,k}={\widehat{\omega }}_{i,k}-{\omega }_i$ , ${\stackrel{\sim }{S}}_{i,k}={\widehat{S}}_{i,k}-S$, $i=\mathrm{1,2,3}$, ${\stackrel{\sim }{P}}_{1,k}={\widehat{P}}_{1,k}-P_1$, ${\stackrel{\sim }{P}}_{2,k}={\widehat{P}}_{2,k}-P_2$ , and $S={\sigma }_M^2$. ${\widehat{\omega }}_{i,k}$, ${\widehat{S}}_{i,k}$, ${\widehat{P}}_{1,k}$, and ${\widehat{P}}_{2,k}$ are estimates of ${\omega }_i$, $S_i$, $P_1$, and $P_2$, respectively.The virtual control laws ${\alpha }_{1,k}$ and ${\alpha }_{2,k}$ and the actual control law $u_k$ are designed as

${\alpha }_{1,k}=-{\widehat{\omega }}_{1,k}^T{\xi }_1-\frac{1}{{\Delta }_k}{z}_{1,k}{\widehat{S}}_{1,k}-c_1{z}_{1,k}+{\widehat{P}}_{1,k}{\dot{y}}_r,(21)$

${\alpha }_{2,k}=-{\widehat{\omega }}_{2,k}^T{\xi }_2-\frac{1}{{\Delta }_k}{z}_{2,k}{\widehat{S}}_{2,k}-c_2{z}_{2,k}+{\dot{\alpha }}_{1,k}-z_{1,k},(22)$

$u_k=-{\widehat{\omega }}_{3,k}^T{\xi }_3-\frac{1}{{\Delta }_k}{z}_{3,k}{\widehat{S}}_{3,k}-c_3{z}_{3,k}+{\widehat{P}}_{2,k}{\dot{\alpha }}_{2,k}-z_{2,k},(23)$

where $c_1$, $c_2$, and $c_3$ are normal parameters that can be designed.

Step 4 Design the parameter update law.

${\dot{\widehat{\omega }}}_{1,k}={\mathrm{\Gamma }}_1{\xi }_1{z}_{1,k},{\dot{\widehat{S}}}_{1,k}={\mathrm{\Gamma }}_2\frac{1}{{\Delta }_k}{z}_{1,k}^2,{\dot{\widehat{P}}}_{1,k}={\mathrm{\Gamma }}_3{\dot{y}}_r{z}_{1,k},(24)$

${\dot{\widehat{\omega }}}_{2,k}={\mathrm{\Gamma }}_4{\xi }_2{z}_{2,k},{\dot{\widehat{S}}}_{2,k}={\mathrm{\Gamma }}_5\frac{1}{{\Delta }_k}{z}_{2,k}^2,(25)$

${\dot{\widehat{\omega }}}_{3,k}={\mathrm{\Gamma }}_6{\xi }_3{z}_{3,k},{\dot{\widehat{S}}}_{3,k}={\mathrm{\Gamma }}_7\frac{1}{{\Delta }_k}{z}_{3,k}^2,{\dot{\widehat{P}}}_{2,k}={\mathrm{\Gamma }}_8{\dot{\alpha }}_{2,k}{z}_{3,k},(26)$

where ${\mathrm{\Gamma }}_i,i=1,\cdots ,8$ are a positive definite diagonal gain matrix of suitable dimension, ${\mathrm{\Gamma }}_i={\mathrm{\Gamma }}_i^T>0$.

Assumption 5 As far as the initial state is concerned, for any $k$, when $t=0$, $x_{1,k}\left(0\right)=y_r\left(0\right)$, ${\widehat{\omega }}_{i,k}\left(0\right)={\widehat{\omega }}_{i,k-1}\left(T\right)$, ${\widehat{S}}_{i,k}\left(0\right)={\widehat{S}}_{i,k-1}\left(T\right)$, ${\widehat{P}}_{1,k}\left(0\right)={\widehat{P}}_{1,k-1}\left(T\right)$, and ${\widehat{P}}_{2,k}\left(0\right)={\widehat{P}}_{2,k-1}\left(T\right)$.

3 Stability analysis

According to the obtained strict feedback model Eq. 2 and the specific controller designed in Section 2.2, the stability analysis of the designed controller will be carried out in the following sections.

Theorem 1 Under the condition that assumptions 1–5 are satisfied and the stability function at the initial equilibrium state is less than any normal number, design virtual control laws (21) and (22), the actual control law (23), and the parameter update law (24–26) can observe that all signals of the closed-loop system are bounded on $\left[0,T\right]$, and the tracking error $z_{i,k}\left(t\right),i=\mathrm{1,2,3}$ converges asymptotically.According to the assumptions, definition, and lemma, it is easy to prove that the conclusion of the theorem holds. The proof process is as follows:$V_{1,k}$ and the derivation process of the error system (13) are as follows:

$\begin{array}{l}{\dot{V}}_{1,k}=z_{1,k}{\dot{z}}_{1,k}+a_1{\stackrel{\sim }{\omega }}_{1,k}^T{\mathrm{\Gamma }}_1^{-1}{\dot{\widehat{\omega }}}_{1,k}+a_1{\mathrm{\Gamma }}_2^{-1}{\stackrel{\sim }{S}}_{1,k}{\dot{\widehat{S}}}_{1,k}+a_1{\mathrm{\Gamma }}_3^{-1}{\stackrel{\sim }{P}}_{1,k}{\dot{\widehat{P}}}_{1,k}\\ =a_1{z}_{1,k}\left(z_{2,k}+{\alpha }_{1,k}+{\omega }_1^T{\xi }_1+{\sigma }_{1,k}-P_1{\dot{y}}_r\right)+a_1{\stackrel{\sim }{\omega }}_{1,k}^T{\mathrm{\Gamma }}_1^{-1}{\dot{\widehat{\omega }}}_{1,k}+a_1{\mathrm{\Gamma }}_2^{-1}{\stackrel{\sim }{S}}_{1,k}{\dot{\widehat{S}}}_{1,k}+a_1{\mathrm{\Gamma }}_3^{-1}{\stackrel{\sim }{P}}_{1,k}{\dot{\widehat{P}}}_{1,k}\\ =a_1{z}_{1,k}\left(z_{2,k}+{\alpha }_{1,k}+{\omega }_1^T{\xi }_1-P_1{\dot{y}}_r\right)+a_1{z}_{1,k}{\sigma }_{1,k}+a_1{\stackrel{\sim }{\omega }}_{1,k}^T{\mathrm{\Gamma }}_1^{-1}{\dot{\widehat{\omega }}}_{1,k}+a_1{\mathrm{\Gamma }}_2^{-1}{\stackrel{\sim }{S}}_{1,k}{\dot{\widehat{S}}}_{1,k}+a_1{\mathrm{\Gamma }}_3^{-1}{\stackrel{\sim }{P}}_{1,k}{\dot{\widehat{P}}}_{1,k}\\ \le a_1{z}_{1,k}\left(z_{2,k}+{\alpha }_{1,k}+{\omega }_1^T{\xi }_1-P_1{\dot{y}}_r\right)+a_1\left|z_{1,k}\right|\left|{\sigma }_{1,k}\right|+a_1{\stackrel{\sim }{\omega }}_{1,k}^T{\mathrm{\Gamma }}_1^{-1}{\dot{\widehat{\omega }}}_{1,k}+a_1{\mathrm{\Gamma }}_2^{-1}{\stackrel{\sim }{S}}_{1,k}{\dot{\widehat{S}}}_{1,k}+a_1{\mathrm{\Gamma }}_3^{-1}{\stackrel{\sim }{P}}_{1,k}{\dot{\widehat{P}}}_{1,k}\\ \le a_1{z}_{1,k}\left(z_{2,k}+{\alpha }_{1,k}+{\omega }_1^T{\xi }_1-P_1{\dot{y}}_r\right)+a_1\left|z_{1,k}\right|{\sigma }_M+a_1{\stackrel{\sim }{\omega }}_{1,k}^T{\mathrm{\Gamma }}_1^{-1}{\dot{\widehat{\omega }}}_{1,k}+a_1{\mathrm{\Gamma }}_2^{-1}{\stackrel{\sim }{S}}_{1,k}{\dot{\widehat{S}}}_{1,k}+a_1{\mathrm{\Gamma }}_3^{-1}{\stackrel{\sim }{P}}_{1,k}{\dot{\widehat{P}}}_{1,k}\\ \le a_1{z}_{1,k}\left(z_{2,k}+{\alpha }_{1,k}+{\omega }_1^T{\xi }_1-P_1{\dot{y}}_r\right)+\frac{a_1}{{\Delta }_k}{z}_{1,k}^2{\sigma }_M^2+\frac{a_1}{4}{\Delta }_k+a_1{\stackrel{\sim }{\omega }}_{1,k}^T{\mathrm{\Gamma }}_1^{-1}{\dot{\widehat{\omega }}}_{1,k}+a_1{\mathrm{\Gamma }}_2^{-1}{\stackrel{\sim }{S}}_{1,k}{\dot{\widehat{S}}}_{1,k}+a_1{\mathrm{\Gamma }}_3^{-1}{\stackrel{\sim }{P}}_{1,k}{\dot{\widehat{P}}}_{1,k}\\ =a_1{z}_{1,k}\left(z_{2,k}+{\alpha }_{1,k}+{\omega }_1^T{\xi }_1-P_1{\dot{y}}_r\right)+\frac{a_1}{{\Delta }_k}{z}_{1,k}^{2}S+\frac{a_1}{4}{\Delta }_k+a_1{\stackrel{\sim }{\omega }}_{1,k}^T{\mathrm{\Gamma }}_1^{-1}{\dot{\widehat{\omega }}}_{1,k}+a_1{\mathrm{\Gamma }}_2^{-1}{\stackrel{\sim }{S}}_{1,k}{\dot{\widehat{S}}}_{1,k}+a_1{\mathrm{\Gamma }}_3^{-1}{\stackrel{\sim }{P}}_{1,k}{\dot{\widehat{P}}}_{1,k}.\end{array}(27)$

$V_{2,k}$ and the derivation process of the error system (14) are as follows:

$\begin{array}{l}{\dot{V}}_{2,k}=z_{2,k}{\dot{z}}_{2,k}+{\stackrel{\sim }{\omega }}_{2,k}^T{\mathrm{\Gamma }}_4^{-1}{\dot{\widehat{\omega }}}_{2,k}+{\mathrm{\Gamma }}_5^{-1}{\stackrel{\sim }{S}}_{2,k}{\dot{\widehat{S}}}_{2,k}+\frac{1}{a_1}{\dot{V}}_{1,k}\\ =z_{2,k}\left(z_{3,k}+{\alpha }_{2,k}+{\omega }_2^T{\xi }_2-{\dot{\alpha }}_{1,k}\right)+z_{2,k}{\sigma }_{2,k}+{\stackrel{\sim }{\omega }}_{2,k}^T{\mathrm{\Gamma }}_4^{-1}{\dot{\widehat{\omega }}}_{2,k}+{\mathrm{\Gamma }}_5^{-1}{\stackrel{\sim }{S}}_{2,k}{\dot{\widehat{S}}}_{2,k}+\frac{1}{a_1}{\dot{V}}_{1,k}\\ \le z_{2,k}\left(z_{3,k}+{\alpha }_{2,k}+{\omega }_2^T{\xi }_2-{\dot{\alpha }}_{1,k}\right)+\left|z_{2,k}\right|\left|{\sigma }_{2,k}\right|+{\stackrel{\sim }{\omega }}_{2,k}^T{\mathrm{\Gamma }}_4^{-1}{\dot{\widehat{\omega }}}_{2,k}+{\mathrm{\Gamma }}_5^{-1}{\stackrel{\sim }{S}}_{2,k}{\dot{\widehat{S}}}_{2,k}+\frac{1}{a_1}{\dot{V}}_{1,k}\\ \le z_{2,k}\left(z_{3,k}+{\alpha }_{2,k}+{\omega }_2^T{\xi }_2-{\dot{\alpha }}_{1,k}\right)+\left|z_{2,k}\right|{\sigma }_M+{\stackrel{\sim }{\omega }}_{2,k}^T{\mathrm{\Gamma }}_4^{-1}{\dot{\widehat{\omega }}}_{2,k}+{\mathrm{\Gamma }}_5^{-1}{\stackrel{\sim }{S}}_{2,k}{\dot{\widehat{S}}}_{2,k}+\frac{1}{a_1}{\dot{V}}_{1,k}\\ \le z_{2,k}\left(z_{3,k}+{\alpha }_{2,k}+{\omega }_2^T{\xi }_2-{\dot{\alpha }}_{1,k}\right)+\frac{1}{{\Delta }_k}{z}_{2,k}^2{\sigma }_M^2+\frac{1}{4}{\Delta }_k+{\stackrel{\sim }{\omega }}_{2,k}^T{\mathrm{\Gamma }}_4^{-1}{\dot{\widehat{\omega }}}_{2,k}+{\mathrm{\Gamma }}_5^{-1}{\stackrel{\sim }{S}}_{2,k}{\dot{\widehat{S}}}_{2,k}+\frac{1}{a_1}{\dot{V}}_{1,k}\\ =z_{2,k}\left(z_{3,k}+{\alpha }_{2,k}+{\omega }_2^T{\xi }_2-{\dot{\alpha }}_{1,k}\right)+\frac{1}{{\Delta }_k}{z}_{2,k}^{2}S+\frac{1}{4}{\Delta }_k+{\stackrel{\sim }{\omega }}_{2,k}^T{\mathrm{\Gamma }}_4^{-1}{\dot{\widehat{\omega }}}_{2,k}+{\mathrm{\Gamma }}_5^{-1}{\stackrel{\sim }{S}}_{2,k}{\dot{\widehat{S}}}_{2,k}+\frac{1}{a_1}{\dot{V}}_{1,k}.\end{array}(28)$

$V_k$ and the derivation process of the error system (15) are as follows:

$\begin{array}{l}{\dot{V}}_k=z_{3,k}{\dot{z}}_{3,k}+a_3{\stackrel{\sim }{\omega }}_{3,k}^T{\mathrm{\Gamma }}_6^{-1}{\dot{\widehat{\omega }}}_{3,k}+a_3{\mathrm{\Gamma }}_7^{-1}{\stackrel{\sim }{S}}_{3,k}{\dot{\widehat{S}}}_{3,k}+a_3{\mathrm{\Gamma }}_8^{-1}{\stackrel{\sim }{P}}_{2,k}{\dot{\widehat{P}}}_{2,k}+a_3{\dot{V}}_{2,k}\\ =a_3{z}_{3,k}\left(u_k+{\omega }_3^T{\xi }_3+{\sigma }_{3,k}-P_{2,k}{\dot{\alpha }}_{2,k}\right)+a_3{\stackrel{\sim }{\omega }}_{3,k}^T{\mathrm{\Gamma }}_6^{-1}{\dot{\widehat{\omega }}}_{3,k}+a_3{\mathrm{\Gamma }}_7^{-1}{\stackrel{\sim }{S}}_{3,k}{\dot{\widehat{S}}}_{3,k}+a_3{\mathrm{\Gamma }}_8^{-1}{\stackrel{\sim }{P}}_{2,k}{\dot{\widehat{P}}}_{2,k}+a_3{\dot{V}}_{2,k}\\ =a_3{z}_{3,k}\left(u_k+{\omega }_3^T{\xi }_3-P_2{\dot{\alpha }}_{2,k}\right)+a_3{z}_{3,k}{\sigma }_{3,k}+a_3{\stackrel{\sim }{\omega }}_{3,k}^T{\mathrm{\Gamma }}_6^{-1}{\dot{\widehat{\omega }}}_{3,k}+a_3{\mathrm{\Gamma }}_7^{-1}{\stackrel{\sim }{S}}_{3,k}{\dot{\widehat{S}}}_{3,k}+a_3{\mathrm{\Gamma }}_8^{-1}{\stackrel{\sim }{P}}_{2,k}{\dot{\widehat{P}}}_{2,k}+a_3{\dot{V}}_{2,k}\\ \le a_3{z}_{3,k}\left(u_k+{\omega }_3^T{\xi }_3-P_2{\dot{\alpha }}_{2,k}\right)+a_3\left|z_{3,k}\right|\left|{\sigma }_{3,k}\right|+a_3{\stackrel{\sim }{\omega }}_{3,k}^T{\mathrm{\Gamma }}_6^{-1}{\dot{\widehat{\omega }}}_{3,k}+a_3{\mathrm{\Gamma }}_7^{-1}{\stackrel{\sim }{S}}_{3,k}{\dot{\widehat{S}}}_{3,k}+a_3{\mathrm{\Gamma }}_8^{-1}{\stackrel{\sim }{P}}_{2,k}{\dot{\widehat{P}}}_{2,k}+a_3{\dot{V}}_{2,k}\\ \le a_3{z}_{3,k}\left(u_k+{\omega }_3^T{\xi }_3-P_2{\dot{\alpha }}_{2,k}\right)+a_3\left|z_{3,k}\right|{\sigma }_M+a_3{\stackrel{\sim }{\omega }}_{3,k}^T{\mathrm{\Gamma }}_6^{-1}{\dot{\widehat{\omega }}}_{3,k}+a_3{\mathrm{\Gamma }}_7^{-1}{\stackrel{\sim }{S}}_{3,k}{\dot{\widehat{S}}}_{3,k}+a_3{\mathrm{\Gamma }}_8^{-1}{\stackrel{\sim }{P}}_{2,k}{\dot{\widehat{P}}}_{2,k}+a_3{\dot{V}}_{2,k}\\ \le a_3{z}_{3,k}\left(u_k+{\omega }_3^T{\xi }_3-P_2{\dot{\alpha }}_{2,k}\right)+\frac{a_3}{{\Delta }_k}{z}_{3,k}^2{\sigma }_M^2+\frac{a_3}{4}{\Delta }_k+a_3{\stackrel{\sim }{\omega }}_{3,k}^T{\mathrm{\Gamma }}_6^{-1}{\dot{\widehat{\omega }}}_{3,k}+a_3{\mathrm{\Gamma }}_7^{-1}{\stackrel{\sim }{S}}_{3,k}{\dot{\widehat{S}}}_{3,k}+a_3{\mathrm{\Gamma }}_8^{-1}{\stackrel{\sim }{P}}_{2,k}{\dot{\widehat{P}}}_{2,k}+a_3{\dot{V}}_{2,k}\\ =a_3{z}_{3,k}\left(u_k+{\omega }_3^T{\xi }_3-P_2{\dot{\alpha }}_{2,k}\right)+\frac{a_3}{{\Delta }_k}{z}_{3,k}^2{\sigma }_M^2+\frac{a_3}{4}{\Delta }_k+a_3{\stackrel{\sim }{\omega }}_{3,k}^T{\mathrm{\Gamma }}_6^{-1}{\dot{\widehat{\omega }}}_{3,k}+a_3{\mathrm{\Gamma }}_7^{-1}{\stackrel{\sim }{S}}_{3,k}{\dot{\widehat{S}}}_{3,k}+a_3{\mathrm{\Gamma }}_8^{-1}{\stackrel{\sim }{P}}_{2,k}{\dot{\widehat{P}}}_{2,k}+a_3{\dot{V}}_{2,k}.\end{array}(29)$

Substitute Eqs 21 and 24 into Eq. 27 to get

${\dot{V}}_{1,k}\le a_1{z}_{1,k}{z}_{2,k}-a_1{c}_1{z}_{1,k}^2+\frac{a_1}{4}{\Delta }_k.(30)$

Substitute Eqs 22 and 25 into Eq. 28 to get

${\dot{V}}_{2,k}\le z_{2,k}{z}_{3,k}-c_1{z}_{1,k}^2-c_2{z}_{2,k}^2+\frac{2}{4}{\Delta }_k.(31)$

Substitute Eqs 23 and 26 into Eq. 29 to get

${\dot{V}}_k\le -a_3{c}_1{z}_{1,k}^2-a_3{c}_2{z}_{2,k}^2-a_3{c}_3{z}_{3,k}^2+\frac{3a_3}{4}{\Delta }_k,(32)$

where for any $r>0$, we have $mn\le \frac{1}{r}{m}^2+\frac{1}{4}{n}^{2}r\left(r={\Delta }_k\right)$.According to Assumption 1, there are $z_{i,k}{\left(0\right)}^2=0\le z_{i,k}{\left(T\right)}^2$ and $i=\mathrm{1,2,3}$, and by Eq. 20, we get

$V_k\left(z_{i,k}\left(0\right),{\widehat{\omega }}_{i,k}\left(T\right),{\widehat{S}}_{i,k}\left(T\right),{\widehat{P}}_{1,k}\left(T\right),{\widehat{P}}_{2,k}\left(T\right)\right)\le V_k\left(z_{i,k}\left(0\right),{\widehat{\omega }}_{i,k}\left(0\right),{\widehat{S}}_{i,k}\left(0\right),{\widehat{P}}_{1,k}\left(0\right),{\widehat{P}}_{2,k}\left(0\right)\right)+{{\displaystyle \int }}_0^T{V}_{k}dt.(33)$

Substituting Eq. 32 into Eq. 33, we get

$\begin{array}{l}{V}_k\left(z_{i,k}\left(0\right),{\widehat{\omega }}_{i,k}\left(T\right),{\widehat{S}}_{i,k}\left(T\right),{\widehat{P}}_{1,k}\left(T\right),{\widehat{P}}_{2,k}\left(T\right)\right)\\ \le V_1\left(z_{i,k}\left(0\right),{\widehat{\omega }}_{i,k}\left(0\right),{\widehat{S}}_{i,k}\left(0\right),{\widehat{P}}_{1,k}\left(0\right),{\widehat{P}}_{2,k}\left(0\right)\right)-{\displaystyle \sum }_{i=1}^3{\displaystyle \sum }_{j=1}^k{{\displaystyle \int }}_0^T{a}_3{c}_i{z}_{i,j}^{2}dt+\frac{3a_3}{4}{\displaystyle \sum }_{j=1}^k{\Delta }_{j}T.\end{array}(34)$

Let $V_0=V_1\left(z_{i,k}\left(0\right),{\widehat{\omega }}_{i,k}\left(0\right),{\widehat{S}}_{i,k}\left(0\right),{\widehat{P}}_{1,k}\left(0\right),{\widehat{P}}_{2,k}\left(0\right)\right)+\frac{3a_3}{4}{\displaystyle \sum }_{j=1}^k{\Delta }_{j}T$ be substituted into Eq. 34, rewritten as

${\displaystyle \sum }_{i=1}^3{\displaystyle \sum }_{j=1}^k{\int }_0^T{a}_3{c}_i{z}_{i,j}^{2}dt\le V_0\left(k\right)-V_k\left(z_{i,k}\left(0\right),{\widehat{\omega }}_{i,k}\left(T\right),{\widehat{S}}_{i,k}\left(T\right),{\widehat{P}}_{1,k}\left(T\right),{\widehat{P}}_{2,k}\left(T\right)\right).(35)$

According to Eq. 5, $\underset{k\to \infty }{\lim }{V}_0\left(k\right)\le V_1+\frac{2a}{4}\left(3a_3\right)T$, $V_0\left(k\right)$ is bounded, and $V_k\left(z_{i,k}\left(0\right),{\widehat{\omega }}_{i,k}\left(T\right),{\widehat{S}}_{i,k}\left(T\right),{\widehat{P}}_{1,k}\left(T\right),{\widehat{P}}_{2,k}\left(T\right)\right)\ge 0$, so

$\underset{k\to \infty }{\lim }{\displaystyle \sum }_{i=1}^3{\int }_0^T{a}_3{c}_i{z}_{i,k}^{2}dt=0.(36)$

According to Eq. 20, for any $k$, $V_k\left(t\right)=V_k\left(0\right)+{\int }_0^t{\dot{V}}_k\left(\tau \right)d\tau$, Eq. 29 is substituted, then

$V_k\left(t\right)=V_k\left(0\right)-{\displaystyle \sum }_{i=1}^3{\int }_0^T{a}_3{c}_i{z}_{i,k}^{2}d\tau +t\frac{3a_3}{4}{\Delta }_k.(37)$

According to Eq. 36, ${\displaystyle \sum }_{i=1}^3{\int }_0^T{a}_3{c}_i{z}_{i,k}^{2}dt$ is bounded. According to Definition 1, ${\Delta }_k$ is bounded, and $t\in \left[0,T\right]$; therefore, $t\frac{3a_3}{4}{\Delta }_k$ is bounded.According to ${\widehat{\omega }}_{i,k}\left(0\right)={\widehat{\omega }}_{i,k-1}\left(T\right)$, ${\widehat{S}}_{i,k}\left(0\right)={\widehat{S}}_{i,k-1}\left(T\right)$, ${\widehat{P}}_{1,k}\left(0\right)={\widehat{P}}_{1,k-1}\left(T\right)$, ${\widehat{P}}_{2,k}\left(0\right)={\widehat{P}}_{2,k-1}\left(T\right)\left(i=\mathrm{1,2,3}\right)$, and Eq. 34, for any $k$, $V_k\left(0,{\widehat{\omega }}_{i,k}\left(T\right),{\widehat{S}}_{i,k}\left(T\right),{\widehat{P}}_{1,k}\left(T\right),{\widehat{P}}_{2,k}\left(T\right)\right)$ is bounded and $V_k\left(0,{\widehat{\omega }}_{i,k}\left(0\right),{\widehat{S}}_{i,k}\left(0\right),{\widehat{P}}_{1,k}\left(0\right),{\widehat{P}}_{2,k}\left(0\right)\right)=V_{k-1}\left(0,{\widehat{\omega }}_{i,k-1}\left(T\right),{\widehat{S}}_{i,k-1}\left(T\right),{\widehat{P}}_{1,k-1}\left(T\right),{\widehat{P}}_{2,k-1}\left(T\right)\right)$ is bounded. It can be seen that for any $k$, $V_k\left(t\right)$, ${\widehat{\omega }}_{i,k}\left(T\right)$, ${\widehat{S}}_{i,k}\left(T\right)$, ${\widehat{P}}_{1,k}\left(T\right)$, and ${\widehat{P}}_{2,k}\left(T\right)$ are bounded. Therefore, $u_k$ and ${\dot{z}}_{i,k}\left(i=\mathrm{1,2,3}\right)$ are bounded, $z_{i,k}$ is consistent and continuous, so $\underset{k\to \infty }{\lim }{z}_{i,k}\left(t\right)=0,\left(i=\mathrm{1,2,3}\right)$.

4 Simulation analysis

According to the control model established in the design part of Section 1,

$\left\{\begin{array}{l}{\dot{x}}_{1,k}=a_1{x}_{2,k}+W_{1,k}\left(x_{1,k},t\right),\\ {\dot{x}}_{2,k}=x_{3,k}+W_{2.k}\left(x_{1,k},x_{2,k},t\right),\\ {\dot{x}}_{3,k}=a_3{u}_k+W_{3,k}\left(x_{2,k},x_{3,k},t\right),\end{array}\right.(38)$

where $W_{1,k}=f_{1,k}\left(x_{1,k}\right)+{\Delta }_{1,k}\left(x_k,t\right)$, $W_{2,k}=f_{2,k}\left(x_{1,k},x_{2,k}\right)+{\Delta }_{2,k}\left(x_k,t\right)$, $W_{3,k}=f_{3,k}\left(x_{2,k},x_{3,k}\right)+{\Delta }_{3,k}\left(x_k,t\right)$, ${\Delta }_{i,k}\left(x_k,t\right),i=\mathrm{1,2,3}$ is the uncertain part, $\left|{\Delta }_{i,k}\left(x_k,t\right)\right|\le {\rho }_i$ , and ${\rho }_i$ is a positive real number and satisfies

$\left\{\begin{array}{l}{f}_{1,k}\left(x_{1,k}\right)=-\frac{g}{V_T}\cos x_{1,k}+{\overline{L}}_0,\\ f_{2,k}\left(x_{1,k},x_{2,k}\right)=\frac{g}{V_T}\cos x_{1,k}-{\overline{L}}_0-{\overline{L}}_{\alpha }{x}_{2,k},\\ f_{3,k}\left(x_{2,k},x_{3,k}\right)=M_{\alpha }{x}_{2,k}+M_q{x}_{3,k},\end{array}\right.(39)$

where $a_1={\overline{L}}_{\alpha }>0,a_3=M_{\delta }>0$.

The ideal trajectory $x_{1d}=\sin t$ is given corresponding to the example hypothesis. Take ${\Delta }_{1,k}=0.01\sin 2t$, ${\Delta }_{2,k}=0.1\cos 2t$, and ${\Delta }_{3,k}=0.05\sin t\cos 2t$.

The unknown physical parameters are selected as follows: ${\overline{L}}_0=-0.1,{\overline{L}}_{\alpha }=0.74,M_{\alpha }=0.1,$ $M_q=-0.02,{andM}_{\delta }=1.36$.

Assume the stable speed $V_T=200m/s$ and $g=9.8m/s^2$, where the initial state of the model takes $x\left(0\right)={\left[000\right]}^T$.

From the controller design part in Section 2, it can be seen that the functions that need to be approximated by the RBF neural network are $\frac{W_1}{{\alpha }_1}$, $W_2$, and $\frac{W_3}{{\alpha }_3}$. Nine hidden nodes are selected, the center of the Gaussian basis function is evenly distributed in the range of $\left[-\mathrm{1,1}\right]$, and the width is 5.3, then the initial values of the network weights are set as

$W_{10}={\left[11.60.10.10.10.10.010.010.010.01\right]}^T,$

$W_{20}={\left[10.0010.010.010.0010.010.010.010.001\right]}^T,$

$W_{30}={\left[300.010.10.010.010.010.000.010.009\right]}^T.$

Let all the initial values $x_{\mathrm{1,0}}\left(0\right)$, $x_{\mathrm{2,0}}\left(0\right)$, and $x_{\mathrm{3,0}}\left(0\right)$ be zero. All the initial values $S_{\mathrm{1,0}}\left(0\right),S_{\mathrm{2,0}}\left(0\right),S_{\mathrm{3,0}}\left(0\right)$ are 0.1, and the initial values $P_{\mathrm{1,0}}\left(0\right)$ and $P_{\mathrm{2,0}}\left(0\right)$ are both 0.01. All the initial errors are zero, ${\rho }_1=0.01$, ${\rho }_2=0.1$, ${\rho }_3=0.05$, $a_{1M}=0.74$, and $a_{3M}=0.36$.

The control parameters are selected under the condition that Lyapunov stability is satisfied. $c_1=23,c_2=3,c_3=40,{\mathrm{\Gamma }}_1=diag\left\{420.10.1220.10.10.10.1\right\},{\mathrm{\Gamma }}_2=70,{\mathrm{\Gamma }}_3=0.1,$

${\mathrm{\Gamma }}_4=diag\left\{370.10.10.10.10.10.10.10.1\right\},{\mathrm{\Gamma }}_5=1,{\mathrm{\Gamma }}_6=diag\left\{400.10.10.10.10.10.10.10.1\right\},{\mathrm{\Gamma }}_7=1000,{\mathrm{\Gamma }}_8=0.1.$

The simulation is carried out under the actual control law $u_k=-{\widehat{\omega }}_{3,k}^T{\xi }_3-\frac{1}{{\Delta }_k}{z}_{3,k}{\widehat{S}}_{3,k}-c_3{z}_{3,k}+{\widehat{P}}_2{\dot{\alpha }}_{2,k}-z_{2,k}$ and the adaptive law ${\dot{\widehat{\omega }}}_{1,\mathit{k}}={\mathrm{\Gamma }}_1{\xi }_1{\mathit{z}}_{1,\mathit{k}}$, ${\dot{\widehat{S}}}_{1,k}={\mathrm{\Gamma }}_2\frac{1}{{\Delta }_k}{z}_{1,k}^2$, ${\dot{\widehat{P}}}_{1,k}={\mathrm{\Gamma }}_3{\dot{y}}_r{z}_{1,k}$, ${\dot{\widehat{\omega }}}_{2,k}={\mathrm{\Gamma }}_4{\xi }_2{z}_{2,k}$, ${\dot{\widehat{S}}}_{2,k}={\mathrm{\Gamma }}_5\frac{1}{{\Delta }_k}{z}_{2,k}^2$, ${\dot{\widehat{\omega }}}_{3,k}={\mathrm{\Gamma }}_6{\xi }_3{z}_{3,k}$, ${\dot{\widehat{S}}}_{3,k}={\mathrm{\Gamma }}_7\frac{1}{{\Delta }_k}{z}_{3,k}^2$, ${\dot{\widehat{P}}}_{2,k}={\mathrm{\Gamma }}_8{\dot{\alpha }}_{2,k}{z}_{3,k}$, and the given initial state. The simulation results are as follows.

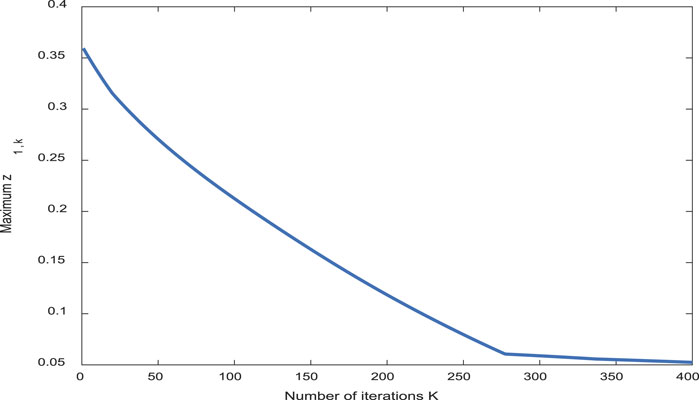
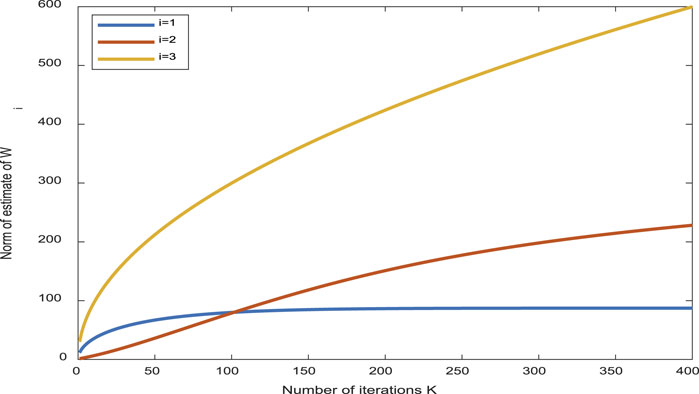
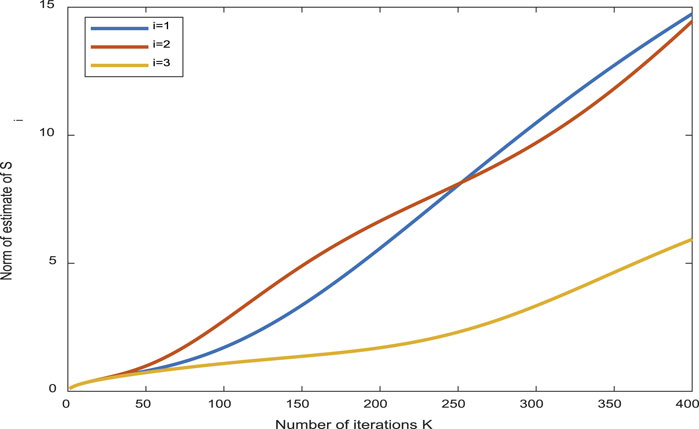
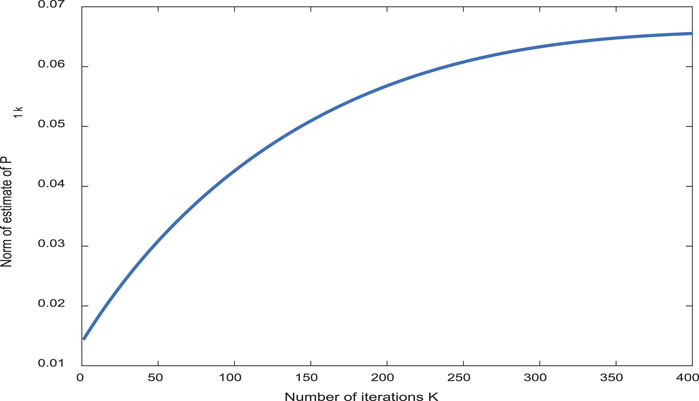
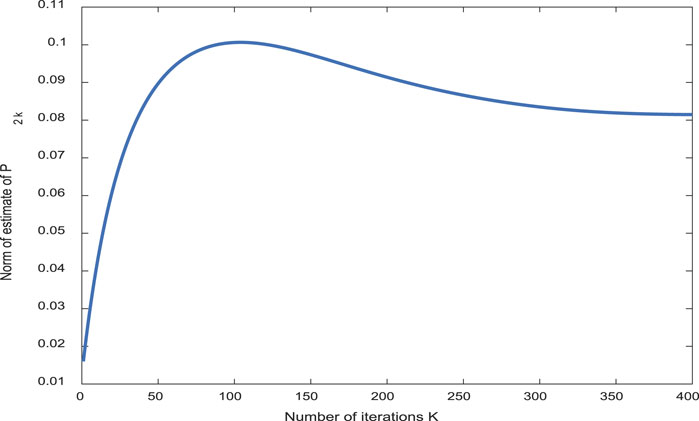
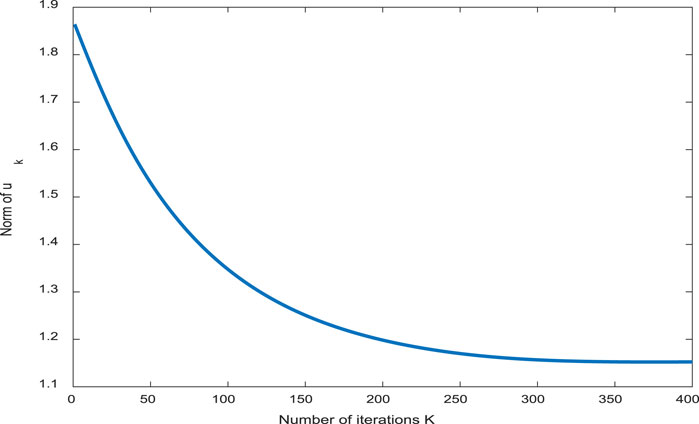
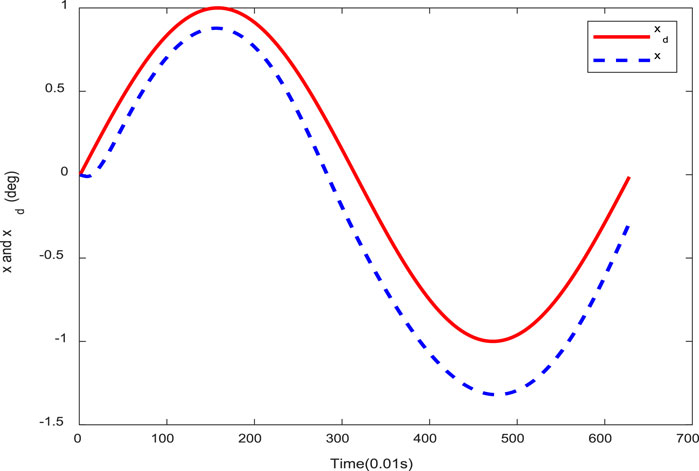
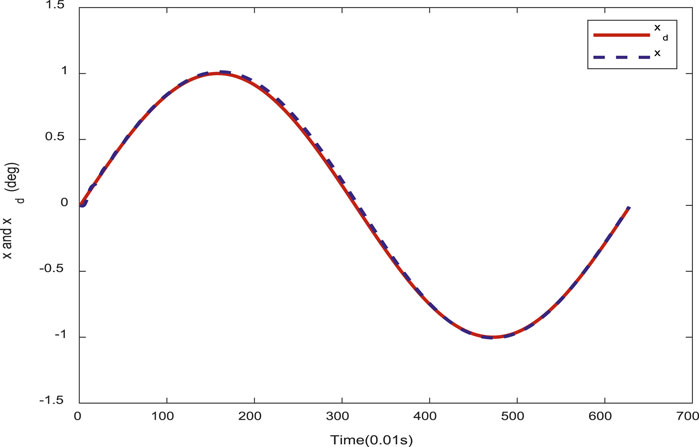
From Figure 2, the inclination error of the aircraft trajectory can basically tend to zero with the increase in the number of iterations. The simulation results from Figures 3–6 show the boundness of the designed parameters. Figure 7 shows that as the number of iterations increases, the control input can remain unchanged, and the stable state of the controller and the control effect are good. By comparing the tracking effect in Figures 8, 9, the tracking effect is more significant with the increase in iteration times.

FIGURE 2

FIGURE 2. Curve of the maximum error $z_{1,k}$ with iteration times.

FIGURE 3

FIGURE 3. Curve of $‖{\widehat{\omega }}_{i,k}‖$ with the number of iterations.

FIGURE 4

FIGURE 4. Curve of $‖{\widehat{S}}_{i,k}‖$ with the number of iterations.

FIGURE 5

FIGURE 5. Curve of $‖{\widehat{P}}_{1,k}‖$ with the number of iterations.

FIGURE 6

FIGURE 6. Curve of $‖{\widehat{P}}_{2,k}‖$ with the number of iterations.

FIGURE 7

FIGURE 7. Curve of $‖u_k‖$ with the number of iterations.

FIGURE 8

FIGURE 8. Trajectory trace graph without iterations.

FIGURE 9

FIGURE 9. Trajectory trace graph for iteration 400.

In summary, the designed neural network adaptive iterative learning controller is suitable for a tracking control in a limited time period and the RBF neural network has a very good effect on approximating any unknown parameters.

5 Conclusion

This paper proposed a new adaptive iterative learning control method for the flight path of the aircraft to complete the tracking control problem in the finite time interval based on the RBF neural network. According to the feedback system in the form of strict feedback abstracted by the longitudinal model of the aircraft, the method of an inversion design is adopted, and the virtual control law is designed to control each subsystem, and finally, the actual control law is obtained by inversion. For each subsystem, a neural network is used to approximate the unknown function in the control, which can greatly improve the control performance of the uncertain system. According to the Lyapunov stability function set by each subsystem, the adaptive law of the neural network that meets the constraints is derived. According to the error between the system output and the ideal trajectory, the adaptive weights and the adjustment parameters are updated to make the entire closed-loop system tend to convergence and stability, and the control objectives of system stability and all signals in a bounded area are achieved. Finally, the effectiveness and feasibility of applying the controller designed by the neural network adaptive iterative learning control method to the aircraft track system are verified by the example simulation.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.

Author contributions

CZ and XT contributed to the conception and design of the study. XT performed the statistical analysis and wrote the first draft of the manuscript. LY wrote sections of the manuscript. All authors contributed to manuscript revision, read, and approved the submitted version.

Funding

This work was supported by the National Natural Science Foundation (NNSF) of China under grants 61603296 and 62073259. This work was also supported by the Key Laboratory of Complex System Control and Intelligent Information Processing in Shaanxi Province.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Zheng C, Yan P, Ding M. Research status and trend of aircraft track planning in Chinese[J]. J Astronautics (2007) 2007(06) 1441–6. doi:10.3321/j.issn:1000-1328.2007.06.001

CrossRef Full Text | Google Scholar

2. Zhuang H, Sun Q, Chen Z, Zeng X. Robust adaptive sliding mode attitude control for aircraft systems based on back-stepping method. Aerospace Sci Tech (2021) 118:107069. doi:10.1016/j.ast.2021.107069

CrossRef Full Text | Google Scholar

3. Yan K, Wu Q. Adaptive tracking flight control for unmanned autonomous helicopter with full state constraints and actuator faults. ISA Trans (2021) 128:32–46. doi:10.1016/j.isatra.2021.11.012

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Wang Y, Hu J. Robust control for a quadrotor aircraft with small overshoot and high-precision position tracking performance. J Franklin Inst (2020) 357(18):13386–409. doi:10.1016/j.jfranklin.2020.09.033

CrossRef Full Text | Google Scholar

5. Yao L. Disturbance observer-based backstepping control for hypersonic flight vehicles without use of measured flight path angle. Chin J Aeronautics (2021) 34(2):396–406. doi:10.1016/j.cja.2020.09.053

CrossRef Full Text | Google Scholar

6. Yang L, Dong C, Zhang W, Wang Q. Phase plane design based fast altitude tracking control for hypersonic flight vehicle with angle of attack constraint. Chin J Aeronautics (2021) 34(2):490–503. doi:10.1016/j.cja.2020.04.026

CrossRef Full Text | Google Scholar

7. Yue F, Wang Y, Sun Z, Xi B, Wu L. Robust modification of nonlinear L1 adaptive flight control system via noise attenuation. Aerospace Sci Tech (2021) 117:106938. doi:10.1016/j.ast.2021.106938

CrossRef Full Text | Google Scholar

8. Yue H, Gong C. Adaptive tracking control for a class of stochastic nonlinearly parameterized systems with time-varying input delay using fuzzy logic systems. J Low Frequency Noise, Vibration Active Control (2022) 41(3):1192–213. doi:10.1177/14613484211045761

CrossRef Full Text | Google Scholar

9. Yue H, Yang W, Li S. Fuzzy adaptive tracking control for a class of nonlinearly parameterized systems with unknown control directions. Iranian J Fuzzy Syst (2019) 16(5):97–112. doi:10.22111/IJFS.2019.4909

CrossRef Full Text | Google Scholar

10. Yu Q, Hou Z. Adaptive fuzzy iterative learning control for high-speed trains with both randomly varying operation lengths and system constraints. IEEE Trans Fuzzy Syst (2021) 29(8):2408–18. doi:10.1109/tfuzz.2020.2999958

CrossRef Full Text | Google Scholar

11. Zhou Z, Wang W, Zhang Y, Yan Q, Cai J. Barrier adaptive iterative learning control for tank gun control systems under nonzero initial error condition. IEEE Access (2022) 10:8664–72. doi:10.1109/access.2022.3144326

CrossRef Full Text | Google Scholar

12. Fei Y, Kong X, Mokbel AAM. Complex dynamics, hardware implementation and image encryption applica tion of multiscroll memeristive hopfield neural network with a novel local active memeristor[J]. IEEE Trans Circuits Systems--II (2022). Express Briefs 1–1. doi:10.1109/TCSII.2022.3218468

CrossRef Full Text | Google Scholar

13. Shen H, Fei Y, Wang C, Sun J. Firing mechanism based on single memristive neuron and double m emristive coupled neurons[J]. Nonlinear Dyn (2022) 110:3807–3822. doi:10.1007/s11071-022-07812-w

CrossRef Full Text | Google Scholar

14. Lin H, Wang C, Sun Y, Ting W. Generating n-scroll chaotic attractors from a memristor-based magne tized hopfield neural network[J]. IEEE Trans Circuits Systems--II (2022). Express Briefs 1–1. doi:10.1109/TCSII.2022.3212394

CrossRef Full Text | Google Scholar

15. Yu F, Shen H, Yu Q, Kong X, Sharma PK, Cai S. Privacy protection of medical data based on multi-scroll memristive hopfield neural network. IEEE Trans Netw Sci Eng (2022) 2022:1–14. doi:10.1109/TNSE.2022.3223930

CrossRef Full Text | Google Scholar

16. Han H, Zhang L, Hou Y, Qiao JF. Nonlinear model predictive control based on a self-organizing recurrent neural network. IEEE Trans Neural Netw Learn Syst (2016) 27(2):402–15. doi:10.1109/tnnls.2015.2465174

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Han H, Wu X, Zhang L, Tian Y, Qiao J. Self-organizing RBF neural network using an adaptive gradient multiobjective particle swarm optimization. IEEE Trans Cybern (2019) 49(1):69–82. doi:10.1109/tcyb.2017.2764744

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Jin X, He T, Wu X, Wang H, Chi J. Robust adaptive neural network-based compensation control of a class of quadrotor aircrafts. J Franklin Inst (2020) 357(17):12241–63. doi:10.1016/j.jfranklin.2020.09.009

CrossRef Full Text | Google Scholar

19. Song J, Yan M, Yang P. Neural adaptive dynamic surface asymptotic tracking control for a class of uncertain nonlinear system. Circuits Syst Signal Process (2020) 40:1673–98. doi:10.1007/s00034-020-01558-9

CrossRef Full Text | Google Scholar

20. Zhang C, Tian X. Non-uniform trajectory tracking adaptive iterative learning control for nonlinear pure-feedback systems with initial state error based on RBF-neural network[C]. In: 2021 40th Chinese Control Conference (CCC); July 26-28, 2021; Shanghai, China (2021). p. 532–9.

Google Scholar

21. Pang Z, Wang T, Liu S. An iterative learning algorithm based on RBF neural network in upper limb rehabilitation robot[J]. In: IEEE 10th Data Driven Control and Learning Systems Conference (DDCLS); May 14-16, 2021; China (2021). p. 293–8.

Google Scholar