Hani J. Kbashi
S. A. Kolpakov- Aston Institute of Photonic Technologies, College of Engineering and Physical Sciences, Aston University, Birmingham, United Kingdom
We reported an experimental study on fast and slow temporal scaling of rogue waves’ emergence in a long (615 m) ring cavity erbium-doped fiber laser. The criterion for distinguishing between the fast and slow rogue waves is a comparison of the event lifetime with the system’s main characteristic time estimated from the decay of an autocorrelation function (AF). Thus, compared with the AF characteristic time, fast optical rogue wave (FORW) events have lifetime duration shorter than the AF decay time, and they appeared due to the mechanism of the pulse-to-pulse interaction and nonlinear pulse dynamics. In contrast, a slow optical rogue wave (SORW) has lifetime duration much longer than the decay time of the AF, which results from the hopping between different attractors. Switching between regimes can be managed by adjusting the in-cavity birefringence.
Introduction
Rogue waves (RWs) are spatiotemporal structures initially introduced in oceanography to describe giant events, colloquially called rare or freak waves. These waves have anomalous amplitudes and result in a destructive impact on nature and society [1]. To be counted as RWs, extreme events should have probabilities higher than events satisfying Gaussian or Rayleigh statistics and have amplitudes exceeding eight standard deviations of the ocean’s surface variations [1]. Meanwhile, an intrinsic scarcity of events and evident technical difficulties to perform full-scale experiments are the main obstacles to understanding and predicting RWs.
Fiber lasers are an ideal platform and perfect candidates for discovering and investigating the formation of single-shot ultrafast rare events such as optical RWs [2–8]. It provides an opportunity to obtain a vast amount of data under laboratory-controlled conditions in a relatively short time. Previously, in the context of mode-locked fiber lasers, the optical RWs mainly have been observed at chaotic bunches of noise-like pulses or soliton rain and dissipative soliton explosions [2, 9–11]. Also, it has been found that optical RWs can be generated in mode-locked lasers due to the interaction of dissipative solitons through the overlapping of their tails or soliton-dispersive wave interactions [12, 13]. An extensive study of the mechanisms of formation of optical RWs has been carried out either experimentally or theoretically in fiber lasers with nonlinearly driven cavities [14], Raman fiber amplifiers and lasers [15], random fiber lasers [16], and fiber lasers via modulation of the pump [17]. On the other hand, hopping between different attractors has also been investigated as a source of optical RW emergence [18, 19]. During the previous investigation, optical RWs were classified as slow and fast depending on the photon lifetime of the active laser medium, which can be used only in the optical system [20].
In this research study, we reported a new RW classification method for the first time. First, we observed both SORWs and FORWs at pump powers close to the lasing threshold in a unidirectional laser experimental setup without a saturable absorber. By adjusting the birefringence of the laser cavity and the polarization of the pump using polarization controllers, we observed many RW patterns that were either previously observed experimentally or predicted theoretically. After that, RW patterns were classified into FORWs and SORWs depending on the AF characteristic time of the laser system. The first one comprises the RW pattern duration faster than the AF characteristic time of the system, which we named FORWs, and the second one is named when the RW event duration is significantly longer than the AF characteristic time (SORW). Furthermore, we classified and illustrated the observed RW patterns depending on the mechanisms of the emergence and then arranged them based on the likelihood frequency of observation.
Fiber laser setup design and characterization
In the experiment, we designed a unidirectional ring cavity fiber laser, as illustrated in Figure 1A. The cavity was assembled with 1 m of the highly concentrated Er3+-doped fiber (Liekki Er 80–8/125) and 614 m of SMF-28 (β2 = −21 ps2/km). A 51-dB dual-stage polarization-insensitive optical isolator (ISO) was used to ensure unidirectional lasing. The 80/20 fiber coupler was used to sample a portion of the signal wave. Unlike mode-locking schemes using nonlinear polarization rotation, only one in-line cavity polarization controller (PC1) was placed inside the cavity. The cavity was pumped via a 1480/1550 WDM using a 1,480 nm laser diode, which had a built-in isolator. The 1,480-nm laser diode has been used in this experiment because the pump absorption bandwidth is located quite close to the lasing bandwidth of 1,550 nm, so pump noise is transferred to the laser emission noise, and this 1,480-nm pump to 1,550-nm signal noise transfer enables the activation of RWs, originating from different types of instabilities. However, the supplied pump power was measured after the pump polarization controller (PC2) and the wavelength division multiplexing but before the Er3+-doped active fiber. A long-cavity fiber laser (615 m) was used in this experiment, inheriting the features of vector resonance multimode and modulation instabilities [21] that lead to the emergence of different types of optical rogue wave events [13, 17, 22] and laser regimes [23–25]. The output signal was detected using an InGaAsUDP-15-IR-2 FC detector with a bandwidth of 17 GHz connected to a 2.5-GHz sampling oscilloscope (Tektronix DPO7254). The oscilloscope has the built-in option of a variable electronic filter for the incoming signal. An optical spectrum analyzer (Yokogawa AQ6317B) and a radio frequency (RF) signal analyzer (FSV Rohde Schwarz; 10 Hz–13.6 GHz) were used to record the laser optical spectrum and RF spectrum, respectively.
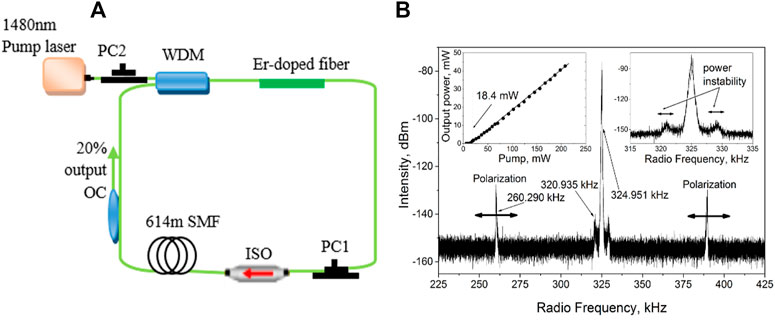
FIGURE 1. (A) Schematic setup of a fiber ring laser, (B) the RF spectrum of the fiber laser; on the left, insert the power versus pump; on the right, insert the amplified RF peak with satellites due to power instability.
The RF spectrum illustrated in Figure 1B shows three simultaneous frequencies. The fundamental central peak corresponds to the laser roundtrip frequency (325 KHz), which matches the roundtrip time (3.077 µs) and cavity length (615 m); two modulation frequency satellites were labeled as polarization, which are related to the in-cavity birefringence-mediated polarization instabilities [18]. The frequency of this modulation depends on birefringence induced in the cavity by PC1. In addition, there are also two small modulation (relaxation and oscillations) frequency satellites close to the fundamental central peak, as shown in the right inset of Figure 1 [21]. These satellites can be controlled via the pump power. The fiber laser has a lasing threshold of 16 mW, calculated from the output versus pump power, as shown in the left inset of Figure 1. We pumped this laser with 18 mW, which is slightly higher than the lasing threshold. The interactions of these three frequencies and the spectra for different types of RWs have been deeply discussed in [21] and motivated us to find temporal metrics that enable to quantify the RW emergence and classify it based on the lifetime, its likelihood, and mechanisms.
Results and discussion
The typical temporal traces (oscilloscope traces) of the fiber laser output around the threshold (18 mW) are recorded in long- and short-time scales in which a large set of pulse clusters can be observed, as illustrated in Figures 2A,B. Autocorrelation functions of the laser system were calculated using the oscilloscope trace with a length of 50 million points and a resolution of 0.1 ns by MATLAB software, and Lags and AF data are saved and analyzed by Origin software. Fast oscillations, which correspond to the roundtrip period and polarization instability, have been removed from the autocorrelation function calculations using a peak detection algorithm, while the small oscillations on the curve of AF correspond to the oscillations of power with the kHz frequency. The shape of AF provided information about the characteristic times of different processes, which have a place in the laser cavity. We found that, for SORW patterns, the system has a linear shape of the AF (Figure 3A), whereas for FORW patterns, the system generates an exponential shape (Figure 3B) of the AF. Therefore, for different laser regimes, the filtered AFs have different shapes.
FIGURE 2. Oscilloscope traces of the (A) SORW and (B) FORW.
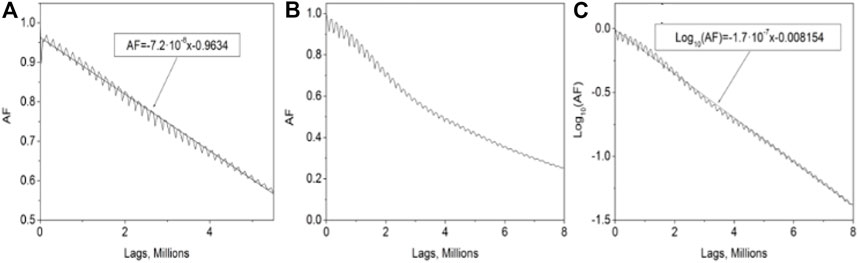
FIGURE 3. Autocorrelation functions; (A) the AF of the SORW pattern, (B) the AF of the observed FORW pattern in the linear scale, and (C) the log scale with linear fitting. In all cases, the length of one lag was 0.1 ns.
We calculated the characteristic time τc of the AF from the fitting line (y = at + b) for both SORWs and FORWs; here, (τc = 1/a) in s. We used x instead of t in the insets of Figure 3 because the scale of the horizontal axis is in lags (0.1 ns per lag). We found that the characteristic times were 1.39 and 0.59 ms for SORWs and FORWs, respectively (the roundtrip time was 3.0773 µs). These times are quite similar to those of the Er+3-doped lasing photon lifetime; because of this, the observed events have been classified as the SORW and FORW. The AF also gives information about the time the system can remember an initially induced perturbation. For instance, when the lifetime of the RW events is significantly longer than the first characteristic time (1.39 ms), as in the case for SORWs, the system loses information about how the pattern developed, and thus, the tail of the events is independent in the front of it (the system forgets how the pattern began while the pattern is still active). Meanwhile, in the case of FORWs, as the event lifetime is shorter than the characteristic time (0.59 ms), the system can remember the shape of the beginning of the RW pattern, and these patterns are affected by the periodic amplification in each roundtrip which can be considered as a kind of memory. Therefore, we have classified these optical RW events as either SORWs or FORWs depending on the ratio of the AF decay time to the events’ lifetime. FORW events have lifetime duration in the part of one roundtrip, which is shorter than the AF decay time (0.59 ms), and SORW events have a longer lifetime (∼200 ms) than the AF decay time.
The responsible mechanism for the emergence of SORW patterns is illustrated in Figure 4. The system seemingly has four amplitude attractors (A0–A3); therefore, the hopping between them (with appropriate frequency and level of background noise) can lead to the surpassing of the RW threshold (8σ). For instance, there is a clear hopping in amplitude from the level of background noise (A0) to a high amplitude (A1), as shown in Figures 4A,B. By tuning the in-cavity polarization controller, more amplitude attractors were observed in one regime, as shown in Figures 4C,D. The difference between these amplitude attractors is the RW event lifetime, where A1 and A2 have the longest event lifetime with about 20 and 8 s, respectively. This situation apparently was similar to the situation observed during the pump modulation [18]. Probably, this happens because polarization modulation instabilities grew inside the laser cavity that performed seemingly to an external pump modulation.
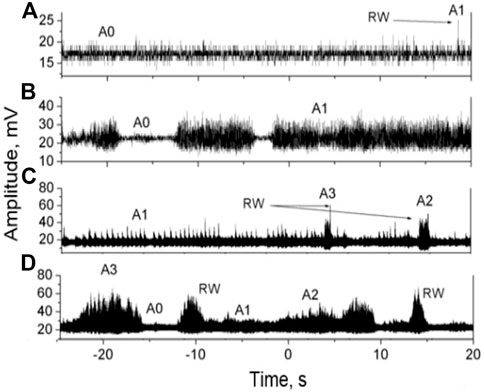
FIGURE 4. In the SORW pattern, the system apparently has four attractors labeled with A0–A3. (A,B) showing the hopping from background noise level A0 to high amplitude A1, (C,D) showing the all attractors A0–A3.
A detailed description of the RW emergence, because of the hopping between the orthogonal states of polarization, is found in our previous work [22]. The polarization instability causes desynchronization of the orthogonal linear states of polarization which takes the form of the chaotic phase difference hopping in the pi radian. As a result, anomalous spikes in power (RWs) appear.
The mechanisms which are responsible for the emergence of the FORW patterns are illustrated in Figure 5; it was based on the resonance pulse–pulse interaction when two pulses are slowly approaching each other and exchanged their energies. Figure 5A elucidates the mechanism of emerging two pulses interacting and forming the RW patterns and then splitting it back to the two pulses. We named this pattern a solitary or lonely RW pattern, which appeared as a result of the interaction between pulses that propagates at different speeds. Similar mechanisms were observed for twins, three sisters, and cross patterns in Figures 5B–D, respectively. In the case of twins RW, the pattern has quite a long lifetime (1 ms) than the lonely (255 µs), three sisters (15.4 µs), and cross (400 ps) patterns. However, it is still less than the system characteristic time that it classified as FORW, which have been widely discussed in [13]. It can also be noticed that the results in Figure 5A belong to the pulse–pulse interaction for about more than 200 roundtrips, whereas the results in Figure 5D are pulse collision within the sub-roundtrip time without any sign of energy transfer between the pulses.
FIGURE 5. FORW, (A) lonely, (B) twins;, (C) three sisters, and (D) cross RW patterns.
The most notable characteristic of the RW process events is the highly skewed probability distribution function (PDF) associated with it. The PDF that corresponds to the SORW pattern is illustrated in Figure 6A. The units of the horizontal scale were normalized to the output voltage and expressed in units of standard deviation (σ). It can be seen from the PDF that due to the optical RW events, the PDF is L-shaped and is significantly different from the PDF of a normal Gaussian distribution. From this result, the probability of SORWs was calculated to be ∼0.195%. The PDF curve has a point of inflection when the abscissa is equal to ∼2 units of σ. The normal output pulses in PDF were fitted with a Gaussian function, while the optical RW event was fitted with a polynomial function. The PDF of the FORW shown in Figure 6B was calculated using the 50-M point-long record oscilloscope trace. We observed that the FORW patterns have a strong asymmetric shape and a large deviation from a Gaussian distribution with a long tail of more than 8 σ from the mean value on the right side of the PDF.
FIGURE 6. PDF of (A) SORW and (B) FORW events.
Finally, we summarize the lifetime, likelihood, and mechanisms behind the emergence of the optical RW patterns, as illustrated in Table 1.
TABLE 1. Observed RW pattern’s lifetime, its likelihood, and mechanism.
In conclusion, the two groups of RW patterns have been observed in a mode-locked fiber laser due to polarization dynamics in the cavity. The first group of the pattern (FORWs) is composed of pulses with a duration significantly less than the AF characteristic time, and it appeared due to the pulse–pulse interaction and nonlinear pulse dynamics. Meanwhile, the second one (SORWs) consists of oscillations with a duration significantly longer than the characteristic time. The mechanism of SORW patterns is different from the mechanism of the FORW patterns and can be explained in terms of hopping between different attractors in a multi-state oscillation system. Most of the patterns were found to be mutually exclusive, which means that only one RW mechanism was realized each time. This, in turn, means that all the patterns of the pulse–pulse interaction (lonely, twins, three sisters, and cross patterns) probably are different cases of the same interaction mechanism.
Data availability statement
The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.
Author contributions
HK, SK, and SS initiated the study. HK built the experimental setup and performed the measurements; all the authors analyzed the data. HK and SS wrote the paper.
Funding
The study was supported by the UK EPSRC Project EP/W002868/1, European Union’s grants Horizon 2020 ETN MEFISTA (861152), and EID MOCCA (814147).
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
1. Onorato M, Residori S, Bortolozzo U, Montina A, Arecchi FT. Rogue waves and their generating mechanisms in different physical contexts. Phys Rep (2013) 528:47–89. doi:10.1016/j.physrep.2013.03.001
2. Lecaplain C, Grelu P, Soto-Crespo JM, Akhmediev N. Dissipative rogue waves generated by chaotic pulse bunching in a mode-locked laser. Phys Rev Lett (2012) 108:233901. doi:10.1103/physrevlett.108.233901
3. Song Y, Wang Z, Wang C, Panajotov K, Zhang H. Recent progress on optical rogue waves in fiber lasers: Status, challenges, and perspectives. Adv Photon (2020) 2(2):024001. doi:10.1117/1.ap.2.2.024001
4. Liu J, Li X, Zhang S, Liu L, Yan D, Wang C. Spectral filtering effect-induced temporal rogue waves in a Tm-doped fiber laser. Opt Express (2021) 29(19):30494. doi:10.1364/oe.434390
5. Du Y, Gao Q, Zeng C, Mao D, Zhao J. Formation and statistical properties of rogue wave in dispersion-managed fiber lasers. Phys Rev A (2021) 103:063504. doi:10.1103/physreva.103.063504
6. Meng F, Lapre C, Billet C, Sylvestre T, Merolla J, Finot C, et al. Intracavity incoherent supercontinuum dynamics and rogue waves in a broadband dissipative soliton laser. Nat Commun (2021) 12:5567. doi:10.1038/s41467-021-25861-4
7. Zhou Y, Chan J, Jalal B. A unified framework for photonic time-stretch systems. Laser Photon Rev (2022) 16:2100524. doi:10.1002/lpor.202100524
8. Luo M, Zhang Z-X, Liu M, Luo A-P, Xu W-C, Luo Z-C. Dissipative rogue waves generated by multi-soliton explosions in an ultrafast fiber laser. Opt Express (2022) 30(12):22143. doi:10.1364/oe.459560
9. Kbashi H, Sergeyev SV, Al Araimi M, Rozhin A. Vector soliton rain. Laser Phys Lett (2019) 16(3):035103. doi:10.1088/1612-202x/aaf89b
10. Sergeyev SV, Eliwa M, Kbashi H. Polarization attractors driven by vector soliton rain. Opt Express (2022) 30(20):35663. doi:10.1364/oe.462491
11. Xu J, Wu J, Ye J, Song J, Yao B, Zhang H, et al. Optical rogue wave in random fiber laser. Photon Res (2020) 8(1):1. doi:10.1364/prj.8.000001
12. Chouli S, Grelu P. Rains of solitons in a fiber laser. Opt Express (2009) 17(14):11776. doi:10.1364/oe.17.011776
13. Kolpakov SA, Kbashi H, Sergeyev SV. Dynamics of vector rogue waves in a fiber laser with a ring cavity. Optica (2016) 3(8):870–5. doi:10.1364/optica.3.000870
14. Solli DR, Ropers C, Koonath P, Jalali B. Optical rogue waves. Nature (2007) 450:1054–7. doi:10.1038/nature06402
15. Hammani K, Finot C, Dudley JM, Millot G. Optical rogue-wave-like extreme value fluctuations in fiber Raman amplifiersOptical rogue-wave-like extreme value fluctuations in fiber Raman amplifiers. Opt Express (2008) 16(21):16467–74. doi:10.1364/oe.16.016467
16. Gao L, Cao Y, Wabnitz S, Ran H, Kong L, Li Y, et al. Polarization evolution dynamics of dissipative soliton fiber lasers. Photon Res (2019) 7(11):1331. doi:10.1364/prj.7.001331
17. Kolpakov S, Kbashi H, Sergeyev S. Slow optical rogue waves in a unidirectional fiber laser. In: 2016 Conference on Lasers and Electro-Optics (CLEO) - San Jose; 5–10 June 2016; CA, United States (2016).
18. Huerta-Cuellar G, Pisarchik AN, Barmenkov YO. Experimental characterization of hopping dynamics in a multistable fiber laser. Phys Rev E (2008) 78(R):035202. doi:10.1103/physreve.78.035202
19. Pisarchik AN, Jaimes-Reategui R, Sevilla-Escoboza R, Huerta-Cuellar G, Taki M. Rogue waves in a multistable system. Phys Rev Lett (2011) 107(27):274101. doi:10.1103/physrevlett.107.274101
20. Gabitov IR, Kueppers F, Shkaryaev M. Statistics of rare events: Errors in optical fiber communication systems. In: Laser Optics 2016 17th international conference; June 2016; Saint-Petersburg, Russia (2016).
21. Sergeyev SV, Kbashi H, Tarasov N, Loiko Y, Kolpakov SA. Vector-resonance-multimode instability. Phys Rev Lett (2017) 118:033904. doi:10.1103/physrevlett.118.033904
22. Kbashi H, Sergeyev SV, Mou C, Garcia AM, Araimi MA, Rozhin A, et al. Bright-dark rogue waves. Annalen der Physik (2018) 530:1700362. doi:10.1002/andp.201700362
23. Kbashi HJ, Sergeyev SV, Al-Araimi M, Rozhin A, Korobko D, Fotiadi A. High-frequency vector harmonic mode locking driven by acoustic resonances. Opt Lett (2019) 44(21):5112–5. doi:10.1364/ol.44.005112
24. Kbashi H, Sergeyev SV, Araimi MA, Rozhin A, Rozhin A. Vector soliton rain. Laser Phys Lett (2019) 16(3):035103. doi:10.1088/1612-202x/aaf89b
Keywords: soliton rain, fiber laser, autocorrelation function, fiber birefringence, rogue wave (RW)
Citation: Kbashi HJ, Kolpakov SA and Sergeyev SV (2022) Fast and slow optical rogue waves in the fiber laser. Front. Phys. 10:1048508. doi: 10.3389/fphy.2022.1048508
Received: 19 September 2022; Accepted: 15 November 2022;
Published: 30 November 2022.
Edited by:
Chong Liu, Northwest University, ChinaReviewed by:
Zhi-Chao Luo, South China Normal University, ChinaJunsong Peng, East China Normal University, China
Copyright © 2022 Kbashi, Kolpakov and Sergeyev. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Hani J. Kbashi, h.kbashi@aston.ac.uk