MERP: Motifs enhanced network embedding based on edge reweighting preprocessing

Network embedding has attracted a lot of attention in different fields recently. It represents nodes in a network into a low-dimensional and dense space while preserving the structural properties of the network. Some methods (e.g. motif2Vec, RUM, and MODEL) have been proposed to preserve the higher-order structures, i.e., motifs in embedding space, and they have obtained better results in some downstream network analysis tasks. However, there still exists a significant challenge because original motifs may include redundant noise edges, and embedding entire motifs into embedding space may adversely affect the performance in downstream tasks. To overcome this problem, we propose a motifs enhancement framework for network embedding, based on edge reweighting. Through edge reweighting, the weight of redundant noise edges between motifs is decreased. Therefore, the effect of redundant noise edges will be reduced in the embedding space. We apply the edge reweighting as a preprocessing phase in network embedding, and construct the motifs enhanced network by incorporating enhanced motifs structures with the original network. By doing this, the embedding vectors from the motifs enhanced network can achieve better performance in downstream network analysis tasks. Extensive experiments are performed on two network analysis tasks (community detection and node classification) with synthetic and real-world datasets. The results show that our framework outperforms state-of-the-art network embedding methods.

1 Introduction

Network embedding, also known as network representation learning, maps the nodes in a network to vectors in a low-dimensional and dense space while preserving various structures and connectivity patterns between nodes [1, 2]. These vectors can be used with existing machine learning algorithms to accomplish downstream network analysis tasks--e.g., node classification [3], link prediction [4], community detection [5], recommendation [6], and anomaly detection [7]. Due to the excellent performance in different network analysis tasks, network embedding has attracted a lot of attention.

From academia and industry. And various network embedding methods have been proposed from different perspectives [1]. To capture the higher-order structural patterns between nodes, lots of works have been presented to integrate higher-order structures into network embedding [8, 9]. As the most common higher-order structures, network motifs are considered building blocks for a complex network, and have been found in various networks--e.g., the networks of neurology, ecology, and biochemistry [10, 11]. Studying network motifs is effective for understanding structures and functions in real-world complex networks [12]. Therefore, lots of network embedding algorithms have been designed to preserve network motifs, such as motif2Vec [13], RUM [14], and MODEL [15], which achieved excellent performance in different network analysis tasks.

However, all these methods are implemented to embed entire network motifs into the embedding space including some redundant noise edges, which may affect the performance of network embedding. We illustrate this situation with an example in Figure 1. Figure 1A shows an original undirected network with two communities. Figure 1B is the motifs from the network in Figure 1A, and we set the triangle to be the motifs of interest. To retain higher-order relationships, previous works preserved all these four motifs in embedding space. However, among these motifs, m3 is constituted by nodes from different communities. Hence, preserving motif m3 will make the distances between nodes 3, 4, and five which belong to different communities closer in embedding space and this may adversely affect the performance in downstream tasks. Therefore, incorporating entire network motifs including redundant noise edges into embedding space will impact the performance of network embedding in downstream tasks.

FIGURE 1

FIGURE 1. An example of network motifs and redundant noise edges. (A) Original network. (B) The motifs of original network.

In this paper, we propose MERP, a Motifs enhanced network embedding based on Edge Reweighting Preprocessing to overcome the above-mentioned problem of the existing methods. Specifically, we first construct the motifs weighted network by incorporating the higher-order structures--i.e., motifs, with first-order structures. Then an iteration motifs enhancement algorithm is designed based on a random walk to re-assign the weights of edges in the motifs weighted network. By edge reweighting, we decrease the weight of redundant noise edges in the motifs. Through iteratively processing this procedure, we obtain the motifs enhanced network. Finally, the final embedding vectors are obtained by projecting the motifs enhanced network with existing network embedding methods. Experiments on synthetic and real-world networks demonstrate that our framework achieves better performance than existing network embedding algorithms in community detection and node classification.

To summarize, the main contributions in this paper are as follows:

• We propose a new framework to incorporate enhanced motifs in network embedding to overcome the problem of preserving redundant noise edges in embedding space, which is commonly existing in previous works.

• We apply an iteration edge reweighting algorithm based on a random walk to re-assign the weight of edges in motifs before network embedding and our algorithm is a general technique that can be easily combined with existing network embedding methods.

• We perform experiments with two typical network analysis tasks, community detection, and node classification, on synthetic and real-world networks to evaluate our approach. Experimental results show that our method improves the state-of-the-art baselines by 0.65%–10.79% (NMI) in community detection task, and 0.21%–2.29% (micro-F1) in node classification task.

The rest of the paper is organized as follows. In section 2, we summarize network embedding research specifically related to network embedding methods with the network motifs. Then we propose our framework with enhanced motifs based on edge reweighting preprocessing in section 3. Section 4 outlines the experimental results on two network analysis tasks: community detection and node classification. Finally, section 5 presents our conclusions and discussions with future works.

2 Related works

Network embedding has attracted a lot of attention in recent years. It learns the low-dimensional representations of nodes in a network and preserves the structure information which aims to close the gap between network analysis and machine learning technologies. In this section, we briefly review the related works. Several comprehensive surveys could refer to [1, 2, 16, 17].

Network motifs have been proven to play an important role in describing the higher-order structural information between nodes in networks. Therefore, preserving the network motifs can improve the performance of network embedding in downstream network analysis tasks. And some works have been proposed to incorporate network motifs in network embedding. Dareddy et al. proposed the motif2Vec [13], which transformed the original heterogeneous network into a motif network by computing the motif adjacency matrices. Through the skip-gram model, the final embedding vectors were obtained and achieved better results in node classification and link prediction tasks. Yu et al. designed a new strategy MotifWalk in RUM to represent the motifs [14], which used each motif as a new node to construct an auxiliary network. The embedding vectors were obtained by executing a random walk on the auxiliary network and had better performance in node classification and network reconstruction. Wang et al. proposed the MODEL algorithm to preserve the network motifs by autoencoder [15]. In MODEL, the first-order similarities were redefined according to common motifs between nodes, and the second-order similarities were determined by the neighbors between the nodes. In the work of HONE [18], Rossi et al. constructed a series matrix to represent network motifs, such as the weighted motif adjacency matrix, the motif transition matrix, the motif Laplacian, and the normalized motif Laplacian. The final embedding vectors were got by solving a minimization problem with different matrices. In MBRep [19], Qian et.al proposed a generalized motif-based higher-order representation learning method. It learned triangle motif embedding in a heterogeneous network using a SkipGram model and had a better performance in link prediction. Ping et.al presented an algorithm LEMON [20] to bridge connectivity and structural similarity in a uniform network representation via motifs.

Although these methods preserve network motifs in different ways and have good performance in different network analysis tasks, all of them incorporate entire network motifs in embedding space. As we have mentioned earlier, there are some redundant noise edges in network motifs making the performance of these methods still have space to improve. In our work MERP, we conduct an iteration algorithm to decrease the weight of redundant noise edges in motifs before incorporating the network motifs in the embedding space. In this way, our method achieves better results in different tasks than the existing methods.

With the development of deep learning in various domains, network embedding based on the deep neural network has drawn increasing research attention and tremendous related works have been proposed [1, 16]. Such as InfoMotif [21], GSN [22], and MBHAN [23], these works incorporated subgraphs or attributed structural roles in GNN and achieved notable performance gains compared with state-of-art GNNs. There are also some network embedding methods designed for specific networks, such as signed networks [24–26], bipartite networks [27–29], dynamic networks [30, 31], and heterogeneous networks [32–34]. In this paper, we mainly focus on the most essential case where only the static, homogeneous network is available.

3 Motifs enhanced network embedding based on edge reweighting preprocessing

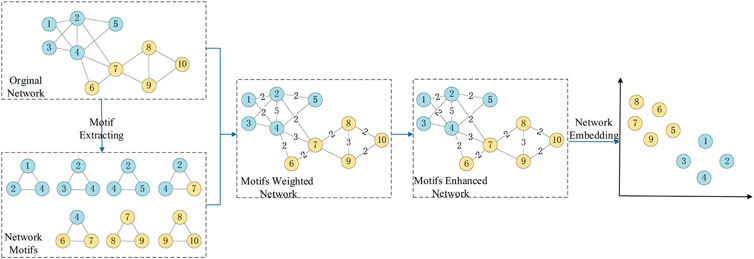
The framework of MERP is shown in Figure 2, which includes three steps. The first step is the extraction and representation of network motifs. In this step, network motifs containing redundant noise edges are extracted and represented as the motifs weighted network. The second step is network motifs enhancement, which constructs the motifs enhanced network by reweighting redundant noise edges in motifs through multiple iterations of the random walk-based method. The third step is network embedding, which projects the motifs enhanced network by existing network embedding methods and preserves the enhanced motifs structures into the embedding space.

FIGURE 2

FIGURE 2. The framework of MERP.

3.1 Motifs weighted network construction

Given an undirected and unweighted network G= (V, E), we can construct the adjacency matrix A from node list V and edge list E, where A is a symmetric matrix and represents the first-order structures of the network G. To get the higher-order structure information of motifs, we can use some existing motifs detection algorithms such as FANMOD [35]. With these tools, the motifs set $M=\left\{m_1,m_2,m_3\dots m_l\right\}$ is extracted from the network G, where each m_i is a motif. By the motifs set $M$, we construct the motifs adjacency matrix $W^M$, where the value of each element $w_{i,j}^M$ in $W^M$ is the number of times that node i and node j appear together in the motifs set M.

For example, in Figure 1A, node two and node three appear in motif m1 and motif m2, so the value of $w_{2,3}^M$ is 2. The motifs adjacency matrix $W^M$ contains all the motifs structures in the network G. However, $W^M$ may have different dimensions with A because some nodes may not be contained in any motif. Furthermore, $W^M$ does not preserve the first-order relationships between nodes. Therefore, we construct the motifs weighted matrix $W^{\prime }$ that combines the adjacency matrix A and the motif adjacency matrix $W^M$ to keep the same nodes set as in the original network and to preserve the first-order structures between nodes.

$\begin{array}{c}{W}^{\prime }=A+W^M\end{array}(1)$

The motifs weighted matrix $W^{\prime }$ not only retains the motifs structures, but also the first-order information between nodes. Some previous motifs-aware network embedding approaches are based on the motifs weighted network and can achieve better results than traditional network embedding methods in some network analysis tasks. However, the motifs weighted matrix $W^{\prime }$ contains the entire motifs including some redundant noise edges. These inter-community motifs cut will be retained in the network embedding vectors, which deteriorates the performance in downstream tasks. Therefore, it needs to filter the noises and reduce the weight of redundant noise edges in motifs. To achieve this goal, we re-assign the weights in the motifs weighted matrix by motifs enhancement.

3.2 Motifs enhancement

As we have described earlier, some motifs are conducted by nodes from different communities, and the edge between these nodes are the redundant noise edges for these edges would make the communities more obscure in the embedding space.

To reduce the influence of redundant noise edges in the motifs weighted matrix, we propose a motifs enhancement method to reduce the weight of these edges.

We use the dynamic behavior of nodes to determine whether two nodes in the motifs belong to the same community. It has proved that a random walker will be stuck for a longer time in the same community than between communities. Thus, random walkers starting from nodes in the same community will behave in a similar way when they randomly walk across the networks. Generally, nodes belonging to the same community have similar dynamic behaviors, while the dynamic behaviors of nodes belonging to different communities have lower similarities. Therefore, the weight between the nodes can be reweighted by the dynamic behavior similarity of the two nodes. If the dynamic behavior similarity between two nodes is low, it means that the two nodes have a high probability of belonging to different communities. The weight of the edges between them can be reduced. Many methods can be used to describe the dynamic behaviors of nodes [36–40]. In this paper, we use the k-step random walk for calculation simplicity [39].

Specifically, the k -step random walk in the network can be calculated by the k -order adjacency matrix. Therefore, for the motifs weighted matrix $W^{\prime }$, we first calculate its diagonal matrix D with the elements shown as follows:

$\begin{array}{c}{d}_{ij}=\{\begin{array}{c}{\displaystyle \sum }_p{W}_{i,p}^{\prime }i=j\\ 0i\ne j\end{array}\end{array}(2)$

Then the transition probability matrix P of motifs weighted network is defined as:

$\begin{array}{c}P=D^{-1}{W}^{\prime }\end{array}(3)$

Each element $p_{ij}$ in P is the transition probability from node $v_i$ to $v_j$ within one step in motifs weighted network.

Then we can calculate the k-step transition probability matrix as following:

$\begin{array}{c}{P}^k=P\cdots P\end{array}(4)$

Each element $P_{ij}^k$ in $P^k$ records the probability that node $v_i$ reaches $v_j$ through k steps random walk. Each row of $P^k$--i.e., $P_{i·}^k$, can be regarded as a vector in n-dimensional space and can be used to represent the dynamic behavior of node $v_i$. To capture all behaviors from order one to order k, we use the transition probability of the first 1∼ k order vectors as the behavior of the node. Therefore, the behavior representation of all nodes can be represented by the sum of the first k-order transition probabilities:

$\begin{array}{c}{R}^k={\displaystyle \sum }_{i=1}^k{P}^i\end{array}(5)$

To measure the similarity of the dynamic behavior between nodes, we can choose a variety of similarity calculation methods, such as Euclidean distance, correlation coefficient, and cosine similarity. Here we use cosine similarity to calculate the behavior similarity between nodes for the cosine similarity can well capture the difference between two vectors in high-dimensional space. Therefore, the dynamic behavior similarity calculation based on cosine similarity is as follows:

$\begin{array}{c}Sim\left(v_i,v_j\right)=\frac{R_i^k\bullet R_j^k}{\parallel R_i^k\parallel \parallel R_j^k\parallel }\end{array}(6)$

If the behavior vector of node $v_i$ and node $v_j$ have high similarity, the corresponding similarity calculation $Sim\left(v_i,v_j\right)$ is close to 1, otherwise, if the behavior vectors of node $v_i$ and node $v_j$ have large differences, the corresponding similarity calculation $Sim\left(v_i,v_j\right)$ is close to 0. Therefore, the similarity $Sim$ can be used to measure whether the edge between two nodes is a redundant noise edge.

For each edge $\left(v_i,v_j\right)$ existing in the motif weighted network, we set its weight to the value of the similarity $Sim\left(v_i,v_j\right)$. In this way, we get a new motifs-weighted network. Then in this new motifs-weighted network, the above weights calculation process is repeated. Through I iterations of calculation, the motifs structures in the motifs weighted network are continuously enhanced. For convenience, we call the final network as the motifs enhanced network and the weights in the motifs enhanced network are marked as $\stackrel{\sim }{W}$, which incorporates the enhanced motifs information between nodes. The outline of motifs enhancement by edge reweighting preprocessing is demonstrated in Algorithm 1.

Whereas, it is time-consuming to calculate $R^k$ in real applications, especially for large-scale networks. To speed up the calculation, we take advantage of the characteristics of network G. Since network G is a general network, the adjacency matrix A is a symmetric matrix. Then both the motifs adjacency matrix W and the motifs weighted matrix $W^{\prime }$ are symmetric matrices.

Although the transition probability matrix P is an asymmetric matrix, P has a symmetric structure. Since

$\begin{array}{c}{D}^{1/2}P{D}^{-1/2}=D^{-1/2}{W}^{\prime }{D}^{-1/2}\end{array}(7)$

The symmetric matrix $D^{-\left(1/2\right)}{\mathrm{W}}^{\prime }{D}^{-\left(1/2\right)}$ has eigen-decomposition $Q\Lambda Q^T$ and Q is orthogonal matrix, $\Lambda =diag\left({\lambda }_1,...{\lambda }_n\right)$.

And we have the equations:

$\begin{array}{c}{D}^{1/2}P{D}^{-1/2}=D^{-1/2}{W}^{\prime }{D}^{-1/2}=Q\Lambda Q^T\end{array}(8)$

$\begin{array}{c}{D}^{1/2}{P}^k{D}^{-1/2}={\left(D^{\frac{1}{2}}P{D}^{-1/2}\right)}^k={\left(Q\Lambda Q^T\right)}^k=Q{\Lambda }^k{Q}^T\end{array}(9)$

So, Equation 4 can be rewritten as:

$\begin{array}{c}{P}^k=D^{-1/2}\left(Q{\Lambda }^k{Q}^T\right)D^{-1/2}\end{array}(10)$

And Equation 5 can be calculated as:

$R^k={\displaystyle \sum }_{i=1}^k{P}^i={\displaystyle \sum }_{i=1}^k{D}^{-1/2}\left(Q{\Lambda }^i{Q}^T\right)D^{-1/2}=D^{-1/2}Q\left({\displaystyle \sum }_{i=1}^k{\Lambda }^i\right)Q^T{D}^{-1/2}(11)$

3.3 Complexity analysis

The time complexity of our algorithm is primarily dominated by the cost of calculating the eigen-decomposition of the transition probability matrix P. For a large-scale network, we could use some algorithms to calculate the first h eigenpairs to approximate the eigen-decomposition of matrix P, such as the Lanczos algorithm [40]. Hence the time complexity for eigen-decomposition is $O\left(t\times n^2\right)$ in the worst case, where t is the average number of nonzero elements in rows of the matrix. And in most instances, transition probability matrix P is sparsity and $t\ll n$. Furthermore, given a network G, the eigen-decomposition step can be calculated offline. The time complexity to calculate cosine similarity between each pair of nodes is $O\left(n^2\right)$. The total time complexity of MERP is $O\left(\left(t+L\right)\times n^2\times I\right)$, where L is the edges number of network and I is the iteration number. And the iteration number I is small, mostly less than 10.

Algorithm 1. Motifs enhanced by edge reweighting

Input: Network G = (V, E), adjacency matrix A of the network G, motifs set M of the network G, step for random walk k, iteration I

Output: weighted matrix $\stackrel{\sim }{W}$ with motifs enhanced information

1: Construct the motifs adjacency matrix $W^M$ from M

2: $W^{\prime }=A+W^M$

3: for m = 0 to I do

4: Calculate the degree matrix D by Equation 2

5: Calculate the transition probability matrix P by $P=D^{-1}{W}^{\prime }$

6: for n = 1 to k do

7: $R^n+=P^n$

8: end for

9: for each edge (i, j) in E do

10: Calculate the similarity $Sim\left(v_i,v_j\right)$of node $v_i$ and $v_j$by Equation 6

11: $w_{ij}^{\prime }=Sim\left(v_i,v_j\right)$

12: end for

13: end for

14: Calculate the final motifs enhanced matrix $\stackrel{\sim }{W}=W^{\prime }$

15: Return $\stackrel{\sim }{W}$

4 Experiments

To evaluate the performance of our method, we perform two different experiments on network analysis tasks: community detection and node classification.

4.1 Community detection

Community detection is to divide nodes into different clusters according to the connection between nodes, which is one of the most important network analysis tasks [41]. There are dense connections between nodes in the same community, while the connections between nodes in different

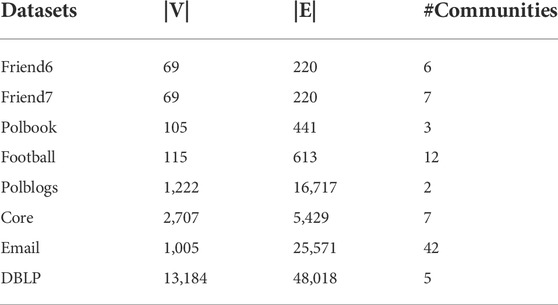
Communities are relatively sparse. To test the effectiveness of our method, we conducted community detection experiments on both synthetic and real-world datasets. Similar to the community detection experiments involved in NE-MRF [42], we first use different network embedding to map the nodes into low-dimensional space. Then these node vectors are clustered into different clusters using the k-means algorithm. To avoid the sensitivity of k-means clustering to the initial centroid, we perform each experiment 5 times and calculated its average value as the final result. With the ground truth community information of these data, we use normalized mutual information (NMI) as the results evaluation metric. The higher the NMI, the closer the result obtained by the method is to the ground truth.

4.1.1 Synthetic datasets

To evaluate the effectiveness of our algorithm, we use the LFR framework to obtain six synthetic networks with known community information [43]. In the LFR framework, both the degree distribution of nodes and the size of communities satisfy the power-law distribution, which is consistent with most real-world networks. We set the main parameters in the LFR framework to construct synthetic networks in our experiments as follows: 1) the number of nodes is 1,000, 2) the average node degree is 20, 3) the maximum node degree is 50, 4) the minimum number of nodes in the community is 50, 5) the maximum number of nodes in the community is 80. The main difference between these six synthetic networks is $\lambda$, which is used to control the ratio of a node’s edges connecting to other nodes in different communities. And the values of $\lambda$ are [0.2, 0.5, 0.6, 0.65, 0.7, 0.8]. The higher the value, the more the node is connected with the nodes in different communities, and the more difficult the community detection task is.

We compare the framework proposed in this article with three well-known network representation learning algorithms (deepWalk [3], node2vec [44], and GraRep [45]). The methods combined our.

Framework with deepWalk, node2vec, and GraRep are called: MERP-D, MERP-N, and MERP-G respectively. We use the default parameters in these algorithms as the setting parameters in our experiments. All embedding dimensions in our experiments are set to 128.

The results of the community detection for synthetic datasets are shown in Figure 3. Compared with traditional methods, our proposed framework has achieved the best results in all six synthetic datasets. On the whole, when $\lambda$ <0.6, both our proposed method and traditional methods can obtain good performance in community detection for the community structures are obvious in LFR networks. When $\lambda$ > 0.7, the community structures are not prominent enough in synthetic networks and the motifs contain more redundant noise edges, making the task of community detection more difficult. However, our method can still achieve marginally better performance than the original algorithms. When $0.6\le \lambda \le 0.7$, our method can achieve better results than traditional algorithms. Specifically, MERP-N can achieve 44.15% higher NMI than the original node2vec method when $\lambda =0.65$. And MERP-D can get 4% NMI higher than the original deepWalk algorithm. Meanwhile, MERP-G is 2% higher than the GraRep method, although GraRep is also a method based on a k-step transition probability matrix.

FIGURE 3

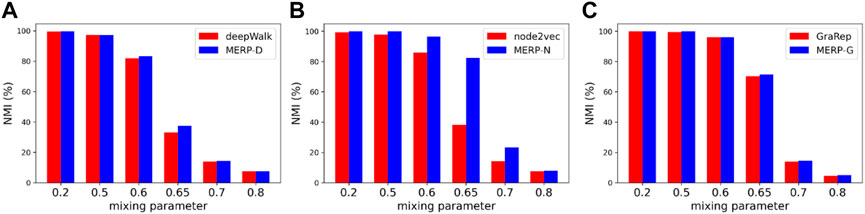
FIGURE 3. Comparison of our method with three embedding methods, (A) deepWalk, (B) node2vec, and (C) GraRep, on LFR benchmark networks with different mixing parameters.

4.1.2 Real-world datasets

In this section, we evaluate the performance of our proposed method on eight real-world datasets with ground truth in the community detection task. The attributes of these eight real-world datasets are shown in Table 1. In this experiment, we compare our framework with deepWalk, node2Vec, GraRep, and MRF-based methods [42]. The MRF-based method incorporates the Markov random field with network embedding and can achieve better performance than other traditional algorithms (e.g. SNMF [46], MNDP [47]) in community detection tasks. And we use the results described in the original paper of the MRF-based method because getting better results by this method requires adjusting a lot of parameters. The community detection results of all methods are shown in Table 2. We see that our methods MERP-D, MERP-N, and MERP-G acquire better results compared with the original methods. We also find that our approach performs better on five out of six networks compared with the MRF-based method. From the experiment results in table 2, we can conclude that our method has comparable performance on the community detection task compared with other higher-order structures preserving network embedding methods.

TABLE 1

TABLE 1. Statistics of real-world datasets.

TABLE 2

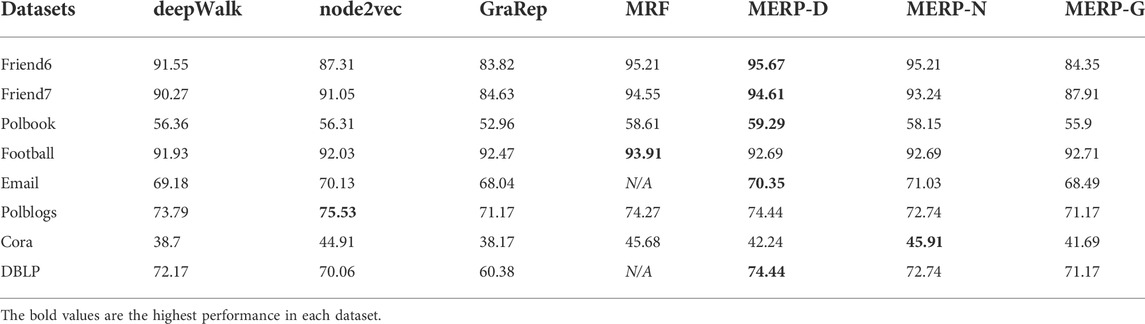
TABLE 2. Performance comparison of different methods on real-world networks (the MRF-based method did not give results on Email and DBLP networks; we mark these with ‘N/A’).

4.1.3 Parameter analysis

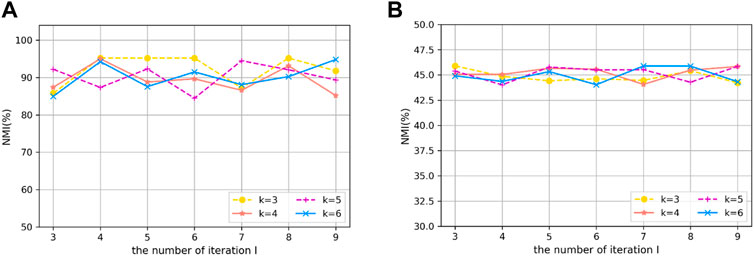
To evaluate the effect of k and I parameters in our framework on community detection tasks, we perform experiments on real-world datasets. In these experiments, the value of random walk step k was changed from 3 to 6, because previous works have shown that community structures in a random walk would more clearly when the step size is less than 6. For different networks having similar performance, we just exhibit the results of our method MERP-N on Friend6 and Cora networks. We show the community detection results NMI (%) with respect to k and I in Figure 4.

FIGURE 4

FIGURE 4. Effect of parameters k and I on community detection task on (A) Friend6 and (B) Cora.

As shown in Figure 4, community detection results have a little change and the performance is relatively stable. Furthermore, we also find that with different parameters MERP-N on both networks still shows competitive performance compared with other methods. As shown in Figure 4B, the worst result is 44.04%, but this result is still better than other results obtained by most of the traditional methods.

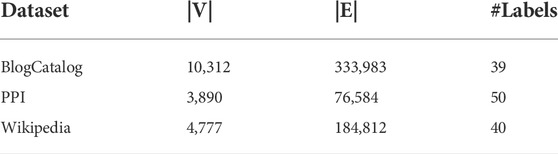
4.2 Node classification

To evaluate our framework in different network analysis tasks, we perform experiments on multi-label node classification. We use three widely used networks for node classification in this section. The details of these networks are shown in Table 3.

TABLE 3

TABLE 3. Statistics of benchmark datasets.

BlogCatalog [48] is an online social network of bloggers, where nodes are bloggers and edges are the friendship network among the bloggers. Node labels represent topics of interest to the bloggers.

Protein-Protein Interactions (PPI) [49] is a subgraph of the PPI network for Homo Sapiens. Nodes represent human proteins and edges represent physical interaction between proteins. Node labels stand for biological states obtained from the hallmark gene sets.

Wikipedia¹ is a words co-occurrence network from the first million bytes of the Wikipedia dump. Nodes are Wikipedia pages and edges are hyperlinks between pages. Labels represent the part-of-speech (POS) tags of pages which are inferred using the Stanford POS-Tagger [50].

And our experimental settings in this section were the same as the NetMF [51]. Firstly, we randomly sampled a ratio of nodes as the training set and the others as the test set. The ratio was changed from 0.1 to 0.9 with the step size being 0.1. Then, we used the one-vs-rest logistic regression model LIBLINEAR² as the classification algorithm. The experiment procedure was repeated 10 times to reduce the effect of different training set and test set. The performance is evaluated in terms of average micro-F1. We also compare our framework with deepWalk, node2vec, and GraRep. Our framework with deepWalk, node2vec, and GraRep are also called MERP-D, MERP-N, and MERP-G, respectively. Finally, Figure 5 shows the results on the three networks in terms of micro-F1.

FIGURE 5

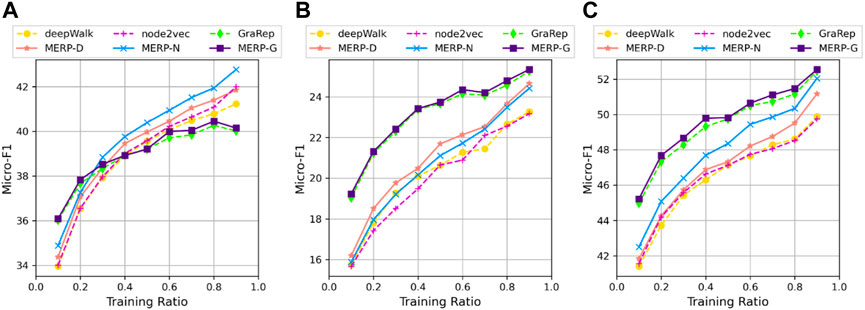
FIGURE 5. Performance evaluation with varying the ratio of training data on three real-world networks with different methods. (A) BlogCatalog network, (B) PPI network, and (C) Wikipedia network.

From the results and the curves in Figure 5, we find that our methods (MERP-D, MERP-N, and MERP-G) can achieve a better (or at least similar) micro-F1 than the original methods (deepWalk, node2vec, and GraRep) on all three real-world datasets.

Furthermore, we can make some interesting observations from Figure 5. We find that GraRep has a better performance than random walk-based methods (node2vec and deepWalk) no matter the ratio of the training set on Wikipedia and PPI networks. And our method MERP-G is still better than the original GraRep on all three networks in all training ratios. In all three networks, the original methods deepWalk and node2vec have similar results. However, in our model, MERP-N has the best results on BlogCatalog and Wikipedia networks while MERP-D has the best performance on the PPI network. To summarize, our proposed method incorporating enhanced motifs in network embedding can achieve significant improvements compared with the original network embedding methods on the node classification task.

4.2.1 Parameter analysis

To analyze the effect of parameters k and I on node classification, we also conducted experiments with MERP-N on the BlogCatalog and Wikipedia datasets. The training ratios varied in the range [0.1, 0.5, 0.9]. The steps k changed in the range [3, 4, 6], and the number of iterations I varied from three to 7.

The node classification results are shown in Figure 6 in terms of micro-F1. From Figure 6, we can see our framework exhibit stable performance with different parameters.

FIGURE 6

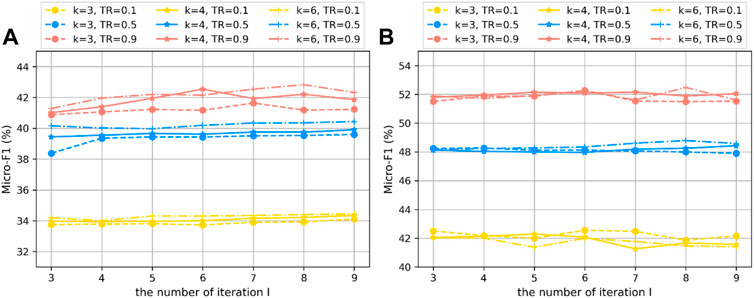
FIGURE 6. Effect of parameters k and I on node classification task on real-world dataset (A) BlogCatalog and (B) Wikipedia.

Specifically, with the same training ratio, the micro-F1 results range within 2\% on all three datasets. This demonstrates that the performance of our method on node classification is insensitive to the setting of the parameters.

5 Conclusion and discussions

In this paper, we proposed a novel motifs enhancement network embedding framework (MERP) based on edge reweighting preprocessing. MERP framework is used to incorporate the enhanced motifs information with local structure information in the original network. By an iteration motifs enhanced algorithm, the weights of motifs between nodes in different communities are decreased. In this way, we reduce the effect of redundant noise edges in motifs. And we applied edge reweighting as a preprocessing stage making nodes’ embedding vectors useful to all kinds of downstream network analysis tasks. Moreover, MERP can be effortlessly applied with the most available network embedding algorithms. Compared with other higher-order structures preserved network embedding methods such as M-NMF [8] and Cosine [9], our method embeds motifs in the network embedding space which is proven to contain rich information and can reveal semantic information of vertices. The experimental results for downstream network analysis tasks: community detection and node classification, as well as the parameters analysis, illustrate that MERP achieves remarkable improvements compared with the existing network embedding methods.

In this study, we mainly focused on normal networks and neglected other different types of networks, such as signed networks, bipartite networks, and heterogeneous networks. And all these networks have been proven to exist motifs. Furthermore, we only analyzed the static networks and not considered dynamic networks which are common in the real world. For future work, we plan to investigate the effects of motifs-enhanced based network embedding on these networks with different types of nodes and edges.

Our method can effectively improve the structure of original networks to enhance the ability of network embedding algorithms. Due to the improvement of network structure, some problems of other network analysis algorithms may also be solved or improved, such as the resolution limit in community detection [52, 53]. Some studies have shown that network enhancement can mitigate the resolution limit and improve traditional community detection algorithms [35, 54]. So, our method can also enhance the ability of traditional algorithms in community detection.

Data availability statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author contributions

SL and JX conceived and planned the experiments. SL and YL carried out the experiments. XR and GL contributed to the interpretation of the results. SL took the lead in writing the manuscript. All authors provided critical feedback and helped shape the research, analysis and manuscript.

Funding

This work was supported in part by the National Natural Science Foundation of China under Grant 60832019 and 61702054, in part by the National Science Foundation of Shaanxi Province under Grant 2020GY-081 and 2022JQ-675, in part by the Shaanxi Key Laboratory of Intelligent Processing for Big Energy Data Open Fund Project under Grant IPBED10, and in part by the Scientific Research Program Funded by Shaanxi Provincial Education Department under Grant 21JK0918.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Footnotes

¹http://mattmahoney.net/dc/text.html.

²https://www.csie.ntu.edu.tw/\∼cjlin/liblinear/.

References

1. Li B, Pi D. Network representation learning: A systematic literature review. Neural Comput Appl (2020) 32:16647–79. doi:10.1007/s00521-020-04908-5

CrossRef Full Text | Google Scholar

2. Cui P, Wang X, Pei J, Zhu W. A survey on network embedding. IEEE Trans Knowl Data Eng (2018) 31(5):833–52. doi:10.1109/tkde.2018.2849727

CrossRef Full Text | Google Scholar

3. Bryan P, Al-Rfou R, Skiena S. Deepwalk: Online learning of social representations. In: Proceedings of the 20th ACM SIGKDD international conference on Knowledge discovery and data mining; August, 2014; New York, USA. (2014). p. 701–10.

Google Scholar

4. Wang Z, Chen C, Li W. Predictive network representation learning for link prediction. In: Proceedings of the 40th international ACM SIGIR conference on research and development in information retrieval; August, 2017; Tokyo, Japan. (2017). p. 969–72.

CrossRef Full Text | Google Scholar

5. Lv S, Xiang J, Feng J, Wang H, Lu G, Li M. Community enhancement network embedding based on edge reweighting preprocessing. J Stat Mech (2020) 2020(10):103403. doi:10.1088/1742-5468/abb45a

CrossRef Full Text | Google Scholar

6. Zhang F, Yuan NJ, Lian D, Xie X, Ma W-Y. Collaborative knowledge base embedding for recommender systems. In: Proceedings of the 22nd ACM SIGKDD international conference on knowledge discovery and data mining; August, 2016; San Francisco, CA, USA. (2016). p. 353–62.

CrossRef Full Text | Google Scholar

7. Ding K, Li J, Bhanushali R, Liu H. Deep anomaly detection on attributed networks. In: Proceedings of the 2019 SIAM International Conference on Data Mining; May, 2019; algary, Alberta, Canada (2019). p. 594–602.

CrossRef Full Text | Google Scholar

8. Wang X, Cui P, Wang J, Pei J, Zhu W, Yang S. Community preserving network embedding. In: Proceedings of the Thirty-First AAAI Conference on Artificial Intelligence; February, 2017; Hilton San Francisco. (2019).

Google Scholar

9. Zhang Y, Lyu T, Zhang Y. Cosine: Community-preserving social network embedding from information diffusion cascades. In: Proceedings of the Thirty-Second AAAI Conference on Artificial Intelligence; Feburuary, 2018; Orleans, Louisiana, USA (2018).

CrossRef Full Text | Google Scholar

10. Milo R, Shen-Orr S, Itzkovitz S, Kashtan N, Chklovskii D, Alon U. Network motifs: Simple building blocks of complex networks. Science (2002) 298(5594):824–7. doi:10.1126/science.298.5594.824

PubMed Abstract | CrossRef Full Text | Google Scholar

11. AustinBenson R, David Gleich F, Leskovec J. Higher-order organization of complex networks. Science (2016) 353(6295):163–6. doi:10.1126/science.aad9029

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Jiang J, Hu Y, Li X, Bin C, Fangcheng F, Zhitao W, Wen O. Analyzing online transaction networks with network motifs. In: Proceedings of the 28th ACM SIGKDD Conference on Knowledge Discovery and Data Mining; Auguest, 2022; Washington, DC (2022). p. 3098–106.

CrossRef Full Text | Google Scholar

13. Reddy Dareddy M, Das M, Yang H. motif2vec: Motif aware node representation learning for heterogeneous networks. In: proceedings of the 2019 IEEE International Conference on Big Data (Big Data); December, 2019; Los Angeles, CA.(2019). p. 1052–9.

CrossRef Full Text | Google Scholar

14. Yu Y, Lu Z, Liu J, Zhao G, Wen J-rong. Rum: Network representation learning using motifs. In: Proceedings of the 2019 IEEE 35th International Conference on Data Engineering (ICDE); April, 2019; Macau, SAR, China. IEEE (2019). p. 1382–93.

CrossRef Full Text | Google Scholar

15. Wang L, Ren J, Xu B, Li J, Luo W, Xia F. Model: Motif-based deep feature learning for link prediction. IEEE Trans Comput Soc Syst (2020) 7(2):503–16. doi:10.1109/tcss.2019.2962819

CrossRef Full Text | Google Scholar

16. Hou M, Ren J, Zhang D, Kong X, Zhang D, Xia F. Network embedding: Taxonomies, frameworks and applications. Comput Sci Rev (2020) 38:100296. doi:10.1016/j.cosrev.2020.100296

CrossRef Full Text | Google Scholar

17. Xue G, Zhong M, Li J, Chen J, Zhai C, Kong R. Dynamic network embedding survey. Neurocomputing (2022) 472:212–23. doi:10.1016/j.neucom.2021.03.138

CrossRef Full Text | Google Scholar

18. Rossi RA, Ahmed NK, Koh E. Higher-order network representation learning. In: Proceedings of the Companion Proceedings of the The Web Conference 2018; April, 2018; Lyon, France. (2018). p. 3–4.

CrossRef Full Text | Google Scholar

19. Hu Q, Fan L, Wang B. MBRep: Motif-based representation learning in heterogeneous networks. Expert Syst Appl (2022) 190:116031. doi:10.1016/j.eswa.2021.116031

CrossRef Full Text | Google Scholar

20. Shao P, Yang Y, Xu S, Wang C. Network embedding via motifs. ACM Trans Knowl Discov Data (2021) 16(3):1–20. doi:10.1145/3473911

CrossRef Full Text | Google Scholar

21. Bouritsas G, Frasca F, Zafeiriou S, Bronstein M. Improving graph neural network expressivity via subgraph isomorphism counting. IEEE Trans Pattern Anal Mach Intell (2022) 1. doi:10.1109/tpami.2022.3154319

CrossRef Full Text | Google Scholar

22. Sankar A, Wang J, Krishnan A, Sundaram H. Self-supervised role learning for graph neural networks. Knowl Inf Syst (2022) 64(8):2091–20121. doi:10.1007/s10115-022-01694-5

CrossRef Full Text | Google Scholar

23. Hu Q, Lin W, Tang M, Jiang J. Mbhan: Motif-based heterogeneous graph attention network. Appl Sci (2022) 12(12):5931. doi:10.3390/app12125931

CrossRef Full Text | Google Scholar

24. Yu L, Yuan T, Zhang J, Chang Y. Learning signed network embedding via graph attention. In: Proceedings of the Thirty-Fourth AAAI Conference on Artificial Intelligence; April, 2020; Louis, USA (2020). p. 4772–9.

Google Scholar

25. Lee Y-C, Seo N, Han K, Kim S-W Asine: Adversarial signed network embedding. In: Proceedings of the 43rd International ACM SIGIR Conference on Research and Development in Information Retrieval; July, 2020. Xi'an, China,(2020) 609–18.

Google Scholar

26. Amin J, Tyler D, Esmailian P, Tang J, KevinChang C-C. Rose: Role-based signed network embedding. In: Proceedings of The Web Conference 2020; April, 2020; Taipei Taiwan (2020). p. 2782–8.

Google Scholar

27. Gao M, Chen L, He X, Zhou A. Bine: Bipartite network embedding. In: Proceedings of the The 41st International ACM SIGIR Conference on Research & Development in Information Retrieval (2018). p. 715–24.

Google Scholar

28. Huang W, Li Y, Yuan F, Fan J, Yang H. Biane: Bipartite attributed network embedding. In: Proceedings of the 43rd international ACM SIGIR conference on research and development in information retrieval; July, 2020; Xi'an, China (2020). p. 149–58.

Google Scholar

29. Cao J, Lin X, Guo S, Liu L, Liu T, Wang B. Bipartite graph embedding via mutual information maximization. In: Proceedings of the 14th ACM International Conference on Web Search and Data Mining; March, 2021; Israel (2021). p. 635–43.

CrossRef Full Text | Google Scholar

30. Hou C, Zhang H, Shan H, Tang K. Glodyne: Global topology preserving dynamic network embedding. In: Proceeding of the IEEE 38th International Conference on Data Engineering; May, 2020; Kuala Lumpur, Malaysia (2020).

Google Scholar

31. Ma L, Zhang Y, Li J, Lin Q, Bao Q, Wang S, et al. Community-aware dynamic network embedding by using deep autoencoder. Inf Sci (2020) 519:22–42. doi:10.1016/j.ins.2020.01.027

CrossRef Full Text | Google Scholar

32. Wang X, Lu Y, Shi C, Wang R, Cui P, Mou S. Dynamic heterogeneous information network embedding with meta-path based proximity. IEEE Trans Knowl Data Eng (2020) 34:1117–32. doi:10.1109/tkde.2020.2993870

CrossRef Full Text | Google Scholar

33. Li X, Shang Y, Cao Y, Li Y, Tan J, Liu Y. Type-aware anchor link prediction across heterogeneous networks based on graph attention network. In: Proceedings of the Thirty-Fourth AAAI Conference on Artificial Intelligence; February, 2020; New York, USA (2020). p. 147–55.

CrossRef Full Text | Google Scholar

34. Wang R, Shi C, Zhao T, Wang X, Ye YF. Heterogeneous information network embedding with adversarial disentangler. IEEE Trans Knowl Data Eng (2021) 1. doi:10.1109/tkde.2021.3096231

CrossRef Full Text | Google Scholar

35. Wernicke S, Rasche F. Fanmod: A tool for fast network motif detection. Bioinformatics (2006) 22(9):1152–3. doi:10.1093/bioinformatics/btl038

PubMed Abstract | CrossRef Full Text | Google Scholar

36. Xiang J, Zhang J, Zheng R, Li X, Li M. Nidm: Network impulsive dynamics on multiplex biological network for disease-gene prediction. Brief Bioinform (2021) 22:bbab080. doi:10.1093/bib/bbab080

PubMed Abstract | CrossRef Full Text | Google Scholar

37. Zhang Z-K, Liu C, Zhan X-X, Lu X, Zhang C-X, Zhang Y-C. Dynamics of information diffusion and its applications on complex networks. Phys Rep (2016) 651:1–34. doi:10.1016/j.physrep.2016.07.002

CrossRef Full Text | Google Scholar

38. Masuda N, Porter MA, Lambiotte R. Random walks and diffusion on networks. Phys Rep (2017) 716:1–58. doi:10.1016/j.physrep.2017.07.007

CrossRef Full Text | Google Scholar

39. Lai D, Lu H, Nardini C. Enhanced modularity-based community detection by random walk network preprocessing. Phys Rev E (2010) 81(6):066118. doi:10.1103/physreve.81.066118

PubMed Abstract | CrossRef Full Text | Google Scholar

40. Parlett BN, Scott DS. The lanczos algorithm with selective orthogonalization. Math Comput (1979) 33(145):217–38. doi:10.1090/s0025-5718-1979-0514820-3

CrossRef Full Text | Google Scholar

41. Wang J, Zhong J, Chen G, Li M, Wu F-xiang, Pan Y. Clusterviz: A cytoscape app for cluster analysis of biological network. Ieee/acm Trans Comput Biol Bioinform (2014) 12(4):815–22. doi:10.1109/tcbb.2014.2361348

CrossRef Full Text | Google Scholar

42. Jin D, You X, Li W, He D, Cui P, Fogelman-Souli´e F¸coise, Chakraborty T. Incorporating network embedding into markov random field for better community detection. In: Proceedings of the AAAI Conference on Artificial Intelligence; Feburary, 2019; Hawaii, USA (2019). p. 160–7. doi:10.1609/aaai.v33i01.3301160

CrossRef Full Text | Google Scholar

43. Lancichinetti A, Fortunato S, Radicchi F. Benchmark graphs for testing community detection algorithms. Phys Rev E (2008) 78(4):046110. doi:10.1103/physreve.78.046110

PubMed Abstract | CrossRef Full Text | Google Scholar

44. Grover A, Leskovec J. node2vec: Scalable feature learning for networks. In: Proceedings of the 22nd ACM SIGKDD international conference on Knowledge discovery and data mining; August, 2016; San Francisco California USA (2016). p. 855–64.

PubMed Abstract | CrossRef Full Text | Google Scholar

45. Cao S, Lu W, Xu Q. Grarep: Learning graph representations with global structural information. In: Proceedings of the 24th ACM international on conference on information and knowledge management; October, 2015; Melbourne. (2015). p. 891–900.

Google Scholar

46. Wang F, Li T, Wang X, Zhu S, Ding C. Community discovery using nonnegative matrix factorization. Data Min Knowl Discov (2011) 22(3):493–521. doi:10.1007/s10618-010-0181-y

CrossRef Full Text | Google Scholar

47. Jin D, Chen Z, He D, Zhang W. Modeling with node degree preservation can accurately find communities. In: Proceedings of the Twenty-Ninth AAAI Conference on Artificial Intelligence; January, 2015; Austin, Texas. (2015).

CrossRef Full Text | Google Scholar

48. Tang L, Liu H. Relational learning via latent social dimensions. In: Proceedings of the 15th ACM SIGKDD international conference on Knowledge discovery and data mining; July, 2009; Paris France. (2009). p. 817–26.

CrossRef Full Text | Google Scholar

49. Stark C, Bobby-Joe B, Chatr-Aryamontri A, Boucher L, Oughtred R, Livstone MS, et al. The biogrid interaction database: 2011 update. Nucleic Acids Res (2010) 39(1):D698–D704. doi:10.1093/nar/gkq1116

PubMed Abstract | CrossRef Full Text | Google Scholar

50. Toutanova K, Klein D, Manning CD, Singer Y. Feature-rich part of-speech tagging with a cyclic dependency network. In: Proceedings of the 2003 conference of the North American chapter of the association for computational linguistics on human language technology; May, 2003; Stroudsburg, PA, U.S.A (2003). p. 173–80.

CrossRef Full Text | Google Scholar

51. Qiu J, Dong Y, Ma H, Li J, Wang K, Tang J. Network embedding as matrix factorization: Unifying deepwalk, line, pte, and node2vec. In: Proceedings of the Eleventh ACM International Conference on Web Search and Data Mining; Feburary, 2018; Los Angeles, California (2018). p. 459–67.

Google Scholar

52. Xiang J, Wang Z-Z, Li H-J, Zhang Y, Li F, Dong L-P, et al. Community detection based on significance optimization in complex networks. J Stat Mech (2017) 2017(5):053213. doi:10.1088/1742-5468/aa6b2c

CrossRef Full Text | Google Scholar

53. Xiang J, Tang Y-N, Gao Y-Y, Liu L, Yi H, Li J-M, et al. Phase transition of surprise optimization in community detection. Physica A: Stat Mech its Appl (2018) 491:693–707. doi:10.1016/j.physa.2017.09.090

CrossRef Full Text | Google Scholar

54. Xiang J, Hu K, Zhang Y, Bao M-H, Tang L, Tang Y-N, et al. Enhancing community detection by using local structural information. J Stat Mech (2016) 2016(3):033405. doi:10.1088/1742-5468/2016/03/033405

CrossRef Full Text | Google Scholar