2D phase behaviors of colloidal ellipsoids and rods

In recent years, the shape of particles has emerged as a key factor influencing their self-assembly and phase behaviors. Understanding the phase behaviors of systems containing shape anisotropic particles remains challenging. In this mini-review, we will summarize our recent experimental studies on the phase behaviors of colloidal systems in which all or part of particles have anisotropic shapes. We focus on two types of shape anisotropic particles, ellipsoids and rods. In particular, it was found that 1) in equilibrium, the anisotropic particles form a nematic phase in 2D, 2) when quenched, they can form a stable glassy state with a two-step glass transition, and 3) when they are dispersed as impurities in a 2D colloidal crystal of spheres, they can destroy the 2D crystal phase. We will discuss the current challenges in the field.

Introduction

Understanding the phase behaviors in condensed matter physics remains a great challenge because many factors including the physical properties of the constituent particles and external environments can influence the phase behaviors. In recent years, colloidal systems have been proposed as excellent model systems to study the self-assembly and phase behaviors because their structures and dynamics can be measured on a single particle scale through video microscopy, which brings great benefits to understanding the mechanism of phase transitions [1, 2]. Due to the development of the synthesis of anisotropic colloidal particles [3–5], new possibilities open up for the studies of the phase behaviors of non-spherical particles in experiments and it is found that the particle shape plays a key role in controlling the self-assembly and phase behaviors [4].

Among various non-spherical colloids, ellipsoids and rods are two typical anisotropic particles. Their phase behaviors have been extensively investigated by simulation and theoretical studies [6–10], which demonstrate that their thermodynamic ground state at high density is a liquid crystal phase even in two dimensions (2D). However, the increase in the density of ellipsoids or rods creates frustration, thus forcing them into a metastable glassy state rather than the equilibrium liquid crystal phase. Therefore, convincing experiments to verify the numerical and theoretical results are urgently needed. On the other hand, previous experimental studies confirm that the ellipsoids are excellent glass-formers [11–13], and their glass transition exhibits a unique feature compared with that of spherical colloids; they experience a two-step glass transition corresponding to the asynchronous freezing of rotational and translational degrees of freedom with increasing particle density. However, the underlying mechanism of the two-step glass transition remains elusive.

The frustration effects due to the shape-anisotropic particles also manifest when a small amount of them are dispersed as impurities in a system of spheres. For example, it is well known that the monodisperse spherical colloids will form a crystal phase at high densities. Once the anisotropic particles are introduced into the system, they serve as impurities. It was found that they have devastating effects on the topological order of the 2D colloidal crystal. Many interesting questions arise as to the physical mechanisms of the impurities effects caused by the anisotropic particles.

In this mini-review, our recent experimental studies on the phase behaviors of colloidal systems containing ellipsoids or rods are summarized. We found that in equilibrium, they form a nematic phase in 2D. When they are quenched, they form a stable 2D colloidal glass. When they are introduced into a system of colloidal spheres as impurities, they cause a crystal-to-glass transition. The current challenges in the field will be discussed.

Formation of nematic phase in 2D

Although colloids provide excellent experimental systems to investigate phase transitions, such as crystallization and glass transition [14, 15], utilizing the colloidal systems for the study of liquid crystal transition, especially in 2D, remains challenging. The main difficulty is that the systems usually fall into the metastable glassy phase hindering the approaching of the equilibrium liquid crystal phase.

In recent work [15], we used a monolayer of superparamagnetic ellipsoid colloidal particles to study for the liquid crystal transition. We found that the free energy barrier between the metastable glassy phase and the equilibrium liquid crystal phase can be overcome by applying an external magnetic field. Before applying the magnetic field, the system holds an isotropic phase at different particle densities, indicating the spontaneous formation of the glass phase at high density (Figure 1A). When applying the magnetic field, the particles align along the field direction resulting in the field-induced nematic phase which is independent of the particle density. After removing the magnetic field, the system of low density relaxes back to an isotropic phase while the system of high density remains in the nematic phase (Figure 1B). This demonstrates an isotropic-to- nematic transition with increasing the particle density, experimentally verifying the formation of the nematic phase in 2D. This equilibrium transition is clarified by calculating the nematic order parameter [7] S ($=1/N{\sum }_i^N\left(\cos \left(2{\theta }_i\right)\right)$, where θ_i is the angle between the particle i and the nematic direction) at different particle densities after removing the magnetic field. S increases for the systems composed of ellipsoids with different aspect ratios (Figure 1C), demonstrating the formation of the nematic phase for all aspect ratio at high particle density, which is consistent with the simulation results [7]. The mechanism of the transition is understood by a local kinetic model in which the effective potential energy (V) in the configuration space is determined [16]. The configuration represents the relative orientation between the nearest neighboring particles. The results demonstrate that the parallel configuration is thermodynamically favorable while the perpendicular configuration is unfavorable at high particle density. This leads to an effective activation barrier, ΔV = V_// - V_⊥, where V_// and V_⊥ represent the potential energies for the parallel and perpendicular configurations, respectively. Such effective activation barrier exhibits an increase with increasing particle density (Figure 1D), which freezes the motion in the orientational degrees of freedom at high particle density. Consequently, the ellipsoids remain at the energy favorable configuration, representing a nematic phase at high particle density. Furthermore, the long ellipsoids corresponding to the large barrier (Figure 1D) facilitate the formation of the nematic phase, which reveals the critical role of the shape anisotropy in the isotropic–nematic phase transition.

FIGURE 1

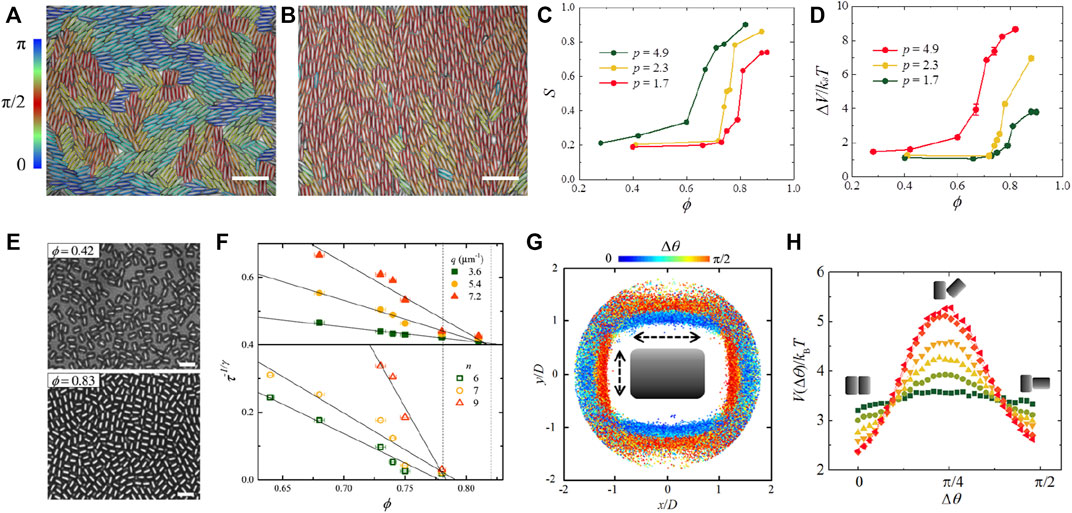
FIGURE 1. (A,B) Spatial distributions of the particle orientation over the bright-field micrographs of monolayers of the ellipsoids with aspect ratio p = 4.9 before applying a magnetic field (A) and after removing the magnetic field (B). The color denotes the orientation of the ellipsoid with respect to the x-axis (see the color bar). (C) Particle density (ϕ) dependent nematic order parameter S for the monolayers of ellipsoids with different aspect ratios after removing the magnetic field. (D) The effective activation barrier as a function of ϕ for three aspect ratios. (A–D) Adapted from [17] with permission of Royal Society of Chemistry. (E) Typical bright-field micrographs of monolayers of the colloidal rods with aspect ratio, p = 1.5. (F) The rotational and translational relaxation times as a function of ϕ, which show two glass transitions (the vertical lines label the two transition points). (G) The heat map of the orientational configuration. Blue and red colors denote the parallel and perpendicular configurations, respectively. (H) The effective potential energy of the orientational configuration at different ϕ: 0.42, 0.64, 0.68, 0.74, 0.78, and 0.83 (from bottom to top at Δθ = π/4). The three typical configurations of rods are shown. (E–H) Adapted from [16] under the terms of the Creative Commons Attribution 4.0 licence.

Two-step glass transition

As mentioned above, the ellipsoids tend to fall into a metastable glass state, which is quite stable in laboratory time scales, at high particle densities. More interestingly, their glass transition shows a two-step process; the increase of the particle density leads to the freezing of rotational motions first and then the freezing of translational motions. Despite the extensive study of the ellipsoidal two-step glass transition by colloidal experiments [11–13], the underlying mechanism is still lacking. Previous studies report that at small aspect ratios (<2.5) of the ellipsoids the local nematic domains disappear and the system transforms from the two-step glass transition to a one-step glass transition [12]. Once attractions are introduced between the ellipsoids with small aspect ratios, the local nematic domains appear and the system experiences the two-step glass transition [13], similar to that of ellipsoids with large aspect ratios (>2.5) [11, 12]. These suggest that the local nematic domains may be the structural origin of the two-step glass transition. However, a recent experimental study of the glass transition of short rods (Figure 1E) reveals that they undergo the two-step glass transition (Figure 1F) with no appearance of the local nematic domains [16]. This calls for a new mechanism for the two-step glass transition. To this end, we proposed [16] the local kinetic model associated with the effective free energy in the configuration space mentioned above to understand the two-step glass transition [16]. By analyzing the heat map of the local configurations (Figure 1G) and their probability distribution, the effective free energy in the orientational configuration space is evaluated. The result demonstrates two energy favorable configurations, parallel and perpendicular configurations, and a significant energy barrier between them at high particle density (Figure 1H). Such energy barrier thus forbids the rotational motions of the particles, but does not affect the translational motions [the particles can move along the axis of the neighboring particles as indicated by the arrows in the heat map (Figure 1F)]. As a result, the rotational and translational motions are decoupled which thus gives rise to the two-step glass transition. Therefore, the energy barrier in the local kinetic model is suggested for the mechanism of the two-step glass transition of the rods, which can apply to the glass transition of ellipsoids. For the ellipsoidal system, the parallel configuration is energy favorable corresponding to the microstructures of local nematic domains and the perpendicular configuration is unfavorable, hence an energy barrier appears which induces the two-step glass transition. When the aspect ratio of the ellipsoids decreases below 2.5, the local nematic domains disappear associated with the negligible energy barrier thus leading the system to a one-step glass transition. In addition, it is worth to note that the two-step glass transition is found independent of the dimension. For 3D ellipsoid systems, it also has been experimentally revealed a liquid glass (orientational glass) phase whose orientational degrees of freedom are frozen but translation is free. This demonstrates the system undergoes the orientational glass transition before the translational glass transition, confirming a two-step glass transition in 3D [18].

2D crystal-to-glass transition due to ellipsoid impurities

Because of the shape mismatch between spheres and anisotropic particles, the anisotropic particles become impurities when their density is low among a system of spheres. We found [19] that the anisotropic impurities can destroy the host crystal phase composed of spheres. This is surprising since they can be viewed as floating disorder. At low density, they are expected to be less destructive than quenched disorder, or random pinning centers. 2D melting transition has been studied using numerical simulations and experimental studies [20–23]. The KTHNY theory [24–26] has been validated. Our observation [19] of the destruction of the 2D crystal phase caused by anisotropic impurities raises new and interesting questions.

In this study [19], a 2D colloidal crystal-to-glass transition due to ellipsoid impurities is investigated experimentally through video microscopy. With increasing the density of the ellipsoid impurity (ϕ), the 2D colloidal lattice is destroyed. This is characterized by Voronoi diagrams (Figure 2A, bottom panel), in which the color represents the number of the nearest neighbors (n_i). At high density, it is clearly observed that the number of particles with n_i ≠ 6 characterizing the defects increases around the ellipsoid impurities, which demonstrates the breakdown of the lattice. To quantify the transition induced by the ellipsoid impurities, the orientational correlation function g₆(r) is calculated (Figure 2B). At low ϕ, g₆(r) displays algebraic decay, indicating that the system holds the quasi-long range orientational order and the ellipsoids act as floating disorder. However, at high ϕ the decay of g₆(r) changes to be exponential. This demonstrates the loss of the quasi-long range orientational order, indicating that the ellipsoid impurity disrupts the host lattice. To illuminate the nature of such transition, the impurity density-dependent correlation length (ξ) of g₆(r) is obtained, which shows an essential singularity ξ ∼ exp (b/|ϕ − ϕ_c|^0.5) with a critical impurity density ϕ_c = 0.049 (Figure 2C), in accordance with the KTHNY theory [24–26]. Such essential singularity is observed in many other experimental studies of 2D melting [20, 27, 28], demonstrating its universality belongs to the KTHNY paradigm of phase transitions. Interestingly, although the defects become pronounced with increasing the impurity density, the elastic moduli characterizing the mechanical properties of the system change nonmonotonically (Figures 2D,E), which are measured from the dispersion relations calculated from displacement covariance matrices [29–31]. At low ϕ, an impurity strengthening behavior, reflected by the increased moduli, is observed, similar to that in metallurgy [32]. When the impurity density rises above ϕ_c, the elastic moduli decrease accompanied by the loss of the quasi-long range orientational order. As predicted by KTHNY theory, the shear modulus should drop to 0 at the critical point, ϕ_c. However, the observation in the experiment shows no sharp drop in shear modulus at ϕ_c. This is reasonable since the moduli are measured at finite time and length scales, and hence the system is considered a glass phase rather than a liquid phase. In addition, the experiments employ the colloidal samples with a constant large packing density, ∼0.89, and varying impurity density [19]. This demonstrates that the system with disordered structures is a glass phase at high impurity density, further characterized by the obvious glassy dynamics [19]. Moreover, the measured elastic moduli show a correlation with the heterogeneous dynamics of the system induced by the increased disordered structures. At high impurity densities beyond ϕ_c, the homogeneous dynamics of the system corresponds to high moduli, which are larger than those of the host crystal phase without impurities; the heterogeneous dynamics of the system corresponds to small moduli, which are lower than those of the host crystal phase.

FIGURE 2

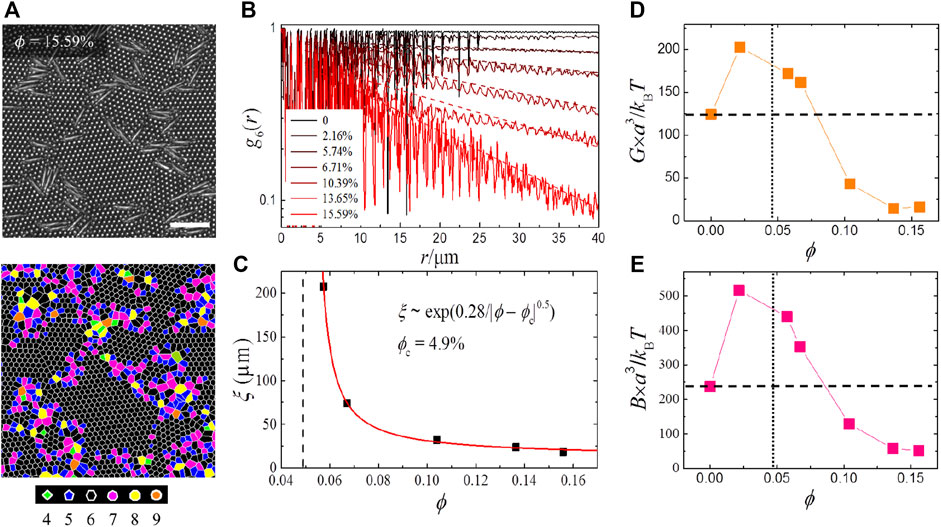
FIGURE 2. (A) Bright-field micrographs of monolayers of spheres with ellipsoid impurities and the corresponding Voronoi diagram. The scale bar is 20 μm. (B) g₆(r) vs. ϕ. The dashed curves are fits of g₆(r) to e^−r/ξ. (C) ξ vs. ϕ. The red line is a fitting curve as indicated. (D,E) Shear and Bulk moduli vs. ϕ. The vertical dotted lines label the critical impurity density. (A–E) Reprinted from [19] with permission of American Physical Society.

Perspectives and challenges

Through the recent colloidal experiments, new insights of the phase behaviors for the system containing ellipsoids or rods are revealed. Nevertheless, there are still lots of challenges. For the nematic phase transition, it has been experimentally verified, while its nature, first-order vs. continuous, remains elusive. The present results suggest that the nature of the transition seems to depend on the anisotropy of the particles (aspect ratio for the ellipsoids). At small anisotropy, the nematic order parameter shows an abrupt increase with increasing the particle density indicating a first-order transition, while at large anisotropy the parameter exhibits a gradual increase suggesting a continuous transition. However, more solid evidences are needed to clarify the nature of the transition. Moreover, besides the nematic phase transition, ellipsoids or rods are predicted to form other interesting phases, such as the smectic phase, depending on their aspect ratio, which has been experimentally observed in suspensions of colloidal rods in 3D [33, 34]. This leaves open the issue whether the same transition will occur in 2D.

Though numerous studies have been paid to understand the nature of glasses, the origin of their apparent rigidity remains poorly understood since there is no long-range order to associate the glasses. For the anisotropic particles, their two-step glass transition is uncovered and the local configurations formed by the particles are found to play a key role in generating the two-step glass transition. It is expected that the local configurations may provide a structural clue to understand the rigidity of glasses. To clarify this, the correlation between the local structures and mechanical properties should be studied.

It is noted that the ellipsoids or rods with small aspect ratios will form a rotator phase, characterized by long-range positional order but short-range orientational order [12, 35]. Although such rotator phase has been experimentally verified in 3D, the corresponding phase behavior formed in 2D remains lacking of experimental evidence. This is an open question that may be studied by utilizing a shape-tunable colloidal system in which particle shapes can be continually switched from ellipsoidal to spherical [36].

The particle shape has been found to play a critical role in the assembly structures. For ellipsoids, they form local nematic domains [11, 12]. In contrast, for rods, the local structures are parallel or perpendicular arrangements [16]. For ellipsoids, the formation of the nematic domains of the ellipsoids depends on the particle aspect ratio [12, 37], but for rod, the aspect ratio seems not to change the local arrangements [16]. These observations suggest that a small difference in particle shape can strongly affect the assembled structures of the particles. Beyond the rod shape, there are lots of other superellipsoid shapes, which can lead to various complex structures and configurations. Therefore, it is envisioned that rich phases will be formed by the superellipsoids [38, 39], which deserve more future studies.

Author contributions

All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.

Funding

This work was financially supported by the National Natural Science Foundation of China (12074275 and 11704269), the Natural Science Foundation of the Jiangsu Higher Education Institutions of China (20KJA150008), and the PAPD program of Jiangsu Higher Education Institutions.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Bo L, Di Z, Yilong H. Assembly and phase transitions of colloidal crystals. Nat Rev Mater (2016) 1:15011–3. doi:10.1038/natrevmats.2015.11

CrossRef Full Text | Google Scholar

2. Anderson VJ, Lekkerkerker HNW. Insights into phase transition kinetics from colloid science. Nature (2002) 416:811–5. doi:10.1038/416811a

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Champion JA, Katare YK, Mitragotri S. Making polymeric micro-and nanoparticles of complex shapes. Proc Natl Acad Sci U S A (2007) 104:11901–4. doi:10.1073/pnas.0705326104

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Glotzer SC, Solomon MJ. Anisotropy of building blocks and their assembly into complex structures. Nat Mater (2007) 6:557–62. doi:10.1038/nmat1949

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Hueckel T, Hocky GM, Sacanna S. Total synthesis of colloidal matter. Nat Rev Mater (2021) 6:1053–69. doi:10.1038/s41578-021-00323-x

CrossRef Full Text | Google Scholar

6. Onsager L. The effects of shape on the interaction of colloidal particles. Ann N Y Acad Sci (1949) 51:627–59. doi:10.1111/j.1749-6632.1949.tb27296.x

CrossRef Full Text | Google Scholar

7. Cuesta JA, Frenkel D. Monte Carlo simulation of two-dimensional hard ellipses. Phys Rev A (1990) 42:2126–36. doi:10.1103/PhysRevA.42.2126

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Martinez-Raton Y, Velasco E, Mederos L. Effect of particle geometry on phase transitions in two-dimensional liquid crystals. J Chem Phys (2005) 122:064903–3540. doi:10.1063/1.1849159

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Bautista-Carbajal G, Odriozola G. Phase diagram of two-dimensional hard ellipses. J Chem Phys (2014) 140:204502. doi:10.1063/1.4878411

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Letz M, Schilling R, Latz A. Ideal glass transitions for hard ellipsoids. Phys Rev E (2000) 62:5173–8. doi:10.1103/PhysRevE.62.5173

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Zheng Z, Wang F, Han Y. Glass transitions in quasi-two-dimensional suspensions of colloidal ellipsoids. Phys Rev Lett (2011) 107:065702. doi:10.1103/PhysRevLett.107.065702

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Zheng Z, Ni R, Wang F, Dijkstra M, Wang Y, Han Y. Structural signatures of dynamic heterogeneities in monolayers of colloidal ellipsoids. Nat Commun (2014) 5:3829. doi:10.1038/ncomms4829

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Mishra CK, Rangarajan A, Ganapathy R. Two-step glass transition induced by attractive interactions in quasi-two-dimensional suspensions of ellipsoidal particles. Phys Rev Lett (2013) 110:188301. doi:10.1103/PhysRevLett.110.188301

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Gasser U, Weeks ER, Schofield A, Pusey PN, Weitz1 DA. Real-space imaging of nucleation and growth in colloidal crystallization. Science (2001) 292:258–62. doi:10.1126/science.1058457

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Weeks ER, Crocker JC, Levitt AC, Schofield A, Weitz1 DA. Three-Dimensional direct imaging of structural relaxation near the colloidal glass transition. Science (2000) 287:627–31. doi:10.1126/science.287.5453.627

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Liu X, Wang H, Zhang Z, Kosterlitz J, Ling XS. Nature of the glass transition in 2D colloidal suspensions of short rods. New J Phys (2020) 22:103066. doi:10.1088/1367-2630/abbfd1

CrossRef Full Text | Google Scholar

17. Tan X, Chen Y, Wang H, Zhang Z, Ling XS. 2D isotropic–nematic transition in colloidal suspensions of ellipsoids. Soft Matter (2021) 17:6001–5. doi:10.1039/d1sm00367d

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Roller J, Laganapan A, Meijer J-M, Zumbusch A. Observation of liquid glass in suspensions of ellipsoidal colloids. Proc Natl Acad Sci U S A (2021) 118:e2018072118. doi:10.1073/pnas.2018072118

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Chen Y, Tan X, Wang H, Zhang Z, Kosterlitz JM, Ling XS. 2D colloidal crystals with anisotropic impurities. Phys Rev Lett (2021) 127:018004. doi:10.1103/PhysRevLett.127.018004

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Han Y, Ha NY, Alsayed AM, Yodh AG. Melting of two-dimensional tunable-diameter colloidal crystals. Phys Rev E (2008) 77:041406. doi:10.1103/PhysRevE.77.041406

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Kapfer SC, Krauth W. Two-Dimensional melting: From liquid-hexatic coexistence to continuous transitions. Phys Rev Lett (2015) 114:035702. doi:10.1103/PhysRevLett.114.035702

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Zahn K, Lenke R, Maret G. Two-stage melting of paramagnetic colloidal crystals in two dimensions. Phys Rev Lett (1999) 82:2721–4. doi:10.1103/PhysRevLett.82.2721

CrossRef Full Text | Google Scholar

23. Thorneywork AL, Abbott JL, Aarts DGAL, Dullens RPA. Two-Dimensional melting of colloidal hard spheres. Phys Rev Lett (2017) 118:158001. doi:10.1103/PhysRevLett.118.158001

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Kosterlitz JM, Thouless DJ. Ordering, metastability and phase transitions in two-dimensional systems. J Phys C: Solid State Phys (1973) 6:1181–203. doi:10.1088/0022-3719/6/7/010

CrossRef Full Text | Google Scholar

25. Halperin BI, Nelson DR. Theory of two-dimensional melting. Phys Rev Lett (1978) 41:121–4. doi:10.1103/PhysRevLett.41.121

CrossRef Full Text | Google Scholar

26. Young AP. Melting and the vector Coulomb gas in two dimensions. Phys Rev B (1979) 19:1855–66. doi:10.1103/PhysRevB.19.1855

CrossRef Full Text | Google Scholar

27. Deutschländer S, Horn T, Löwen H, Maret G, Keim P. Two-Dimensional melting under quenched disorder. Phys Rev Lett (2013) 111:098301. doi:10.1103/PhysRevLett.111.098301

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Keim P, Maret G, Grünberg HHV. Frank’s constant in the hexatic phase. Phys Rev E (2007) 75:031402. doi:10.1103/PhysRevE.75.031402

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Still T, Goodrich CP, Chen K, Yunker PJ, Schoenholz S, Liu AJ, et al. Phonon dispersion and elastic moduli of two-dimensional disordered colloidal packings of soft particles with frictional interactions. Phys Rev E (2014) 89:012301. doi:10.1103/PhysRevE.89.012301

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Keim P, Maret G, Herz U, von Grunberg HH. Harmonic lattice behavior of two-dimensional colloidal crystals. Phys Rev Lett (2004) 92:215504. doi:10.1103/PhysRevLett.92.215504

PubMed Abstract | CrossRef Full Text | Google Scholar

31. Chen K, Ellenbroek WG, Zhang ZX, Chen DTN, Yunker PJ, Henkes S, et al. Low-frequency vibrations of soft colloidal glasses. Phys Rev Lett (2010) 105:025501. doi:10.1103/PhysRevLett.105.025501

PubMed Abstract | CrossRef Full Text | Google Scholar

32. Cottrell AH, Bilby BA. Dislocation theory of yielding and strain ageing of iron. Proc Phys Soc A (1949) 62:49–62. doi:10.1088/0370-1298/62/1/308

CrossRef Full Text | Google Scholar

33. Kuijk A, Byelov DV, Petukhov AV, Blaaderena Av, Imhof A. Phase behavior of colloidal silica rods. Faraday Discuss (2012) 159:181–99. doi:10.1039/C2FD20084H

CrossRef Full Text | Google Scholar

34. Kuijk A, Troppenz T, Filion L, Imhof A, Roij Rv, Dijkstraa M, et al. Effect of external electric fields on the phase behavior of colloidal silica rods. Soft Matter (2014) 10:6249–55. doi:10.1039/C4SM00957F

PubMed Abstract | CrossRef Full Text | Google Scholar

35. Liu B, Besseling TH, Hermes M, Demirörs AF, Imhof A, Blaaderen Av. Switching plastic crystals of colloidal rods with electric fields. Nat Commun (2014) 5:3092. doi:10.1038/ncomms4092

PubMed Abstract | CrossRef Full Text | Google Scholar

36. Wang H, Li B, Yodh AG, Zhang Z. Stimuli-responsive shape switching of polymer colloids by temperature-sensitive absorption of solvent. Angew Chem Int Ed (2016) 55:9952–5. doi:10.1002/anie.201604294

PubMed Abstract | CrossRef Full Text | Google Scholar

37. Zheng Z, Ni R, Wang Y, Han Y. Translational and rotational critical-like behaviors in the glass transition of colloidal ellipsoid monolayers. Sci Adv (2021) 7:eabd1958. doi:10.1126/sciadv.abd1958

PubMed Abstract | CrossRef Full Text | Google Scholar

38. Rossi L, Soni V, Ashton DJ, Pine DJ, Philipse AP, Chaikin PM, et al. Shape-sensitive crystallization in colloidal superball fluids. Proc Natl Acad Sci U S A (2015) 112:5286–90. doi:10.1073/pnas.1415467112

PubMed Abstract | CrossRef Full Text | Google Scholar

39. Meijer J-M, Pal A, Ouhajji S, Lekkerkerker HNW, Philipse AP, Petukhov AV. Observation of solid–solid transitions in 3D crystals of colloidal superballs. Nat Commun (2017) 8:14352. doi:10.1038/ncomms14352

PubMed Abstract | CrossRef Full Text | Google Scholar