Multiple lump solutions of the (2+1)-dimensional sawada-kotera-like equation

In this paper, 1-lump solution and 2-lump solution of a (2 + 1)-dimensional Sawada-Kotera-like equation are obtained by means of the Hirota’s bilinear method and long wave limit method. The propagation orbits, velocities and the collisions among waves are analyzed. By setting the parameter values, the dynamic characteristics of the obtained solutions are shown in 3D and density plots. These conclusions enrich the dynamical theory of higher-dimensional nonlinear dispersive wave equations.

1 Introduction

Nonlinear evolution equations can be used to simulate various nonlinear phenomena in the real world, which appear in fluid mechanics [1–3], optical fibers[4], applied mathematics[5–7], chemistry and biology[8–10], etc. In recent years, searching for exact solutions of nonlinear evolution equations has attracted considerable attention, such as lump solutions[11–16], soliton solutions[17–21] and breather solutions[22–25].

The (2 + 1)-dimensional Sawada–Kotera equation:

$5u_x{u}^2+5u{u}_y+5u_{\mathit{xxx}}u+5u_x{\partial }_x^{-1}{u}_y+5u_{xx}{u}_x-u_t+5u_{\mathit{xxy}}+u_{\mathit{xxxxx}}-5{\partial }_x^{-1}{u}_{yy}=0,(1)$

has important and wide applications in conformal field theory, quantum gravity field theory and conserved current of Liouville equation[26–28]. Soliton solutions[29–31], lump solutions[32,33], travelling wave solutions[34] and some other exact solutions[35] of Eq. 1 have been detailed. In this paper, we mainly consider the (2 + 1)-dimensional Sawada-Kotera-like equation[36]:

$\begin{array}{ll}\hfill & -180{\partial }_x^{-1}{u}_{yy}-36u_t+180u_{\mathit{xxy}}+30u_{xx}uw+15u_{\mathit{xxx}}{w}^2+180u_{x}v+180u{u}_y+135u_x{u}^2\hfill \\ \hfill & +90u_{\mathit{xxx}}u-30u_{xx}{u}_x+15u^{3}w+35u_{x}u{w}^2+5u^2{w}^3+\frac{5}{36}u{w}^5+\frac{20}{3}{u}_{xx}{w}^3+\frac{5}{4}{u}_x{w}^4=0,\hfill \end{array}(2)$

in which ∂⁻¹ represents the partial integration operator. Eq. 2 is gained from Eq. 1 by the generalized bilinear method[36]. When v_x = u_y and ω_x = u, Eq. 2 can be reduced to Eq. 1. And Eq. 2 is different from the Sawada-Kotera-like equations which have been mentioned by [32,37].As far as we known, multiple lump solutions of Eq. 2 have not been presented in any existing articles. Classic lump, generalized lump solutions and new rogue wave solutions of Eq. 2 have been obtained by [36]. In this paper, we will study multiple lump solutions of Eq. 2. In Section 2, we construct 1-lump solution and 2-lump solution of Eq. 2 by employing the Hirota’s bilinear method and long wave limit method. The dynamical behaviors of the solutions are analyzed in Section 3. Section 4 is our conclusions.

2 1-lump solution and 2-lump solution

The long wave limit method is an effective method to generate M-lump solutions from N-soliton solutions[38–44]. In this section, we will construct the 1-lump solution and 2-lump solution of Eq. 2. As a preparation for constructing 1-lump solution and 2-lump solution of Eq. 2, we first study the N-soliton solutions[45]. With the aid of the variable transformation

$u=6{\left(\ln f\right)}_{xx},\omega =6{\left(\ln f\right)}_x,\nu =6{\left(\ln f\right)}_{xy},(3)$

Eq. 2 can be transformed into a bilinear form[36]:

$\begin{array}{ll}\hfill \left(D_{5,x}^6+5D_{5,y}{D}_{5,x}^3-5D_{5,y}^2-D_{5,x}{D}_{5,t}\right)f\cdot f& =-2f_{tx}f-10f_{yy}f+10f_{\mathit{xxxy}}f+2f_x{f}_t-30f_{\mathit{xxy}}{f}_x+10f_y^2-10f_y{f}_{\mathit{xxx}}+30f_{xy}{f}_{xx}+30f_{\mathit{xxxx}}{f}_{xx}-20f_{\mathit{xxx}}^2=0,\hfill \end{array}(4)$

where D_t, D_x, and D_y are the bilinear derivative operators, which can be defined by generalized D operator[46]:

$D_{p,x_1}^{n_1}\dots D_{p,x_M}^{n_M}\left(f\cdot f\right)={\left.\prod _{i=1}^M{\left(\frac{\partial }{\partial x_i}+\alpha \frac{\partial }{\partial x_i^{\prime }}\right)}^{n_i}f\left(x_1,\dots ,x_M\right)f\left(x_1^{\prime },\dots ,x_M^{\prime }\right)\right|}_{x_1^{\prime }=x_1,\dots ,x_M^{\prime }=x_M}.(5)$

It means that Eq. 3 are solutions of Eq. 2 if and only if f is a solution of Eq. 4. Based on the Hirota’s bilinear method, the N-soliton solutions of Eq. 4 have been obtained[45]:

$f=f_N=\sum _{\mu =\mathrm{0,1}}\exp \left(\sum _{i=1}^N{\mu }_i{\eta }_i+\sum _{i<j}^N{\mu }_i{\mu }_j{A}_{ij}\right),(6)$

where

${\eta }_i=k_i\left(x+p_{i}y+{\omega }_{i}t\right)+{\eta }_i^0,{\omega }_i=k_i^4+5k_i^2{p}_i-5p_i^2,$

$\exp A_{ij}=\frac{k_i^4-3k_i^3{k}_j+k_j^4+{\left(p_i-p_j\right)}^2-3k_i{k}_j\left(k_j^2+p_i+p_j\right)+k_i^2\left(4k_j^2+2p_i+p_j\right)+k_j^2\left(p_i+2p_j\right)}{k_i^4+3k_i^3{k}_j+k_j^4+{\left(p_i-p_j\right)}^2+3k_i{k}_j\left(k_j^2+p_i+p_j\right)+k_i^2\left(4k_j^2+2p_i+p_j\right)+k_j^2\left(p_i+2p_j\right)},(7)$

with k_i, p_i and ${\eta }_i^0$ are arbitrary constants,$\sum _{\mu =\mathrm{0,1}}$is the summation of possible combinations of μ_i = 0, 1(i = 1, 2⋯N).By taking a limit of ${\eta }_i^0=-1,k_i\to 0(i=\mathrm{1,2},\cdots N)$ and considering all the k_i in the same asymptotic order in Eq. 6, we have

$f_N=\prod _{i=1}^N{\theta }_i+\frac{1}{2}\sum _{i,j}^N{B}_{ij}\prod _{s\ne i,j}^N{\theta }_s+\cdots +\frac{1}{M!2^M}\sum _{i,j,\dots ,p,q}^N\stackrel{M}{\overbrace{B_{ij}{B}_{kl}\dots B_{pq}}}\prod _{m\ne i,j,k,l,\dots ,p,q}^N{\theta }_m+\cdots ,(8)$

where

${\theta }_i=x+y{p}_i-5t{p}_i^2,B_{ij}=-\frac{6\left(p_i+p_j\right)}{{\left(p_i-p_j\right)}^2},(9)$

and ${\sum }_{i,j,\cdots N}^N$ represents the summation over all possible compositions of i, j, ⋯p, q, which are taken different values from 1, 2, ⋯N. Taking N = 2M in Eq. 8 and $p_{M+i}=p_i^{*}\left(i=\mathrm{1,2},\dots ,M\right)$ in Eq. 9, where “*” denotes the complex conjugation, the M-lump solutions to Eq. 4 can be obtained.In the case of N = 2, Eq. 8 is changed into

$f_2={\theta }_1{\theta }_2+B_{12},(10)$

where ${\theta }_1=x+y{p}_1-5t{p}_1^2$, ${\theta }_2=x+y{p}_2-5t{p}_2^2$, $B_{12}=-\frac{6\left(p_1+p_2\right)}{{\left(p_1-p_2\right)}^2}$. If we take $p_2=p_1^{\ast }=a-b\ast I$, where a and b are real constants, I is an imaginary number unit, Eq. 10 is changed into

$f_2=\frac{3a}{b^2}+25a^4{t}^2+50a^2{b}^2{t}^2+25b^4{t}^2-10a^{2}tx+10b^{2}tx+x^2-10a^{3}ty-10a{b}^{2}ty+2axy+a^2{y}^2+b^2{y}^2,(11)$

then we can obtain the 1-lump solution of Eq. 2:

$\begin{array}{ll}\hfill u& =6{\left(\ln f_2\right)}_{xx}\hfill \\ \hfill & =-\left\{12b^2\left[25a^4{b}^2{t}^2+25b^6{t}^2+b^2{x}^2-10a^3{b}^{2}ty+a\left(-3+30b^{4}ty+2b^{2}xy\right)\right.\right.\hfill \\ \hfill & \left.\left.+b^4\left(10tx-y^2\right)+a^2{b}^2\left(-150b^2{t}^2-10tx+y^2\right)\right]\right\}\left[25a^4{b}^2{t}^2+25b^6{t}^2+b^2{x}^2-10a^3{b}^{2}ty\right.\hfill \\ \hfill & {\left.+a\left(3-10b^{4}ty+2b^{2}xy\right)+a^2{b}^2\left(50b^2{t}^2-10tx+y^2\right)+b^4\left(10tx+y^2\right)\right]}^{-2}.\hfill \end{array}(12)$

This wave keeps moving on the line $y=-\frac{2ax}{a^2+b^2}$, the velocity along the x-axis is v_x = x + 5b²t + 5a²t, and the velocity along the y-axis is v_y = y − 10 at.In the case of N = 4, Eq. 8 is changed into

$f4={\theta }_1{\theta }_2{\theta }_3{\theta }_4+B_{12}{\theta }_3{\theta }_4+B_{13}{\theta }_2{\theta }_4+B_{14}{\theta }_2{\theta }_3+B_{23}{\theta }_1{\theta }_4+B_{24}{\theta }_1{\theta }_3+B_{34}{\theta }_1{\theta }_2+B_{12}{B}_{34}+B_{13}{B}_{24}+B_{14}{B}_{23},(13)$

where ${\theta }_i=x+y{p}_i-5t{p}_i^2$, $B_{ij}=-\frac{6\left(p_i+p_j\right)}{{\left(p_i-p_j\right)}^2},(1\le i<j\le 4)$ and $p_1=p_2^{*}=a_1+b_{1}I{p}_3=p_4^{*}=a_2+b_{2}I$. Substituting Eq. 13 into Eq. 3, we can obtain 2-lump solution of Eq. 2:

$\begin{array}{ll}\hfill u& =6\ln {\left(f_4\right)}_{xx}\hfill \\ \hfill & =\left[-6{\left({\beta }_1+{\beta }_2+{\beta }_3+{\beta }_4+{\beta }_5+{\beta }_6+{\beta }_7\right)}^2+12\left({\beta }_8+{\beta }_9+{\beta }_{10}+{\beta }_{11}\right)\left({\beta }_{12}+{\beta }_{13}+{\beta }_{14}+{\beta }_{15}+{\beta }_{16}\right)\right]\hfill \\ \hfill & \times {\left(-{\beta }_{12}-{\beta }_{13}-{\beta }_{14}-{\beta }_{15}-{\beta }_{16}\right)}^{-2},\hfill \end{array}(14)$

where

${\beta }_1=6\left(p_1+p_3\right){\alpha }_2{\left(p_1-p_3\right)}^{-2}+6\left(p_2+p_3\right){\alpha }_1{\left(p_2-p_3\right)}^{-2},$

${\beta }_2=6\left(p_1+p_2\right){\alpha }_3{\left(p_1-p_2\right)}^{-2}-{\alpha }_1{\alpha }_2{\alpha }_3,{\beta }_3=6\left(p_1+p_4\right)\left({\alpha }_2+{\alpha }_3\right){\left(p_1-p_4\right)}^{-2},$

${\beta }_4=6\left(p_2+p_4\right){\alpha }_1+6\left(p_2+p_4\right){\alpha }_3{\left(p_2-p_4\right)}^{-2},{\beta }_5=6\left(p_3+p_4\right)\left({\alpha }_1+{\alpha }_2\right){\left(p_3-p_4\right)}^{-2},$

${\beta }_6=6\left(p_1+p_2\right){\alpha }_4{\left(p_1-p_2\right)}^{-2}-{\alpha }_1{\alpha }_2{\alpha }_4,{\beta }_7=6\left(p_1+p_3\right){\alpha }_4{\left(p_1-p_3\right)}^{-2}+6\left(p_2+p_3\right){\alpha }_4{\left(p_2-p_3\right)}^{-2},$

${\beta }_8={\alpha }_1{\alpha }_3{\alpha }_4,{\beta }_9={\alpha }_2{\alpha }_3{\alpha }_4,{\beta }_{10}={\alpha }_1{\alpha }_3+{\alpha }_2{\alpha }_3,$

${\beta }_{11}={\alpha }_1{\alpha }_2-6\left(p_1+p_2\right){\left(p_1-p_2\right)}^{-2}-6\left(p_1+p_3\right){\left(p_1-p_3\right)}^{-2}-6\left(p_2+p_3\right){\left(p_2-p_3\right)}^{-2},$

${\beta }_{12}={\alpha }_1{\alpha }_4-6\left(p_1+p_4\right){\left(p_1-p_4\right)}^{-2}-6\left(p_2+p_4\right){\left(p_2-p_4\right)}^{-2}-6\left(p_3+p_4\right){\left(p_3-p_4\right)}^{-2},$

${\beta }_{13}={\alpha }_2{\alpha }_4+{\alpha }_3{\alpha }_4,$

${\beta }_{14}=36\left(p_2+p_3\right)\left(p_1+p_4\right){\left[\left(p_2-p_3\right)\left(p_1-p_4\right)\right]}^{-2}-6\left(p_1+p_4\right){\alpha }_2{\alpha }_3{\left(p_1-p_4\right)}^{-2},$

${\beta }_{15}=36\left(p_1+p_3\right)\left(p_2+p_4\right){\left[\left(p_1-p_3\right)\left(p_2-p_4\right)\right]}^{-2}-6\left(p_2+p_4\right){\alpha }_1{\alpha }_3{\left(p_2-p_4\right)}^{-2},$

${\beta }_{16}=36\left(p_1+p_2\right)\left(p_3+p_4\right){\left[\left(p_1-p_2\right)\left(p_3-p_4\right)\right]}^{-2}-6\left(p_3+p_4\right){\alpha }_1{\alpha }_2{\left(p_3-p_4\right)}^{-2},$

${\beta }_{17}=-6\left(p_1+p_3\right){\alpha }_2{\alpha }_4{\left(p_1-p_3\right)}^{-2},{\beta }_{18}=-6\left(p_2+p_3\right){\alpha }_1{\alpha }_4{\left(p_2-p_3\right)}^{-2},$

${\beta }_{19}=-6\left(p_1+p_2\right){\alpha }_3{\alpha }_4{\left(p_1-p_2\right)}^{-2},{\beta }_{20}={\alpha }_1{\alpha }_2{\alpha }_3{\alpha }_4,$

in which ${\alpha }_i=x+y{p}_i-5t{p}_i^2,\left(i=\mathrm{1,2,3,4}\right)$. The wave keeps moving along the line $y_1=-\frac{2a_{1}x}{{a_1}^2+{b_1}^2}$, $y_2=-\frac{2a_{2}x}{{a_2}^2+{b_2}^2}$.

Figures 1–2, show the evolution of the 1-lump solution Eq. 12 and 2-lump solution Eq. 14 with the time variation. Figure 1 show the 1-lump waves for Eq. 2 under a = 1, b = 1 but with the different values of (a) and (d) t = −1, (b) and (e) t = 0, (c) and (f) t = 1. Figure 2 are the 2-lump waves for Eq. 2 with parameters a₁ = 1, $a_2=\frac{1}{3}$, b₁ = 1, $b_2=\frac{1}{2}$ with the different values of (a) and (d) t = −1, (b) and (e) t = 0, (c) and (f) t = 1. Figures 1D,E,F are the density plot of Figures 1A,B,C separately and Figures 2D,E,F are the density plot of Figures 2A,B,C respectively.

FIGURE 1

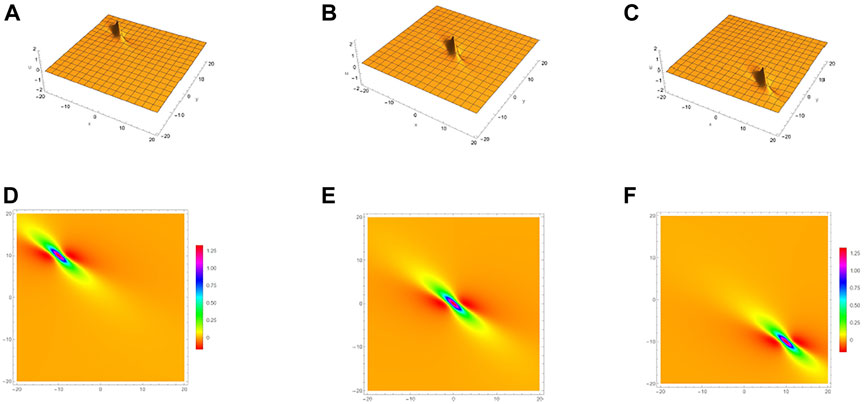
FIGURE 1. 1-lump solution Eq. 12 for Eq. 2 with a = 1, b = 1: (A) t = −1; (B) t = 0; (C) t = 1; (D), (E), (F) are the density plot of (A), (B), (C) respectively.

FIGURE 2

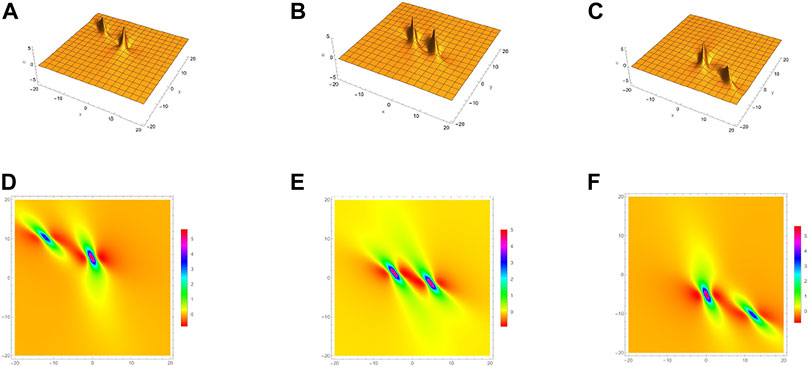
FIGURE 2. 2-lump solution Eq. 14 for Eq. 2 with a₁ = 1, $a_2=\frac{1}{3}$, b₁ = 1, $b_2=\frac{1}{2}$: (A) t = −1; (B) t = 0; (C) t = 1; (D), (E), (F) are the density plot of (A), (B), (C) respectively.

3 Conclusion

In this paper, we have presented the 1-lump solution Eq. 12 and 2-lump solution Eq. 14 of the (2 + 1)-dimensional Sawada-Kotera-like Eq. 2 by using a variable transformation. Dynamical features and density distributions of the presented solutions have been depicted through plots. It is expected that these results can be useful to understand the dynamical behavior of relevant fields in physics.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

FQ: work out the whole idea of this paper, including method and writing. SL: some calculations and writing of the paper. ZL: polish the whole paper. PW: check the English gramma.

Funding

The study is supported by the key project of Beijing Social Science Foundation “strategic research on improving the service quality of capital logistics based on big data technology (18GLA009)”.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Ablowitz MJ, Segur H. On the evolution of packets of water waves. J Fluid Mech (1979) 92:691–715. doi:10.1017/S0022112079000835

CrossRef Full Text | Google Scholar

2. Liu F-Y, Gao Y-T, Yu X, Li L-Q, Ding C-C, Wang D. Lie group analysis and analytic solutions for a (2+1)-dimensional generalized bogoyavlensky–konopelchenko equation in fluid mechanics and plasma physics. Eur Phys J Plus (2021) 136:656–14. doi:10.1140/epjp/s13360-021-01469-x

CrossRef Full Text | Google Scholar

3. Zhao Y-W, Xia J-W, Lü X. The variable separation solution, fractal and chaos in an extended coupled (2+1)-dimensional burgers system. Nonlinear Dyn (2022) 108:4195–205. doi:10.1007/s11071-021-07100-z

CrossRef Full Text | Google Scholar

4. Liu J-G, Osman M, Zhu W-H, Zhou L, Ai G-P. Different complex wave structures described by the hirota equation with variable coefficients in inhomogeneous optical fibers. Appl Phys B (2019) 125:175–9. doi:10.1007/s00340-019-7287-8

CrossRef Full Text | Google Scholar

5. Xu T, Liu C, Qi F, Li C, Meng D. New double wronskian solutions of the whitham-broer-kaup system: Asymptotic analysis and resonant soliton interactions. J Nonlinear Math Phys (2021) 24:116. doi:10.1080/14029251.2017.1282248

CrossRef Full Text | Google Scholar

6. Qi F-H, Huang Y-H, Wang P. Solitary-wave and new exact solutions for an extended (3+1)-dimensional jimbo–miwa-like equation. Appl Math Lett (2020) 100:106004. doi:10.1016/j.aml.2019.106004

CrossRef Full Text | Google Scholar

7. Lou S, Hao X. Linear superposition in the general heavenly equation. Phys Lett A (2022) 443:128203. doi:10.1016/j.physleta.2022.128203

CrossRef Full Text | Google Scholar

8. Xu T, Chen Y, Li M, Meng D-X. General stationary solutions of the nonlocal nonlinear Schrödinger equation and their relevance to the pt-symmetric system. Chaos (2019) 29:123124. doi:10.1063/1.5121776

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Xu T, Lan S, Li M, Li L-L, Zhang G-W. Mixed soliton solutions of the defocusing nonlocal nonlinear Schrödinger equation. Physica D: Nonlinear Phenomena (2019) 390:47–61. doi:10.1016/j.physd.2018.11.001

CrossRef Full Text | Google Scholar

10. Epstein IR. Nonlinear oscillations in chemical and biological systems. Physica D: Nonlinear Phenomena (1991) 51:152–60. doi:10.1016/0167-2789(91)90228-2

CrossRef Full Text | Google Scholar

11. Ma W-X. Lump solutions to the kadomtsev–petviashvili equation. Phys Lett A (2015) 379:1975–8. doi:10.1016/j.physleta.2015.06.061

CrossRef Full Text | Google Scholar

12. Lü X, Wang J-P, Lin F-H, Zhou X-W. Lump dynamics of a generalized two-dimensional boussinesq equation in shallow water. Nonlinear Dyn (2017) 91:1249–59. doi:10.1007/s11071-017-3942-y

CrossRef Full Text | Google Scholar

13. Ding L, Ma W-X, Chen Q, Huang Y. Lump solutions of a nonlinear pde containing a third-order derivative of time. Appl Math Lett (2021) 112:106809. doi:10.1016/j.aml.2020.106809

CrossRef Full Text | Google Scholar

14. Chen S-J, Lü X. Lump and lump-multi-kink solutions in the (3+1)-dimensions. Commun Nonlinear Sci Numer Simulation (2022) 109:106103. doi:10.1016/j.cnsns.2021.106103

CrossRef Full Text | Google Scholar

15. Lü X, Chen S-J. New general interaction solutions to the kpi equation via an optional decoupling condition approach. Commun Nonlinear Sci Numer Simulation (2021) 103:105939. doi:10.1016/j.cnsns.2021.105939

CrossRef Full Text | Google Scholar

16. Lü X, Chen S-J. Interaction solutions to nonlinear partial differential equations via hirota bilinear forms: One-lump-multi-stripe and one-lump-multi-soliton types. Nonlinear Dyn (2021) 103:947–77. doi:10.1007/s11071-020-06068-6

CrossRef Full Text | Google Scholar

17. Ma W-X. N-soliton solution and the Hirota condition of a (2+1)-dimensional combined equation. Mathematics Comput Simulation (2021) 190:270–9. doi:10.1016/j.matcom.2021.05.020

CrossRef Full Text | Google Scholar

18. Dong J-J, Li B, Yuen M. Soliton molecules and mixed solutions of the (2+1)-dimensional bidirectional sawada–kotera equation. Commun Theor Phys (2020) 72:025002. doi:10.1088/1572-9494/ab6184

CrossRef Full Text | Google Scholar

19. Wang D, Huang Y, Yong X, Zhang J. Rational soliton solutions of the nonlocal nonlinear Schrödinger equation by the kp reduction method. Int J Mod Phys B (2019) 33:1950362. doi:10.1142/s0217979219503624

CrossRef Full Text | Google Scholar

20. Chen S-J, Lü X. Observation of resonant solitons and associated integrable properties for nonlinear waves. Chaos, Solitons & Fractals (2022) 163:112543. doi:10.1016/j.chaos.2022.112543

CrossRef Full Text | Google Scholar

21. Yin Y-H, Lü X, Ma W-X. Bäcklund transformation, exact solutions and diverse interaction phenomena to a (3+1)-dimensional nonlinear evolution equation. Nonlinear Dyn (2021) 108:4181–94. doi:10.1007/s11071-021-06531-y

CrossRef Full Text | Google Scholar

22. Liu J-G, Zhu W-H. Multiple rogue wave, breather wave and interaction solutions of a generalized (3+1)-dimensional variable-coefficient nonlinear wave equation. Nonlinear Dyn (2021) 103:1841–50. doi:10.1007/s11071-020-06186-1

CrossRef Full Text | Google Scholar

23. Tan W. Evolution of breathers and interaction between high-order lump solutions and N-solitons (N → ∞) for Breaking Soliton system. Phys Lett A (2019) 383:125907. doi:10.1016/j.physleta.2019.125907

CrossRef Full Text | Google Scholar

24. Zhao Z, He L. M-lump, high-order breather solutions and interaction dynamics of a generalized $$(2 + 1)$$-dimensional nonlinear wave equation. Nonlinear Dyn (2020) 100:2753–65. doi:10.1007/s11071-020-05611-9

CrossRef Full Text | Google Scholar

25. Hao X. Nonlocal symmetries and molecule structures of the kdv hierarchy. Nonlinear Dyn (2021) 104:4277–91. doi:10.1007/s11071-021-06530-z

CrossRef Full Text | Google Scholar

26. Sawada K, Kotera T. A method for finding n-soliton solutions of the kdv equation and kdv-like equation. Prog Theor Phys (1974) 51:1355–67. doi:10.1143/PTP.51.1355

CrossRef Full Text | Google Scholar

27. Konopelchenko B, Dubrovsky V. Some new integrable nonlinear evolution equations in 2+1 dimensions. Phys Lett A (1984) 102:15–7. doi:10.1016/0375-9601(84)90442-0

CrossRef Full Text | Google Scholar

28. An H, Feng D, Zhu H. General $${\varvec{M}}$$-lump, high-order breather and localized interaction solutions to the $$\varvec{2+1}$$-dimensional Sawada–Kotera equation. Nonlinear Dyn (2019) 98:1275–86. doi:10.1007/s11071-019-05261-6

CrossRef Full Text | Google Scholar

29. Lü X, Geng T, Zhang C, Zhu H-W, Meng X-H, Tian B. Multi-soliton solutions and their interactions for the (2+1)-dimensional sawada-kotera model with truncated painlevé expansion, hirota bilinear method and symbolic computation. Int J Mod Phys B (2009) 23:5003–15. doi:10.1142/S0217979209053382

CrossRef Full Text | Google Scholar

30. Lü X. New bilinear bäcklund transformation with multisoliton solutions for the (2+1)-dimensional sawada-kotera model. Nonlinear Dyn (2014) 76:161–8. doi:10.1007/s11071-013-1118-y

CrossRef Full Text | Google Scholar

31. Debin K, Rezazadeh H, Ullah N, Vahidi J, Tariq KU, Akinyemi L. New soliton wave solutions of a (2+1)-dimensional sawada-kotera equation. J Ocean Eng Sci (2022). doi:10.1016/j.joes.2022.03.007

CrossRef Full Text | Google Scholar

32. Zhang H-Q, Ma W-X. Lump solutions to the ( $$\mathbf 2+1 $$ 2 + 1 )-dimensional Sawada–Kotera equation. Nonlinear Dyn (2016) 87:2305–10. doi:10.1007/s11071-016-3190-6

CrossRef Full Text | Google Scholar

33. Huang L-L, Chen Y. Lump solutions and interaction phenomenon for (2+1)-dimensional sawada-kotera equation. Commun Theor Phys (2017) 67:473. doi:10.1088/0253-6102/67/5/473

CrossRef Full Text | Google Scholar

34. Wang X, Zhao Q, Jia M, Lou S. Novel travelling wave structures for (2+1)-dimensional sawada-kotera equation. Appl Math Lett (2022) 124:107638. doi:10.1016/j.aml.2021.107638

CrossRef Full Text | Google Scholar

35. Qi Z, Chen Q, Wang M, Li B. New mixed solutions generated by velocity resonance in the $$(2+1)$$-dimensional Sawada–Kotera equation. Nonlinear Dyn (2022) 108:1617–26. doi:10.1007/s11071-022-07248-2

CrossRef Full Text | Google Scholar

36. Zhang R-F, Li M-C, Al-Mosharea E, Zheng F-C, Bilige S. Rogue waves, classical lump solutions and generalized lump solutions for sawada–kotera-like equation. Int J Mod Phys B (2022) 36. 2250044. doi:10.1142/s0217979222500448

CrossRef Full Text | Google Scholar

37. Du Y-H, Yun Y-S, Ma W-X. Rational solutions to two sawada–kotera-like equations. Mod Phys Lett B (2019) 33:1950108. doi:10.1142/s0217984919501082

CrossRef Full Text | Google Scholar

38. Ablowitz MJ, Satsuma J. Solitons and rational solutions of nonlinear evolution equations. J Math Phys (1978) 19:2180. doi:10.1063/1.523550

CrossRef Full Text | Google Scholar

39. Satsuma J, Ablowitz MJ. Two-dimensional lumps in nonlinear dispersive systems. J Math Phys (1979) 20:1496–503. doi:10.1063/1.524208

CrossRef Full Text | Google Scholar

40. Zhao Z, He L, Gao Y. Rogue wave and multiple lump solutions of the (2+1)-dimensional benjamin-ono equation in fluid mechanics. Complexity (2019) 2019:1–18. doi:10.1155/2019/8249635

CrossRef Full Text | Google Scholar

41. Chen S-J, Lü X, Li M-G, Wang F. Derivation and simulation of the m-lump solutions to two (2+1)-dimensional nonlinear equations. Phys Scr (2021) 96:095201. doi:10.1088/1402-4896/abf307

CrossRef Full Text | Google Scholar

42. Zhao Z, He L. M-lump and hybrid solutions of a generalized (2+1)-dimensional Hirota–Satsuma–Ito equation. Appl Math Lett (2021) 111:106612. doi:10.1016/j.aml.2020.106612

CrossRef Full Text | Google Scholar

43. Zhang W-J, Xia T-C. Solitary wave, m-lump and localized interaction solutions to the (4+1)-dimensional fokas equation. Phys Scr (2020) 95:045217. doi:10.1088/1402-4896/ab6a3f

CrossRef Full Text | Google Scholar

44. He X-J, Lü X. M-lump solution, soliton solution and rational solution to a (3+1)-dimensional nonlinear model. Math Comput Simulation (2022) 197:327–40. doi:10.1016/j.matcom.2022.02.014

CrossRef Full Text | Google Scholar

45. Satsuma J. N-soliton solution of the two-dimensional korteweg-devries equation. J Phys Soc Jpn (1976) 40:286–90. doi:10.1143/jpsj.40.286

CrossRef Full Text | Google Scholar

46. Ma W-X. Generalized bilinear differential equations. Stud Nonlinear Sci (2011) 2:140–4. Available at: researchgate.net/publication/284931775.

Google Scholar