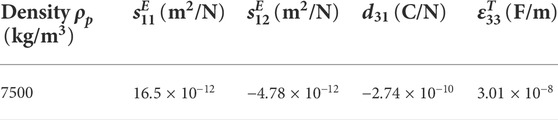Polynomial eigenvalue solution for elastic wave prediction of piezoelectric shunting arrays

This paper presents a polynomial eigenvalue solution to predict the propagation behaviors of elastic wave in piezoelectric shunting arrays. Based on the Bloch theorem, one independent unit cell is selected to conduct the dynamic characteristic analysis instead of infinity. The reduced form of the discretized governing equations is first derived by the standard finite element procedures. To facilitate the subsequent acquisition of dispersion relationship, the dynamic stiffness matrix is then partitioned into a block matrix. Through applying the periodic boundary conditions, a polynomial eigenvalue equation concerning complex propagation constant is finally obtained. The wave propagation and attenuation characteristics in arbitrary directions are investigated using the above methodology. The results demonstrate that the present method can provide very accurate and reliable solutions for wave propagation prediction of piezoelectric shunting arrays.

1 Introduction

Over the past several decades, the propagation of elastic waves including bulk waves [1] and surface waves [2] in phononic crystals (PCs) has attracted a great deal of interest [3, 4]. Due to the existence of band gaps, PCs have many potential applications, such as elastic wave filters and vibration isolation. There are two main mechanisms for the formation of band gaps, namely, Bragg scattering (BS) [5] and locally resonant (LR) [6]. Compared with the BS mechanism, the LR one allows the acquisition of low-frequency band gaps with the structure of small dimensions. Hence, researchers prefer to use the LR PCs for the reduction of vibration noise in practical engineering [7]. However, for the traditional PCs, the non-adjustable characteristics of band gaps restrict their practical application, especially for structures with variable working conditions. By combining the piezoelectric shunt damping technology [8, 9] with PCs theory, piezoelectric shunt arrays (PSA) which belong to a new type of PCs emerged. The tunable characteristics of shunt circuits allow the band gaps to be adjusted over desired frequency range. However, due to the existence of complex wave vectors caused by the piezoelectric shunt damping, it is not an easy work to predict the band structures of PSA using the traditional numerical approaches.

The transfer matrix method [10, 11] is the first numerical algorithm used in band structures simulation of PSA. Based on this approach, Thorp [12] et al. studied the attenuation and localization of elastic wave propagation in a piezoelectric resistive-inductive-shunted rod. Airoldi and Ruzzene [13] investigated the wave propagation characteristics of a periodic beam with shunted piezoelectric patches. Wang [14] et al. analyzed the vibration attenuation effects of piezoelectric beams connected by an enhanced resonant shunting circuit. However, this algorithm is restricted to one-dimensional system, which is not suitable for practical engineering applications. In order to obtain the two-dimensional band structures of PSA, the enhanced plane wave expansion (PWE) method [15] emerged. Lian [16] et al. analyzed the effect of circuit parameters on the LR band gaps in a piezoelectric PC plate with resonant shunting circuits. Chen [17] et al. studied the band gap characteristics of piezoelectric metamaterial plate with interface circuits. Compared with the conventional PWE, the enhanced PWE can provide more accurate results and has a good convergence. But it is difficult to predict the attenuation degree of elastic waves due to the neglect of information on amplitude attenuation in the wave vectors. With the rapid development of computational mechanics, researchers have gradually applied the finite element method for the prediction of wave propagation and attenuation in PSA. Spadoni [18] et al. analyzed the wave propagation and subsequent vibrations in plates with periodic shunted piezoelectric patches. Gardonio [19] et al. realized the effective control of bending vibration in thin plate by self-tuning PSA. Although the propagation properties can be obtained in some specific directions, these studies rarely concern the arbitrarily oriented ones. By using the ‘fsolve’ function in Matlab, Chen [20] et al. predicted the propagation behaviors of elastic wave in arbitrary directions in PSA. However, several numerical defects still exist, for example, initial value sensitivity and tendency to converge to wrong results. Later, Wen [21] et al. proposed a wave field transformation method to analyze the directionality of dispersion relationships when elastic waves propagate in PSA. But this method suffers from the complication formulations and the low computational efficiency, which limits its practical application.

In order to facilitate the prediction of propagation characteristics in arbitrary directions, developing a new algorithm which can cure the above mentioned drawbacks seems more feasible. In this work, we further present a polynomial eigenvalue solution (PES) to predict the propagation behaviors of elastic wave in PSA. As the structure is periodic in the x-y plane, one independent unit cell is selected for the dynamic characteristic analysis instead of infinity. Based on the classic Kirchhoff hypothesis and standard finite element procedures, rectangular element with corner nodes is first employed to obtain the discretized system equations [22]. To acquire the dispersion relationship conveniently, the dynamic stiffness matrix is then partitioned into a block matrix. By implementing the Bloch theorem, a polynomial eigenvalue equation concerning complex propagation constants is further obtained. Through a simple transformation, a linear eigenvalue equation is finally derived, from which the dispersion relationships of PSA can be easily derived. In order to examine the performance of the proposed algorithm, the wave propagation behaviors of a semi-covered piezoelectric periodic plate connecting with a inductance-resistance circuit are in detail studied. The results reveal that the present PES can provide very accurate and reliable numerical predictions for the wave propagation characteristics in arbitrary directions in PSA.

2 Methods

2.1 Theoretical basis

Consider a piezoelectric shunt system consisting of a host plate and arrays of shunted piezoelectric patches, the periodic plate behaves as a two-dimensional infinite waveguide propagating transverse waves. Based on the Bloch theorem, one independent unit cell is selected to conduct the dynamic characteristic analysis, as illustrated in Figure 1A. The divided regions of the unit cell contain two different structural types, i.e., one is the single-layer plate without piezoelectric patches attached, the other is a composite plate consisting of a host plate and piezoelectric patches connecting with a circuit. Noteworthy, the polarization directions of the piezoelectric patches are same.

FIGURE 1

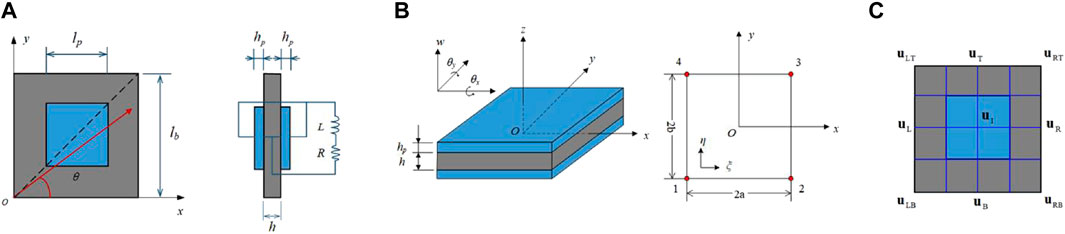
FIGURE 1. (A) The square unit cell; (B) Composite plate structure and rectangular element in x-y plane; (C) A typical mesh arrangement for the domain discretization.

As the existence of piezoelectric patches, the electromechanical coupling effect needs to be considered for the dynamic analysis of the unit cell. The stress-charge form of the constitutive equations for a piezoelectric material can be written as [23].

$\left[\begin{array}{c}{\mathbf{\sigma }}_p\\ {\mathbf{D}}_{\mathit{e}}\end{array}\right]=\left[\begin{array}{cc}{\mathbf{c}}^{\mathit{E}}& -\mathbf{e}\\ {\mathbf{e}}^{\mathbf{T}}& {\epsilon }^s\end{array}\right]\left[\begin{array}{c}{\mathbf{\epsilon }}_{\mathit{p}}\\ \mathbf{E}\end{array}\right](1)$

where, ${\mathbf{\sigma }}_p$ and ${\mathbf{\epsilon }}_p$ are the mechanical stress vector and the mechanical strain vector, respectively; ${\mathbf{D}}_e$ and $\mathbf{E}$ represent the electric displacement vector and the electric field vector on the piezoelectric patches electrode, separately; ${\epsilon }^s$ is the permittivity matrix; $\mathbf{e}$ denotes the matrix of piezoelectric stress constants; ${\mathbf{c}}^E$ is the stiffness matrix of piezoelectric material.

In order to obtain the subsequent discretized governing equations, the energy functional of the whole unit cell is presented. Here, only the energy functional of the composite plate with piezoelectric patches attached is discussed. According to the Lagrange’s equations, the energy functional $L$ of the composite plate can be described as

$L=T-U+U_e(2)$

where, $T$ is the kinetic energy, $U$ is the potential energy and $U_e$ is the electric energy, which can be expressed as

$T=\frac{1}{2}{\int }_{{\Omega }_b}{\rho }_b{\dot{w}}^{2}d{\Omega }_b+\frac{1}{2}{\int }_{{\Omega }_p}{\rho }_p{\dot{w}}^{2}d{\Omega }_p(3)$

$U=\frac{1}{2}{\int }_{{\Omega }_b}{\mathbf{\epsilon }}_{\mathit{b}}^{\mathbf{T}}{\mathbf{\sigma }}_{\mathit{b}}d{\Omega }_b+\frac{1}{2}{\int }_{{\Omega }_p}{\mathbf{\epsilon }}_{\mathit{p}}^{\mathbf{T}}{\mathbf{\sigma }}_{\mathit{p}}d{\Omega }_p(4)$

$U_e=\frac{1}{2}{\int }_{{\Omega }_p}{\mathbf{E}}^{\mathbf{T}}{\mathbf{D}}_{\mathit{e}}d{\Omega }_p(5)$

where, $\rho$ is the density; $w$ denotes the element displacement. Note that, the subscript ‘b’ and ‘p’ represent the quantities corresponding to host plate and piezoelectric shunting, respectively.

To gain the wave propagation characteristics in the whole PSA, the periodic boundary conditions need to be imposed. The Bloch theorem explains this behavior, which can be described in what follows. According to the lattice theory, the whole two-dimensional lattice structure can be seen as the result of translating the unit cell along the basis vectors ${\mathbf{\alpha }}_{\mathbf{1}}$ and ${\mathbf{\alpha }}_{\mathbf{2}}$ [24]. Let $\mathbf{R}\left(\mathbf{r}\right)$ represent the displacement of a lattice point located at the position $\mathbf{r}\left(x,y\right)$, which can be expressed as

$\mathbf{R}\left(\mathbf{r}\right)=\mathbf{R}{\mathrm{e}}^{\left(\mathrm{i}\omega t-\mathbf{k}\cdot \mathbf{r}\right)}(6)$

in which, R is the amplitude of displacement vector and $\mathbf{k}$ is the wave vector. The position of other ones based on this lattice point can be given by

${\mathbf{r}}^{n_1,n_2}=\mathbf{r}+n_1{\mathbf{\alpha }}_1+n_{\mathbf{2}}{\mathbf{\alpha }}_{\mathbf{2}}(7)$

where, the n₁ and n₂ are integers related to periodicity. Putting ${\mu }_x=-\mathbf{k}\cdot {\mathbf{\alpha }}_{\mathbf{1}}$ and ${\mu }_y=-\mathbf{k}\cdot {\mathbf{\alpha }}_{\mathbf{2}}$, the displacement of lattice points located at the position ${\mathrm{r}}^{n_1,n_2}$ can be given by

$\mathbf{R}\left({\mathbf{r}}^{n_1,n_2}\right)=\mathbf{R}\left(\mathbf{r}\right){\mathbf{e}}^{n_1{\mu }_x+n_2{\mu }_y}(8)$

2.2 Basic formulations of the PES

This section presents the basic formulations of PES for wave propagation prediction of PSA in detail. To perform the numerical investigation, both the finite element discretization and the Bloch theorem are utilized, which will be detailedly discussed in the following.

2.2.1 Finite element discretization

Based on the Bloch theorem, only one unit cell is selected for the dynamic analysis. The composite plate structure, which is used to represent the wave propagation characteristics, is shown in Figure 1B. In order to implement the investigation, a set of four-node rectangular elements with corner nodes [22] are first adopted to discrete the problem domain. According to the Kirchhoff hypothesis, the relationship between the vertical deflection $w$ and the rotation ${\theta }_x$ about x-axis, as well as the rotation ${\theta }_y$ about y-axis, can be defined as

$\{\begin{array}{c}{\theta }_x=\frac{\partial w}{\partial y}\\ {\theta }_y=-\frac{\partial w}{\partial x}\end{array}(9)$

Using the standard finite element procedure, the generalized deflection $w$ within an element can be interpolated using

$w={\mathbf{\text{Nu}}}^{\mathit{e}}(10)$

where, $\mathrm{N}$ is the element shape function; ${\mathrm{u}}^e$ is the element displacement vector that can be written as

${\mathbf{u}}^e={\left[\begin{array}{cccc}{\mathbf{u}}_1& {\mathbf{u}}_2& {\mathbf{u}}_3& {\mathbf{u}}_4\end{array}\right]}^{\mathrm{T}}(11)$

in which, ${\mathrm{u}}_i=\left\{w_i,{\theta }_{xi},{\theta }_{yi}\right\}\left(i=\mathrm{1,2,3,4}\right)$ is the nodal displacement vector.

To clearly illustrate Eq.10, N can be explicitly expressed using

$\mathbf{N}=\left[\begin{array}{cccc}{\mathbf{N}}_1& {\mathbf{N}}_2& {\mathbf{N}}_3& {\mathbf{N}}_4\end{array}\right](12)$

in which

$\begin{array}{cc}{\mathbf{N}}_{\mathit{i}}=\frac{1}{8}\left(1+{\xi }_0\right)\left(1+{\eta }_0\right){\left[\begin{array}{c}2+{\xi }_0+{\eta }_0-{\xi }^2-{\eta }^2\\ b{\eta }_i\left(1-{\eta }^2\right)\\ -a{\xi }_i\left(1-{\xi }^2\right)\end{array}\right]}^{\mathrm{T}}& \left(i=\mathrm{1,2,3,4}\right)\end{array}(13)$

with

$\{\begin{array}{c}{\xi }_0=\xi {\xi }_i,\\ {\eta }_0=\eta {\eta }_i,\end{array}\begin{array}{c}\xi =\left(x-x_c\right)/a\\ \eta =\left(y-y_c\right)/b\end{array}(14)$

where, $\xi$ and $\eta$ are the normalized coordinates; $x_c$ and $y_c$ are the coordinates of the centroid O; $a$ and $b$ are the half lengths of side; the values of ${\xi }_i$ and ${\eta }_i$ can be found in Ref. [22].

Based on the relationship between stain and displacement, the relevant strain vector related to the host plate and the piezoelectric patches can be written as

$\mathbf{\epsilon }={\left\{\begin{array}{ccc}{\epsilon }_x& {\epsilon }_y& {\gamma }_{xy}\end{array}\right\}}^{\mathrm{T}}=z\mathbf{L}w(15)$

in which, L denotes the differential operator with the form of

$\mathbf{L}={\left\{-\frac{{\partial }^2}{\partial x^2},-\frac{{\partial }^2}{\partial y^2},-2\frac{{\partial }^2}{\partial x\partial y}\right\}}^{\mathrm{T}}(16)$

The stress-strain relationship for the host plate of PSA can be written as

${\mathbf{\sigma }}_b=\mathbf{D}{\mathbf{\epsilon }}_b(17)$

where, the matrix $\mathrm{D}$ is the constitutive coefficient that can be found in Ref. [22].

In order to represent the electromechanical coupling effect of the piezoelectric shunt system, the potential degree of freedom (DOF) should also be included in the kinetic analysis. Consider the fact that the potential on the electrode of piezoelectric patch is equal everywhere, a potential DOF $\phi$ namely the electric potential difference is introduced for the whole unit cell, which can be expressed as

$\phi =E{h}_p(18)$

in which, E is the electric field intensity in z-axis direction; $h_p$ denotes the thickness of piezoelectric patch.

According to the Hamilton principle, the energy functional $L$ in Eq. 2 should be at a minimum to reach equilibrium-stability state. Substituting Eqs 1 and 10, 15, 17 and 18 into Eq. 2, the discretized system equations for the dynamic characteristics of unit cell corresponding to the PSA can then be derived as follows [15, 25]

${\mathbf{M}}_{uu}\ddot{\mathbf{u}}+{\mathbf{K}}_{uu}\mathbf{u}+{\mathbf{K}}_{u\phi }\phi =\mathbf{f}(19)$

${\mathbf{K}}_{\phi u}\mathbf{u}+{\mathrm{K}}_{\phi \phi }\phi =q(20)$

in which, $\mathbf{u}$ is the nodal displacements vector of the whole unit cell; $\mathbf{f}$ is the system forces vector; $q$ is the total charge; ${\mathbf{M}}_{uu}$, ${\mathbf{K}}_{uu}$ and ${\mathbf{K}}_{u\phi }$ are the assembled mass, stiffness and coupling matrices, respectively. ${\mathbf{K}}_{\phi u}$ is the transpose matrix of ${\mathbf{K}}_{u\phi }$. Note that, ${\mathrm{K}}_{\phi \phi }$ is a scalar, which is opposite to the total capacitance of the piezoelectric patches at constant strain.

Assuming that the displacement $\mathbf{u}$ is a small harmonic perturbation which satisfies

$\mathbf{u}={\text{ue}}^{i\omega t}(21)$

where, $\omega$ denotes the angular frequency; u represents the amplitude of the displacement. Under the same hypothesis, the relationship between the total charge $q\left(\omega \right)$ and the electric potential difference $\phi \left(\omega \right)$ can then be written as

$q\left(\omega \right)=\frac{\phi \left(\omega \right)}{i\omega Z\left(\omega \right)}(22)$

in which, $Z\left(\omega \right)$ is the complex impedance and $i=\sqrt{-1}$. On its substitution into Eq. 20, $\phi \left(\omega \right)$ can be rewritten as

$\phi \left(\omega \right)={\left[\frac{1}{i\omega Z\left(\omega \right)}-K_{\phi \phi }\right]}^{-1}{\mathbf{K}}_{\phi u}\mathbf{u}(23)$

Substituting Eqs 21, 23 into Eq. 19, we can finally obtain

${\mathbf{K}}_D\left(\omega \right)\mathbf{u}=\mathbf{f}(24)$

where, ${\mathbf{K}}_D\left(\omega \right)$ is the dynamic stiffness matrix with the form of

${\mathbf{K}}_D\left(\omega \right)={\mathbf{K}}_{uu}-{\omega }^2{\mathbf{M}}_{uu}+{\mathbf{K}}_{u\phi }{\left[\frac{1}{i\omega Z\left(\omega \right)}-K_{\phi \phi }\right]}^{-1}{\mathbf{K}}_{\phi u}(25)$

2.2.2 Bloch analysis

To study the wave propagation behaviors of the whole PSA, the periodic boundary conditions are introduced in this subsection. As shown in Figure 1C, the nodal displacements $\mathrm{u}$ and forces $\mathrm{f}$ have been divided according to their relative positions in the unit cell, which can be expressed using

$\mathbf{u}={\left[\begin{array}{ccc}{\mathbf{u}}_I& {\mathbf{u}}_B& \begin{array}{ccc}{\mathbf{u}}_T& {\mathbf{u}}_L& \begin{array}{ccc}{\mathbf{u}}_R& {\mathbf{u}}_{LB}& {\begin{array}{ccc}{\mathbf{u}}_{RB}& {\mathbf{u}}_{LT}& \mathbf{u}\end{array}}_{RT}\end{array}\end{array}\end{array}\right]}^T(26)$

$\mathbf{f}={\left[\begin{array}{ccc}\mathbf{0}& {\mathbf{f}}_B& \begin{array}{ccc}{\mathbf{f}}_T& {\mathbf{f}}_L& \begin{array}{ccc}{\mathbf{f}}_R& {\mathbf{f}}_{LB}& {\begin{array}{ccc}{\mathbf{f}}_{RB}& {\mathbf{f}}_{LT}& \mathbf{f}\end{array}}_{RT}\end{array}\end{array}\end{array}\right]}^{\mathrm{T}}(27)$

Based on the periodic conditions and equilibrium conditions [24], the Bloch boundary conditions can be written as

$\{\begin{array}{c}{\mathbf{u}}_T={\mathrm{e}}^{{\mu }_y}{\mathbf{u}}_{{\rm B}},{\mathbf{u}}_R={\mathrm{e}}^{{\mu }_x}{\mathbf{u}}_L\\ {\mathbf{u}}_{LT}={\mathrm{e}}^{{\mu }_y}{\mathbf{u}}_{LB},{\mathbf{u}}_{RB}={\mathrm{e}}^{{\mu }_x}{\mathbf{u}}_{LB},{\mathbf{u}}_{RT}={\mathrm{e}}^{{\mu }_x+{\mu }_y}{\mathbf{u}}_{LB}\end{array}(28)$

$\{\begin{array}{c}{\mathbf{f}}_{{\rm B}}+{\mathrm{e}}^{-{\mu }_y}{\mathbf{f}}_T=0,{\mathbf{f}}_L+{\mathrm{e}}^{-{\mu }_x}{\mathbf{f}}_R=0\\ {\mathbf{f}}_{LB}+{\mathrm{e}}^{-{\mu }_x}{\mathbf{f}}_{RB}+{\mathrm{e}}^{-{\mu }_y}{\mathbf{f}}_{LT}+{\mathrm{e}}^{-{\mu }_x-{\mu }_y}{\mathbf{f}}_{RT}=0\end{array}(29)$

in which, $\left({\mu }_x{,\mu }_y\right)$ are propagation constants that are normally complex numbers, i.e., ${\mu }_j={\alpha }_{\mathrm{j}}+\mathrm{i}{\beta }_{\mathrm{j}}\left(\mathrm{j}=\mathrm{x},\mathrm{y}\right)$. The real part ${\alpha }_j$ is attenuation constant which indicates the amplitude decay of elastic wave propagating from one unit cell to the next. The imaginary part ${\beta }_j$ is phase constant which denotes the phase change of elastic waves propagation.

Putting ${\mathrm{e}}^{{\mu }_x}={\lambda }_{\mathrm{x}}$ and ${\mathrm{e}}^{{\mu }_y}={\lambda }_{\mathrm{y}}$, the matrix form of Eqs 28, 29 can be further expressed by

$\{\begin{array}{c}\mathbf{u}=\mathbf{T}\left({\lambda }_x,{\lambda }_y\right)\widehat{\mathbf{u}}\\ {\mathbf{T}}^{\mathrm{T}}\left(1/{\lambda }_x,1/{\lambda }_y\right)\mathbf{f}=0\end{array}(30)$

in which

$\widehat{\mathbf{u}}={\left[\begin{array}{cccc}{\mathbf{u}}_I& {\mathbf{u}}_B& {\mathbf{u}}_L& {\mathbf{u}}_{LB}\end{array}\right]}^{\mathrm{T}}(31)$

$\mathbf{T}\left({\lambda }_x,{\lambda }_y\right)={\left[\begin{array}{ccccccccc}\mathbf{I}& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& \mathbf{I}& \mathbf{I}{\lambda }_y& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& \mathbf{I}& \mathbf{I}{\lambda }_x& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& \mathbf{I}& \mathbf{I}{\lambda }_x& \mathbf{I}{\lambda }_y& \mathbf{I}{\lambda }_x{\lambda }_y\end{array}\right]}^{\mathrm{T}}(32)$

2.2.3 The acquirement of propagation constant

This subsection formulates a polynomial eigenvalue equation to obtain the propagation constant on the basis of periodic boundary conditions and dynamic equilibrium equation. To facilitate the subsequent acquisition of propagation constant, ${\mathbf{K}}_D\left(\omega \right)$ can be rewritten in the form of block matrix

${\mathbf{K}}_D\left(\omega \right)=\left[\begin{array}{ccccccccc}{\mathbf{K}}_{II}& {\mathbf{K}}_{IB}& {\mathbf{K}}_{IT}& {\mathbf{K}}_{IL}& {\mathbf{K}}_{IR}& {\mathbf{K}}_{ILB}& {\mathbf{K}}_{IRB}& {\mathbf{K}}_{ILT}& {\mathbf{K}}_{IRT}\\ {\mathbf{K}}_{BI}& {\mathbf{K}}_{BB}& {\mathbf{K}}_{BT}& {\mathbf{K}}_{BL}& {\mathbf{K}}_{BR}& {\mathbf{K}}_{BLB}& {\mathbf{K}}_{BRB}& {\mathbf{K}}_{BLT}& {\mathbf{K}}_{BRT}\\ {\mathbf{K}}_{TI}& {\mathbf{K}}_{TB}& {\mathbf{K}}_{TT}& {\mathbf{K}}_{TL}& {\mathbf{K}}_{TR}& {\mathbf{K}}_{TLB}& {\mathbf{K}}_{TRB}& {\mathbf{K}}_{TLT}& {\mathbf{K}}_{TRT}\\ {\mathbf{K}}_{LI}& {\mathbf{K}}_{LB}& {\mathbf{K}}_{LT}& {\mathbf{K}}_{LL}& {\mathbf{K}}_{LR}& {\mathbf{K}}_{LLB}& {\mathbf{K}}_{LRB}& {\mathbf{K}}_{LLT}& {\mathbf{K}}_{LRT}\\ {\mathbf{K}}_{RI}& {\mathbf{K}}_{RB}& {\mathbf{K}}_{RT}& {\mathbf{K}}_{RL}& {\mathbf{K}}_{RR}& {\mathbf{K}}_{RLB}& {\mathbf{K}}_{RRB}& {\mathbf{K}}_{RLT}& {\mathbf{K}}_{RRT}\\ {\mathbf{K}}_{LBI}& {\mathbf{K}}_{LBB}& {\mathbf{K}}_{LBT}& {\mathbf{K}}_{LBL}& {\mathbf{K}}_{LBR}& {\mathbf{K}}_{LBLB}& {\mathbf{K}}_{LBRB}& {\mathbf{K}}_{LBLT}& {\mathbf{K}}_{LBRT}\\ {\mathbf{K}}_{RBI}& {\mathbf{K}}_{RBB}& {\mathbf{K}}_{RBT}& {\mathbf{K}}_{RBL}& {\mathbf{K}}_{RBR}& {\mathbf{K}}_{RBLB}& {\mathbf{K}}_{RBRB}& {\mathbf{K}}_{RBLT}& {\mathbf{K}}_{RBRT}\\ {\mathbf{K}}_{LTI}& {\mathbf{K}}_{LTB}& {\mathbf{K}}_{LTT}& {\mathbf{K}}_{LTL}& {\mathbf{K}}_{LTR}& {\mathbf{K}}_{LTLB}& {\mathbf{K}}_{LTRB}& {\mathbf{K}}_{LTLT}& {\mathbf{K}}_{LTRT}\\ {\mathbf{K}}_{RTI}& {\mathbf{K}}_{RTB}& {\mathbf{K}}_{RTT}& {\mathbf{K}}_{RTL}& {\mathbf{K}}_{RTR}& {\mathbf{K}}_{RTLB}& {\mathbf{K}}_{RTRB}& {\mathbf{K}}_{RTLT}& {\mathbf{K}}_{RTRT}\end{array}\right](33)$

Substituting Eqs. 30, 33 into Eq.24, a polynomial eigenvalue equation, depending on $\omega$, ${\lambda }_x$ and ${\lambda }_y$, can be obtained and expressed in the following form

$\left[{\mathbf{K}}_{D0}+{\mathbf{K}}_{D1}{\lambda }_x+{\mathbf{K}}_{D2}{\lambda }_y+{\mathbf{K}}_{D3}{\lambda }_x^2+{\mathbf{K}}_{D4}{\lambda }_y^2+{\mathbf{K}}_{D5}{\lambda }_x{\lambda }_y+{\mathbf{K}}_{D6}{\lambda }_x^2{\lambda }_y+{\mathbf{K}}_{D7}{\lambda }_x{\lambda }_y^2+{\mathit{K}}_{D8}{\lambda }_x^2{\lambda }_y^2\right]\widehat{\mathbf{u}}=0(34)$

in which, the coefficient matrices are shown in Appendix A. It is difficult to directly obtain ${\lambda }_x$ and ${\lambda }_y$ through a given $\omega$ as the solution conditions of polynomial eigenvalue equation are not satisfied [26]. Consider the fact that ${\mu }_x$ and ${\mu }_y$ can be represented by wave vector $\mathrm{k}$ in $x$ and $y$ directions [27, 28], then we can get

$\frac{{\mu }_y}{{\mu }_x}=\tan \left(\theta \right)(35)$

in which, θ is the wave propagation angle.

To make Eq. 34 solvable, the following two requirements need to be satisfied: 1) the ratio ${\mu }_y/{\mu }_{\mathrm{x}}=m_2/m_1$ is rational; 2) $m_2$ and $m_1$ are integers with no common divisor. Hence, the propagation constants can be further expressed using ${\mu }_x=m_1\delta$ and ${\mu }_y=m_2\delta$ where $\delta$ is the quantity without practical meaning. By introducing $\tau =e^{\delta }$, Eq. 34 can be rewritten as

$\begin{array}{l}[{\mathbf{K}}_{D0}+{\mathbf{K}}_{D1}{\tau }^{m_1}+{\mathbf{K}}_{D2}{\tau }^{m_2}+{\mathbf{K}}_{D3}{\tau }^{2m_1}+{\mathbf{K}}_{D4}{\tau }^{2m_2}+{\mathbf{K}}_{D5}{\tau }^{m_1+m_2}+{\mathbf{K}}_{D6}{\tau }^{2m_1+m_2}\\ +{\mathbf{K}}_{D7}{\tau }^{m_1+2m_2}+{\mathbf{K}}_{D8}{\tau }^{2m_1+2m_2}]\stackrel{\wedge }{\mathbf{u}}=0\end{array}(36)$

Through a simple transformation process, Eq. 36 can be further expressed using

$\left[\mathbf{Q}-\tau \mathbf{I}\right]\widehat{\mathbf{U}}=\mathbf{0}(37)$

with

$\mathbf{Q}=\left[\begin{array}{cccc}-{\mathbf{K}}_{Dm}^{-1}{\mathbf{K}}_{D\left(m-\mathbf{1}\right)}& \cdots & -{\mathbf{K}}_{Dm}^{-1}{\mathbf{K}}_{D1}& -{\mathbf{K}}_{Dm}^{-1}{\mathbf{K}}_{D0}\\ \mathbf{I}& & & ⋮\\ & \ddots & & \\ & & \mathbf{I}& 0\end{array}\right](38)$

$\widehat{\mathbf{U}}=\left\{\begin{array}{c}{\tau }^{m-1}\widehat{\mathbf{u}}\\ ⋮\\ \tau \widehat{\mathbf{u}}\\ \widehat{\mathbf{u}}\end{array}\right\}(39)$

in which, ${\mathbf{K}}_{Dm}\ne 0$ and $m=2m_1+2m_2$

Obviously, Eq. 37 is a linear eigenvalue problem which is easier to solve. When the propagation angular frequency $\omega$ and the tangent value $\tan \left(\theta \right)$ are given, $\delta$ can be easily derived. The propagation constant ${\mu }_{\theta }$ in arbitrary direction $\theta$ can be finally calculated using

${\mu }_{\theta }=\delta \sqrt{m_1^2+m_2^2}(40)$

It can be seen from Eq. 40 that ${\mu }_{\theta }$ varies with the changes of $\delta$, $m_1$ and $m_2$. Therefore, when $\theta$ is determined, the relationship between ${\mu }_{\theta }$ and $\omega$ can be easily obtained to represent the propagation behaviors of elastic wave.

3 Results

The present formulation has been coded using MATLAB program. In what follows, a typical numerical example is carefully studied to illustrate the accuracy and reliability of our PES. In addition, the wave propagation and attenuation in arbitrary directions are also investigated using the above methodology.

The host plate is epoxy with Young’s modulus $E=4.35\text{GPa}$, Poisson’s ratio $\upsilon =0.37$ and mass density ${\rho }_b=1180{\text{kg}/\mathrm{m}}^3$. The piezoelectric patch is PZT-5H. Table 1 and Table 2 list the related material and geometric parameters used in this study.

TABLE 1

TABLE 1. Material parameters of the PZT-5H.

TABLE 2

TABLE 2. Geometric parameters of the unit cell.

Moreover, the shunt circuit is a serial resistive-inductive network, hence the complex impedance Z becomes

$Z\left(\omega \right)=R+i\omega L(41)$

where, the shunt resistance and inductance value are selected to be 100Ω and 0.2H [20], respectively.

3.1 Accuracy of the PES

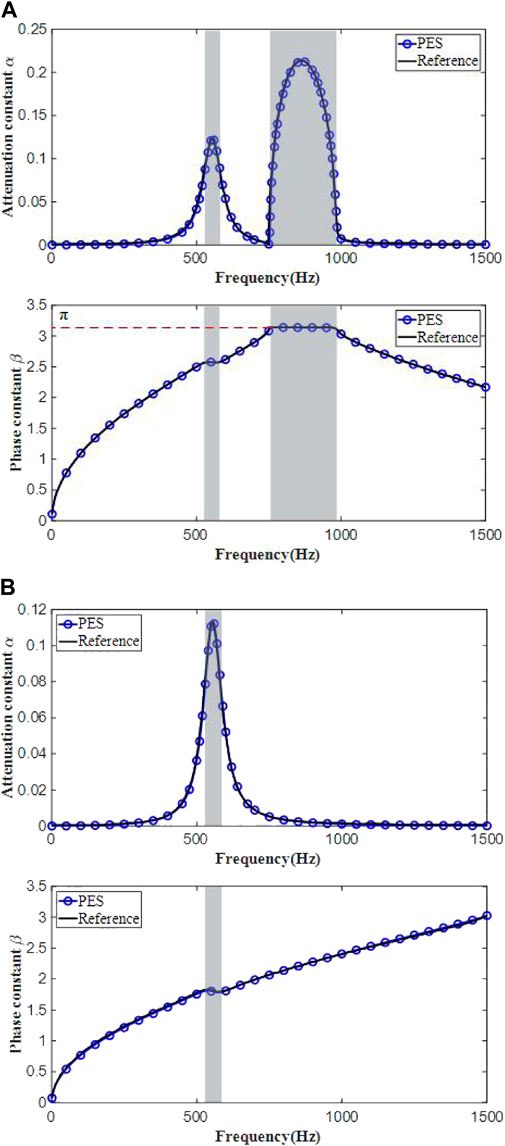
To implement this investigation, the problem domain is first discretized using 16 four-node rectangular elements. As the elastic wave can propagate in arbitrary directions, two representative wave propagation angle, namely θ = 0 and θ = π/4, are selected to study the wave propagation and attenuation characteristics. Because the exact solutions are unknown for this case, the numerical results verified by commercial software ANSYS and experiment [20] are taken as the reference.

The attenuation constant a and phase constant ß obtained using both algorithms by varying the frequency from 0 Hz to 1,500 Hz are plotted in Figure 2. It can be observed that 1) For θ = 0, there are two band gaps in the considered frequency range. The first band gap named the locally resonant gap is about 525 Hz–580 Hz, while the second one called the Bragg gap is about 750 Hz–985 Hz. 2) For θ = π/4, only one band gap exists which is about 527 Hz–582 Hz. 3) Whatever the wave propagation angle is, the attenuation constant in the band gap increases with the growth of frequency. However, it decreases gradually after reaching the maximum at the center of frequency range. 4) The maximum value of phase constant can only be $\pi$ in the considered frequency range. The Bloch theorem contributes to this phenomenon. 5) For the ranges and widths of the band gaps, together with the amplitude of the central band structures, the PES can always give very accurate numerical predictions compared with the reference. Therefore, the effectiveness and accuracy of the present method is confirmed.

FIGURE 2

FIGURE 2. Variations in propagation constant with frequency at: (A) θ = 0; (B) θ = π/4.

3.2 Convergence study

In order to further verify the reliability of our PES, the convergence property of the present method is investigated in this package. Differ from the previous subsection, two representative directions, namely tan(θ) = 0.2 and tan(θ) = 1, are studied in this part. The attenuation constants and phase constants versus the increase of element number N are plotted in Figure 3. It can be observed from these figures that 1) With the increase of element number, the range and width of the band gaps change very little. However, the attenuation constant near the center of band gaps decreases continuously. 2) In the direction of tan(θ) = 0.2, the phase constants obtained using 16, 64 and 144 elements are almost the same. Hence, very accurate results can be obtained with few number of elements. 3) In the direction of tan(θ) = 1, the phase constants obtained using 64 and 144 elements are slightly smaller than that obtained using 16 elements. 4) The numerical results calculated using 64 and 144 elements are almost overlapped, which means that the present model could give very stable numerical predictions with a coarse mesh discretization. Therefore, the convergence of the present method is confirmed.

FIGURE 3

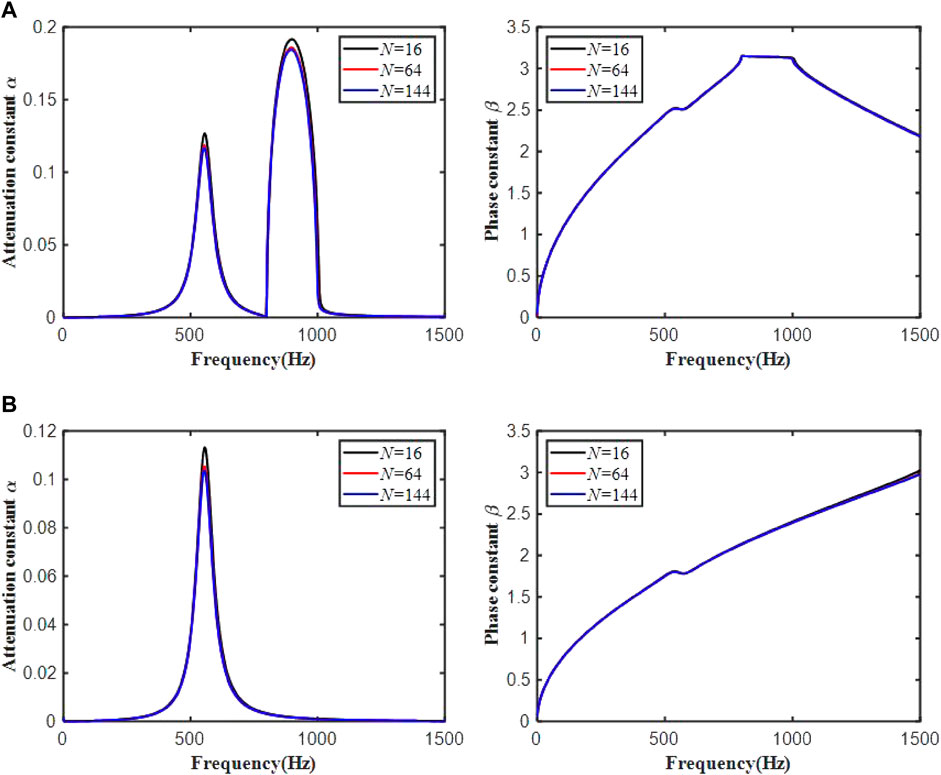
FIGURE 3. Convergence of propagation constants with different amount of elements: (A) tan(θ) = 0.2; (B) tan(θ) = 1.

3.3 Directionality of the wave propagation and attenuation

Based on the previous findings and discussion, it can be found that the Bragg gap and the locally resonant gap differ from each other greatly with the change of direction. In order to clearly reveal the evolution of band gaps, the directionality of the wave propagation and attenuation are further studied in this part.

According to the symmetry of square unit cell as shown in Figure 1A, the propagation constant in arbitrary direction can be obtained by sweeping θ from 0 to π/4, i. e

${\mu }_{\theta }=\{\begin{array}{c}{\mu }_{\theta }\\ {\mu }_{\pi /2-\theta }\end{array}\begin{array}{c}0\le \theta \le \pi /4\\ \pi /4<\theta \le \pi /2\end{array}(42)$

Therefore, the tangent value is taken from 0 to 1.

Figure 4A depicts the band gaps vary with tangent values, in which the color spectra represents the magnitude of attenuation constant. It can be seen from the figure that (1) A complete band gap is first observed in the frequency range of 525–580 Hz. As locally resonant gap is strongly related to the resonance of shunting circuits, the band width changes very little with direction. In other words, it is a typically full band gap in all directions. 2) The frequency range of Bragg gap increases with the growth of tangent value. However, due to the frequency of lower boundary increases faster than that of upper boundary, the band width decreases until it vanishes. The Bragg gap is mainly induced by the impedance mismatch between the piezoelectric patches and the substrate plate. With the wave propagation angle θ increases, it gradually reaches impedance matching. Hence, the Bragg gap is distinctly directional.

FIGURE 4

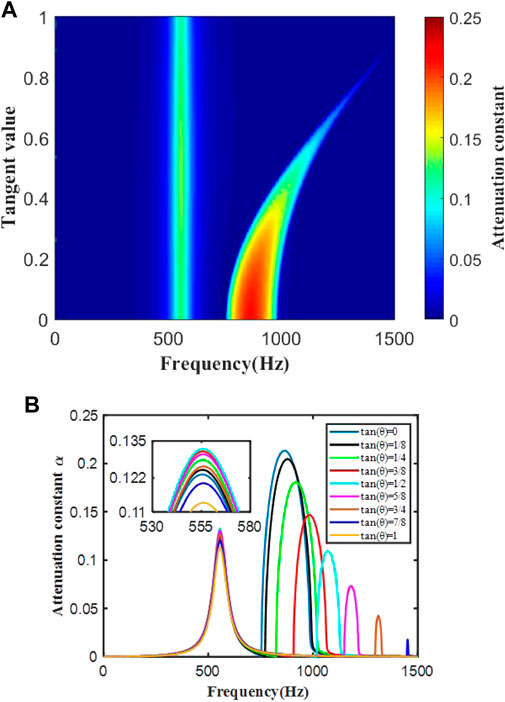
FIGURE 4. (A) Variation in band gaps with different tangent values; (B) Variations in attenuation constant with different tangent values.

To further investigate the attenuation degree of elastic waves in different directions, the attenuation constant obtained using the present algorithm is also outlined in Figure 4B. Here, nine different tangent values are considered, namely tan(θ) = 0, 0.125, 0.25, 0.375, 0.5, 0.625, 0.75, 0.875 and 1.0. It can be found that 1) The amplitude of attenuation constant near the center of locally resonant gap increases with the growth of tangent value. However, it decreases quickly after reaching the maximum when the tangent value is about 0.5. 2) The maximum of attenuation constant within Bragg gap decreases with the increase of tangent value. Combing with Figure 4A, when the tangent value is about 0.9, it eventually equals zero.

Based on these preliminary findings, we can further conclude that the PES can be seen a good choice for the prediction of wave propagation and attenuation in arbitrary direction.

4 Conclusion

In this work, a polynomial eigenvalue solution is formulated for predicting the propagation behaviors of elastic wave in arbitrary directions in piezoelectric shunting arrays. Based on the Bloch theorem, the wave propagation in PSA is evaluated through the dynamic analysis of one unit cell. A typical square plate with shunted piezoelectric patches is investigated in detail to study the accuracy, convergence and effectiveness of PES. The results show that the present method can provide very accurate numerical solutions compared with the reference. Besides, the proposed formulation can give very stable and convergent numerical predictions with a coarse mesh discretization. The variations of band gaps and attenuation constant with the wave propagation angle are finally investigated, which can verify the effectiveness of PES. Through the obtained results, the present algorithm is thus a strong competitor to other solutions in the analysis of wave propagation and attenuation in arbitrary directions in PSA.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

HY implemented the research, analyzed the data and wrote the manuscript. GW conceptualized the idea, discussed all the results and conducted the proof reading. All authors have read and agreed the published version of the manuscript.

Funding

This work was supported by the National Natural Science Foundation of China (12072099, 11832011) and the Natural Science Foundation of Hebei Province of China (A2021202023).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Appendix A

The coefficient matrices for any combination of ${\lambda }_x$ and ${\lambda }_y$ in Eq. 34 are elaborated below.

${\mathbf{K}}_{\mathrm{D}0}=\left[\begin{array}{cccc}0& 0& 0& 0\\ 0& 0& 0& 0\\ 0& 0& 0& 0\\ {\mathbf{K}}_{\text{RTI}}& {\mathbf{K}}_{\text{RTB}}& {\mathbf{K}}_{\text{RTL}}& {\mathbf{K}}_{\text{RTLB}}\end{array}\right]$(A.1)

${\mathbf{K}}_{\mathrm{D}1}=\left[\begin{array}{cccc}0& 0& 0& 0\\ {\mathbf{K}}_{\text{TI}}& {\mathbf{K}}_{\text{TB}}& {\mathbf{K}}_{\text{TL}}& {\mathbf{K}}_{\text{TLB}}\\ 0& 0& 0& 0\\ {\mathbf{K}}_{\text{LTI}}& {\mathbf{K}}_{\text{LTB}}& {\mathbf{K}}_{\text{RTR}}+{\mathbf{K}}_{\text{LTL}}& {\mathbf{K}}_{\text{LTLB}}+{\mathbf{K}}_{\text{RTRB}}\end{array}\right]$(A.2)

${\mathbf{K}}_{\mathrm{D}\mathbf{2}}=\left[\begin{array}{cccc}0& 0& 0& 0\\ 0& 0& 0& 0\\ {\mathbf{K}}_{\text{RI}}& {\mathbf{K}}_{\text{RB}}& {\mathbf{K}}_{\text{RL}}& {\mathbf{K}}_{\text{RLB}}\\ {\mathbf{K}}_{\text{RBI}}& {\mathbf{K}}_{\text{RBB}}+{\mathbf{K}}_{\text{RTT}}& {\mathbf{K}}_{\text{RBL}}& {\mathbf{K}}_{\text{RBLB}}+{\mathbf{K}}_{\text{RTLT}}\end{array}\right]$(A.3)

${\mathbf{K}}_{\mathrm{D}\mathbf{3}}=\left[\begin{array}{cccc}0& 0& 0& 0\\ 0& 0& {\mathbf{K}}_{\text{TR}}& {\mathbf{K}}_{\text{TRB}}\\ 0& 0& 0& 0\\ 0& 0& {\mathbf{K}}_{\text{LTR}}& {\mathbf{K}}_{\text{LTRB}}\end{array}\right]$(A.4)

${\mathbf{K}}_{\mathrm{D}\mathbf{4}}=\left[\begin{array}{cccc}0& 0& 0& 0\\ 0& 0& 0& 0\\ 0& {\mathbf{K}}_{\text{RT}}& 0& {\mathbf{K}}_{\text{RLT}}\\ 0& {\mathbf{K}}_{\text{RBT}}& 0& {\mathbf{K}}_{\text{RBLT}}\end{array}\right]$(A.5)

${\mathbf{K}}_{\mathrm{D}\mathbf{5}}=\left[\begin{array}{cccc}{\mathbf{K}}_{\text{II}}& {\mathbf{K}}_{\text{IB}}& {\mathbf{K}}_{\text{IL}}& {\mathbf{K}}_{\text{ILB}}\\ {\mathbf{K}}_{\text{BI}}& {\mathbf{K}}_{\text{BB}}+{\mathbf{K}}_{\text{TT}}& {\mathbf{K}}_{\text{BL}}& {\mathbf{K}}_{\text{BLB}}+{\mathbf{K}}_{\text{TLT}}\\ {\mathbf{K}}_{\text{LI}}& {\mathbf{K}}_{\text{LB}}& {\mathbf{K}}_{\text{LL}}+{\mathbf{K}}_{\text{RR}}& {\mathbf{K}}_{\text{LLB}}+{\mathbf{K}}_{\text{RRB}}\\ {\mathbf{K}}_{\text{LBI}}& {\mathbf{K}}_{\text{LBB}}+{\mathbf{K}}_{\text{LTT}}& {\mathbf{K}}_{\text{LBL}}+{\mathbf{K}}_{\text{RBR}}& {\mathbf{K}}_{\text{LBLB}}+{\mathbf{K}}_{\text{RBRB}}+{\mathbf{K}}_{\text{LTLT}}+{\mathbf{K}}_{\text{RTRT}}\end{array}\right]$(A.6)

${\mathbf{K}}_{\mathrm{D}\mathbf{6}}=\left[\begin{array}{cccc}0& 0& {\mathbf{K}}_{\text{IR}}& {\mathbf{K}}_{\text{IRB}}\\ 0& 0& {\mathbf{K}}_{\text{BR}}& {\mathbf{K}}_{\text{TRT}}+{\mathbf{K}}_{\text{BRB}}\\ 0& 0& {\mathbf{K}}_{\text{LR}}& {\mathbf{K}}_{\text{LRB}}\\ 0& 0& {\mathbf{K}}_{\text{LBR}}& {\mathbf{K}}_{\text{LBRB}}+{\mathbf{K}}_{\text{LTRT}}\end{array}\right]$(A.7)

${\mathbf{K}}_{\mathrm{D}\mathbf{7}}=\left[\begin{array}{cccc}0& {\mathbf{K}}_{\text{IT}}& 0& {\mathbf{K}}_{\text{ILT}}\\ 0& {\mathbf{K}}_{\text{BT}}& 0& {\mathbf{K}}_{\text{BLT}}\\ 0& {\mathbf{K}}_{\text{LT}}& 0& {\mathbf{K}}_{\text{LLT}}+{\mathbf{K}}_{\text{RRT}}\\ 0& {\mathbf{K}}_{\text{LBT}}& 0& {\mathbf{K}}_{\text{LBLT}}+{\mathbf{K}}_{\text{RBRT}}\end{array}\right]$(A.8)

${\mathbf{K}}_{\mathrm{D}\mathbf{8}}=\left[\begin{array}{cccc}0& 0& 0& {\mathbf{K}}_{\text{IRT}}\\ 0& 0& 0& {\mathbf{K}}_{\text{BRT}}\\ 0& 0& 0& {\mathbf{K}}_{\text{LRT}}\\ 0& 0& 0& {\mathbf{K}}_{\text{LBRT}}\end{array}\right]$(A.9)

References

1. Wang YF, Wang YS, Laude V. Wave propagation in two-dimensional viscoelastic metamaterials. Phys Rev B (2015) 92:104110. doi:10.1103/PhysRevB.92.104110

CrossRef Full Text | Google Scholar

2. Zhang SY, Wang YF, Wang YS. Evanescent surface acoustic waves in 1D viscoelastic phononic crystals. J Appl Phys (2021) 129:245111. doi:10.1063/5.0046004

CrossRef Full Text | Google Scholar

3. Kushwaha MS, Halevi P, Dobrzynski L, Djafari-Rouhani B. Acoustic band structure of periodic elastic composites. Phys Rev Lett (1993) 71(13):2022–2025. doi:10.1103/PhysRevLett.71.2022

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Martínez-Sala R, Sancho J, Sánchez JV, Gómez V, Llinares J, Meseguer F. Sound attenuation by sculpture. Nature (1995) 378(6554):241. doi:10.1038/378241a0

CrossRef Full Text | Google Scholar

5. Foehr A, Bilal OR, Huber SD, Daraio C. Spiral-based phononic plates: From wave beaming to topological insulators. Phys Rev Lett (2018) 120 (20):205501. doi:10.1103/PhysRevLett.120.205501

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Liu ZY, Zhang XX, Mao YW, Zhu YY, Yang ZY, Chan CT, et al. Locally resonant sonic materials. Science (2000) 289(5485):1734–1736. doi:10.1126/science.289.5485.1734

PubMed Abstract | CrossRef Full Text | Google Scholar

7. He ZC, Hu JY, Li E. An uncertainty model of acoustic metamaterials with random parameters. Comput Mech (2018) 62(5):1023–1036. doi:10.1007/s00466-018-1548-y

CrossRef Full Text | Google Scholar

8. Forward RL. Electronic damping of vibrations in optical structures. Appl Opt (1979) 18(5):690–697. doi:10.1364/AO.18.000690

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Hagood NW, Flotow von A. Damping of structural vibrations with piezoelectric materials and passive electrical networks. J Sound Vibration (1991) 146 (2):243–268. doi:10.1016/0022-460x(91)90762-9

CrossRef Full Text | Google Scholar

10. Guo X, Liu H, Zhang K, Duan HL. Dispersion relations of elastic waves in two-dimensional tessellated piezoelectric phononic crystals. Appl Math Model (2018) 56:65–82. doi:10.1016/j.apm.2017.11.037

CrossRef Full Text | Google Scholar

11. Hou ZL, Fu XJ, Liu YY. Calculational method to study the transmission properties of phononic crystals. Phys Rev B (2004) 70(1):014304. doi:10.1103/PhysRevB.70.014304

CrossRef Full Text | Google Scholar

12. Thorp O, Ruzzene M, Baz A. Attenuation and localization of wave propagation in rods with periodic shunted piezoelectric patches. Smart Mater Struct (2001) 10(5):979–989. doi:10.1088/0964-1726/10/5/314

CrossRef Full Text | Google Scholar

13. Airoldi L, Ruzzene M. Design of tunable acoustic metamaterials through periodic arrays of resonant shunted piezos. New J Phys (2011) 13 (11):113010. doi:10.1088/1367-2630/13/11/113010

CrossRef Full Text | Google Scholar

14. Wang G, Wang JW, Chen SB, Wen JH. Vibration attenuations induced by periodic arrays of piezoelectric patches connected by enhanced resonant shunting circuits. Smart Mater Struct (2011) 20(12):125019. doi:10.1088/0964-1726/20/12/125019

CrossRef Full Text | Google Scholar

15. Sugino C, Ruzzene M, Erturk A. An analytical framework for locally resonant piezoelectric metamaterial plates. Int J Sol Structures (2020) 182:281–294. doi:10.1016/j.ijsolstr.2019.08.011

CrossRef Full Text | Google Scholar

16. Lian ZY, Jiang S, Hu HP, Dai LX, Chen XD, Jiang W. An enhanced plane wave expansion method to solve piezoelectric phononic crystal with resonant shunting circuits. Shock and Vibration (2016) 2016: 4015363. doi:10.1155/2016/4015363

CrossRef Full Text | Google Scholar

17. Chen ZS, Xiong YP, Wei YX. Binary-Like topology optimization of piezoelectric metamaterial plate with interface circuits using extended plane wave expansion method. Appl Sci (2021) 11(11):5191. doi:10.3390/app11115191

CrossRef Full Text | Google Scholar

18. Spadoni A, Ruzzene M, Cunefare K. Vibration and wave propagation control of plates with periodic arrays of shunted piezoelectric patches. J Intell Mater Syst Structures (2019) 20(8):979–990. doi:10.1177/1045389x08100041

CrossRef Full Text | Google Scholar

19. Gardonio P, Zientek M, Dal Bo L. Panel with self-tuning shunted piezoelectric patches for broadband flexural vibration control. Mech Syst Signal Process (2019) 134:106299. doi:10.1016/j.ymssp.2019.106299

CrossRef Full Text | Google Scholar

20. Chen SB, Wang G, Wen JH, Wen XS. Wave propagation and attenuation in plates with periodic arrays of shunted piezo-patches. J Sound Vibration (2013) 332:1520–1532. doi:10.1016/j.jsv.2012.11.005

CrossRef Full Text | Google Scholar

21. Wen JH, Chen SB, Wang G, Yu DL, Wen XS. Directionality of wave propagation and attenuation in plates with resonant shunting arrays. J Intell Mater Syst Structures (2016) 27(1):28–38. doi:10.1177/1045389X14560361

CrossRef Full Text | Google Scholar

22. Zienkiewicz OC, Taylor RL, Fox DD. The finite element method for solid and structural mechanics. 7th ed. Oxford: Butterworth-Heinemann (2014).

Google Scholar

23. Airoldi L, Ruzzene M. Wave propagation control in beams through periodic multi-Branch shunts. J Intell Mater Syst Structures (2011) 22 (14):1567–1579. doi:10.1177/1045389X11408372

CrossRef Full Text | Google Scholar

24. Farzbod F, Leamy MJ. The treatment of forces in Bloch analysis. J Sound Vib (2009) 325:545–551. doi:10.1016/j.jsv.2009.03.035

CrossRef Full Text | Google Scholar

25. Casadei F, Ruzzene M, Dozio L, Cunefare KA. Broadband vibration control through periodic arrays of resonant shunts: Experimental investigation on plates. Smart Mater Struct (2010) 19:015002. doi:10.1088/0964-1726/19/1/015002

CrossRef Full Text | Google Scholar

26. Dedieu JP, Tisseur F. Perturbation theory for homogeneous polynomial eigenvalue problems. Linear Algebra Its Appl (2003) 358:71–94. doi:10.1016/s0024-3795(01)00423-2

CrossRef Full Text | Google Scholar

27. Mace BR, Manconi E. Modelling wave propagation in two-dimensional structures using finite element analysis. J Sound Vibration (2008) 318:884–902. doi:10.1016/j.jsv.2008.04.039

CrossRef Full Text | Google Scholar

28. Langley RS. Wave motion and energy flow in cylindrical shells. J Sound Vibration (1994) 169(1):29–42. doi:10.1006/j.svi.1994.1004

CrossRef Full Text | Google Scholar