Toward a high-precision mass–energy test of the equivalence principle with atom interferometers

The equivalence principle (EP) is a basic assumption of the general relativity. The quantum test of the equivalence principle with atoms is an important way to examine the applicable scope of the current physical framework so as to discover new physics. Recently, we extended the traditional pure mass or energy tests of the equivalence principle to the joint test of mass–energy by atom interferometry (Zhou et al.,Phys.Rev.A 104,022822). The violation parameter of mass is constrained to η₀ = (−0.8 ± 1.4) × 10^–10 and that of internal energy to η_E = (0.0 ± 0.4) × 10^–10 per reduced energy ratio. Here, we first briefly outline the joint test idea and experimental results, and then, we analyze and discuss how to improve the test accuracy. Finally, we report the latest experimental progress toward a high-precision mass–energy test of the equivalence principle. We realize atom interference fringes of 2T = 2.6 s in the 10-m long-baseline atom interferometer. This free evolution time T, to the best of our knowledge, is the longest duration realized in the laboratory, and the corresponding resolution of gravity measurement is 4.5 × 10⁻¹¹ g per shot.

Introduction

Einstein’s equivalence principle (EP) is one of the basic assumptions of general relativity. The EP includes the weak equivalence principle (WEP), local Lorentz invariance (LLI), and local position invariance (LPI). On one side, violation of the EP implies the need to modify the general relativity. On the other side, new physical theories, which attempt to unify the gravity theory and the standard model, require EP violation [1]. All these factors inspire the passion on the experimental test of the EP. Since the last century, the accuracy of EP tests using free fall [2], torsion balances [3], satellites [4], and lunar laser ranging [5] has been continuously improved. The highest precision of the EP tests is currently achieved by the satellite experiment at the level of 10^–15 [4].

One of the most important lessons given by physics in the 20th century is that the laws of physics in the macroscopic world are not suitable for all situations in the Universe. In the microscopic world, the law is quantum mechanics. The EP holds true despite the increasing precision of tests at the macroscopic scale, and then, whether the EP differs in the microscopic world becomes a more curious issue. A macroscopic object is well characterized by its mass and composition, but to describe a microscopic particle, we need to use more attributes, such as the spin, the internal energy states, the superposition, and entanglement of the states. Thus, quantum tests of the EP with microscopic particles can provide far richer information than macroscopic tests, and they are the direct methods to find possible couplings between gravity and microscopic properties. Neutrons were first used for the microscopic particle EP test in 1970s, but due to the difficulty of neutron control, the testing accuracy was only 10^–4 [6]. Nowadays, due to development of laser cooling, trapping, and manipulating techniques, atoms have been widely applied for precision measurement. The accuracy of the EP test using atom interferometers has gradually approached the most accurate EP test using a macroscopic object in less than two decades. The abundant quantum properties of atoms have produced diverse directions [7–10] for the EP test.

The first experiment of the atom-based EP test in 2004 has shown the main characteristic for this area: both traditional mass (${}^{85}\mathrm{R}\mathrm{b}$ and ${}^{87}\mathrm{R}\mathrm{b}$) and beyond mass (different quantum states of ${}^{85}\mathrm{R}\mathrm{b}$) tests were conducted. For the EP tests with different masses, there are isotopes of rubidium (${}^{85}\mathrm{R}\mathrm{b}$ and ${}^{87}\mathrm{R}\mathrm{b}$) [7,8,11–13], strontium (${}^{87}\mathrm{S}\mathrm{r}$ and ${}^{88}\mathrm{S}\mathrm{r}$) [14], and also of different alkali-metal atom pairs like ${}^{87}\mathrm{R}\mathrm{b}$ and ${}^{39}\mathrm{K}$ [15,16]. The EP test experiment based on the combination of alkali metals and alkaline earth metals (rubidium and ytterbium) [17] with greater difference in mass is also in progress. The EP tests beyond mass include different internal states (corresponding to different energy) [7,13,18,19], spin [14,20], quantum statistics [14], and quantum superposition [19]. In addition, the experiment based on quantum entanglement [21] has also been proposed. As for the test accuracy, the test based on mass is 10^–4 to 10^–12, while beyond mass, it is 10^–7 to 10^–10.

The research requirements of fundamental physics, such as high-precision testing of the EP of microscopic particles, have greatly promoted the development of long-baseline atom interferometers and related technologies [17,22,23]. These techniques include atom source preparation (large number, ultra-low temperature dual-species atom source, and coherently accelerated atomic fountain [8]), cold atom interference (dual-species common-mode noise suppression [8,11], large momentum transfer [24], shear interference detection [25]), large length–diameter ratio magnetic shield [26,27], narrow-line width, and high-power laser technology [28,29]. The long-baseline atom interferometer has achieved the separation of half-meter-scale matter waves [30], the measurement of the space–time curvature [31], and the observation of gravitational AB effects [32]. Research schemes for mid-band gravitational wave detection [33,34] and dark matter detection [35] based on long-baseline atom interferometers have been proposed. Projects based on the large-scale atom interferometer, such as MIGA [36], ZAIGA [37], AION [38], and MAGIS100 [39], have also been proposed. These projects could lead to the development of long-baseline atom interferometers as new additions to future research facilities.

In the following, we briefly describe the theory and experiments of the joint mass–energy test of the EP, analyze the current challenges for high-precision mass–energy tests, and report the latest experimental research progress of the 10-m atom interferometer in Wuhan.

Joint mass–energy test of the equivalence principle

Different from the EP test based on macroscopic objects, microscopic particles such as atoms can be used for both mass and beyond-mass tests of the EP, as well as the joint test with multiple quantum properties, which provides more information than a single-attribute test (see more details in [13]).

Theory

For the joint test of the EP with mass and energy, the gravitational mass of the test body, m_g, can be expressed as a sum of different types of mass–energy and the violation terms of the EP:

$m_g=\sum _A\left(1+{\eta }^A\right)\frac{E^A}{c^2}=m_i+\sum _A{\eta }^A\frac{E^A}{c^2},(1)$

where $m_i={\sum }_A\frac{E^A}{c^2}$ is the inertial mass, A represents different kinds of interaction, E^A is the corresponding energy, c is the speed of light, and η^A is the violation parameter of the EP. If there is no violation of the EP, then η^A = 0.

In this experiment, we use ${}^{85}\mathrm{R}\mathrm{b}$ and ${}^{87}\mathrm{R}\mathrm{b}$ atom pairs with different hyperfine energy levels. The inertial mass is equal to the sum of the masses of the lower ground state and the internal mass–energy. Then, Eq. 1 is rewritten as follows:

$m_g=m_i+\alpha m_0+\beta \frac{\mathrm{\Delta }E}{c^2},(2)$

where $m_i=m_0+\frac{\mathrm{\Delta }E}{c^2}$, and m₀ is the rest mass of lower ground state atoms. α is the mass violation parameter of rubidium atoms, and β is the internal energy violation parameter. ΔE is the internal energy, namely, the difference between the lower ground state and the upper ground state of rubidium atoms (Figure 1A).

FIGURE 1

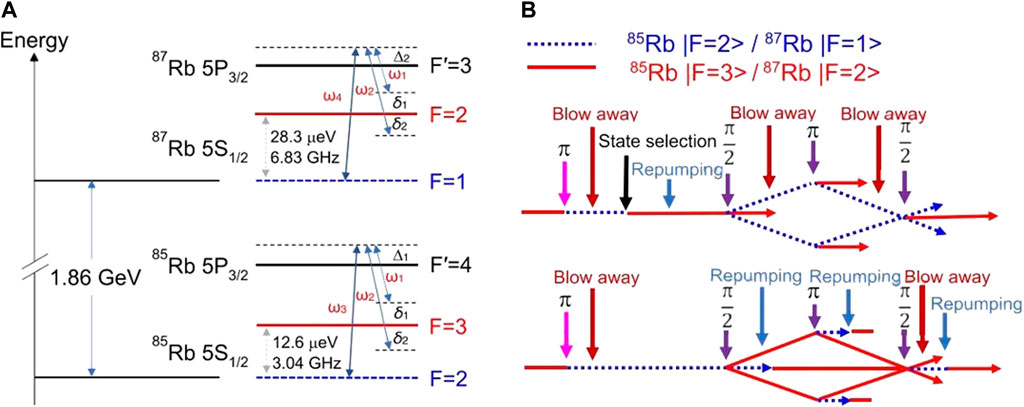
FIGURE 1. Scheme of 4WDR-e for the dual-species atom interferometer of ${}^{85}\mathrm{R}\mathrm{b}-{}^{87}\mathrm{R}\mathrm{b}$. (A) Energy level of the two species. The laser frequencies of ω₁, ω₂ and ω₃ are used for ${}^{85}\mathrm{R}\mathrm{b}$ atoms, while ω₁, ω₂ and ω₄ for ${}^{87}\mathrm{R}\mathrm{b}$ atoms. (B) Scheme of 4WDR-e. The blue dashed line represents lower ground state atoms, and the red solid line represents upper energy ground state atoms. The atom interferometer in the 4WDR-e scheme works in both lower and upper ground states, while in the 4WDR scheme, it works only in the lower ground state (the upper one in (B)).

For the EP test, the greater the difference in mass and in energy, the better outcomes we may receive. However, when choosing a quantum test system, not only the aforementioned factors should be considered but also technical factors such as common-mode noise suppression should be taken into account. In the existing experiments of the EP test of atoms, the combination of rubidium and potassium has the biggest difference in the test mass, while the isotope of rubidium achieves the best common-mode noise suppression ratio, and the isotope of strontium can be conducted with much more different energy states. Our current joint mass–energy test of the EP combines the mass test of rubidium isotope atoms and the energy difference test of two hyperfine energy levels, in which the ratio between the mass corresponding to the energy and the rest mass is 10^–16. For the isotope of strontium and their energy difference of the optical clock transition ($5{}^1\mathrm{S}_0$-$5{}^3\mathrm{P}_0$, which is five orders of magnitude greater than rubidium), the ratio is approximately 10^–11, which will be attractive.

Considering the rubidium isotope and the energy difference of their hyperfine energy levels, Eq. 2 is rewritten as follows.

$\begin{array}{cc}\hfill & m_g^{87}=m_i^{87}+{\alpha }^{87}{m}_0^{87}+\beta \frac{\mathrm{\Delta }{E}^{87}}{c^2}\hfill \\ \hfill & m_g^{85}=m_i^{85}+{\alpha }^{85}{m}_0^{85}+\beta \frac{\mathrm{\Delta }{E}^{85}}{c^2}.\hfill \end{array}(3)$

Thus, for the joint mass and energy test, the Eötvös parameter is

$\eta \equiv 2\frac{\left(m_g^{85}/m_i^{85}\right)-\left(m_g^{87}/m_i^{87}\right)}{\left(m_g^{85}/m_i^{85}\right)+\left(m_g^{87}/m_i^{87}\right)}.(4)$

For the different combinations of ${}^{85}\mathrm{R}\mathrm{b}|F=2\rangle$, ${}^{85}\mathrm{R}\mathrm{b}|F=3\rangle$, ${}^{87}\mathrm{R}\mathrm{b}|F=1\rangle$, and ${}^{87}\mathrm{R}\mathrm{b}|F=2\rangle$, we apply Eq. 3 into Eq. 4 and take the denominator approximately equal to 1, thus obtaining the Eötvös parameters of the four paired combinations as follows.

$\begin{array}{cc}\hfill & {\eta }_1={\eta }_0,\hfill \\ \hfill & {\eta }_2={\eta }_0-\beta {ϵ}^{85},\hfill \\ \hfill & {\eta }_3={\eta }_0+\beta {ϵ}^{87},\hfill \\ \hfill & {\eta }_4={\eta }_0+\beta \left({ϵ}^{87}-{ϵ}^{85}\right).\hfill \end{array}(5)$

where η₀ is the violation parameter of mass, and η₁, η₂, η₃ and η₄ are corresponding to the four combined measurements of ${}^{87}\mathrm{R}\mathrm{b}|F=1\rangle -{}^{85}\mathrm{R}\mathrm{b}|F=2\rangle$, ${}^{87}\mathrm{R}\mathrm{b}|F=2\rangle -{}^{85}\mathrm{R}\mathrm{b}|F=2\rangle$, ${}^{87}\mathrm{R}\mathrm{b}|F=1\rangle -{}^{85}\mathrm{R}\mathrm{b}|F=3\rangle$, and ${}^{87}\mathrm{R}\mathrm{b}|F=2\rangle -{}^{85}\mathrm{R}\mathrm{b}|F=3\rangle$, respectively, ϵ⁸⁵ and ϵ⁸⁷ are the dimensionless energy scale factors, which are proportional to the energy of photons. We use the parameter η_E to represent the violation parameter of the reduced energy ratio a, where η_E = βa and $a=h{\nu }_0/m_i^{85}{c}^2$ ($m_i^{85}$ is the inertial mass of ${}^{85}\mathrm{R}\mathrm{b}$ atoms, ν₀ = 1 GHz). The values of ϵ⁸⁵ and ϵ⁸⁷ are listed as follows.

$\begin{array}{cc}\hfill & {ϵ}^{85}\equiv \frac{\mathrm{\Delta }{E}^{85}}{m_{i0}^{85}{c}^2},\hfill \\ \hfill & {ϵ}^{87}\equiv \frac{\mathrm{\Delta }{E}^{87}}{m_{i0}^{87}{c}^2}.\hfill \end{array}(6)$

4WDR scheme and experiment result

The main obstacle in combining two kinds of atoms and their specific quantum states in experiments is the technical complexity. A series of requirements need to be met in the experiment, including maintaining the same specified quantum state during the interference process, realizing the common-mode noise suppression of different species of atoms, acquiring the same Rabi frequency for dual-species atoms, ensuring the cancellation of the AC Stark frequency shift. For the joint test, we also need to change the internal state and realize the differential measurement of different combinations on the basis of maintaining all the aforementioned conditions.

By extending the 4WDR scheme, which has been developed in 2015 [11,40,41], we realize the 4WDR-e scheme (Figure 1B) [13], which meets the requirement of the joint mass–energy test of the EP. Actually, the 4WDR scheme has great advantages, including low power requirement for Raman lasers, symmetry of the interference path, single internal state during the interference path, and a high common-mode noise suppression ratio of two isotope species. But for using the blow-away laser during the interference path, the atom interferometer can only work at the lower ground states (namely, ${}^{87}\mathrm{R}\mathrm{b}|F=1\rangle$ and ${}^{85}\mathrm{R}\mathrm{b}|F=2\rangle$). We develop a new technique (called 4WDR-e) to make it possible to work at the upper ground states (namely, ${}^{87}\mathrm{R}\mathrm{b}|F=2\rangle$ and ${}^{85}\mathrm{R}\mathrm{b}|F=3\rangle$) by using a repumping laser to destroy the interference path of the atoms in the lower ground state. With this 4WDR-e scheme, the EP with rubidium atoms works on both the lower and the upper ground states. Compared with the Bragg’s diffraction method, this method can achieve differential measurement of a high common-mode rejection ratio without changing the frequency and intensity ratio of the coherent laser when combining the different internal states of two species.

We have achieved the dual-species atom interferometer of ${}^{85}\mathrm{R}\mathrm{b}-{}^{87}\mathrm{R}\mathrm{b}$ based on 4WDR in 2015 [11], for choosing the free evolution time T = 70.96 ms and integrating for 3,200 s. The statistical uncertainty reaches η = 8 × 10^–9. After evaluating the systematic errors carefully, we improved the mass test of the EP to η = (2.8 ± 3.0) × 10^–8. With the adaptation of the 4WDR-e scheme, we used the different internal state combinations of two isotope species for the EP test, and the statistical uncertainty of each combination reaches η = 2.5 × 10^–10. After the evaluation of systematic errors, we get the measurement result for four combinations as follows: η₁ = (1.5 ± 3.2) × 10^–10 (for ${}^{87}\mathrm{R}\mathrm{b}|F=1\rangle -{}^{85}\mathrm{R}\mathrm{b}|F=2\rangle$), η₂ = (−0.6 ± 3.7) × 10^–10 (for ${}^{87}\mathrm{R}\mathrm{b}|F=2\rangle -{}^{85}\mathrm{R}\mathrm{b}|F=2\rangle$), η₃ = (−2.5 ± 4.1) × 10^–10 (for ${}^{87}\mathrm{R}\mathrm{b}|F=1\rangle -{}^{85}\mathrm{R}\mathrm{b}|F=3\rangle$), and η₄ = (−2.7 ± 3.6) × 10^–10 (for ${}^{87}\mathrm{R}\mathrm{b}|F=2\rangle -{}^{85}\mathrm{R}\mathrm{b}|F=3\rangle$). Thus, we give the violation parameters of mass and energy simultaneously, where the mass violation parameter is η₀ = (−0.8 ± 1.4) × 10^–10 and the energy violation parameter is η_E = (0.0 ± 0.4) × 10^–10 per reduced energy ratio.

High-precision mass–energy test of the equivalence principle with atom interferometers

To achieve a higher precision joint mass–energy EP test, there are two main challenges: improving the measuring resolution and reducing the systematic error.

When speaking about the measuring resolution, we need to extend the free evolution time from 203 ms to 1.4 s first, which means the full use of the 10-m atom interferometer baseline. Also, the resolution is expressed as follows.

$\frac{\delta \varphi }{\varphi }\sim \frac{1}{k_{\text{eff}}g{T}^2}\frac{\pi }{\mathrm{S}\mathrm{N}\mathrm{R}\sqrt{t/T_c}},(7)$

where k_eff is the effective wave vector of double diffraction Raman lasers, T is the free evolution time, SNR is the signal-to-noise ratio, which is proportional to the fringe contrast and the square root of the atom numbers involved in the interference, t is the total measurement time, and T_c is the duration of a single shot. When these parameters are given as k_eff = 3.2 × 10⁷ rad/m, T = 1.4 s, SNR = 200, t = 10⁵ s, T_c = 10 s, the resolution of the atom interferometer will be $\frac{\delta \varphi }{\varphi }\simeq 3\times 10^{-13}$.

The aforementioned resolution depends on the ultra-cold dual-species source and the techniques for the full 10-m double diffraction atom interferometer and should be integrated continuously for more than a whole day. Thanks to the state labeling in the 4WDR scheme, which makes it possible to detect the atoms in different internal states without large separation in space, we can use the full effective length of the magnetic shield to achieve an atom interferometer-based differential measurement with the longest free evolution time of 2T = 2.8 s (Figure 2).

FIGURE 2

FIGURE 2. 10-m baseline atom interferometer in APM-CAS: the height of the vacuum tube and magnetic shield are 12 and 11.4 m, respectively. APM-CAS represents the new name of the institute, that is, the Innovation Academy for Precision Measurement Science and Technology, Chinese Academy of Sciences [23].

The ultra-cold dual-species source is needed for a high SNR and small systematic errors in the atom interferometer. Thus, we will adapt both the optical dipole trap and optical lattice to prepare ${}^{85}\mathrm{R}\mathrm{b}$ and ${}^{87}\mathrm{R}\mathrm{b}$ atom sources, with the temperature of 100 nK and the atomic number of 10⁵. We utilize the sympathetic cooling scheme to acquire cold ${}^{85}\mathrm{R}\mathrm{b}$ atoms and then use atomic lensing to acquire the dual-species ultra-cold atom source for the EP test. To obtain a minor systematic error in the experiment, we adapt two different trapping frequencies through two consecutive stages during the atomic lensing process, thus achieving the best combination of initial velocity, position, and temperature. In addition, compared with the magnetic trap, the optical dipole trap can be closed faster, and the atoms can be prepared in the initial state |m_F = 0⟩. We use the small-size 795-nm laser beam (rubidium D1 transitions: $5{}^2\mathrm{S}_{1/2}$-$5{}^2\mathrm{P}_{1/2}$) as the lattice laser to accelerate the atoms and then combine the beam with the 780-nm Raman laser (rubidium D2 transitions: $5{}^2\mathrm{S}_{1/2}$-$5{}^2\mathrm{P}_{3/2}$) through a dichroic mirror, thus achieving the spatial coupling between the lattice lasers with the Raman lasers.

Considering the sensitivity of the atom interferometer will improve by more than two orders of magnitude over our 2021 experimental results, although there are five orders of magnitude for common-mode vibration noise suppression (which given by δk/k, where δk is the difference of the effective vector of Raman beams), the vibration noise can still be the main noise in our experiment. Thus, we will isolate the vibration noise and suppress the laser phase noise.

Among the systematic errors, the gravity gradient is the main error source for the EP test. This error can be made less sensitive by switching the frequency of the middle Raman pulse, which has been applied in the G measurement and the EP test [42,43]. For our 4WDR-e scheme, although it has great advantages in choosing and detecting the internal state, it is difficult to suppress the systematic error due to the gravity gradient. This difficulty arises from the wide range of frequency shifting during the interference process, for example, the frequency shift for the middle Raman pulse should be as large as 300 MHz for 2T = 2.8 s. It is quite difficult in our scheme to realize the frequency shift, while keeping the Rabi frequency changing simultaneously and guaranteeing the compensation of the AC Stark shift. To solve this problem, we should extend the 4WDR-e scheme a step forward, by changing the frequency locking point of the Raman lasers to achieve a large frequency shift of the middle Raman pulse and adding another laser to compensate for the AC Stark shift. This scheme will implement the gravity gradient cancellation method mentioned previously. For the initial central position with the difference of ±100 μm of the two species, the gravity gradient effect can be reduced for two orders of magnitude after compensation, and the influence on the systematic error is lower than 10^–12.

As for other systematic errors, they will be reduced further by improving the simultaneity of the ultra-cold atom source and optimizing other parameters. For instance, the AC Stark shift can be reduced by stabilizing the laser intensity from 2% to 0.1%, and the uncertainty will be lower than 1 × 10^–12 [13]. By improving the performance of magnetic shielding, we can estimate that the systematic error of the quadratic Zeeman shift will be reduced to 1.6 × 10^–13 with a magnetic field strength of 1,000 nT and the inhomogeneity of 1.7 nT inside the interference region [27]. The Coriolis effect due to the rotation of the Earth was 2.9 × 10^–8 in 2015 [11] and 4 × 10^–11 in 2020 after compensating for the rotation of the Raman laser’s mirror [44]. It will be suppressed to the 10^–13 level due to the use of the ultra-cold atom source and compensating the rotation of Raman laser’s mirror with 10 nrad/s accuracy. The wavefront distortion will also be suppressed to be lower than 10^–12 in the future by an expansion rate selection method [45]. Thus, the expected accuracy of the future joint mass–energy test is 10^–12 ∼ 10^–13.

Technical improvements and recent experimental results of the long-baseline atom interferometer

Based on the previous 10-m atom interferometer platform and the continuous improvement of the EP test [11,13], we have made a series of progress with the goal of a high-precision joint mass–energy EP test recently. The first thing is preparing dual species ultra-cold atoms by an optical dipole trap. Figure 3A shows the photograph of the ultra-cold atom cloud. The next step is launching the atoms upward to achieve coherently accelerated atomic fountain after loading them adiabatically into a vertical 795-nm lattice laser. We improved the 4WDR-e scheme to meet the needs of suppressing vibration noise and gravity gradient effects. We have also made improvements on other unit techniques, such as the detection scheme of the phase shear readout [25], the highly stable AOM-based optical system [46,47], and the new magnetic shield with 8 nT residual magnetic field [27]. Figure 3B shows the atom interferometer fringe based on the cold atom source and the 4WDR scheme. All these improvements pave the way for a high-precision joint mass–energy test.

FIGURE 3

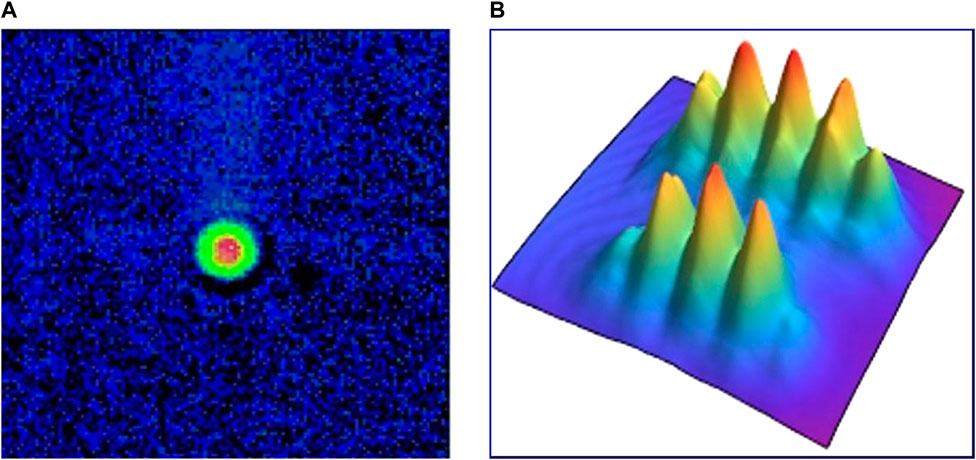
FIGURE 3. (A) ${}^{87}\mathrm{R}\mathrm{b}$ atoms in the optical dipole trap. There are 4 × 10⁵ atoms at 500 nK after the evaporative cooling. (B) Dual-species interference fringe for T = 203 m. The upper ground state for ${}^{85}\mathrm{R}\mathrm{b}$ atoms with the resolution of 1.5 × 10^–9 g and the lower ground state for ${}^{87}\mathrm{R}\mathrm{b}$ atoms of 1.0 × 10^–9 g.

For the 10-m long-baseline atom interferometer, the ultra-cold atom source and the coherent acceleration will help improve the fringe contrast and the measurement resolution, respectively. In addition, the small initial size of the atom cloud will also reduce the systematic error for the EP test. However, the techniques for the ultra-cold atom source are quite complex, and the atom numbers may not be more than 10⁶ when the temperature reaches 100 nK, while for 3 × 10⁹ atoms at 10 μK, there can still be 4 × 10⁶ atoms with the velocity distribution corresponding to 100 nK after polarization gradient cooling (PGC), but the acquiring of the source can be much easier. Thus, for a similar SNR, the cold atom source can also be quite attractive for the measurement with long free evolution time and high stability (such as the atom interferometer in space). The main challenge for the 10-m atom interferometer on Earth is the achievement of the high efficiency and low-temperature atom fountain. Although we get the falling signal of the atoms after being launched upward 12 m in early days, due to the high temperature and the small detectable number of atoms, the corresponding atom interference signal has not been observed previously.

We improved the moving molasses technique for the atom fountain by launching a downward-launching upward-PGC timing scheme. For a moving molasses atom fountain, the launching and PGC process need 2 ∼ 3 ms. When we launch atoms with an initial velocity of v₀ = 14 m/s from the center of 30-mm diameter laser beams, the atoms will move out of the laser beams before the PGC process. However, after launching the atoms downward first, the atom will move longer time in the beam area and will be fully speeding up and cooling down. This improvement leads to a 5-times stronger atom fountain signal than that in 2021 [46]. We achieved the interference fringe with 2T = 2.6 s for ${}^{87}\mathrm{R}\mathrm{b}$ (Figure 4); there are 10⁵ atoms being detected finally, which corresponds to 200 nK, with the contrast of the spatial fringe of 45%. This is the longest free evolution time atom interferometer we know. Using principal component analysis for the row data, we acquire the phase uncertainty of 12 mrad for a single interference fringe, which corresponds to the single-shot gravity measurement resolution of δg/g = δϕ/(k_effgT²) = 4.5 × 10^–11. This is also the highest resolution based on moving molasses for the cold atom interferometer.

FIGURE 4

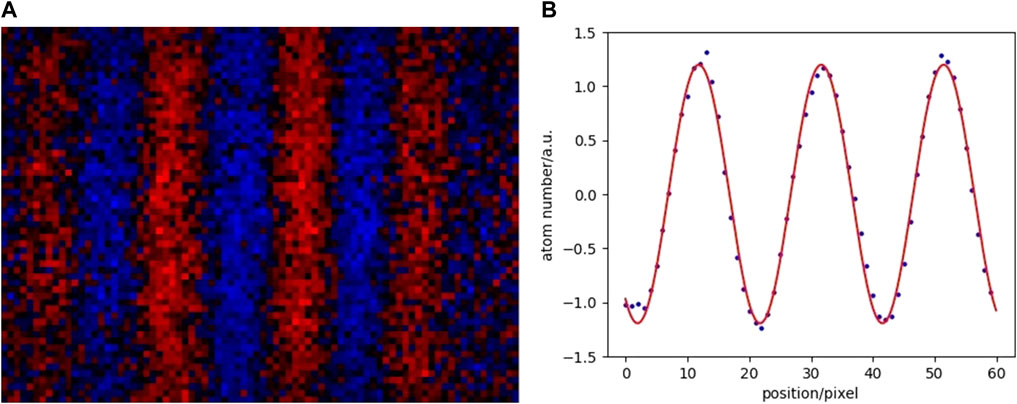
FIGURE 4. (A) Interference fringe for 2T = 2.6 s acquired by an EMCCD, each point is binning from eight pixels, corresponding to 0.32 mm in real space. (B) Vertical binning result after the Gaussian correction for atoms and the laser beams. The phase uncertainty of a single interference fringe is 12 mrad, which correspond to the single-shot gravity measurement resolution to be 4.5 × 10^–11 g.

Conclusion and outlook

In this paper, we have outlined the atom interferometer-based EP test, the theory and result of the joint mass–energy EP test, and the development of the 10-m atom interferometer in APM-CAS. For achieving the high-precision joint mass–energy EP test, we made a series of progress and acquired an interference fringe of 2T = 2.6 s, which is the longest free evolution time of the atom interferometer on Earth, and the corresponding resolution of gravity measurement is 4.5 × 10^–11 g per shot. Finally, the combination of a 10-m atom interferometer and an ultra-cold atom source based on an optical dipole trap will pave the way for the 10^–12 ∼ 10^–13 level joint mass–energy EP test. The 10-m atom interferometer will serve as a high precision matter wave sensor for the ZAIGA project, which will also be applied for the detection of the gravitational wave and dark matter.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material. Further inquiries can be directed to the corresponding authors.

Author contributions

LZ, JW, and M-SZ conceived the experiments. LZ, S-TY, and CH realized the atom interferometer setup and the 4WDR-e scheme. CH, Y-HJ, J-JJ, and ZH contributed to its laser system and operated the shear interference part both for the experiment and data analysis presented in this manuscript, while R-DX, QW, and Z-XL performed the BEC part. LZ, S-TY, D-FG, ML, W-TN, JW, and M-SZ provided major input to the manuscript, and all authors critically reviewed and approved the final version.

Funding

This work was supported by the Chinese Academy of Sciences Project for Young Scientists in Basic Research (Grant No. YSBR-055), the Hubei Provincial Science and technology major project (ZDZX2022000001), the Hubei Provincial Natural Science Foundation of China (2022CFA096), National Natural Science Foundation of China (91536221, 12174403, 91736311), Innovation Program for Quantum Science and Technology (2021ZD0300603), and Strategic Priority Research Program of the Chinese Academy of Sciences (XDB21010100).

Acknowledgments

The authors thank Huilin Wan, Yan Wang, Huanyao Sun, Qunfeng Cheng, Zongyuan Xiong, and Jiaqi Zhong for their contributions to the apparatus or key technology.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Will CM. The confrontation between general relativity and experiment. Living Rev Relativ (2014) 17:4. doi:10.12942/lrr-2014-4

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Niebauer TM, McHugh MP, Faller JE. Galilean test for the fifth force. Phys Rev Lett (1987) 59:609–12. doi:10.1103/PhysRevLett.59.609

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Zhu L, Liu Q, Zhao HH, Gong QL, Yang SQ, Luo P, et al. Test of the equivalence principle with chiral masses using a rotating torsion pendulum. Phys Rev Lett (2018) 121:261101. doi:10.1103/PhysRevLett.121.261101

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Touboul P, Métris G, Rodrigues M, Bergé J, Robert A, Baghi Q, et al. MICROSCOPE mission: Final results of the test of the equivalence principle. Phys Rev Lett (2022) 129:121102. doi:10.1103/PhysRevLett.129.121102

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Williams JG, Turyshev SG, Boggs DH. Progress in lunar laser ranging tests of relativistic gravity. Phys Rev Lett (2004) 93:261101. doi:10.1103/PhysRevLett.93.261101

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Koester L. Verification of the equivalence of gravitational and inertial mass for the neutron. Phys Rev D (1976) 14:907–9. doi:10.1103/PhysRevD.14.907

CrossRef Full Text | Google Scholar

7. Fray S, Diez CA, Hänsch TW, Weitz M. Atomic interferometer with amplitude gratings of light and its applications to atom based tests of the equivalence principle. Phys Rev Lett (2004) 93:240404. doi:10.1103/PhysRevLett.93.240404

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Asenbaum P, Overstreet C, Kim M, Curti J, Kasevich MA. Atom-Interferometric test of the equivalence principle at the 10⁻¹² level. Phys Rev Lett (2020) 125:191101. doi:10.1103/PhysRevLett.125.191101

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Safronova MS, Budker D, DeMille D, Kimball DFJ, Derevianko A, Clark CW. Search for new physics with atoms and molecules. Rev Mod Phys (2018) 90:025008. doi:10.1103/RevModPhys.90.025008

CrossRef Full Text | Google Scholar

10. Tino G, Cacciapuoti L, Capozziello S, Lambiase G, Sorrentino F. Precision gravity tests and the einstein equivalence principle. Prog Part Nucl Phys (2020) 112:103772. doi:10.1016/j.ppnp.2020.103772

CrossRef Full Text | Google Scholar

11. Zhou L, Long S, Tang B, Chen X, Gao F, Peng W, et al. Test of equivalence principle at10⁻⁸ Level by a dual-species double-diffraction Raman atom interferometer. Phys Rev Lett (2015) 115:013004. doi:10.1103/PhysRevLett.115.013004

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Bonnin A, Zahzam N, Bidel Y, Bresson A. Simultaneous dual-species matter-wave accelerometer. Phys Rev A (2013) 88:043615. doi:10.1103/PhysRevA.88.043615

CrossRef Full Text | Google Scholar

13. Zhou L, He C, Yan ST, Chen X, Gao DF, Duan WT, et al. Joint mass-and-energy test of the equivalence principle at the 10⁻¹⁰ level using atoms with specified mass and internal energy. Phys Rev A (2021) 104:022822. doi:10.1103/PhysRevA.104.022822

CrossRef Full Text | Google Scholar

14. Tarallo MG, Mazzoni T, Poli N, Sutyrin DV, Zhang X, Tino GM. Test of einstein equivalence principle for 0-spin and half-integer-spin atoms: Search for spin-gravity coupling effects. Phys Rev Lett (2014) 113:023005. doi:10.1103/PhysRevLett.113.023005

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Schlippert D, Hartwig J, Albers H, Richardson LL, Schubert C, Roura A, et al. Quantum test of the universality of free fall. Phys Rev Lett (2014) 112:203002. doi:10.1103/PhysRevLett.112.203002

CrossRef Full Text | Google Scholar

16. Barrett B, Antoni-Micollier L, Chichet L, Battelier B, Lévèque T, Landragin A, et al. Dual matter-wave inertial sensors in weightlessness. Nat Commun (2016) 7:13786. doi:10.1038/ncomms13786

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Hartwig J, Abend S, Schubert C, Schlippert D, Ahlers H, Posso-Trujillo K, et al. Testing the universality of free fall with rubidium and ytterbium in a very large baseline atom interferometer. New J Phys (2015) 17:035011. doi:10.1088/1367-2630/17/3/035011

CrossRef Full Text | Google Scholar

18. Zhang K, Zhou MK, Cheng Y, Chen LL, Luo Q, Xu WJ, et al. Testing the universality of free fall by comparing the atoms in different hyperfine states with Bragg diffraction*. Chin Phys. Lett. (2020) 37:043701. doi:10.1088/0256-307x/37/4/043701

CrossRef Full Text | Google Scholar

19. Rosi G, D’Amico G, Cacciapuoti L, Sorrentino F, Prevedelli M, Zych M, et al. Quantum test of the equivalence principle for atoms in coherent superposition of internal energy states. Nat Commun (2017) 8:15529. doi:10.1038/ncomms15529

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Duan XC, Deng XB, Zhou MK, Zhang K, Xu WJ, Xiong F, et al. Test of the universality of free fall with atoms in different spin orientations. Phys Rev Lett (2016) 117:023001. doi:10.1103/PhysRevLett.117.023001

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Geiger R, Trupke M. Proposal for a quantum test of the weak equivalence principle with entangled atomic species. Phys Rev Lett (2018) 120:043602. doi:10.1103/PhysRevLett.120.043602

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Dimopoulos S, Graham PW, Hogan JM, Kasevich MA. Testing general relativity with atom interferometry. Phys Rev Lett (2007) 98:111102. doi:10.1103/PhysRevLett.98.111102

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Zhou L, Xiong Z, Yang W, Tang B, Peng W, Hao K, et al. Development of an atom gravimeter and status of the 10-meter atom interferometer for precision gravity measurement. Gen Relativ Gravit (2011) 43:1931–42. doi:10.1007/s10714-011-1167-9

CrossRef Full Text | Google Scholar

24. Müller H, Chiow SW, Long Q, Herrmann S, Chu S. Atom interferometry with up to 24-photon-momentum-transfer beam splitters. Phys Rev Lett (2008) 100:180405. doi:10.1103/PhysRevLett.100.180405

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Sugarbaker A, Dickerson SM, Hogan JM, Johnson DMS, Kasevich MA. Enhanced atom interferometer readout through the application of phase shear. Phys Rev Lett (2013) 111:113002. doi:10.1103/PhysRevLett.111.113002

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Wodey E, Tell D, Rasel E, Schlippert D, Baur R, Kissling U, et al. A scalable high-performance magnetic shield for very long baseline atom interferometry. Rev Scientific Instr (2020) 91:035117. doi:10.1063/1.5141340

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Ji YH, Zhou L, Yan S, He C, Zhou C, Barthwal S, et al. An actively compensated 8 nT-level magnetic shielding system for 10-m atom interferometer. Rev Scientific Instr (2021) 92:083201. doi:10.1063/5.0053971

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Chiow S, Herrmann S, Müller H, Chu S. 6W, 1 kHz linewidth, tunable continuous-wave near-infrared laser. Opt Express (2009) 17:5246–50. doi:10.1364/OE.17.005246

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Kim M, Notermans R, Overstreet C, Curti J, Asenbaum P, Kasevich MA. 40 W, 780 nm laser system with compensated dual beam splitters for atom interferometry. Opt Lett (2020) 45:6555–8. doi:10.1364/OL.404430

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Kovachy T, Asenbaum P, Overstreet C, Donnelly C, Dickerson S, Sugarbaker A, et al. Quantum superposition at the half-metre scale. Nature (2015) 528:530–3. doi:10.1038/nature16155

PubMed Abstract | CrossRef Full Text | Google Scholar

31. Asenbaum P, Overstreet C, Kovachy T, Brown DD, Hogan JM, Kasevich MA. Phase shift in an atom interferometer due to spacetime curvature across its wave function. Phys Rev Lett (2017) 118:183602. doi:10.1103/PhysRevLett.118.183602

PubMed Abstract | CrossRef Full Text | Google Scholar

32. Overstreet C, Asenbaum P, Curti J, Kim M, Kasevich MA. Observation of a gravitational Aharonov-Bohm effect. Science (2022) 375:226–9. doi:10.1126/science.abl7152

PubMed Abstract | CrossRef Full Text | Google Scholar

33. Tino GM, Vetrano F. Is it possible to detect gravitational waves with atom interferometers? Class Quan Grav. (2007) 24:2167–78. doi:10.1088/0264-9381/24/9/001

CrossRef Full Text | Google Scholar

34. Gao D, Ju P, Zhang B, Zhan M. Gravitational-wave detection with matter-wave interferometers based on standing light waves. Gen Relativ Gravit (2011) 43:2027–36. doi:10.1007/s10714-011-1173-y

CrossRef Full Text | Google Scholar

35. Zhao W, Mei X, Gao D, Wang J, Zhan M. Ultralight scalar dark matter detection with ZAIGA. Int J Mod Phys D (2022) 31 (5):2250037. doi:10.1142/S0218271822500377

CrossRef Full Text | Google Scholar

36. Canuel B, Bertoldi A, Amand L, Pozzo di Borgo E, Chantrait T, Danquigny C, et al. Exploring gravity with the miga large scale atom interferometer. Sci Rep (2018) 8:14064. doi:10.1038/s41598-018-32165-z

PubMed Abstract | CrossRef Full Text | Google Scholar

37. Zhan M, Wang J, Ni WT, Gao D, Wang G, He L, et al. Zaiga: Zhaoshan long-baseline atom interferometer gravitation antenna. Int J Mod Phys D (2019) 29:1940005. doi:10.1142/S0218271819400054

CrossRef Full Text | Google Scholar

38. Badurina L, Bentine E, Blas D, Bongs K, Bortoletto D, Bowcock T, et al. AION: An atom interferometer observatory and network. J Cosmol Astropart Phys (2020) 2020:011. doi:10.1088/1475-7516/2020/05/011

CrossRef Full Text | Google Scholar

39. Abe M, Adamson P, Borcean M, Bortoletto D, Bridges K, Carman SP, et al. Matter-wave atomic gradiometer interferometric sensor (MAGIS-100). Quan Sci. Technol. (2021) 6:044003. doi:10.1088/2058-9565/abf719

CrossRef Full Text | Google Scholar

40. Lévèque T, Gauguet A, Michaud F, Pereira Dos Santos F, Landragin A. Enhancing the area of a Raman atom interferometer using a versatile double-diffraction technique. Phys Rev Lett (2009) 103:080405. doi:10.1103/PhysRevLett.103.080405

PubMed Abstract | CrossRef Full Text | Google Scholar

41. Malossi N, Bodart Q, Merlet S, Lévèque T, Landragin A, Santos FPD. Double diffraction in an atomic gravimeter. Phys Rev A (2010) 81:013617. doi:10.1103/PhysRevA.81.013617

CrossRef Full Text | Google Scholar

42. D’Amico G, Rosi G, Zhan S, Cacciapuoti L, Fattori M, Tino GM. Canceling the gravity gradient phase shift in atom interferometry. Phys Rev Lett (2017) 119:253201. doi:10.1103/PhysRevLett.119.253201

PubMed Abstract | CrossRef Full Text | Google Scholar

43. Overstreet C, Asenbaum P, Kovachy T, Notermans R, Hogan JM, Kasevich MA. Effective inertial frame in an atom interferometric test of the equivalence principle. Phys Rev Lett (2018) 120:183604. doi:10.1103/PhysRevLett.120.183604

PubMed Abstract | CrossRef Full Text | Google Scholar

44. Duan WT, He C, Yan ST, Ji YH, Zhou L, Chen X, et al. Suppression of Coriolis error in weak equivalence principle test using ⁸⁵Rb-⁸⁷Rb dual-species atom interferometer*. Chin Phys. B (2020) 29:070305. doi:10.1088/1674-1056/ab969a

CrossRef Full Text | Google Scholar

45. Hu J, Chen X, Fang J, Zhou L, Zhong J, Wang J, et al. Analysis and suppression of wave-front-aberration phase noise in weak-equivalence-principle tests using dual-species atom interferometers. Phys Rev A (2017) 96:023618. doi:10.1103/PhysRevA.96.023618

CrossRef Full Text | Google Scholar

46. He C, Yan S, Zhou L, Barthwal S, Xu R, Zhou C, et al. All acousto-optic modulator laser system for a 12 m fountain-type dual-species atom interferometer. Appl Opt (2021) 60:5258–65. doi:10.1364/AO.429965

PubMed Abstract | CrossRef Full Text | Google Scholar

47. Xu R, Wang Q, Yan S, Hou Z, He C, Ji Y, et al. Modular-assembled laser system for a long-baseline atom interferometer. Appl Opt (2022) 61:4648–54. doi:10.1364/AO.458361

PubMed Abstract | CrossRef Full Text | Google Scholar